CGRAP: A Web Server for Coarse-Grained Rigidity Analysis of Proteins

Abstract

Elucidating protein rigidity offers insights about protein conformational changes. An understanding of protein motion can help speed drug development, and provide general insights into the dynamic behaviors of biomolecules. Existing rigidity analysis techniques employ fine-grained, all-atom modeling, which has a costly run-time, particularly for proteins made up of more than 500 residues. In this work, we introduce coarse-grained rigidity analysis, and showcase that it provides flexibility information about a protein that is similar in accuracy to an all-atom modeling approach. We assess the accuracy of the coarse-grained method relative to an all-atom approach via a comparison metric that reasons about the largest rigid clusters of the two methods. The apparent symmetry between the all-atom and coarse-grained methods yields very similar results, but the coarse-grained method routinely exhibits 40% reduced run-times. The CGRAP web server outputs rigid cluster information, and provides data visualization capabilities, including a interactive protein visualizer.

1. Introduction

Directly observing how proteins flex and bend is not possible because the timescales involved are microseconds for conformational transitions and down to nanoseconds for sidechain fluctuations [1]. Information about protein motion is critical nonetheless to understanding a wide range of biophysical phenomena, including ligand and drug design [2], and understanding of protein-protein docking [3]. X-ray crystallography based approaches pose significant limitations because they offer a single, averaged static screenshot of a protein in its most stable crystallographic state [4]. Wet-lab experimental techniques such as nuclear magnetic resonance (NMR) are able to produce ensembles of conformations, but even they have limitations [5]. There are a variety of computational approaches that are available, some developed prior to 2000, that complement wet-lab techniques [6,7,8].

In past works, combinatorial pebble-game approaches for identifying the rigid and flexible regions of proteins have been developed [9]. Those approaches, albeit fast and efficient, assumed an all-atom modeling approach. Consequently, they did not scale well when the count of residues in the protein was more than 500; biomolecules composed of more than 1000 residues needed tens of minutes of compute time. There are currently upwards of 40,000 proteins in the PDB with 1000 or more residues, and thus it is not possible to analyze their rigidity in near real-time using existing all-atom based approaches.

For this work, we present a novel and first-ever coarse-grained pebble-game rigidity analysis method. Our motivation is to reduce in complexity the mechanical model of a protein, but whose analysis nonetheless yields similar results to the all-atom approach. Our coarse-grained approach works because of the structural symmetry that exists between the two methods. Both approaches reason about the degrees of freedom among the residues; the all-atom approach builds a mechanical model at the atomic level, whereas the coarse-grained approach in CGRAP reasons about a mechanical model at the residue level.

Like our previous all-atom combinatorial approach [9], our coarse-grained approach builds a mechanical model of a biomolecule, from which an associated graph is built, which is then analyzed using a pebble game algorithm, to infer which portions of the protein are members of rigid clusters. We developed our coarse-grained approach in which all residues are modeled as a single body in the mechanical model of the protein, which is in stark contrast to all other all-atom approaches. Consequently, this vastly reduces the complexity of the associated graph relative to an all-atom modeling approach, which provides a vast speedup, allowing up to a 50% reduction in run-time.

2. Background and Related Work

Computational-based approaches for identifying the rigid regions of proteins dates back to the late 1990s. ASU-FIRST, and KINARI, are the two most popular approaches, which we describe here.

2.1. Rigidity Analysis

The study of rigidity dates back to James Clerk Maxwell’s pioneering work in the 1800s on trusses [10], and more recently work by Laman [11] and Tay [12]. Michael Thorpe and others in the past few decades have performed pioneering work in rigidity of biomolecules [13,14]. Analyzing the rigidity of biomolecular structures involves multiple steps. First, the placement of bonds and other stabilizing interactions among the atoms of a protein is used to compose a mechanical model of composed of bodies, bars and hinges, in what is known as a bar-and-joint-framework. From the mechanical model, an associated multigraph is built, in which bodies represent the vertices, while covalent bonds, along with stabilizing interactions such as hydrogen bonds and hydrophobic interactions among the bodies in the mechanical model, represent the edges. The number of edges between any two nodes in the multigraph represents the type of bond that exists between the two corresponding bodies in the mechanical model of the molecule. The body-bar-hinge framework allows analyzing two- and three-dimensional structures [11]. Efficient pebble game algorithms permit analyzing the body-bar-hinge-framework [15,16], and thus permit inferring the flexible and rigid regions of biomolecues.

2.2. MSU-FIRST and FlexWeb

MSU-FIRST was the the first protein rigidity analysis software suite. It was a patented command-line program dependent on a mechanical model (called bar-and-joint) of a protein, and which utilized a heuristic pebble game algorithm for 3D bar-and-joint structures [17]. An extension to it was ASU-FIRST, which was made available through the FlexWeb server. ASU-FIRST, unlike MSU-FIRST, identified hydrogen bonds using its own internal function, and it implemented a variant of the Mayo energy potential [18] to calculate their energies. FlexWeb is no longer publicly available.

2.3. KINARI

KINARI is the second generation protein rigidity analysis software suite that was developed in 2011, whose web server [9] offered a variety of visualization tools to explore the rigid and flexible regions of proteins. Although the KINARI codebase via a library is still available [19], the visualization capabilities of KINARI Web are no longer operational. KINARI uses HBPLUS [20] to identify hydrogen bonds, which implements a slightly different variant of the Mayo energy function. The primary difference between KINARI and FlexWeb is how atoms are modeled. KINARI makes a mechanical model where rigid bodies of atoms are connected by hinges which are rotatable bonds, while FlexWeb models the protein using a special kind of multi-graph, in which vertices represent atoms and an edge represents the loss of a single degree of freedom between the atoms. Although the modeling of atoms and their interactions is different among KINARI and FlexWeb, their rigidity results are comparable [21]. KINARI has been used widely, for a variety of applications, including modeling the motions of loops [22], to infer the effects of protein point substitutions [23], to sampling protein conformational pathways [24].

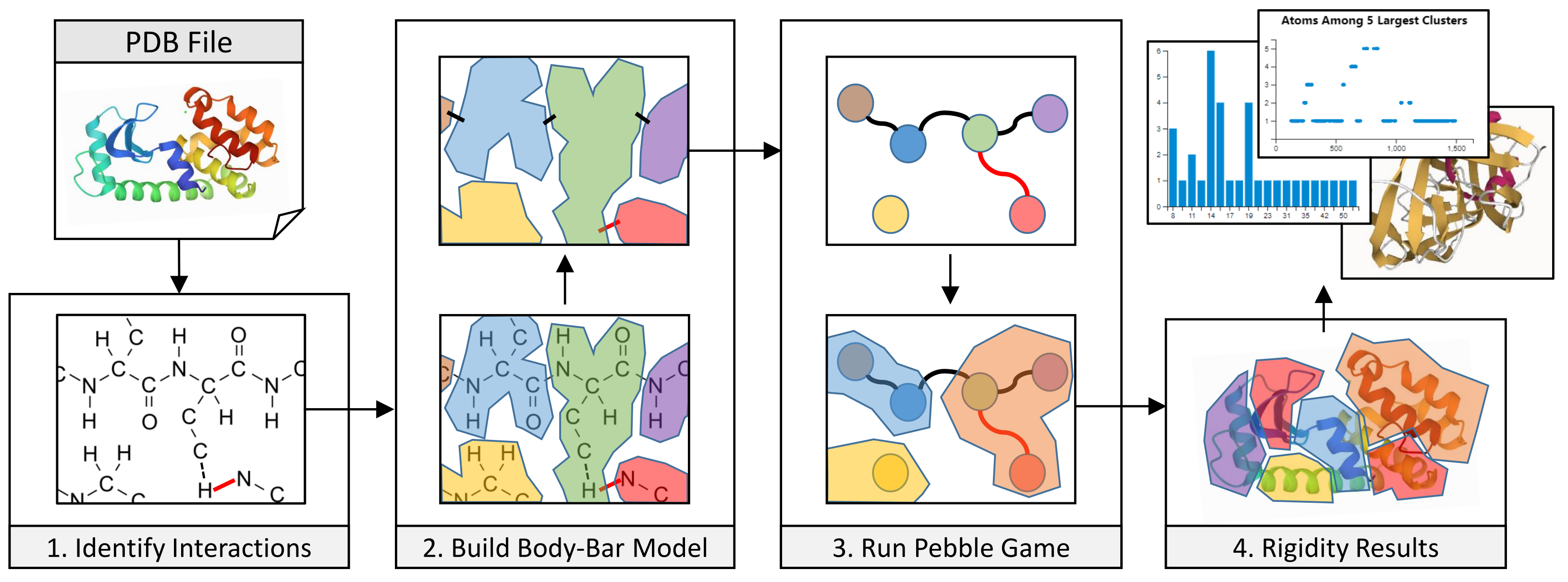
3. Methods

The CGRAP web server implements the first-ever coarse-grained rigidity analysis of proteins, and includes a visualizer to explore the rigid regions of a biomolecule. In this section, we present the coarse-grained rigidity analysis approach, and present a metric to quantitatively compare KINARI’s all-atom rigidity analysis to the coarse-grained rigidity results of CGRAP. The rigidity analysis method implemented in CGRAP involves a coarse-grain representation of a protein, from which a mechanical model is built. It is converted to an associated graph, which is analyzed using a pebble game algorithm, which indirectly infers the rigid regions of the biomolecule in the PDB file. The flexible regions of a protein are composed of those atoms that are not members of the larger rigid clusters, and are only indirectly identified by CGRAP. Explicitly identifying the flexible regions of a protein we leave to future work. The entire compute pipeline is summarized in Figure 1.

3.1. Coarse-Grained Body-Bar Mechanical Model

Similar to ASU-FIRST and KINARI, CGRAP identifies covalent bonds and stabilizing interactions such as hydrogen bonds and hydrophobic interactions among the atoms of a user-identified PDB file. If CGRAP is invoked on a PDB file whose structure was resolved X-ray crystallographically, CGRAP identifies and adds hydrogen atoms.

Next, the atoms and bonds in the PDB file are modelled as a mechanical framework. It is at this stage that the coarse-grained approach differs significantly from KINARI and FlexWeb, which employ an all-atom approach. In KINARI’s (left portion of Figure 2), each atom along with the atoms that it directly bonds to, are modeled as a body. Thus, a single residue is composed of many bodies. In CGRAP, however, all of the atoms in a residue are modeled as a single body (right portion of Figure 2). Because the molecular framework of the KINARI approach is fine-grained with a residue made up of many bodies, but in CGRAP, all atoms of a residue are represented by a single body, the resulting mechanical models of both approaches differ greatly (Figure 3).

3.2. Coarse-Grained Associated Graph

From the mechanical model, CGRAP builds an associated multigraph, on which the (6,6) pebble game algorithm [15] is run. Each body in the mechanical model is represented as a node in the associated multigraph, and bonds between the bodies of the mechanical model are modeled as edges. Here, also, CGRAP differs significantly from KINARI. In KINARI’s, any two atoms that constitute the end-points of a rotatable bond, when contained in two overlapping bodies (atoms A and B, among the blue and red bodies in Figure 2 left), are modeled as two nodes in the associated graph. In the all-atom approach, between such two nodes, there are placed 5 edges in the associated graph, to model the 1 degree of freedom of a hinge joint. In CGRAP, because a node in the graph represents an entire residue, there are far fewer nodes in the multigraph. Ultimately it is the reduced number of bodies in the mechanical model in CGRAP, and thus associated graph, that permits a significant speedup of the pebble game algorithm. For PDB file 6udw for example, in the all-atom modeling approach employed by KINARI, there are 38 vertices and 232 edges in the associated graph, but in CGRAP, there are 19 vertices and 128 edges. The body-bar mechanical model in CGRAP has on average 49% fewer bodies than KINARI’s body-bar-hinge framework.

In CGRAP, because there are no overlapping bodies, the only chemical bonds are those that exist between residues, including single covalent bonds, disulfide bonds, hydrogen bonds, and hydrophobic interactions. In KINARI, hinges, hydrophobic interactions, hydrogen bonds, and single covalent bonds are modeled as 3, 5, 5, and 5 bars, respectively, where an increased number of bars represents mechanically fewer degrees of freedom, and biophysically represents a greater bond strength. In KINARI, the default modeling is that single covalent bonds are modeled as hinges, which represent 1 degree of rotational freedom among two bodies that each contain the two atoms engaged in a stabilizing interaction (Figure 2 left).

In CGRAP, to attain coarse-grained rigidity results that matched best with the all-atom approach, we performed a parameter sweep of the modeling options for all bond types. For hydrogen bonds, hydrophobic tethers, single covalent bonds, and double covalent bonds, all 4096 combinations of these 4 were modelled as a hinge, 1–6 bars, or nothing, and this was tested on a subset of 10 proteins. The accuracy was determined using our TLCCS metric (see Section 3.3). After narrowing down the models to those that consistently performed well, then increasing the subset of proteins tested on to 100, the most accurate modelling for CGRAP was found when hydrogen bonds were modeled as 6 bars, hydrophobic tethers as 5 bars, covalent bonds as 2 bars, and double covalent bonds as zero bars. These are the default modeling options for CGRAP.

3.3. Metrics for Rigidity Analysis Comparison

To assess the ability of the coarse-grained approach relative to the all-atom analysis performed by KINARI, we developed a metric for comparing the first and second largest rigid clusters of both methods. The metric, Two Largest Cluster Comparison Score (TLCCS), takes into account the size differences between the largest and second-largest clusters of KINARI and CGRAP, as well the percent of atoms that overlap between the two methods’ largest clusters. We chose to rely on the two largest rigid clusters only because these represent the most prominent rigid components of a protein, which represent the rigidity that exists at the domain level [25].

TLCCS takes the percent of overlapping atoms ($\frac{\mathrm{num} \mathrm{overlapping} \mathrm{atoms}}{\mathrm{num} \mathrm{atoms} \mathrm{in} \mathrm{all}-\mathrm{atom} \mathrm{approach}}$) between the two models’ largest clusters and divides them by 1 + the percent difference of the sizes between the two models’ first and second largest clusters. This ensures the relevant information about the largest two clusters, and therefore the most important factors of a protein’s rigidity, are used as the measure of rigid cluster comparison. The closer TLCCS is to 1, the more similar the two largest rigid clusters are among the two modeling approaches.

$$TLCCS=\frac{\frac{AALC\cap CGLC}{AALCS}}{1+\frac{|AALCS-CGLCS|+|AASLCS-CGSLCS|}{AALCS}}$$

where AA = all-atom rigidity analysis, CG = coarse-grained rigidity analysis, LCS = largest cluster size, and SLCS = second largest cluster size.

3.4. Server

The web server for CGRAP is at http://cgrap.cs.wwu.edu (accessed on 16 November 2021). The server is Scala-based and uses the Play web framework, Bootstrap, and jQuery [26]. Portions of CGRAP are also written in TypeScript and transpiled for the browser using Webpack. CGRAP runs in a Docker container behind an nginx reverse-proxy on an Azure Cloud VM and is deployed via an automated CI/CD build/deployment pipeline on Azure DevOps. On the landing page, the user inputs the PDB ID and chain to be analyzed. CGRAP identifies hydrogen atoms, bonds, and stabilizing interactions (Step 1, Figure 1), builds the body-bar mechanical model (Step 2, Figure 1), runs the pebble game (Step 3, Figure 1), and from the pebble game results infers the rigid regions of the protein, which are shown via a protein interactive visualizer accompanied with several plots detailing the specifics of rigid clusters (Step 4, Figure 1). The resulting analysis of the protein is displayed using the Molstar 3D visualizer [27], which offers a variety of data visualization features for rotating, zooming in on, highlighting, etc., the protein and its rigid clusters. Interactive graphs made with D3.js [28] are displayed as well, showing the distribution of rigid clusters and the atoms among the five largest clusters.

4. Results

To showcase the utility of CGRAP relative to KINARI’s all-atom approach, we analyzed the rigidity of 9046 proteins using both methods. For each protein, we tallied the run-time of both approaches, and calculated the TLCCS score (

Table 1. KINARI all-atom versus CGRAP Rigidity Analysis. LC = Largest Cluster. SLC = Second Largest Cluster. #Prot = number of proteins in bin. RT${}_{\mathit{avg}}$ = CGRAP’s run-time as percentage of KINARI’s run-time. #A${}_{\mathit{avg}}$ = average count of atoms among all proteins in that bin. $\Delta$Size${}_{\mathit{LC},\mathit{SLC}}$ = difference in size (count of atoms) among the LC and SLC. $\Delta$SLC${}_{\mathit{avg}}$ = difference in size (count of atoms) for the SLC. LC${}_{\mathit{overlap}}$ = the percentage of atoms in the LC in the all-atom approach that also are in the LC via CGRAP. See Section 3.3 for a motivation for these metrics.

Bin	#Prot	RT${}_{\mathit{avg}}$	#A${}_{\mathit{avg}}$	$\mathbf{\Delta }$Size${}_{\mathit{LC},\mathit{SLC}}$	$\mathbf{\Delta }$SLC${}_{\mathit{avg}}$	LC${}_{\mathit{overlap}}$	TLCCS${}_{\mathit{avg}}$
$best$	2133	66%	5358	12%	46	83%	0.73
$excellent$	2292	67%	4847	20%	68	80%	0.65
very good	1993	68%	4311	34%	121	76%	0.56
$good$	1058	68%	4227	69%	295	72%	0.43
$fair$	1570	70%	3795	184%	322	49%	0.21

). We group the 9046 proteins into 5 bins based on TLCCS scores: best (TLCCS > 0.7), excellent (0.7 > TLCCS > 0.6), very good (0.6 > TLCCS > 0.5), good (0.5 > TLCCS > 0.4), and fair (0.4 > TLCCS). We chose the names for the bins based on the fact that for all proteins except for those in the fair bin, rigidity results for the coarse-grained method were still visually very similar to the all-atom approach. The highest TLCCS score recorded was 0.85 for PDB file 4j9t.

In addition to the numeric metric, we also developed an in-house Python script for displaying the rigid clusters of a protein. This was needed because KINARI Web no longer provides visualization capabilities of the rigidity results, but we needed to visually compare the rigidity of a protein as determined via KINARI’s all-atom approach versus CGRAP.

4.1. Bin: $Best$

The 2133 proteins in the $best$ bin had a CGRAP run-time that was 33.3% faster than KINARI, yet the CGRAP rigidity results were very similar to that of the all-atom approach. This represents the best trade-off of accuracy for speed gain. An example protein from the $best$ bin is 5ers (Figure 4). The largest cluster changed from 3060 atoms in the all-atom approach, to 3054 atoms using CGRAP, and the second largest cluster changed from 1049 atoms to 1206. A total of 72% of the atoms in the largest cluster using KINARI are contained in the largest cluster identified using CGRAP. PDB files 1yvs and 5kw5, are additional examples of proteins whose rigidity results via CGRAP are very similar relative to KINARI’s all-atom approach (Figure 5 and Figure 6), but which still saw a significant speedup in compute time using CGRAP’s coarse-grained approach.

4.2. Bin: $Excellent$

The average run-time decrease using CGRAP in this bin was 32.6% relative to the run-time of KINARI’s all-atom rigidity analysis. An example protein from this bin is 2yym (Figure 7), whose largest cluster changed from 4827 atoms in the all-atom analysis, to 5970, and the second largest cluster changed from 159 atoms to 202. A total of 82% of the atoms in the largest cluster as identified using KINARI were contained in the largest cluster found by CGRAP.

4.3. Bin: Very Good

The average run-time of the coarse-grained rigidity analysis approach decrease in this bin was 31.9% relative to KINARI’s all-atom approach. An example protein from the very good bin is 1b5v (Figure 8), whose largest cluster changed from 717 atoms in the all-atom approach to 1190 in CGRAP, and the second largest cluster changed from 458 to 342 atoms. A total of 91% of the atoms in the all-atom approach largest cluster are contained in the largest cluster identified by CGRAP.

4.4. Bin: $Good$

The average run-time decrease of the coarse-grained approach in this bin was 31.4% relative to KINARI’s all-atom rigidity analysis. An example protein that was earmarked as a $good$ tradeoff of accuracy loss for speed gain, using TLCCS, is 5utd (Figure 9). The largest cluster changed from 1001 atoms in the all-atom approach to 1847 in CGRAP, and the second largest cluster changed from 207 atoms to 98. A total of 81% of the atoms in the all-atom model’s largest cluster are contained in the largest cluster identified via CGRAP. Although 5utd’s TLCCS score was just 0.45, note that visually, CGRAP’s rigidity results are still very similar to KINARI’s all-atom rigidity analysis.

4.5. Bin: $Fair$

The average run-time decrease using CGRAP in this bin was 29.6% relative to KINARI’s all-atom rigidity analysis. An example protein that we considered a $fair$ tradeoff of accuracy for speed gain is 6fs9 (Figure 10). The largest cluster changed from 627 atoms to 1973, and the second largest cluster changed from 231 atoms to 129. A total of 75% of the atoms in the all-atom model’s largest cluster are contained in the largest cluster identified via CGRAP.

4.6. Large Proteins

In addition to assessing the quality of CGRAP’s results relative to KINARI’s all-atom approach, we also looked closely at very large proteins, because their coarse-grained rigidity analysis is poised to realize significant speedup relative to KINARI’s all-atom approach. Indeed the quality of CGRAP’s results for very large proteins, is also very good, indicating that the small loss of accuracy is nonetheless a fair tradeoff for the reduced time needed to preform the analysis. Proteins 2v0c, 4l78, and 5yna (Figure 11, Figure 12 and Figure 13) are three such proteins.

PDB file 2v0c is composed of 13,070 atoms and rigidity analysis using CGRAP had a speedup of 40%, or 98 s, relative to the run-time of KINARI’s all-atom approach. The largest cluster changed from 6928 atoms in the all-atom approach to 7462 via CGRAP, and the second largest cluster changed from 1578 atoms to 2219. A total of 79% of the atoms in the largest cluster identified using KINARI are contained in the largest cluster identified using CGRAP.

PDB file 5yna is made up of 15,829 atoms, and analyzing its rigidity using CGRAP was 36% faster, or a savings of 130 s, versus the run-time of KINARI. The largest cluster changed from 9608 atoms in the all-atom approach to 9397 in the results from CGRAP, and the second largest cluster changed from 1209 atoms to 1289. A total of 74% of the atoms in the largest cluster as inferred via KINARI are contained in the largest cluster as inferred via CGRAP.

PDB file 4l78, the largest protein that we analyzed, is made up of 19,489 atoms among 1285 residues. Using CGRAP we saw a speedup of 38%, or 202 s, relative to KINARI. The largest cluster changed from 13,352 atoms in the output of KINARI to 15,418 atoms in the output of CGRAP, and the second largest cluster changed from 113 atoms to 119. A total of 85% of the atoms the largest rigid cluster via KINARI are contained in the largest cluster identified using CGRAP.

4.7. Speedup Using CGRAP

All-in-all, the speedup of using a coarse-grained approach as implemented in CGRAP relative to the all-atom approach in KINARI, is shown in Figure 14. Proteins larger than about 2000 atoms routinely saw a reduced run-time of 35% relative to the all-atom approach, and upwards of 50% reduced run-times.

5. Discussion

The ultimate goal of our coarse-grained approach is to reduce the run-time of the pebble game for protein rigidity analysis, but at the same time minimize the loss of accuracy.

We see from the data (Table 1 and Figure 14) that CGRAP does in fact reduce the run-time for nearly all proteins compared to an all-atom approach, with an average run-time reduction of 32.5%. Some run-times via a coarse-grained approach were reduced as much as 50% relative to the all-atom method implemented in KINARI. Larger proteins can require up to tens of minutes of compute time via an all-atom rigidity analysis approach, so a 40–50% reduction in run-time via a coarse-grained approach permits a user to nearly double the number of proteins that can be analyzed otherwise.

The TLCCS metric reveals that in many cases, the coarse-grained approach implemented via CGRAP produced rigidity results that are very comparable to the all-atom rigidity analysis approach (Table 1). The 6418 proteins among the $best$, $excellent$ and very good bins of proteins as assessed via TLCCS represent 70% of all proteins that we studied. In addition, even those proteins whose coarse-grained rigidity analysis we deemed as $good$ relative to the all-atom KINARI method, still often identified the two largest clusters as being located near to where they are in the all-atom approach, and otherwise bear a noticeable resemblance to the all-atom modeling method (Figure 9).

Those proteins for which a coarse-grained rigidity analysis yielded results that were $fair$ relative to an all-atom approach represent 17% of the proteins that we tested (Figure 10 is an example). Fortunately, as can be seen in Table 1, those proteins also represent the smallest proteins in our data set of 9046 PDF files, with an average size of 3795 atoms. Thus, a rule of thumb might be that proteins larger than 5000 atoms be analyzed via a coarse-grained approach, whose results will be good relative to an all-atom approach, but whose speed gain will nonetheless be significant.

Our analysis of several very large proteins for which a coarse-grained analysis worked well, we consider extra noteworthy. The three proteins in Figure 11, Figure 12 and Figure 13 are among the largest proteins that we analyzed, and whose quality of their rigidity results via CGRAP we calculate as $best$ when compared to the all-atom approach. For these, the largest and second largest clusters are at the correct positions and are approximately the same size of the largest and second largest clusters in the all-atom approach.

6. Conclusions

In this work, we present the first coarse-grained, residue-level rigidity analysis approach that models proteins as body-bar structures, and analyzes their rigidity via a pebble game algorithm. Relative to an all-atom approach that is available via KINARI, we show quantitatively via a comparison metric that the results of our coarse-grained rigidity analysis are often very comparable to the all-atom approach, while routinely requiring 40% less compute time, and sometimes exhibiting a speedup of up to 50%. Such a speedup in run-time, while not jeopardizing accuracy, can facilitate a timely comparative analyses of many protein variants. This is especially true of very large proteins, as for example the spike protein of SARS-Cov2, which is made up for 1281 residues (PDB 6vxx), whose mutations have significant implications in the global efforts to combat the COVID-19 pandemic.