Investigation on the Prediction of Cardiovascular Events Based on Multi-Scale Time Irreversibility Analysis
Abstract
:1. Introduction
2. Materials and Methods
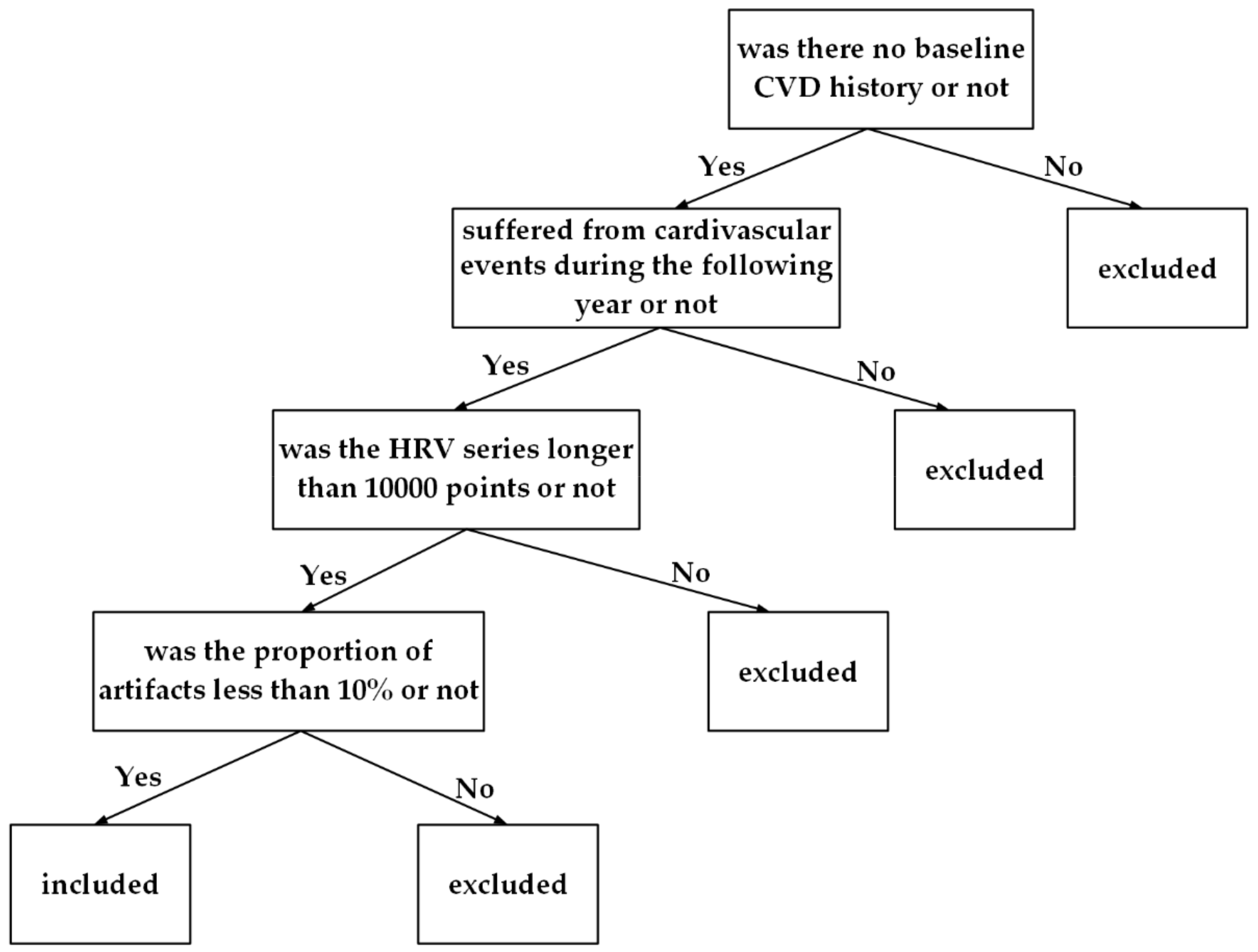
2.1. Participants
2.2. Multi-Scale Time Irreversibility Analysis
2.3. Conventional HRV Analysis
2.4. Classification of CVD and Non-CVD Participants by Random Forest (RF) Algorithm
2.4.1. The Basic Principle of DT
2.4.2. Bagging Ensemble Learning Algorithm
2.4.3. RF Algorithm
| Algorithm 1: Random forest |
| Input: original sample set D; number of decision tree T |
| Output: strong learner G |
| 1 For t = 1, 2, …, T 2 request size-N’ data Dt by bootstrapping with D; 3 obtain tree gt with random feature selection; 4 return G = Uniform({gt }); |
2.5. Statistical Analysis
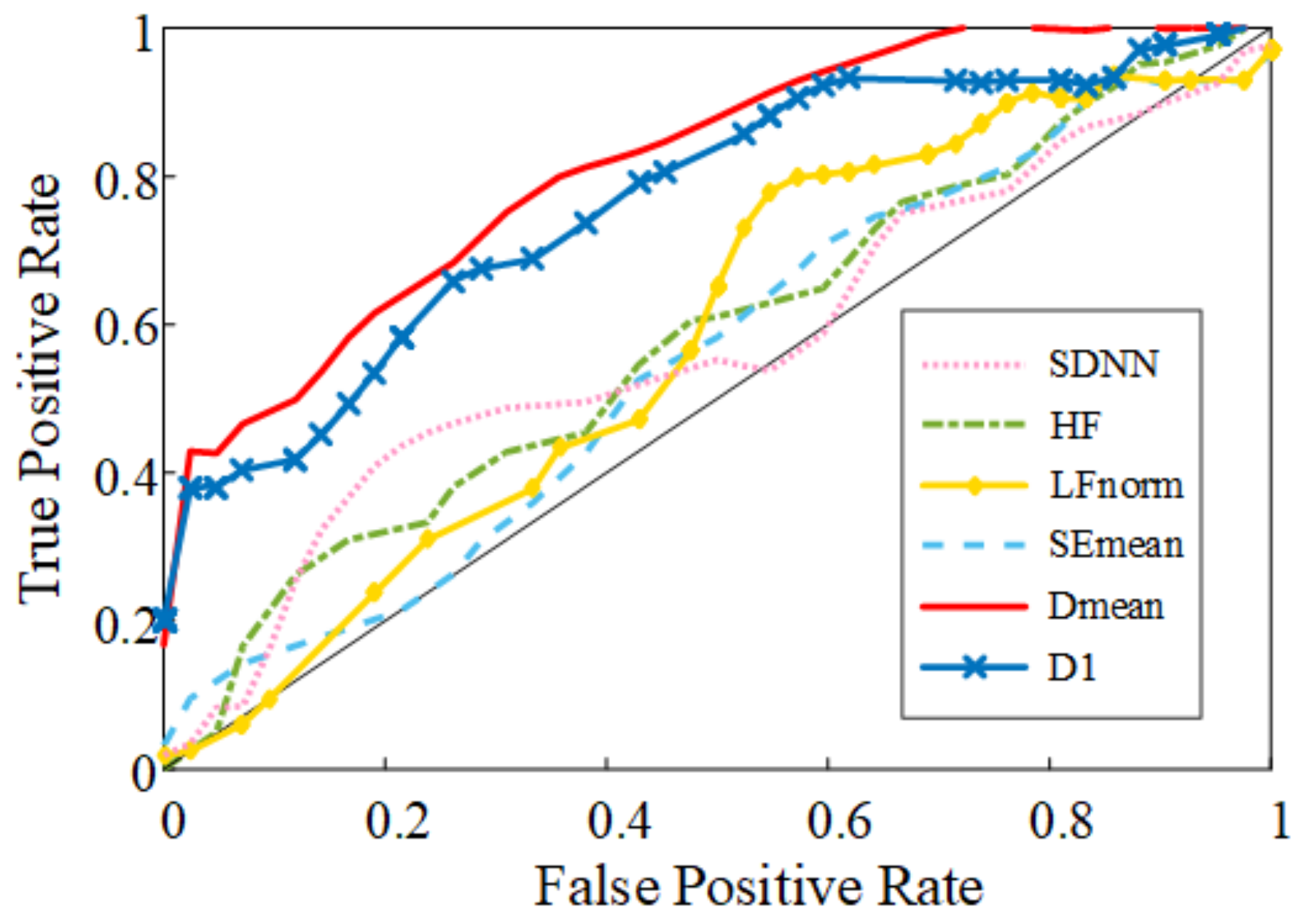
3. Results
4. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Health Organization. Cardiovascular Diseases (CVDs). Available online:https://www.who.int/news-room/fact-sheets/detail/cardiovascular-diseases-(cvds) (accessed on 20 June 2021).
- Harris, P.R.E. The Normal Electrocardiogram: Resting 12-Lead and Electrocardiogram Monitoring in the Hospital. Crit. Care Nurs. Clin. N. Am. 2016, 28, 281–296. [Google Scholar] [CrossRef] [PubMed]
- María, E.R.; Lluís, C.; Ramos, C.J.; Cleofé, Z.M.; Sara, M.; José, A.; Jesús, C.-M. Reduced heart rate variability predicts fatigue severity in individuals with chronic fatigue syndrome/myalgic encephalomyelitis. J. Transl. Med. 2020, 18, 4. [Google Scholar] [CrossRef]
- Yan, X.; Zhang, L.; Li, J.; Du, D.; Hou, F. Entropy-Based Measures of Hypnopompic Heart Rate Variability Contribute to the Automatic Prediction of Cardiovascular Events. Entropy 2020, 22, 241. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karavaev, A.S.; Ishbulatov, Y.M.; Ponomarenko, V.I.; Bezruchko, B.P.; Kiselev, A.R.; Prokhorov, M.D. Autonomic control is a source of dynamical chaos in the cardiovascular system. Chaos 2019, 29, 121101. [Google Scholar] [CrossRef]
- Humeau-Heurtier, A.; Mahé, G.; Chapeau-Blondeau, F.; Rousseau, D.; Abraham, P. Study of time reversibility/irreversibility of cardiovascular data: Theoretical results and application to laser Doppler flowmetry and heart rate variability signals. Phys. Med. Biol. 2012, 57, 4335–4351. [Google Scholar] [CrossRef] [PubMed]
- Kennel, M.B. Testing time symmetry in time series using data compression dictionaries. Phys. Rev. E Stat. Nonlin. Soft. Matter. Phys. 2004, 69, 056208. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Yang, D.; Wang, L.; Wang, K. Classifying of welding time series based on multi-scale time irreversibility analysis and extreme learning machine. Chaos Solitons Fractals 2020, 139, 110040. [Google Scholar] [CrossRef]
- Lucia, U.; Grisolia, G.; Kuzemsky, A.L. Time, Irreversibility and Entropy Production in Nonequilibrium Systems. Entropy 2020, 22, 887. [Google Scholar] [CrossRef]
- Xia, J.; Shang, P.; Wang, J.; Shi, W. Classifying of financial time series based on multiscale entropy and multiscale time irreversibility. Phys. A Stat. Mech. Its Appl. 2014, 400, 151–158. [Google Scholar] [CrossRef]
- Yao, W.; Dai, J.; Perc, M.; Wang, J.; Yao, D.; Guo, D. Permutation-based time irreversibility in epileptic electroencephalograms. Nonlinear Dyn. 2020, 100, 907–919. [Google Scholar] [CrossRef]
- Zanin, M.; Güntekin, B.; Aktürk, T.; Hanoğlu, L.; Papo, D. Time Irreversibility of Resting-State Activity in the Healthy Brain and Pathology. Front. Physiol. 2019, 10, 1619. [Google Scholar] [CrossRef]
- Cammarota, C.; Rogora, E. Time reversal, symbolic series and irreversibility of human heartbeat. Chaos Solitons Fractals 2006, 32, 1649–1654. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Broken asymmetry of the human heartbeat: Loss of time irreversibility in aging and disease. Phys. Rev. Lett. 2005, 95, 198102. [Google Scholar] [CrossRef] [PubMed]
- Chladekova, L.; Czippelova, B.; Turianikova, Z.; Tonhajzerova, I.; Calkovska, A.; Baumert, M.; Javorka, M. Multiscale time irreversibility of heart rate and blood pressure variability during orthostasis. Physiol. Meas. 2012, 33, 1747–1756. [Google Scholar] [CrossRef]
- Tonhajzerova, I.; Ondrejka, I.; Chladekova, L.; Farsky, I.; Visnovcova, Z.; Calkovska, A.; Jurko, A.; Javorka, M. Heart rate time irreversibility is impaired in adolescent major depression. Prog. Neuropsychopharmacol. Biol. Psychiatry 2012, 39, 212–217. [Google Scholar] [CrossRef] [PubMed]
- Spiegel, K.; Tasali, E.; Leproult, R.; Van Cauter, E. Effects of poor and short sleep on glucose metabolism and obesity risk. Nat. Rev. Endocrinol. 2009, 5, 253–261. [Google Scholar] [CrossRef] [PubMed]
- Faraut, B.; Boudjeltia, K.Z.; Vanhamme, L.; Kerkhofs, M. Immune, inflammatory and cardiovascular consequences of sleep restriction and recovery. Sleep Med. Rev. 2012, 16, 137–149. [Google Scholar] [CrossRef]
- Born, J.; Wilhelm, I. System consolidation of memory during sleep. Psychol. Res. 2012, 76, 192–203. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ma, Y.; Hou, F.; Yang, A.C.; Ahn, A.C.; Fan, L.; Peng, C.-K. Symbolic dynamics of electroencephalography is associated with the sleep depth and overall sleep quality in healthy adults. Phys. A Stat. Mech. Its Appl. 2018, 513, 22–31. [Google Scholar] [CrossRef]
- Ford, D.E.; Cooper-Patrick, L. Sleep disturbances and mood disorders: An epidemiologic perspective. Depress. Anxiety 2001, 14, 3–6. [Google Scholar] [CrossRef]
- Song, Y.; Blackwell, T.; Yaffe, K.; Ancoli-Israel, S.; Redline, S.; Stone, K.L. Relationships between sleep stages and changes in cognitive function in older men: The MrOS Sleep Study. Sleep 2015, 38, 411–421. [Google Scholar] [CrossRef] [Green Version]
- Blackwell, T.; Yaffe, K.; Ancoli-Israel, S.; Schneider, J.L.; Cauley, J.A.; Hillier, T.A.; Fink, H.A.; Stone, K.L. Poor sleep is associated with impaired cognitive function in older women: The study of osteoporotic fractures. J. Gerontol. A Biol. Sci. Med. Sci. 2006, 61, 405–410. [Google Scholar] [CrossRef] [Green Version]
- Aslan, S.; Erbil, N.; Tezer, F.I. Heart Rate Variability During Nocturnal Sleep and Daytime Naps in Patients With Narcolepsy Type 1 and Type 2. J. Clin. Neurophysiol. 2019, 36, 104–111. [Google Scholar] [CrossRef]
- Bazilio, D.S.; Bonagamba, L.G.H.; Moraes, D.J.A.; Machado, B.H. Cardiovascular and respiratory profiles during the sleep-wake cycle of rats previously submitted to chronic intermittent hypoxia. Exp. Physiol. 2019, 104, 1408–1419. [Google Scholar] [CrossRef] [PubMed]
- Morris, C.J.; Purvis, T.E.; Hu, K.; Scheer, F.A. Circadian misalignment increases cardiovascular disease risk factors in humans. Proc. Natl. Acad. Sci. USA 2016, 113, E1402–E1411. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Neufeld, E.V.; Carney, J.J.; Dolezal, B.A.; Boland, D.M.; Cooper, C.B. Exploratory Study of Heart Rate Variability and Sleep among Emergency Medical Services Shift Workers. Prehosp. Emerg. Care 2017, 21, 18–23. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nakayama, N.; Miyachi, M.; Tamakoshi, K.; Negi, K.; Watanabe, K.; Hirai, M. Increased Activity in Patients with Cardiovascular Risk Factors Increases Heart Rate Variability. West J. Nurs. Res. 2020, 42, 431–436. [Google Scholar] [CrossRef]
- Eguchi, K.; Schwartz, J.E.; Pickering, T.G.; Hoshide, S.; Ishikawa, J.; Shimada, K.; Kario, K. Increased heart rate variability during sleep is a predictor for future cardiovascular events in patients with type 2 diabetes. Hypertens. Res. 2010, 33, 737–742. [Google Scholar] [CrossRef]
- Ulmer, C.S.; Hall, M.H.; Dennis, P.A.; Beckham, J.C.; Germain, A. Posttraumatic stress disorder diagnosis is associated with reduced parasympathetic activity during sleep in US veterans and military service members of the Iraq and Afghanistan wars. Sleep 2018, 41, zsy174. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, L.; Wu, H.; Zhang, X.; Wei, X.; Hou, F.; Ma, Y. Sleep heart rate variability assists the automatic prediction of long-term cardiovascular outcomes. Sleep Med. 2020, 67, 217–224. [Google Scholar] [CrossRef]
- Fang, S.C.; Wu, Y.L.; Tsai, P.S. Heart Rate Variability and Risk of All-Cause Death and Cardiovascular Events in Patients With Cardiovascular Disease: A Meta-Analysis of Cohort Studies. Biol. Res. Nurs. 2020, 22, 45–56. [Google Scholar] [CrossRef]
- Dean, D.A.; Goldberger, A.L.; Mueller, R.; Kim, M.; Rueschman, M.; Mobley, D.; Sahoo, S.S.; Jayapandian, C.P.; Cui, L.; Morrical, M.G.; et al. Scaling Up Scientific Discovery in Sleep Medicine: The National Sleep Research Resource. Sleep 2016, 39, 1151–1164. [Google Scholar] [CrossRef] [Green Version]
- Pan, J.; Tompkins, W.J. A real-time QRS detection algorithm. IEEE Trans. Biomed. Eng. 1985, 32, 230–236. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef] [Green Version]
- Hou, F.; Zhuang, J.; Bian, C.; Tong, T.; Chen, Y.; Yin, J.; Qiu, X.; Ning, X. Analysis of heartbeat asymmetry based on multi-scale time irreversibility test. Phys. A Stat. Mech. Its Appl. 2009, 389, 754–760. [Google Scholar] [CrossRef]
- Hou, F.; Ning, X.; Zhuang, J.; Huang, X.; Fu, M.; Bian, C. High-dimensional time irreversibility analysis of human interbeat intervals. Med. Eng. Phys. 2011, 33, 633–637. [Google Scholar] [CrossRef]
- Camm, A.J.; Malik, M.; Bigger, J.T.; Breithardt, G.; Cerutti, S.; Cohen, R.J.; Coumel, P.; Fallen, E.L.; Kennedy, H.L.; Kleiger, R.E.; et al. Heart rate variability: Standards of measurement, physiological interpretation and clinical use. Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology. Circulation 1996, 93, 1043–1065. [Google Scholar]
- Fernández-Delgado, M.; Cernadas, E.; Barro, S.; Amorim, D. Do we need hundreds of classifiers to solve real world classification problems? J. Mach. Learn. Res. 2014, 15, 3133–3181. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Bayar, B.; Stamm, M.C. Constrained Convolutional Neural Networks: A New Approach Towards General Purpose Image Manipulation Detection. IEEE Trans. Inf. Forensics Secur. 2018, 13, 2691–2706. [Google Scholar] [CrossRef]
- Stramba-Badiale, M.; Fox, K.M.; Priori, S.G.; Collins, P.; Daly, C.; Graham, I.; Jonsson, B.; Schenck-Gustafsson, K.; Tendera, M. Cardiovascular diseases in women: A statement from the policy conference of the European Society of Cardiology. Eur. Heart J. 2006, 27, 994–1005. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hubert, H.B.; Feinleib, M.; McNamara, P.M.; Castelli, W.P. Obesity as an independent risk factor for cardiovascular disease: A 26-year follow-up of participants in the Framingham Heart Study. Circulation 1983, 67, 968–977. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goldberger, A.L.; Peng, C.K.; Lipsitz, L.A. What is physiologic complexity and how does it change with aging and disease? Neurobiol. Aging 2002, 23, 23–26. [Google Scholar] [CrossRef]
- Porta, A.; Guzzetti, S.; Montano, N.; Gnecchi-Ruscone, T.; Furlan, R.; Malliani, A. Time Reversibility in Short-Term Heart Period Variability. In Proceedings of the 2006 Computers in Cardiology, Valencia, Spain, 17–20 September 2006; IEEE: Piscataway, NJ, USA, 2008; pp. 77–80. [Google Scholar]
- Porta, A.; D’Addio, G.; Bassani, T.; Maestri, R.; Pinna, G.D. Assessment of cardiovascular regulation through irreversibility analysis of heart period variability: A 24 hours Holter study in healthy and chronic heart failure populations. Philos. Trans. A Math Phys. Eng. Sci. 2009, 367, 1359–1375. [Google Scholar] [CrossRef] [PubMed]


| Variable | Non-CVD Group | CVD Group | p |
|---|---|---|---|
| 1, M [Q1, Q3] | 9.52 [7.92, 11.65] | 6.53 [2.6, 8.83] | <0.001 |
| 2, M [Q1, Q3] | 7.13 [4.99, 8.59] | 3.46 [1.92, 6.12] | <0.001 |
| 3, Mean ± SD | 7.43 ± 3.08 | 4.15 ± 2.54 | <0.001 |
| 4, Mean ± SD | 7.6 ± 3.32 | 4.12 ± 2.83 | <0.001 |
| 5, M [Q1, Q3] | 7.1 [5.75, 9.07] | 3.17 [2.13, 5.8] | <0.001 |
| 6, Mean ± SD | 7.02 ± 3.47 | 4.07 ± 2.73 | <0.001 |
| 7, Mean ± SD | 6.61 ± 3.25 | 4.21 ± 2.47 | <0.001 |
| 8, Mean ± SD | 6.29 ± 3.09 | 3.99 ± 2.53 | <0.001 |
| 9, M [Q1, Q3] | 5.93 [3.65, 8.01] | 3.01 [1.84, 4.87] | <0.001 |
| 10, M [Q1, Q3] | 5.84 [3.72, 7.22] | 3.2 [2.32, 5.78] | 0.002 |
| Variable | β | SE | OR (95% CI) | p |
|---|---|---|---|---|
| 1 | −0.297 | 0.079 | 0.743 (0.636–0.868) | <0.001 |
| 2 | −0.316 | 0.090 | 0.729 (0.611–0.870) | <0.001 |
| 3 | −0.451 | 0.111 | 0.637 (0.513–0.791) | <0.001 |
| 4 | −0.379 | 0.096 | 0.685 (0.567–0.826) | <0.001 |
| 5 | −0.365 | 0.093 | 0.694 (0.578–0.833) | <0.001 |
| 6 | −0.320 | 0.091 | 0.726 (0.607–0.868) | <0.001 |
| 7 | −0.291 | 0.093 | 0.747 (0.623–0.896) | 0.002 |
| 8 | −0.285 | 0.091 | 0.752 (0.629–0.899) | 0.002 |
| 9 | −0.316 | 0.100 | 0.729 (0.600–0.886) | 0.002 |
| 10 | −0.282 | 0.101 | 0.754 (0.619–0.919) | 0.005 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Yang, Q.; Li, J.; Hou, F. Investigation on the Prediction of Cardiovascular Events Based on Multi-Scale Time Irreversibility Analysis. Symmetry 2021, 13, 2424. https://doi.org/10.3390/sym13122424
Wu X, Yang Q, Li J, Hou F. Investigation on the Prediction of Cardiovascular Events Based on Multi-Scale Time Irreversibility Analysis. Symmetry. 2021; 13(12):2424. https://doi.org/10.3390/sym13122424
Chicago/Turabian StyleWu, Xiaochuan, Qianru Yang, Jin Li, and Fengzhen Hou. 2021. "Investigation on the Prediction of Cardiovascular Events Based on Multi-Scale Time Irreversibility Analysis" Symmetry 13, no. 12: 2424. https://doi.org/10.3390/sym13122424
APA StyleWu, X., Yang, Q., Li, J., & Hou, F. (2021). Investigation on the Prediction of Cardiovascular Events Based on Multi-Scale Time Irreversibility Analysis. Symmetry, 13(12), 2424. https://doi.org/10.3390/sym13122424





