Synchronous Steady State Solutions of a Symmetric Mixed Cubic-Superlinear Schrödinger System
Abstract
:1. Introduction
2. NLS Systems Mathematical Physics Overview
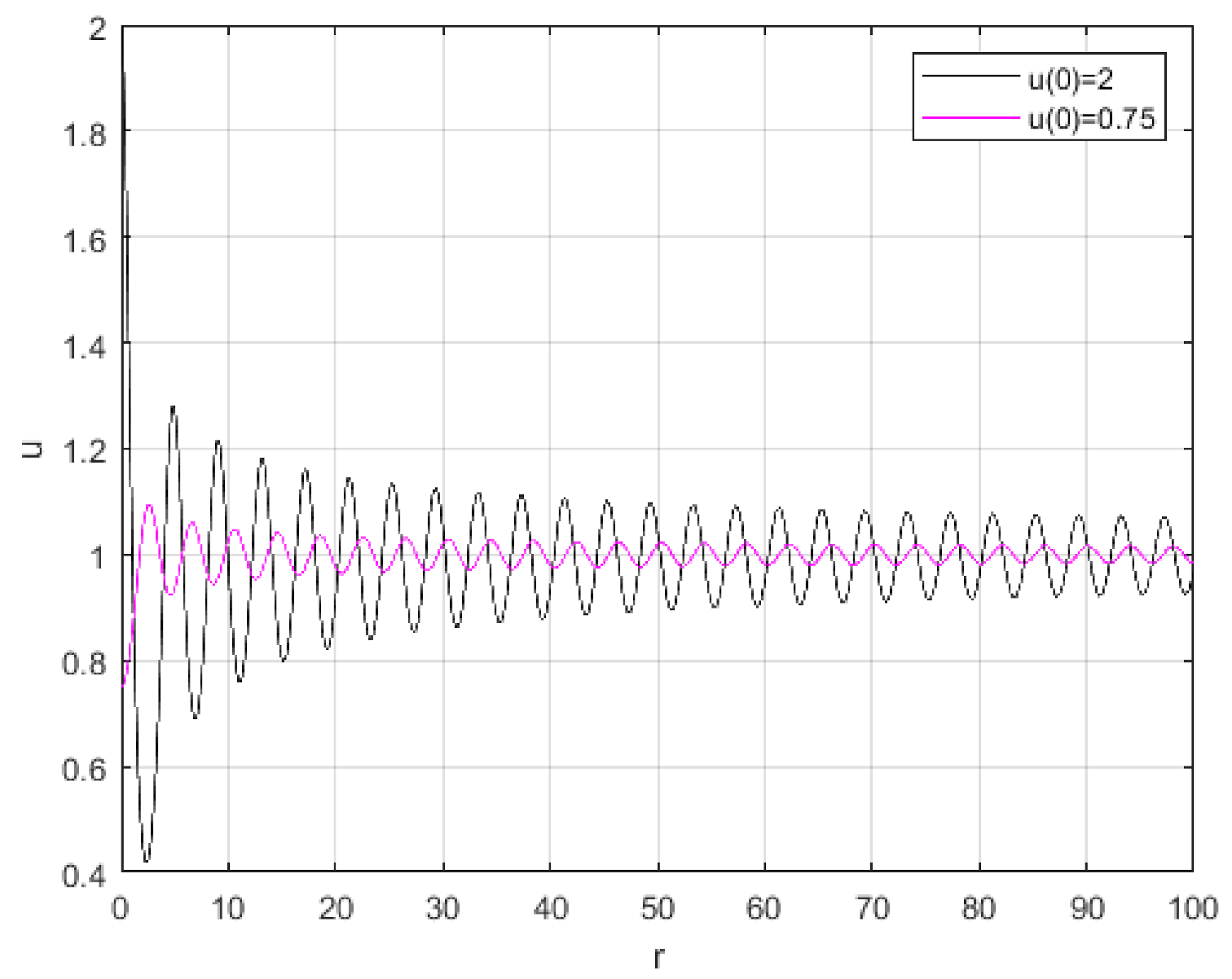
3. The Steady State Problem
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
- i.
- .
- ii.
- there exists constants such that , .
- iii.
- there exists such that .
References
- Abazari, R. Numerical simulation of coupled nonlinear Schrödinger equation by RDTM and comparison with DTM. J. Appl. Sci. 2011, 11, 3454–3463. [Google Scholar] [CrossRef] [Green Version]
- Ambrosetti, A.; Colorado, E. Standing waves of some coupled nonlinear Schrödinger equations. J. Lond. Math. Soc. 2007, 75, 67–82. [Google Scholar] [CrossRef]
- Bartsch, T.; Wang, Z.-Q. Note on ground states of nonlinear Schrödinger systems. J. Part. Diff. Equ. 2006, 19, 200–207. [Google Scholar]
- Bahri, A.; Lions, P.L. Morse index of some min-max critical points. I. Application to multiplicity results. Commun. Pure Appl. Math. 1988, 41, 1027–1037. [Google Scholar] [CrossRef]
- Bermudez, R.F. Coupled system of nonlinear Schrödinger and Korteweg-de Vries equations. Master’s Thesis in Mathematical Engineering, Universidad Carlos III de Madrid. arXiv 2016, arXiv:1609.06655v2. [Google Scholar]
- Geng, X.G.; Liu, H.; Zhu, J. Initial-boundary value problems for the coupled nonlinear Schrödinger equation on the half-line. Stud. Appl. Math. 2015, 135, 310–346. [Google Scholar] [CrossRef]
- He, Y.; Qin, D.; Chen, D. Ground state solutions for Hamiltonian elliptic systems with super or asymptotically quadratic nonlinearity. Bound Value Probl. 2019, 2019, 158. [Google Scholar] [CrossRef] [Green Version]
- Ling, L.M.; Zhao, L.C.; Guo, B.L. Darboux transformation and classification of solution for mixed coupled nonlinear Schrödinger equations. Commun. Nonlinear Sci. Num. Simul. 2016, 32, 285–304. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.L.; Wang, Z.-Q. Ground states and bound states of a nonlinear Schrödinger system. Adv. Nonlinear Stud. 2010, 10, 175–193. [Google Scholar] [CrossRef]
- Pomponio, A. Coupled nonlinear Schrödinger systems with potentials. J. Differ. Equ. 2006, 227, 258–281. [Google Scholar] [CrossRef] [Green Version]
- Sirakov, B. Least energy solitary waves for a system of nonlinear Schrödinger equations in Rn. Comm. Math. Phys. 2007, 271, 199–221. [Google Scholar] [CrossRef]
- Tian, S.F. Initial-boundary value problems for the general coupled nonlinear Schrödinger equation on the interval via the Fokas method. J. Differ. Equ. 2017, 262, 506–558. [Google Scholar] [CrossRef]
- Tian, R.-S.; Wang, Z.-Q. Multiple solitary wave solutions of nonlinear Schrödinger systems. Topol. Methods Nonlinear Anal. 2011, 37, 203–223. [Google Scholar]
- Wan, Y.; Avila, A.I. Multiple solutions of a coupled nonlinear Schrödinger system. J. Math. Anal. Appl. 2007, 334, 1308–1325. [Google Scholar] [CrossRef] [Green Version]
- Willem, M. Minimax Theorems; Birkhauser: Boston, MA, USA, 1996. [Google Scholar]
- Dhar, A.K.; Das, K.P. Fourth-order nonlinear evolution equation for two Stokes wave trains in deep water. Phys. Fluids A Fluid Dyn. 1991, 3, 3021. [Google Scholar] [CrossRef]
- Menyuk, C.R. Stability of solitons in birefringent optical fibers. II. Arbitrary amplitudes. J. Opt. Soc. Am. B 1988, 5, 392–402. [Google Scholar] [CrossRef]
- Kanna, T.; Lakshmanan, M.; Dinda, P.T.; Akhmediev, N. Soliton collisions with shape change by intensity redistribution in mixed coupled nonlinear Schrödinger equations. Phys. Rev. E 2006, 73, 026604. [Google Scholar] [CrossRef] [Green Version]
- Lin, T.C.; Wei, J.C. Ground state of N coupled nonlinear Schrödinger equations in Rn; n ≥ 3. Commun. Math. Phys. 2005, 255, 629–653. [Google Scholar] [CrossRef]
- Liu, W.-M.; Kengne, E. Schrödinger Equations in Nonlinear Systems; Springer Nature Singapore Pte Ltd.: Singapore, 2019. [Google Scholar]
- Prytula, V.; Vekslerchik, V.; Perez-Garcia, V.M. Collapse in coupled nonlinear Schrödinger equations: Sufficient conditions and applications. Physica D 2009, 238, 1462–1467. [Google Scholar] [CrossRef] [Green Version]
- Sirakov, B.; Soares, S. Soliton solutions to systems of coupled Schrödinger equations of Hamiltonian type. Trans. Am. Math. Soc. Am. Math. Soc. 2010, 362, 5729–5744. [Google Scholar] [CrossRef] [Green Version]
- Bluman, G.; Kumei, S. Symmetries and Differential Equations; Springer: New York, NY, USA, 1989. [Google Scholar]
- Ibragimov, N.H. CRC Handbook of Lie Group Analysis of Differential Equations; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Mawhin, J.; Willem, M. Critical Point Theory and Hamiltonian System; Springer: New York, NY, USA, 1989. [Google Scholar]
- Noris, B.; Ramos, M. Existence and bounds of positive solutions for a nonlinear Schrödinger system. Proc. AMS 2010, 138, 1681–1692. [Google Scholar] [CrossRef] [Green Version]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer: New York, NY, USA, 1986. [Google Scholar]
- Ovsiannikov, L.V. Group Analysis of Differential Equations; Nauka: Moscow, Russia, 1978. [Google Scholar]
- Xu, J. Initial-boundary value problem for the two-component nonlinear Schrödinger equation on the half-line. J. Nonlinear Math. Phys. 2016, 23, 167–189. [Google Scholar] [CrossRef] [Green Version]
- Yan, F.; Hua, C.; Liu, H.; Liu, Z. Lie symmetry analysis and exact solutions for the coupled Kuramoto-Sivashinsky Equations. In Proceedings of the 2011 Fourth International Workshop on Chaos-Fractals Theories and Applications, Hangzhou, China, 19–22 October 2011; IEEE Computer Soc.: Piscataway, NJ, USA, 2011; pp. 61–65. [Google Scholar]
- Porsezian, K.; Nakkeeran, K. Optical soliton propagation in a coupled system of the nonlinear Schrödinger equation and the Maxwell-Bloch equations. J. Mod. Opt. 1995, 42, 1953–1958. [Google Scholar] [CrossRef]
- Mitchell, M.; Chen, Z.; Shih, M.; Segev, M. Self-trapping of partially spatially incoherent light. Phys. Rev. Lett. 1996, 77, 490493. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Terracini, S.; Verzini, G. Multipulse phase in k-mixtures of Bose-Einstein condenstates. Arch. Rat. Mech. Anal. 2009, 194, 717–741. [Google Scholar] [CrossRef] [Green Version]
- Ruegg, C.; Cavadini, N.; Furrer, A.; Gudel, H.-U.; Kramer, K.; Mutka, H.; Wildes, A.; Habicht, K.; Vorderwischu, P. Bose-Einstein condensation of the triplet states in the magnetic insulator TlCuCl3. Nature 2003, 423, 62–65. [Google Scholar] [CrossRef]
- Bahrami, M.; Großardt, A.; Donadi, S.; Bassi, A. The Schrödinger-Newton equation and its foundations. New J. Phys. 2014, 16, 115007. [Google Scholar] [CrossRef]
- Belmonte-Beitia, J. A note on radial nonlinear Schrödinger systems with nonlinearity spacially modulated. Electron. J. Differ. Equ. 2008, 2008, 1–6. [Google Scholar]
- Belmonte-Beitia, J.; Perez-García, V.M.; Torres, P.J. Solitary waves for linearly coupled nonlinear Schrödinger equations with inhomogeneous coefficients. J. Nonlinear Sci. 2009, 19, 437–451. [Google Scholar] [CrossRef] [Green Version]
- Farah, L.G.; Pastor, A. Scattering for a 3D coupled nonlinear Schrödinger system. J. Math. Phys. 2017, 58, 071502. [Google Scholar] [CrossRef]
- Ma, L.; Zhao, L. Uniqueness of ground states of some coupled nonlinear Schrödinger systems and their application. J. Differ. Equ. 2008, 245, 2551–2565. [Google Scholar] [CrossRef] [Green Version]
- Belmonte-Beitia, J.; Perez-García, V.M.; Brazhnyi, V. Solitary waves in coupled nonlinear Schrödinger equations with spatially inhomogeneous nonlinearities. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 158–172. [Google Scholar] [CrossRef] [Green Version]
- Su, J.; Tian, R.; Wang, Z.-Q. Positive solutions of doubly coupled multicomponent nonlinear Schrödinger systems. Discret. Contin. Dyn. Syst. 2019, 15, 2143–2161. [Google Scholar] [CrossRef] [Green Version]
- Tian, R. Existence and Multiplicity Results on Standing Wave Solutions of Some Coupled Nonlinear Schrödinger Equations. Ph.D. Thesis, Utah State University, Logan, UT, USA, 2013. [Google Scholar]
- Vijayajayanthi, M.; Kanna, T.; Lakshmanan, M. Bright-dark solitons and their collisions in mixed N-coupled nonlinear Schrödinger equations. Phys. Rev. A 2008, 77, 013820. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.-Q.; Meng, X.-H.; Xu, T.; Li, L.-L.; Tian, B. Interactions of bright solitons for the (2+1)-dimensional coupled nonlinear Schrödinger equations from optical fibres with symbolic computation. Phys. Scr. 2007, 75, 537–542. [Google Scholar] [CrossRef]
- Agrawal, G.P. Nonlinear Fiber Optics; Academic Press: New York, NY, USA, 1995. [Google Scholar]
- Chakravarty, S.; Ablowitz, M.J.; Sauer, J.R.; Jenkins, R.B. Multisoliton interactions and wavelength-division multiplexing. Opt. Lett. 1995, 20, 136–138. [Google Scholar] [CrossRef]
- Mollenauer, L.F.; Evangelides, S.G.; Gordon, J.P. Wavelength division multiplexing with solitons in ultra-long distance transmission using lumped amplifiers. J. Lightwave Technol. 1991, 9, 362. [Google Scholar] [CrossRef]
- Aitchison, J.S.; Weiner, A.M.; Silberberg, Y.; Leaird, D.E.; Oliver, M.K.; Jackel, J.L.; Smith, P.W.E. Experimental observation of spatial soliton interactions. Opt. Lett. 1991, 16, 15–17. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hioe, F.T. Solitary waves for two and three coupled nonlinear Schrödinger equations. Phys. Rev. E 1998, 58, 6700. [Google Scholar] [CrossRef]
- Hioe, F.T. Solitary waves for N coupled nonlinear Schrödinger equations. Phys. Rev. Lett. 1999, 82, 1152–1155. [Google Scholar] [CrossRef]
- Hioe, F.T.; Salter, T.S. Special set and solutions of coupled nonlinear Schrödinger equations. J. Phys. A Math. Gen. 2002, 35, 8913–8928. [Google Scholar] [CrossRef]
- Shalaby, M.; Reynaud, F.; Barthelemy, A. Experimental observation of spatial soliton interactions with a π/2 relative phase difference. Opt. Lett. 1992, 17, 778–780. [Google Scholar] [CrossRef] [PubMed]
- Zhida, Y. Multi-soliton solutions of coupled nonlinear Schrödinger equations. J. Chin. Phys. Lett. 1987, 4, 185–187. [Google Scholar] [CrossRef]
- Berkhoer, A.L.; Zakharov, V.E. Self excitation of Waves with different polarizations in nonlinear media. JETP 1970, 31, 486–490. [Google Scholar]
- Bhakta, J.C.; Gupta, M.R. Stability of solitary wave solutions of simultaneous nonlinear Schrödinger equations. J. Plas. Phys. 1982, 28, 379–383. [Google Scholar] [CrossRef]
- Gupta, M.R.; Som, B.K.; Dasgupta, B. Coupled nonlinear Schrödinger equations for Langmuir and elecromagnetic waves and extension of their modulational instability domain. J. Plasma Phys. 1981, 25, 499–507. [Google Scholar] [CrossRef]
- Benci, V.; Fortunato, D.F. Solitary waves of the nonlinear Klein-Gordon equation coupled with Maxwell equations. Rev. Math. Phys. 2002, 14, 409–420. [Google Scholar] [CrossRef]
- Brezis, H.; Nirenberg, L. Positive solutions of non linear elliptic equations involving critical Sobolev exponents. Comm. Pure. Appl. Math. 1983, 36, 437–477. [Google Scholar] [CrossRef]
- Ben Mabrouk, A.; Ben Mohamed, M.L. On some critical and slightly super-critical sub-superlinear equations. Far East J. Appl. Math. 2006, 23, 73–90. [Google Scholar]
- Mabrouk, A.B.; Ben Mohamed, M.L. Nodal solutions for some nonlinear elliptic equations. Appl. Math. Comput. 2007, 186, 589–597. [Google Scholar] [CrossRef]
- Mabrouk, A.B.; Ben Mohamed, M.L.; Omrani, K. Finite difference approximate solutions for a mixed sub-superlinear equation. Appl. Math. Comput. 2007, 187, 1007–1016. [Google Scholar] [CrossRef]
- Berestycki, H.; Lions, P.L. Nonlinear scalar field equations I and II. Arch. Rat. Anal. 1983, 82, 333–345, 347–375. [Google Scholar]
- Chteoui, R.; Ben Mabrouk, A.; Ounaies, H. Existence and properties of radial solutions of a sublinear elliptic equation. J. Part. Diff. Eq. 2015, 28, 1–9. [Google Scholar]
- Strauss, W.A. Existence of solitary waves in higher dimensions. Commun. Math. Phys. 1977, 55, 149–162. [Google Scholar] [CrossRef]
- Quaas, A.; Sirakov, B. Existence and non-existence results for fully nonlinear elliptic systems. Indiana Univ. Math. J. 2009, 58, 751–788. [Google Scholar] [CrossRef] [Green Version]
- Zhou, S.; Cheng, X. Numerical solution to coupled nonlinear Schrödinger equations on unbounded domains. Math. Comput. Simul. 2010, 80, 2362–2373. [Google Scholar] [CrossRef]
- Pinar, Z.; Deliktas, E. Solution behaviors in coupled Schrödinger equations with full-modulated nonlinearities. AIP Conf. Proc. 2017, 1815, 080019. [Google Scholar]
- Ping, L.; Lou, S.Y. Coupled nonlinear Schrödinger equation: Symmetries and exact solutions. Commun. Theor. Phys. 2009, 51, 27–34. [Google Scholar] [CrossRef]
- Bezia, A.; Ben Mabrouk, A.; Betina, K. Lyapunov-Sylvester operators for (2+1)-Boussinesq equation. Electron. J. Differ. Equ. 2016, 286, 1–19. [Google Scholar]
- Aminikhah, H.; Pournasiri, F.; Mehrdoust, F. A novel effective approach for systems of coupled Schrödinger equation. Pramana J. Phys. Indian Acad. Sci. 2016, 86, 19–30. [Google Scholar] [CrossRef]
- Rasouli, S.H.; Choubin, M. The Nehari manifold approach for a class of n × n nonlinear elliptic systems. Monatshefte Math. 2014, 173, 605–623. [Google Scholar] [CrossRef]
- Liu, H. Ground states of linearly coupled Schrödinger systems. Electron. J. Differ. Equ. 2017, 5, 1–10. [Google Scholar]
- Guo, Y.; Wang, J.M.; Zhao, D.X. Stability of an interconnected Schrödinger-heat system in a torus region. Math. Methods Appl. Sci. 2016, 39, 3735–3749. [Google Scholar] [CrossRef]
- Benrhouma, M. Existence and uniqueness of solutions for a singular semilinear elliptic system. Nonlinear Anal. 2014, 107, 134–146. [Google Scholar] [CrossRef]
- Benrhouma, M. Existence of solutions for a semilinear elliptic system. ESAIM Control Optim. Calc. Var. 2013, 19, 574–586. [Google Scholar] [CrossRef] [Green Version]
- Saanouni, T. A note on coupled focusing nonlinear Schrödinger equations. J. Appl. Anal. Int. J. 2016, 95, 2063–2080. [Google Scholar] [CrossRef] [Green Version]
- Chteoui, R.; Aljohani, A.F.; Ben Mabrouk, A. Classification and simulation of chaotic behaviour of the solutions of a mixed nonlinear Schrödinger system. Electron. Res. Arch. 2020. [Google Scholar] [CrossRef]
- Kajikyia, R. Necessary and sufficient condition for existence and uniqueness of nodal solutions to sublinear elliptic equations. Adv. Diff. Equ. 2001, 11, 1317–1346. [Google Scholar]
- Kajikiya, R. Infinitely many radially symmetric solutions of certain semilinear elliptic equations. Hiroshima Math. J. 1991, 21, 557–585. [Google Scholar] [CrossRef]
- Kajikiya, R. Existence and asymptotic behavior of nodal solutions for semilinear elliptic equations. J. Differ. Equ. 1993, 106, 238–256. [Google Scholar] [CrossRef] [Green Version]
- Kajikiya, R. Nodal solutions of superlinear elliptic equations in symmetric domains. Adv. Math. Sci. Appl. 1993, 3, 219–266. [Google Scholar]
- Kajikiya, R. A critical point theorem related to the symmetric mountain pass lemma and its applications to elliptic equations. J. Funct. Anal. 2005, 225, 352–370. [Google Scholar] [CrossRef] [Green Version]
- Kajikiya, R. Radially symmetric solutions of semilinear elliptic equations, existence and Sobolev estimates. Hiroshima Math. J. 1991, 21, 111–161. [Google Scholar] [CrossRef]
- Kajikiya, R.; Tanaka, K. Existence of infinitely many solutions for some superlinear elliptic equations. J. Math. Anal. Appl. 1990, 149, 313–321. [Google Scholar] [CrossRef] [Green Version]
- Kajikiya, R. Multiple solutions of sublinear Lane-Emden elliptic equations. Calc. Var. 2006, 26, 29–48. [Google Scholar] [CrossRef]
- Chteoui, R.; Ben Mabrouk, A.; Cattani, C. Mixed concave-convex sub-superlinear Schrödinger equation: Survey and development of some new cases. In Nonlinear Analysis and Global Optimization; Rassias, T.M., Pardalos, P.M., Eds.; Springer Optimization and Its Applications: Berlin/Heidelberg, Germany, 2021; Volume 167. [Google Scholar] [CrossRef]
- Chteoui, R.; Aljohani, A.F.; Ben Mabrouk, A. Lyapunov-Sylvester computational method for numerical solutions of a mixed cubic-superlinear Schrödinger system. Eng. Comput. 2021. [Google Scholar] [CrossRef]
- Ambrosetti, A.; Rabinowitz, P.H. Dual variational methods in critical point theory and applications. J. Funct. Anal. 1973, 14, 349–381. [Google Scholar] [CrossRef] [Green Version]
- Ekeland, I. On the variational principle. J. Math. Anal. Appl. 1974, 47, 324–353. [Google Scholar] [CrossRef] [Green Version]
- Ekeland, I. Nonconvex minimization problems. Bull. Am. Math. Soc. New Ser. 1979, 1, 443–474. [Google Scholar] [CrossRef] [Green Version]
- Nehari, Z. On a class of nonlinear second-order differential equations. Trans. Am. Math. Soc. 1960, 95, 101–123. [Google Scholar] [CrossRef]
- Nehari, Z. Characteristic values associated with a class of nonlinear second-order differential equations. Acta Math. 1961, 105, 141–175. [Google Scholar] [CrossRef]
- Nehari, Z. A nonlinear oscillation problem. J. Differ. Equ. 1969, 5, 452–460. [Google Scholar] [CrossRef] [Green Version]
- Robinson, J. A survey of Ekeland’s Variational Principle and Related Theorems and Applications. Master’s Thesis, University of Nevada, Las Vegas, NV, USA, 2014. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chteoui, R.; Aljohani, A.F.; Ben Mabrouk, A. Synchronous Steady State Solutions of a Symmetric Mixed Cubic-Superlinear Schrödinger System. Symmetry 2021, 13, 190. https://doi.org/10.3390/sym13020190
Chteoui R, Aljohani AF, Ben Mabrouk A. Synchronous Steady State Solutions of a Symmetric Mixed Cubic-Superlinear Schrödinger System. Symmetry. 2021; 13(2):190. https://doi.org/10.3390/sym13020190
Chicago/Turabian StyleChteoui, Riadh, Abdulrahman F. Aljohani, and Anouar Ben Mabrouk. 2021. "Synchronous Steady State Solutions of a Symmetric Mixed Cubic-Superlinear Schrödinger System" Symmetry 13, no. 2: 190. https://doi.org/10.3390/sym13020190
APA StyleChteoui, R., Aljohani, A. F., & Ben Mabrouk, A. (2021). Synchronous Steady State Solutions of a Symmetric Mixed Cubic-Superlinear Schrödinger System. Symmetry, 13(2), 190. https://doi.org/10.3390/sym13020190





