Bootstrapped Motion of an Agent on an Adaptive Resource Landscape

Abstract

We theoretically show that isolated agents that locally and symmetrically consume resources and sense positive resource gradients can generate constant motion via bootstrapped resource gradients in the absence of any externally imposed gradients, and we show a realization of this motion using robots. This self-generated agent motion can be coupled with neighboring agents to act as a spontaneously broken symmetry seed for emergent collective dynamics. We also show that in a sufficiently weak externally imposed gradient, it is possible for an agent to move against an external resource gradient due to the local resource depression on the landscape created by an agent. This counter-intuitive boot-strapped motion against an external gradient is demonstrated with a simple robot system on an light-emitting diode (LED) light-board.

1. Introduction

In biology, it is often assumed that agents do not actively influence their environment, but rather passively respond to the environment. For example, at the simplest level of chemotaxis [1,2,3,4], it is assumed that agents sense gradients and move along the gradients, but do not generate or influence the gradients themselves. While the agents’ movements are changed by chemotaxis, in the absence of any gradients, it is assumed that the agents still have a zero-gradient inherent speed.

However, chemotactic agents, such as Escherichia coli and Dictyostelium, can explore complex topologies, such as mazes and fractals, much more rapidly and efficiently than a response to an imposed gradient alone would predict [5,6]. This occurs if agents do not just follow an imposed gradient passively, but also influence the surrounding environment by consuming and producing chemicals [7,8,9]. This emergent self-generated gradient creates a back-reaction, which helps the agents navigate through non-trivial complex geometries.

This paper presents a fundamental mechanism involving spontaneous symmetry breaking by which individual agents can self-generate motion to solve the complex topologies that nature presents and even show the ability to back out of a dead-end path that would otherwise trap an agent. The next step will be to let the agents interact with each other and look for emergent large-scale symmetry breaking.

2. Approach

We present a scenario where an agent consumes local resources symmetrically and responds to the self-generated resource depression by moving up an emergent self-generated gradient. This emergent self-generated gradient creates a back-reaction, which the agents then use to move away from their self-generated resource depression. In effect, they run from their shadow, but the shadow follows them. The analysis predicts that an agent initially at rest with no inherent motion can bootstrap to a constant motion under certain conditions of resource consumption, resource recovery, and sensitivity to resources. The transition from “zero-point” fluctuations to a constant velocity vector is a spontaneous symmetry-breaking process [10].

There are two kinds of resource environments that show this bootstrap effect. The actively recovering environment, “recovering environment”, can be considered as one where each pixel of the environment has the same recovery time $\tau$ and the resource does not diffuse. The resource could be considered as trees that are cut down and grow back at some rate, for example. The other environment is a passively diffusing or “diffusive recovering”, and can be viewed as one where the resource diffuses in from an infinite source with some characteristic diffusion coefficient D. This kind of resource could be considered as oil that is removed through a well in a very large field, and the oil diffuses back into the well. The physical systems of interest are described in Figure 1.

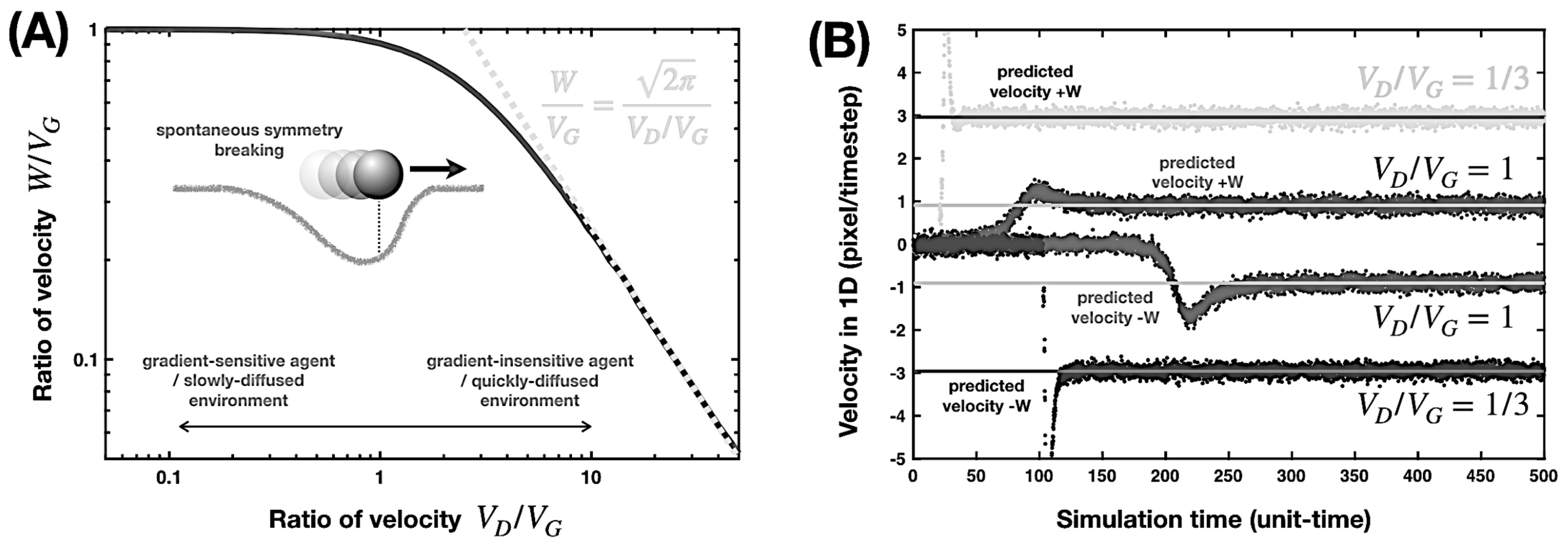
2.1. Actively Recovering Environment

It is assumed that an agent in the presence of a resource field $I(\overrightarrow{x},t)$ will follow the field gradient with the velocity vector ${\partial }_t\overrightarrow{X}$ given by:

$${\partial }_t\overrightarrow{X}=\kappa \nabla I(\overrightarrow{x},t){|}_{\overrightarrow{x}=\overrightarrow{X}\left(t\right)},$$

(1)

where $\overrightarrow{X}\left(t\right)$ is the position of the agent at time t and $\kappa$ is its sensitivity to the resource gradient. For a recovering environment of infinitely large size and local relaxation time $\tau$, the agent influences the environment around it with rate $\gamma$ and radius of influence $\sigma$:

$${\partial }_{t}I(\overrightarrow{x},t)-\frac{1}{\tau }\left(I_{*}-I(\overrightarrow{x},t)\right)=-\gamma e^{-\frac{{\left(\overrightarrow{x}-\overrightarrow{X}\left(t\right)\right)}^2}{2{\sigma }^2}},$$

(2)

$I_{*}$ is the natural homogeneous amount of resources in the environment when no agent is present. The environment’s response can be obtained from:

$$I(\overrightarrow{x},t)=I_{*}-\gamma {\int }_{{\mathbb{R}}^{\mathcal{D}}}{d}^{\mathcal{D}}{\overrightarrow{x}}^{\prime }{\int }_{\mathbb{R}}d{t}^{\prime }G(\overrightarrow{x}-{\overrightarrow{x}}^{\prime },t-t^{\prime })e^{-\frac{{\left({\overrightarrow{x}}^{\prime }-\overrightarrow{X}\left(t^{\prime }\right)\right)}^2}{2{\sigma }^2}},$$

(3)

where $\mathcal{D}$ is the number of spatial dimensions, Green’s function is given by

$$G(\overrightarrow{x}-{\overrightarrow{x}}^{\prime },t-t^{\prime })=\mathsf{\Theta }(t-t^{\prime }){\delta }^{\left(\mathcal{D}\right)}(\overrightarrow{x}-{\overrightarrow{x}}^{\prime })e^{-\frac{t-t^{\prime }}{\tau }},$$

(4)

${\delta }^{\mathcal{D}}$ is the $\mathcal{D}$-dimensional Dirac delta function, and $\mathsf{\Theta }$ is the Heaviside function:

$$\mathsf{\Theta }(\xi \le 0)=0,\mathsf{\Theta }(\xi >0)=1.$$

(5)

There exists a constant non-zero-velocity solution in the $\widehat{k}$-direction, $\overrightarrow{X}\left(t\right)=Wt\widehat{k}$, where $W>0$. Using this relation to calculate the resource field from Equations (3) and (4), and using the result in Equation (1) and integrating ${\int }_{{\mathbb{R}}^{\mathcal{D}}}{d}^{\mathcal{D}}{\overrightarrow{x}}^{\prime }$, we arrive at:

$$W=\frac{\kappa \gamma }{{\sigma }^2}{\int }_{{\mathbb{R}}^{+}}d{t}^{″}\left(W{t}^{″}\right)e^{-\frac{t^{″}}{\tau }-\frac{{\left(W{t}^{″}\right)}^2}{2{\sigma }^2}},$$

(6)

where $t^{″}=t-t^{\prime }$. The derivation for this equation is given in Appendix A. After the integration ${\int }_{{\mathbb{R}}^{+}}d{t}^{\prime }$ and rearranging, the terms yield:

$$\frac{1}{2}{\left(\frac{V_R}{V_G}\right)}^2={\left(\frac{V_R}{\sqrt{2}W}\right)}^2\left(1-\sqrt{\pi }\left(\frac{V_R}{\sqrt{2}W}\right)e^{{\left(\frac{V_R}{\sqrt{2}W}\right)}^2}\mathrm{Erfc}\left(\frac{V_R}{\sqrt{2}W}\right)\right),$$

(7)

where Erfc is the complementary error function, defining the recovering velocity $V_R=\sigma /\tau$ and the gradient-following velocity $V_G=\sqrt{\kappa \gamma }$. From the right-hand side (R.H.S.), using the inequality for variable $\xi =V_R/\sqrt{2}W\ge 0$:

$$\frac{1}{2}\ge {\xi }^2\left(1-\sqrt{\pi }\xi e^{{\xi }^2}\mathrm{Erfc}\left(\xi \right)\right){|}_{\xi \ge 0}\ge 0,$$

(8)

yields the condition for the $W>0$ solution to exist:

$$\frac{1}{2}{\left(\frac{V_R}{V_G}\right)}^2<\frac{1}{2}\Rightarrow V_R<V_G.$$

(9)

Physically, this means that the bootstrap motion of constant velocity will not appear if the agent is not gradient-sensitive enough or if the environment recovery rate is too fast. Near the pitchfork transition $V_G\gg V_G-V_R>0$, the “critical behavior” is described by a scaling law $W/V_G\propto {(1-V_R/V_G)}^{1/2}$ [11], which is shown in Figure 2A. In the limit $V_R\ll V_G$, when the agent is very gradient-sensitive or the environment recovery rate is extremely slow, the solution is approximately $W\approx V_G$.

For general values of $V_R$ and $V_G$, the bootstrap velocity W can be evaluated numerically (see Figure 2A). A simulation was performed to verify the theoretical analysis, with a small randomness added to the velocity to trigger the symmetry breaking (see Figure 2B,C). The details for the simulation are given in Appendix B.

2.2. Passively Diffusive Environment

For a diffusive environment that is infinitely large and initially homogeneous $I(\overrightarrow{x},t\to -\infty )=I_{*}$, the field Equation (2) is changed to:

$${\partial }_{t}I(\overrightarrow{x},t)-D{\nabla }^{2}I(\overrightarrow{x},t)=-\gamma e^{-\frac{{\left(\overrightarrow{x}-\overrightarrow{X}\left(t\right)\right)}^2}{2{\sigma }^2}},$$

(10)

where D is the diffusion coefficient of the resource. The environment response can be similarly obtained from (3), but using Green’s function given by

$$G(\overrightarrow{x}-{\overrightarrow{x}}^{\prime },t-t^{\prime })=\mathsf{\Theta }(t-t^{\prime })\frac{e^{-\frac{{(\overrightarrow{x}-{\overrightarrow{x}}^{\prime })}^2}{4D(t-t^{\prime })}}}{{\left(4\pi D(t-t^{\prime })\right)}^{\mathcal{D}/2}}.$$

(11)

For the sake of simplicity, consider a one-dimensional space $\mathcal{D}=1$ and solve for a constant non-zero velocity solution $X\left(t\right)=Wt$, where $W>0$. Using this relation to calculate the chemical field from Equations (3) and (11), then putting this result into Equation (1), we arrive at:

$$W=\frac{2}{\sqrt{\pi }}\kappa \gamma {\int }_{\mathbb{R}}d{x}^{\prime }{\int }_{{\mathbb{R}}^{+}}d{t}^{″}\frac{x^{\prime }{e}^{-\frac{x^{\prime 2}}{4D{t}^{″}}-\frac{{\left(x^{\prime }-W{t}^{″}\right)}^2}{2{\sigma }^2}}}{{\left(4\pi D{t}^{″}\right)}^{3/2}},$$

(12)

where $t^{″}=t-t^{\prime }$. After integration ${\int }_{\mathbb{R}}d{x}^{\prime }$ and a change of variable $t^{‴}=2D{t}^{″}/{\sigma }^2$, this equation is equivalent to:

$$1={\left(\frac{V_G}{V_D}\right)}^2{\int }_{{\mathbb{R}}^{+}}d{t}^{‴}\frac{t^{‴}{e}^{-\frac{1}{2}{\left(\frac{W}{V_D}\right)}^2\frac{t^{‴2}}{1+t^{‴}}}}{{\left(1+t^{‴}\right)}^{3/2}},$$

(13)

defining the diffusive velocity $V_D=2D/\sigma$ and noting that $V_G=\sqrt{\kappa \gamma }$ is the gradient-following velocity.

When $W\ll V_D$, Equation (13) can be approximated as:

$$1\approx {\left(\frac{V_G}{V_D}\right)}^2{\int }_{{\mathbb{R}}^{+}}d{t}^{‴}\frac{e^{-\frac{1}{2}{\left(\frac{W}{V_D}\right)}^2{t}^{‴}}}{\sqrt{t^{‴}}}\Rightarrow W\approx \sqrt{2\pi }{\left(\frac{V_G}{V_D}\right)}^2{V}_D,$$

(14)

which can only be satisfied in the regime $V_G\ll V_D$, which physically corresponds to the fast-diffusion/gradient-insensitive limit.

When $W\gg V_D$, again, the approximation yields:

$$1\approx {\left(\frac{V_G}{V_D}\right)}^2{\int }_{{\mathbb{R}}^{+}}d{t}^{‴}{t}^{‴}{e}^{-\frac{1}{2}{\left(\frac{W}{V_D}\right)}^2{t}^{‴2}}\Rightarrow W\approx V_G,$$

(15)

which can only be satisfied in the regime $V_G\gg V_D$. This physically corresponds to the slow-diffusion/gradient-sensitive limit. It should be noted that this is in agreement with the previous section, as the field dynamics disappear when $\tau \to \infty$ and $D\to 0$.

For general values of $V_D$ and $V_G$, the bootstrap velocity W can be evaluated numerically (see Figure 3A). Simulations to verify the theoretical analysis were also done, with a small randomness in velocity to trigger the symmetry breaking (see Figure 3B). The details for the simulation are given in Appendix C.

3. Retrograde Movement against an Applied Gradient

Up to this point, all isolated agents generate a bootstrapped gradient and follow it. In the presence of other agents, externally applied gradients can be imposed on an agent. Rather non-intuitively, in the presence of an externally applied, sufficiently weak gradient, the combination of the imposed slope of the gradient $\nabla I_{*}$ and the local resource hole being dug by an agent makes it possible for an agent to go against the gradient $\overrightarrow{V}\uparrow \downarrow \nabla I_{*}$. Figure 4A,B are illustrations of how propagation against an external resource gradient can happen.

Mathematically, consider a constant slope $\nabla I_{*}=-S\widehat{k}$ where $S\ge 0$ in the $\widehat{k}$-direction; we will look for the solution $X\left(t\right)=Wt\widehat{k}$ where $W>0$. We will also estimate the maximum value of S for which propagation against the gradient is still possible at some simple limits.

3.1. Actively Recovering Environment

For the recovering environment, in the present of the applied gradient, Equation (6) becomes:

$$W+\kappa S=\frac{\kappa \gamma }{{\sigma }^2}{\int }_{{\mathbb{R}}^{+}}d{t}^{\prime }\left(W{t}^{\prime }\right)e^{-\frac{t^{\prime }}{\tau }-\frac{{\left(W{t}^{\prime }\right)}^2}{2{\sigma }^2}}.$$

(16)

After the integration ${\int }_{{\mathbb{R}}^{+}}d{t}^{\prime }$ and rearranging the terms, this yields:

$$\frac{\sqrt{2}\kappa S}{V_R}=-\frac{1}{\left(\frac{V_R}{\sqrt{2}W}\right)}+\frac{\left(\frac{V_R}{\sqrt{2}W}\right)}{\frac{1}{2}{\left(\frac{V_R}{V_G}\right)}^2}\left(1-\sqrt{\pi }\left(\frac{V_R}{\sqrt{2}W}\right)e^{{\left(\frac{V_R}{\sqrt{2}W}\right)}^2}\mathrm{Erfc}\left(\frac{V_R}{\sqrt{2}W}\right)\right).$$

(17)

Note that $V_R=\sigma /\tau$ is the recovering velocity and $V_G=\sqrt{\kappa \gamma }$ is the gradient-following velocity. This equation allows one to find the bootstrap velocity W that an agent can have against an external gradient S.

The maximum gradient $\max \left(S\right)$ against which an agent can move is determined from the largest value of the function of variable $\xi =V_R/\sqrt{2}W\ge 0$ on the R.H.S. of (17):

$$\max \left(S\right)=\frac{V_R}{\sqrt{2}\kappa }\max \left(-\frac{1}{\xi }+\frac{\xi \left(1-\sqrt{\pi }\xi e^{{\xi }^2}\mathrm{Erfc}\left(\xi \right)\right)}{\frac{1}{2}{\left(\frac{V_R}{V_G}\right)}^2}\right){|}_{\xi \ge 0}.$$

(18)

In the limit $V_R\ll V_G$, when the agent is very gradient-sensitive or the environment recovery rate is extremely slow, inside the $\max (\dots )$ on the R.H.S. of (18), we can neglect the first term $-1/\xi$. The upper value of the nominator of the second term can be found numerically to be $\approx 0.25$ at around $\xi \approx 0.82$, indicating that the maximum slope for a cell to go against is $\max \left(S\right)\approx 0.35\gamma /V_R$.

3.2. Passively Diffusive Environment

The presence of an external gradient in the diffusive environment physically corresponds to a constant flux ${\overrightarrow{J}}_{*}=-D\nabla I_{*}=DS\widehat{k}$ of a resource diffusing in the $\widehat{k}$-direction. For this setting, in one-dimensional space $\mathcal{D}=1$, Equation (12) becomes:

$$W+\kappa S=\frac{2\kappa \gamma }{\sqrt{\pi }}{\int }_{\mathbb{R}}d{x}^{\prime }{\int }_{{\mathbb{R}}^{+}}d{t}^{\prime }\frac{x^{\prime }{e}^{-\frac{x^{\prime 2}}{4D{t}^{\prime }}-\frac{{\left(x^{\prime }-W{t}^{\prime }\right)}^2}{2{\sigma }^2}}}{{\left(4\pi D{t}^{\prime }\right)}^{3/2}}.$$

(19)

After the integration ${\int }_{\mathbb{R}}d{x}^{\prime }$ and a change of variable $t^{″}=2D{t}^{\prime }/{\sigma }^2$, this is equivalent to:

$$1+\frac{\kappa S}{W}={\left(\frac{V_G}{V_D}\right)}^2{\int }_{{\mathbb{R}}^{+}}d{t}^{″}\frac{t^{″}{e}^{-\frac{1}{2}{\left(\frac{W}{V_D}\right)}^2\frac{t^{″2}}{1+t^{″}}}}{{\left(1+t^{″}\right)}^{3/2}}.$$

(20)

Note that $V_D=2D/\sigma$ is the diffusive velocity. This equation allows one to find the bootstrap velocity W that an agent can attain against the gradient S.

In the limit $V_G\ll V_D$, which corresponds to the fast-diffusion/gradient-insensitive regime, following (14), we approximate the integral with the assumption $W\ll V_D$, which is consistent with the following result:

$$1+\frac{\kappa S}{W}\approx \sqrt{2\pi }{\left(\frac{V_G}{V_D}\right)}^2\left(\frac{V_D}{W}\right)\Rightarrow W\approx \sqrt{2\pi }{\left(\frac{V_G}{V_D}\right)}^2{V}_D-\kappa S.$$

(21)

Here, the applied gradient only contributes a linear shift to the bootstrap velocity. The maximum applied gradient that still allows $W>0$ is estimated by:

$$\max \left(S\right)=\frac{\sqrt{2\pi }{V}_D}{\kappa }{\left(\frac{V_G}{V_D}\right)}^2.$$

(22)

4. Results: The Robotic Experiment

The theory presented here shows that gradient-following agents influence the surrounding environment, use the resource back-reaction, and can go against an applied resource gradient. It is possible to test these ideas with a form of synthetic life, namely robots rather than living cells, which are quite complex. Further, analog/digital robots can move on analog resource landscapes [12], rather than working with digital simulations alone.

A test of these concepts was done with a physical system consisting of robots on an interactive light-emitting diode (LED) light-board, as shown in Figure 5A. The experimental settings for the three robots are shown in Figure 5B. The robots moved only in response to the local light-intensity gradient at their positions on the LED light-board with rotational noise, as shown in the movie contained in the Supplementary movie smovie01.mp4. The robots influenced the landscape they moved on by locally dimming the light intensity, and the shadow generated by the presence of a robot could recover once the robot moved away. With a constant imposed light-intensity gradient in the background, not only was there bootstrapped field-drive motion, but back-propagation events going against the background gradient were also observed, as shown in Supplementary movie smovie02.mp4. In that experiment, due to rotational noise, one of the robots spontaneously changed its original direction and started going against the gradient with an average bootstrap velocity that was slower than those of the other two, as shown in the trajectory plot in Figure 5C.

5. Conclusions

We have found that, due to spontaneous symmetry breaking, an agent can bootstrap itself to a constant motion via a self-generated gradient in a recovering environment and in a diffusive environment. While the symmetry-breaking process only appears in a certain region of parameter space for an agent in a recovering environment, it always emerges for an agent in a diffusive environment.

There are limitations to this work. The resource field can be depleted without renewal, which makes Equations (2) and (10) become much more complicated. The rate $\gamma$ and the radius of influence $\sigma$ for a biological agent are usually not constants, but are rather functions that depend on the surrounding resource field. We did not consider any of those non-linear effects. We also note that the above mathematical analysis will not be applicable to an agent moving in a liquid medium, since convective effects should be taken into account. Finally, we only considered isolated agents, not a swarm of agents interacting not only with the environment, but with each other. In summary, this work still scratches the surface of a potentially deep topic.