Mixed Convection of Silica–Molybdenum Disulphide/Water Hybrid Nanoliquid over a Rough Sphere

Abstract

A steady combined convective motion over a rough sphere with hybrid nanoparticles is analyzed. We have considered silica (SiO₂) and molybdenum disulphide (MoS₂) nanoadditives which are added in H₂O to form MoS₂–SiO₂/H₂O hybrid nanoliquid. The partial differential equations describing the boundary layer flow characteristics are reduced into non-dimensional form with appropriate non-similar reduction. It should be noted that the governing equations have been written using the conservation laws of mass, momentum and energy. These considered equations allow simulating the analyzed phenomenon using numerical techniques. Implicit finite difference approximation and technique of Quasilinearization are utilized to work out the dimensionless control equations. The influence of various physical characteristics included in this challenge, such as the velocity fields and temperature patterns, is investigated. The study of border gradients is performed, which deals with the skin friction and energy transport strength. The plots of computational outcomes are considered, which ascertain that velocity distribution reduces, whilst coefficient of friction at the surface, energy transport strength and temperature distribution augment for enhancing values of hybrid nanofluid. For enhancing magnitude of combined convection parameter, dimensionless velocity distribution, surface drag coefficient and energy transport strength enhance, while temperature distribution diminishes. High impact of hybrid nanofluid on energy transport strength and the surface friction compared to the host liquid and mono nanofluid in presence/absence of surface roughness is shown. Velocity distribution enhances for rising values of velocity ratio parameter. Enhancing values of frequency parameter rise the friction at the surface and energy transport strength. It is also examined that the hybrid nanofluid has a maximum temperature for the blade-shaped nanoparticles and has a low temperature for the spherical-shaped nanoparticles.

1. Introduction

The transport behavior of nanofluids can be described using, for example, Buongiorno’s model [1] and Tiwari and Das approach [2]. In Buongiorno’s approach, the nanoparticles’ slip velocity is not zero considering seven possible slip phenomena including thermophoresis, Magnus effect, inertia, Brownian motion, diffusiophoresis, gravity and fluid drainage. Tiwari and Das model [2] can be considered as an effective model with formulae for heat conductivity and dynamic viscosity that are greater than in the case of regular liquids. Therefore, Tiwari and Das approach can be considered as a homogeneous model which is different from Buongiorno’s model.

Nanofluid is a combination of host fluid and nano-sized solid particles [3]. Scientists are in search of better type of liquid in order to enhance the thermal efficiency of different engineering systems. Taking into account such investigation, the hybrid nanofluid as a combination of base liquid and several different types of nanoparticles, can have high thermal conductivity compared to mono nanofluid and hybrid nanofluids can be considered as the advanced forms of nanofluid. Hybrid nanofluids have heat transfer applications in numerous engineering fields such as, manufacturing, naval structures, transportation, acoustics, defense, micro fluidics, medical etc. [4,5,6]. Thus, Waini et al. [7] have analyzed the combined convection hybrid nanoliquid circulation about a vertical border and their results reveal that the energy transport strength diminishes in shrinking case. In the work of Dinarvand et al. [8], hybrid nanofluid flow past a wedge by considering titanium and copper nanoparticles has been analyzed. Rostami et al. [5] have scrutinized the combined convection of a hybrid silica-alumina nanofluid and their results ascertain that the hybrid nanofluid has high energy transport strength than the base fluid. Moreover, many other researchers have worked by considering the different combination of nanoparticles for hybrid nanofluids such as, Ag-TiO₂, CuO-MgO, Cu-Al₂O₃ and MWCNTs-Fe₂O₄-SWCNTs, etc. [9,10,11,12,13]. Since, many authors such as Maraj et al. [14], Ghadikolaei et al. [15], Khan et al. [16], etc., have studied the water containing Molybdenum disulphide and Silica nanoparticles, considering the either of one or both nanoparticles. Chemical attributes of molybdenum disulfide including capabilities of lubrication, heat conductivity and thermal capacitance are employed in various engineering systems [17]. In addition, Silicon oxide (silica) is widely applied in energy transport applications and it can be successfully use as nano-inclusions [18]. The work of these authors has motivated us to perform the present research and therefore, we have investigated the current problem.

Some kinds of nanoadditives have been employed by some scientists in theoretical and experimental researches. Among the various types of nanoadditives, one of them is known as molybdenum disulfide nanoadditives. Such nanoadditives are rarely employed in the papers particularly in theoretical researches. MoS₂ is characterized by large band gaps structure which is related to the structure of grapheme and as a result, MoS₂ is employed in different engineering systems [19,20,21,22,23,24,25,26]. Moreover, chemical attributes of MoS₂ can be applied in various mechanical systems [23]. MoS₂ particles have been coated with copper to improve their combination with the copper particles for the sintering [24]. Further, silicon is widely spread element on earth after oxygen [25]. Silicon has very useful attributes that illustrates many different applications of this element in various fields. Silicon chips have essentially changed different technical systems including electronics, space and aviation industry, and others. Silicon is used in photovoltaic panels that characterize the high efficiency and suitability. Silicon oxide (silica) is widely employed in energy transport applications and it can be successfully applied as a nanoadditive [18].

In many branches of science and technology, the notion of mixed convection flow can be applied. Correspondingly, combined convection flows play a crucial role in the operation of thermal processing, such as in heated or cooled enclosures and electrical power supply, ventilation and air conditioning systems in atmospheric and ocean circulation, electronic equipment and thermal distribution in buildings [27,28,29]. In particular, owing to its prevalence in engineering fields, the combined convection flow around the sphere has been stimulated by several researchers. The examination of heat transport in combined convective motion over a sphere helps in polymer and fiber industries. Different investigators have studied a combined convective boundary layer motion over a sphere. Combined convective motion around a solid sphere was studied by Salleh et al. [30], taking Newtonian warming into the consideration and their outcomes exhibit that the dimensionless velocity and temperature patters can be reduced with Pr. In addition, Rashad et al. [31] examined the combined convective motion past a sphere and authors have ascertained that the chemical effects are noticeable for energy transport strength. Further, many researchers also analyzed the combined convective water boundary layer flow over a sphere [32,33].

Many scientists have also examined the hybrid nanofluid circulation over different geometries. Recently, Waini et al. [34] have scrutinized combined convective motion with Cu-Al₂O₃/H₂O nanoliquid past a surface and their results reveal that the surface drag coefficient lessens for opposing buoyancy flow, while it boosts for assisting buoyancy flow. Further, Muhammad et al. [35] have analyzed combined convection over a curved surface with MWCNT-Cu/H₂O hybrid nanofluid and the obtained outcomes ascertain that the fluid velocity enhances for combined convection parameter. Bognar et al. [36] have studied the nanofluid flow over a uniformly moving plate considering different nanoparticles and their outcomes reveal that the values of velocity and temperature are greater for alumina nanoparticles compared to titania and magnetite particles. In addition, Bognar and Hriczo [37] have studied the ferrofluids behavior over a flat sheet under the variable magnetic field influence. They have revealed that a rise of the ferromagnetic parameter characterizes the velocity reduction and temperature augmentation. Many researchers have also worked on the combination of silica and molybdenum nanoparticles by considering various base fluids such as water, ethylene glycol, etc. [38,39].

The one feature that tests micro-irregularities presented in the surface texture, is the surface roughness. The roughness analysis was initiated by Nikuradse [40] where he explored the roughness effects on surface drag coefficient. Owen and Thompson [41] have examined the influence of roughness on energy transport strength, while Dawson and Trass [42] have investigated its influence on Sherwood number. Sedahmed and Shemilt [43] have examined the forced convection behavior owing to the border roughness. Patil et al. [44] have investigated the nanosuspension combined convection motion over a rough sphere and their outcome reveals that with suitable choice of roughness and combined convection parameter the point of separation can be delayed. In addition, Patil et al. [45] have analyzed nanoliquid motion about a moving plate and their outcome shows that the friction at the surface enhances.

Taking into account this brief literature review, it can be found that investigation of the combined convective flow of molybdenum silica/water hybrid nanofluid about a rough sphere has not been studied earlier. The novelty of the present analysis includes the following points:

–

combined convective flow over a rough sphere;

–

impact of molybdenum-silica/water hybrid nanofluid on flow structures and heat patterns;

–

effect of surface roughness on hydro- and thermodynamics.

The modeled governing equations and their boundary constraints are affected to the appropriate non-similar reduction. Further, the obtained relations are attempted for solution transformations by employing the method of Quasilinearization and the implicit finite difference approximation [44,45].

2. Mathematical Analysis

Herein, we investigate the viscous, laminar, incompressible combined convection motion around a sphere. Here R is the sphere size. Let T_w and T_∞ be the temperature at the border and away from the surface. The geometry and the configuration of the flow system are schematically presented in Figure 1. Here x is the curvilinear coordinate over the sphere border, while coordinate y is perpendicular it. The section r(x) explains the contour of the considered object.

The surface roughness is modeled in terms of large frequency and low amplitude sinusoidal waves. The control equations representing the hybrid nanosuspension flow variations are [2,7,42,43,44,45]:

$$\frac{\partial (ru)}{\partial x}+\frac{\partial (rv)}{\partial y}=0$$

(1)

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\frac{{\mu }_{hnf}}{{\rho }_{hnf}}\frac{{\partial }^{2}u}{\partial y^2}+\frac{{\left(\rho \beta \right)}_{hnf}}{{\rho }_{hnf}}g(T-T_{\infty })sin\left(\frac{x}{R}\right)+U_e\frac{d{U}_e}{dx}$$

(2)

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{k_{hnf}}{{\left(\rho c_p\right)}_{hnf}}\frac{{\partial }^{2}T}{\partial y^2}$$

(3)

Prescribed border constraints are

$$\begin{array}{l}\mathrm{At}y=0:u=U_w\left(x\right)=U_0\alpha sin\left(\frac{nx}{R}\right),v=0,T=T_W\\ \mathrm{As}y\to \infty :u\to U_e\left(x\right)=\frac{3}{2}{U}_{\infty }sin\left(\frac{x}{R}\right),T\to T_{\infty }\end{array}\}$$

(4)

Here, u indicates the nanosuspension velocity component over x coordinate, v indicates the nanosuspension velocity component over y axis and hybrid nanofluid temperature is indicated T. Further, ρ_hnf, μ_hnf, (ρc_p)_hnf, (ρβ)_hnf and k_hnf denote the density, viscosity, thermal capacitance, heat expansion coefficient and heat conductivity of the hybrid nanosuspension. Following Khan et al. [36], Devi and Devi [46], Rostami et al. [5] and Waini et al. [7], the chemophysical attributes for mono and hybrid nanosuspensions are provided in

Table 1. Chemo-physical attributes of hybrid nanosuspension [2,5,36,46].

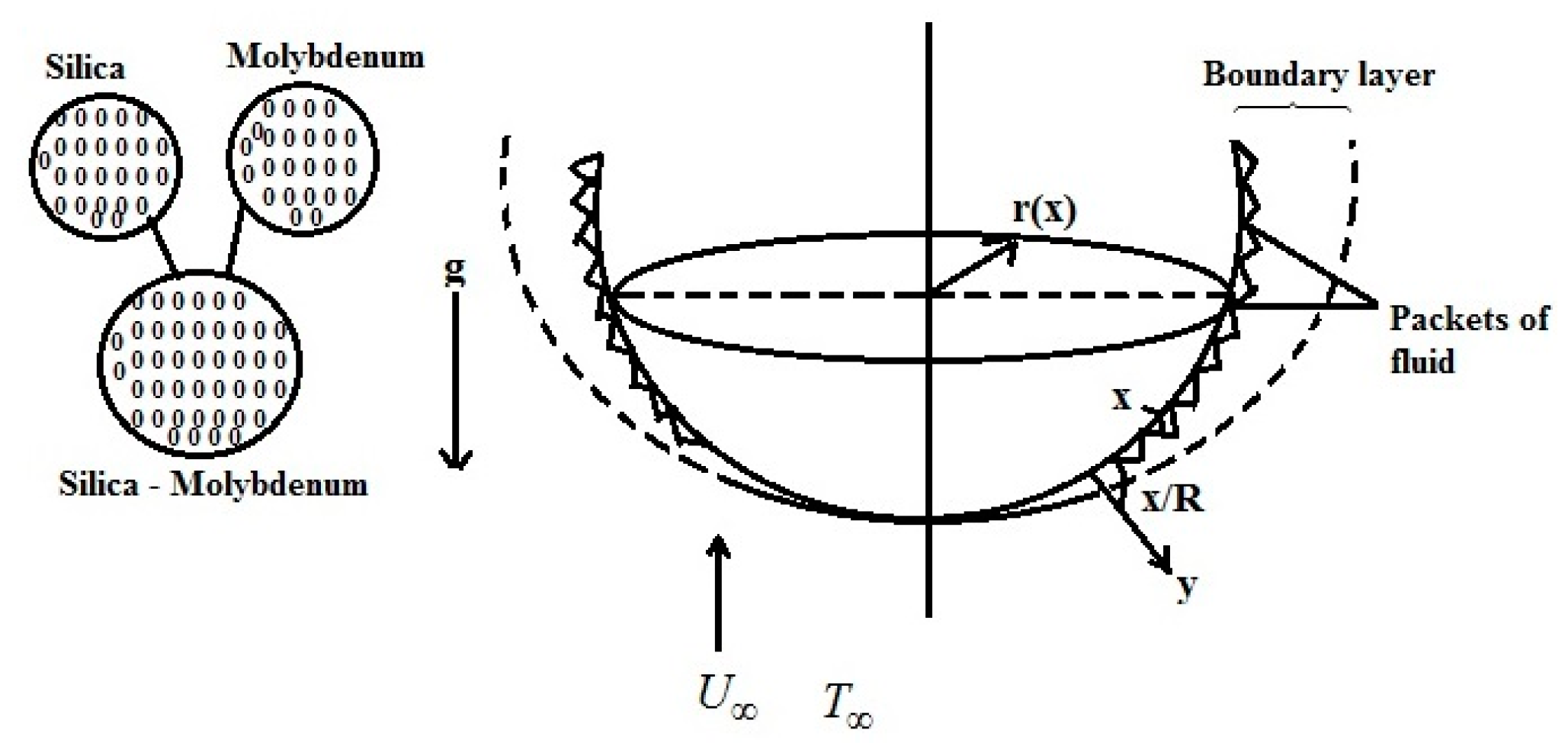
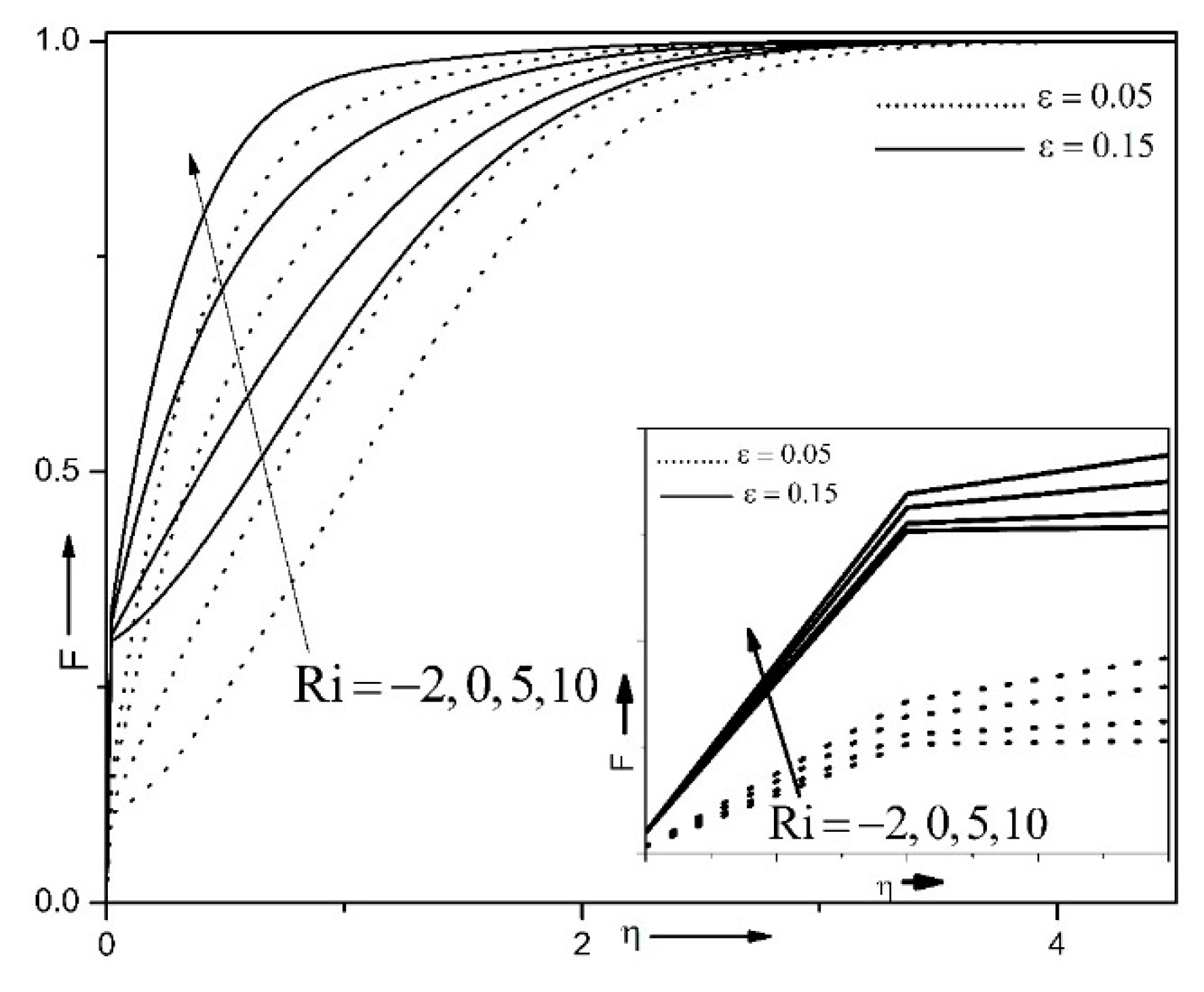
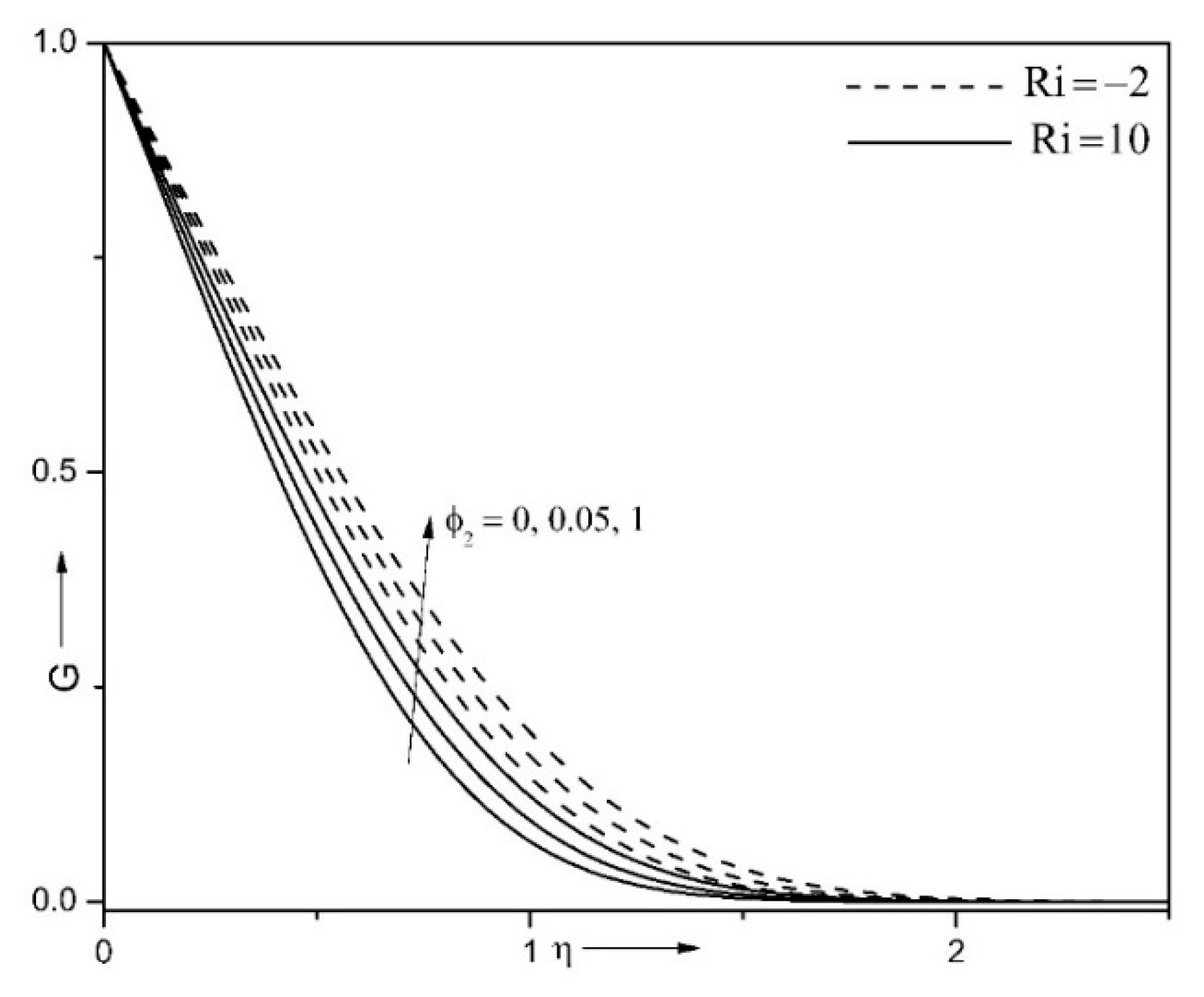
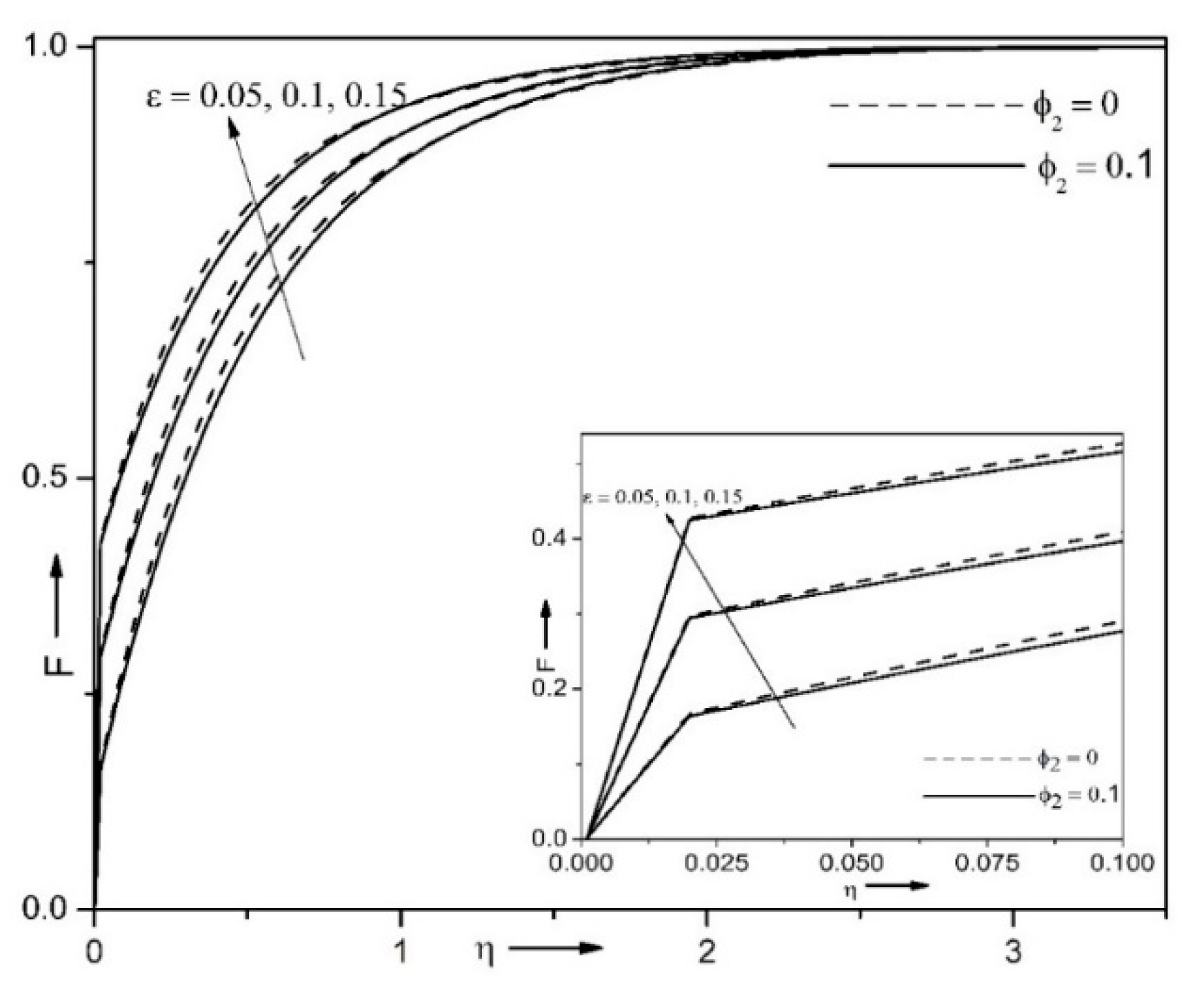
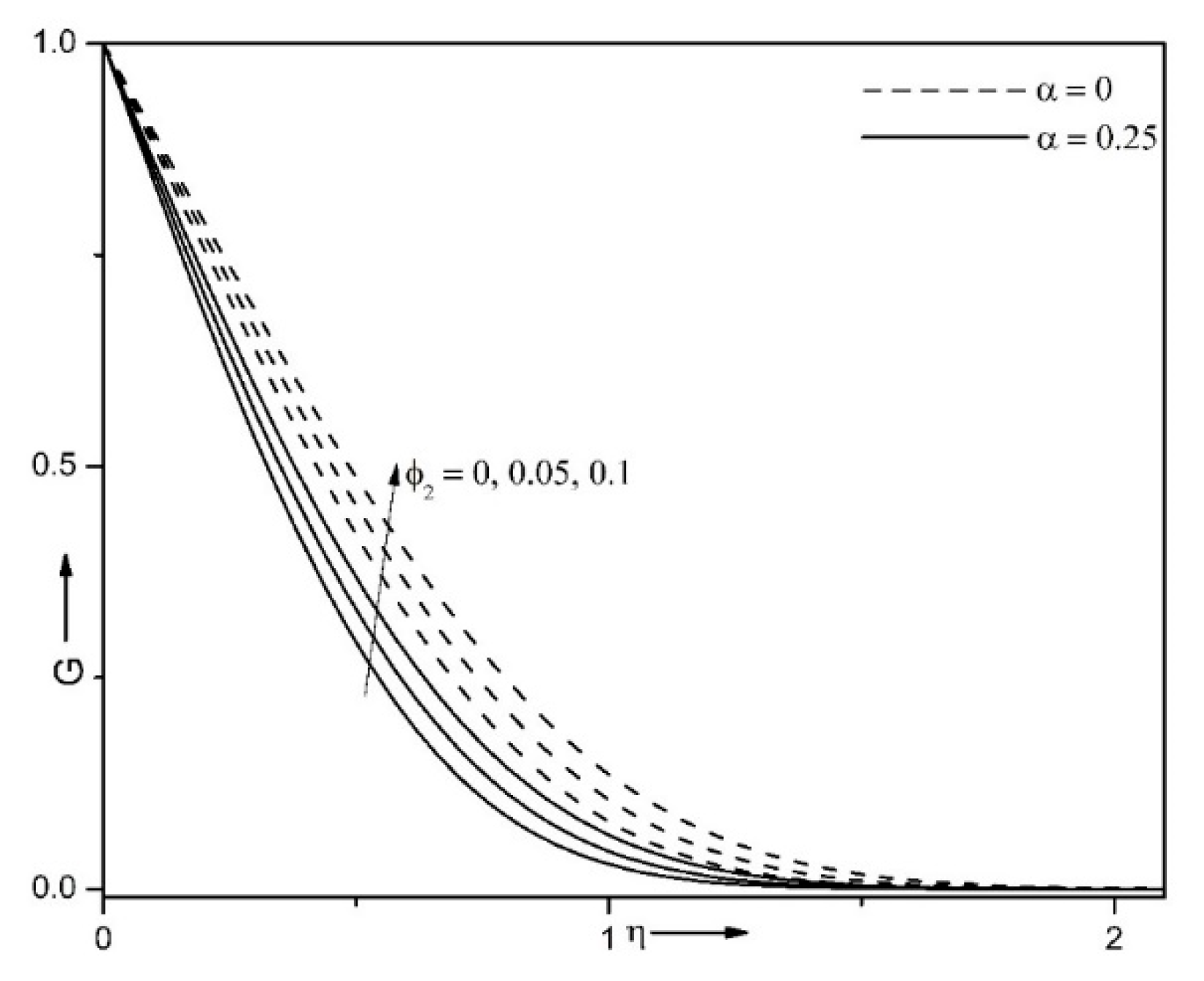
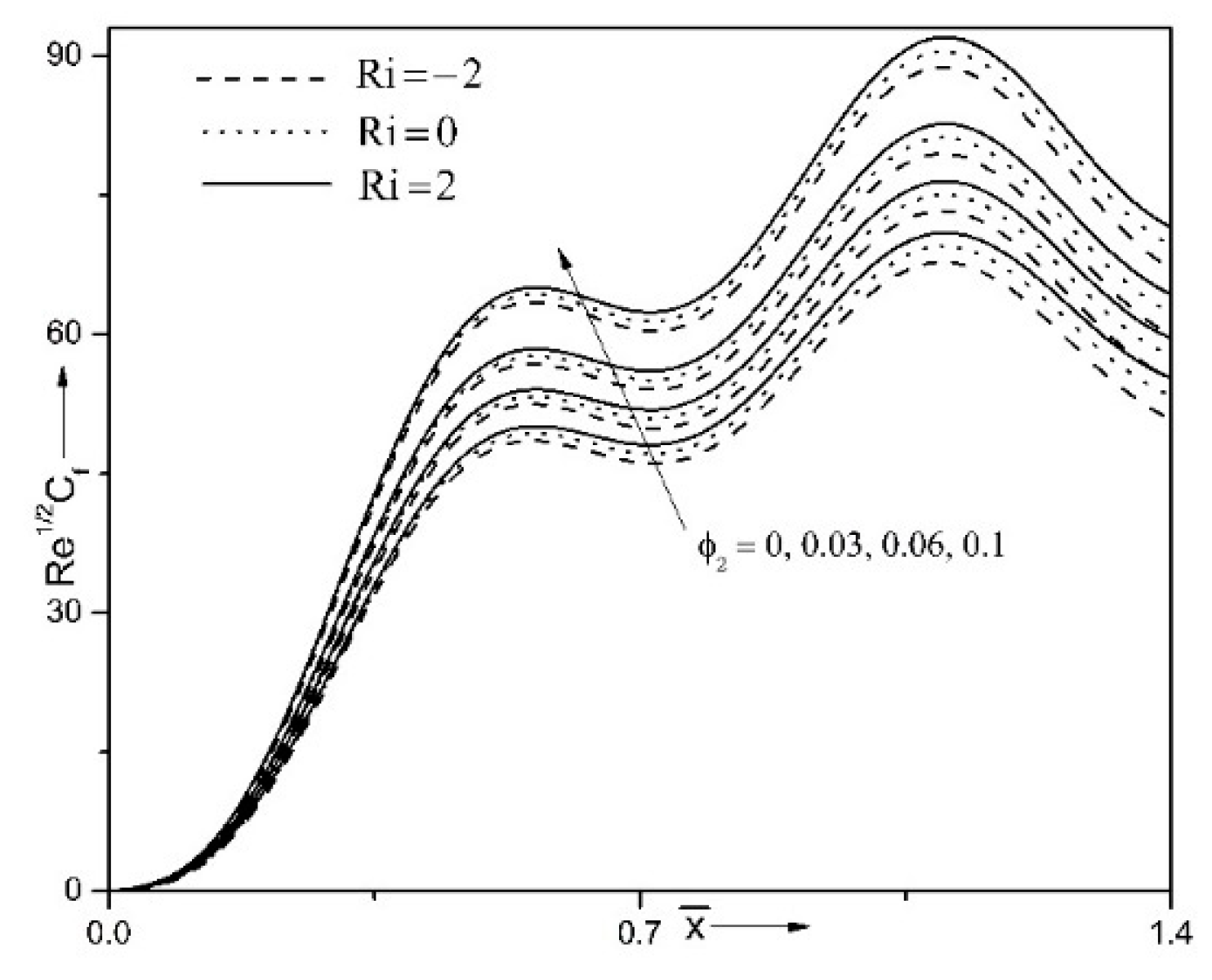
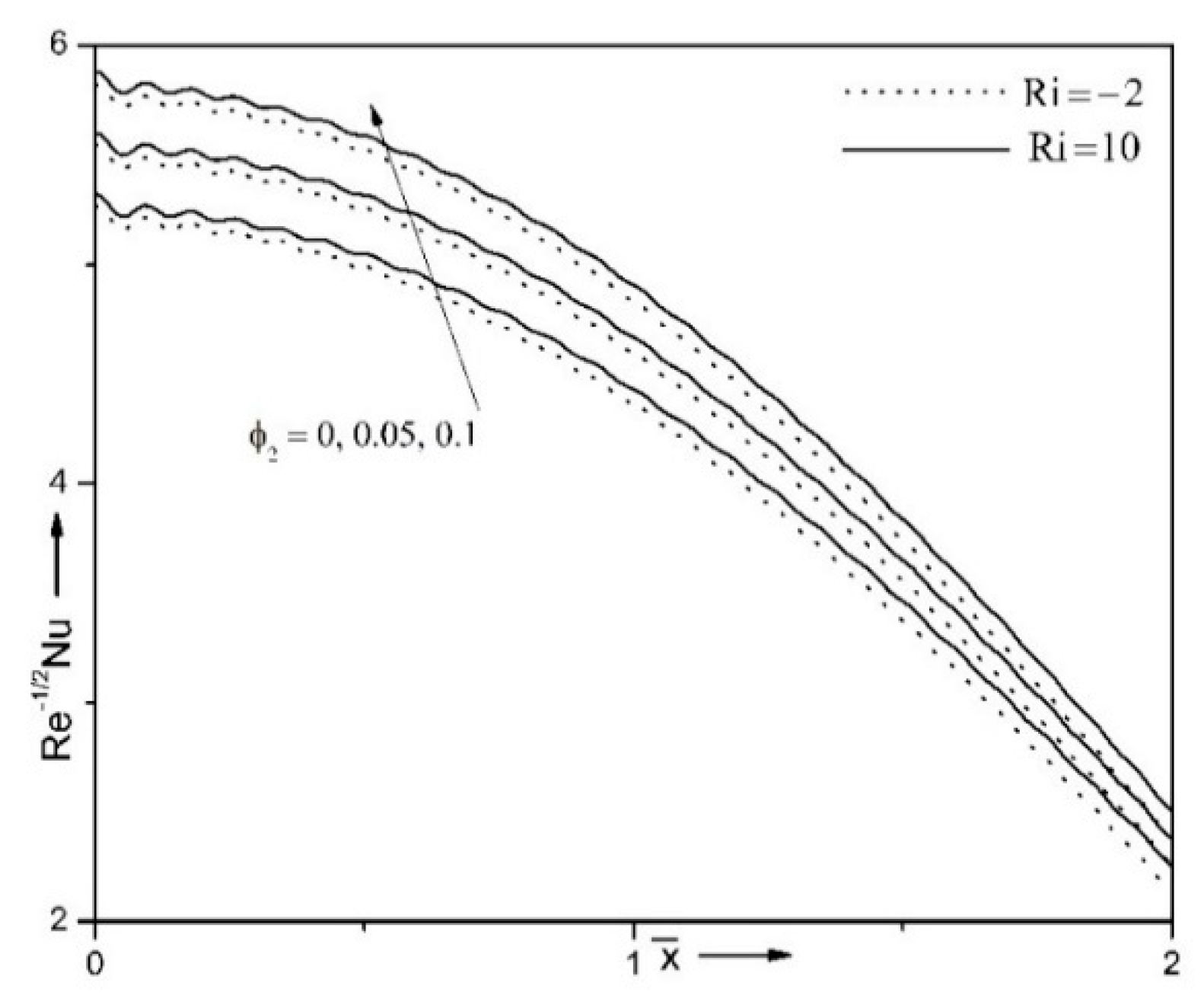
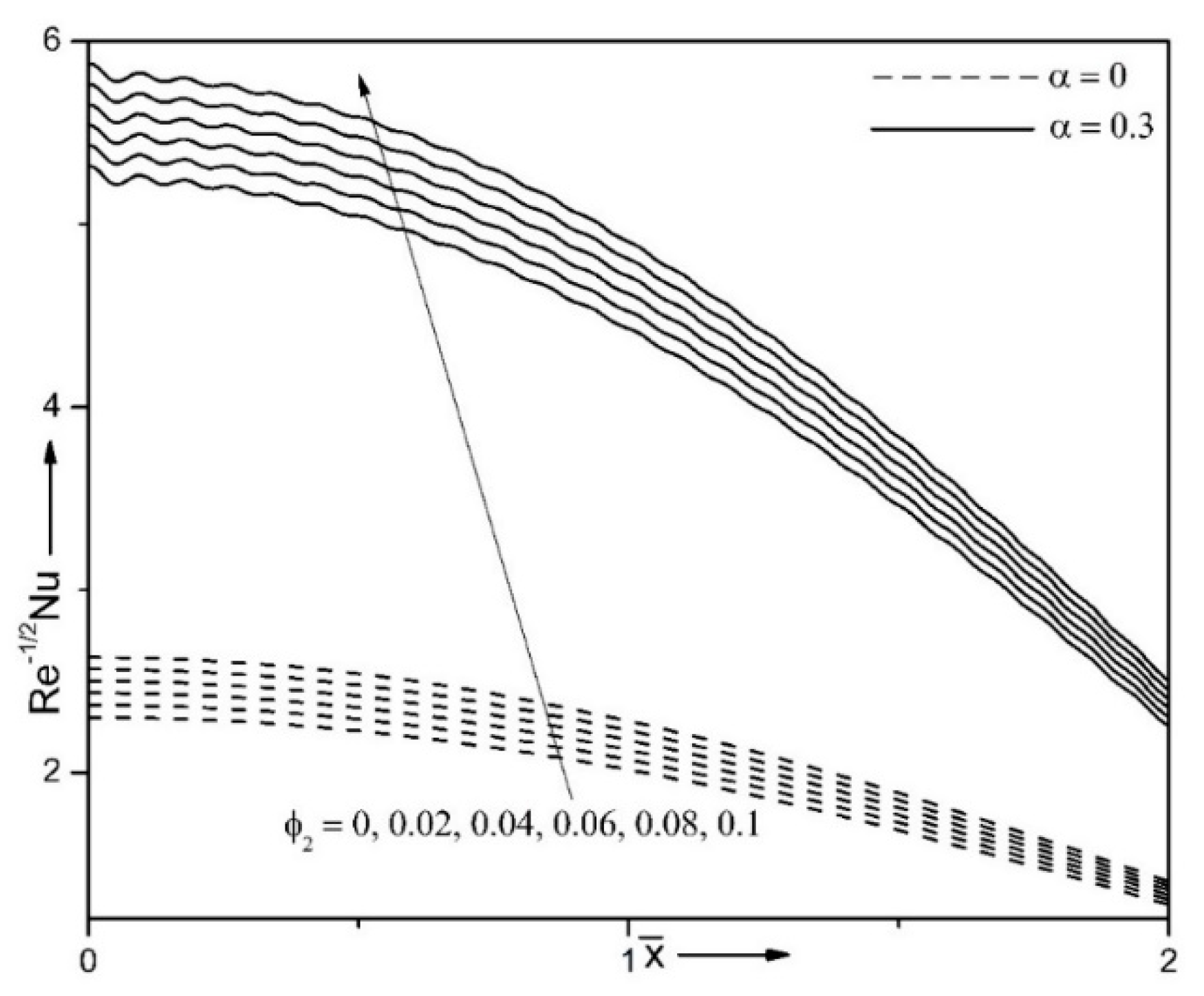
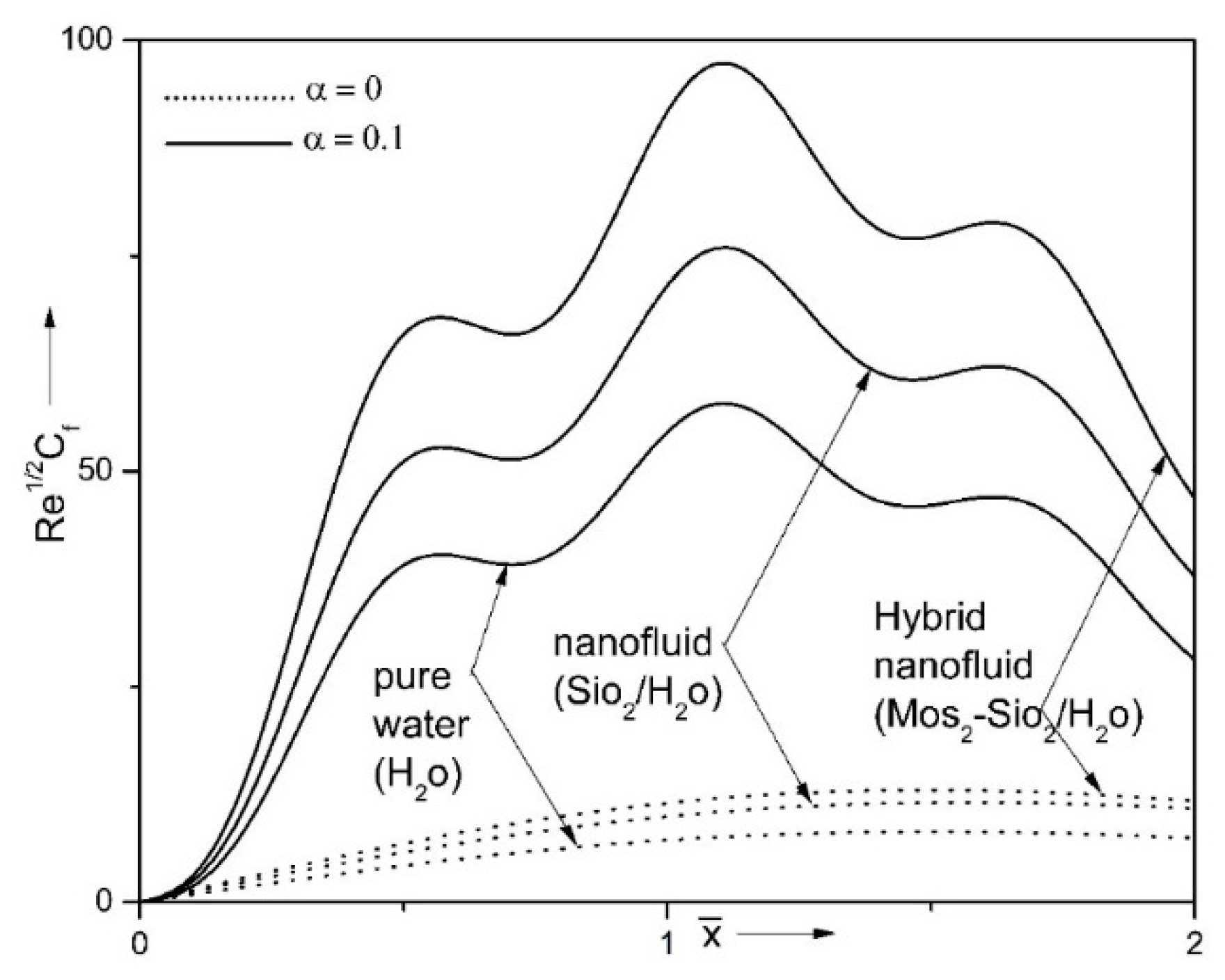
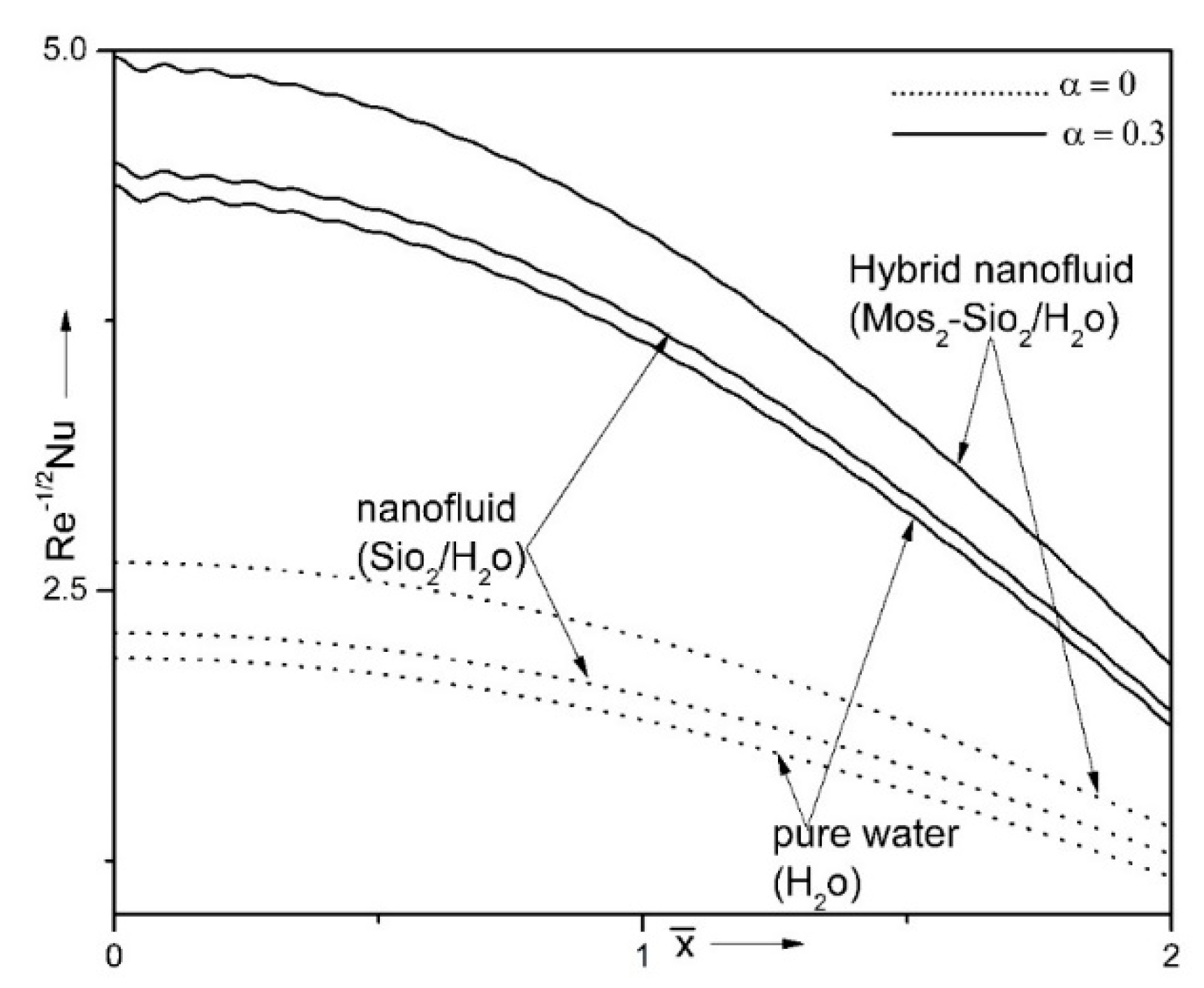
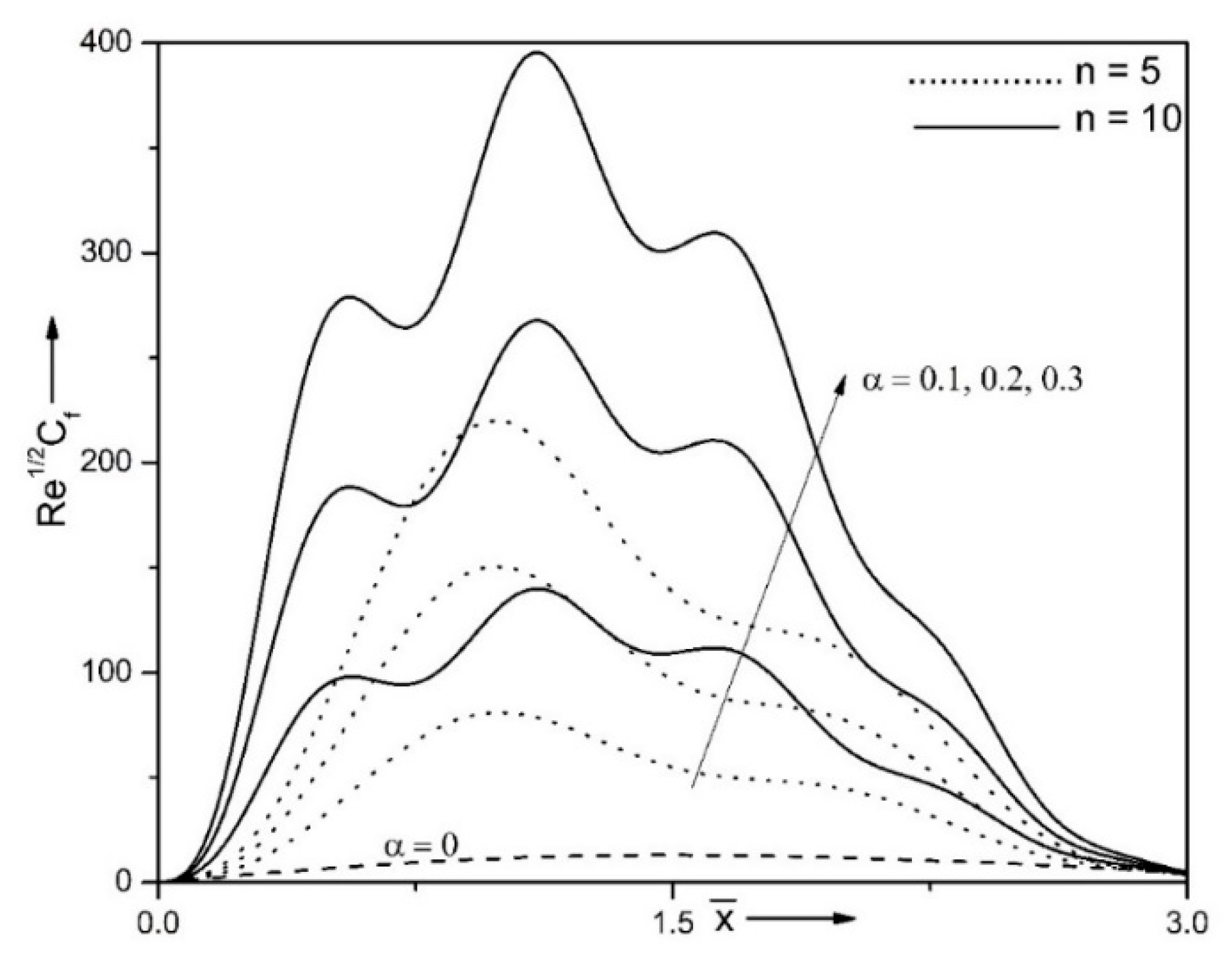
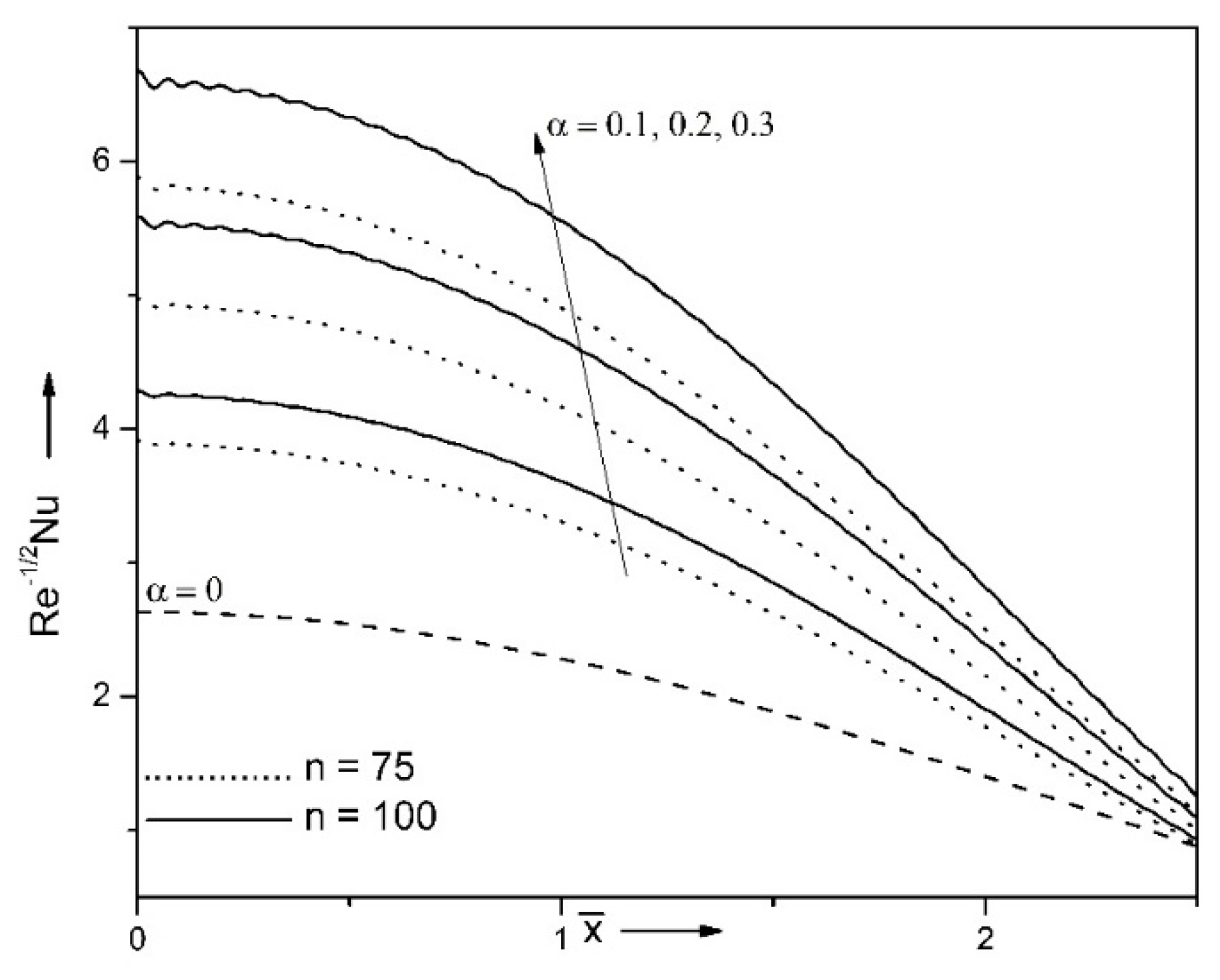
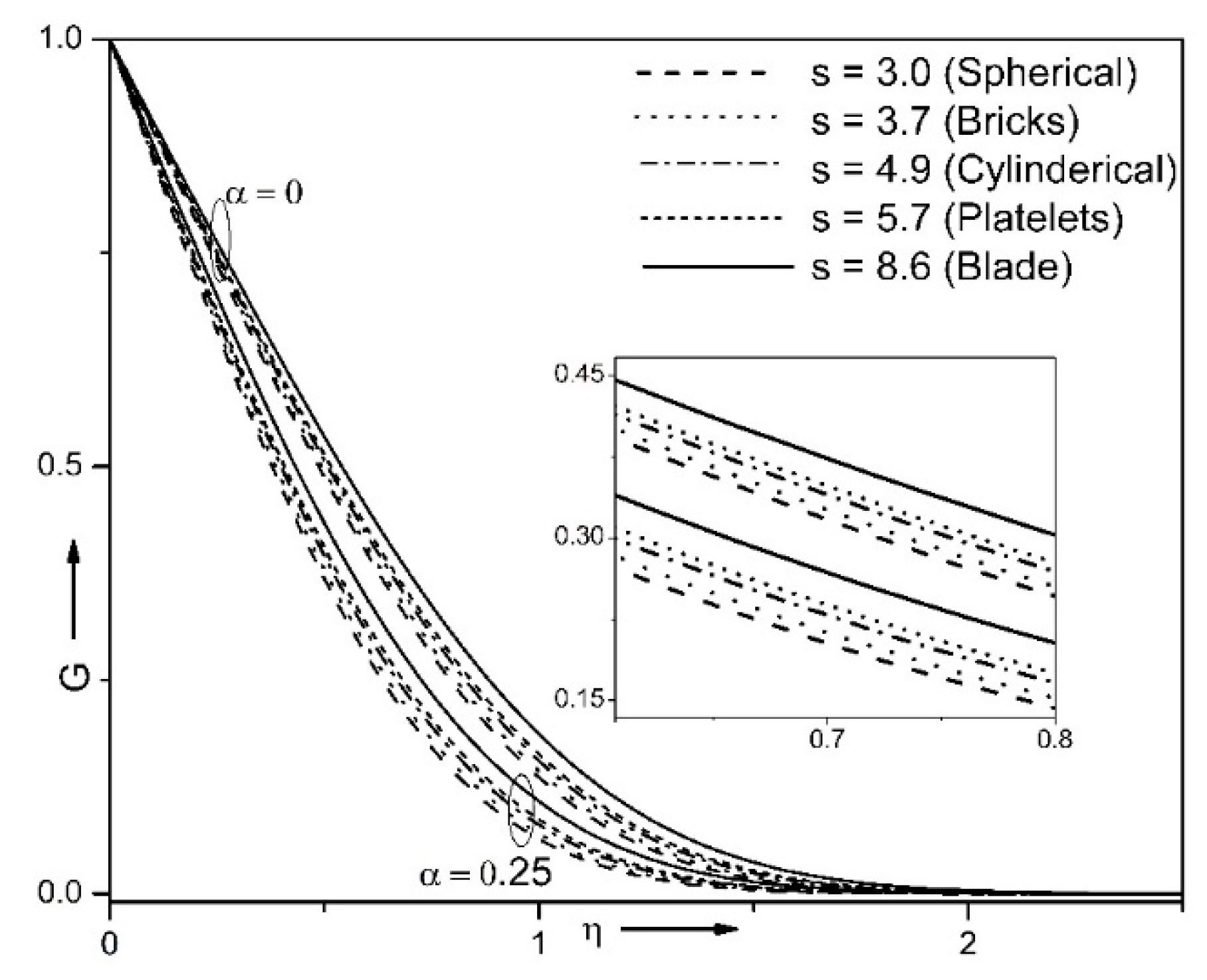
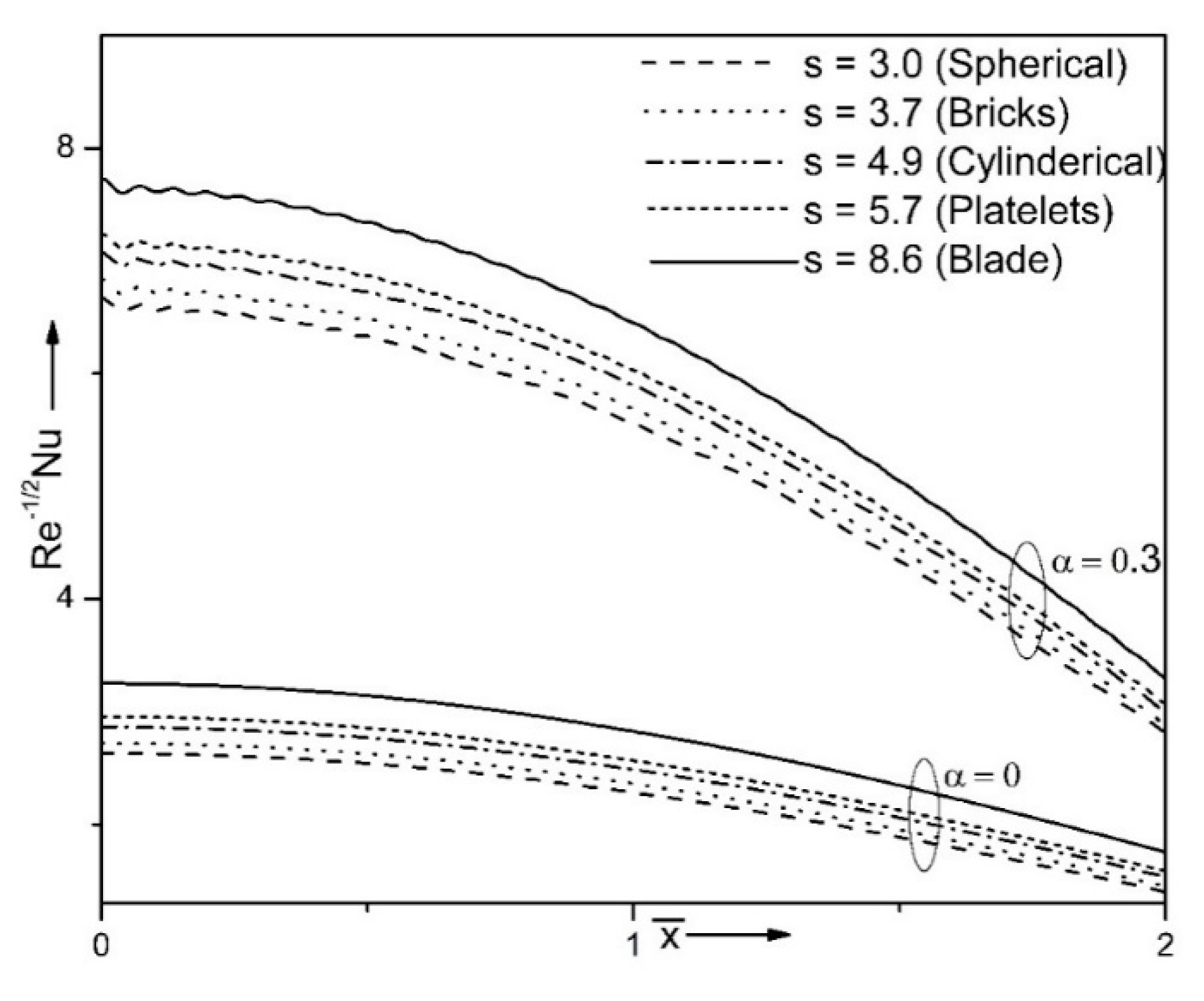
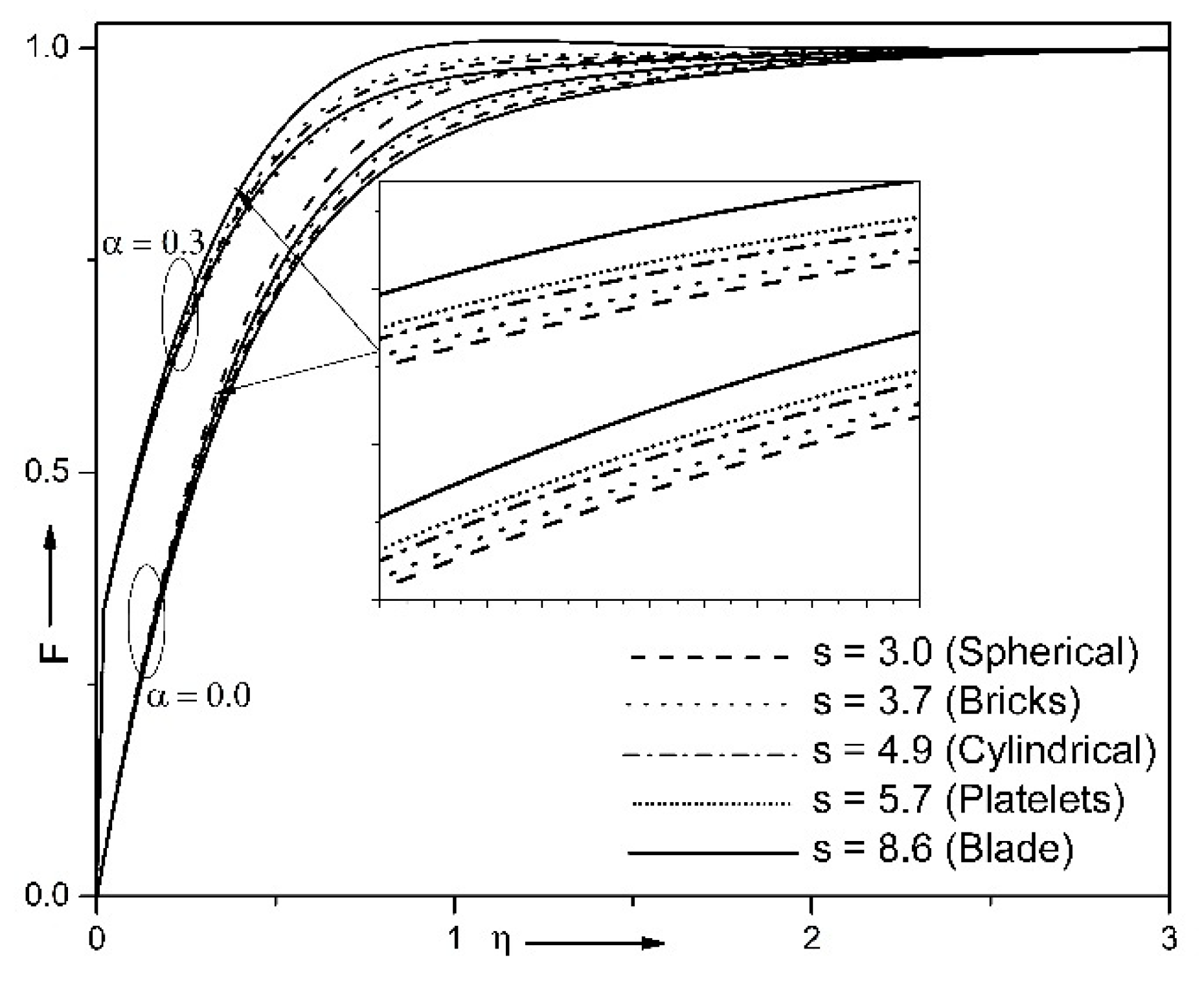
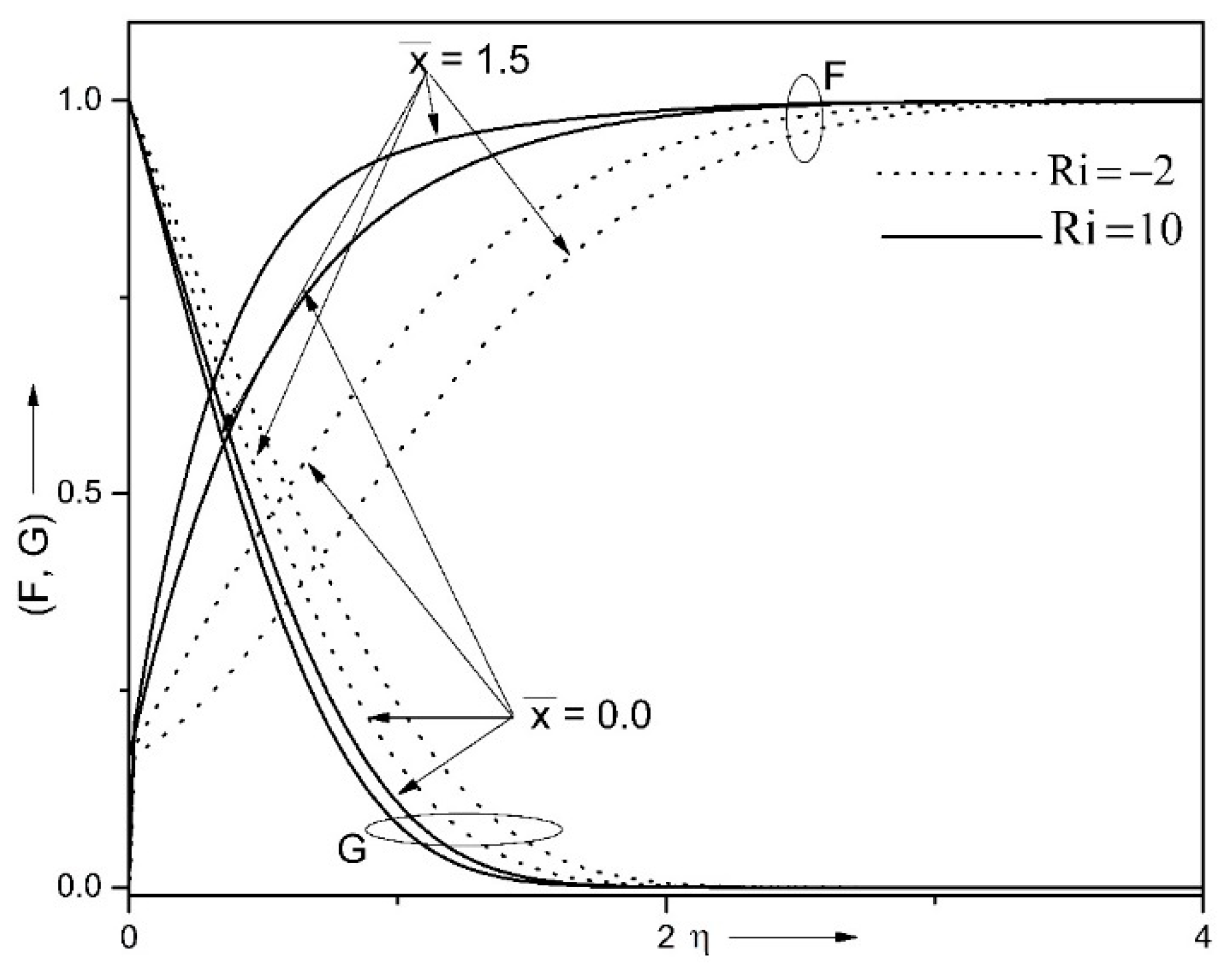
Properties	Nanofluid	Hybrid Nanofluid
Dynamic viscosity	${\mu }_{nf}=\frac{{\mu }_f}{{\left(1-{\varphi }_1\right)}^{2.5}}$	${\mu }_{hnf}=\frac{{\mu }_f}{{\left(1-{\varphi }_1\right)}^{2.5}{\left(1-{\varphi }_2\right)}^{2.5}}$
Density	${\rho }_{nf}=\left(1-{\varphi }_1\right){\rho }_f+{\varphi }_1{\rho }_{s_1}$	${\rho }_{hnf}=\left[{\varphi }_2{\rho }_{s_2}+\left(1-{\varphi }_2\right)\left\{\begin{array}{l}{\varphi }_1{\rho }_{s_1}+\\ \left(1-{\varphi }_1\right){\rho }_f\end{array}\right\}\right]$
Thermal conductivity	$k_{nf}=k_f\frac{k_{s_1}+2k_f-2{\varphi }_1\left(k_f-k_{s_1}\right)}{k_{s1}+2k_f+{\varphi }_1\left(k_f-k_{s_1}\right)}$	$k_{hnf}=k_{nf}\frac{k_{s_2}+2k_{nf}-2{\varphi }_2\left(k_{nf}-k_{s_2}\right)}{k_{s_2}+2k_{nf}+{\varphi }_2\left(k_{nf}-k_{s_2}\right)}$ with $k_{nf}=k_f\frac{k_{s_1}+2k_f-2{\varphi }_1\left(k_f-k_{s_1}\right)}{k_{s1}+2k_f+{\varphi }_1\left(k_f-k_{s_1}\right)}$
Thermal expansion coefficient	${\left(\rho \beta \right)}_{nf}=\left(1-{\varphi }_1\right){\left(\rho \beta \right)}_f+{\varphi }_1{\left(\rho \beta \right)}_{s_1}$	${\left(\rho \beta \right)}_{hnf}=\left[\begin{array}{l}{\varphi }_2{\left(\rho \beta \right)}_{s_2}+\\ \left(1-{\varphi }_2\right)\left\{\begin{array}{l}{\varphi }_1{\left(\rho \beta \right)}_{s_1}+\\ \left(1-{\varphi }_1\right){\left(\rho \beta \right)}_f\end{array}\right\}\end{array}\right]$
Heat capacitance	${\left(\rho c_p\right)}_{hnf}=\left(1-{\varphi }_1\right){\left(\rho c_p\right)}_f+{\varphi }_1{\left(\rho c_p\right)}_{s_1}$	${\left(\rho c_p\right)}_{hnf}=\left[\begin{array}{l}{\varphi }_2{\left(\rho c_p\right)}_{s_2}+\\ \left(1-{\varphi }_2\right)\left\{\begin{array}{l}{\varphi }_1{\left(\rho c_p\right)}_{s_1}+\\ \left(1-{\varphi }_1\right){\left(\rho c_p\right)}_f\end{array}\right\}\end{array}\right]$

.

In Table 1, volume fractions of silica and molybdenum disulphide nanoparticles are indicated by φ₁ and φ₂, respectively where φ₁ = φ₂ = 0 is meant to be the regular liquid. The hybrid nanosuspension includes 0.1 volume fraction of SiO₂ (i.e., φ₁) and the concentration of MoS₂ is changed from 0 to 0.1 $\left(0\le {\varphi }_2\le 0.1\right)$.

Table 2. Chemo-physical attributes of host liquid and nanoadditives [5,14,15,16].

Properties	Water	SiO2	MoS2
cp (J·kg−1·K−1)	4179	730	397.746
ρ (kg·m−3)	997.1	2650	5060
k (W·m−1·K−1)	0.613	1.5	34.5
Β × 10−5 (K−1)	21.0	42.7	2.8242

demonstrates the chemical attributes of the nanoadditives and the host liquid (see Maraj et al. [14], Rostami et al. [5], Ghadikolae et al. [15] and Khan et al. [16]).

Meanwhile,

Table 3. Type of nanoadditives with their geometry parameter values [3].

Nanoparticles Type	Geometry Parameter
Spherical	3.0
Bricks	3.7
Cylindrical	4.9
Platelets	5.7
Blade	8.6

shows the different shape impacts on governing parameters. Further, the solid components of SiO₂ and MoS₂ are denoted by the subscripts s₁ and s₂, respectively. The subscripts hnf, f and nf and denotes hybrid nanoliquid, base liquid and nanoliquid respectively.

Following non-similarity parameters as in Patil et al. [44,47], Rajakumar et al. [32] and Roy et al. [33] are employed. The non-similarity transformations and resulting flow variables are as follows:

$$\begin{array}{l}\xi ={{\displaystyle \underset{0}{\overset{x}{\int }}\frac{U_e}{U_{\infty }}\left(\frac{r}{R}\right)}}^{2}d\left(\frac{x}{R}\right)\eta ={\left(\frac{Re}{2\xi }\right)}^{\frac{1}{2}}\left(\frac{U_e}{U_{\infty }}\right)\left(\frac{r}{R}\right)\frac{y}{R},F=f_{\eta },\\ \psi (x,y)=U_{\infty }R{\left(\frac{2\xi }{Re}\right)}^{\frac{1}{2}}f\left(\xi ,\eta \right),u=\left(\frac{R}{r}\right)\frac{\partial \psi }{\partial y},v=-\left(\frac{R}{r}\right)\frac{\partial \psi }{\partial x},G=\frac{T-T_{\infty }}{T_W-T_{\infty }}\end{array}\}$$

(5)

In view of Equation (5), we have

$$\begin{array}{l}u=U_{e}F\\ v=-\left(\frac{R}{r}\right)U_{\infty }R{\left(\frac{2\xi }{Re}\right)}^{1/2}\left\{\frac{f}{2\xi }{\xi }_x+\frac{3}{2R}{sin}^3\left(\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$R$}\right.\right)f_{\xi }+\frac{2\eta }{R}cot\left(\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$R$}\right.\right)F-\frac{\eta {\xi }_{x}F}{2\xi }\right\}\end{array}$$

Let

$$a_{11}=\frac{{\mu }_{hnf}}{{\mu }_f},a_{12}=\frac{{\rho }_{hnf}}{{\rho }_f},a_{13}=\frac{{\left(\rho \beta \right)}_{hnf}}{{\left(\rho \beta \right)}_f},a_{14}=\frac{k_{hnf}}{k_f},a_{15}=\frac{{\left(\rho c_p\right)}_{hnf}}{{\left(\rho c_p\right)}_f},a_{16}=\frac{a_{11}}{a_{12}},a_{17}=\frac{a_{13}}{a_{11}},$$

and

$$a_{18}=\frac{a_{14}}{a_{15}}$$

Now, utilizing the transformations (5), Equations (1)–(3) are reduced as below and Equation (1) is satisfied identically.

$$F_{\eta \eta }+\frac{\gamma \left(\xi \right)\left(1-F^2\right)}{a_{16}}+\frac{f{F}_{\eta }}{a_{16}}+\frac{2\xi }{a_{16}}\left[F_{\eta }{f}_{\xi }-F{F}_{\xi }\right]+a_{17}Ri\cdot m(\overline{x})\cdot G=0$$

(6)

$$G_{\eta \eta }+\frac{Pr\cdot f{G}_{\eta }}{a_{18}}+\frac{2Pr\cdot \xi }{a_{18}}\left(G_{\eta }{f}_{\xi }-F{G}_{\xi }\right)=0$$

(7)

The employed border conditions are given below:

$$\begin{array}{l}\mathrm{At}\eta =0:F\left(\xi ,0\right)=\frac{2}{3}\epsilon \alpha \frac{sin\left(n\overline{x}\right)}{sin\left(\overline{x}\right)},G\left(\xi ,0\right)=1,\\ \mathrm{As}\eta \to \infty :F\left(\xi ,\infty \right)=1,G\left(\xi ,\infty \right)=0.\end{array}\}$$

(8)

The non-dimensional characteristics arising in this research are:

$$\begin{array}{l}Ri=\frac{Gr}{R{e}^2},Gr=\frac{g{\beta }_f\left(T_w-T_{\infty }\right)R^3}{{\nu }_f^2},Re=\frac{U_{\infty }R}{{\nu }_f},m\left(\overline{x}\right)=\frac{8{\left(1-cos\left(\overline{x}\right)\right)}^2\left(2+cos\left(\overline{x}\right)\right)}{27{sin}^4\left(\overline{x}\right)},\\ \gamma \left(\xi \right)=\frac{2\xi }{U_e}\frac{d{U}_e}{d\xi },\epsilon =\frac{U_0}{U_{\infty }},Pr=\frac{{\mu }_f{\left(c_p\right)}_f}{k_f}\end{array}$$

Furthermore,$f(\xi ,\eta )={\displaystyle \underset{0}{\overset{\eta }{\int }}Fd\eta +f_w;\mathrm{where}{f}_w=0}$ denotes an impermeable surface.

The velocity profile in the mainstream current is given below:

$$\frac{U_e}{U_{\infty }}=\frac{3}{2}sin\left(\overline{x}\right),\frac{r}{R}=sin\left(\overline{x}\right),\overline{x}=\frac{x}{R}$$

(9)

Therefore, ξ and γ(ξ) can be expressed in $\overline{x}$ as below:

$$\xi =\frac{S_1^2{S}_3}{2},\gamma \left(\overline{x}\right)=\frac{2cos\left(\overline{x}\right)S_3}{3S_2^2}$$

where

$$S_1=1-cos\left(\overline{x}\right),S_2=1+cos\left(\overline{x}\right),S_3=2+cos\left(\overline{x}\right)$$

(10)

The above equations, that are expressed in terms of ξ, are rewritten in $\overline{x}$, using the following relation:

$$\xi \frac{\partial }{\partial \xi }=B\left(\overline{x}\right)\frac{\partial }{\partial \overline{x}}$$

(11)

where

$$B\left(\overline{x}\right)=\frac{tan\left(\frac{\overline{x}}{2}\right)S_3}{3S_2}$$

(12)

In view of Equations (11) and (12), Equations (6) and (7) become as follows

$$F_{\eta \eta }+\frac{\gamma \left(\overline{x}\right)\left(1-F^2\right)}{a_{16}}+\frac{f{F}_{\eta }}{a_{16}}+\frac{2B\left(\overline{x}\right)}{a_{16}}\left[F_{\eta }{f}_{\overline{x}}-F{F}_{\overline{x}}\right]+a_{17}Ri\cdot m\left(\overline{x}\right)\cdot G=0$$

(13)

$$G_{\eta \eta }+\frac{Pr\cdot f{G}_{\eta }}{a_{18}}+\frac{2Pr\cdot B\left(\overline{x}\right)}{a_{18}}\left(G_{\eta }{f}_{\overline{x}}-F{G}_{\overline{x}}\right)=0$$

(14)

The relevant border constraints are

$$\begin{array}{l}\mathrm{At}\eta =0:F\left(\overline{x},0\right)=\frac{2}{3}\epsilon \alpha \frac{sin\left(n\overline{x}\right)}{sin\left(\overline{x}\right)},G\left(\overline{x},0\right)=1\\ \mathrm{As}\eta \to \infty :F\left(\overline{x},\infty \right)=1,G\left(\overline{x},\infty \right)=0\end{array}\}$$

(15)

All parameters and non-dimensional characteristics that arise in the analysis are described in Nomenclature. The gradients at the sphere are:

surface drag parameter

$$C_f=a_{11}\frac{9sin\left(\overline{x}\right)S_2{S}_3{}^{-1/2}{F}_{\eta }\left(\overline{x},0\right)}{2R{e}^{1/2}},R{e}^{1/2}{C}_f=a_{11}\frac{9}{2}sin\left(\overline{x}\right)S_2{S}_3{}^{-1/2}{F}_{\eta }\left(\overline{x},0\right)$$

(16)

and energy transport strength

$$Nu=-a_{14}\frac{3}{2}{S}_2{S}_3{}^{-1/2}R{e}^{1/2}{G}_{\eta }\left(\overline{x},0\right),R{e}^{-1/2}Nu=-a_{14}\frac{3}{2}{S}_2{S}_3{}^{-1/2}{G}_{\eta }\left(\overline{x},0\right)$$

(17)

3. Method of Analysis

Equations (13) and (14) are linearized employing the Quasilinearization method in the form:

$$F_{\eta }{{}_{\eta }}^{i+1}+A_1^i{F}_{\eta }^{i+1}+A_2^i{F}_{\overline{x}}^{i+1}+A_3^i{F}^{i+1}+A_4^i{G}^{i+1}=A_5^i$$

(18)

$$G_{\eta \eta }{}^{i+1}+B_1^i{G}_{\eta }{}^{i+1}+B_2^i{G}_{\overline{x}}^{i+1}+B_3^i{F}^{i+1}=B_4^i$$

(19)

Here the parameters at the (i + 1)th iteration are found by using the known ith iterative coefficients. The non-dimensional border conditions become

$$\begin{array}{l}{F}^{i+1}=\frac{2}{3}\epsilon \alpha \frac{sin\left(n\overline{x}\right)}{sin\left(\overline{x}\right)},G^{i+1}=1,\mathrm{at}\eta =0,\\ F^{i+1}=1,G^{i+1}=0,\mathrm{at}\eta ={\eta }_{\infty }\end{array}\}$$

(20)

where boundary layer edge is denoted by η_∞.

Parameters in Equations (18) and (19) are

$$\begin{array}{l}{A}_1^i=\frac{a_{12}}{a_{11}}\left(2B\left(\overline{x}\right)f_{\overline{x}}+f\right),A_2^i=-\frac{a_{12}}{a_{11}}2B\left(\overline{x}\right)F,A_3^i=-\frac{a_{12}}{a_{11}}\left[2B\left(\overline{x}\right)F_{\overline{x}}+2\gamma \left(\overline{x}\right)F\right],\\ A_4^i=\frac{a_{13}}{a_{11}}Ri\cdot m\left(\overline{x}\right),A_5^i=-\frac{a_{12}}{a_{11}}\left(2B\left(\overline{x}\right)F{F}_{\overline{x}}+\gamma \left(\overline{x}\right)\left(F^2+1\right)\right),B_1^i=\frac{a_{15}}{a_{14}}Pr\left(2B\left(\overline{x}\right)f_{\overline{x}}+f\right),\\ B_2^i=-2\frac{a_{15}}{a_{14}}Pr\cdot B\left(\overline{x}\right)F,B_3^i=-2\frac{a_{15}}{a_{14}}Pr\cdot B\left(\overline{x}\right)G_{\overline{x}},B_4^i=-2\frac{a_{15}}{a_{14}}Pr\cdot B\left(\overline{x}\right)F{G}_{\overline{x}}.\end{array}$$

Numerical solutions to the Equations (18) and (19) with the border constraints (20) were worked out through implicit finite difference approximation, where the backward and central differences are employed. The obtained algebraic set is solved employing the Varga’s algorithm [48]. The step size $\Delta \overline{x}=0.01$ is chosen along $\overline{x}$ direction and $\Delta \eta =0.01$ is chosen along η direction. When the present and previous iterations difference is low than 0.0001, the iteration process is stopped.

4. Results and Discussion

Molybdenum disulphide and silica/water combination of nanoparticles is taken for the present investigation. In the present model, 0.1 volume fraction of silica (φ₁) is included to the host liquid (H₂O) and accordingly molybdenum disulphide (φ₂) is introduced with numerous concentrations to obtain MoS₂-SiO₂/water hybrid nanosuspension. By considering the different combination of nanoparticles, the similar approach has been investigated by many researchers [46,49,50]. The surface roughness is modeled in terms of large frequency and low amplitude sinusoidal waves. The frequency characteristic (n) and low variable (α) are employed for 5 ≤ n ≤ 100 and 0 ≤ α ≤ 0.3. The smooth border is denoted using α = 0, whilst the rough border is denoted using α ≠ 0 [44,51]. As curvilinear $\overline{x}$ and y coordinates are perpendicular one another, the angle between these coordinates is taken as π/2. The magnitude ε = 0 characterizes the no-slip condition at the border, i.e., smooth border. The empirical shape factor s for nanoparticles is calculated using the formula s = ψ/3, where ψ is the sphericity. As per the Hamilton and Crosser approach [52], sphericity is the proportion of sphere area to the border area of physical particles with the same volumes. In the numerical computation, we have considered Pr = 7 that demonstrates the water as the host liquid, and it is constant throughout the investigation [30,53].

Figure 2 exhibits the effect of combined convection characteristic (Ri) and velocity ratio characteristic (ε) on velocity pattern $\left\{F\left(\overline{x},\eta \right)\right\}$. Rising values of combined parameter boost the nanosuspension velocity. Enhancing magnitudes of combined convection parameter specify higher significant impact of forced convection. Thus, the velocity of the fluid augments with the forced convection. In addition, in existence of rough surface (α = 0.1), velocity slip is noticed close to the surface. That is, abrupt jump arises close to sphere with roughness. Moreover, the characteristic (ε) is determined as the ratio between the slip velocity and the ambient circulation velocity. Thus, as the velocity ratio characteristic (ε) augments, the velocity of the liquid is enhanced.

Figure 3 displays the impact of combined convection parameter (Ri) and volume fraction (φ₂) on temperature distribution $\left\{G\left(\overline{x},\eta \right)\right\}$. For enhancing values of combined convection characteristic, the temperature of the liquid diminishes. The difference between the wall temperature and ambient flow temperature increases, for increasing values of Ri, which reduces the fluid temperature. Further, for escalating magnitude of volume fraction (φ₂), the temperature of the liquid augments. The liquid heat conductivity enhances for enhancing magnitude of volume fraction (φ₂) and rises the capacity of the hybrid nanofluid to conduct more heat, which enhances the temperature of the liquid.

Figure 4 displays the impact of velocity ratio characteristic (ε) and volume fraction (φ₂) on velocity profile $\left\{F\left(\overline{x},\eta \right)\right\}$. For enhancing magnitudes of concentration (φ₂) the velocity of the liquid diminishes. It is clear that the velocity of the fluid is larger in absence of nanoparticles compared its presence, for each corresponding value of ε. For increasing values of φ₂ the hybrid nanofluid becomes denser and concentrated. Moreover, velocity of the fluid enhances with enhancing values of velocity ratio characteristic. This is caused because the larger value of velocity ratio characteristic indicates more slip at the border that raises the liquid velocity.

Figure 5 presents the impact of small parameter (α) and volume fraction (φ₂) on temperature profile $\left\{G\left(\overline{x},\eta \right)\right\}$. Temperature of the liquid diminishes with enhance in this small parameter. As we seen that the fluid temperature diminishes more in rough surface (α ≠ 0) case compared to smooth surface (α = 0). Such phenomenon can be explained by the packets of fluid that are captured in the troughs formed owing to the surface roughness. It experiences slip at the wall of the sphere, when the liquid flows about the rough sphere and this enhances the velocity of the liquid. The growth of the liquid velocity yields more fluid movement across the wall of the sphere and this diminishes the liquid’s temperature. In addition, the liquid’s temperature enhances with rise in the volume fraction (φ₂). It is very clear that hybrid nanofluid has greater thermal conductivity than that of base fluid. Physically, it means that the nanoparticles with high thermal conductivity allow intensifying the heat transference and an inclusion of such nanoparticles enhances energy transport with a rise of the temperature.

Figure 6 and Figure 7 portray the impact of combined convection characteristics (Ri) and volume fraction (φ₂) on surface drag coefficient $\left({\mathrm{Re}}^{1/2}{C}_f\right)$ and energy transport strength $\left({\mathrm{Re}}^{-1/2}Nu\right)$. Surface drag coefficient and energy transport strength are enhanced for rising values of combined convection characteristic. The positive magnitudes of Ri illustrate the essential impact of free convection over the forced one. Thus, the buoyancy force inside the liquid intensifies the liquid motion and as a result it augments frictions at the surface. In addition, the drop between the border temperature and free stream temperature enhances for rising values of Ri, which increases the energy transport strength from wall to fluid. Further, for enhancing values of volume fraction (φ₂), the friction at the surface and the energy transport strength enhance. This is because addition of nanoparticles in the host liquid leads to intensifying its temperature and as a result one can find an intensification of the energy transport.

Figure 8 portrays the influence of small parameter (α) and volume fraction (φ₂) on energy transport strength $\left({\mathrm{Re}}^{-1/2}Nu\right)$. The energy transport strength boosts with enhancing nanoparticle volume fraction (φ₂). The physical reason is that these nanoparticles which are characterized by large heat conductivity display the augmentation of the energy transport coefficient because this parameter is directly proportional to heat conductivity. Further, heat transfer rate enhances with enhance in the small parameter. The sinusoidal waves are observed in presence of surface roughness. This is because the sphere has more area owing to the presence of roughness and thereby intensifies the heat transfer in a larger quantity from the sphere into the ambient fluid.

Figure 9 and Figure 10 show the comparison of hybrid nanofluid (MoS₂-SiO₂/H₂O), mono nanofluid (SiO₂/H₂O) and base liquid (H₂O) with various values of small parameter (α) for the surface drag coefficient $\left({\mathrm{Re}}^{1/2}{C}_f\right)$ and energy transport strength $\left({\mathrm{Re}}^{-1/2}Nu\right)$. Energy transport strength and coefficient of friction at the border are enhanced for hybrid nanosuspension compared to mono nanofluid and regular liquid. In addition, the friction and rate of heat transfer high for rough surface (α ≠ 0) case compared to smooth surface (α = 0) and sinusoidal waves are seen in presence of rough surface (α ≠ 0). Hence, we can conclude that the hybrid nanofluid has more thermal conductivity than that of nanofluid and base fluid due to the rising magnitudes of nanoparticles concentration fundamentally designate the quicker heat transmission from surface of the cylinder to ambient fluid, this boosts the thermal conductivity and consequently temperature of hybrid nanofluid, which causes the intensive enhance in the magnitudes of temperature profile and rate of heat transfer coefficient, significantly.

Figure 11 and Figure 12 exhibit the impact of α and n on surface drag parameter $\left({\mathrm{Re}}^{1/2}{C}_f\right)$ and energy transport strength $\left({\mathrm{Re}}^{-1/2}Nu\right)$. Coefficient of friction at the surface and the Nusselt number are enhanced for enhancing values of frequency parameter and non-zero values of small parameter (α ≠ 0). It is highlighted that, for regardless magnitudes of frequency coefficient the lines merge all together in smooth surface (α = 0) case. The sinusoidal variations are observed in rough surface (α ≠ 0) case. The amplitude of the sinusoidal waves enhances with intensifying values of small parameter, while the number of sinusoidal variations enhances as rise in n. Hence, the roughness of the surface has an essential influence on the liquid motion in comparison to the smooth surface. In addition, at $\overline{x}=0.5$ and n = 100, the friction at the surface enhances about 55%, when α varies from 0.1 to 0.3.

Figure 13 and Figure 14 explain the influence of shape factor with various values of small parameter on temperature profile $\left\{G\left(\overline{x},\eta \right)\right\}$ and energy transport strength $\left({\mathrm{Re}}^{-1/2}Nu\right)$. The graphical results reveal that, for all considered shapes such as, spherical, bricks, cylindrical, platelets and blade, there is an overall enhance in the values of $\left\{G\left(\overline{x},\eta \right)\right\}$ and $\left({\mathrm{Re}}^{-1/2}Nu\right)$. Particle shape has an essential influence on the heat exchange performance. Their impact can be observed in the chemo-physical attributes of the hybrid nanosuspension. Among the considered shapes, blade-shaped particles give the high heat performance compared to the platelets, cylindrical and bricks, and sphere-shaped particles give the low heat performance. Further, enhancing values of small parameter, the temperature profile lessens, while Nusselt number augments. Physically, addition of nanoparticles in the regular liquid leads to the temperature growth, so an intensification of the Nusselt number is quite obvious. For instance, at $\overline{x}=0.5$ the heat transfer rate enhances about 16%, from spherical to blade shaped nanoparticles type in presence of rough surface.

Taking into account an influence of the considered shapes of nanoparticles on velocity profiles (see Figure 15) it is possible to highlight that the blade-shaped particles give the highest growth of the velocity in comparison with other studied shapes, and spherical-shaped particles illustrate the formation of the smallest velocity. Further, a rise of small parameter reflects a growth of the velocity profile.

Figure 16 explains the impact of non-similarity parameter and combined convection parameter on velocity distribution $\left\{F\left(\overline{x},\eta \right)\right\}$ and temperature distribution $\left\{G\left(\overline{x},\eta \right)\right\}$. Velocity profile reduces while, temperature profile boosts in absence of non-similarity variable in opposing buoyancy flow case. Further, opposite outcomes are observed in presence of non-similarity parameter in assisting buoyancy motion case. Reason is that $\overline{x}$ directs as a favorable pressure drop. Intensifying magnitudes of combined convection coefficient augments the velocity distribution while, reduces the temperature distribution. It is clear from figure that the velocity of liquid is more pronounced for larger Ri in assisting motion variant. Physically, more buoyancy force is generated for greater values of Ri, which gave the maximum energy to the moving fluid, and such heat creates the confrontation in the circulation. The opposing model was scrutinized for the velocity in opposing flow version. In addition, it ascertains that the temperature and thermal boundary layer are diminished owing to Ri in the considered circulations.

To verify the accuracy of the computational approach, the obtained outcomes found for several values of Ri, by setting all characteristics values to zero except Pr = 0.7 are compared with the outcomes of Rajakumar et al. [32] in Figure 17 and it is obtained that the outcomes are well agreed.

Table 4. Comparison of hybrid nanofluid (φ₁ = 0.1 and φ₂ = 0.1) and mono nanofluid (φ₁ = 0.1 and φ₂ = 0.0) for different magnitudes of combined convection coefficient (Ri) at smooth and rough surfaces, for skin-friction coefficient and energy transport strength when $\overline{x}=0.5$, n = 10, ε = 0.1.

Combined Convection Parameter (Ri)		Mono Nanofluid (φ1 = 0.1 and φ2 = 0.0)		Hybrid Nanofluid (φ1 = 0.1 and φ2 = 0.1)
		Re1/2Cf	Re−1/2Nu	Re1/2Cf	Re−1/2Nu
Ri = −2	smooth surface (α = 0)	1.91924	1.73737	2.76707	2.07747
Ri = 0		2.68659	1.85759	3.54184	2.18376
Ri = 3		3.71230	1.99284	4.60356	2.30996
Ri = 6		4.64655	2.10531	5.58725	2.41753
Ri = 10		5.79680	2.22851	6.81020	2.54115
Ri = −2	rough surface (α = 0.25)	115.67549	2.11400	150.75397	2.46100
Ri = 0		116.33356	2.19692	151.43079	2.53750
Ri = 3		117.24895	2.30142	152.38640	2.63768
Ri = 6		118.10291	2.39003	153.28743	2.72483
Ri = 10		119.17278	2.49174	154.42511	2.82653

shows the influence of different values of combined convection parameter for mono nanofluid and hybrid nanofluid for skin-friction coefficient and energy transport strength. A rise of Ri reflects an increase in heat transport strength and friction at the surface for both the mono nanofluid and hybrid nanofluid. In addition, it is clear that, the hybrid nanofluid values are comparatively larger than that of nanofluid, for skin-friction coefficient as well as energy transport strength in smooth surface case. In addition, it is seen that the same trend is observed in rough surface case.

Table 5. Comparison values of energy transport strength (Re^−1/2Nu) with published outcomes for different magnitudes of $\overline{x}$ and Ri for Pr = 0.7.

	Nazar et al. [54]			Mohamed et al. [55]			Present Results
$\overline{\mathit{x}}$	Ri = −1	Ri = 0	Ri = 1	Ri = −1	Ri = 0	Ri = 1	Ri = −1	Ri = 0	Ri = 1
00	0.7870	0.8162	0.8463	0.7858	0.8150	0.8406	0.7918	0.8180	0.8426
100	0.7818	0.8112	0.8371	0.7809	0.8103	0.8362	0.7778	0.8139	0.8385
200	0.7669	0.7974	0.8239	0.7615	0.7967	0.8232	0.7729	0.8008	0.8254
300	0.7422	0.7746	0.8024	0.7719	0.7741	0.8018	0.7497	0.7792	0.8054
400	0.7076	0.7429	0.7725	0.7074	0.7425	0.7721	0.7134	0.7475	0.7737
500	0.6624	0.7022	0.7345	0.6624	0.7032	0.7354	0.6754	0.7081	0.7377

demonstrates the comparison with previous published data illustrating a very good agreement. It presents the values of heat transfer rate against $\overline{x}$ and Ri. The negative magnitudes of mixed convection coefficient (Ri < 0) indicate the opposing buoyant flow, while Ri > 0 is for assisting buoyant flow. From Table 5, it is clear that Nusselt number is a reducing relation of $\overline{x}$.

5. Conclusions

The current investigation explores the combined convective flow of silica–molybdenum disulphide/water nanosuspension over a rough sphere. The influences of varying small parameter, mixed convection, concentration of nanoadditives and frequency characteristic on the non-dimensional velocity and temperature distributions, surface drag coefficient and energy transport strength are investigated and explained with the help of different graphs. From the detailed analysis of the obtained results, the following vital observations are made:

–

the hybrid nanofluid augments the temperature, as well as Nusselt number at the wall;

–

velocity distribution is reduced, while friction at the surface enhances in the case of hybrid nanofluid;

–

slip exists near the surface of the sphere owing to roughness, which yields steep jump in the liquid velocity close to the border;

–

for enhancing magnitudes of small parameter, the friction at the surface and the Nusselt number are enhanced;

–

skin-friction parameter and the Nusselt number are boosted for hybrid nanoliquid on comparison with mono nanofluid and the base fluid;

–

skin-friction parameter and the Nusselt number have the highest values for blade-shaped nanoadditives and lowest value is found for spherical-formed nanoparticles.