Next Article in Journal
On the Trace Anomaly of the Chaudhuri–Choi–Rabinovici Model
Previous Article in Journal
Supramolecular Chirogenesis in Bis-Porphyrin: Crystallographic Structure and CD Spectra for a Complex with a Chiral Guanidine Derivative
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Symmetry
Volume 13
Issue 2
10.3390/sym13020272
symmetry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Handed Mirror Symmetry Breaking at the Photo-Excited State of π-Conjugated Rotamers in Solutions

by
Puhup Puneet
1,*,
Sajan Singh
1,
Michiya Fujiki
2,* and
Bhanu Nandan
1,*
1
Department of Textile and Fibre Engineering, Indian Institute of Technology Delhi (IITD), Delhi 110016, India
2
Division of Materials Science, Graduate School of Science and Technology, Nara Institute of Science and Technology, 8916-5 Takayama, Ikoma, Nara 630-0036, Japan
*
Authors to whom correspondence should be addressed.
Symmetry 2021, 13(2), 272; https://doi.org/10.3390/sym13020272
Submission received: 12 January 2021 / Revised: 30 January 2021 / Accepted: 1 February 2021 / Published: 5 February 2021
Browse Figures
Versions Notes

Abstract

:
The quest to decode the evolution of homochirality of life on earth has stimulated research at the molecular level. In this study, handed mirror symmetry breaking, and molecular parity violation hypotheses of systematically designed π-conjugated rotamers possessing anthracene and bianthracene core were evinced via circularly polarized luminescence (CPL) and circular dichroism (CD). The CPL signals were found to exhibit a (−)-sign, and a handed dissymmetry ratio, which increased with viscosity of achiral solvents depending on the rotation barrier of rotamers. The time-resolved photoluminescence spectroscopy and quantum efficiency measurement of these luminophores in selected solvents reinforced the hypothesis of a viscosity-induced consistent increase of the (−)-sign handed CPL signals.

Graphical Abstract

1. Introduction

The fundamental building blocks of life on planet earth are dominated by one of the enantiomer pairs, for instance, l-amino acids and d-sugars. However, they are supposed to be energetically equivalent to another enantiomer and should obey the parity conservation law of mirror symmetry [1,2,3,4,5]. Several theoretical investigations have utilized handed mirror symmetry breaking (MSB) via molecular parity violation (MPV) to explain the natural selection of one enantiomer over the other in biological systems [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]. The MPV hypothesis is based on the idea of parity-violating weak neutral current (PV-WNC), owing to the electron–nuclei interaction facilitated by massive neutral Z0-boson (91 GeV). Consequently, one enantiomer is stabilized slightly in terms of energy by −Epv; conversely, the other is destabilized by +Epv and the energy difference is known as the parity-violating weak energy difference (∆Epv) [7,8,32,33,34]. Based on the MPV hypothesis, various reports have estimated that the ∆Epv between mirror-image enantiomers is extremely small (10−8–10−14 kcal mol–1), which corresponds to the enantiomeric excess (ee) of only 10−9–10−15 %, i.e., excess of one molecule in the racemic mixture of 1011–1017 molecules [14,35,36]. Practically, the detection of such a tiny chiral bias is still a significant challenge owing to the detection limits of conventional spectroscopic methods such as achiral UV-Visible, IR, NMR, ESR, microwave spectrometers and enantioselective column chromatography [37,38,39,40]. To make the MPV detectable by spectroscopic measurements, several methods have been postulated to amplify the signals. For instance, linear amplification of faint Epv by the connotation of molecules to polymers and crystals [6], and a small influence of PV-originating oscillation on parity conserving electromagnetic (PC-EM)-originating quantum oscillation of imaginary chiral molecules in a double-well (DW) potential [11]. Additional theoretical models of real and imaginary molecules have been referred to in several innovative reports, along with experimental attempts [6,7,8,12,13,14,16,17,18,20,25,26,27,28,29,41,42,43,44,45,46]. Recent reports highlight the advance in the realm of MPV [47,48,49,50].
Recently, one of the authors (M.F.) and coworkers reported astonishing results from a comprehensive circularly polarized luminescene (CPL) and circular dichroism (CD) spectroscopic data set of nearly fifty non-rigid luminophore rotamers without stereogenic centers [42,43]. On controlling the tunneling barrier (Eb), all these luminophores revealed step-like and consistent alteration in Kuhn’s dissymmetry factor (glum) with only (–)-sign CPL signals with changes in the viscosity of the achiral solvents. They provided a possible explanation for the result, which was that although these non-rigid luminophores are made of lighter atoms possessing non-zero spin–orbit interaction (ζ, kcal·mol−1) [ζ = 0.1 (C), 0.2 (N), 0.4 (O), 0.7 (F), 1.0 (S)], a large number of photoexcited luminophores (>1010–1016) confined in a cuvette interacted with focused incident light beams. Subsequently, the faint ∆Epv on the order of 10−8–10−14 kcal·mol−1 was resonantly amplified to a detectable level to produce CPL chiroptical signals during a synchronized spontaneous radiation process [43]. The authenticity of the results were verified by studying luminophores with an enantiomeric chiral center and achiral D2h-symmetric fused aromatics (naphthalene, anthracene, tetracene, and pyrene). The mirror-image CPL and CD spectra were observed for the luminophores with chiral centers, whereas no detectable CPL and CD spectra were observed for the rigid fused aromatics.
CPL spectroscopy may be a promising tool to experimentally observe molecular parity violation effects:however, a moredetailed theoretical understanding and experimental investigations are requiredto understand the relationships between MPV with (–)-sign glum, photodynamics, quantum efficiency, and solvent viscosity. Moreover, it is not yet known whether this approach is consistent with other synthetic π- molecular and polymeric rotamers associated with different directions (horizontal and/or vertical) of π-conjugation and rotational barriers.
Based on previous reports [42,43], we rationally synthesized three non-rigid extended π-conjugated luminophores. These luminophores consist of anthracene (single horizontal and verticle conjugation axis), bis-anthracene (single horizontal and double vertical conjugation axes), and biphenyl moieties (single horizontal conjugation axis) as twistable cores in the right- or left-hand geometries, which commonly carry two floppy trans-styryl moieties as labile pendants that provide excellent solubility to a broad range of organic solvents. These rotamers possess different rotational barriers that were tunable with the apparent viscosity of achiral solvents, resulting in alterations in chiroptical spectroscopic response. More importantly, handed MSB phenomena was evinced by (–)-sign glum associated with no dominant CD signals for luminophores dissolved in a series of achiral alcohols. For a comprehensive study, we comparedthe obtained similar (–)-sign CPL signals of an unsubstituted twistable bi-aryl compound and chain-like π-conjugated polymer in solutions. Subsequently, the MPV effect of these luminophores observed by CPL spectroscopy was complemented by time-resolved photoluminescence spectroscopy (TRPL), relative quantum efficiency (Φf) measurements and change in dipole moment. The photophysical and chiroptical properties predicted by density functional theory (DFT) and time-dependent DFT (TD-DFT) calculations of luminophores consistently supported the experimental observations.

2. Materials and Methods

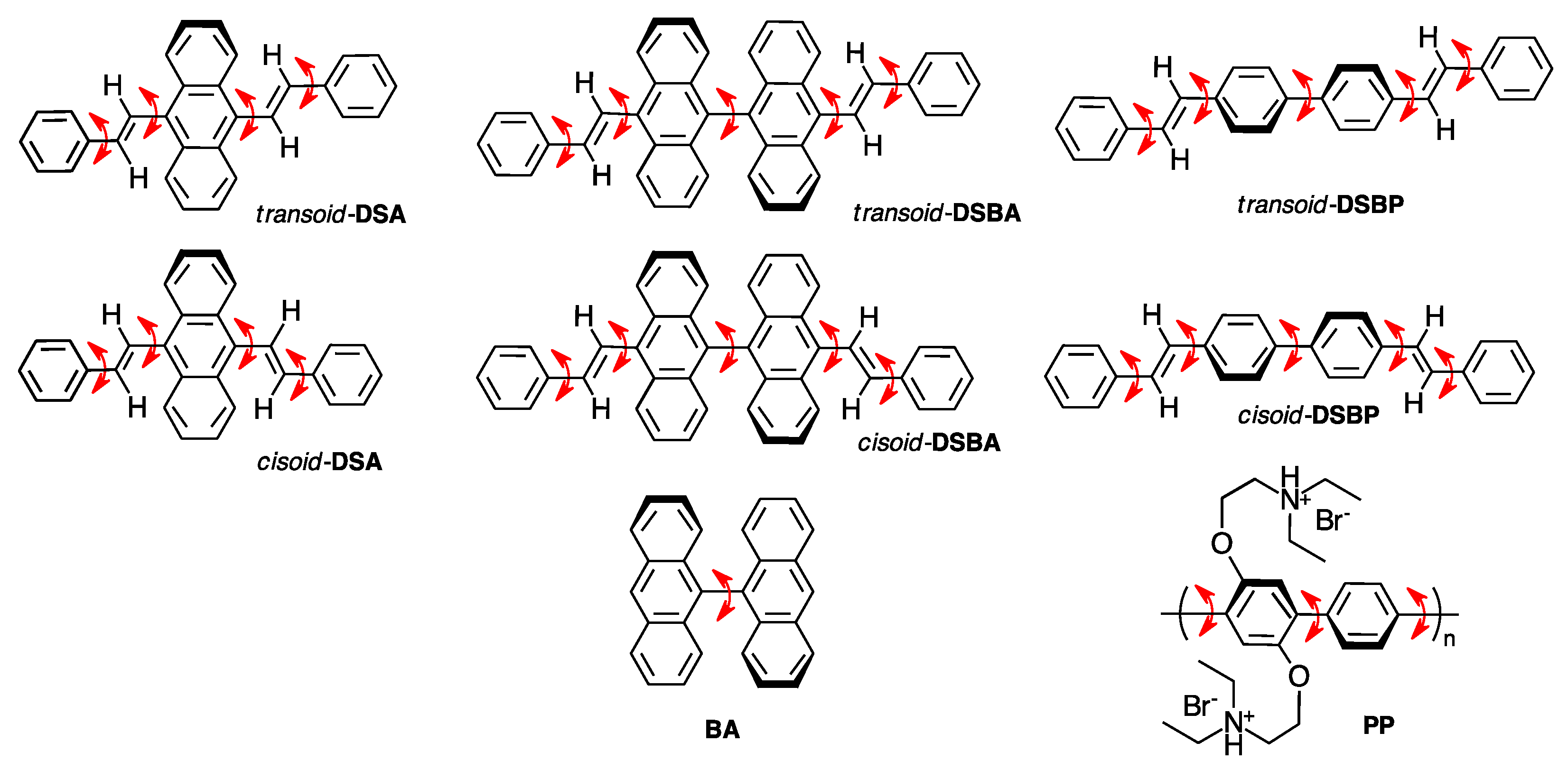
2.1. Synthesis and Characterization of Luminophores

Synthesis of 4,4′-distyryl-1,1′-biphenyl (DSA): this was synthesized according to the literature [50]. 9,10-Dibromobianthracene (200 mg, 0.595 mmol), styrene (148 mg, 1.428 mmol), K3PO4 (0.63 g, 2.975 mmol), and Pd(OAc)2 (26.7 mg, 0.119 mmol) were dissolved in dry dimethylacetamide (40 mL). The reaction mixture was heated to 110 °C and stirred for 24 h. The hot reaction mixture was allowed to cool to room temperature, then it was poured into water. The crude product was extracted twice with CHCl3 (60 mL) and the combined organic extracts were dried over Na2SO4. The solvent was evaporated to 5 mL; the product crystallized after addition of hexane and isolated as a yellow solid (40% yield).
Synthesis of 10,10′-distyryl-9,9′-bianthracene (DSBA): 10,10′-Dibromo-9,9′-bianthracene (200 mg, 0.39 mmol), styrene (97 mg, 0.93 mmol), K3PO4 (0.41 g, 1.95 mmol), and Pd(OAc)2 (17.5 mg, 0.078 mmol) were dissolved in dry dimethylacetamide (40 mL). The reaction mixture was heated to 110 °C and stirred for 24 h. The hot reaction mixture was allowed to cool down to room temperature, then it was poured into water. The product was extracted twice with CHCl3 (60 mL) and the combined organic extracts were dried over Na2SO4. The solvent was evaporated to 5 mL; the product crystallized after addition of hexane and isolated as a yellow solid (45% yield). 1H-NMR (δ in ppm 400 MHz, CDCl3): 8.55 (d, 4H, ArH), 8.13 (d, 4H, ArH), 7.81 (d, 4H, ArH), 7.54 (m, 4H, ArH), 7.45 (m, 8H, ArH), 7.19 (s, 4H, CH=CH), 7.14 (s, 2H, ArH). M/z = 558.41 g/mol (MALDI-TOF).
Synthesis of 4,4′-distyryl-1,1′-biphenyl (DSBP): 4,4′-Dibromo-1,1′-biphenyl (200 mg, 0.64 mmol), styrene (160 mg, 1.53 mmol), K3PO4 (0.68 g, 3.2 mmol), and Pd(OAc)2 (28.8 mg, 0.12 mmol) were dissolved in dry dimethylacetamide (30 mL). The reaction mixture was heated to 110 °C and stirred for 24 h. The hot reaction mixture was allowed to cool down to room temperature, then it was poured into water. The product was extracted twice with CHCl3 (60 mL) and the combined organic extracts were dried over Na2SO4. The solvent was evaporated to 5 mL; the product crystallized after addition of hexane and isolated as a solid (29 % yield). 1H-NMR (δ in ppm 400 MHz, CDCl3): 7.66 (d, 4H, ArH), 7.62 (d, 4H, ArH), 7.57 (d, 4H, ArH), 7.40 (t, 4H, ArH), 7.30 (m, 2H), 7.18 (s, 4H, CH=CH). M/z = 358 g/mol (Maldi-tof).

2.2. Preparation of Sample Solutions

First, a stock solution of luminophore (10–3 M) was prepared in a suitable organic solvent. For DSA and DSBA, chloroform was used as the stock solution as solvent, and for DSBP, methanol was used as a stock solution as solvent. Premeasured aliquots of stock solution were added to 1.9–2.1 mL of the desired liquid in a cylindrical quartz cuvette using a micro-syringe and diluted with a range of solvents followed by vigorous shaking by hand to minimize the incorporation of external (chiral) dust, fiber, particles. It was confirmed that the mixed solution was a scattering-free, transparent homogeneous solution before the CD and CPL measurements.

2.3. Instrumentation

Simultaneous measurements of CD and UV-visible spectra were done at room temperature using a cylindrical quartz cuvette with path lengths of 10 mm (JASCO J-820 spectropolarimeter, Hachioji, Tokyo, Japan). The cylindrical cuvette appears to provide precise CD measurements as compared to rectangular cuvettes. To ensure reliability, one or two accumulations of the spectra were recorded. Similarly, simultaneous measurements of CPL and PL spectra were performed on a JASCO CPL-200 spectrofluoropolarimeter using cylindrical quartz cuvettes at room temperature. The reliability of the measurements was ensured by recording two to three accumulations of spectra.
The NMR spectra were measured with a Bruker-400 MHz; the mass spectra were measured with a Bruker (Bengaluru, Karnataka, India) UltrafleXtreme MALDI-TOF/TOF mass spectrometer; luminescence lifetime decay was recorded with time correlated single photon counting (TCSPC) using Edinburgh Instruments (Kirkton Campus, Livingston, UK) FLSP920 time-resolved fluorescence spectrometer. A pulsed laser diode (377 nm) with a pulse repetition rate of 500 kHz was employed for the mean lifetime measurements.

3. Results

DSA, DSBA, and DSBP (Chart 1) were synthesized according to Section 2.1. For comparison, we investigated two commercial rotamers, including 9,9′-bianthracene (BA) and poly{[2,5-bis(2-(N,N-diethylammoniumbromide)ethoxy)-1,4-phenylene]-alt-1,4-pheynlene (PP) (Chart 1). BA is a core moiety of DSBA and PP is regarded as an extension of multiple cores in DSBP. The CPL and CD spectra of all luminophores were measured in a series of linear alkane mono-ols and diols with different viscosities at 25 °C, ranging from 0.59 cP and 7.0 cP. The CPL signals for all the three luminophores were of (−)-sign, which kept on increasing in relation to the viscosity of the solvent, whereas they remained CD-silent irrespective of the viscosity of the solvent. The non-aggregated molecular conformations of these molecules were investigated in this study by performing chiroptical measurements in dilute solutions (10−6–10−5 M). However, if we consider the optical properties of DSA, for instance, and compare it with the predicted UV-Visible spectra of cis-DSA and trans-DSA during CD and CPL measurements (Figure S15, Supplementary Material (SM)), it is difficult to determine whether cis or trans isomer is involved. 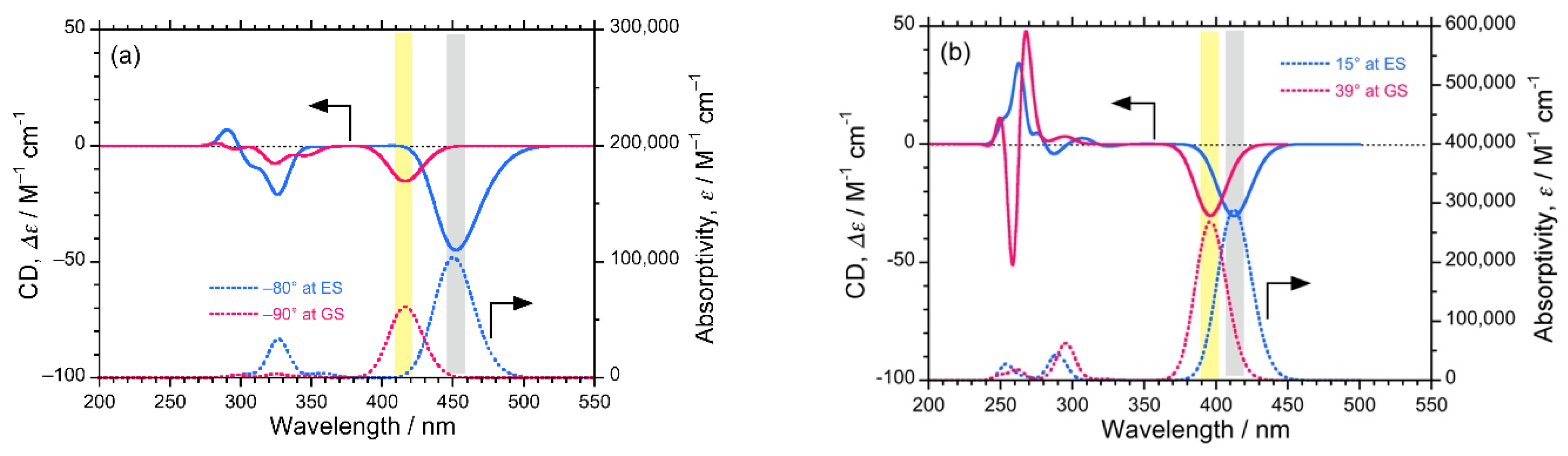An experimental observation indicated there was a transoid–cisoid conformational transition arising from the rapid rotational transition of two labile styryl groups.

3.1. Chiroptical Properties

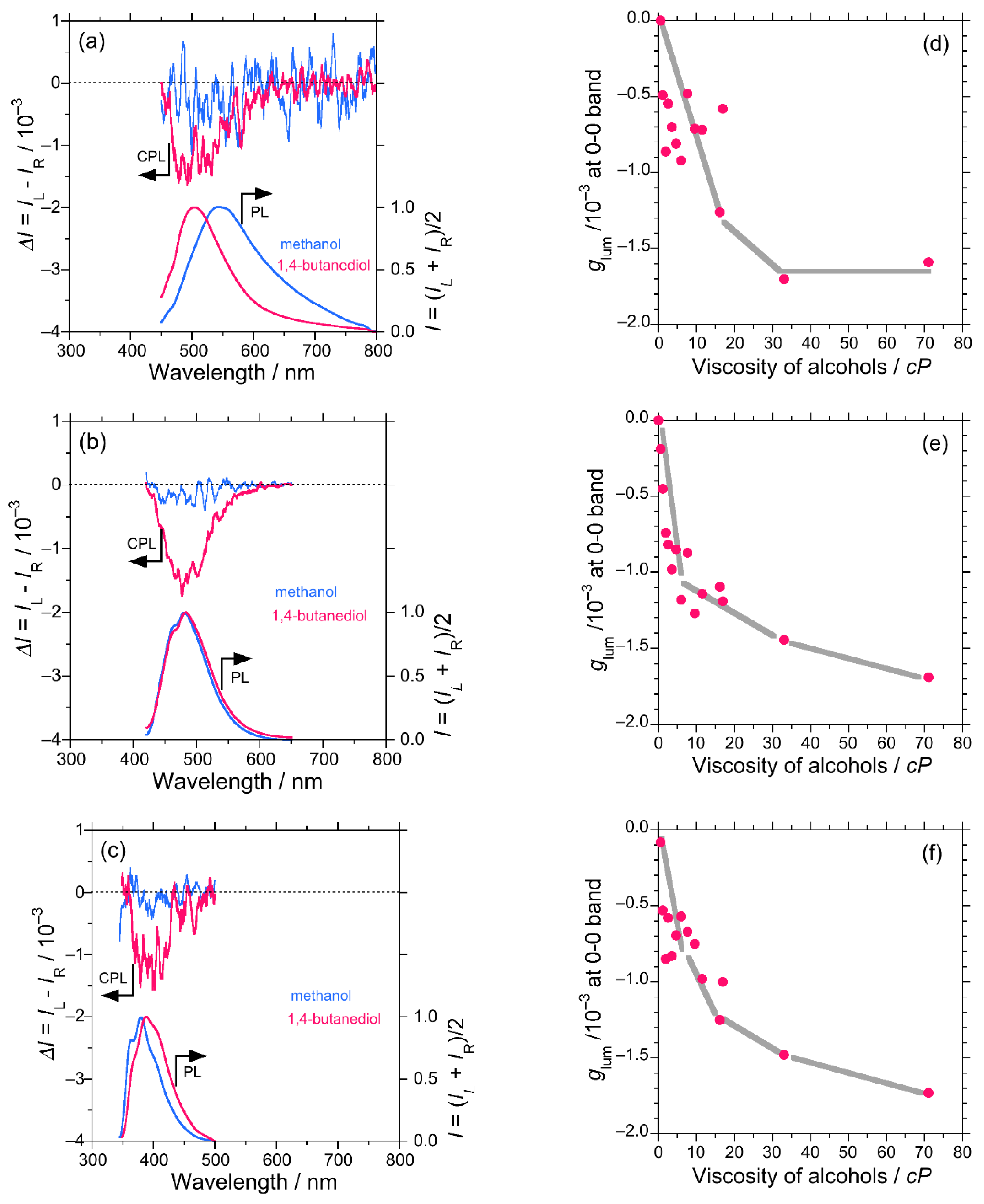
3.1.1. DSA

In the case of DSA, the CPL profile (glum) observed in methanol and 1,4-butanediols were compared. The signal intensity was much higher in 1,4-butanediol (glum = −1.7 × 10−3) as compared to that in methanol (glum = −0.5 × 10−3) (Figure 1a). Also, the CPL–viscosity plot shows a cluster of data points for glum for lower viscosity solvents, an increasing tendency for higher viscosity solvents and becomes nearly constant with viscosity of more than 33 cP (Figure 1d). This behavior can be attributed to the labile flip-flop motion of the π-extended styryl group until the media is sufficiently viscous. Once the rotational freedom was fully restricted due to molasses in the media, DSA molecules adopted a time-averaged stable conformation, which revealed mainly (–)-sign CPL signals. Anomalous behavior was observed in the emission properties of DSA in the diols, where a significant blue shift was observed along with intense CPL signals. The observed blueshift may occur, possibly, due to the formation of an intermolecular OH-π adduct of DSA with diol molecules. It distorted the rotational degree of styryl units. Hence, the extension of π-conjugation was moderated. As a result, emission phenomenon approaches a blue-shifted anthracene type behavior.

3.1.2. DSBA and BA

DSBA possesses a bianthracene core and owing to an inherent substantial intramolecular steric hindrance, DSBA remains at a twisted angle of (90.07°) with D2h-like molecular symmetry or exact D2-symmetry based on an optimized structure by DFT calculations (Table S6 in SM). This geometry of the molecule should not display any obvious CPL signal owing to the nearly achiral D2h-like symmetry of the core. The photoluminescence (PL) spectra showed two emission bands, namely, 0-0 and 0-1 vibronic bands. As the viscosity of the media increased, the (–)-sign CPL signal at the 0-0, 0-1 vibronic bands increased consistently (Figure 1d,e). Figure 1b demonstrates the CPL profile and stronger CPL intensity in more viscous 1,4-butanediol (glum = −1.7 × 10−3) as compared to less viscous methanol (glum = −0.3 × 10−3). This result infers that the viscous medium enforces the molecular rotation of the bianthracene core more significantly as compared to DSA, owing to the relatively high rotational barrier height of the bianthracene core. Since most of the PL and CPL signals of DSBA come from the bianthracene core, the effect of the OH/π-interaction with diols was not observed. To support the hypothesis of viscosity dependent twisting of the bianthracene core, BA was examined through CD and CPL measurements. Similar to the case of DSBA, the chiroptical properties of BA in methanol, ethanol, and 1-propanol exhibited a linear increase in the (–)-sign CPL signal with an increase in the viscosity of the solvents (Figure S14, SM).
Moreover, theoretical calculations were employed for BA with a forced twist angle as a function of the dihedral angle between two anthracene units ranging from 30° and 90°. In the case of BA, the ground state energy increased exponentially with a decrease in twist angle (Figure S13, SM). This implies that one has to raise the ground state energy of BA to achieve a smaller twist angle, which no longer remains in the pseudo-D2h-symmetry. Thus, BA can adopt a time-averaged right (R)- or left (L)-state. In this study, we achieved mechanical twisting of BA and the bianthracene core of DSBA with an enhancement in the viscosity of the solvent.

3.1.3. DSBP and PP

DSBP possesses a built-in twisted biphenyl core owing to its inherent intra-molecular twisting capability. DSBP revealed a similar consistent increase in the (–)-sign CPL signal with the viscosity of the solvent at two vibronic bands in PL and CPL (0-0 and 0-1) spectra (Figure 1c–f).
For additional comparison, we measured the chiroptical properties of PP, which is an oligomer with several phenylene units. The oligomer PP showed an intense (–)-sign CPL signal, even in a very low viscous methanol. In higher viscosity solvents, the (–)-sign CPL signal appeared to have saturated, and a negligible effect on CPL intensity was observed (Figure S14, SM). Hence, a high degree of polymerization of π-conjugated units is assumed to have a similar effect as luminophores in the highly viscous environment due to the long chains and their sluggish movements. Moreover, the intense CPL signals can be accredited to enhanced π-conjugation along the main chain, whereas (–)-sign signal is maintained because of the handed conformation locked by the long main-chain lengths.

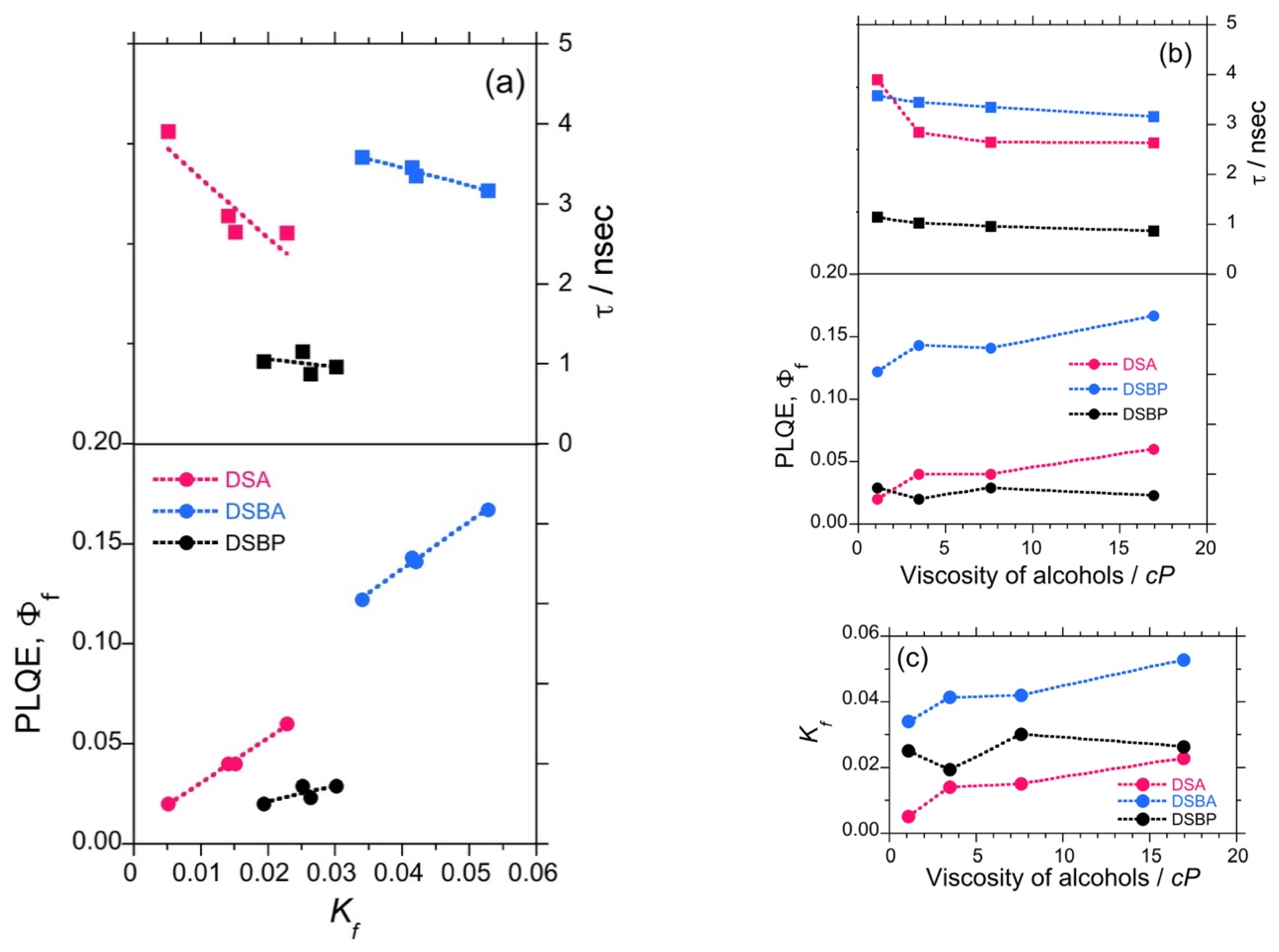
3.1.4. Mean Excited-State Lifetime and Relative Quantum Efficiency of DSA, DSBA and DSBP

It is commonly understood in chemistry that molecules in the photoexcited state lose energy via a non-radiative decay channel. In principle, the non-radiative loss can be curbed if molecular rotational and vibrational modes are restricted in viscous solvents [48,49]. To collect more evidence on the parity-violating (–)-sign CPL enhancement with the viscosity of the solvent, the mean excited state lifetime (τ)of luminophores and relative Φf were measured as a function of viscosity in selected solvents (ethanol = 1.19 cP (25 °C), n-pentanol = 3.47 cP (25 °C), n-octanol = 7.59 cP (25 °C), and n-undecanol = 16.95 cP (25 °C)).
The τ values for DSA, DSBA, and DSBP reduced linearly with an increase in the viscosity of the solvent (Figure 2b). This signifies that the excitons emit faster, which is associated with a lesser probability of non-radiative decay in a viscous environment. Similarly, the relative Φf showed an increasing tendency for DSA and DSBA, whereas it remained almost constant with slight fluctuations for DSBP (Figure 2b and Tables S3–S5, SM). Using these values, the rate of radiative decay (Kf) was calculated (Kf = Φf/τ). The profile of Kf vs. τ exhibited a linear decreasing trend, and Kf vs. Φf showed an increasing trend (Figure 2a) of DSA, DSBA, and DSBP. The Kf value for DSA and DSBA showed an increasing tendency with the viscosity of the solvent, whereas the Kf value for DSBP remained almost constant with slight fluctuations (Figure 2c). This implies that the τ, Φf, and Kf values are complementary to the intensified characteristics of parity-violating handed CPL signals along with time-averaged handed conformation of luminophores in a DW for DSA and DSBA. In the case of DSBP, no significant increasing tendency was observed for Φf and Kf, however, a consistent decreasing trend of τ suggests that the CPL signals intensify with an increase in the viscosity of the solvent.

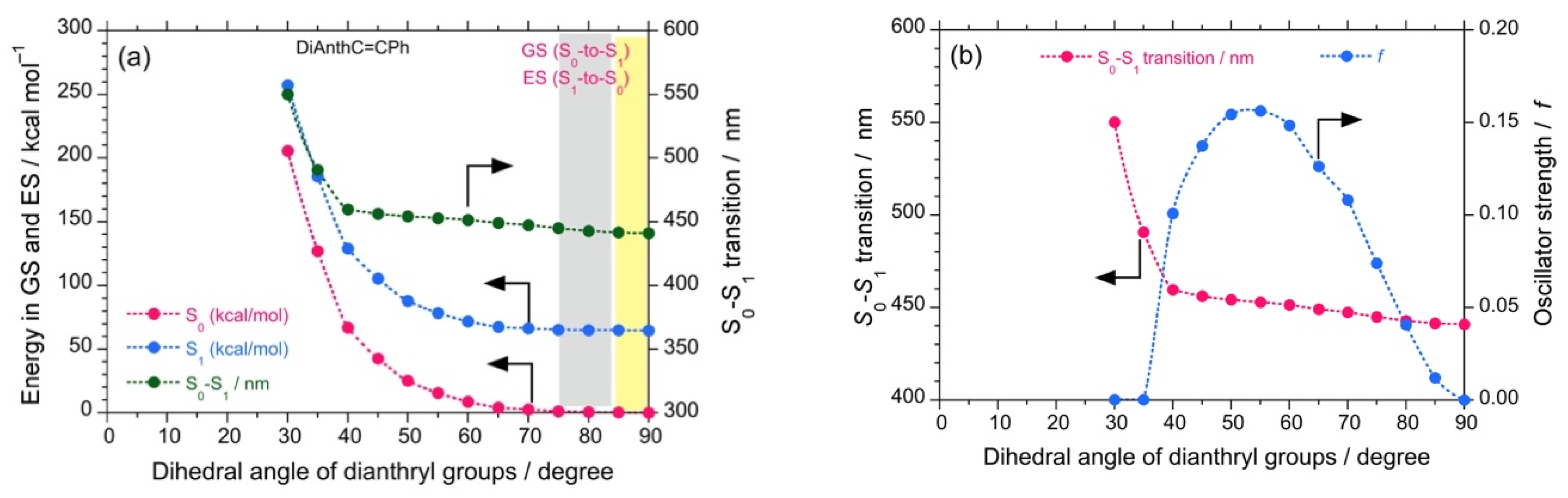
3.1.5. Changes in Dipole Moment and Theoretical Calculations

The change in dipole moment ∆µ (= µe − µg) was calculated according to the literature [51,52] (Section 5, SM). In the case of DSA and DSBA, their ∆µ values were found to be 9.66 D and 7.74 D, respectively. The change in dipole moment in the excited state as compared to the ground state is directly correlated to the nature of the luminophore in the excited state and its intramolecular charge transfer state. Such a high ∆µ for DSA and DSBA strongly supports the presence of a twisted intramolecular charge-transfer state (TICT) in the excited state. The twisting of luminophores caused them to have a higher polarity in the excited state, which ultimately resulted in the high ∆µ values. Contrarily, the ∆µ value of DSBP was 2.79 D, which is moderate compared to DSA and DSBA; however, experimentally, we still observed dominant CPL signals with an increase in viscosity of the solvent. These behaviors can be explained by the DFT-optimized structure and HOMOs-and-LUMOs of luminophores. The DSA and DSBA possess anthracene and bianthracene cores, respectively, which contribute to the vertical conjugation (longer axis of the anthracene ring) along with the horizontal conjugation (shorter axis of the ring). Hence, TICT is more dependent on the twisting of anthracene and bianthracene core [53]. In the case of DSBP, because only the horizontal conjugation is possible, the TICT does not dominate to yield the high ∆µ value. The CPL measurements are more sensitive, hence, the ∆µ value of 2.79 D appeared to produce sufficiently large CPL signals.
Theoretical calculations were also performed to investigate the properties of the luminophores at several intramolecular twisted states. The DSA possesses a stable anthracene core but two twistable styryl groups at each end. These two variables would significantly increase the number of twisted states. For simplicity, we omitted such calculations. The twisted states of DSBP containing biphenyl core were generated hypothetically by varying the dihedral angles of the biphenyl core from 5°–90° with an interval of 5°, while keeping the dihedral angle of the styryl groups as optimized (~53°). By employing these structures, single-point energy calculations were performed using DFT and TD-DFT (B3LYP, 6-311G). The plots of energy at the ground state (GS) and excited state (ES) vs. the dihedral angle of biphenyl core reveals that, although DSBP at GS remains with a dihedral angle of 39°, DSBP adopts a conformation with a dihedral angle of ~15° at the ES (Figure 3a). Such an extensive twisting capability is correlated with small rotational barriers (1–2 kcal mol–1) for the biphenyl group at GS and ES. As a result, the molecule is expected to lose absorbed photoexcited energy by non-radiative decay pathways.
Correspondingly, the estimated oscillator strength (f) showed a slight increase from 2.07 at GS to 2.15 at ES, which can be directly correlated with the Φf values. These results infer that DSBP at ES adopts a stable handed conformation with a dihedral angle of ~15°. This arises from the small energy barrier of rotation and loss of photoexcited energy as a non-radiative decay pathway, even in fluidic viscous solvents. Such an energy loss coupled with a slight increase in f value results in almost constant values of Φf and Kf (Kf = Φf/τ). However, the consistent increase of (–)-sign CPL signals is attributed to the decrease of τ value associated with an increase of viscosity of the solvent. Moreover, the deeper energy well with the dihedral angle at GS and moderately deep energy well at ES suggest appreciable tunneling through the energy barrier to adopt a right-handed conformation, which is a one-way route for the excitons because of slight stabilization of the right-hand state by ∆Epv.
Further, the plot of the dihedral angle vs. the lowest transition energy (eV, nm) reveals a change in the lowest transition energy from 3.54 eV (349 nm) at GS to 3.39 eV (362 nm) at ES, which also complements the experimental observations of a large Stokes shift (from 330 nm to 393 nm, ~4850 cm−1 or 0.60 eV) (Figure 3b). Similarly, DSBA possesses a bianthryl core; its twisted states were generated hypothetically by varying the dihedral angles of bianthryl core from 30°–90° with an interval of 5° while keeping the dihedral angle of styryl groups optimized (~53°). By employing these twisted structures, single-point energy calculations were performed using DFT and TD-DFT (B3LYP, 6-311G).
The plots of energy at GS and ES as a function of the dihedral angle of biphenyl core revealed that DSBA remains at GS with a dihedral angle of 90.07° and subsequently adopts a conformation with a dihedral angle of ~80° at ES. The energy profile reveals a much higher energy barrier for intra-molecular rotation as compared to DSBP, which increased exponentially with a decrease in the dihedral angle of bianthryl core. Therefore, only a small intra-molecular reorganization could be observed from GS to ES (Figure 4a). Further, the f value as a function of the dihedral angle showed an increase in f from GS (0.00079) to ES (0.04063) owing to the small intra-molecular reorganization due to a large rotational barrier (Figure 4b). As a result, when the viscosity of the solvent was increased, consistent increases in Φf and Kf values of DSBA were observed, associated with the decrease in τ value. This tendency is significantly supported by the corresponding (–)-sign CPL signals.
Additionally, to ensure the authenticity of the experimentally observed (–)-CPL signals of the luminophores, we predicted CD spectra at GS and ES with the corresponding dihedral angles of biphenyl and bianthryl core by performing DFT/TD-DFT calculations (Figure 5). The predicted CD spectra at ES corresponds to CPL signals. In the case of DSBP, the predicted CD spectra at both GS and ES showed a significant (–)-sign Cotton band with comparable intensities. The similar intensity at GS and ES also complements the anomalous behavior of DSBP, i.e., the minimal increase in f and loss of energy via intra-molecular reorganization (Figure 5b). Conversely, for DSBA, a significant (–)-sign Cotton band was observed at GS, whereas a lot of intense signal was observed at ES owing to the intramolecular twisting and subsequent increase of Φf and f (Figure 5a). These predicted CD spectra indisputably support the experimental observations.

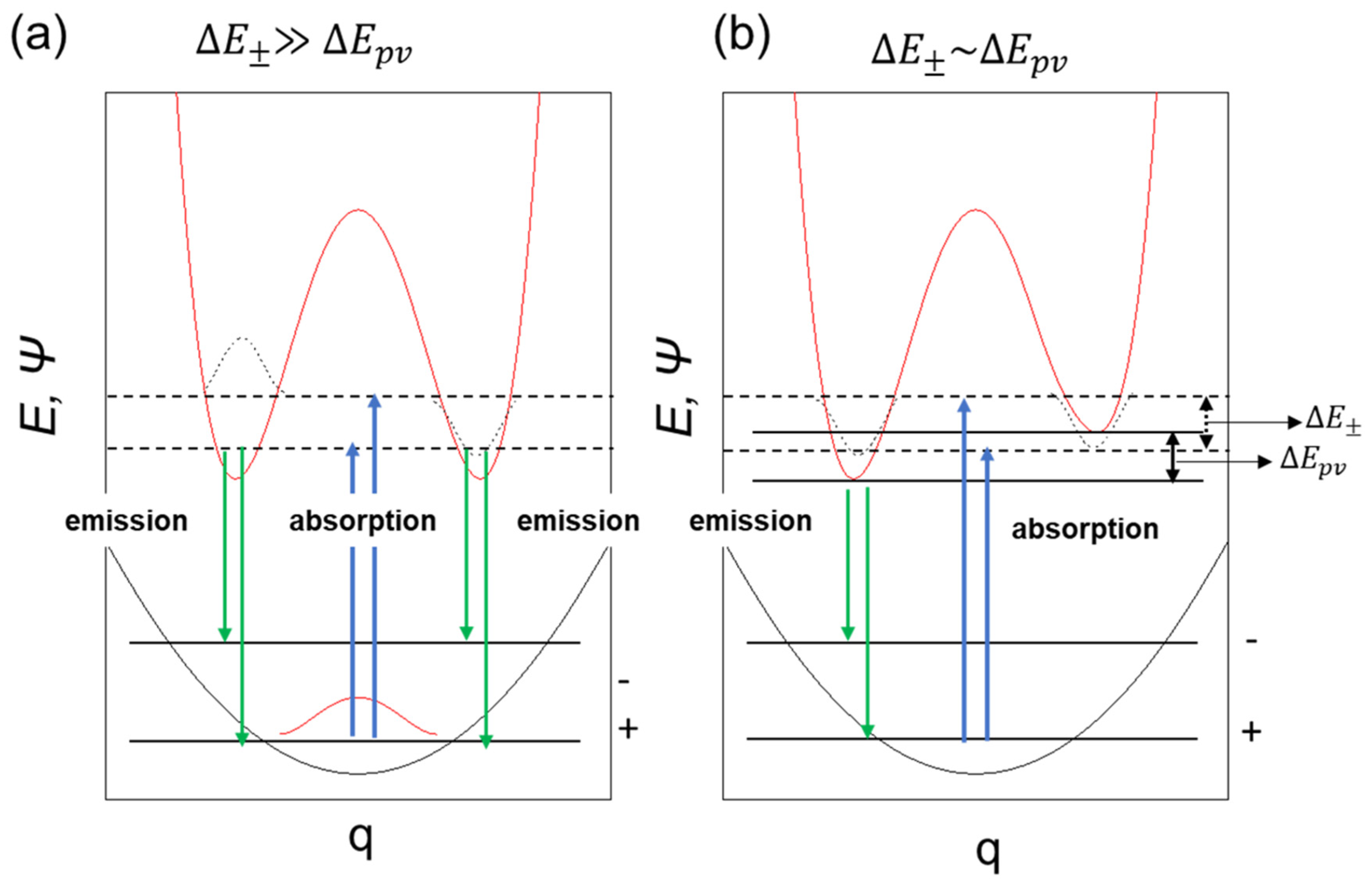
4. Discussion

The experimental observation of variation in glum for luminophores in relation to the viscosity of the solvent is evident from Figure 1, indicating handed MSB via MPV. The systematic study of critical photophysical properties such as τ, Φf, and Kf, revealed the photodynamics of luminophores at the excited state, which could be significantly modulated with changes in the viscosity of the media (Figure 2), whereas ∆µ depended on the presence of TICT (Section 5, ESI). Consequently, variations in GS and ES energy with dihedral angle predicted by DFT calculations supported the hypothesis of viscosity-dependent rotational freedom (Figure 3 and Figure 4). It is known that viscosity of the solvent can be directly correlated with the quantum tunneling energy barrier (Eb) of left- and right-handed states of chiral molecules [26,42], thus, one can speculate that rotamers studied here exhibit variation in handed chiroptical signals via variations in Eb. However, one can still be skeptical about the experimental observation of such as small bias in MSB via MPV, and a suitable theoretical model should be adopted that builds on several theoretical treatments and models. According to the theoretical treatment suggested by Hegstorm and McDermott [42], Quack et al. [27], and Bargueño [28], the chiral bias of eigenstates of chiral forms of molecules Ψ(±), is given by cos2β − sin2β = cos 2β, where β is the mixing angle ranging 0° to 45° and
cos   2 β = Δ E pv ( Δ E pv ) 2 + δ 2   ≈   Δ E pv δ
where δ is half of the tunneling splitting (∆E±).
(i)
In the case of molecules delocalizing rapidly between the left-handed and right-handed states, we have ∆E± >> ∆Epv, giving β→45°. Hence, cos β = sin β = (1/√2), which allows one to recover the parity eigenstates Ψ(±).For example, ammonia-like molecules remain in a superposition of left-handed and right-handed states because the tunneling time is in milliseconds.
(ii)
Molecules exhibiting stable handed forms have ∆Epv >> ∆E±, giving β→0. In this case, the energy eigenstates tend to become handed states, for example, biomolecules with stable chiral states.
(iii)
Other molecules that form the subject of the current study have ∆Epv and ∆E± that are comparable in magnitude. These molecules would remain in a superposition but with a minor and measurable bias to one side, of the order cos 2β.
For a typical polyatomic molecule with a ∆Epv of 10−16 kT, and a ∆E± of the order 10−10 kT, we get ∆Epv/δ = 10−6. With this insight, instead of looking at the very weak ∆Epv/kT, which employs the measurement of differences in the enantiomeric population based on Boltzmann distribution, one can measure ∆Epv/δ, which should possibly be measured by commonly employed spectropolarimeters. The notable examples are Faraday polarimeters to measure the electroweak optical rotation of atoms and cavity ring-down polarimeters for selected molecules. Hegstorm and McDermott further argue that any molecular property P exhibiting opposite sign for enantiomers would behave as
P± = ∓ P1 cos2β
In relation to the theoretical treatments presented above [27,28,42], Bouchiat et al. estimated theoretically that the degree of circular polarization of cesium vapor, lead vapor, and molecular oxygen gas, arising from parity-violating weak neutral current (WNC) is mediated by massive neutral Z0 boson (91 GeV) [54]. Actually, physicists have succeeded in measuring an optical rotation dispersion (ORD) spectrum of atomic lead vapor at 1240 nm as an absorption mode [50]. Moreover, Quack has proposed a method for the preparation of molecules in well-defined parity states, evolving with time and selective probing to an electronic excited state [54]. Later, Berger suggested a comprehensive method to probe molecules that are achiral at the ground state (∆E± >> ∆Epv) but due to the influence of parity violating potential in the excited state may acquire opposite parity [55]. This method also predicts the possibility of a smaller tunneling splitting barrier at excited states (smaller ∆E±), which would be comparable to parity violating energy, i.e., ∆E± ~ ∆Epv. Further, this approach may not only improve the ability to measure the magnitude of ∆Epv, but also widens the possible designs of realistic molecules that can be probed with electronic excitation. An emerging spectroscopic technique to study the effect of chirality in electronic excited states of the molecules is circularly polarized luminescence (CPL) spectroscopy). Notably, Bouchiat’s team detected a high-resolution PL-detective CD spectrum of cesium vapor by monitoring a near-infrared emission (6P1/2–7S1/2 transition at 1360 nm) upon circularly polarized photoexcitation of forbidden 6S1/2–7S1/2 transition at 539 nm [56]; similar to the fluorescence-detective circular dichroism spectroscopy, the so-called FD-CD technique that is equivalent to the present technique.
Based on the theoretical predictions, followed by the experimental attempts discussed above, one can hypothesize that experimental detection of MPV may be possible when proper luminophore rotamers with ∆Epv ~ ∆E± are employed under carefully controlled conditions at ambient temperature, using the state-of-the-art CPL and CD spectropolarimeters.
Thus far, several experimental studies have validated the MSB hypothesis in the quest to understand the differences in physical and optical properties of enantiomeric compounds [53,57,58,59,60,61]. With regard to the linear amplification model and the phase transition models at the far-from-equilibrium, when large numbers (>1010–1016) of enantiomeric luminophores are photoexcited macroscopically in a chorus to the first excited S1 state, the extreme small ee, and feeble ∆Epv may be greatly enhanced to a detectable level. It is understood that, in the case of enantiomeric rotamers in a symmetrical DW at the S1 state, the enantiomers may promptly oscillate between L- and R-states with time; subsequently time-averaged CPL signals are produced. Moreover, if enantiomers of rotamers with time are considered in dissymmetrical DW at the S1 state, they may favor a one-way route via quantum tunneling, mediated by a weak neutral current mediated by Z0 boson.
Figure 6 illustrates a system that is achiral at the ground state (∆E± >> ∆Epv) but due to the influence of parity-violating potential at the electronic excited state, may acquire inversed parity, which can be probed by radiative decay. This scenario led us to assume that only (+)- or (–)-sign CPL signals could be detectable via handed rotational and flip-flop motions.

5. Conclusions

Regarding the MPV hypothesis, we collected comprehensive experimental data from photoexcited MSB for three non-rigid π-conjugated rotamers (DSA, DSBA, and DSBP), and for comparison, BA and PP using CPL spectroscopy. DSA, DSBA, and DSBP carrying two floppy styryl groups were rationally designed and synthesized. The values of τ and Φf in selective solvents were obtained, followed by the calculated Kf value, which agreed with an enhanced radiative decay process when the viscosity of the solvents increased. Several theoretical calculations, including the effect of solvent viscosity on the τ and Φf [52] values provided new insight into the behavior of these luminophore rotamers at GS and ES and complemented all the present experimental observations. Our findings offer experimental templates for rationally designing non-rigid π-conjugated molecules [62], polymers, and supramolecules [50] as luminophores rotamers at ES to detect similar MPV effects, revealing only (–)-sign CPL signals and/or non-mirror-image CPL spectra, as mentioned above.

Supplementary Materials

The following are available online at https://www.mdpi.com/2073-8994/13/2/272/s1, Figure S1: 1H-NMR spectrum (a) and MALDI-TOF spectrum (b) of DSBA; Figure S2: 1H-NMR spectrum (a) and MALDI-TOF spectrum (b) of DSBP; Figure S3: CPL spectra of DSA in methanol (a), ethanol (b), n-propanol (c), n-butanol (d), n-pentanol (e), n-hexanol (f), n-heptanol (g), n-octanol (h), n-nonanol (i), n-decanol (j), n-undecanol (k), ethyleneglycol (l), 1,3-propanediol (m), 1,4-butanediol (n); Figure S4: CD spectra of DSA in methanol (a), ethanol (b), n-propanol (c), n-butanol (d), n-pentanol (e), n-hexanol (f), n-heptanol (g), n-octanol (h), n-nonanol (i), n-decanol (j), n-undecanol (k), 1,3-propanediol (l), 1,4-butanediol (m); Figure S5: CPL spectra of DSBA in methanol (a), ethanol (b), n-propanol (c), n-butanol (d), n-pentanol e), n-hexanol (f), n-heptanol (g), n-octanol (h), n-nonanol (i), n-decanol (j), n-undecanol (k), ethyleneglycol (l), 1,3-propanediol (m), 1,4-butanediol (n); Figure S6: CD spectra of DSBA in methanol (a), ethanol (b), n-propanol (c), n-butanol (d), n-pentanol (e), n-hexanol (f), n-heptanol (g), n-octanol (h), n-nonanol (i), n-decanol (j), n-undecanol (k), 1,3-propanediol (l), 1,4-butanediol (m); Figure S7: CPL spectra of DSBP in methanol ol (a), ethanol (b), n-propanol (c), n-butanol (d), n-pentanol e), n-hexanol (f), n-heptanol (g), n-octanol (h), n-nonanol (i), n-decanol (j), n-undecanol (k), ethyleneglycol (l), 1,3-propanediol (m), 1,4-butanediol (n); Figure S8: CD spectra of DSBP in methanol (a), ethanol (b), n-propanol (c), n-butanol (d), n-pentanol (e), n-hexanol (f), n-heptanol (g), n-octanol (h), n-nonanol (i), n-decanol (j), n-undecanol (k), 1,3-propanediol (l), 1,4-butanediol (m); Figure S9: CPL spectra of BA in methanol (a), ethanol (b), n-propanol (c); Figure S10: CPL spectra of PP in methanol (a), ethanol (b), n-propanol (c), n-butanol (d), n-pentanol e), n-hexanol (f), n-heptanol (g), n-octanol (h), n-nonanol (i), n-decanol (j), n-undecanol (k); Figure S11: CD spectra of PP in methanol (a), ethanol (b), n-propanol (c), n-butanol (d), n-pentanol (e), n-hexanol (f), n-heptanol (g), n-octanol (h), n-nonanol (i), n-decanol (j), n-undecanol (k), D2O (l), Figure S11: CD spectra of PP in methanol (a), ethanol (b), n-propanol (c), n-butanol (d), n-pentanol (e), n-hexanol (f), n-heptanol (g), n-octanol (h), n-nonanol (i), n-decanol (j), n-undecanol (k), D2O (l); Figure S12: Plot of va–vf vs. f(ε, n) and va + vf vs. f(ε, n) + 2g(n) for DSA in various alcohols; Figure S13: Plot of va-vf vs. f(ε, n) and va + vf vs. f(ε, n) + 2g(n) for DSBA in various alcohols; Figure S14: Plot of va–vf vs. f(ε, n) and va + vf vs. f(ε, n) + 2g(n) for DSBP in various alcohols; Figure S15: Photographs of solid state emission of DSA (a), DSBA (b) and DSBP (c); Figure S16: Graph of forced dihedral angle vs. ground state energy of BA; Figure S17: Graph of glum vs. viscosity of the solvent for DA (a) and PP (b); Figure S18: Experimental and predicted UV-Visible spectra of DSA obtained with TD-DFT (B3LYP, 6-311G basis set). Table S1: Table of solvent parameters; Table S2: Table of transition dipole moment values for DSA, DSBA, and DSBP; Table S3: Table of Kf, Φ and τ values of DSA in selected solvents; Table S4: Table of Kf, Φ and τ values of DSBA in selected solvents; Table S5: Table of Kf, Φf, and τ values of DSBP in selected solvents; Table S6: Optimized structure, HOMO and LUMO of DSA, DSBA, and DSBP obtained with DFT (B3LYP functional, 6-311G basis set) using Gaussian 09 (rev D.01) and GaussView5.

Author Contributions

Three luminophores, DSA, DSBA, and DSBP, were synthesized and characterized by P.P. and B.N. The chiroptical properties of five luminophores (DSA, DSBA, DSBP, BA, and PP) were co-measured and co-verified by P.P. and M.F, who was a technical staffer at NAIST using CPL-200 and CD J820 spectrometers located in a lab of M.F. The spectrometers were routinely maintained and calibrated with ethanol solutions (0.4 wt/v) of D-/L-camphor by Yasuo Nakanishi who is a JASCO engineer. The relative quantum efficiency using 9,10-diphenylanthracene (Φf 0.97 in cyclohexane) as a standard was measured and preliminarily analyzed by M.F., and P.P. Theoretical calculation obtained with Gaussian09 package was carried out by P.P. and M.F. The lifetime of PL was measured and analyzed by S.S., P.P., and B.N. The manuscript was co-written by P.P., M.F., and B.N. Requests for all original raw and processed data sets, should be sent to P.P. ([email protected]) and M.F. ([email protected]). All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by a grant from the Department of Science and Technology, India (SR/NM/NS-1439/2014).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data may be available on request.

Acknowledgments

P.P. is thankful to the SERB, Department of Science and Technology, India for a National Post-Doctoral Fellowship. Thanks to Seiko Amazumi (S.A.) for co-measurement and co-verification of CD and CPL spectra.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

  1. Breslow, R. A likely possible origin of homochirality in amino acids and sugars on prebiotic earth. Tetrahedron Lett. 2011, 52, 2028–2032. [Google Scholar] [CrossRef]
  2. Harada, K.; Fox, S.W. Thermal Synthesis of Natural Amino-Acids from a Postulated Primitive Terrestrial Atmosphere. Nat. Cell Biol. 1964, 201, 335–336. [Google Scholar] [CrossRef] [PubMed]
  3. Hanafusa, H.; Akabori, S. Polymerization of Aminoacetonitrile. Bull. Chem. Soc. Jpn. 1959, 32, 626–630. [Google Scholar] [CrossRef] [Green Version]
  4. Miller, S.L. A Production of Amino Acids Under Possible Primitive Earth Conditions. Science 1953, 117, 528–529. [Google Scholar] [CrossRef] [Green Version]
  5. Wigner, E. Einige Folgerungen aus der Schrödingerschen Theorie für die Termstrukturen. Eur. Phys. J. A 1927, 43, 624–652. [Google Scholar] [CrossRef]
  6. Yamagata, Y. A hypothesis for the asymmetric appearance of biomolecules on earth. J. Theor. Biol. 1966, 11, 495–498. [Google Scholar] [CrossRef]
  7. Rein, D.W. Some remarks on parity violating effects of intramolecular interactions. J. Mol. Evol. 1974, 4, 15–22. [Google Scholar] [CrossRef] [PubMed]
  8. Letokhov, V. On difference of energy levels of left and right molecules due to weak interactions. Phys. Lett. A 1975, 53, 275–276. [Google Scholar] [CrossRef]
  9. Fujiki, M. Mirror Symmetry Breaking in Helical Polysilanes: Preference between Left and Right of Chemical and Physical Origin. Symmetry 2010, 2, 1625–1652. [Google Scholar] [CrossRef] [Green Version]
  10. Keszthelyi, L. Origin of the asymmetry of biomolecules and weak interaction. Orig. life Evol. Biosph. 1977, 8, 299–340. [Google Scholar] [CrossRef] [PubMed]
  11. Harris, R.; Stodolsky, L. Quantum beats in optical activity and weak interactions. Phys. Lett. B 1978, 78, 313–317. [Google Scholar] [CrossRef]
  12. Hegstrom, R.A.; Rein, D.W.; Sandars, P.G.H. Calculation of the parity nonconserving energy difference between mirror-image molecules. J. Chem. Phys. 1980, 73, 2329–2341. [Google Scholar] [CrossRef]
  13. Mason, S.F.; Tranter, G.E. Energy inequivalence of peptide enantiomers from parity non-conservation. J. Chem. Soc. Chem. Commun. 1983, 117–119. [Google Scholar] [CrossRef]
  14. Mason, S.; Tranter, G. The parity-violating energy difference between enantiomeric molecules. Mol. Phys. 1984, 53, 1091–1111. [Google Scholar] [CrossRef]
  15. Barron, L.D. Symmetry and molecular chirality. Chem. Soc. Rev. 1986, 15, 189–223. [Google Scholar] [CrossRef]
  16. Quack, M. Structure and Dynamics of Chiral Molecules. Angew. Chem. Int. Ed. 1989, 28, 571–586. [Google Scholar] [CrossRef]
  17. Hegstrom, R.A.; Kondepudi, D.K. The Handedness of the Universe. Sci. Am. 1990, 262, 108–115. [Google Scholar] [CrossRef]
  18. Salam, A. The role of chirality in the origin of life. J. Mol. Evol. 1991, 33, 105–113. [Google Scholar] [CrossRef]
  19. MacDermott, A.J. Electro weak enantioselection and the origin of life. Orig. Life Evol. Biosph. 1995, 25, 191–199. [Google Scholar] [CrossRef]
  20. Kikuchi, O.; Kiyonaga, H. Parity-violating energy shift of helical n-alkanes. J. Mol. Struct. Theochem. 1994, 312, 271–274. [Google Scholar] [CrossRef]
  21. Avetisov, V.; Goldanskii, V. Mirror symmetry breaking at the molecular level. Proc. Natl. Acad. Sci. USA 1996, 93, 11435–11442. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  22. Bonner, W.A. Enantioselective autocatalysis. IV. Implications for parity violation effects. Orig. Life Evol. Biosph. 1996, 26, 27–45. [Google Scholar] [CrossRef]
  23. Szabó-Nagy, A.; Keszthelyi, L. Demonstration of the parity-violating energy difference between enantiomers. Proc. Natl. Acad. Sci. USA 1999, 96, 4252–4255. [Google Scholar] [CrossRef] [Green Version]
  24. Compton, R.N.; Pagni, R.M. The Chirality of Biomolecules. Adv. At. Mol. Opt. Phys. 2002, 48, 219–261. [Google Scholar] [CrossRef]
  25. Schwerdtfeger, P.; Gierlich, J.; Bollwein, T. Large Parity-Violation Effects in Heavy-Metal-Containing Chiral Compounds. Angew. Chem. Int. Ed. 2003, 42, 1293–1296. [Google Scholar] [CrossRef]
  26. MacDermott, A.; Hegstrom, R. A proposed experiment to measure the parity-violating energy difference between enantiomers from the optical rotation of chiral ammonia-like “cat” molecules. Chem. Phys. 2004, 305, 55–68. [Google Scholar] [CrossRef]
  27. Quack, M.; Stohner, J.; Willeke, M. High-Resolution Spectroscopic Studies and Theory of Parity Violation in Chiral Molecules. Annu. Rev. Phys. Chem. 2008, 59, 741–769. [Google Scholar] [CrossRef]
  28. Bargueño, P.; Gonzalo, I.; De Tudela, R.P.; Gonzalo, I. Detection of parity violation in chiral molecules by external tuning of electroweak optical activity. Phys. Rev. A 2009, 80. [Google Scholar] [CrossRef] [Green Version]
  29. Dorta-Urra, A.; Peñate-Rodríguez, H.C.; Bargueño, P.; Rojas-Lorenzo, G.; Miret-Artés, S. Dissipative geometric phase and decoherence in parity-violating chiral molecules. J. Chem. Phys. 2012, 136, 174505. [Google Scholar] [CrossRef] [Green Version]
  30. Famiano, M.A.; Boyd, R.N.; Kajino, T.; Onaka, T.; Mo, Y. Amino Acid Chiral Selection Via Weak Interactions in Stellar Environments: Implications for the Origin of Life. Sci. Rep. 2018, 8, 8833. [Google Scholar] [CrossRef] [Green Version]
  31. Daussy, C.; Marrel, T.; Amy-Klein, A.; Nguyen, C.T.; Bordé, C.J.; Chardonnet, C. Limit on the Parity Nonconserving Energy Difference between the Enantiomers of a Chiral Molecule by Laser Spectroscopy. Phys. Rev. Lett. 1999, 83, 1554–1557. [Google Scholar] [CrossRef]
  32. Lee, T.D.; Yang, C.N. Question of Parity Conservation in Weak Interactions. Phys. Rev. 1956, 104, 254–258. [Google Scholar] [CrossRef]
  33. Wu, C.S.; Ambler, E.; Hayward, R.W.; Hoppes, D.D.; Hudson, R.P. Experimental Test of Parity Conservation in Beta Decay. Phys. Rev. 1957, 105, 1413–1415. [Google Scholar] [CrossRef]
  34. Quantum Systems in Chemistry and Physics. Concepts Methods Appl. Quantum Syst. Chem. Phys. 2012, 26, 47–76. [CrossRef]
  35. Quack, M. How Important is Parity Violation for Molecular and Biomolecular Chirality? Angew. Chem. Int. Ed. 2002, 41, 4618–4630. [Google Scholar] [CrossRef]
  36. Soncini, A.; Faglioni, F.; Lazzeretti, P. Parity-violating contributions to nuclear magnetic shielding. Phys. Rev. A 2003, 68, 033402. [Google Scholar] [CrossRef]
  37. Arimondo, E.; Glorieux, P.; Oka, T. Observation of inverted infrared lamb dips in separated optical isomers. Opt. Commun. 1977, 23, 369–372. [Google Scholar] [CrossRef]
  38. Crassous, J.; Monier, F.; Dutasta, J.-P.; Ziskind, M.; Daussy, C.; Grain, C.; Chardonnet, C. Search for Resolution of Chiral Fluorohalogenomethanes and Parity-Violation Effects at the Molecular Level. Chem. Phys. Chem. 2003, 4, 541–548. [Google Scholar] [CrossRef] [PubMed]
  39. Lahamer, A.S.; Mahurin, S.M.; Compton, R.N.; House, D.; Laerdahl, J.K.; Lein, M.; Schwerdtfeger, P. Search for a Parity-Violating Energy Difference between Enantiomers of a Chiral Iron Complex. Phys. Rev. Lett. 2000, 85, 4470–4473. [Google Scholar] [CrossRef]
  40. Robert, J.-B.; Barra, A. NMR and parity nonconservation. Experimental requirements to observe a difference between enantiomer signals. Chirality 2001, 13, 699–702. [Google Scholar] [CrossRef]
  41. Darquié, B.; Stoeffler, C.; Shelkovnikov, A.; Daussy, C.; Amy-Klein, A.; Chardonnet, C.; Zrig, S.; Guy, L.; Crassous, J.; Soulard, P.; et al. Progress toward the first observation of parity violation in chiral molecules by high-resolution laser spectroscopy. Chirality 2010, 22, 870–884. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  42. Fujiki, M.; Koe, J.R.; Mori, T.; Kimura, Y. Questions of Mirror Symmetry at the Photoexcited and Ground States of Non-Rigid Luminophores Raised by Circularly Polarized Luminescence and Circular Dichroism Spectroscopy: Part 1. Oligofluorenes, Oligophenylenes, Binaphthyls and Fused Aromatics. Molecules 2018, 23, 2606. [Google Scholar] [CrossRef] [Green Version]
  43. Fujiki, M.; Koe, J.R.; Amazumi, S. Questions of Mirror Symmetry at the Photoexcited and Ground States of Non-Rigid Luminophores Raised by Circularly Polarized Luminescence and Circular Dichroism Spectroscopy. Part 2: Perylenes, BODIPYs, Molecular Scintillators, Coumarins, Rhodamine B, and DCM. Symmetry 2019, 11, 363. [Google Scholar] [CrossRef] [Green Version]
  44. Norrgard, E.B.; Barker, D.S.; Eckel, S.; Fedchak, J.A.; Klimov, N.N.; Scherschligt, J. Nuclear-spin dependent parity violation in optically trapped polyatomic molecules. Commun. Phys. 2019, 2, 1–6. [Google Scholar] [CrossRef] [Green Version]
  45. Eills, J.; Blanchard, J.W.; Bougas, L.; Kozlov, M.G.; Pines, A.; Budker, D. Measuring molecular parity nonconservation using nuclear-magnetic-resonance spectroscopy. Phys. Rev. A 2017, 96, 042119. [Google Scholar] [CrossRef] [Green Version]
  46. Sang, Y.; Liu, M. Symmetry Breaking in Self-Assembled Nanoassemblies. Symmetry 2019, 11, 950. [Google Scholar] [CrossRef] [Green Version]
  47. Emeis, C.; Oosterhoff, L. Emission of circularly-polarised radiation by optically-active compounds. Chem. Phys. Lett. 1967, 1, 129–132. [Google Scholar] [CrossRef]
  48. Ribó, J.M.; Hochberg, D.; Crusats, J.; El-Hachemi, Z.; Moyano, A. Spontaneous mirror symmetry breaking and origin of biological homochirality. J. R. Soc. Interface 2017, 14, 20170699. [Google Scholar] [CrossRef]
  49. Ribó, J.M.; Hochberg, D. Chemical Basis of Biological Homochirality during the Abiotic Evolution Stages on Earth. Symmetry 2019, 11, 814. [Google Scholar] [CrossRef] [Green Version]
  50. He, J.; Xu, B.; Chen, F.; Xia, H.; Li, K.; Ye, L.; Tian, W. Aggregation-Induced Emission in the Crystals of 9,10-Distyrylanthracene Derivatives: The Essential Role of Restricted Intramolecular Torsion. J. Phys. Chem. C 2009, 113, 9892–9899. [Google Scholar] [CrossRef]
  51. Ii, G.J.; Jackson, W.R.; Choi, C.Y.; Bergmark, W.R. Solvent effects on emission yield and lifetime for coumarin laser dyes. Requirements for a rotatory decay mechanism. J. Phys. Chem. 1985, 89, 294–300. [Google Scholar] [CrossRef]
  52. Nadaf, Y.; Mulimani, B.; Gopal, M.; Inamdar, S. Ground and excited state dipole moments of some exalite UV laser dyes from solvatochromic method using solvent polarity parameters. J. Mol. Struct. Theochem. 2004, 678, 177–181. [Google Scholar] [CrossRef]
  53. Kozlova, S.; Gabuda, S.P. Thermal properties of Zn2(C8H4O4)2•C6H12N2 metal-organic framework compound and mirror symmetry violation of dabco molecules. Sci. Rep. 2017, 7, 11505. [Google Scholar] [CrossRef]
  54. Quack, M. On the measurement of the parity violating energy difference between enantiomers. Chem. Phys. Lett. 1986, 132, 147–153. [Google Scholar] [CrossRef]
  55. Berger, R. Molecular parity violation in electronically excited states. Phys. Chem. Chem. Phys. 2002, 5, 12–17. [Google Scholar] [CrossRef]
  56. Bouchiat, M.-A.; Pottier, L.; Howard, R.E.; Jackel, L.D.; Mankiewich, P.M.; Skocpol, W.J. Optical Experiments and Weak Interactions. Science 1986, 234, 1203–1210. [Google Scholar] [CrossRef] [PubMed]
  57. Wang, W.; Yi, F.; Ni, Y.; Zhao, Z.; Jin, X.; Tang, Y. Parity Violation of Electroweak Force in Phase Transitions of Single Crystals of D- and L-Alanine and Valine. J. Biol. Phys. 2000, 26, 51–65. [Google Scholar] [CrossRef] [PubMed]
  58. Pagni, R.M.; Compton, R.N. Asymmetric Synthesis of Optically Active Sodium Chlorate and Bromate Crystals. Cryst. Growth Des. 2002, 2, 249–253. [Google Scholar] [CrossRef]
  59. Scolnik, Y.; Portnaya, I.; Cogan, U.; Tal, S.; Haimovitz, R.; Fridkin, M.; Elitzur, A.C.; Deamer, D.W.; Shinitzky, M. Subtle differences in structural transitions between poly-l- and poly-d-amino acids of equal length in water. Phys. Chem. Chem. Phys. 2005, 8, 333–339. [Google Scholar] [CrossRef]
  60. Kodona, E.K.; Alexopoulos, C.; Panou-Pomonis, E.; Pomonis, P.J. Chirality and helix stability of polyglutamic acid enantiomers. J. Colloid Interface Sci. 2008, 319, 72–80. [Google Scholar] [CrossRef]
  61. Albert, S.; Arn, F.; Bolotova, I.; Chen, Z.; Fábri, C.; Grassi, G.; Lerch, P.; Quack, M.; Seyfang, G.; Wokaun, A.; et al. Synchrotron-Based Highest Resolution Terahertz Spectroscopy of the ν24Band System of 1,2-Dithiine (C4H4S2): A Candidate for Measuring the Parity Violating Energy Difference between Enantiomers of Chiral Molecules. J. Phys. Chem. Lett. 2016, 7, 3847–3853. [Google Scholar] [CrossRef] [PubMed]
  62. Inamdar, S.; Nadaf, Y.; Mulimani, B. Ground and excited state dipole moments of exalite 404 and exalite 417 UV laser dyes determined from solvatochromic shifts of absorption and fluorescence spectra. J. Mol. Struct. Theochem. 2003, 624, 47–51. [Google Scholar] [CrossRef]
Symmetry 13 00272 ch001 550
Chart 1. Chemical structure of luminophore rotamers. The arrow in red represents the labile rotation axis. DSA, DSBA, and DSBP show less-polar transoid and polar cisoid vinylic conformers.
Chart 1. Chemical structure of luminophore rotamers. The arrow in red represents the labile rotation axis. DSA, DSBA, and DSBP show less-polar transoid and polar cisoid vinylic conformers.
Symmetry 13 00272 ch001
Symmetry 13 00272 g001 550
Figure 1. Comparison of the CPL and photo-luminescence (PL) spectra in methanol and 1,4-butanediol for DSA excited at 420 nm (a), DSBA excited at 390 nm (b), and DSBP excited at 320 nm (c). The glum values at 0-0 PL band extremum of DSA (d), DSBA (e), and DSBP (f) as a function of the viscosity of alcohol, respectively: methanol (0.55 cP), ethanol (1.09 cP), n-propanol (1.96 cP), n-butanol (2.59 cP), n-pentanol (3.47 cP), n-hexanol (4.59 cP), n-heptanol (5.97 cP), n-octanol (7.59 cP), n-nonanol (9.51 cP), n-decanol (11.50 cP), ethylene glycol (16.1 cP), n-undecanol (16.95 cP), 1,3-propandiol (33.0 cP), and 1,4-butanediol (71.0 cP) [42,43].
Figure 1. Comparison of the CPL and photo-luminescence (PL) spectra in methanol and 1,4-butanediol for DSA excited at 420 nm (a), DSBA excited at 390 nm (b), and DSBP excited at 320 nm (c). The glum values at 0-0 PL band extremum of DSA (d), DSBA (e), and DSBP (f) as a function of the viscosity of alcohol, respectively: methanol (0.55 cP), ethanol (1.09 cP), n-propanol (1.96 cP), n-butanol (2.59 cP), n-pentanol (3.47 cP), n-hexanol (4.59 cP), n-heptanol (5.97 cP), n-octanol (7.59 cP), n-nonanol (9.51 cP), n-decanol (11.50 cP), ethylene glycol (16.1 cP), n-undecanol (16.95 cP), 1,3-propandiol (33.0 cP), and 1,4-butanediol (71.0 cP) [42,43].
Symmetry 13 00272 g001
Symmetry 13 00272 g002 550
Figure 2. Relationships between radiative decay rate (Kf), photoluminescence lifetime (τ), and quantum yield (Φf) of DSA (red filled circles and squares), DSBA (blue filled circles and squares), and DSBP (black filled circles and squares) (a), the relationship between Φf, τ and the viscosity of four alcohols (b), and the relationship between Kf and the solvent viscosity (c). The solvents are ethanol 1.19 cP (25 °C), n-pentanol 3.47 cP (25 °C), n-octanol 7.59 cP (25 °C), and n-undecanol 16.95 cP (25 °C)) [48,49].
Figure 2. Relationships between radiative decay rate (Kf), photoluminescence lifetime (τ), and quantum yield (Φf) of DSA (red filled circles and squares), DSBA (blue filled circles and squares), and DSBP (black filled circles and squares) (a), the relationship between Φf, τ and the viscosity of four alcohols (b), and the relationship between Kf and the solvent viscosity (c). The solvents are ethanol 1.19 cP (25 °C), n-pentanol 3.47 cP (25 °C), n-octanol 7.59 cP (25 °C), and n-undecanol 16.95 cP (25 °C)) [48,49].
Symmetry 13 00272 g002
Symmetry 13 00272 g003 550
Figure 3. The calculated energy (DFT/TD-DFT, B3LYP, 6-311G) for DSBP at GS (blue filled circles) and ES (red filled circles) and oscillator strength (green filled circles) as a function of dihedral angle of biphenyl groups (a). The lowest transition energy (left-side ordinate in eV, red filled circles and right-side ordinate in nm, blue filled circles) as a function of dihedral angle of biphenyl groups (b).
Figure 3. The calculated energy (DFT/TD-DFT, B3LYP, 6-311G) for DSBP at GS (blue filled circles) and ES (red filled circles) and oscillator strength (green filled circles) as a function of dihedral angle of biphenyl groups (a). The lowest transition energy (left-side ordinate in eV, red filled circles and right-side ordinate in nm, blue filled circles) as a function of dihedral angle of biphenyl groups (b).
Symmetry 13 00272 g003
Symmetry 13 00272 g004 550
Figure 4. The calculated energy, S0-S1 (in kcal mol–1, green filled circles) obtained with DFT/TD-DFT, B3LYP, 6-311G) for DSBA at GS (red filled circles) and ES (blue filled circles) as a function of the dihedral angle of bianthryl groups (a). The S0-S1 transition (in nm, red filled circles) and oscillator strength (f, blue filled circles) as a function of the dihedral angle of bianthryl groups (b).
Figure 4. The calculated energy, S0-S1 (in kcal mol–1, green filled circles) obtained with DFT/TD-DFT, B3LYP, 6-311G) for DSBA at GS (red filled circles) and ES (blue filled circles) as a function of the dihedral angle of bianthryl groups (a). The S0-S1 transition (in nm, red filled circles) and oscillator strength (f, blue filled circles) as a function of the dihedral angle of bianthryl groups (b).
Symmetry 13 00272 g004
Symmetry 13 00272 g005 550
Figure 5. The predicted CD (top) and UV-visible (bottom) spectra of DSBA (a) and DSBP (b) at GS (red lines) and ES (blue lines).
Figure 5. The predicted CD (top) and UV-visible (bottom) spectra of DSBA (a) and DSBP (b) at GS (red lines) and ES (blue lines).
Symmetry 13 00272 g005
Symmetry 13 00272 g006 550
Figure 6. A schematic model of symmetrical double-well (a) and dis-symmetrical double-well in the photoexcited state (b) coupled with single well in the ground state.
Figure 6. A schematic model of symmetrical double-well (a) and dis-symmetrical double-well in the photoexcited state (b) coupled with single well in the ground state.
Symmetry 13 00272 g006
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Puneet, P.; Singh, S.; Fujiki, M.; Nandan, B. Handed Mirror Symmetry Breaking at the Photo-Excited State of π-Conjugated Rotamers in Solutions. Symmetry 2021, 13, 272. https://doi.org/10.3390/sym13020272

AMA Style

Puneet P, Singh S, Fujiki M, Nandan B. Handed Mirror Symmetry Breaking at the Photo-Excited State of π-Conjugated Rotamers in Solutions. Symmetry. 2021; 13(2):272. https://doi.org/10.3390/sym13020272

Chicago/Turabian Style

Puneet, Puhup, Sajan Singh, Michiya Fujiki, and Bhanu Nandan. 2021. "Handed Mirror Symmetry Breaking at the Photo-Excited State of π-Conjugated Rotamers in Solutions" Symmetry 13, no. 2: 272. https://doi.org/10.3390/sym13020272

APA Style

Puneet, P., Singh, S., Fujiki, M., & Nandan, B. (2021). Handed Mirror Symmetry Breaking at the Photo-Excited State of π-Conjugated Rotamers in Solutions. Symmetry, 13(2), 272. https://doi.org/10.3390/sym13020272

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop