Design of a Hyperbolic Metamaterial as a Waveguide for Low-Loss Propagation of Plasmonic Wave
Abstract
:1. Introduction
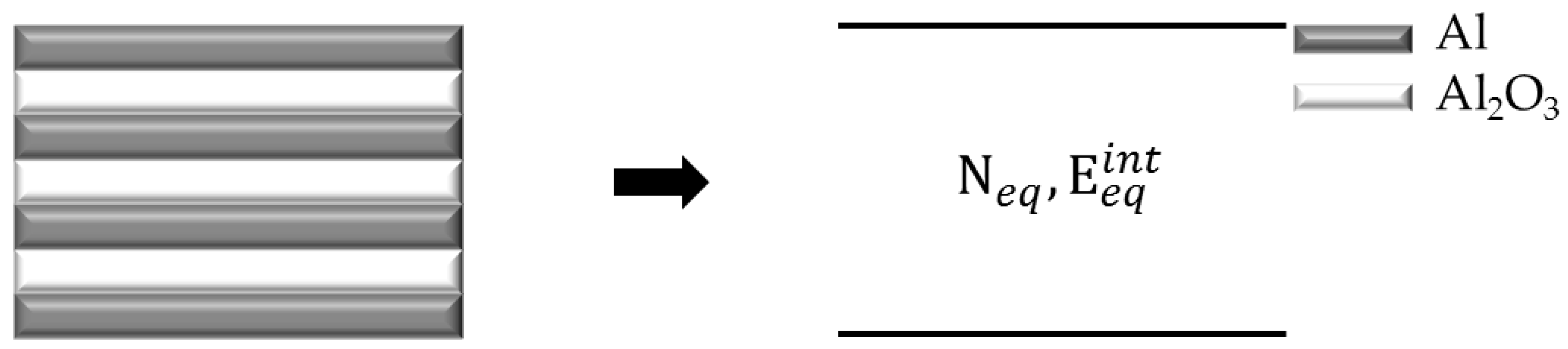
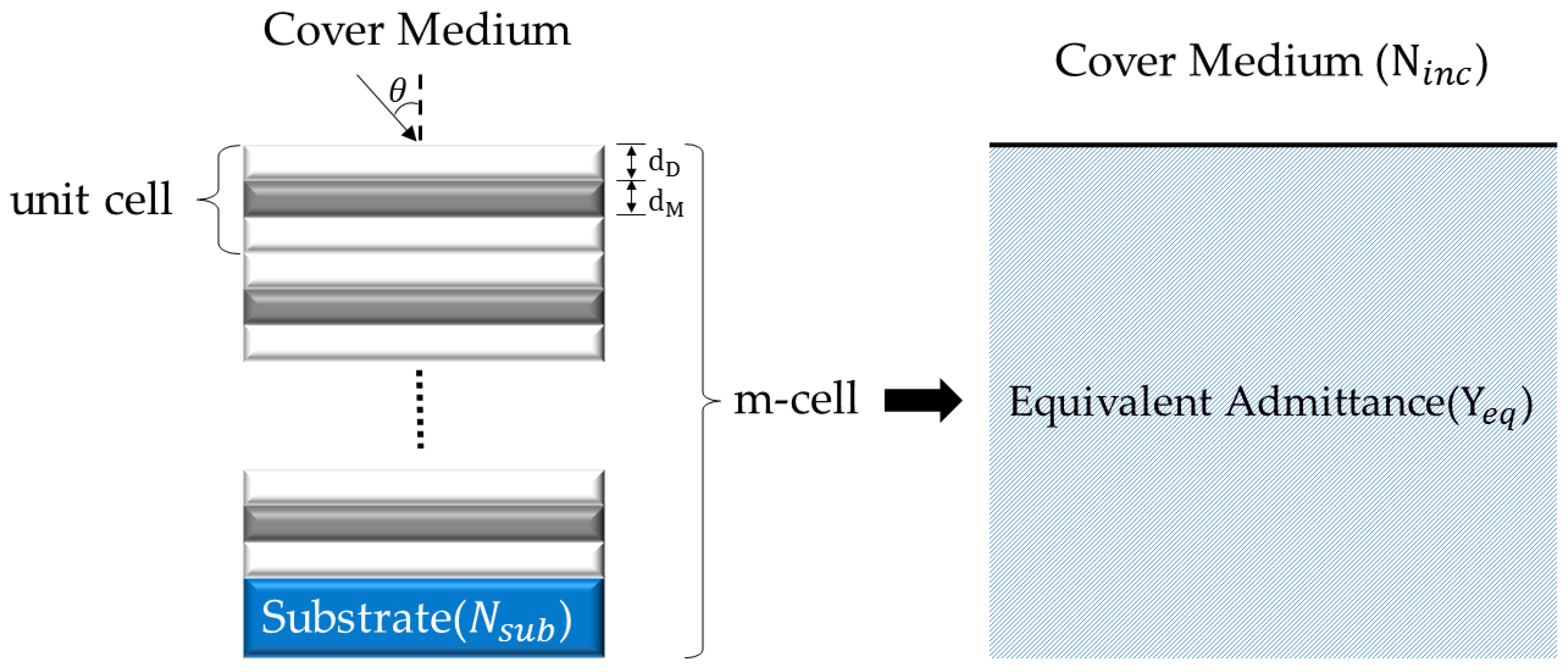
2. Materials and Methods
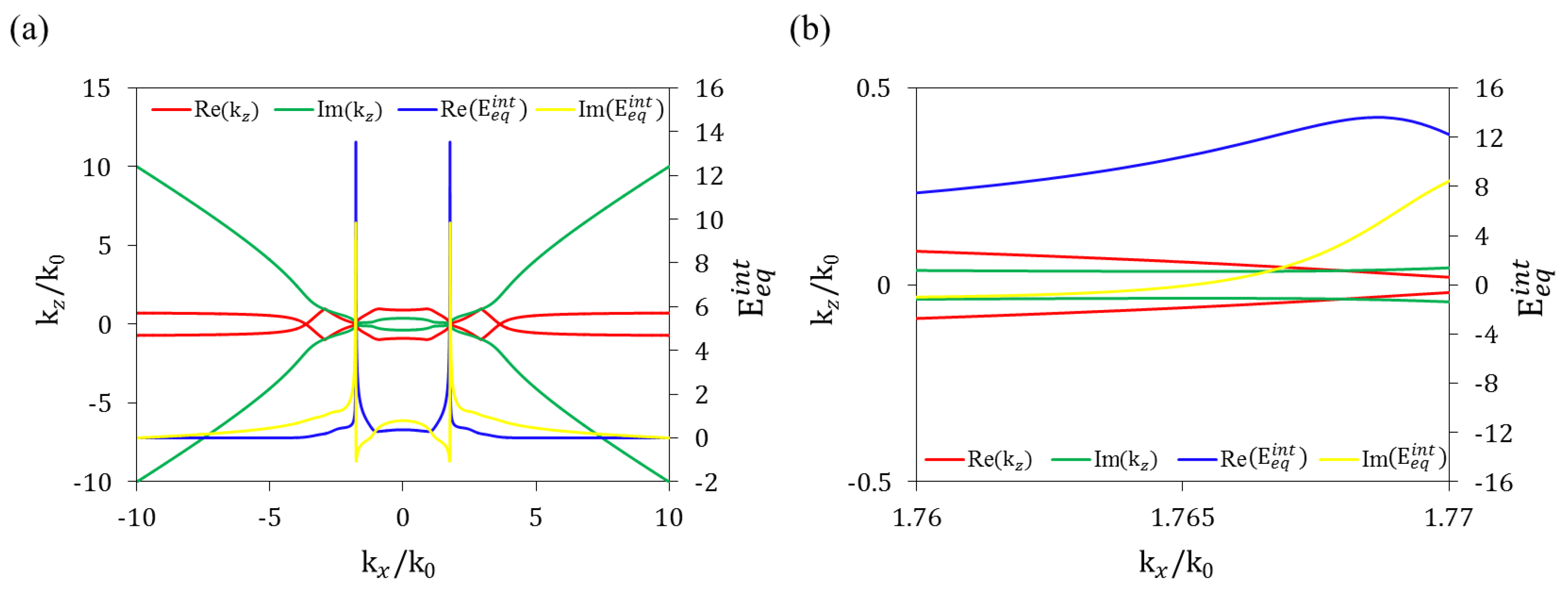
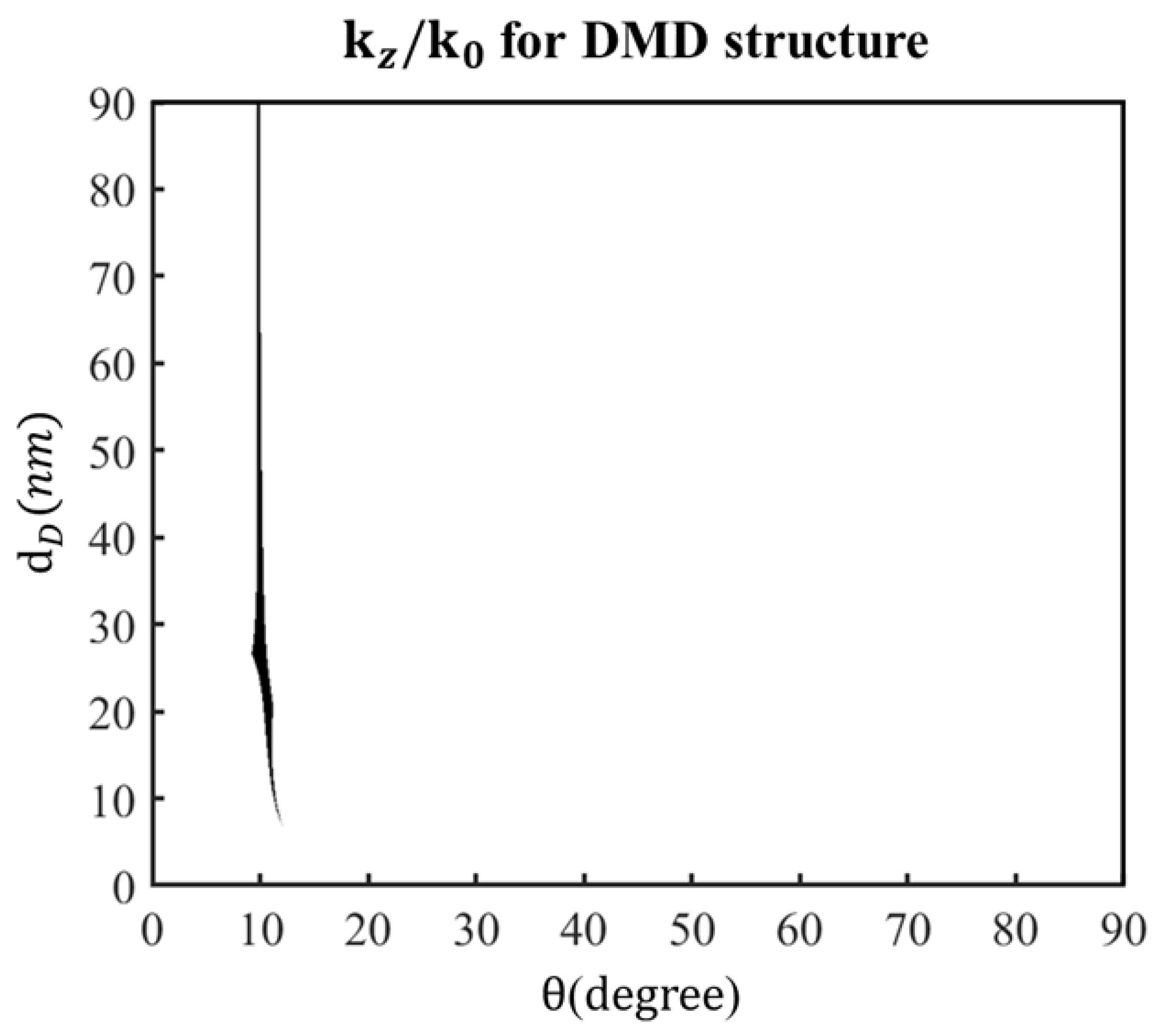
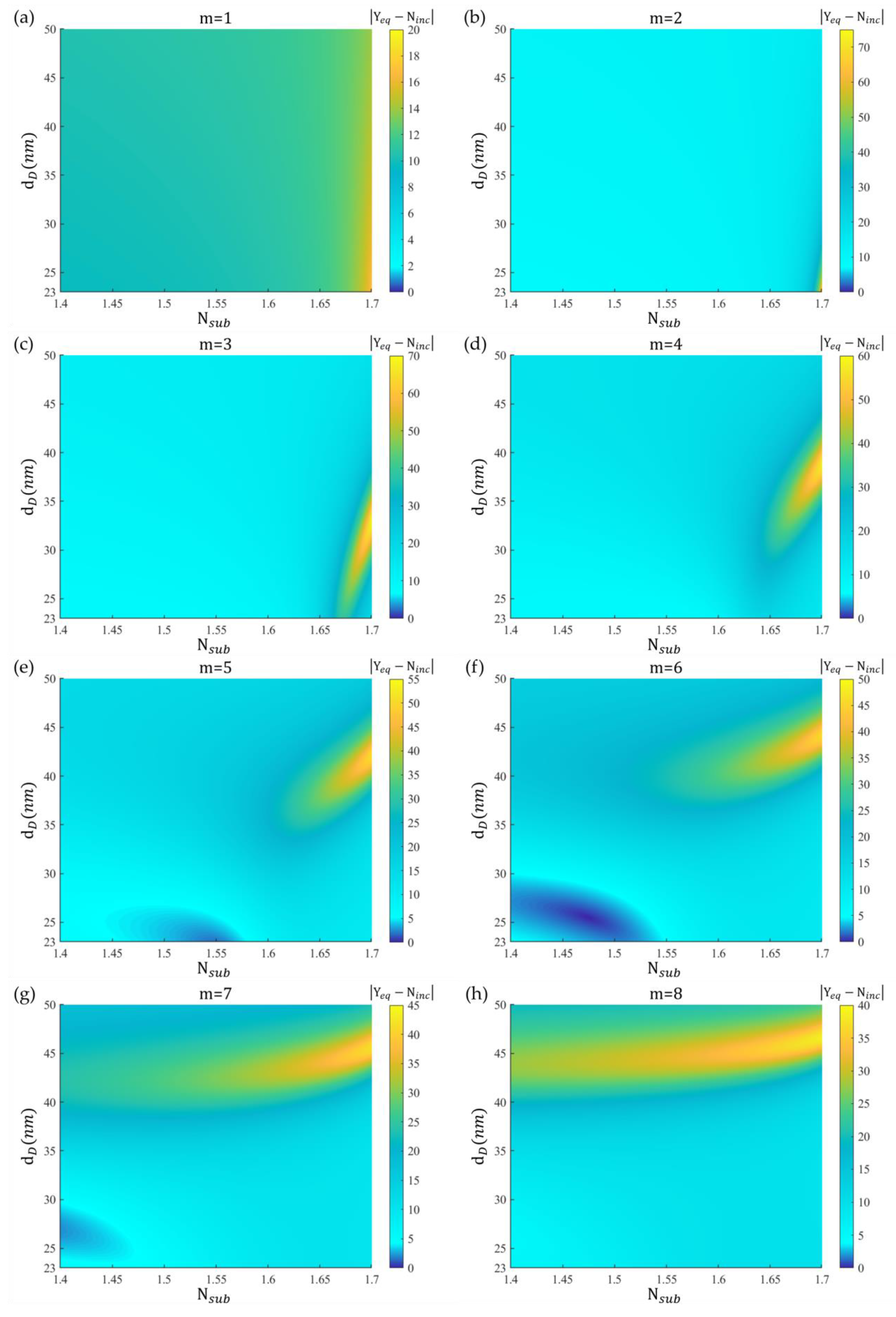
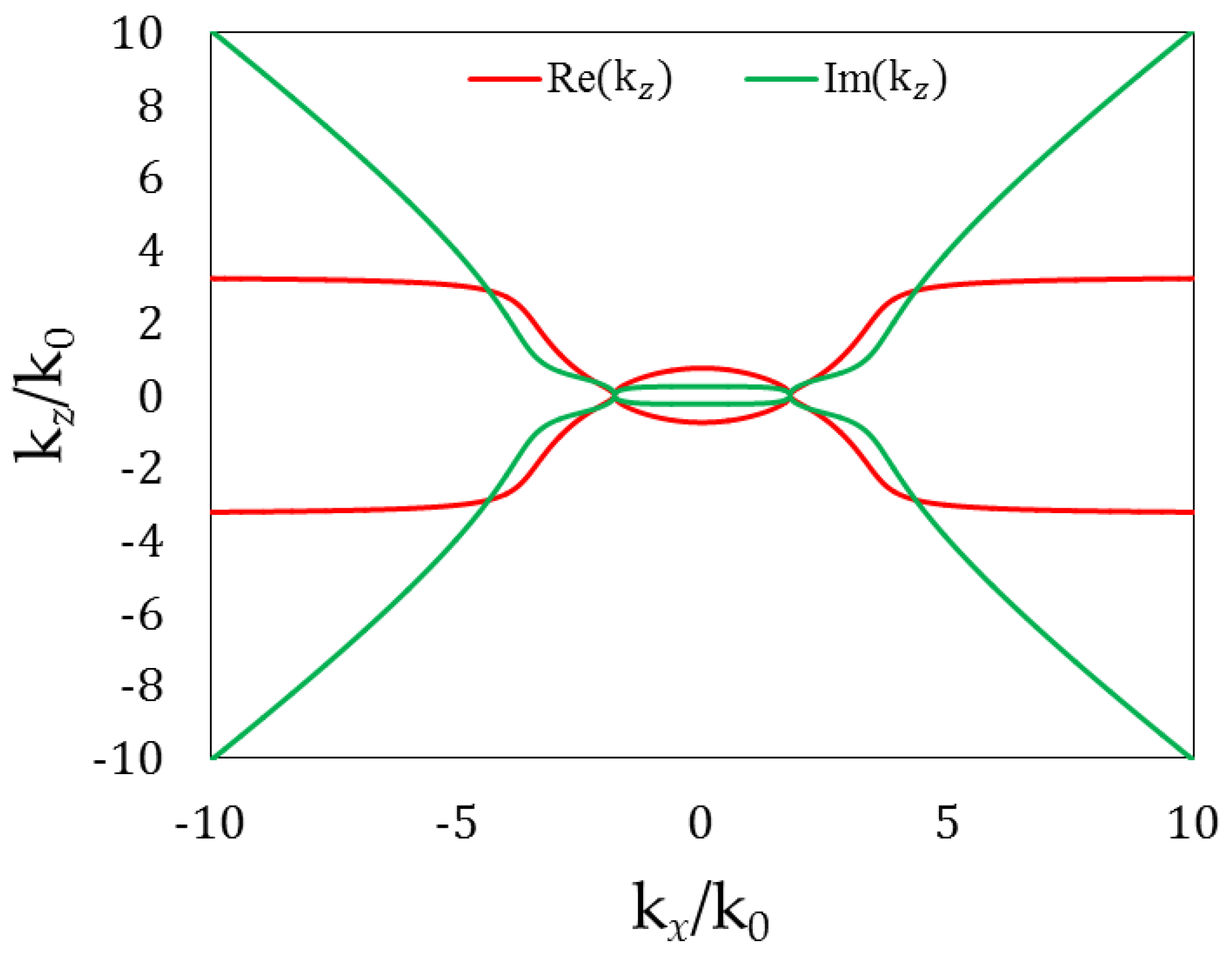
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cai, W.; Shalaev, V.M. Optical Metamaterials; Springer: Berlin, Germany, 2010; Volume 10. [Google Scholar]
- Poddubny, A.; Iorsh, I.; Belov, P.; Kivshar, Y. Hyperbolic metamaterials. Nat. Photonics 2013, 7, 948–957. [Google Scholar] [CrossRef]
- Peragut, F.; Cerutti, L.; Baranov, A.; Hugonin, J.; Taliercio, T.; Wilde, Y.D.; Greffet, J. Hyperbolic metamaterials and surface plasmon polaritons. Optica 2017, 4, 1409–1415. [Google Scholar] [CrossRef]
- Huo, P.; Zhang, S.; Liang, Y.; Lu, Y.; Xu, T. Hyperbolic Metamaterials and Metasurfaces: Fundamentals and Applications. Adv. Opt. Mater. 2019, 7, 1801616. [Google Scholar] [CrossRef]
- Lee, H.; Liu, Z.; Xiong, Y.; Sun, C.; Zhang, X. Development of optical hyperlens for imaging below the diffraction limit. Opt. Express 2007, 15, 15886–15891. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Lee, H.; Xiong, Y.; Sun, C.; Zhang, X. Far-field optical hyperlens magnifying sub-diffraction-limited objects. Science 2007, 315, 1686. [Google Scholar] [CrossRef] [Green Version]
- Rho, J.; Ye, Z.; Xiong, Y.; Yin, X.; Liu, Z.; Choi, H.; Bartal, G.; Zhang, X. Spherical hyperlens for two-dimensional sub-diffraction imaging at visible frequencies. Nat. Commun. 2010, 1, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Lu, D.; Liu, Z. Hyperlenses and metalenses for far-field super-resolution imaging. Nat. Commun. 2012, 3, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y.; Fung, K.H.; Xu, J.; Ma, H.; Jin, Y.; He, S.; Fang, N.X. Ultrabroadband light absorption by a sawtooth anisotropic metamaterial slab. Nano Lett. 2012, 12, 1443–1447. [Google Scholar] [CrossRef] [Green Version]
- Riley, C.T.; Smalley, J.S.; Brodie, J.R.; Fainman, Y.; Sirbuly, D.J.; Liu, Z. Near-perfect broadband absorption from hyperbolic metamaterial nanoparticles. Proc. Natl. Acad. Sci. USA 2017, 114, 1264–1268. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. Perfect metamaterial absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Zhao, Y.; Ma, J.; Wang, C.; Cui, J.; Du, C.; Luo, X. Sub-diffraction-limited interference photolithography with metamaterials. Opt. Express 2008, 16, 13579–13584. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Zeng, B.; Wang, C.; Luo, X. Breaking the feature sizes down to sub-22 nm by plasmonic interference lithography using dielectric-metal multilayer. Opt. Express 2009, 17, 21560–21565. [Google Scholar] [CrossRef] [PubMed]
- Zhu, P.; Shi, H.; Guo, L.J. SPPs coupling induced interference in metal/dielectric multilayer waveguides and its application for plasmonic lithography. Opt. Express 2012, 20, 12521–12529. [Google Scholar] [CrossRef] [PubMed]
- Liang, G.; Chen, X.; Zhao, Q.; Guo, L.J. Achieving pattern uniformity in plasmonic lithography by spatial frequency selection. Nanophotonics 2018, 7, 277–286. [Google Scholar] [CrossRef]
- Poddubny, A.N.; Belov, P.A.; Kivshar, Y.S. Spontaneous radiation of a finite-size dipole emitter in hyperbolic media. Phys. Rev. A 2011, 84, 023807. [Google Scholar] [CrossRef] [Green Version]
- Jin, Y.; Xiao, S.; Mortensen, N.A.; He, S. Arbitrarily thin metamaterial structure for perfect absorption and giant magnification. Opt. Express 2011, 19, 11114–11119. [Google Scholar] [CrossRef] [Green Version]
- Feng, S. Loss-induced omnidirectional bending to the normal in ϵ-near-zero metamaterials. Phys. Rev. Lett. 2012, 108, 193904. [Google Scholar] [CrossRef] [Green Version]
- Dyachenko, P.N.; Molesky, S.; Petrov, A.Y.; Störmer, M.; Krekeler, T.; Lang, S.; Ritter, M.; Jacob, Z.; Eich, M. Controlling thermal emission with refractory epsilon-near-zero metamaterials via topological transitions. Nat. Commun. 2016, 7, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Sun, L.; Yang, X.; Wang, W.; Gao, J. Diffraction-free optical beam propagation with near-zero phase variation in extremely anisotropic metamaterials. J. Opt. 2015, 17, 035101. [Google Scholar] [CrossRef] [Green Version]
- Yoo, D.; Nguyen, N.-C.; Martín Moreno, L.; Mohr, D.A.; Carretero-Palacios, S.; Shaver, J.; Peraire, J.; Ebbesen, T.W.; Oh, S.-H. High-Throughput Fabrication of Resonant Metamaterials with Ultrasmall Coaxial Apertures via Atomic Layer Lithography. Nano Lett. 2016, 16, 2040–2046. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Castaño, M.; Zheng, H.; García-Pomar, J.L.; Vallée, R.; Mihi, A.; Ravaine, S. Tunable index metamaterials made by bottom-up approaches. Nanoscale Adv. 2019, 1, 1070–1076. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Zhang, C.; Yang, F.; Liang, G.; Li, Q.; Guo, L.J. Plasmonic lithography utilizing epsilon near zero hyperbolic metamaterial. ACS Nano 2017, 11, 9863–9868. [Google Scholar] [CrossRef] [PubMed]
- Wood, B.; Pendry, J.; Tsai, D. Directed subwavelength imaging using a layered metal-dielectric system. Phys. Rev. B 2006, 74, 115116. [Google Scholar] [CrossRef] [Green Version]
- Ferrari, L.; Wu, C.; Lepage, D.; Zhang, X.; Liu, Z. Hyperbolic metamaterials and their applications. Prog. Quantum Electron. 2015, 40, 1–40. [Google Scholar] [CrossRef]
- Bergman, D.J. The dielectric constant of a composite material—A problem in classical physics. Phys. Rep. 1978, 43, 377–407. [Google Scholar] [CrossRef]
- Popov, V.; Lavrinenko, A.V.; Novitsky, A. Surface waves on multilayer hyperbolic metamaterials: Operator approach to effective medium approximation. Phys. Rev. B 2018, 97, 125428. [Google Scholar] [CrossRef] [Green Version]
- Sukham, J.; Takayama, O.; Mahmoodi, M.; Sychev, S.; Bogdanov, A.; Tavassoli, S.H.; Lavrinenko, A.V.; Malureanu, R. Investigation of effective media applicability for ultrathin multilayer structures. Nanoscale 2019, 11, 12582–12588. [Google Scholar] [CrossRef] [PubMed]
- Mahmoodi, M.; Tavassoli, S.H.; Takayama, O.; Sukham, J.; Malureanu, R.; Lavrinenko, A.V. Existence Conditions of High-k Modes in Finite Hyperbolic Metamaterials. Laser Photon. Rev. 2019, 13, 1800253. [Google Scholar] [CrossRef] [Green Version]
- Jen, Y.J.; Liu, W.C. Design a Stratiform Metamaterial with Precise Optical Property. Symmetry 2019, 11, 1464. [Google Scholar] [CrossRef] [Green Version]
- Kildishev, A.V.; Cai, W.; Chettiar, U.K.; Yuan, H.K.; Sarychev, A.K.; Drachev, V.P.; Shalaev, V.M. Negative refractive index in optics of metal–dielectric composites. J. Opt. Soc. Am. B 2006, 23, 423–433. [Google Scholar] [CrossRef]
- Jen, Y.J.; Lakhtakia, A. Response to “Comment on ‘Silver/silicon dioxide/silver sandwich films in the blue-to-red spectral regime with negative-real refractive index” Appl. Phys. Lett. 2012, 101, 156101. [Google Scholar]
- Macleod, H.A. Thin-Film Optical Filters, 3rd ed.; Institute of Physics Publishing: Bristol, UK, 1986. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, Y.-C.; Chan, T.-L.; Lee, C.-C.; Jen, Y.-J.; Ma, W.-C. Design of a Hyperbolic Metamaterial as a Waveguide for Low-Loss Propagation of Plasmonic Wave. Symmetry 2021, 13, 291. https://doi.org/10.3390/sym13020291
Chang Y-C, Chan T-L, Lee C-C, Jen Y-J, Ma W-C. Design of a Hyperbolic Metamaterial as a Waveguide for Low-Loss Propagation of Plasmonic Wave. Symmetry. 2021; 13(2):291. https://doi.org/10.3390/sym13020291
Chicago/Turabian StyleChang, Ya-Chen, Teh-Li Chan, Cheng-Chung Lee, Yi-Jun Jen, and Wei-Chieh Ma. 2021. "Design of a Hyperbolic Metamaterial as a Waveguide for Low-Loss Propagation of Plasmonic Wave" Symmetry 13, no. 2: 291. https://doi.org/10.3390/sym13020291
APA StyleChang, Y.-C., Chan, T.-L., Lee, C.-C., Jen, Y.-J., & Ma, W.-C. (2021). Design of a Hyperbolic Metamaterial as a Waveguide for Low-Loss Propagation of Plasmonic Wave. Symmetry, 13(2), 291. https://doi.org/10.3390/sym13020291





