Fractional-Order Analysis of Modified Chua’s Circuit System with the Smooth Degree of 3 and Its Microcontroller-Based Implementation with Analog Circuit Design
Abstract
1. Introduction
2. The Modified Chua’s Circuit System with the Smooth Degree of 3
3. Fractional-Order Model of Modified Chua’s Circuit
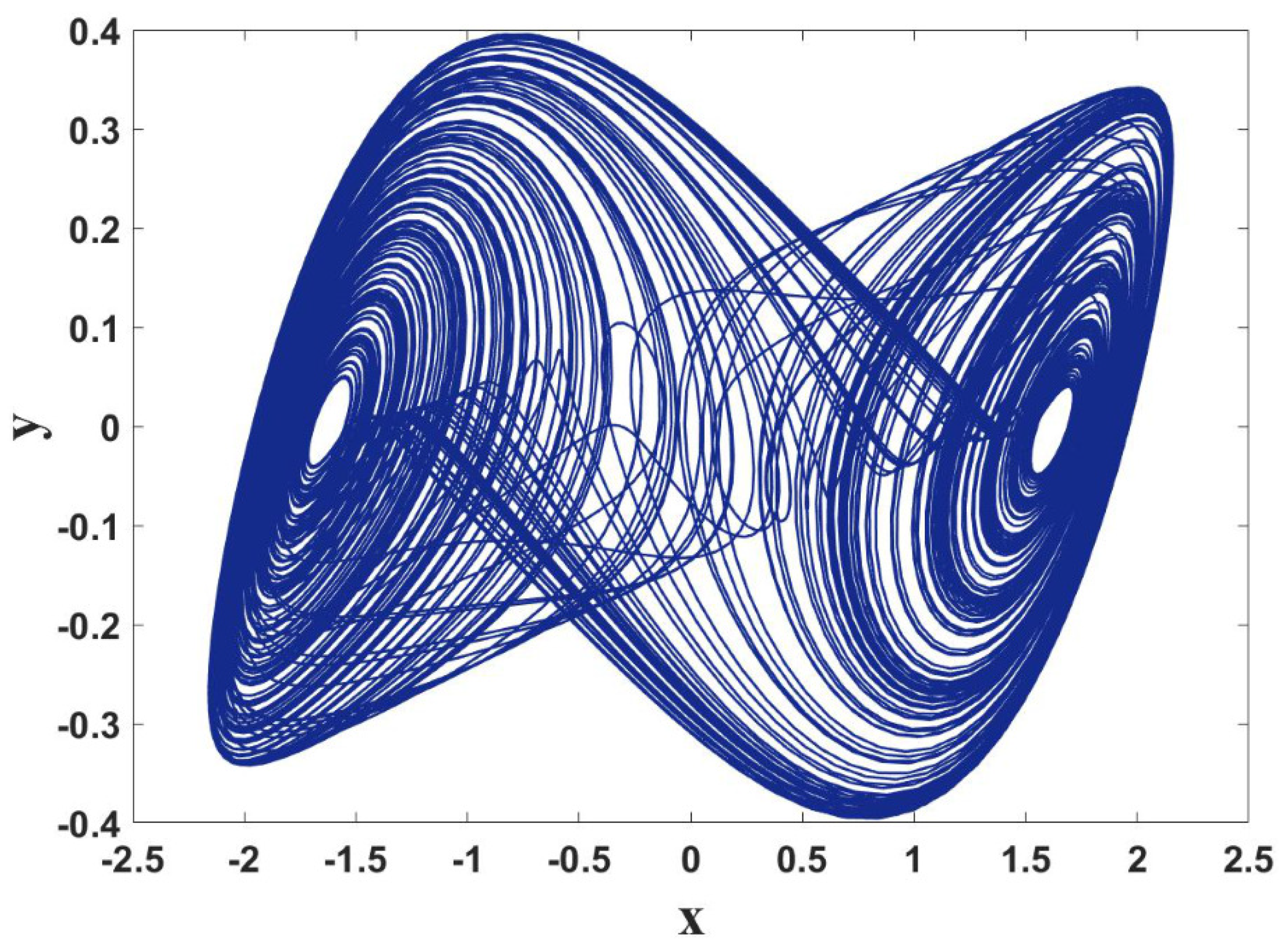
4. Dynamical Properties of the FOABS System
4.1. Lyapunov Exponents
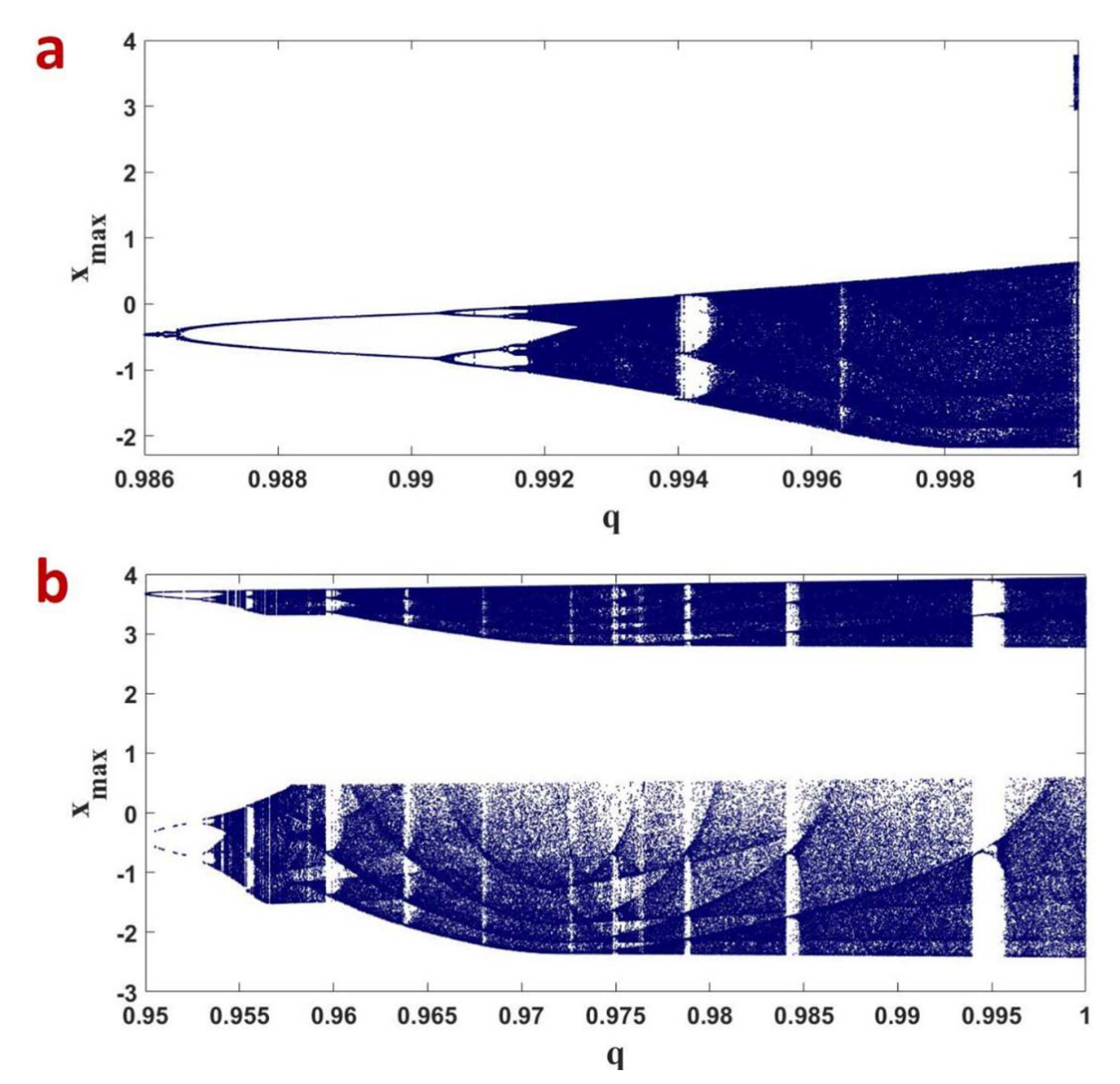
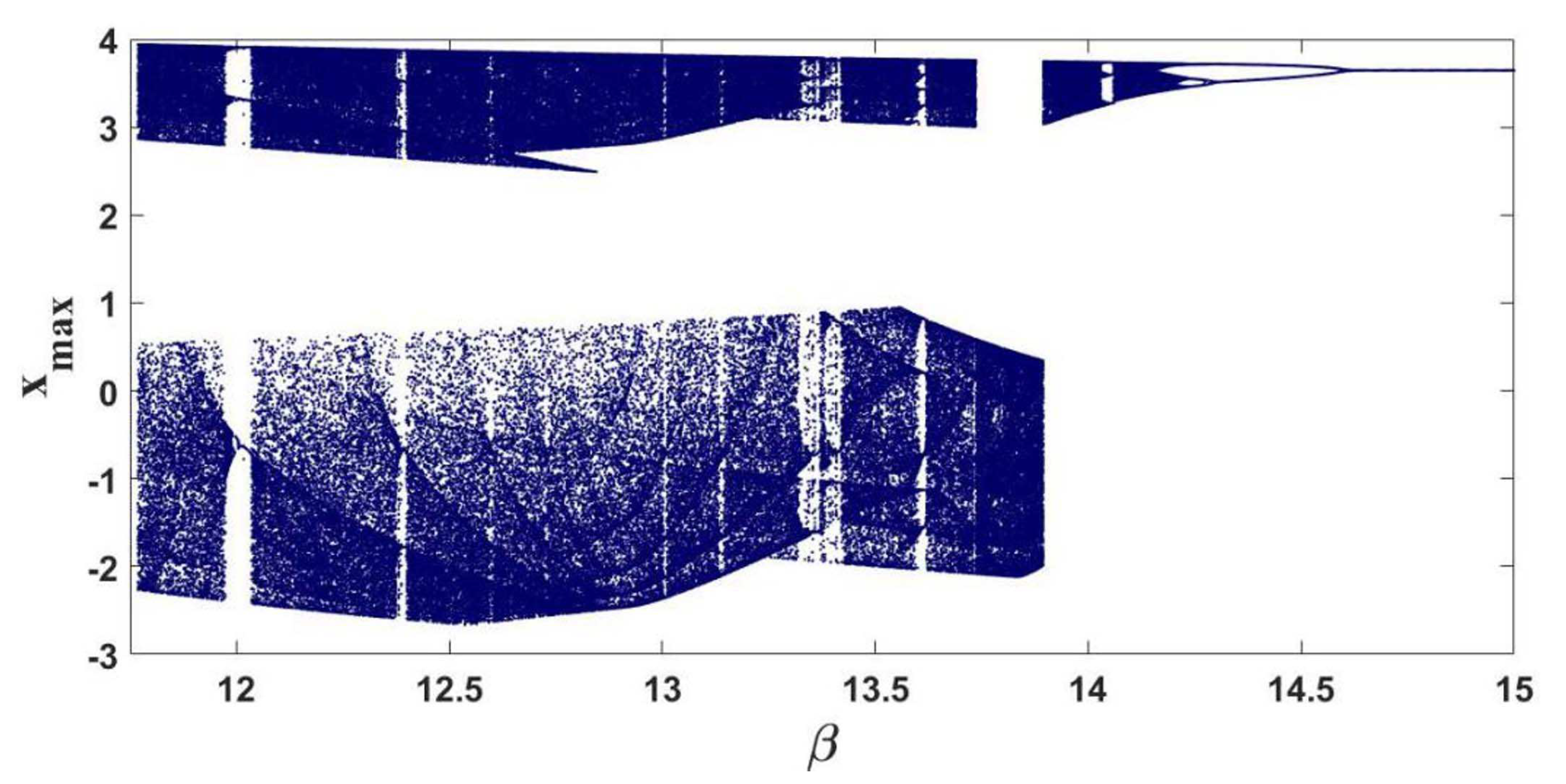
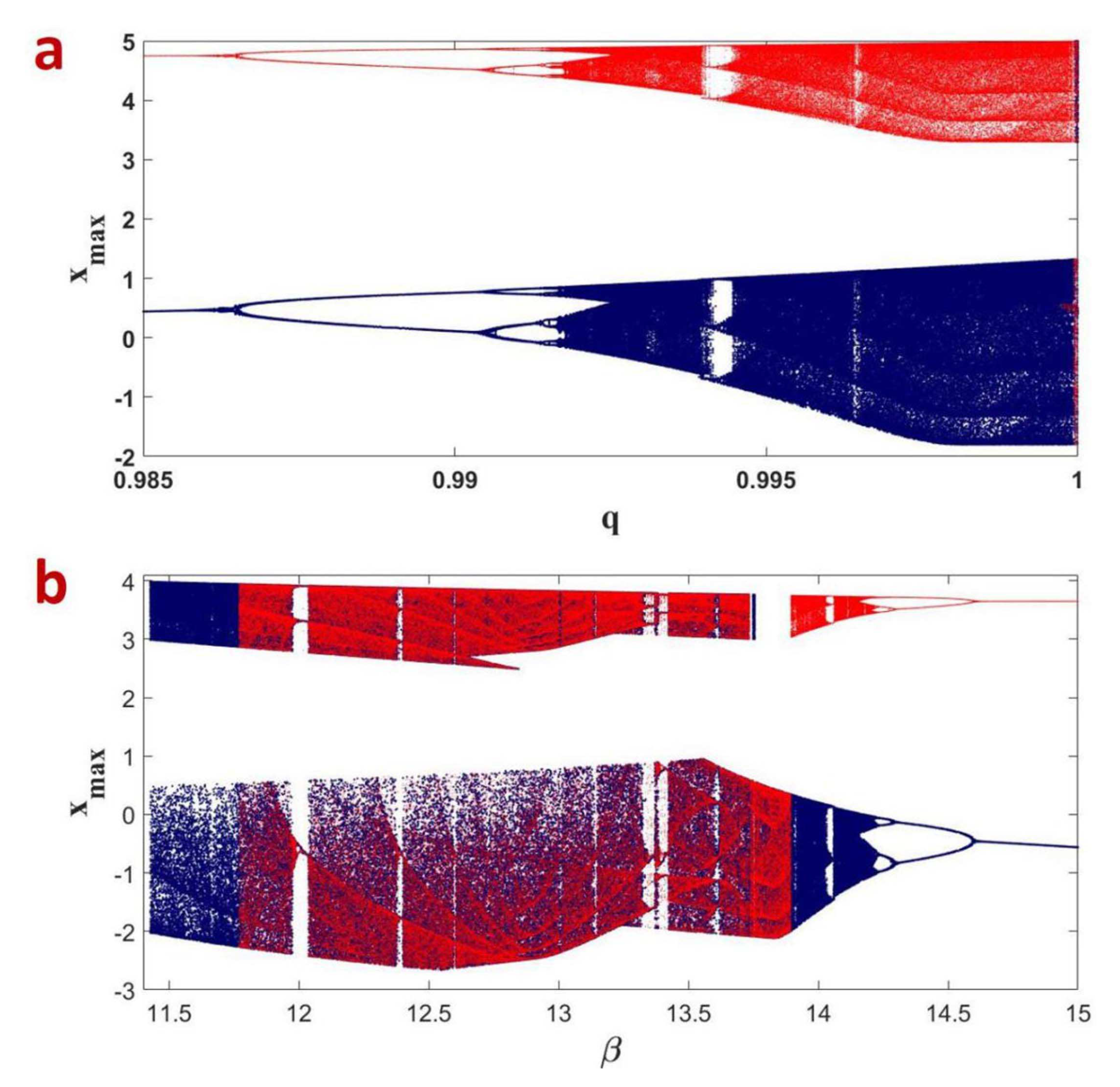
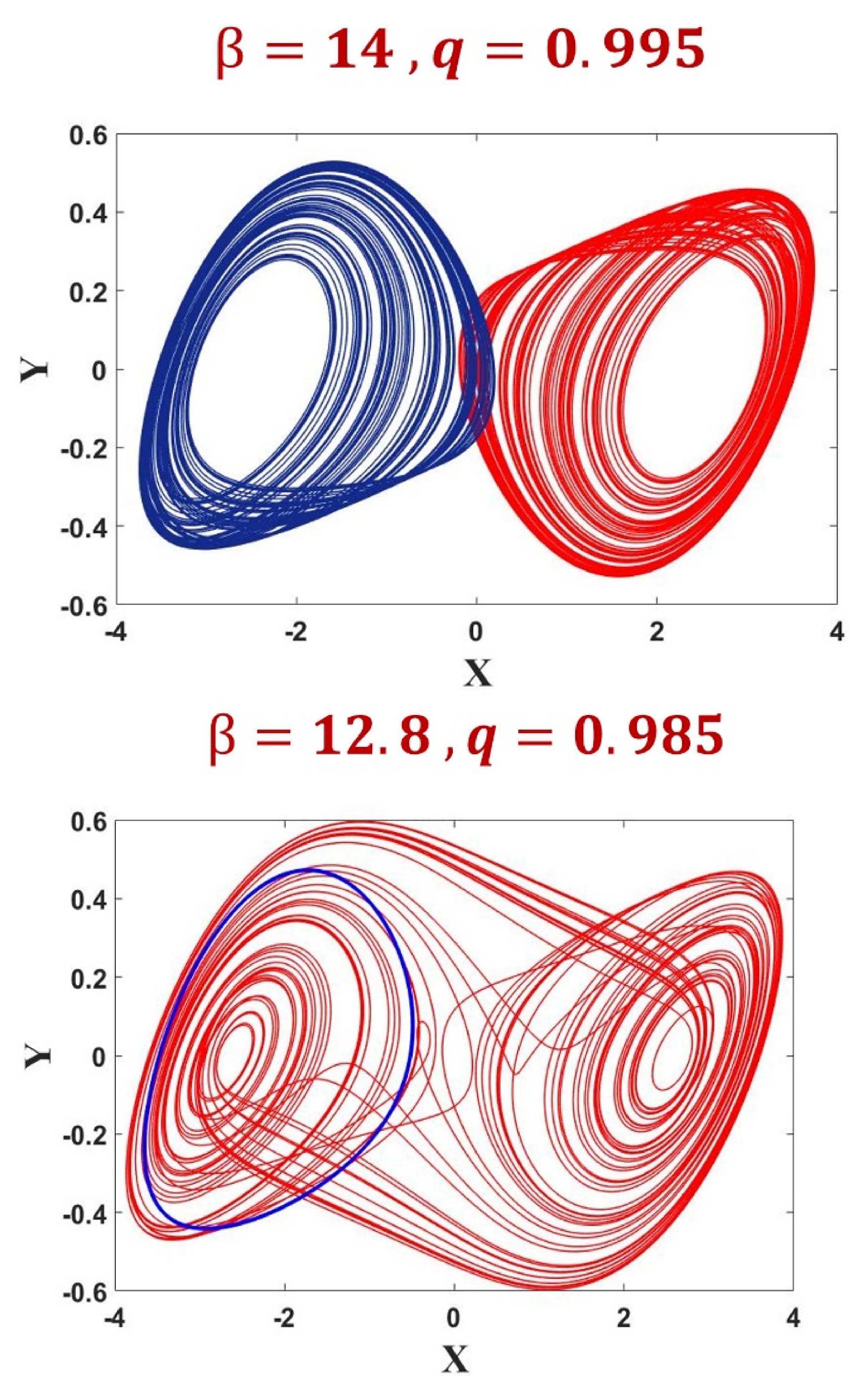
4.2. Route to Chaos
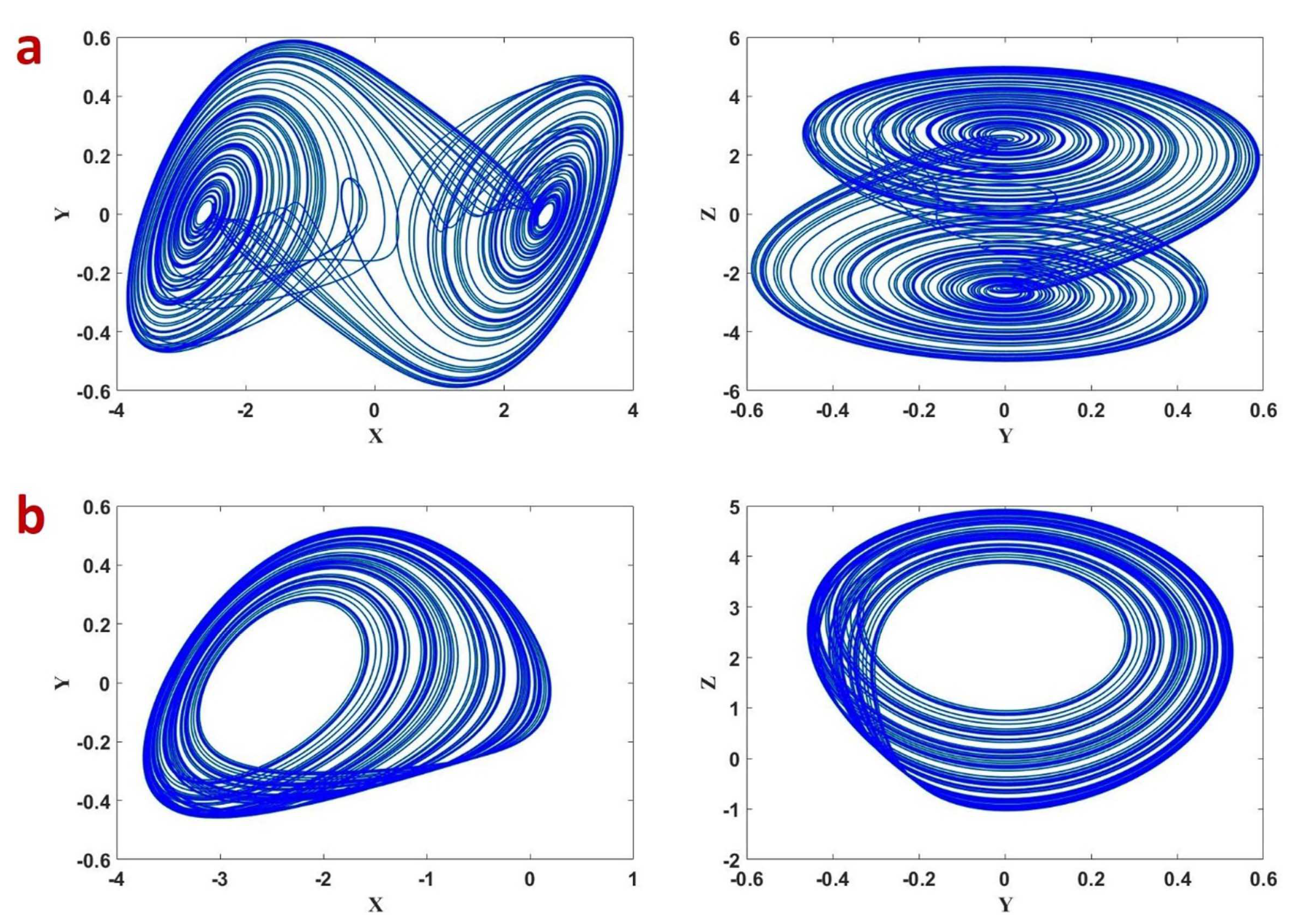
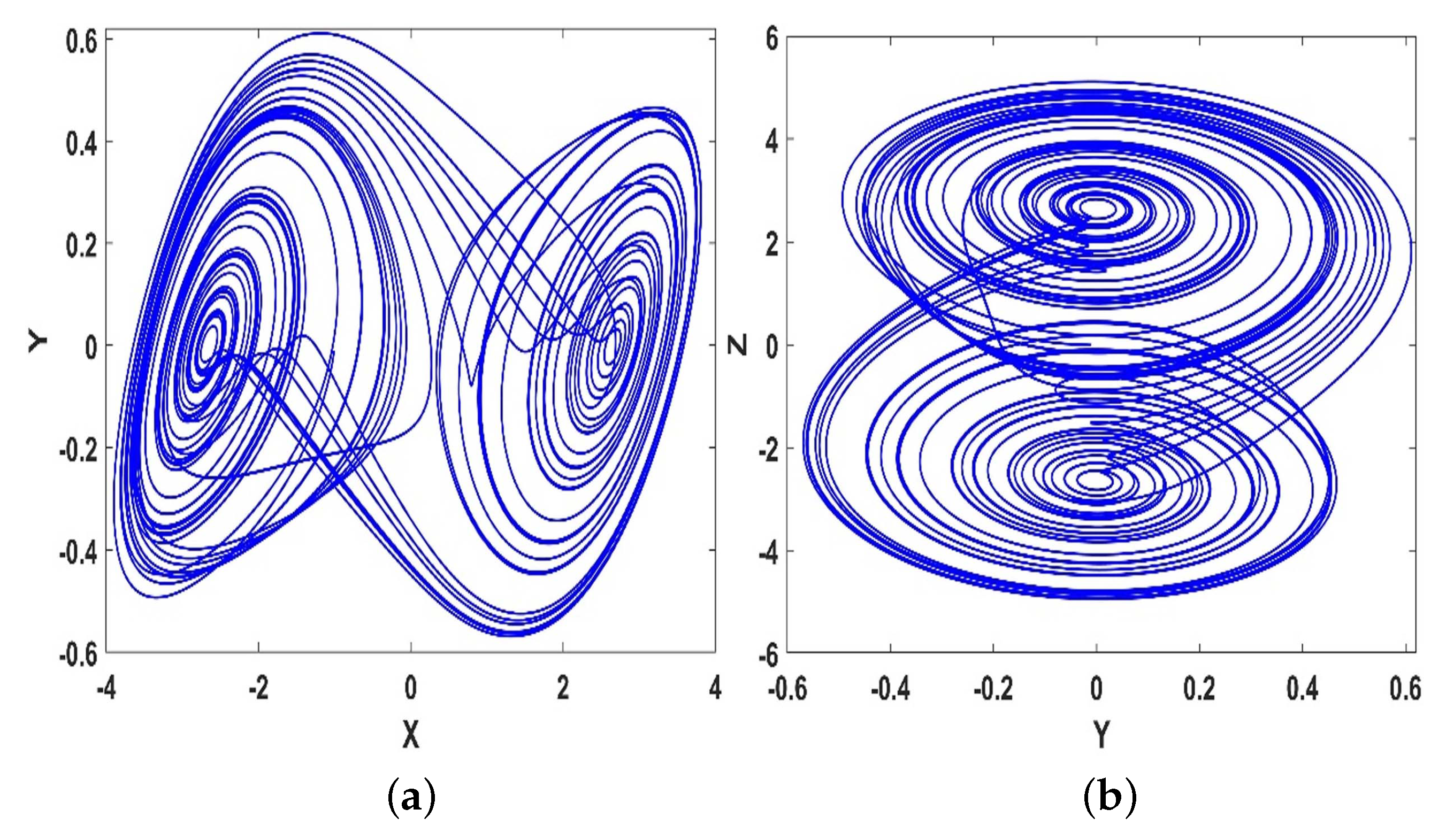
4.3. Multistability and Coexisting Attractors
5. Microcontroller-Based Implementation of FOABS System
6. Electronic Circuit Realization of Modified Chua’s Circuit (1)
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Rossler, O.E. An equation for continuous chaos. Phys. Rev. A 1976, 57, 397–398. [Google Scholar] [CrossRef]
- Chua, L.O.; Lin, G.N. Canonical realization of Chua’s circuit family. IEEE Trans. Circuits Syst. 1990, 37, 885–902. [Google Scholar] [CrossRef]
- Chen, G.; Ueta, T. Yet another chaotic attractor. Int. J. Bifur. Chaos 1999, 9, 1465–1466. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V. Hidden attractors in dynamical systems: From hidden oscillations in Hilbert-Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits. Int. J. Bifur. Chaos 2013, 23, 1330002. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V.; Vagaitsev, V.I. Ocalization of hidden Chua’s attractors. Phys. Lett. A 2011, 375, 2230–2233. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V.; Vagaitsev, V.I. Hidden attractor in smooth Chua systems. Phys. D Nonlinear Phenom. 2012, 241, 1482–1486. [Google Scholar] [CrossRef]
- Murillo-Escobar, M.A.; Cruz-Hernandez, C.; Abundiz-Perez, F.; Lopez-Gutierrez, R.M. Implementation of an improved chaotic encryption algorithm for real-time embedded systems by using a 32-bit microcontroller. Microprocess. Microsyst. 2016, 45, 297–309. [Google Scholar] [CrossRef]
- Janakiraman, S.; Thenmozhi, K.; Rayappan, J.B.B.; Amirtharajan, R. Lightweight chaotic image encryption algorithm forMicroprocess Microsystem, real-time embedded system: Implementation and analysis on 32-bit microcontroller. Microprocess. Microsyst. 2018, 56, 1–12. [Google Scholar] [CrossRef]
- Murillo-Escobar, M.A.; Cruz-Hernandez, C.; Abundiz-Perez, F.; Lopez-Gutierrez, R.M. A robust embedded biometric authentication system based on fingerprint and chaotic encryption. Expert Syst. Appl. 2015, 42, 8198–8211. [Google Scholar] [CrossRef]
- Kacar, S. Analog circuit and microcontroller based RNG application of a new easy realizable 4D chaotic system. Optik 2016, 127, 9551–9561. [Google Scholar] [CrossRef]
- Acho, L. discrete-time chaotic oscillator based on the logistic map: A secure communication scheme and a simple experiment using Arduino. J. Franklin Inst. 2015, 352, 3113–3121. [Google Scholar] [CrossRef]
- Ojo, K.S.; Adelakun, A.O.; Oluyinka, A.A. Synchronisation of cyclic coupled Josephson junctions and its microcontroller-based implementation. Pramana 2019, 92, 77. [Google Scholar] [CrossRef]
- Matouk, A.E.; Agiza, H.N. Bifurcations, chaos and synchronization in ADVP circuit with Parallel resistor. J. Math. Anal. Appl. 2008, 341, 259–269. [Google Scholar] [CrossRef]
- Agiza, H.N.; Matouk, A.E. Adaptive synchronization of Chua’s circuits with fully unknown parameters. Chaos Solitons Fractals 2006, 28, 219–227. [Google Scholar] [CrossRef]
- Tang, K.S.; Man, K.F.; Zhong, G.Q.; Chen, G.R. Modified Chua’s circuit with x|x|. Control Theory Appl. 2003, 20, 223–227. [Google Scholar]
- Tang, F.; Wang, L. An adaptive active control for the modified Chua’s circuit. Phys. Lett. A 2005, 346, 342–346. [Google Scholar] [CrossRef]
- Fu, S.; Meng, X.; Lu, Q. Stability and boundary equilibrium bifurcations of modified Chua’s circuit with smooth degree of 3*. Appl. Math. Mech. (Engl. Ed.) 2015, 36, 1639–1650. [Google Scholar] [CrossRef]
- Tolba, M.F.; AbdelAty, A.M.; Soliman, N.S.; Said, L.A.; Madian, A.H.; Azar, A.T.; Radwan, A.G. FPGA implementation of two fractional order chaotic systems. AEU-Int. J. Electron. Commun. 2017, 78, 162–172. [Google Scholar] [CrossRef]
- Petras, I. Fractional-Order Nonlinear Systems; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- MacDonald, C.L.; Bhattacharya, N.; Sprouse, B.P.; Silva, G.A. Efficient computation of the Grünwald-Letnikov fractional diffusion derivative using adaptive time step memory. J. Comput. Phys. 2015, 297, 221–236. [Google Scholar] [CrossRef]
- Yuste, S.B.; Acedo, L. On an explicit finite difference method for fractional diffusion equations. SIAM J. Numer. Anal. 2005, 42, 1862. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: London, UK, 1998. [Google Scholar]
- El-Sayed, A.M.A.; Nour, H.M.; Elsaid, A.; Matouk, A.E.; Elsonbaty, A. Dynamical behaviors, circuit realization, chaos control and synchronization of a new fractional order hyperchaotic system. Appl. Math. Model. 2016, 40, 3516–3534. [Google Scholar] [CrossRef]
- El-Sayed, A.M.A.; Elsonbaty, A.; Elsadany, A.A.; Matouk, A.E. Dynamical analysis and circuit simulation of a new fractional-order hyperchaotic system and its discretization. Int. J. Bifurc. Chaos 2016, 26, 1650222. [Google Scholar] [CrossRef]
- Matouk, A.E. A novel fractional-order system: Chaos, hyperchaos and applications to linear control. J. Ournal. Appl. Comput. Mech. 2020. [Google Scholar] [CrossRef]
- Matouk, A.E.; Khan, I. Complex dynamics and control of a novel physical model using nonlocal fractional differential operator with singular kernel. J. Adv. Res. 2020, 24, 463–474. [Google Scholar] [CrossRef] [PubMed]
- Al-khedhairi, A.; Matouk, A.E.; Khan, I. Chaotic dynamics and chaos control for the fractional-order geomagnetic field model. Chaos Solitons Fractals 2019, 128, 390–401. [Google Scholar] [CrossRef]
- Rajagopal, K.; Karthikeyan, A.; Duraisamy, P.; Weldegiorgis, R.; Tadesse, G. Bifurcation, chaos and its control in a fractional order power system model with uncertainties. Asian J. Control. 2019, 21, 184–193. [Google Scholar] [CrossRef]
- Rajagopal, K.; Pham, V.T.; Alsaadi, F.E.; Alsaadi, F.E.; Karthikeyan, A.; Duraisamy, P. Multistability and coexisting attractors in a fractional order Coronary artery system. Eur. Phys. J. Spec. Top. 2018, 227, 837–850. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Danca, M.F. Lyapunov exponents of a class of piecewise continuous systems of fractional order. Nonlinear Dyn. 2015, 81, 227–237. [Google Scholar] [CrossRef]
- Hale, J.K. Forward and backward continuation for neutral functional differential equations. J. Differ. Equ. 1970, 9, 168–181. [Google Scholar] [CrossRef]
- Wei, Z.; Moroz, I.; Sprott, J.C.; Akgul, A.; Zhang, W. Hidden hyperchaos and electronic circuit application in a 5D self-exciting homopolar disc dynamo. Chaos Interdiscip. J. Nonlinear Sci. 2017, 27, 033101. [Google Scholar] [CrossRef] [PubMed]
- Volos, C.; Akgul, A.; Pham, V.-T.; Stouboulos, I.; Kyprianidis, I. A simple chaotic circuit with a hyperbolic sine function and its use in a sound encryption scheme. Nonlinear Dyn. 2017, 89, 1047–1061. [Google Scholar] [CrossRef]
- Pham, V.-T.; Akgul, A.; Volos, C.; Jafari, S.; Kapitaniak, T. Dynamics and circuit realization of a no-quilibrium chaotic system with a boostable variable. AEU-Int. J. Electron. Commun. 2017, 78, 134. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Xiao, L.; Rajagopal, K.; Akgul, A.; Cicek, S.; Aricioglu, B. Fractional-Order Analysis of Modified Chua’s Circuit System with the Smooth Degree of 3 and Its Microcontroller-Based Implementation with Analog Circuit Design. Symmetry 2021, 13, 340. https://doi.org/10.3390/sym13020340
Wang J, Xiao L, Rajagopal K, Akgul A, Cicek S, Aricioglu B. Fractional-Order Analysis of Modified Chua’s Circuit System with the Smooth Degree of 3 and Its Microcontroller-Based Implementation with Analog Circuit Design. Symmetry. 2021; 13(2):340. https://doi.org/10.3390/sym13020340
Chicago/Turabian StyleWang, Junxia, Li Xiao, Karthikeyan Rajagopal, Akif Akgul, Serdar Cicek, and Burak Aricioglu. 2021. "Fractional-Order Analysis of Modified Chua’s Circuit System with the Smooth Degree of 3 and Its Microcontroller-Based Implementation with Analog Circuit Design" Symmetry 13, no. 2: 340. https://doi.org/10.3390/sym13020340
APA StyleWang, J., Xiao, L., Rajagopal, K., Akgul, A., Cicek, S., & Aricioglu, B. (2021). Fractional-Order Analysis of Modified Chua’s Circuit System with the Smooth Degree of 3 and Its Microcontroller-Based Implementation with Analog Circuit Design. Symmetry, 13(2), 340. https://doi.org/10.3390/sym13020340






