Three-Species Lotka-Volterra Model with Respect to Caputo and Caputo-Fabrizio Fractional Operators
Abstract
:1. Introduction
2. Definitions
Fractional Calculus
3. Modeling
3.1. Three-Species Lotka-Volterra Model
3.2. Existence of Solutions
3.3. Uniqueness of Solutions
4. Stability of the Model
4.1. Stability of the Factional-Order System
- (1)
- (2)
- (3)
- (4)
- (1)
- (2)
- (3)
- (4)
4.2. Stability of the LV Model with the CF Derivative
4.2.1. The First Equilibrium
4.2.2. The Second Equilibrium
4.2.3. The Third Equilibrium
4.2.4. The Fourth Equilibrium
4.2.5. The Fifth Equilibrium
5. Numerical Algorithm
6. Numerical Results
6.1. Example 1
6.2. Example 2
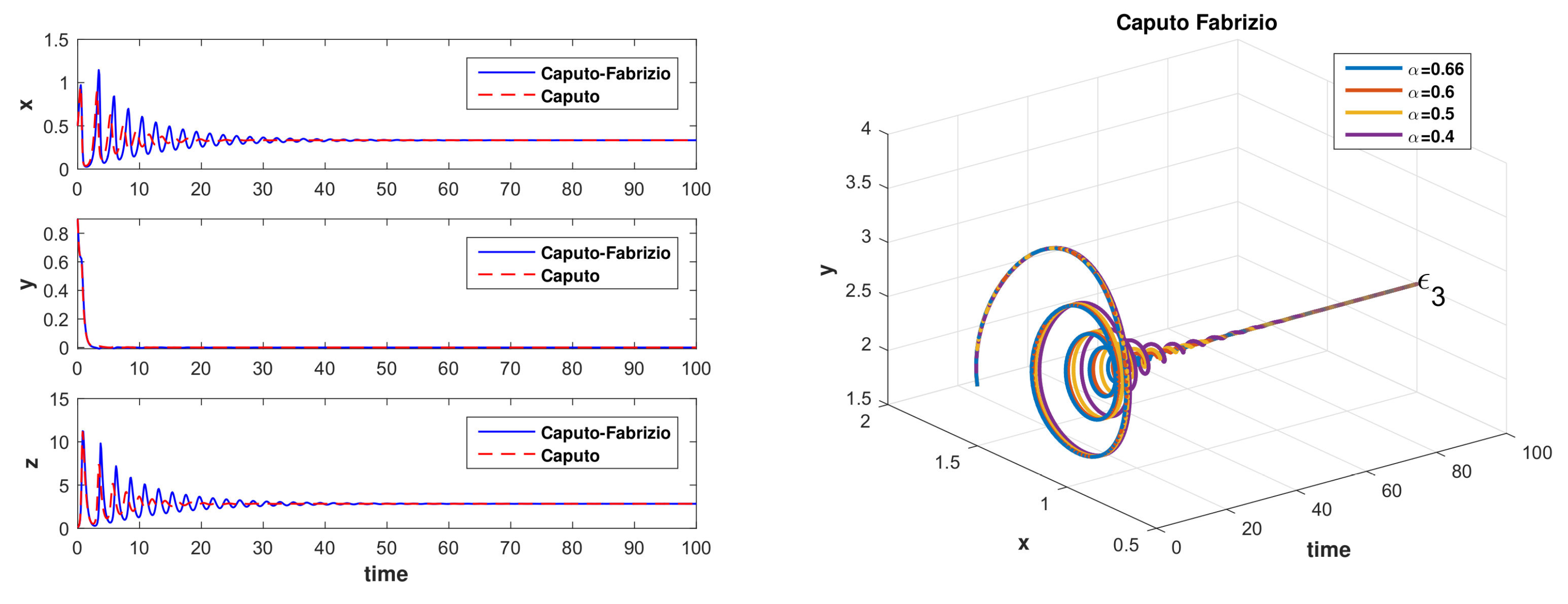
6.3. Example 3
6.4. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Naik, P.A.; Owolabi, K.M.; Yavuz, M.; Zu, J. Chaotic dynamics of a fractional order HIV-1 model involving AIDS-related cancer cells. Chaos Solitons Fractals 2020, 140, 110272. [Google Scholar] [CrossRef]
- Kilbas, A.A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier Science Limited: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Naik, P.A.; Zu, J.; Owolabi, K.M. Global dynamics of a fractional order model for the transmission of HIV epidemic with optimal control. Chaos Solitons Fractals 2020, 138, 109826. [Google Scholar] [CrossRef] [PubMed]
- Karaagac, B.; Owolabi, K.M.; Nisar, K.S. Analysis and dynamics of illicit drug use described by fractional derivative with mittag-leffler kernel. CMC-Comput. Mater. Cont. 2020, 65, 1905–1924. [Google Scholar]
- Owolabi, K.M. High-dimensional spatial patterns in fractional reaction-diffusion system arising in biology. Chaos Solitons Fractals 2020, 134, 109723. [Google Scholar] [CrossRef]
- Owolabi, K.M. Computational techniques for highly oscillatory and chaotic wave problems with fractional-order operator. Eur. Phys. J. Plus 2020, 135, 1–23. [Google Scholar] [CrossRef]
- Saeedian, M.; Khalighi, M.; Azimi-Tafreshi, N.; Jafari, G.R.; Ausloos, M. Memory effects on epidemic evolution: The susceptible-infected-recovered epidemic model. Phys. Rev. E 2017, 95, 022409. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ghalib, M.M.; Zafar, A.A.; Hammouch, Z.; Riaz, M.B.; Shabbir, K. Analytical results on the unsteady rotational flow of fractional-order non-newtonian fluids with shear stress on the boundary. Discret. Contin. Dyn. Syst.-S 2020, 13, 683. [Google Scholar]
- Baleanu, D.; Jajarmi, A.; Mohammadi, H.; Rezapour, S. A new study on the mathematical modelling of human liver with Caputo–Fabrizio fractional derivative. Chaos Solitons Fractals 2020, 134, 109705. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 1–13. [Google Scholar]
- Losada, J.; Nieto, J. Properties of a new fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 87–92. [Google Scholar]
- Caputo, M.; Fabrizio, M. Applications of new time and spatial fractional derivatives with exponential kernels. Prog. Fract. Differ. Appl. 2016, 2, 1–11. [Google Scholar] [CrossRef]
- Atangana, A.; Alkahtani, B. Controlling the wave movement on the surface of shallow water with the Caputo–Fabrizio derivative with fractional order. Chaos Solitons Fractals 2016, 89, 539–546. [Google Scholar]
- Moore, E.J.; Sirisubtawee, S.; Koonprasert, S. A Caputo–Fabrizio fractional differential equation model for HIV/AIDS with treatment compartment. Adv. Differ. Equ. 2019, 2019, 200. [Google Scholar] [CrossRef] [Green Version]
- Bushnaq, S.; Khan, S.A.; Shah, K.; Zaman, G. Mathematical analysis of HIV/AIDS infection model with Caputo-Fabrizio fractional derivative. Cogent Math. Stat. 2018, 5, 1432521. [Google Scholar] [CrossRef]
- Arshad, S.; Baleanu, D.; Defterli, O.; Shumaila. A numerical framework for the approximate solution of fractional tumor-obesity model. Int. J. Model. Simulation Sci. Comput. 2018, 10, 1941008. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Machado, J.T. A critical analysis of the Caputo–Fabrizio operator. Commun. Nonlinear Sci. Numer. Simul. 2018, 59, 608–611. [Google Scholar] [CrossRef]
- Loh, J.R.; Isah, A.; Phang, C.; Toh, Y.T. On the new properties of Caputo–Fabrizio operator and its application in deriving shifted Legendre operational matrix. Appl. Numer. Math. 2018, 132, 138–153. [Google Scholar] [CrossRef]
- Qureshi, S.; Rangaig, N.A.; Baleanu, D. New numerical aspects of Caputo-Fabrizio fractional derivative operator. Mathematics 2019, 7, 374. [Google Scholar] [CrossRef] [Green Version]
- Toh, Y.T.; Phang, C.; Loh, J.R. New predictor-corrector scheme for solving nonlinear differential equations with Caputo-Fabrizio operator. Math. Methods Appl. Sci. 2018, 42, 175–185. [Google Scholar] [CrossRef] [Green Version]
- Atangana, A.; Owolabi, K.M. New numerical approach for fractional differential equations. Math. Model. Nat. Phenom. 2018, 13, 3. [Google Scholar] [CrossRef] [Green Version]
- Das, S.; Gupta, P. A mathematical model on fractional Lotka–Volterra equations. J. Theor. Biol. 2011, 277, 1–6. [Google Scholar] [CrossRef]
- Calin-Adrian, C. Banking system: Three level Lotka-Volterra Model. Procedia Econ. Financ. 2012, 3, 251–255. [Google Scholar]
- Volterra, V. Variazioni e Fluttuazioni del Numero di Individui in Specie Animali Conviventi; Atti della R. Accademia Nazionale dei Lincei, C. Ferrari: Rome, Italy, 1927. [Google Scholar]
- Gonze, D.; Lahti, L.; Raes, J.; Faust, K. Multi-stability and the origin of microbial community types. ISME J. 2017, 11, 2159. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, E.; El-Sayed, A.; El-Saka, H. Equilibrium points, stability and numerical solutions of fractional-order predator-prey and rabies models. J. Math. Anal. Appl. 2007, 325, 542–553. [Google Scholar] [CrossRef] [Green Version]
- Samardzija, N.; Greller, L.D. Explosive route to chaos through a fractal torus in a generalized Lotka-Volterra model. Bull. Math. Biol. 1988, 50, 465–491. [Google Scholar] [CrossRef]
- Elettreby, M.; Al-Raezah, A.A.; Nabil, T. Fractional-order model of two-prey one-predator system. Math. Probl. Eng. 2017, 2017, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Owolabi, K.M. Numerical approach to chaotic pattern formation in diffusive predator–prey system with Caputo fractional operator. Numer. Methods Partial. Differ. Equ. 2021, 37, 131–151. [Google Scholar] [CrossRef]
- Naik, P.A.; Yavuz, M.; Qureshi, S.; Zu, J.; Townley, S. Modeling and analysis of COVID-19 epidemics with treatment in fractional derivatives using real data from pakistan. Eur. Phys. J. Plus 2020, 135, 1–42. [Google Scholar] [CrossRef]
- Amirian, M.M.; Towers, I.; Jovanoski, Z.; Irwin, A.J. Memory and mutualism in species sustainability: A time-fractional Lotka-Volterra model with harvesting. Heliyon 2020, 6, e04816. [Google Scholar] [CrossRef]
- Selvam, A.G.M.; Dhineshbabu, R.; Vianny, D.A. Analysis of a fractional order prey-predator model (3-species). Glob. J. Comput. Sci. Math. 2015, 5, 95–102. [Google Scholar]
- Gonze, D.; Coyte, K.Z.; Lahti, L.; Faust, K. Microbial communities as dynamical systems. Curr. Opin. Microbiol. 2018, 44, 41–49. [Google Scholar] [CrossRef]
- Eklöf, A.; Ebenman, B. Species loss and secondary extinctions in simple and complex model communities. J. Anim. Ecol. 2006, 75, 239–246. [Google Scholar] [CrossRef] [PubMed]
- Haerter, J.O.; Mitarai, N.; Sneppen, K. Food web assembly rules for generalized Lotka-Volterra equations. PLoS Comput. Biol. 2016, 12, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Kreyszig, E. Introductory Functional Analysis with Applications; Wiley: New York, NY, USA, 1978; Volume 1. [Google Scholar]
- Hunter, J.K.; Nachtergaele, B. Applied Analysis; World Scientific: Singapore, 2001. [Google Scholar]
- Conway, J.B. A Course in Functional Analysis; Springer: Berlin/Heidelberg, Germany, 2019; Volume 96. [Google Scholar]
- Yavuz, M.; Sene, N. Stability analysis and numerical computation of the fractional predator–prey model with the harvesting rate. Fractal Fract. 2020, 4, 35. [Google Scholar] [CrossRef]
- Matignon, D. Stability results for fractional differential equations with applications to control processing. Comput. Eng. Syst. Appl. 1996, 2, 963–968. [Google Scholar]
- Li, H.; Cheng, J.; Li, H.b.; Zhong, S.R.M. Stability analysis of a fractional-order linear system described by the Caputo-Fabrizio Derivative. Mathematics 2019, 7, 200. [Google Scholar] [CrossRef] [Green Version]
- Garrappa, R. On linear stability of predictor–corrector algorithms for fractional differential equations. Int. J. Comput. Math. 2010, 87, 2281–2290. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Dadras, S.; Momeni, H. Control of a fractional-order economical system via sliding mode. Phys. A Stat. Mech. Its Appl. 2010, 389, 2434–2442. [Google Scholar] [CrossRef]
- Najafi, E.; Babuska, R.; Lopes, G. A fast sampling method for estimating the domain of attraction. Nonlinear Dyn. 2016, 86, 823–834. [Google Scholar] [CrossRef] [Green Version]
- Tarasov, V.E. Caputo–Fabrizio operator in terms of integer derivatives: Memory or distributed lag? Comput. Appl. Math. 2019, 38, 113. [Google Scholar] [CrossRef]





| Equilibrium Points | Conditions |
|---|---|
| Always exists | |
| Always exists | |
| and | |
| and | |
| , and or , or and |
| Fixed Points | Caputo Derivative | CF Operator |
|---|---|---|
| Always saddle | ||
| and | and or and | |
or and | ||
or and | ||
or (see Equations (48)–(50)) |
| Example 1 | C | CF | C | CF | |||
| Coefficient | Equilibrium | Eigenvalues | |||||
| ✗ | ✗ | ✗ | ✓ | ||||
| ✗ | ✗ | ✗ | ✓ | ||||
| ✓ | ✓ | ✓ | ✓ | ||||
| ✗ | ✗ | ✗ | ✓ | ||||
| Not Acceptable | ✗ | ✗ | ✗ | ✗ | |||
| Example 2 | C | CF | |||||
| Coefficient | Equilibrium | Eigenvalues | |||||
| ✗ | ✓ | ||||||
| ✗ | ✓ | ||||||
| ✗ | ✗ | ||||||
| ✗ | ✓ | ||||||
| ✓ | ✗ | ||||||
| Example 3 | C | CF | |||||
| Coefficient | Equilibrium | Eigenvalues | |||||
| ✗ | ✓ | ||||||
| ✗ | ✓ | ||||||
| ✓ | ✓ | ||||||
| ✗ | ✓ | ||||||
| Not Acceptable | ✗ | ✓ | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalighi, M.; Eftekhari, L.; Hosseinpour, S.; Lahti, L. Three-Species Lotka-Volterra Model with Respect to Caputo and Caputo-Fabrizio Fractional Operators. Symmetry 2021, 13, 368. https://doi.org/10.3390/sym13030368
Khalighi M, Eftekhari L, Hosseinpour S, Lahti L. Three-Species Lotka-Volterra Model with Respect to Caputo and Caputo-Fabrizio Fractional Operators. Symmetry. 2021; 13(3):368. https://doi.org/10.3390/sym13030368
Chicago/Turabian StyleKhalighi, Moein, Leila Eftekhari, Soleiman Hosseinpour, and Leo Lahti. 2021. "Three-Species Lotka-Volterra Model with Respect to Caputo and Caputo-Fabrizio Fractional Operators" Symmetry 13, no. 3: 368. https://doi.org/10.3390/sym13030368
APA StyleKhalighi, M., Eftekhari, L., Hosseinpour, S., & Lahti, L. (2021). Three-Species Lotka-Volterra Model with Respect to Caputo and Caputo-Fabrizio Fractional Operators. Symmetry, 13(3), 368. https://doi.org/10.3390/sym13030368







