Nonlinear Dynamics of Wave Packets in Tunnel-Coupled Harmonic-Oscillator Traps
Abstract
:1. Introduction
2. The Symmetric System
2.1. The Coupled Equations
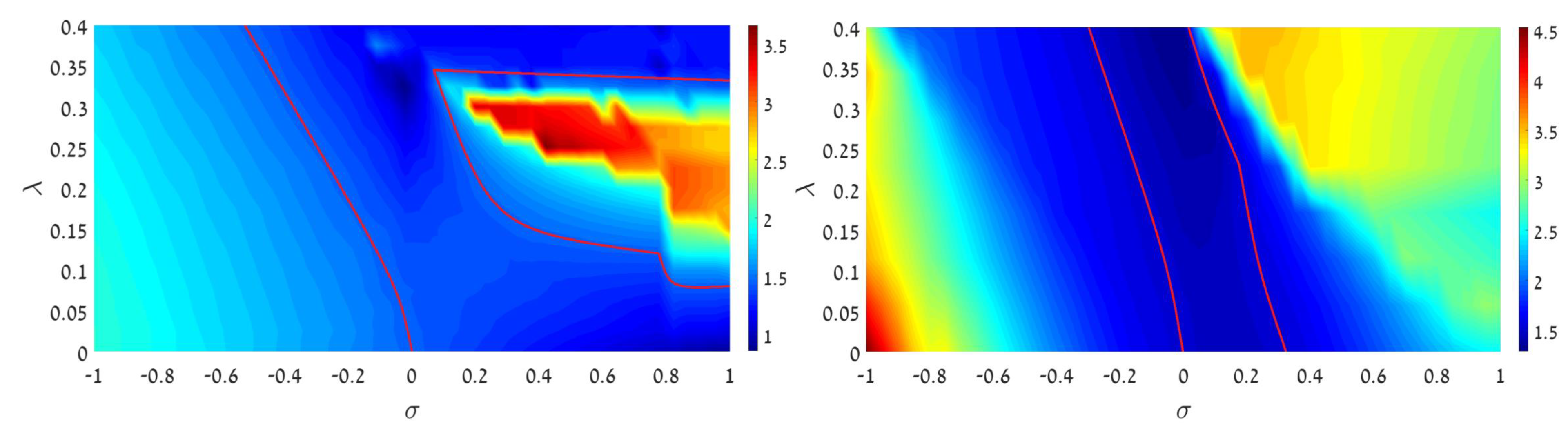
2.2. The Transition from Regular to Chaotic Dynamics
2.3. Spontaneous Symmetry Breaking (SSB) between the Coupled Components
3. The Half-Trapped System
3.1. The Linearized System: Analytical and Numerical Results
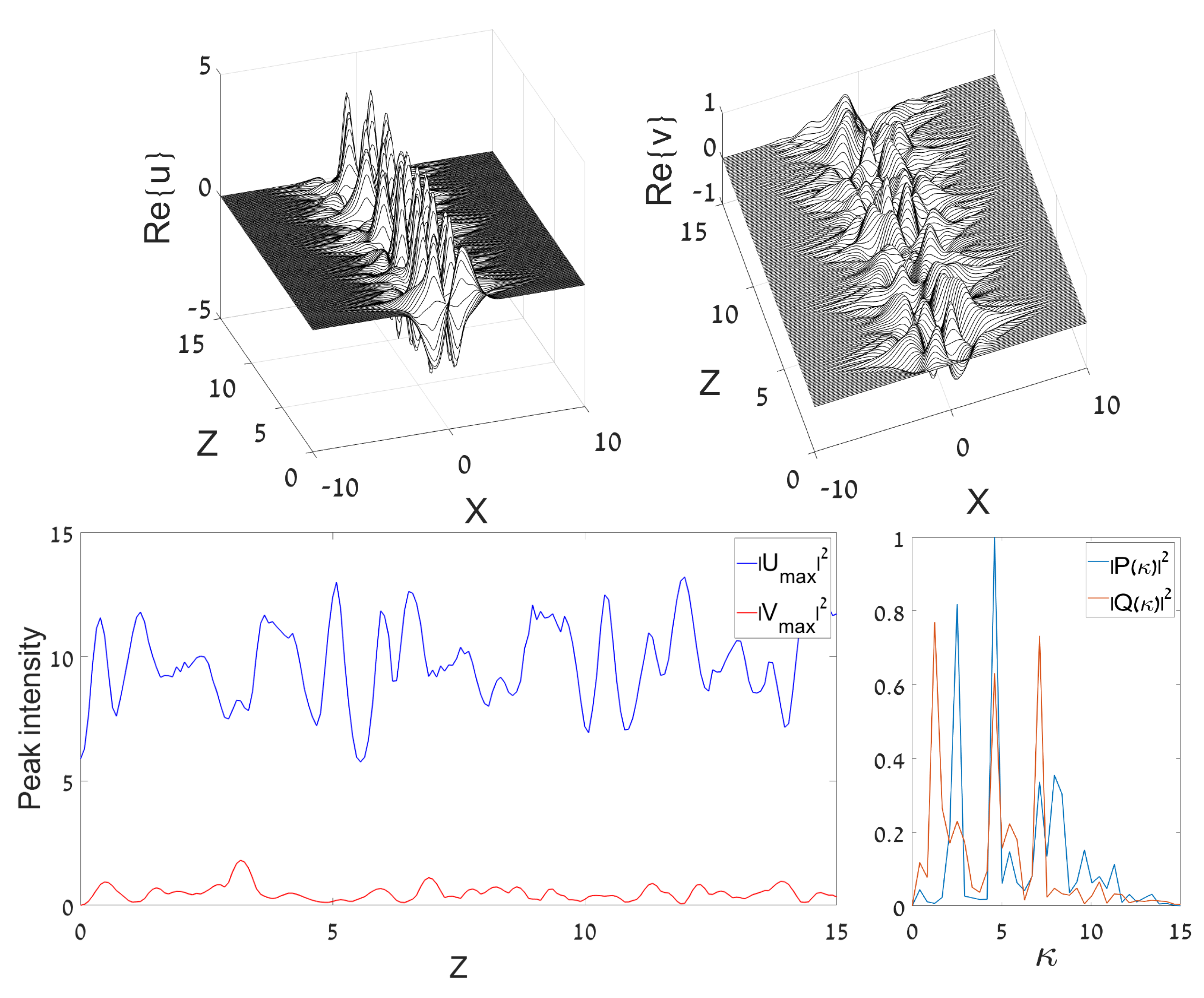
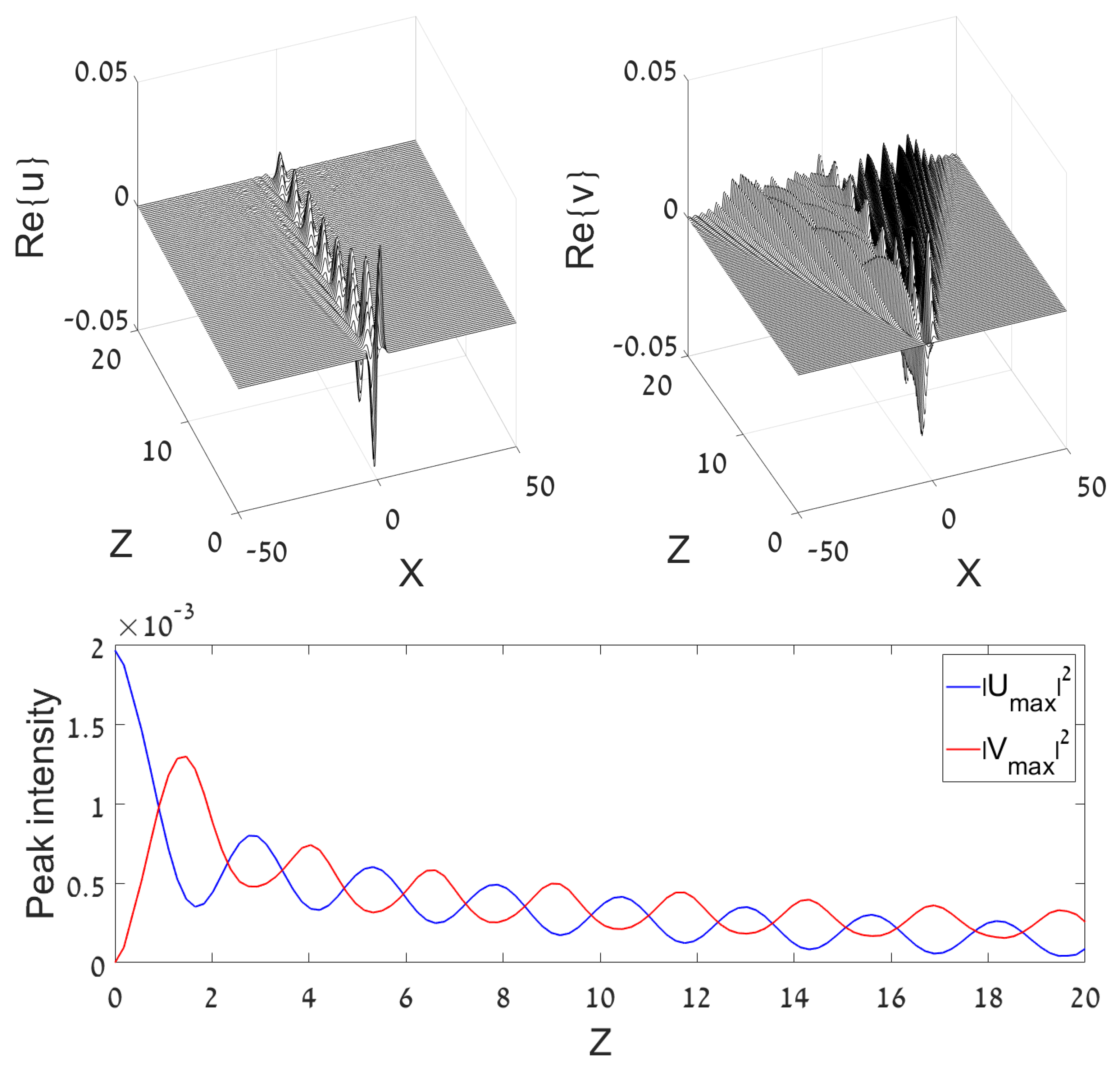
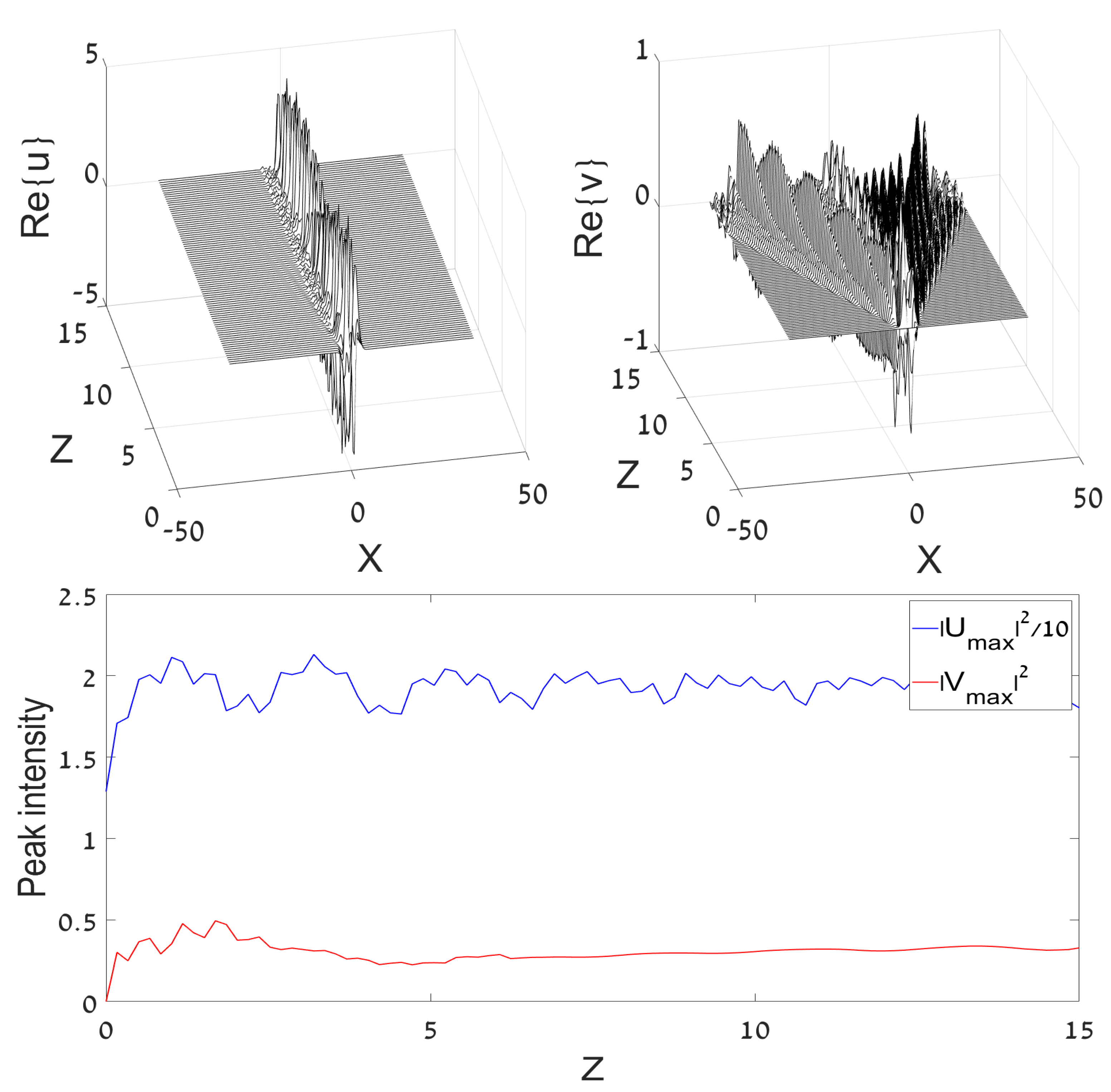
3.1.1. Emission of Radiation in the Untrapped Component
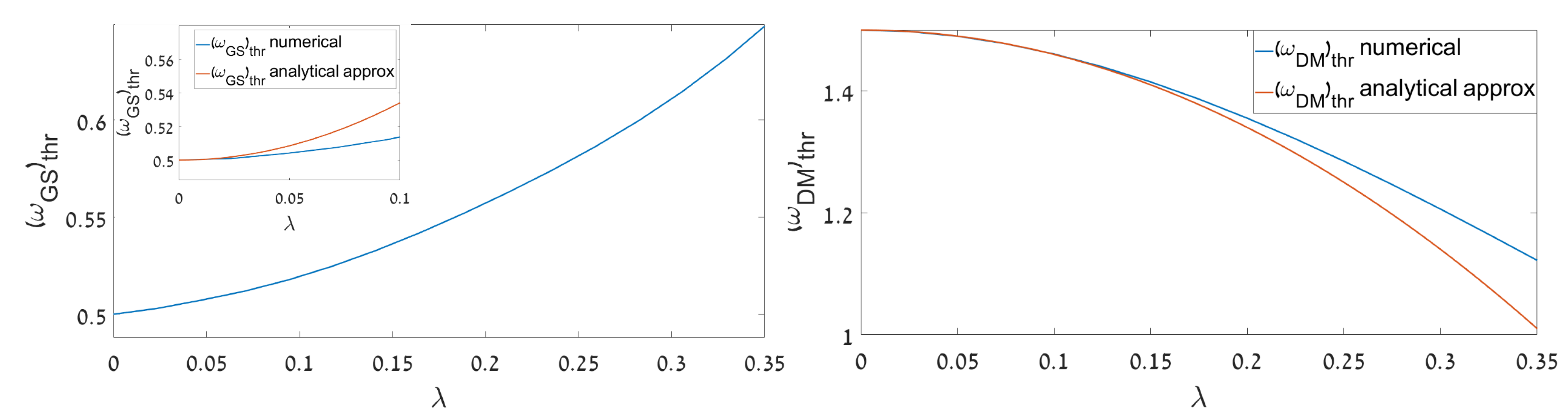
3.1.2. The Shift of the GS and DM Existence Thresholds at Small Values of Coupling Constant
3.1.3. The Analysis for Large Values of
3.1.4. Exact Solutions for One- and Two-Dimensional Bound States in the Continuum (BIC) in the Linear System
3.2. The Nonlinear Half-Trapped System
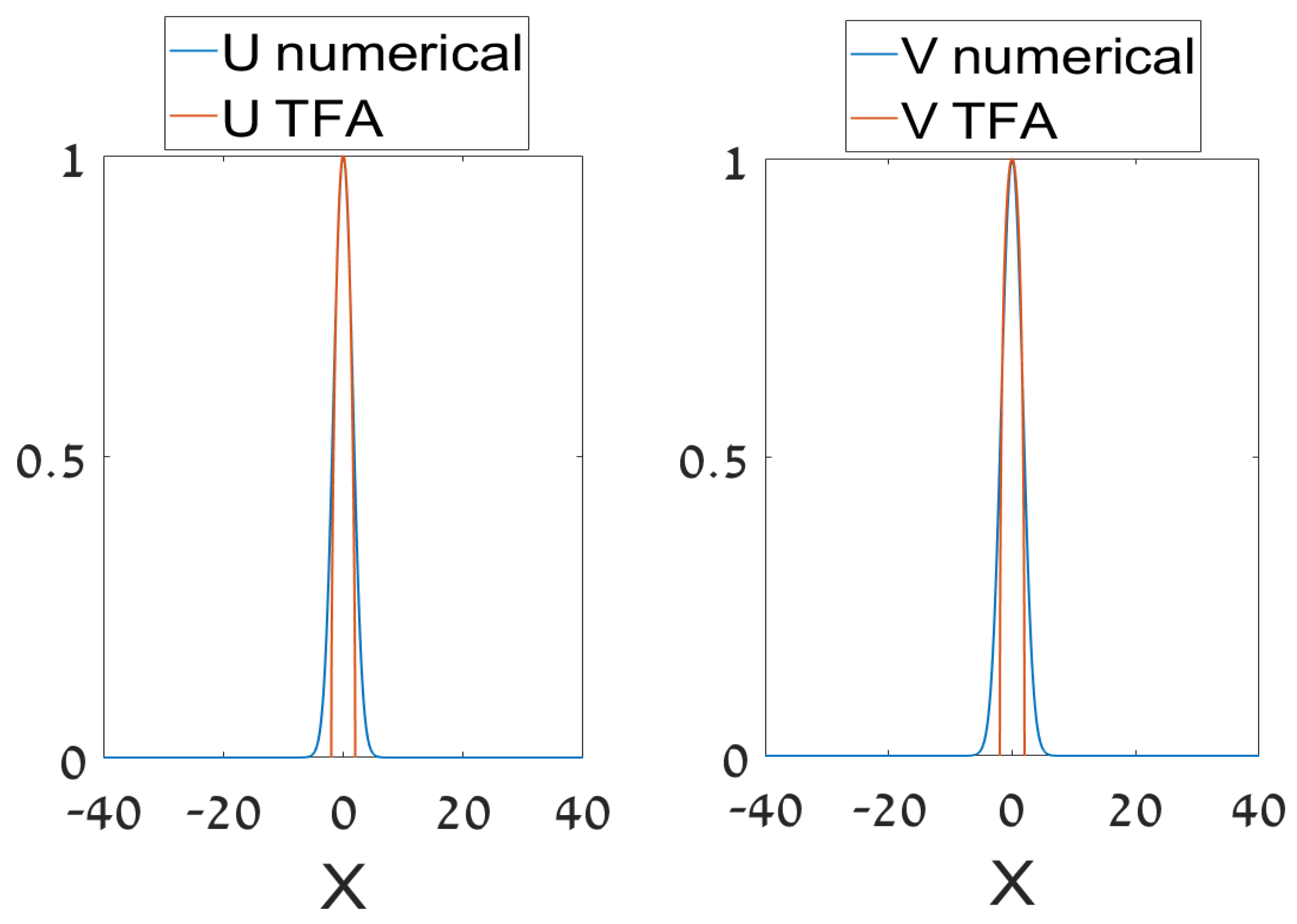
3.2.1. The Thomas–Fermi Approximation (TFA)
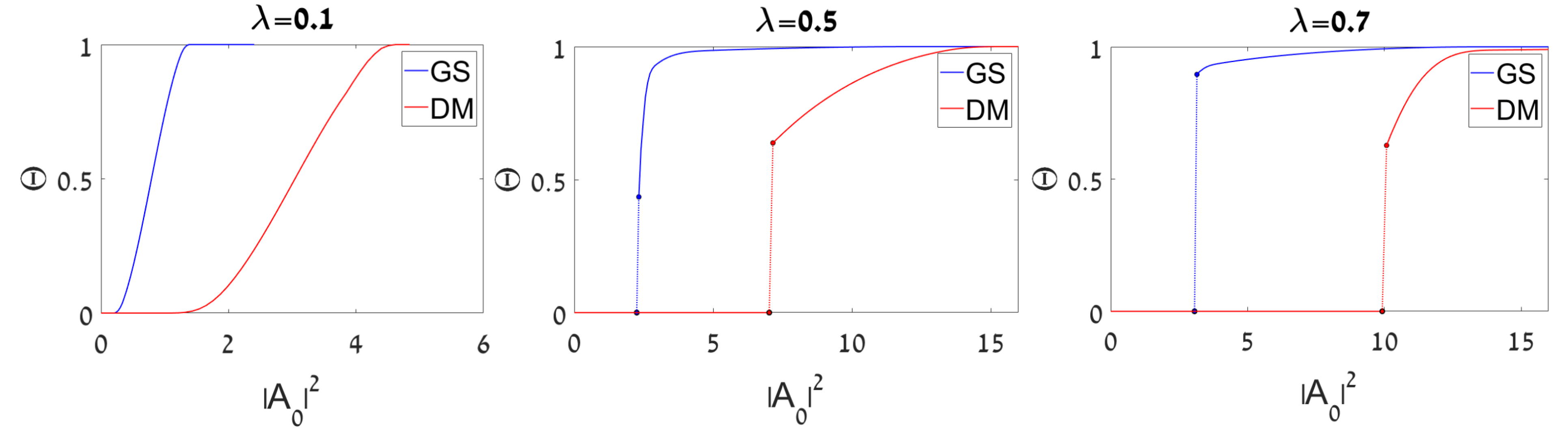
3.2.2. Existence Boundaries for Nonlinear States
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pethick, C.J.; Smith, H. Bose-Einstein Condensation in Dilute Gases; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Pitaevskii, L.P.; Stringari, S. Bose-Einstein Condensation; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Kevrekidis, P.G.; Frantzeskakis, D.J.; Carretero-Gonz ález, R. Emergent Nonlinear Phenomena in Bose-Einstein Condensates: Theory and Experiment; Springer: Heidelberg, Germany, 2008. [Google Scholar]
- Schneider, B.I.; Feder, D.L. Numerical approach to the ground and excited states of a Bose-Einstein condensed gas confined in a completely anisotropic trap. Phys. Rev. A 1999, 59, 2232–2242. [Google Scholar] [CrossRef] [Green Version]
- Adhikari, S.K. Numerical solution of the two-dimensional Gross-Pitaevskii equation for trapped interacting atoms. Phys. Lett. A 2000, 265, 91–96. [Google Scholar] [CrossRef] [Green Version]
- Busch, T.; Anglin, J.R. Motion of dark solitons in trapped Bose-Einstein condensates. Phys. Rev. Lett. 2000, 84, 2298–2301. [Google Scholar] [CrossRef] [Green Version]
- Kivshar, Y.S.; Alexander, T.J.; Turitsyn, S.K. Nonlinear modes of a macroscopic quantum oscillator. Phys. Lett. 2001, 278, 225–230. [Google Scholar] [CrossRef] [Green Version]
- Alexander, T.J.; Bergé, L. Ground states and vortices of matter-wave condensates and optical guided waves. Phys. Rev. E 2002, 65, 026611. [Google Scholar] [CrossRef] [Green Version]
- Huang, G.; Szeftel, J.; Zhu, S. Dynamics of dark solitons in quasi-one-dimensional Bose-Einstein condensates. Phys. Rev. A 2002, 65, 053605. [Google Scholar] [CrossRef]
- Parker, N.G.; Proukakis, N.P.; Leadbeater, M.; Adams, C.S. Soliton-sound interactions in quasi-one-dimensional Bose-Einstein condensates. Phys. Rev. Lett. 2003, 90, 220401. [Google Scholar] [CrossRef]
- Pelinovsky, D.E.; Frantzeskakis, D.J.; Kevrekidis, P.G. Oscillations of dark solitons in trapped Bose-Einstein condensates. Phys. Rev. E 2005, 72, 016615. [Google Scholar] [CrossRef] [Green Version]
- Brazhnyi, V.A.; Konotop, V.V. Stable and unstable vector dark solitons of coupled nonlinear Schrödinger equations: Application to two-component Bose-Einstein condensates. Phys. Rev. E 2005, 72, 026616. [Google Scholar] [CrossRef] [Green Version]
- Parker, N.G.; Proukakis, N.G.; Adams, C.S. Dark soliton decay due to trap anharmonicity in atomic Bose-Einstein condensates. Phys. Rev. A 2010, 81, 033606. [Google Scholar] [CrossRef] [Green Version]
- Bland, T.; Parker, N.G.; Proukakis, N.P.; Malomed, B.A. Probing quasi-integrability of the Gross-Pitaevskii equation in a harmonic-oscillator potential. J. Phys. B Atomic Mol. Opt. Phys. 2018, 51, 205303. [Google Scholar] [CrossRef] [Green Version]
- Raghavan, S.; Agrawal, G.P. Spatiotemporal solitons in inhomogeneous nonlinear media. Opt. Commun. 2000, 180, 377–382. [Google Scholar] [CrossRef]
- Zezyulin, D.A.; Alfimov, G.L.; Konotop, V.V. Nonlinear modes in a complex parabolic potential. Phys. Rev. A 2010, 81, 013606. [Google Scholar] [CrossRef]
- Charalampidis, E.G.; Kevrekidis, P.G.; Frantzeskakis, D.J.; Malomed, B.A. Dark-bright solitons in coupled NLS equations with unequal dispersion coefficients. Phys. Rev. E 2015, 91, 012924. [Google Scholar] [CrossRef] [Green Version]
- Mayteevarunyoo, T.; Malomed, B.A.; Skryabin, D.V. One- and two-dimensional modes in the complex Ginzburg-Landau equation with a trapping potential. Opt. Exp. 2018, 26, 8849–8865. [Google Scholar] [CrossRef] [Green Version]
- Leib, M.; Deppe, F.; Marx, A.; Gross, R.; Hartmann, M.J. Networks of nonlinear superconducting transmission line resonators. New J. Phys. 2012, 14, 075024. [Google Scholar] [CrossRef] [Green Version]
- Kivshar, Y.S.; Agrawal, G.P. Optical Solitons: From Fibers to Photonic Crystals; Academic Press: San Diego, CA, USA, 2003. [Google Scholar]
- Morsch, O.; Oberthaler, M. Dynamics of Bose-Einstein condensates in optical lattices. Rev. Modern Phys. 2006, 78, 179–215. [Google Scholar] [CrossRef]
- Joannopoulos, J.D.; Johnson, S.G.; Winn, J.N.; Meade, R.D. Photonic Crystals: Molding the Flow of Light; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Skorobogatiy, M.; Yang, J. Fundamentals of Photonic Crystal Guiding; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Cerda-Mendez, E.A.; Sarkar, D.; Krizhanovskii, D.N.; Gavrilov, S.S.; Biermann, K.; Skolnick, M.S.; Santos, P.V. Exciton-polariton gap solitons in two-dimensional lattices. Phys. Rev. Lett. 2013, 111, 146401. [Google Scholar] [CrossRef]
- Brazhnyi, V.A.; Konotop, V.V. Theory of nonlinear matter waves in optical lattices. Modern Phys. Lett. B 2004, 18, 627–651. [Google Scholar] [CrossRef] [Green Version]
- Sakaguchi, H.; Malomed, B.A. Dynamics of positive- and negative-mass solitons in optical lattices and inverted traps. J. Phys. B 2004, 37, 1443–1459. [Google Scholar] [CrossRef] [Green Version]
- Zakharov, V.E.; Manakov, S.V.; Novikov, S.P.; Pitaevskii, L.P. Theory of Solitons: Inverse Scattering Method; English translation: Consultants Bureau, New York, 1984; Nauka: Moscow, Russia, 1980. [Google Scholar]
- Zakharov, V.; Dias, F.; Pushkarev, A. One-dimensional wave turbulence. Phys. Rep. 2004, 398, 1–65. [Google Scholar] [CrossRef]
- Mazets, I.E.; Schmiedmayer, J. Thermalization in a quasi-one-dimensional ultracold bosonic gas. New J. Phys. 2010, 12, 055023. [Google Scholar] [CrossRef]
- Cockburn, S.P.; Negretti, A.; Proukakis, N.P.; Henkel, C. Comparison between microscopic methods for finite-temperature Bose gases. Phys. Rev. A 2011, 83, 043619. [Google Scholar] [CrossRef] [Green Version]
- Grisins, P.; Mazets, I.E. Thermalization in a one-dimensional integrable system. Phys. Rev. A 2011, 84, 053635. [Google Scholar] [CrossRef] [Green Version]
- Thomas, K.F.; Davis, M.J.; Kheruntsyan, K.V. Thermalization of a quantum Newton’s cradle in a one-dimensional quasicondensate. Phys. Rev. A 2021, 103, 023315. [Google Scholar] [CrossRef]
- Merhasin, M.I.; Malomed, B.A.; Driben, R. Transition to miscibility in a binary Bose-Einstein condensate induced by linear coupling. J. Phys. B 2005, 38, 877–892. [Google Scholar] [CrossRef]
- Nistazakis, H.E.; Frantzeskakis, D.J.; Kevrekidis, P.G.; Malomed, B.A.; Carretero-Gonzalez, R. Bright-dark soliton complexes in spinor Bose-Einstein condensates. Phys. Rev. A 2008, 77, 033612. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Li, Y.; Malomed, B.A.; Salasnich, L. Spontaneous symmetry breaking of fundamental states, vortices, and dipoles in two and one-dimensional linearly coupled traps with cubic self-attraction. Phys. Rev. A 2016, 96, 033621. [Google Scholar] [CrossRef] [Green Version]
- Decker, M.; Ruther, M.; Kriegler, C.E.; Zhou, J.; Soukoulis, C.M.; Linden, S.; Wegener, M. Strong optical activity from twisted-cross photonic metamaterials. Opt. Lett. 2009, 34, 2501–2503. [Google Scholar] [CrossRef] [PubMed]
- Ballagh, R.J.; Burnett, K.; Scott, T.F. Theory of an output coupler for Bose-Einstein condensed atoms. Phys. Rev. Lett. 1997, 78, 1607–1611. [Google Scholar] [CrossRef]
- Öhberg, P.; Stenholm, S. Internal Josephson effect in trapped double condensates. Phys. Rev. A 1999, 59, 3890–3895. [Google Scholar] [CrossRef]
- Son, D.T.; Stephanov, M.A. Domain walls of relative phase in two-component Bose-Einstein condensates. Phys. Rev. A 2002, 65, 063621. [Google Scholar] [CrossRef] [Green Version]
- Jenkins, S.D.; Kennedy, T.A.B. Dynamic stability of dressed condensate mixtures. Phys. Rev. A 2003, 68, 053607. [Google Scholar] [CrossRef]
- Malomed, B.A. (Ed.) Spontaneous Symmetry Breaking, Self-Trapping, and Josephson Oscillations; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Hung, N.V.; Tai, L.X.T.; Bugar, I.; Longobucco, M.; Buzcy ński, R.; Malomed, B.A.; Trippenbach, M. Reversible ultrafast soliton switching in dual-core highly nonlinear optical fibers. Opt. Lett. 2020, 45, 5221–5224. [Google Scholar]
- Mineev, V.P. The theory of the solution of two near-ideal Bose gases. Zh. Eksp. Teor. Fiz. 1974, 67, 263–272, [English translation: Sov. Phys. JETP 1974, 40, 132–136]. [Google Scholar]
- Malomed, B.A. Solitons and nonlinear dynamics in dual-core optical fibers. In Handbook of Optical Fibers; Peng, G.-D., Ed.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 421–474. [Google Scholar]
- Tratnik, M.V.; Sipe, J.E. Bound solitary waves in a birefringent optical fiber. Phys. Rev. A 1988, 38, 2011–2017. [Google Scholar] [CrossRef]
- Paré, C.; Orjańczyk, M.F. Approximate model of soliton dynamics in all-optical couplers. Phys. Rev. A 1990, 41, 6287. [Google Scholar] [CrossRef]
- Maimistov, A.I. Propagation of a light pulse in nonlinear tunnel-coupled optical waveguides. Kvant. Elektron. 1991, 18, 758, [English translation: Sov. J. Quantum Electron. 1991, 21, 687].. [Google Scholar] [CrossRef]
- Uzunov, I.M.; Muschall, R.; Goelles, M.; Kivshar, Y.S.; Malomed, B.A.; Lederer, F. Pulse switching in nonlinear fiber directional couplers. Phys. Rev. E 1995, 51, 2527–2536. [Google Scholar] [CrossRef]
- Abbarchi, M.; Amo, A.; Sala, V.G.; Solnyshkov, D.D.; Flayac, H.; Ferrier, L.; Sagnes, I.; Galopin, E.; Lemaître, A.; Malpuech, G.; et al. Macroscopic quantum self-trapping and Josephson oscillations of exciton polaritons. Nat. Phys. 2013, 9, 275. [Google Scholar] [CrossRef]
- Milburn, G.J.; Corney, J.; Wright, E.M.; Walls, D.F. Quantum dynamics of an atomic Bose-Einstein condensate in a double-well potential. Phys. Rev. A 1997, 55, 4318. [Google Scholar] [CrossRef] [Green Version]
- Smerzi, A.; Fantoni, S.; Giovanazzi, S.; Shenoy, S.R. Quantum coherent atomic tunneling between two trapped Bose-Einstein condensates. Phys. Rev. Lett. 1997, 79, 4950. [Google Scholar] [CrossRef] [Green Version]
- Albiez, M.; Gati, R.; Fölling, J.; Hunsmann, S.; Cristiani, M.; Oberthaler, M.K. Direct observation of tunneling and nonlinear self-trapping in a single bosonic Josephson junction. Phys. Rev. Lett. 2005, 95, 010402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shin, Y.; Jo, G.-B.; Saba, M.; Pasquini, T.A.; Ketterle, W.; Pritchard, D.E. Optical weak link between two spatially separated Bose-Einstein condensates. Phys. Rev. Lett. 2005, 95, 170402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Levy, S.; Lahoud, E.; Shomroni, I.; Steinhauer, J. The a.c. and d.c. Josephson effects in a Bose–Einstein condensate. Nature 2007, 449, 579–583. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Y.; Malomed, B.A. Josephson oscillations of chirality and identity in two-dimensional solitons in spin-orbit-coupled condensates. Phys. Rev. Res. 2020, 2, 033214. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Malomed, B.A. Symmetry breaking in a two-component system with repulsive interactions and linear coupling. Comm. Nonlin. Sci. Num. Sim. 2020, 92, 105496. [Google Scholar] [CrossRef]
- Panoiu, N.-C.; Malomed, B.A.; Osgood, R.M., Jr. Semidiscrete solitons in arrayed waveguide structures with Kerr nonlinearity. Phys. Rev. A 2008, 78, 013801. [Google Scholar] [CrossRef] [Green Version]
- Stillinger, F.H.; Herrick, D.R. Bound states in continuum. Phys. Rev. A 1975, 11, 446–454. [Google Scholar] [CrossRef]
- Kodigala, A.; Lepetit, T.; Gu, Q.; Bahari, B.; Fainman, Y.; Kante, B. Lasing action from photonic bound states in continuum. Nature 2017, 54, 196–199. [Google Scholar] [CrossRef]
- Midya, B.; Konotop, V.V. Coherent-perfect-absorber and laser for bound states in a continuum. Opt. Lett. 2018, 43, 607–610. [Google Scholar] [CrossRef]
- Champneys, A.R.; Malomed, B.A.; Yang, J.; Kaup, D.J. “Embedded solitons”: Solitary waves in resonance with the linear spectrum. Physica D 2001, 152–153, 340–354. [Google Scholar] [CrossRef] [Green Version]
- Ananikian, D.; Bergeman, T. Gross-Pitaevskii equation for Bose particles in a double-well potential: Two-mode models and beyond. Phys. Rev. A 2006, 73, 013604. [Google Scholar] [CrossRef] [Green Version]
- Kartashov, Y.V.; Konotop, V.V.; Vysloukh, V.A. Dynamical suppression of tunneling and spin switching of a spin-orbit-coupled atom in a double-well trap. Phys. Rev. A 2018, 97, 063609. [Google Scholar] [CrossRef] [Green Version]
- Kivshar, Y.S.; Malomed, B.A. Dynamics of solitons in nearly integrable systems. Rev. Mod. Phys. 1989, 61, 763–915. [Google Scholar] [CrossRef]
- Iooss, G.; Joseph, D.D. Elementary Stability Bifurcation Theory; Springer: New York, NY, USA, 1980. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics; Nauka Publishers: Moscow, Russia, 1974. [Google Scholar]
- Kartashov, Y.V.; Konotop, V.V.; Torner, L. Bound states in the continuum in spin-orbit-coupled atomic systems. Phys. Rev. A 2017, 96, 033619. [Google Scholar] [CrossRef] [Green Version]
- dos Santos, M.C.P.; Malomed, B.A.; Cardoso, W.B. Double-layer Bose-Einstein condensates: A quantum phase transition in the transverse direction, and reduction to two dimensions. Phys. Rev. E 2020, 102, 042209. [Google Scholar] [CrossRef] [PubMed]
- Fetter, A.L.; Feder, D.L. Beyond the Thomas-Fermi approximation for a trapped condensed Bose-Einstein gas. Phys. Rev. A 1998, 58, 3185–3194. [Google Scholar] [CrossRef] [Green Version]
- Sakaguchi, H.; Malomed, B.A. Solitons in combined linear and nonlinear lattice potentials. Phys. Rev. A 2010, 81, 013624. [Google Scholar] [CrossRef] [Green Version]
- Vakhitov, N.G.; Kolokolov, A.A. Stationary solutions of the wave equation in a medium with nonlinearity saturation. Radiophys. Quant. Electron. 1973, 16, 783–789. [Google Scholar] [CrossRef]
- Bergé, L. Wave collapse in physics: Principles and applications to light and plasma waves. Phys. Rep. 1998, 303, 259–370. [Google Scholar] [CrossRef]
- Fibich, G. The Nonlinear Schrödinger Equation: Singular Solutions and Optical Collapse; Springer: Heidelberg, Germany, 2015. [Google Scholar]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hacker, N.; Malomed, B.A. Nonlinear Dynamics of Wave Packets in Tunnel-Coupled Harmonic-Oscillator Traps. Symmetry 2021, 13, 372. https://doi.org/10.3390/sym13030372
Hacker N, Malomed BA. Nonlinear Dynamics of Wave Packets in Tunnel-Coupled Harmonic-Oscillator Traps. Symmetry. 2021; 13(3):372. https://doi.org/10.3390/sym13030372
Chicago/Turabian StyleHacker, Nir, and Boris A. Malomed. 2021. "Nonlinear Dynamics of Wave Packets in Tunnel-Coupled Harmonic-Oscillator Traps" Symmetry 13, no. 3: 372. https://doi.org/10.3390/sym13030372
APA StyleHacker, N., & Malomed, B. A. (2021). Nonlinear Dynamics of Wave Packets in Tunnel-Coupled Harmonic-Oscillator Traps. Symmetry, 13(3), 372. https://doi.org/10.3390/sym13030372