An Incremental and Backward-Conflict Guided Method for Unfolding Petri Nets

Abstract

The unfolding technique of Petri net can characterize the real concurrency and alleviate the state space explosion problem. Thus, it is greatly suitable to analyze/check some potential errors in concurrent systems. During the unfolding process of a Petri net, the calculations of configurations, cuts, and cut-off events are the key factors for the unfolding efficiency. However, most of the unfolding methods do not specify a highly efficient calculations on them. In this paper, we reveal some recursive relations and structural properties of these factors. Subsequently, we propose an improved method for computing configurations and cuts. Meanwhile, backward conflicts are used to guide the calculations of cut-off events. Moreover, a case study and a series of experiments are done to illustrate the effectiveness and application scenarios of our methods.

1. Introduction

Nowadays, concurrent systems have been successfully applied to various scenarios, e.g., large-scale websites, railway traffic systems, and telecom operation-support systems. Although high concurrency can indeed enhance their performance and throughput, it easily leads to some errors, such as deadlocks, a lack of synchronization, and data inconsistencies, especially when a concurrent system deals with a great amount of data. For example, Apache Httpd (an open-source web server) suffered from deadlocks that were caused by its unix mutex (https://www.sqlite.org/src/info/a6c30be214, (accessed on 2 January 2021)). The errors of data inconsistency in an IPO (Initial Public Offering) Cross system made NASDAQ (Nasdaq OMX Group, Inc, NewYork, USA ) lose $13 million in May, 2012 (https://www.computerworld.com/article/2727012/nasdaq-s-facebook-glitch-came-from-race-conditions.html, (accessed on 5 January 2021)). Therefore, some model-checking-based methods are proposed for checking the correctness and reliability of concurrent systems. Petri net is widely used to model and verify concurrent systems due to its great capability of explicitly specifying parallelism, concurrency, and synchronization [1,2,3]. The classical reachability graph (CRG) of Petri net is a commonly used technique for checking deadlocks, reachability, and soundness of concurrent systems [4,5,6]. However, this technique easily has the problem of the state space explosion because it is based on the interleaving semantics [7] of concurrent events/actions. The interleaving semantics of CRG only considers the partial orders of business activities, and utilizes the global states of concurrent systems to describe and analyze their behaviors. Thus, a CRG needs to find out all precedence relations between activities, generate successor states, and eventually form some symmetry diamond structures.

When compared with the reachability-graph-based method, the unfolding technique [8] of Petri nets can both alleviate the state space explosion problem and characterize the concurrency relations because it is based on the true concurrency semantics. In fact, some methods are proposed to conduct a concurrency analysis of Petri nets, such as reachability set [9], concurrent sequential automata [10], and c-exact hypergraphs [11]. By comparison, the  unfolding technique uses an acyclic net to represent all behaviors of a Petri net. On the one hand, this acyclic net can directly record all concurrent operations. On the other hand, it uses a much smaller space to store all states especially when a system has many concurrent events/actions. If a Petri net is unbounded or it is bounded but has a repeatedly firable action sequence, its unfolding is naturally infinite. Thus, an important task in this case is to determine a cut-off event and obtain a finite complete prefix (FCP) of infinite unfoldings. Currently, there have been many methods of Petri nets to generate an FCP [12], such as ERV (“ERV” is the abbreviation of authors: Esparza, Romer, and Vogler) unfolding, directed unfolding (DU), and  merged process (MP). ERV [13] is a classical unfolding method, which proposes partial orders and improves the McMillan’s unfolding algorithm [8]. The merged process [14] generates a condensed unfolding of a Petri net’s behavior based on merged conditions. Directed unfolding [15] utilizes heuristic functions to guide the unfolding of Petri nets towards the desired states. Moreover, these unfolding techniques have been successfully applied to many fields, e.g., fault diagnosis [16], Artificial Intelligence (AI) planning [17], and test cases generation [18].

For these methods of generating an FCP, the calculations of configurations, cuts, and cut-off events greatly affect the unfolding efficiency of a Petri net. These related calculations make up an absolutely significant share ($70\%$) of the total unfolding time, as shown in Figure 1. However, most unfolding techniques do not specify a highly efficient calculations on them. On the one hand, the  existing computing approaches of configurations and cuts depend on a lot of repetitive work. On the other hand, once a new event is generated and added into a given prefix, the current methods still need to match it up with all existing events so as to determine whether it is a cut-off event.

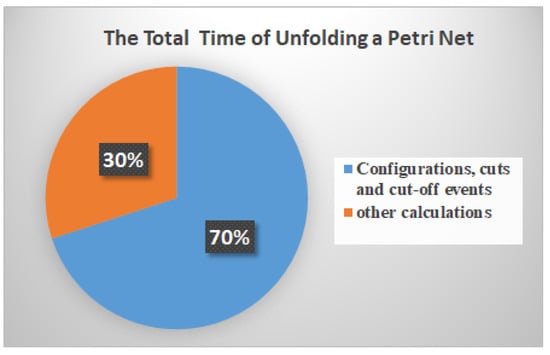
Figure 1. The ratios of different kinds of calculations (e.g., configurations, cuts, and cut-off events) to the total time of unfolding a Petri net (The statistics come from our experiments on The BPM Academic Initiative Model Collection. https://bpmai.org/download/index.html (accessed on 10 December 2020)).

In this paper, we reveal some deep properties of configuration, cuts, and cut-off events, and then utilize recursion formulas and characterized structures to improve these calculations. Some algorithms are developed to perform these calculations and generate finite complete prefixes (FCPs). What is more, all of these improvements can be applied into the existing unfolding techniques and they contribute to the related model checkings.

The main contributions are summarized, as follows:

(1)

Incremental methods are proposed to calculate configurations, cuts and concurrent conditions.

(2)

Backward conflicts are used to guide the determination of cut-off events.

(3)

A tool is developed to implement our improved methods for unfolding a Petri net.

2. Related Work

2.1. The Unfolding Techniques of Petri Nets

McMillan [8] initially proposed the net unfolding technique with partial-order semantics of Petri nets. As an improvement of McMillan’s unfoldings, Esparza et al. [13] proposed a family of algorithms (i.e., ERV unfolding method) to construct a finite complete prefix. Whereafter, its parallel unfolding [19] came up. Khomenko et al. [20] proposed a cutting context to determine static cut-off events and generate canonical prefixes. Bonet et al. [12] generalized the notion of cutting context and provided a user-oriented framework of the unfolding technique. Couvreur et al. [21] proposed a new model of branching processes without any finiteness or safeness assumptions, which are suitable for describing the behavior of general Petri nets. Bonet [15] utilized the problem-specific information as a heuristic function to guide the unfolding of Petri net towards the desired marking. Rodriguez et al. [22] combined partial order reductions (POR) with net unfoldings to tackle the state space explosion problem. Chatain et al. [23] proposed a goal-driven unfolding technique with model reduction to explore the minimal configurations that can lead to a given marking.

These studies of unfolding methods mainly focus on how to generate a smaller FCP by unfolding a Petri net, or explore different kinds of Petri net unfoldings, e.g.,  unbound Petri net [24], timed Petri net [25], colored Petri net [26], contextual Petri net [27], and Nested Petri nets (NP-net) [28]. However, they easily have a low efficiency in the calculations of configurations, cuts, and cut-off events. We propose an improved method for unfolding a Petri net in this paper in order to solve this problem.

2.2. Model Checking Based on Petri Net Unfolding

The unfolding technique of Petri net has been widely used in model checking, e.g.,  diagnosing faults in asynchronous discrete event systems [16], making a concurrent planning [17], generating test cases for multi-threads [18], and checking deadlock [29], soundness [5], reachability, and coverability [30].

McMillan [8] first used the unfolding technique to verify asynchronous circuits. De León et al. [31] presented a test generation algorithm for a complete test suite w.r.t. concurrent conformance relation based on the unfolding of IOPN. Jezequel et al. [32] extended a distributed unfolding technique with time stamps to build testers for distributed systems. Saarikivi et al. [33,34] computed the minimal test suites for multi-threaded programs based on unfolding techniques. Liu et al. [5] proposed the basic unfolding of Petri net to check the soundness of workflow systems. Lutz-Ley et al. [35] analyzed the stability of discrete event systems that are based on the unfolding technique of Petri net. Meyer et al. [36] translated finite control processes into a safe Petri net, and utilized the unfolding-based method to verify Mobile Systems. Ponce-de-Leon et al. [37] used the unfolding technique of Petri net to discover a process model. Weidlich et al. [38] calculated the behavioral consistency of process models based on Petri-net unfoldings. Xiang et al. [39] used the unfolding of PD-net to detect the errors of data inconsistency.

When compared with these model checking methods, we can more effectively check errors of concurrent systems based on our unfolding method, since it records as much contextual information as possible and improves the calculational efficiency of Petri net unfolding.

3. Basic Notations

Some basic notations are introduced in this section, e.g., Petri net, occurrence net, and branching process.

Definition 1.

A net is a triple $N=(P,T,F)$, where

(1) 

P and T are two disjoint and finite sets, which are, respectively, called place set and transition set; and,

(2) 

$F\subseteq (P\times T)\cup (T\times P)$ is a flow relation.

A marking of a net is a mapping M: $P\to \mathbb{N}$, where $\mathbb{N}=\{0,1,2,\cdots \}$ is a set of non-negative integers. In this paper, a multiset of places represents a marking. A Petri net is a net N with an initial marking $M_0$, and denoted as $\Sigma =(N,M_0)$. For a node $x\in P\cup T$, its pre-set is denoted as ${}^{•}x=\left\{y\right|y\in P\cup T\wedge (y,x)\in F\}$ and post-set $x^{•}=\left\{y\right|y\in P\cup T\wedge (x,y)\in F\}$. For a node set $X\subseteq P\cup T$, its pre-set is ${}^{•}X={\bigcup }_{x\in X}{}^{•}x$ and post-set $X^{•}={\bigcup }_{x\in X}{x}^{•}$. Furthermore, ${}^{•}$${}^{•}x$=$\{x^{\prime }$|$x^{\prime }\in {}^{•}X\wedge X={}^{•}x\}$ and $x^{•}$${}^{•}$=$\{x^{\prime }$| $x^{\prime }\in X^{•}\wedge X=x^{•}\}$ are called prep-set and postp-set of x, respectively. Especially, if x is a transition, then ${}^{•}$${}^{•}x$ (resp.$x^{•}$${}^{•}$ ) is called prep-transitions (resp. posp-transitions).

Given a Petri net $\Sigma =(P,T,F,M_0)$, a transition $t\in T$ is enabled at a marking M if $\forall p\in P$: $p\in {}^{•}t\Rightarrow M\left(t\right)\ge 1$, which is denoted by $M[t⟩$. After firing an enabled transition t at M, a new marking $M^{\prime }$ is generated and denoted as $M[t⟩M^{\prime }$, where ∀p∈P: $M^{\prime }\left(p\right)=M\left(p\right)-1$ if $p\in {}^{•}t\setminus t^{•}$; $M^{\prime }\left(p\right)=M\left(p\right)+1$ if $p\in t^{•}\setminus {}^{•}t$; and, otherwise, $M^{\prime }\left(p\right)=M\left(p\right)$. A marking $M^{\prime }$ is reachable from another marking M, if there exists a firing transition sequence $t_1$$t_2$⋯$t_n$ such that $M[t_1$⟩$M_1[t_2$⟩$M_2$⋯$M_{n-1}[t_n$⟩$M^{\prime }$. The set of reachable markings from M is denoted by $R\left(M\right)$. For example, Figure 2a is a Petri net, where ${}^{•}{t}_0=\{p_0,p_1\}$, $t_0^{••}=\{t_2,t_3\}$, $M_0\left(p_0\right)=M_0\left(p_1\right)=M_0\left(p_2\right)=1$, $M_0[t_0⟩M_1$ and $M_1=p_2+p_3+p_4$.

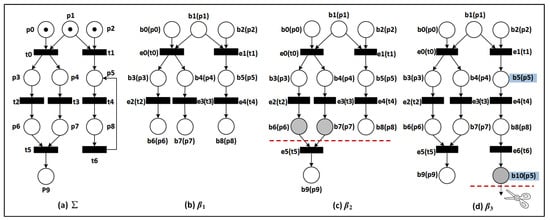
Figure 2. A Petri net $\Sigma$ and its branching processes ${\beta }_1$, ${\beta }_2$ and ${\beta }_3$.

Definition 2

(Causality, conflict and concurrency). In an acyclic net $N=$ (P, T, F), given two nodes x, y∈P∪T,

(1) 

x and y are incausality, which is denoted by x ≤ y, if the net contains a path from x to y. Especially, if $x\ne y$, it is denoted as x < y.

(2) 

x and y are inconflict, which is denoted by $x\#y$, if ∃$t_1,t_2$$\in T$: ${}^{•}{t}_1$∩${}^{•}{t}_2$≠∅, $t_1$≤x, and $t_2$ ≤ y; or,

(3) 

x and y are inconcurrency, denoted by xcoy, if there is neither $x<y$, nor $y<x$, nor $x\#y$.

For the example of Figure 2b, the nodes $e_1$ and $e_4$ are in causality, $e_0$ and $e_1$ are in conflict, and $b_3$ and $b_4$ are in concurrency.

An occurrence net is a special net, and its formal definition is given, as follows.

Definition 3

(Occurrence net [8]). A net $N=(P,T,F)$ is called an occurrence net if

(1) 

$\forall x,y\in P\cup T$: $x<y\Rightarrow y\nless x$;

(2) 

$\forall p\in P$: $|{}^{•}p|\le 1$; and,

(3) 

no transition is in self-conflict, i.e., $\forall t\in T$:$\neg (t\#t)$.

In an occurrence net, places and transitions are usually called conditions and events, respectively. In general, we use $O=(B$, E, $G)$ to denote an occurrence net, where B, E, and G are, respectively, sets of conditions, events, and arcs. $Min\left(O\right)$ is the set of minimal elements of $B\cup E$ with respect to the causal relation, i.e., $\forall x\in Min\left(O\right):{}^{•}x=\mathsf{\varnothing }$. For example, Figure 2b is an occurrence net, where $Min\left(O\right)=\{b_0,b_1,b_2\}$.

Based on occurrence net, a branching process of a Petri net is defined, as follows.

Definition 4

(Branching process [13]). Let $(N,M_0)=(P$, T, F, $M_0$) be a Petri net. $(O,h)$ is a branching process of $(N,M_0)$ if the occurrence net $O=$$(B$, E, G) and the homomorphism $h:B\cup E\to P\cup T$ satisfy:

(1) 

$h\left(B\right)\subseteq P$ and $h\left(E\right)\subseteq T$;

(2) 

for every $e\in E$, the restriction of h onto ${}^{•}e$ (resp., $e^{•}$)) is a bijection between ${}^{•}e$ and ${}^{•}h\left(e\right)$ (resp., between $e^{•}$ and $h{\left(e\right)}^{•}$);

(3) 

the restriction of h onto $Min\left(O\right)$ is a bijection between $Min\left(O\right)$ and $M_0$; and,

(4) 

for every $e_1$,$e_2$$\in E$, if ${}^{•}{e}_1={}^{•}{e}_2$ and $h\left(e_1\right)=h\left(e_2\right)$, then $e_1=e_2$.

Definition 5

(Prefix). Let $(O_i,h_i)$=$(B_i$, $E_i$, $G_i$, $h_i)$ be two branching processes of a Petri net where $i\in 1,2$. $(O_1,h_1)$ is a prefix of $(O_2,h_2)$ if $B_1\subseteq B_2\wedge E_1\subseteq E_2$.

For example, Figure 2b–d are three branching processes of Figure 2a, where Figure 2b is a prefix of Figure 2c, and  Figure 2c is a prefix of Figure 2d.

4. The Existing Unfolding Method of Petri Nets

4.1. Finite Complete Prefix

All of the branching processes of a Petri net $\Sigma$ form a partially ordered set w.r.t. the binary relation prefix. Its greatest element is called Unfolding of $\Sigma$, which is denoted as $Unf(\Sigma )$. In order to generate the unfolding of a Petri net, some related definitions and calculations are introduced, such as configuration, co-set, and cut-off event.

Definition 6

(Configuration [8]). A configuration C of a branching process is defined as a set of events, such that C is causally closed (i.e., $e\in C\Rightarrow \forall e^{\prime }\le e$: $e^{\prime }\in C$) and conflict-free (i.e., $\forall e,e^{\prime }$∈$C:$$\neg (e\#e^{\prime })$).

A local configuration of an event e is $\left[e\right]=$$\{e^{\prime }$|$e^{\prime }\le e$, $e^{\prime }$∈$E\}$. Especially, if an event set $E^{\prime }$ satisfies $\forall e_1,e_2\in E^{\prime }$: $e_1$$co$$e_2$, then its local configuration is $\left[E^{\prime }\right]={\bigcup }_{e\in E^{\prime }}\left[e\right]$. The set of all (resp. local) configurations of a branching process $\beta$ is denoted by $C_{\beta }$ (resp. $C_{\beta }^L$). Obviously, a (local) configuration represents a possible partial run of a Petri net [8].

A set of conditions is a co-set if its elements are pairwise in concurrency relation. A cut is a maximal co-set with respect to the set inclusion relation ⊂. The set of all cuts of a branching process $\beta$ is denoted by $C{T}_{\beta }$. For the example of Figure 2c, $\left[e_5\right]$ = $\{e_0$, $e_2$, $e_3,e_5\}$, $[e_2,e_3]$=$\{e_0$, $e_2$, $e_3\}$ and $\{b_2,b_9\}$ is a cut.

In fact, configurations, cuts, and reachable markings are closely connected by the following formulas [13], i.e.,

$$\begin{array}{c}Cut\left(C\right)=(Min\left(O\right)\cup C^{•}){\setminus }^{•}C\end{array}$$

(1)

$$\begin{array}{c}M=Mark\left(C\right)=h\left(Cut\right(C\left)\right)\end{array}$$

(2)

where C is a finite configuration of a branching process $\beta$, $M\in R\left(M_0\right)$ is a reachable marking, $Cut:C_{\beta }\to C{T}_{\beta }$ is a cut function that maps a configuration set into a cut set, and the function $Mark:C_{\beta }$→$R\left(M_0\right)$ represents the reachable marking by firing a finite configuration. Especially, M is called a local marking if $M=Mark\left(C\right)\wedge \exists e\in E:C=\left[e\right]$. For the example of Figure 2c, $Cut\left(\left[e_5\right]\right)$ = $\{b_2,b_9\}$ and $Mark\left(\left[e_5\right]\right)=p_2+p_9$.

Although the unfolding records all the running information of a Petri net, it is infinite if there exists an infinite firing transition sequence. For example, the unfolding of Figure 2a is infinite, because there is a loop from $t_4$ to $t_6$. Thus, it is hard to utilize an infinite unfolding to analyze a concurrent system. In order to solve this problem, a finite and complete prefix (FCP) [4,5,39] is proposed.

A prefix $Fin$ is an FCP if it satisfies finiteness and completeness, i.e.,

• $Fin$ only contains finitely many events and conditions; and,
• for every reachable marking M there exists a configuration C in $Fin$ such that $Mark\left(C\right)=M$, and for every transition t enabled by M there exists a configuration $C\cup \left\{e\right\}$ such that $e\notin C$ and e is labeled by t.

4.2. The Classical Algorithm for Generating an FCP

In order to generate an FCP, cut-off events (Definition. 7) are proposed to determine which events are not added into a given prefix when guaranteeing its finiteness and completeness. In other words, the unfolding of Petri net is truncated by cut-off events. For the example of Figure 2d, $e_6$ is a cut-off event, because $Mark\left(\left[e_6\right]\right)$=$Mark\left(\left[e_1\right]\right)$=$\{p_0$, $p_5\}$ and $\left[e_1\right]$${<}_e$$\left[e_6\right]$, where ${<}_e$ is an adequate order and was first used in Petri net unfolding by Esparza et al. [13].

Definition 7

(Cut-off event). Let β be a prefix, and $e_1$, $e_2$ be two events. The event $e_2$ is a cut-off event if $\left[e_1\right]⊲\left[e_2\right]\wedge Mark\left(\left[e_1\right]\right)$=$Mark(\left[e_2\right]$), where ⊲ is an adequate order that is a strict well-founded partial order on a set of prefix and it refines ⊂, i.e., $C_1\subset C_2\Rightarrow C_1⊲C_2$.

An FCP can be generated with many unfolding methods. In general, their basic idea is that for a given finite prefix, one of its possible extensions (corresponding to enabled transitions) is selected and added into it if the possible extension is not a cut-off event; and, then, for this new finite prefix, the above operation is continually conducted until all of the possible extensions are cut-off events or there is no possible extension. In this basic process, possible extensions are those transitions that can be added into a given prefix, while cut-off events determine its boundaries and scales. Corresponding to the basic idea, Algorithm 1 [13] shows a general method for producing an FCP. In this algorithm, the function $PosExtend\left(Fin\right)$ is used to calculate all possible extensions of a given prefix $Fin$, i.e.,

$$\begin{array}{c}PosExtend\left(Fin\right)=\left\{\right(t,X\left)\right|X\subset B,t\in T,Xisaco-set,\\ h\left(X\right)={}^{•}tand(t,X)\notin Fin\}.\end{array}$$

(3)

Algorithm 1 A finite complete prefix (FCP) algorithm

Require:

A Petri net $\Sigma$;

Ensure :

A finite complete prefix $Fin$ of $Unf(\Sigma )$;

1: $Cutoff:=\varnothing$; /*Cut-off events*/ 2: $Fin:=\varnothing$; 3: Add instances of the places from $M_0$ into $Fin$ 4: $Pe:=PosExtend\left(Fin\right)$; 5: while$Pe\ne \varnothing$do 6:   Choose an event e from $Pe$; 7:   if$\left[e\right]\cap Cutoff\ne \varnothing$then 8:     Extend $Fin$ with e and $e^{•}$∪${}^{•}e$; 9: $Pe:=PosExtend\left(Fin\right)$; 10:     if e is a cutoff event then 11: $Cutoff:=Cutoff\cup \left\{e\right\}$; 12:     end if 13:   else 14: $pe:=pe\setminus \left\{e\right\}$; 15:   end if 16: end while 17: return$Fin$;

4.3. Discussion

Many unfolding methods of generating FCPs have been proposed based on Algorithm 1, such as merged process and directed unfolding. Although these methods can generate different FCPs for a given Petri net, all of them cannot work without the calculations of configurations, cuts (or concurrent conditions), and cut-off events, since they are performed according to Definitions 6 and 7 and Equations (1)–(3). Obviously, these calculations can directly affect the unfolding efficiency of Petri nets. However, the  related computing methods of configurations, cuts, and cut-off events easily suffer from the following problems:

(1) 

The repeated calculations of configurations and cuts.

The calculations of configurations and cuts need to be repeatedly conducted without considering the causality and recurrence relations between events. For example, in order to calculate the local configuration of $e_6$ in Figure 2d, it needs to find out all of the events that are in casuality with it. Thus, we can get $\left[e_6\right]$ = $\{e_1$, $e_4$, $e_6\}$ according to Definition 6. In fact, some events of $\left[e_6\right]$ have been previously obtained by calculating the local configurations of $e_6$’s prep-sets. This is because $e_4<e_6$ and $\forall e\in \left[e_4\right]:e<e_4\Rightarrow e<e_6$. Similarly, in order to calculate the cut of $\left[e_6\right]$, it needs to find out all the pre-/post-sets of $\left[e_6\right]$, i.e., $Cut\left(\left[e_6\right]\right)$ = ($Min\left({\beta }_3\right)$$\cup {\left[e_6\right]}^{•}{)\setminus }^{•}\left[e_6\right]$. In fact, some results can be calculated by $e_6$’s prep-sets since their local configurations have been obtained.

(2) 

The blindness in determining cut-off events.

According to the definition of cut-off events, we know that, once a new event is generated and added into a given prefix, it needs to match with all of the existing events, so as to determine whether it is a cut-off event. For example, if we determine whether $e_6$ is a cut-off event in ${\beta }_3$ of Figure 2d, it has to find out one event e from the existing event set $\{e_0,e_1,e_2,e_3,e_4,e_5\}$ satisfying $\left[e\right]⊲\left[e_6\right]\wedge Mark\left[e\right]$=$Mark\left[e_6\right]$. In fact, some transitions with certain structures correspond to these cut-off events. Hence, we can utilize them to guide the determination of cut-off events rather than the blind matchings with all events.

5. An Improved Computing Method for Unfolding Petri Nets

In this section, we propose an incremental and backward-conflict guided method for calculating configurations, cuts, and  cut-off events. Furthermore, an  improved unfolding algorithm is developed to do some model checkings.

5.1. The Incremental Calculations of Configurations and Cuts

We can easily derive Lemma 1 because a configuration is causally closed and conflict-free.

Lemma 1.

(1) 

$\left[e\right]=\left[{}^{••}e\right]\cup \left\{e\right\}$;

(2) 

${\left[e\right]}^{•}={\left[{}^{••}e\right]}^{•}\cup e^{•}=\left({\bigcup }_{e^{\prime }\in {}^{••}e}{\left[e^{\prime }\right]}^{•}\right)\cup e^{•}$;

(3) 

${}^{•}\left[e\right]={}^{•}\left[{}^{••}e\right]\cup {}^{•}e=\left({\bigcup }_{e^{\prime }\in {}^{••}e}{}^{•}\left[e^{\prime }\right]\right)\cup {}^{•}e$.

From Lemma 1, we can find that the local configuration of an event can be recursively calculated by its prep-sets. Furthermore, these prep-sets can also compute the post-/pre-set of this local configuration.

In this paper, all of the local configurations can be represented by a configuration matrix. Thus, once a new event is added into a given prefix, its new local configuration can be calculated by Lemma 1, and a new configuration matrix of this prefix is accordingly updated. Figure 3 shows the configuration matrices of ${\beta }_1$ and ${\beta }_2$ in Figure 2b,c, respectively. From  Figure 3, we can find that the local configuration of $e_5$ can be calculated by a logical OR operation on the local configurations of $e_2$ and $e_3$ in the configuration matrix of ${\beta }_1$.

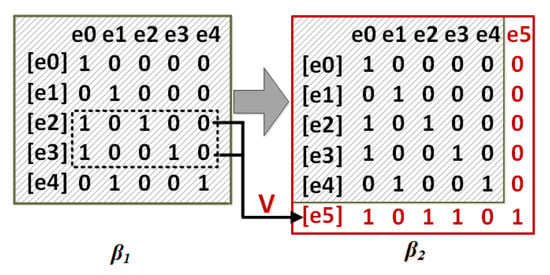
Figure 3. The configuration matrices of Figure 2b,c.

We propose the following theorems to reveal the recursive relations between an event and its prep-sets in order to improve the calculations of cuts.

Theorem 1.

If C is a configuration of a branching process β, then there exists a set of events $E^{\prime }\subseteq C$ satisfying $\left[E^{\prime }\right]=C$, where $E^{\prime }=\{e\in C|\forall e^{\prime }\in C\setminus \left\{e\right\}:e\nless e^{\prime }\}$.

Proof. 

If $e\in \left[E^{\prime }\right]$, then $e\in C$. It is assumed that $\exists e^{\prime }\in C:e^{\prime }\notin \left[E^{\prime }\right]$. From this assumption, we can easily get $e^{\prime }\notin E^{\prime }$. Because C is a configuration, then $\exists e^{\prime \prime }\in E:e^{\prime }\le e^{\prime \prime }$. However, $e^{\prime \prime }\in E$. Obviously, it contradicts the above assumption. Hence, if $e^{\prime }\in C$, then $e^{\prime }\in \left[E^{\prime }\right]$. Therefore, $\left[E^{\prime }\right]=C$.    □

According to Theorem 1, we can further obtain the following formula.

$$\begin{array}{c}Cut\left(C\right)=(Min\left(O\right)\cup {\left[E^{\prime }\right]}^{•}){\setminus }^{•}\left[E^{\prime }\right]=\\ (Min\left(O\right)\cup \bigcup _{i=1}^k{\left[e_i\right]}^{•})\setminus \bigcup _{i=1}^k{}^{•}\left[e_i\right]\end{array}$$

(4)

where $C=\left[E^{\prime }\right]$ and $E^{\prime }={\bigcup }_{i=1}^k{e}_i$. Especially, if  $C=\left[e\right]$ and $e\in E$, then

$$\begin{array}{c}Cut\left(\left[e\right]\right)=(Min\left(O\right)\cup {\left[e\right]}^{•})\setminus {}^{•}\left[e\right]=\\ (Min\left(O\right)\cup e^{•}\cup \bigcup _{e^{\prime }\in {}^{••}e}{\left[e^{\prime }\right]}^{•})\setminus ({}^{•}e\cup \bigcup _{e^{\prime }\in {}^{••}e}{}^{•}\left[e^{\prime }\right])\end{array}$$

(5)

Theorem 2.

Let e be an event of a branching process. If the pre-event set of e is a non-empty set, i.e., ${}^{•}$${}^{•}e$≠∅, then $Cut\left(\right[e\left]\right)$=$\left(Cut\right([{}^{•}$${}^{•}e\left]\right)$∪$e^{•})$∖${}^{•}e$.

Proof. 

From Equation (2), we can obtain $Cut\left(\right[e\left]\right)$= ($Min\left(O\right)$∪${\left[e\right]}^{•})$∖${}^{•}\left[e\right]$. Let $S={}^{•}$${}^{•}e$. If $S\ne$∅, then $Cut\left(\right[e\left]\right)$= ($Min\left(O\right)$∪ (${\left[S\right]}^{•}$∪$e^{•}\left)\right)$∖ (${}^{•}\left[S\right]$∪${}^{•}e$) = (($Min\left(O\right)$∪${\left[S\right]}^{•}$) ∖ (${}^{•}\left[S\right]$∪${}^{•}e$)) ∪ ($e^{•}$∖ (${}^{•}\left[S\right]$∪${}^{•}e$)). Since $e^{•}$∩${}^{•}\left[S\right]$=∅ and $e^{•}$∩${}^{•}e$=∅, then $Cut\left(\right[e\left]\right)$= ((($Min\left(O\right)$∪${\left[S\right]}^{•}$ ) ∖${}^{•}\left[S\right]$) ∖${}^{•}e$) ∪$e^{•}$= ($Cut\left[S\right]$∖${}^{•}e$) ∪$e^{•}$= ($Cut\left[S\right]$∪$e^{•}$) ∖${}^{•}e$.    □

Based on Theorem 2 and Equation(5), we can utilize these recursive relations between an event and its prep-set to calculate the related cuts. For the example of Figure 2c, $Cut\left(\left[e_4\right]\right)=(Cut\left(\left[e_1\right]\right)$∪$e_4^{•})$∖${}^{•}{e}_4$$=\{b_0,b_8\}$, where $e_1={}^{•}$${}^{•}{e}_4$ and $Cut\left(\left[e_1\right]\right)=\{b_0,b_5\}$.

Therefore, the contexts (Definition  8) of every event can be computed and recorded during the process of producing an FCP. What is more, they can be reused in the subsequent calculations of another events. For the example of Figure 2c, the context of $e_4$ is $\zeta \left(e_4\right)$=$(\left[e_4\right]$, ${}^{•}\left[e_4\right]$, ${\left[e_4\right]}^{•}$, $Cut\left(\left[e_4\right]\right))$$=(\{e_1,e_4\}$, $\{b_1,b_2,b_5\}$, $\{b_5,b_8\}$, $\{b_0,b_8\})$, and it can be reused to calculate the context of $e_6$, since $e_4={}^{•}$${}^{•}{e}_6$.

Definition 8

(Context). The context of an event e is a four-tuple $\zeta \left(e\right)=(\left[e\right],{}^{•}\left[e\right],{\left[e\right]}^{•},Cut\left(\left[e\right]\right))$.

Although Equation (3) gives the calculation of possible extensions, it is not easy to find out all of the co-sets in the unfolding process of Petri nets. For example, if we determine whether the transition $t_5$ can be added into the prefix ${\beta }_1$ in Figure 2b, it has to find out all related concurrent conditions from the existing ones. In fact, we can utilize the concurrency relation of the prep-sets of a condition to recursively calculate its concurrent conditions, and then compute all possible extensions.

Therefore, in order to determine whether a transition t can be added into a given prefix $\beta$, it is necessary to find a co-set X in $\beta$ much more efficiently, which satisfies $h\left(X\right)$=${}^{•}t$ and $(t,X)$∉$\beta$. Because of the fact that concurrent conditions make up a co-set, we can utilize the recursive relation between an event and its prep-sets to improve their calculations.

Stefan Romer [40] gives this recursive relation, and  shows that the concurrent conditions of one condition can be recursively calculated by its prep-sets. That is, if $Cob\left(b\right)=\left\{b^{\prime }\right|b$$co$$b^{\prime },b^{\prime }\in B\}$ denotes the concurrent conditions of a condition b, then

$$\begin{array}{c}Cob\left(b\right)=\bigcap _{b^{\prime }\in {}^{••}b}Cob\left(b^{\prime }\right).\end{array}$$

(6)

For the example of Figure 2c, $Cob\left(b_9\right)=Cob\left(b_6\right)\cap Cob\left(b_7\right)=\{b_2,b_7\}\cap \{b_2,b_6\}=\left\{b_2\right\}$ and ${}^{••}{b}_9=\{b_6,b_7\}$.

In this paper, all the concurrent relations of conditions can be represented by a concurrency matrix. Thus, once a new event is added into a given prefix, the new concurrent conditions can be calculated by Equation (6), and  a new concurrency matrix is accordingly updated. Figure 4 shows the concurrency matrices of ${\beta }_1$ and ${\beta }_2$ in Figure 2b,c, respectively. From  Figure 4, we can find that the concurrent conditions of $b_9$ can be calculated by a logical AND operation on the concurrent conditions of $b_6$ and $b_7$ in the concurrency matrix of ${\beta }_1$.

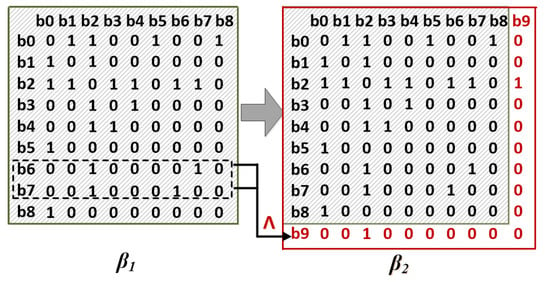
Figure 4. The concurrency matrices of Figure 2b,c.

Based on the recursive calculation of concurrent conditions, we give a specific algorithm for calculating possible extensions, as shown in Algorithm 2.

Algorithm 2 Possible extension algorithm

Require:

A prefix $\beta$ and its concurrency matrix A of conditions;

Ensure :

A set of possible extensions $Pe$;

1: for each $t\in T$ do 2:   Find out a set of event X such that $h\left(X\right)$=${}^{•}t$; 3:   if X is a co-set in A and ($t,X$) ∉$Pe$ then 4:     Add ($t,X$) into $Pe$; 5:     According to Equation (6), calculate the concurrent conditions of the new event and update A; 6:   end if 7: end for 8: return$Pe$;

5.2. The Backward-Conflict Guided Calculations of Cut-Off Events

According to the definition of cut-off events (Definition 7) and Theorem 2, our incremental calculations of configurations and cuts are also conductive to the determination of cut-off events since they are closely related with these calculations. In this part, we utilize backward conflicts (Definition 9) [17] to further guide the calculations/matchings of cut-off events.

Definition 9

(Backward conflict). Two different transitions, $t_1$ and $t_2$, are in backward conflict if $t_1^{•}$ ∩ $t_2^{•}$ ≠ ∅.

As is well known, the initial marking $M_0$ of a Petri net is possibly equal to the Mark function value of the local configuration of an event e in a prefix, i.e., $Mark\left(\left[e\right]\right)=M_0$. In fact, this event is a cut-off event, and it guarantees the finiteness and completeness of this prefix. Therefore, in order to efficiently calculate cut-off events in this case, we first transform the places with tokens and input transitions into backward-conflict structures (Notice that this transformation does not affect the properties of original Petri nets). That is to say, if there exists a place p in a Petri net $\Sigma$ that satisfies $M_0\left(p\right)>0\wedge \left|p^{•}\right|>0$, we add a new place $p^{\prime }$, a new transition $t^{\prime }$ and some arcs (i.e.,  flow relations $\left\{p^{\prime }\right\}\times \left\{t^{\prime }\right\}$ and $\left\{t^{\prime }\right\}\times \left\{p\right\}$ ) into $\Sigma$. Meanwhile, the new initial marking becomes $M_0^{\prime }$, and it satisfies $M_0^{\prime }[t^{\prime }⟩M_0$∧$M_0^{\prime }\left(p^{\prime }\right)=M_0\left(p\right)$∧$M_0^{\prime }\left(p\right)=0$. Figure 5 shows this transformation process of a Petri net before unfolding it.

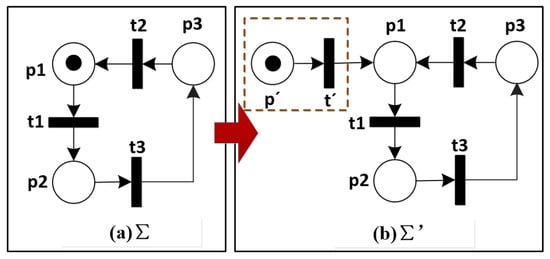
Figure 5. The pre-process of a Petri net before unfolding it.

After transforming into some backward-conflicts, we can use these structures to guide the related matchings with certain existing events, so as to determine cut-off events.

Lemma 2.

If an event $e_2$ is a cut-off event of a branching process with respect to an event $e_1$, then $\exists e_1^{\prime }\in \left[e_1\right]$: $h{\left(e_1^{\prime }\right)}^{•}$∩$h{\left(e_2\right)}^{•}\ne \varnothing$∧$\exists e_2^{\prime }\in \left[e_2\right]$: $h{\left(e_2^{\prime }\right)}^{•}$∩$h{\left(e_1\right)}^{•}\ne \varnothing$.

Proof. 

From the definition of cut-off events, we can get $Mark\left[e_1\right]$=$Mark\left[e_2\right]$ and $Cut\left[e_1\right]$=$Cut\left[e_2\right]$. It is assumed that there is no event $e_1^{\prime }\in \left[e_1\right]$ satisfying $h{\left(e_1^{\prime }\right)}^{•}$∩$h{\left(e_2\right)}^{•}\ne \varnothing$, then $\exists e_x\in E\setminus \left[e_1\right]$: $h{\left(e_x\right)}^{•}$∩$h{\left(e_2\right)}^{•}\ne \varnothing$. Hence, $e_x\nless e_1$∧$e_1\nless e_x$. No matter that $e_x\#e_1$ or $e_x$$co$$e_1$, it cannot satisfy $Cut\left[e_1\right]$=$Cut\left[e_2\right]$. Therefore, $\exists e_1^{\prime }\in \left[e_1\right]$: $h{\left(e_1^{\prime }\right)}^{•}$∩$h{\left(e_2\right)}^{•}\ne \varnothing$. Similarly, we can come to the other conclusion that $\exists e_2^{\prime }\in \left[e_2\right]$: $h{\left(e_2^{\prime }\right)}^{•}$∩$h{\left(e_1\right)}^{•}\ne \varnothing$.    □

For example, $e_6$ is a cut-off event with respect to $e_1$ in Figure 2d, where $h{\left(e_6\right)}^{•}$∩$h{\left(e_1\right)}^{•}\ne \varnothing$. In fact, the transitions $h\left(e_6\right)$ and $h\left(e_1\right)$ are in backward conflict. Therefore, Lemma 2 shows the relation between cutoff events and backward-conflict transitions. Furthermore, we can determine whether an event is a cutoff event only when it corresponds to a backward-conflict transition.

Specifically, a function of possible cut-off transitions with respect to a Petri net $\Sigma$ is given to guide the determination of cut-off events in this paper, i.e.,

$$\begin{array}{c}PosCutoff(\Sigma )=\{t\in T|\exists p\in P:t\in {}^{•}p\wedge {\left(\right|}^{•}p|>1)\}.\end{array}$$

(7)

Furthermore, we can easily get the following theorem.

Theorem 3.

Let Σ be a Petri net and β be a branching process of Σ. If e is a cut-off event of β, then $h\left(e\right)\in PosCutoff(\Sigma )$.

According to Theorem 3, we match a new event with $PosCutoff(\Sigma )$ to determine whether it is a cut-off event. For the example of Figure 2d, $e_6$ is a cut-off event with respect to $e_1$, where $t_1^{•}$∩$t_6^{•}$≠∅, $PosCutoff(\Sigma )$ = $\{t_1,t_6\}$, and $h\left(e_6\right)\in PosCutoff(\Sigma )$.

5.3. An Improved Algorithm for Generating an FCP

Based on the above new calculations of configurations, cuts, and cut-off events, we propose an improved method for unfolding a Petri net, as shown in Figure 6. Corresponding to this basic process, we develop an incremental and backward-conflict guided algorithm for generating an FCP, as shown in Algorithm 3.

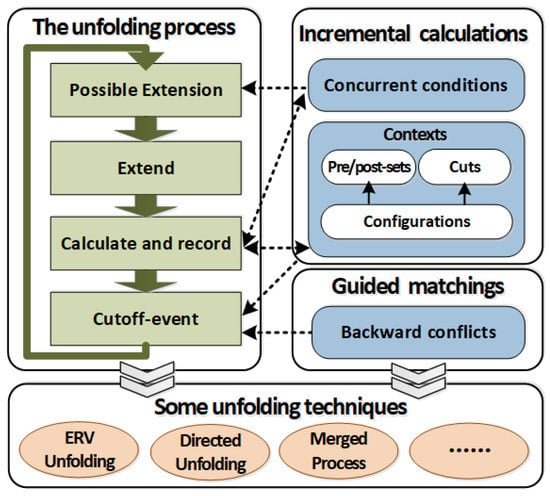
Figure 6. The basic process of our improved method for unfolding a Petri net.

• The contexts of events are calculated in Lines 10–15 according to Equation (5) and Theorem 2.
• Algorithm 2 is utilized to calculate the possible extensions.
• Linked hash tables are used to store the contexts of events and concurrent conditions, which contribute to the calculations of set operations in Equations (4) and (5).
• Cut-off events are determined by Theorem 3, and  Lines 19–22 correspond to this point.

Algorithm 3 An incremental and backward-conflict guided algorithm for generating an FCP

Require:

A Petri net $\Sigma$;

Ensure :

A finite complete prefix $Fin$ of $Unf(\Sigma )$;

(1) Initialize

1: $Fin:=\varnothing$; 2: $Hash:=\varnothing$; /*The contexts of events*/ 3: $Cutoff:=\varnothing$; /*Cut-off events*/ 4: Pre-process $\Sigma$ and transform some structures into backward conflicts; 5: $Pc:=PosCutoff(\Sigma )$; /*Backward-conflict transitions*/

(2) Unfolding process

6: Add the place instances from $M_0$ into $Fin$; 7: $Pe:=PosExtend\left(Fin\right)$; /*Algorithm 2*/ 8: while$Pe\ne \varnothing$do 9:   Choose a minimal event $e:=(t,X)$ with respect to an adequate order in $Pe$ such that $h\left(e\right)=t$; 10:    if $\left[e\right]\cap Cutoff==\varnothing$then 11:    Extend $Fin$ with e and $e^{•}$∪${}^{•}e$; 12:     if $|{}^{•}$${}^{•}$$e|==1$then 13: $\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}Cut\left(\right[e\left]\right)$$:=$ ($Cut\left(\left[e^{\prime }\right]\right)$∪$e^{•})$∖${}^{•}e$, where $e^{\prime }$∈${}^{•}$${}^{•}e$; 14:    else 15: $\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}Cut\left(\right[e\left]\right)$$:=$$(Min\left(O\right)\cup e^{•}\cup {\bigcup }_{e^{\prime }\in {}^{••}e}{\left[e^{\prime }\right]}^{•})\setminus ({}^{•}e\cup {\bigcup }_{e^{\prime }\in \setminus {}^{••}e}{}^{•}\left[e^{\prime }\right])$ 16:    end if 17: $\hspace{1em}\hspace{1em}\hspace{1em}Hash.put(e,\zeta (e\left)\right)$; /*Record the context of e*/ 18: $\hspace{1em}\hspace{1em}\hspace{1em}Pe:=PosExtend\left(Fin\right)$; /*Algorithm 2*/ 19:     if$h\left(e\right)\in Pc$then 20:     Determine whether e is a cutoff event through $Hash$ and $Pc$; 21:     if e is a cutoff event then 22: $\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}Cutoff:=Cutoff\cup \left\{e\right\}$; 23:     end if 24:    end if 25:   else 26: $\hspace{1em}\hspace{1em}\hspace{1em}pe:=pe\setminus \left\{e\right\}$; 27:   end if 28: end while 29: Delete events, conditions and arcs that are caused by pre-processing $\Sigma$. 30: return$Fin$;

5.4. The Validation of Our Improved Unfolding Method

The prefix generated by Algorithm 3 is finite and complete, since it is the same as that by the classical unfolding. What is more, our new computing methods can improve the unfolding efficiency of Petri nets as compared with Algorithm 1 due to the fact that recursive relations, contextual information, and backward conflicts are considered in our specified calculations. Moreover, the result of our improved method is guaranteed by the following factors. On the one hand, we derive Equations (4)–(6) according to Lemma 1, Theorems 1 and 2. Based on these Equations, we can utilize the prep-transition $e^{\prime }$ (i.e., predecessor) of an event e to calculate its cuts if $|{}^{•}$${}^{•}$$e|=1$ (Algorithm 3). That is, $Cut\left(\right[e\left]\right)$$:=$ ($Cut\left(\left[e^{\prime }\right]\right)$∪$e^{•})$∖${}^{•}e$, where $e^{\prime }$∈${}^{•}$${}^{•}e$. Otherwise, some calculated contextual results (Definition 8) can be directly reused in order to compute the cuts of e. By comparison, the classical unfolding methods need a lot of repetitive calculations of pre-sets and post-sets for each event in $\left[e\right]$. Thus, our improved unfolding method saves much time in the runtime of calculating configurations and cuts. On the other hand, we match a new event with $PosCutoff(\Sigma )$ (Equation (7)) to determine whether it is a cut-off event according to Lemma 2 and Theorem 3. By comparison, the classical unfolding methods need to match a new event with all existing events. What is more, the time complexity of classical unfolding methods is generally $O\left(L^2\right)$, while our improved calculation is $O\left(KL\right)$, where L is the number of total events and K is the number of events that map to $PosCutoff(\Sigma )$. Note that, K is much less than L (i.e., $K<<L$) with the increase of L. Thus, our improved unfolding method saves much time in the runtime of calculating cut-off events. Nevertheless, our method takes up more space than the classical unfolding, because it needs to store many more contextual results.

5.5. Model Checkings Based on the Improved Unfolding Method

Our improved computing method for unfolding Petri nets can be applied to many model checkings.

(1) 

Embedded into the existing unfolding techniques

The new calculations of configurations, cuts, concurrent conditions (possible extensions), and cut-off events can be applied in various kinds of unfolding techniques, e.g., ERV unfolding, merged process and directed unfolding. As is well known, ERV unfolding proposes a new classical algorithm for improving the McMillan’s unfolding. The merged process (MP) generates a condensed unfolding of a Petri net’s behavior. Directed unfolding (DU) utilizes heuristic functions to guide the unfolding process of Petri nets. Given these unfolding techniques, our improved computing methods can replace their calculations of configurations, cuts, and cut-off events. Meanwhile, our new calculations can be further combined with partial orders, merged conditions and heuristic functions in their related unfolding methods of Petri nets. By this means, our new computing methods can enhance these unfolding techniques and improve their model checkings.

(2) 

Checking reachability, properly completed, and deadlocks

Some errors can be detected based on the unfolding techniques. In this paper, we refer to some previous studies [5,34,37,41,42], and utilize our improvements to efficiently check reachability [15,30], properly completed [43,44] and deadlocks [45,46].

• Reachability
  On the one hand, we can utilize the directed unfolding technique [15] to verify the reachability of markings or places. On the other hand, some incremental calculations of configurations (e.g., configuration matrix) can be used to check whether a transition is reachable to the other one in the execution of a Petri net. That is, given two transitions $t_1,t_2\in T$ and two events $e_i,e_j\in E$, if the configuration matrix A of an FCP satisfies $A_{(i,j)}=1\wedge h\left(e_i\right)=t_1\wedge h\left(e_j\right)=t_2$, then we can come to the conclusion that $t_2$ is reachable to $t_1$. Notice that $e_i$ and $e_j$ are, respectively, the i-th and j-th elements of E.
• Properly completed
  As is well known, a WF-net $\Sigma =(N,M_0)$ is properly completed if it satisfies $\forall M\in R\left(M_0\right):M\left(o\right)>0\Rightarrow M=\left\{o\right\}$, where o is the sink place [44]. In order to verify this property, we can determine whether there exist some conditions that are concurrent with sink conditions (i.e., corresponding to the sink places) in our concurrency matrix. If these conditions exist, they indicate that $\Sigma$ is not properly completed or sound.
• Deadlocks
  Because the context of an event is calculated in our improved unfolding method, we can utilize its cuts and Mark functions to check deadlocks, i.e., a marking M is a deadlock if $\exists e\in E:M=Mark\left(\right[e\left]\right)$ and no transition $t\in T$ is enabled at M.

6. Case Study

In order to illustrate the application scenarios of our improved method for unfolding Petri nets, a case study of airport check-in is given, as follows.

A passenger must check in at theairport before boarding an airplane. Figure 7 shows the basic business process of an airport check-in system (IBM: https://www.ibm.com/developerworks/rational/library/2802.html, (accessed on 5 January 2021)). In this business process, the passengers’ reservations are first checked. If their reservations are correct, these passengers can choose/change their seats. Otherwise, the incorrect reservations are sent to the airport travel agency. After choosing seats, the airport can receive the passengers’ baggages and print their receipts. Meanwhile, the boarding cards are concurrently printed. Finally, all travel of the documents is provided to passengers.

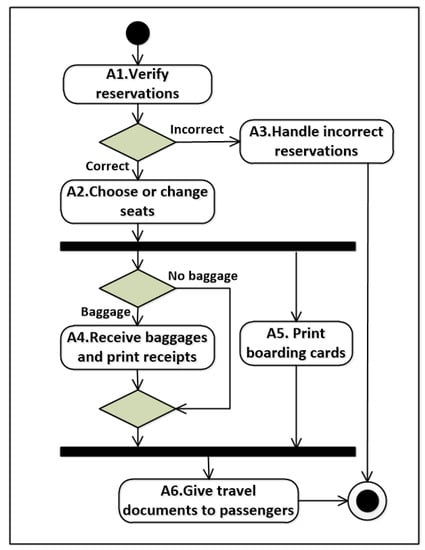
Figure 7. The business process of an airport check-in system.

As for the above business process, we first use a Petri net $\Sigma$ of Figure 8a to model it. Table 1 lists the meanings of all transitions in $\Sigma$, where the backward-conflict transition set is $\{t_2,t_7,t_4,t_5\}$. Thus, we can obtain the possible cut-off transitions, i.e.,

$$PosCutoff(\Sigma )=\{t_2,t_7,t_4,t_5\}.$$

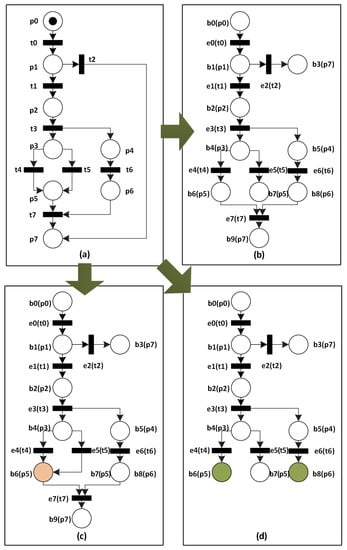
Figure 8. (a) A Petri net $\Sigma$ that models an airport check-in system; (b) the ERV unfolding of $\Sigma$; (c) the merged process of $\Sigma$; and, (d) the directed unfolding of $\Sigma$, where $p_5+p_6$ is a reachable marking.

Table 1. Activities.

Transition	Activity	Transition	Activity
$t_0$	Verify reservations	$t_4$	Receive baggages and print receipts
$t_1$	Choose/change seats	$t_5$	–
$t_2$	Handle incorrect reservations	$t_6$	Print boarding cards
$t_3$	–	$t_7$	Give travel documents to passengers

According to Algorithm 3, we unfold $\Sigma$ and generate its FCP, as shown in Figure 8b. During this unfolding process, Table 2 records all contexts of events and Figure 9 shows the incremental calculations of configurations and concurrent conditions. Meanwhile, backward-conflict transitions are utilized to guide the matchings between events $e_4$ and $e_5$, where $Mark\left(\left[e_4\right]\right)$=$Mark\left(\left[e_5\right]\right)$ and $\left[e_4\right]$${<}_e$$\left[e_5\right]$. Thus, $e_5$ is a cut-off event with respect to $e_4$.

Table 2. The contexts of events.

Events	Contexts
	Local Configurations ($\left[\mathit{e}\right]$)	Pre-Sets (${}^{•}\left[\mathit{e}\right]$)	Post-Sets (${\left[\mathit{e}\right]}^{•}$)	Cuts ($\mathbf{Cut}\left(\right[\mathit{e}\left]\right)$)
$e_0$	$\left\{e_0\right\}$	$\left\{b_0\right\}$	$\left\{b_1\right\}$	$\left\{b_1\right\}$
$e_1$	$\{e_0,e_1\}$	$\{b_0,b_1\}$	$\{b_1,b_2\}$	$\left\{b_2\right\}$
$e_2$	$\{e_0,e_2\}$	$\{b_0,b_1\}$	$\{b_1,b_3\}$	$\left\{b_3\right\}$
$e_3$	$\{e_0,e_1,e_3\}$	$\{b_0,b_1,b_2\}$	$\{b_1,b_2,b_4,b_5\}$	$\{b_4,b_5\}$
$e_4$	$\{e_0,e_1,e_3,e_4\}$	$\{b_0,b_1,b_2,b_4\}$	$\{b_1,b_2,b_4,b_6\}$	$\{b_5,b_6\}$
$e_5$	$\{e_0,e_1,e_3,e_5\}$	$\{b_0,b_1,b_2,b_4\}$	$\{b_1,b_2,b_4,b_7\}$	$\{b_5,b_7\}$
$e_6$	$\{e_0,e_1,e_3,e_6\}$	$\{b_0,b_1,b_2,b_5\}$	$\{b_1,b_2,b_5,b_8\}$	$\{b_4,b_8\}$
$e_7$	$\{e_0,e_1,e_3,e_4,e_6,e_7\}$	$\{b_0,b_1,b_2,b_4,b_5,b_6,b_8\}$	$\{b_1,b_2,b_4,b_6,b_8,b_9\}$	$\left\{b_9\right\}$
$e_8$	$\{e_0,e_1,e_3,e_5,e_6,e_8\}$	$\{b_0,b_1,b_2,b_4,b_5,b_7,b_8\}$	$\{b_1,b_2,b_4,b_5,b_7,b_8,b_{10}\}$	$\left\{b_{10}\right\}$

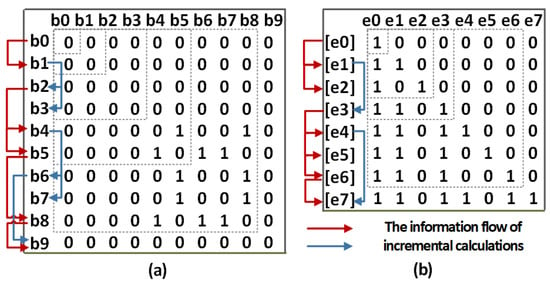
Figure 9. (a) The incremental calculations of concurrent conditions; (b) the incremental calculations of configurations.

Additionally, we can generate a merged process and directed unfolding of $\Sigma$, respectively, as shown in Figure 8c,d. Based on these unfoldings, we can verify some properties, such as deadlocks, properly completed, and reachability.

(1)

There is no deadlock in $\Sigma$ because there always exist enabled transitions at any local markings (except for the final state).

(2)

$\Sigma$ is properly completed, because no condition is concurrent with the sink condition $b_9$ in the concurrency matrix of Figure 9a.

(3)

Because events $b_6$ and $b_8$ are included in the directed unfolding and satisfy $h\left(b_6\right)=p_5$∧$h\left(b_8\right)=p_6$∧$b_{6}co{b}_8$, the marking $\{p_5,p_6\}$ is reachable from the initial marking $\left\{p_0\right\}$.

(4)

According to the configuration matrix of Figure 9b, the transition $t_0$ is reachable to the transition $t_7$ in the execution of $\Sigma$, since the events $e_0$ and $e_7$ satisfy $e_0\in \left[e_7\right]$∧$h\left(e_0\right)=t_0$∧$h\left(e_7\right)=t_7$.

From this case study, we can find that our improved computing method for unfolding a Petri net is feasible, and its result is correct. Moreover, this method can be applied to different unfolding techniques and model checkings.

7. Experiments and Results

7.1. Data Collections and Tool

The experiments in this paper are respectively done on the benchmarks of BPM_AIMC (The BPM Academic Initiative Model Collection: https://bpmai.org/download/index.html (accessed on 30 December 2020)) and Dining Philosophers [41]. BPM_AIMC is a famous data collection of formal models, and it has 100 + Petri nets. By now, this benchmark has been utilized by hundreds of academic institutes. The n-Dining-Philosopher is a classical problem in the synchronization of concurrent events/actions, and we can use Petri nets to formalize this problem, where n is from two to 20. For these two benchmarks, we use our tool DICER (DICER is developed based on PIPE (an open source tool), which can unfold Petri nets and PD-nets, and detect errors of data inconsistency.) [39] to implement the new methods and conduct a group of experiments.

7.2. Implementation and Results

In order to illustrate the unfolding efficiency of our improved computing method, we compare it with some unfolding methods in terms of runtime, such as ERV unfolding, merged process (MP), and directed unfolding (DU). That is, our improved calculations of configurations/cuts, concurrent conditions, and cut-off events are applied to these unfolding techniques, i.e., improved ERV unfolding (IERV), improved merged process (IMP), and improved directed unfolding (IDU), respectively.

(1)

The experiments on BPM_AIM

Because to the fact that Petri nets in BPM_AIMC are JSON documents, we first utilize the parsers of JSON and XML to transform them into some PNML (Petri Net Markup Language) [47] documents, which can be loaded by DICER. After getting PNML-based Petri nets, we select bounded ones from them with more than 10 transitions. Meanwhile, we assume that their initial places only have one token. Finally, we import 37 Petri nets of BPM_AIMC into DICER, and then generate their unfoldings. All of these experiments are done in a PC with Intel Core i5-2400 CPU (3.10GHz) and 4.0G memory.

Figure 10, Figure 11 and Figure 12 are the results of our experiments on BPM_AIMC. From Figure 10, we can see that IERV spends less time than ERV to generate an FCP. Similarly, IMP (resp. IDU) takes less time than MP (resp. DU). Obviously, our improved computing method is more effective than others in the runtime of unfolding Petri nets, although the scale of BPM_AIMC is not too large in reality.

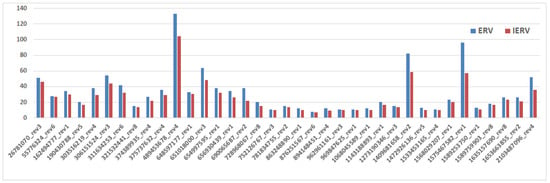
Figure 10. The unfolding time (ms) of Esparza, Romer, and Vogler (ERV) and improved ERV unfolding (IERV), where ERV is an unfolding technique and IERV applies our improved computing method to ERV.

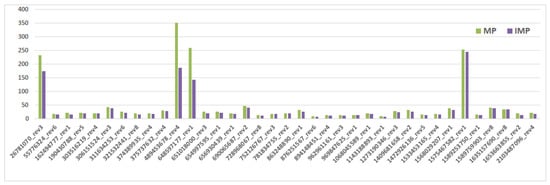
Figure 11. The unfolding time (ms) of merged process (MP) and IMP, where MP is an unfolding technique and IMP applies our improved computing method to MP.

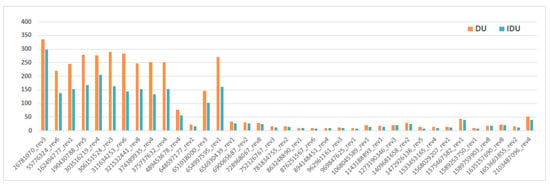
Figure 12. The unfolding time (ms) of directed unfolding (DU) and IDU, where DU is an unfolding technique and IDU applies our improved computing method to DU.

(2)

The experiments on Dining Philosophers

Some experiments are done on Dining Philosophers in order to further show the advantage of our method. We first import 10 Petri nets of Dining Philosophers into DICER, and then generate their unfoldings. For example, Figure 13 shows a Petri net of two-philosophers’ dining problem in DICER.

Figure 13. The Petri net of 2-philosophers’ dining problem in DICER.

Figure 14a–c are the results of our experiments on Dining Philosophers. From these results, we can see that ERV (resp. MP, DU) spends much more time than IERV (resp. IMP, IDU) to generate FCPs with the increment of n philosophers.

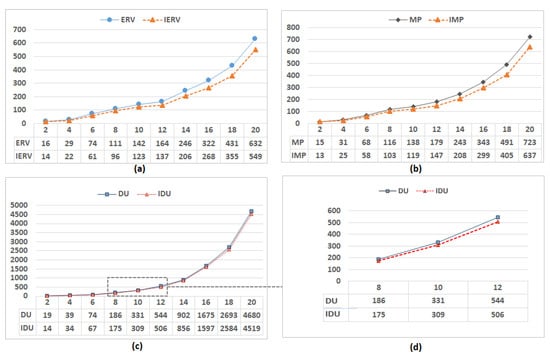
Figure 14. The unfolding time (ms) of different unfolding techniques on n-philosophers’ dining problem, where n is from 2 to 20. (a) IERV vs. ERV; (b) IMP vs. MP; (c) IDU vs. DU; and, (d) is a part of (c).

8. Conclusions

Concurrent systems easily suffer from some errors, such as deadlocks, lack of synchronization, and data inconsistencies. Although reachability-graph-based methods are proposed to check these errors, they generally have the problems of state space explosion. This is because these methods are based on the interleaving semantics, and the need to consider all partial orders of business activities to analyze their global behaviors of concurrent systems. By comparison, the unfolding technique of Petri net can characterize the real concurrency and alleviate the state space explosion problem, since it uses an acyclic net to represent the system running. Thus, it is greatly suitable to analyze/check some potential errors in a concurrent system.

As for the unfolding technique of Petri nets, the calculations of configurations, cuts, and cut-off events are key factors that make up an absolutely significant share of the total unfolding time. However, most of the unfolding methods do not specify highly efficient calculations on them. They mainly focus on how to generate a smaller FCP, or explore different kinds of Petri net unfoldings and their model checkings. In fact, their calculations of configurations and cuts need a lot of repetitive work, and new events need to match them up with all existing events so as to determine whether they are cut-off events. In order to solve these problems, we propose an improved computing method for unfolding Petri nets. Some recursion formulas and theorems are derived to calculate configurations and cuts. Backward conflicts are used to guide the determinations of cut-off events. Furthermore, we develop some improved algorithms for generating FCPs.

In the future work, we plan to carry out the following studies:

(1)

we apply our new calculations with heuristic functions into many more model checkings of concurrent systems;

(2)

timed concurrent systems are simulated and analyzed based on the unfolding techniques of Petri nets; and,

(3)

we explore the unfolding-based technique of WFD-net [48] to check concurrency bugs [49,50,51].