Towards a Novel Computer-Aided Optimization of Microreactors: Techno-Economic Evaluation of an Immobilized Enzyme System
Abstract
:1. Introduction
2. Materials and Methods
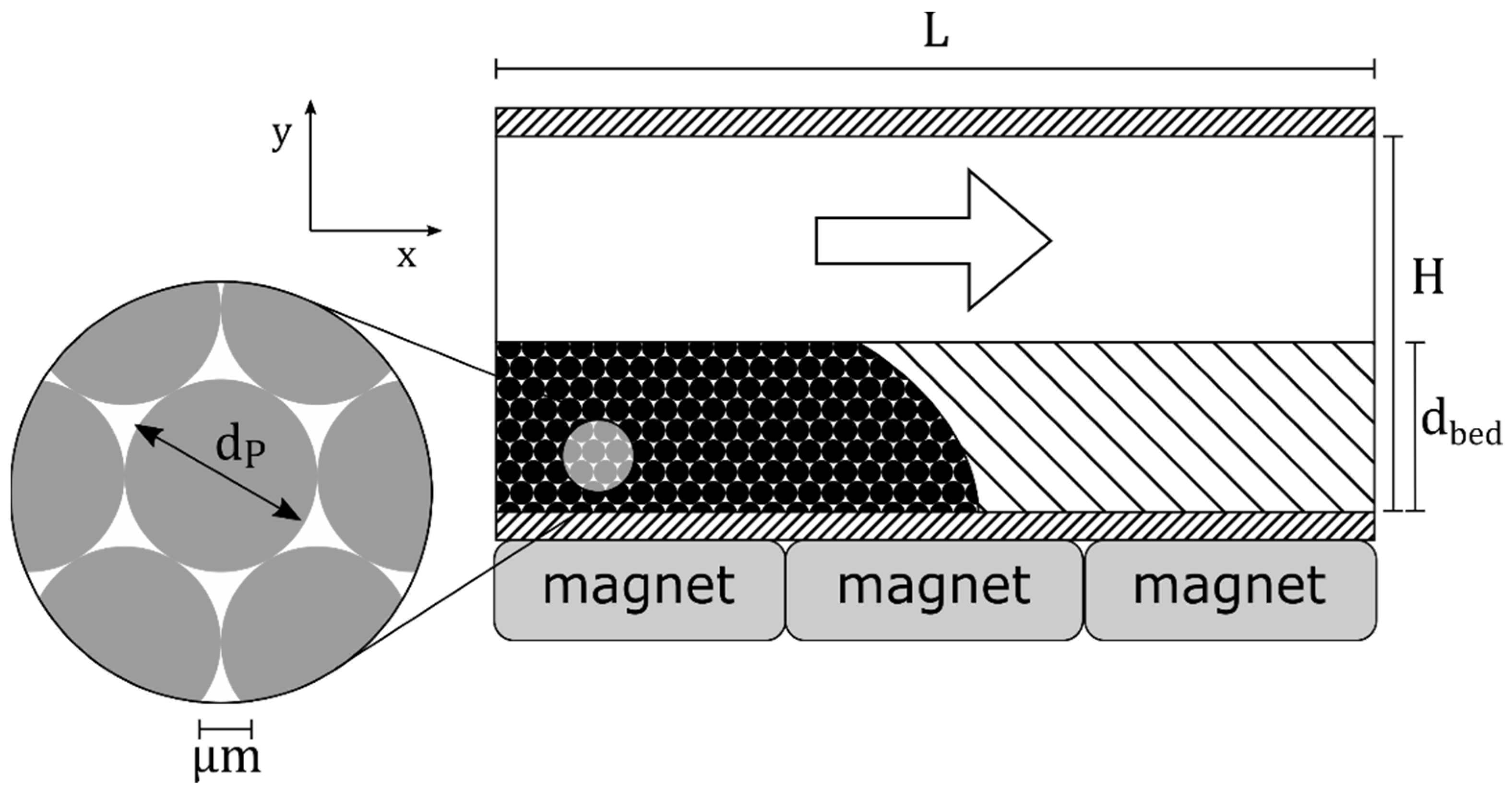
2.1. Reactor System
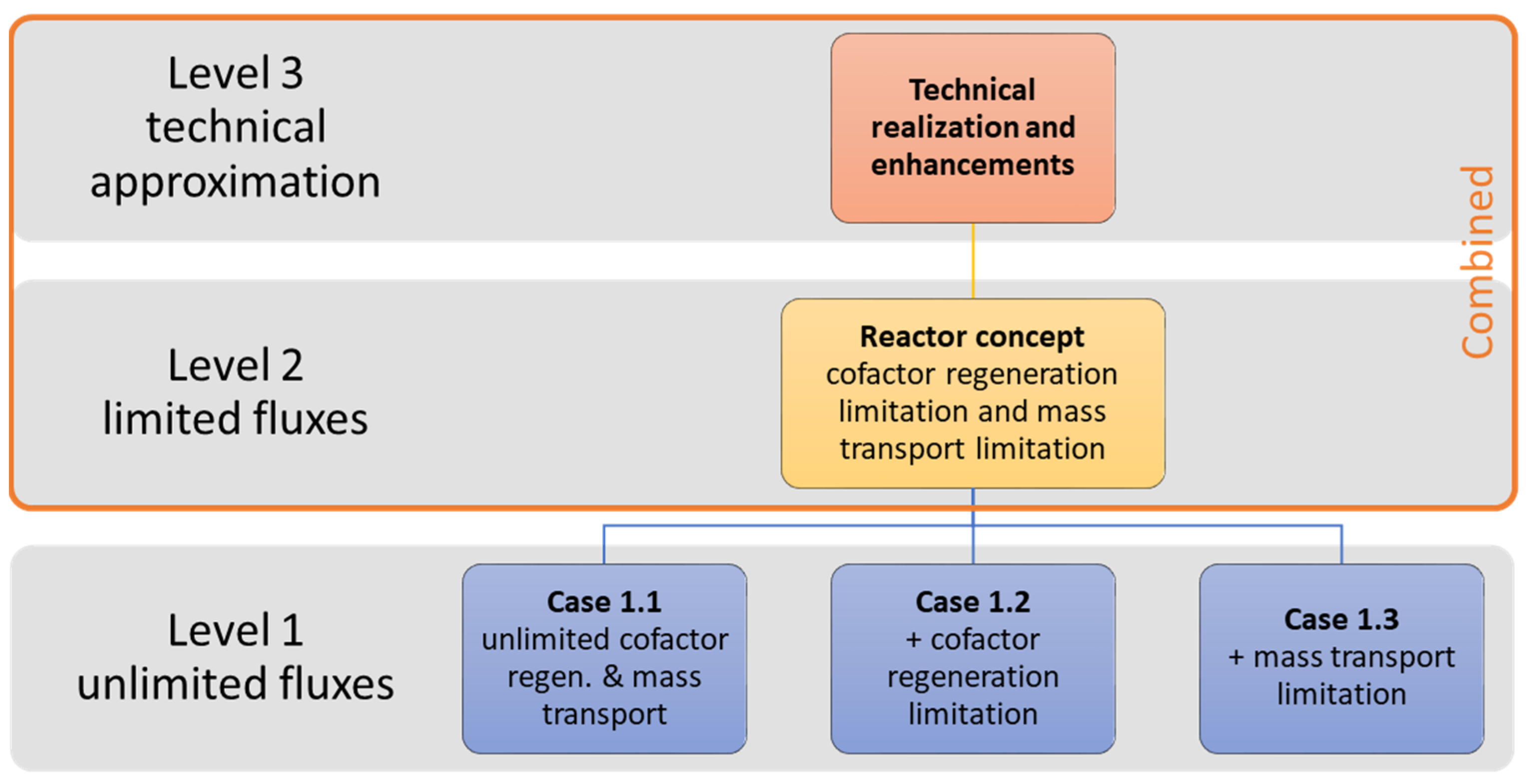
2.2. Systematic Design Methodology
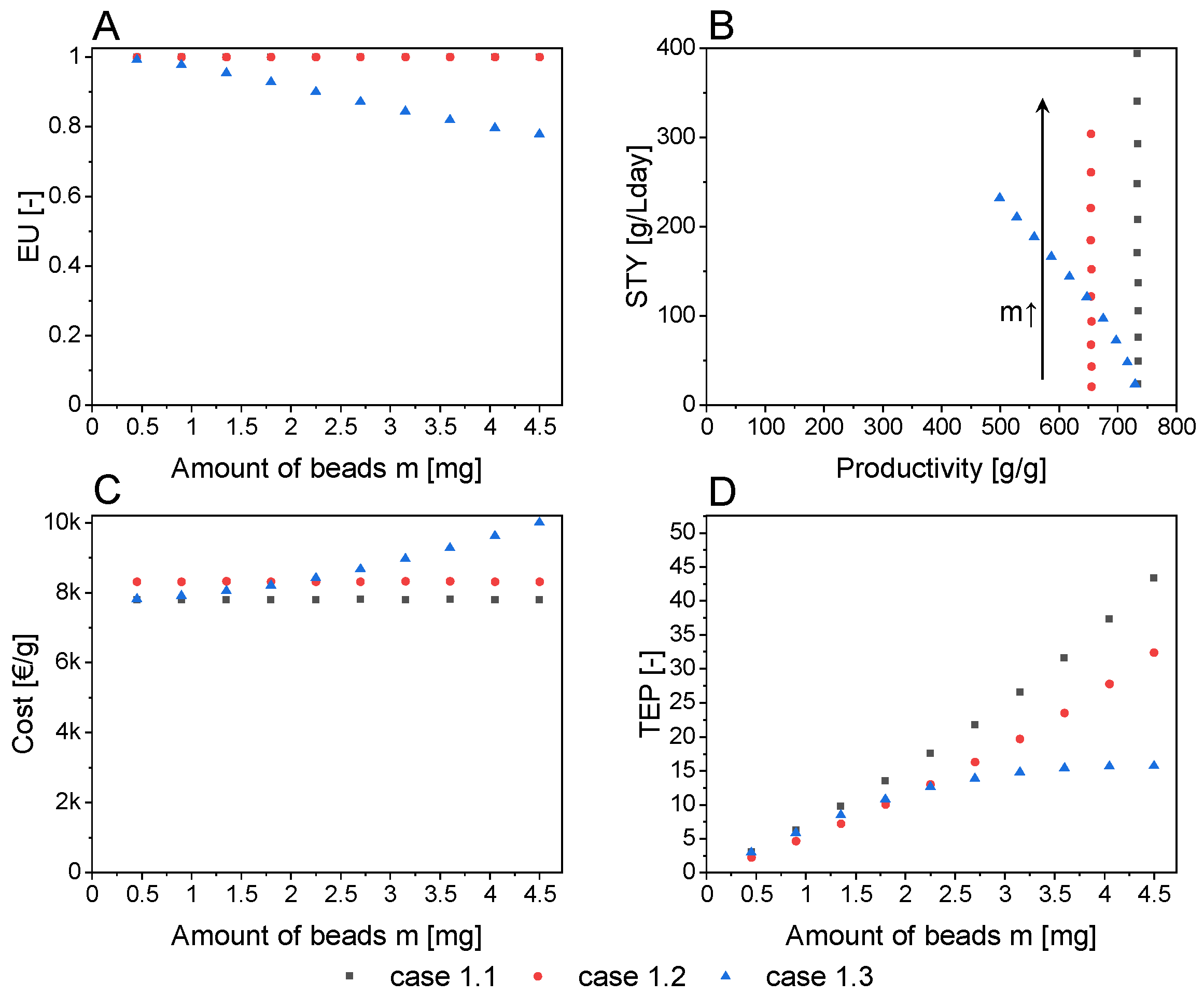
- Case 1.1—unlimited cofactor regeneration and mass transport
- Case 1.2—unlimited cofactor regeneration (mass transport limitation)
- Case 1.3—unlimited mass transport (cofactor regeneration limitation)
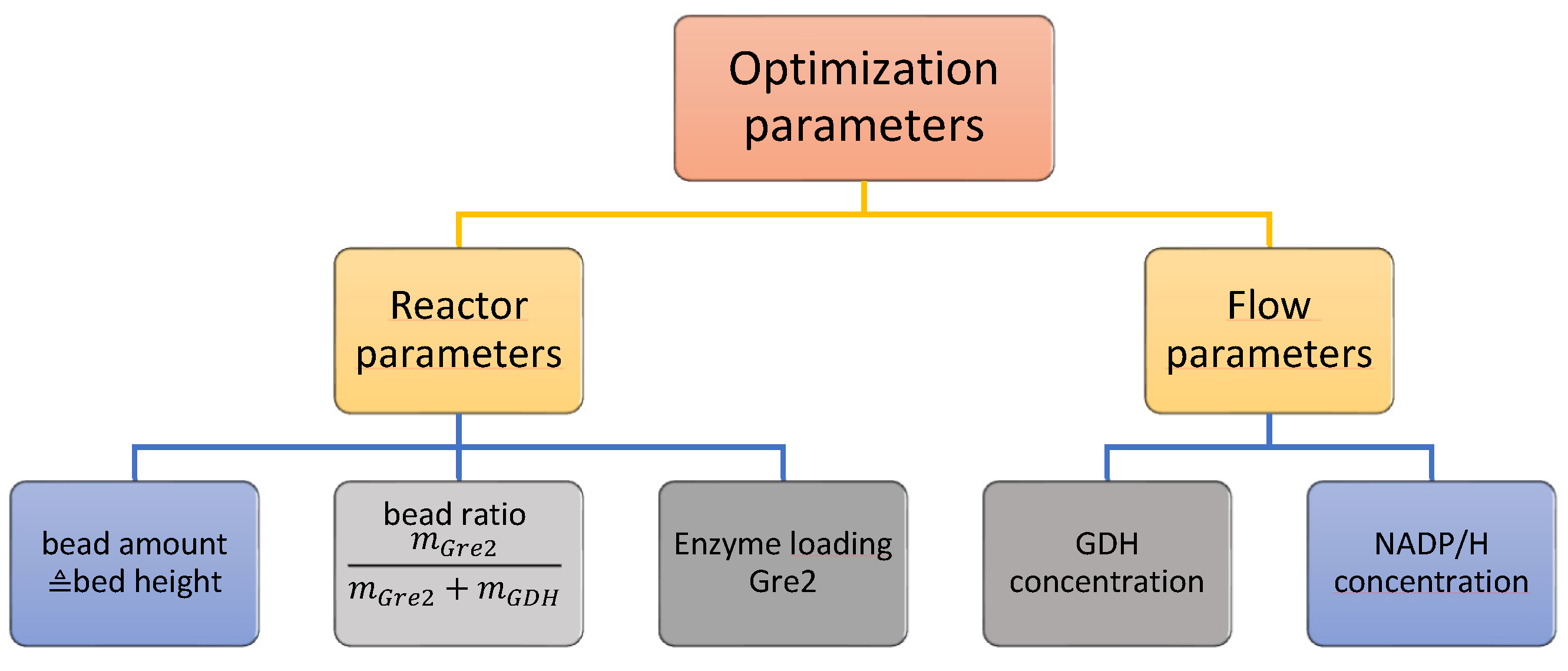
2.3. Optimization Methodology
2.3.1. Measure of Process Economics
2.3.2. Boundary Conditions
2.3.3. Techno-Economic Performance (TEP)
3. Results and Discussion
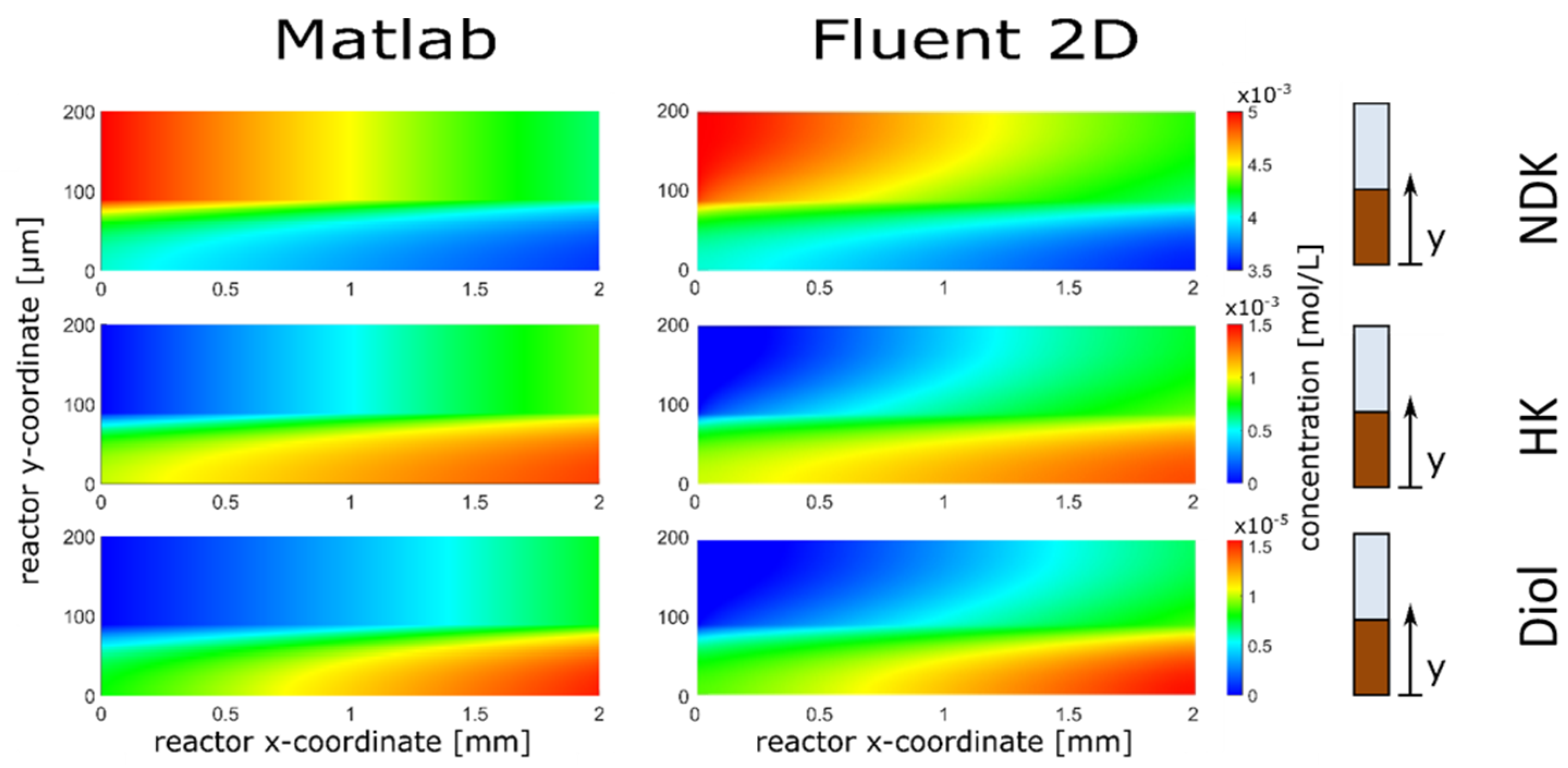
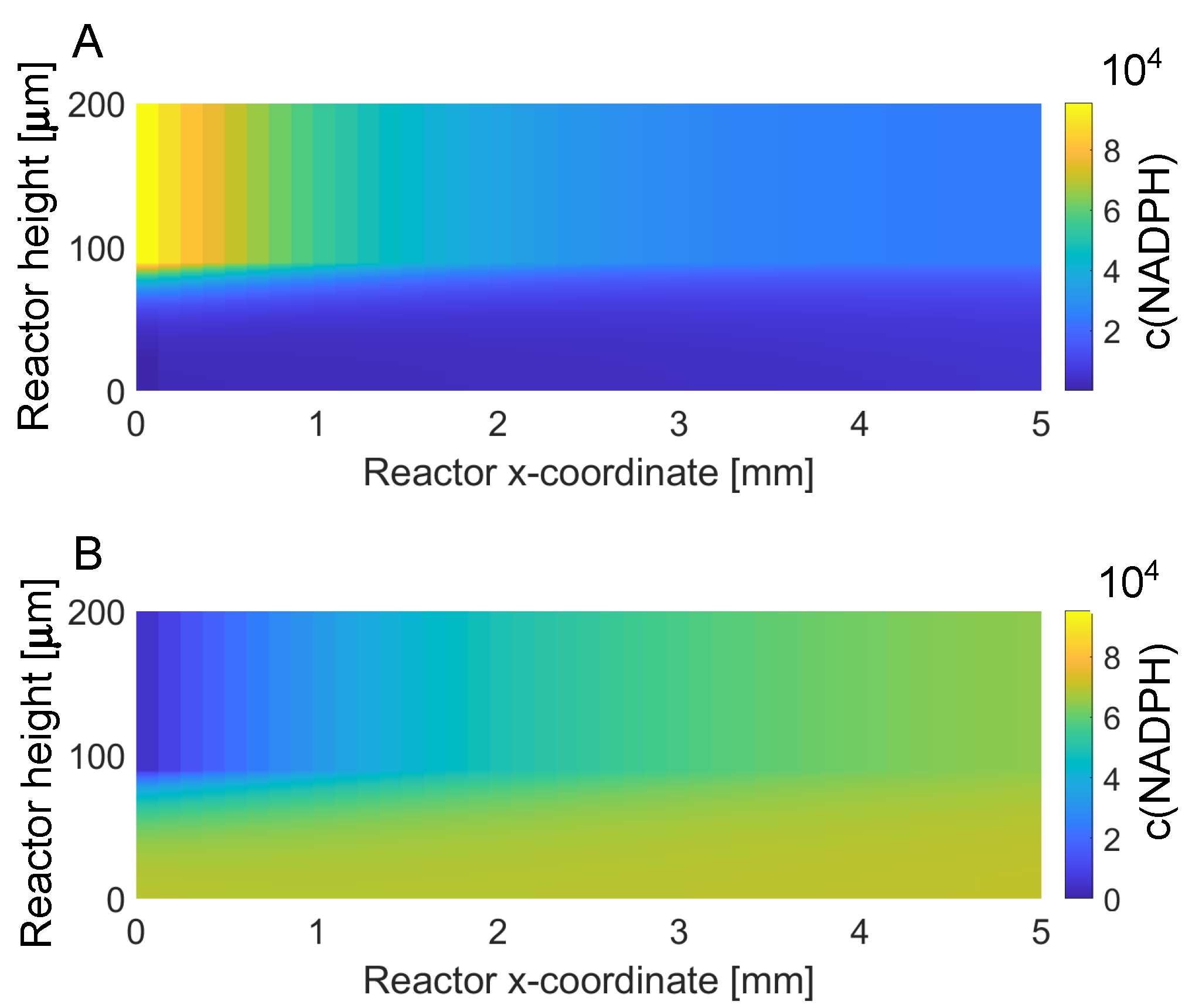
3.1. Reactor Model
3.2. GDH Immobilization
3.3. Level 1: Infinite Fluxes
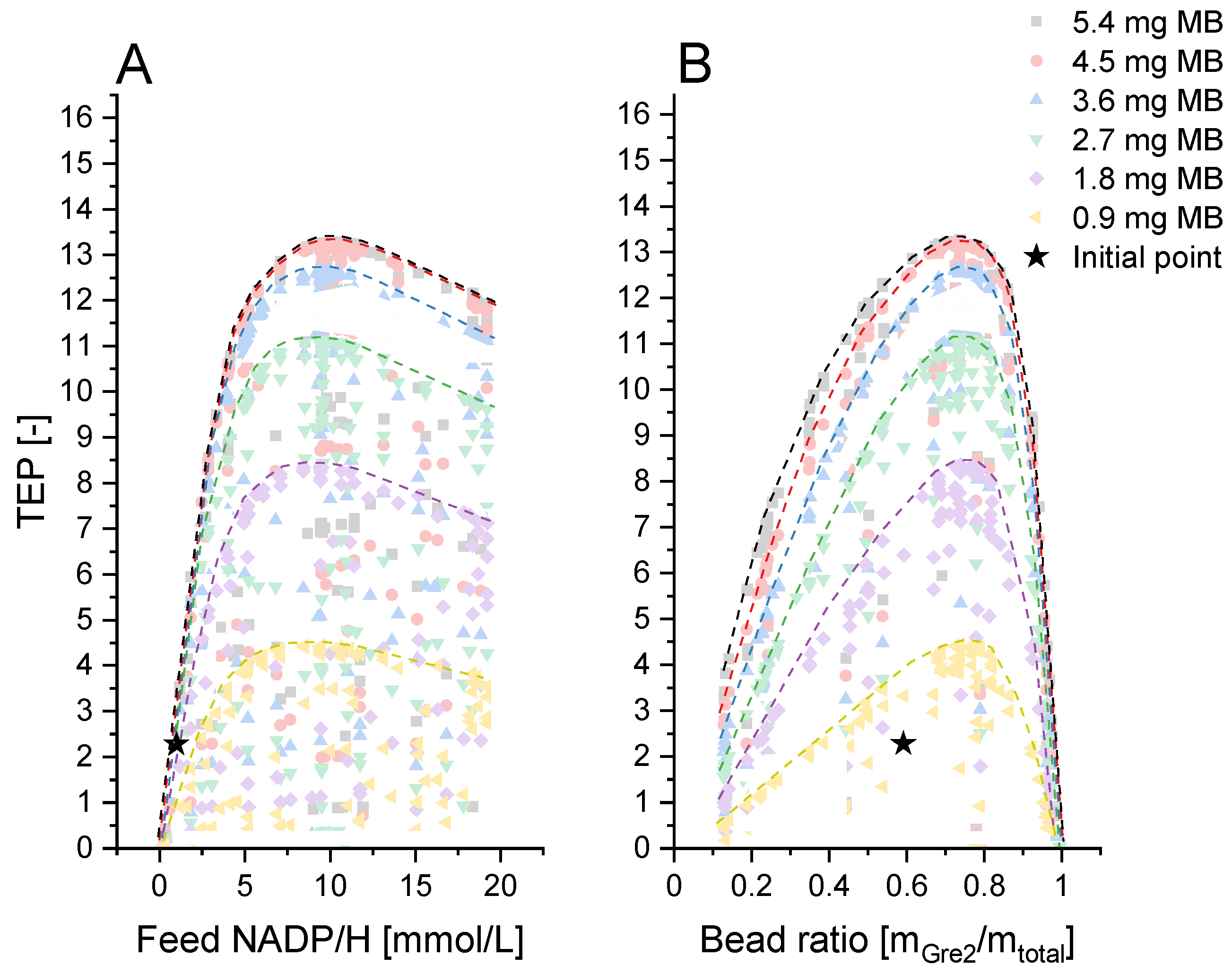
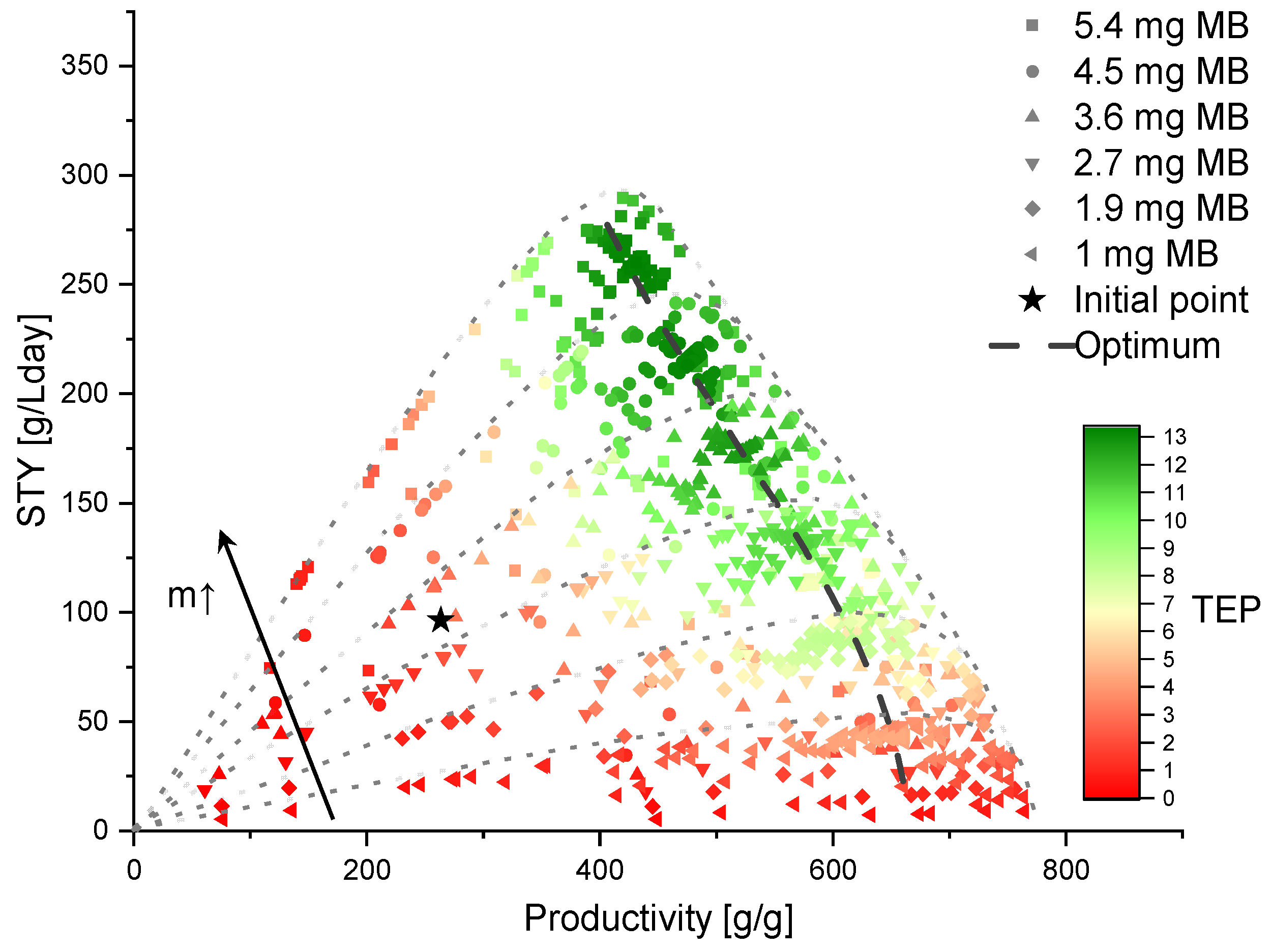
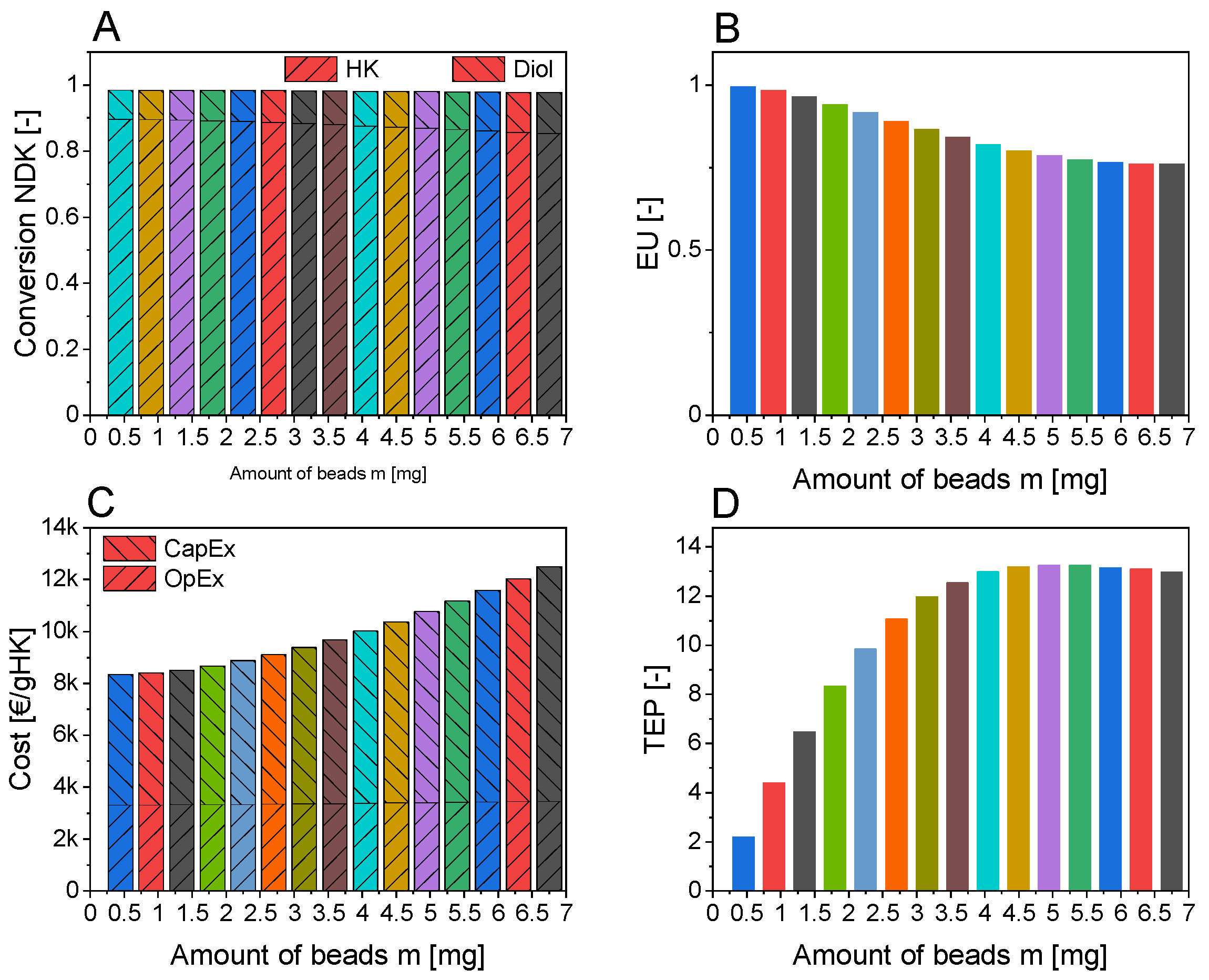
3.4. Levels 2 and 3: (Technical) Reactor Concept
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hickey, A.M.; Marle, L.; McCreedy, T.; Watts, P.; Greenway, G.M.; Littlechild, J.A. Immobilization of thermophilic enzymes in miniaturized flow reactors. Biochem. Soc. Trans. 2007, 35, 1621–1623. [Google Scholar] [CrossRef] [PubMed]
- Matsuura, S.-I.; Ishii, R.; Itoh, T.; Hamakawa, S.; Tsunoda, T.; Hanaoka, T.; Mizukami, F. Immobilization of enzyme-encapsulated nanoporous material in a microreactor and reaction analysis. Chem. Eng. J. 2011, 167, 744–749. [Google Scholar] [CrossRef]
- Plutschack, M.B.; Pieber, B.; Gilmore, K.; Seeberger, P.H. The Hitchhiker’s Guide to Flow Chemistry II. Chem. Rev. 2017, 117, 11796–11893. [Google Scholar] [CrossRef] [PubMed]
- Wiles, C.; Watts, P. Improving chemical synthesis using flow reactors. Expert Opin. Drug Discov. 2007, 2, 1487–1503. [Google Scholar] [CrossRef] [PubMed]
- Kockmann, N. Transport Phenomena in Micro Process Engineering; Springer Science & Business Media: Berlin, Germany, 2007; ISBN 3540746188. [Google Scholar]
- Vorbach, M.; Bohn, L.; Kotthaus, M.; Kraut, M.; Pöchlauer, P.; Wenka, A.; Schubert, K. Achema 2006: 28. Internat. Ausstellungskongreß für Chemische Technik, Umweltschutz und Biotechnologie, Frankfurt, 15.-19.Mai 2006 Book of Abstracts; Dechema e.v.: Frankfurt am Main, Germany, 2006; First Large-Scale Application of Microreaction Technology within Commercial Chemical Production of DSM. [Google Scholar]
- Proctor, L.; Dunn, P.J.; Hawkins, J.M.; Wells, A.S.; Williams, M.T. Continuous Processing in the Pharmaceutical Industry. In Green Chemistry in the Pharmaceutical Industry; Dunn, P.J., Wells, A.S., Williams, M.T., Eds.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2010; pp. 221–242. ISBN 9783527629688. [Google Scholar]
- Bornscheuer, U.T.; Huisman, G.W.; Kazlauskas, R.J.; Lutz, S.; Moore, J.C.; Robins, K. Engineering the third wave of biocatalysis. Nature 2012, 485, 185–194. [Google Scholar] [CrossRef] [PubMed]
- Faber, K. Biotransformations in Organic Chemistry; Springer: Berlin, Germany, 1992. [Google Scholar]
- Wang, X.; Saba, T.; Yiu, H.H.P.; Howe, R.F.; Anderson, J.A.; Shi, J. Cofactor NAD(P)H Regeneration Inspired by Heterogeneous Pathways. Chem 2017, 2, 621–654. [Google Scholar] [CrossRef] [Green Version]
- Rabe, K.S.; Müller, J.; Skoupi, M.; Niemeyer, C.M. Cascades in Compartments: En Route to Machine-Assisted Biotechnology. Angew. Chem. Int. Ed. Engl. 2017, 56, 13574–13589. [Google Scholar] [CrossRef] [PubMed]
- Cao, L.; van Langen, L.; Sheldon, R.A. Immobilised enzymes: Carrier-bound or carrier-free? Curr. Opin. Biotechnol. 2003, 14, 387–394. [Google Scholar] [CrossRef]
- Foley, A.M.; Maguire, A.R. The Impact of Recent Developments in Technologies which Enable the Increased Use of Biocatalysts. Eur. J. Org. Chem. 2019, 2019, 3713–3734. [Google Scholar] [CrossRef]
- Zhu, Y.; Chen, Q.; Shao, L.; Jia, Y.; Zhang, X. Microfluidic immobilized enzyme reactors for continuous biocatalysis. React. Chem. Eng. 2020, 5, 9–32. [Google Scholar] [CrossRef]
- Bitterwolf, P.; Ott, F.; Rabe, K.S.; Niemeyer, C.M. Imine Reductase Based All-Enzyme Hydrogel with Intrinsic Cofactor Regeneration for Flow Biocatalysis. Micromachines 2019, 10, 783. [Google Scholar] [CrossRef] [Green Version]
- Dall’Oglio, F.; Contente, M.L.; Conti, P.; Molinari, F.; Monfredi, D.; Pinto, A.; Romano, D.; Ubiali, D.; Tamborini, L.; Serra, I. Flow-based stereoselective reduction of ketones using an immobilized ketoreductase/glucose dehydrogenase mixed bed system. Catal. Commun. 2017, 93, 29–32. [Google Scholar] [CrossRef]
- Weiser, D.; Bencze, L.C.; Bánóczi, G.; Ender, F.; Kiss, R.; Kókai, E.; Szilágyi, A.; Vértessy, B.G.; Farkas, Ö.; Paizs, C.; et al. Phenylalanine Ammonia-Lyase-Catalyzed Deamination of an Acyclic Amino Acid: Enzyme Mechanistic Studies Aided by a Novel Microreactor Filled with Magnetic Nanoparticles. Chembiochem 2015, 16, 2283–2288. [Google Scholar] [CrossRef]
- Ender, F.; Weiser, D.; Nagy, B.; Bencze, C.L.; Paizs, C.; Pálovics, P.; Poppe, L. Microfluidic multiple cell chip reactor filled with enzyme-coated magnetic nanoparticles—An efficient and flexible novel tool for enzyme catalyzed biotransformations. J. Flow Chem. 2016, 6, 43–52. [Google Scholar] [CrossRef]
- Santis, P.D.; Meyer, L.-E.; Kara, S. The rise of continuous flow biocatalysis-fundamentals, very recent developments and future perspectives. React. Chem. Eng. 2020, 16, 852. [Google Scholar] [CrossRef]
- Baronas, R.; Kulys, J.; Petkevičius, L. Modelling the enzyme catalysed substrate conversion in a microbioreactor acting in continuous flow mode. Nonlinear Anal. 2018, 23, 437–458. [Google Scholar] [CrossRef] [Green Version]
- Strniša, F.; Bajić, M.; Panjan, P.; Plazl, I.; Sesay, A.M.; Žnidaršič-Plazl, P. Characterization of an enzymatic packed-bed microreactor: Experiments and modeling. Chem. Eng. J. 2018, 350, 541–550. [Google Scholar] [CrossRef]
- Pribec, I.; Urbic, T.; Plazl, I. Modelling Reaction-Diffusion Dynamics in Microsystems. In Proceedings of the 26th European Symposium on Computer Aided Process Engineering, Portorož, Slovenia, 12–15 June 2016; Elsevier: Amsterdam, The Netherland, 2016; pp. 1623–1628. [Google Scholar]
- Marques, M.P.C.; Fernandes, P.; Cabral, J.M.S.; Žnidaršič-Plazl, P.; Plazl, I. On the feasibility of in situ steroid biotransformation and product recovery in microchannels. Chem. Eng. J. 2010, 160, 708–714. [Google Scholar] [CrossRef]
- van Daele, T.; Fernandes del Pozo, D.; van Hauwermeiren, D.; Gernaey, K.V.; Wohlgemuth, R.; Nopens, I. A generic model-based methodology for quantification of mass transfer limitations in microreactors. Chem. Eng. J. 2016, 300, 193–208. [Google Scholar] [CrossRef]
- Schlereth, D.; Hinrichsen, O. A fixed-bed reactor modeling study on the methanation of CO2. Chem. Eng. Res. Des. 2014, 92, 702–712. [Google Scholar] [CrossRef]
- Brown, S.R.; Staff, M.; Lee, R.; Love, J.; Parker, D.A.; Aves, S.J.; Howard, T.P. Design of Experiments Methodology to Build a Multifactorial Statistical Model Describing the Metabolic Interactions of Alcohol Dehydrogenase Isozymes in the Ethanol Biosynthetic Pathway of the Yeast Saccharomyces cerevisiae. ACS Synth. Biol. 2018, 7, 1676–1684. [Google Scholar] [CrossRef]
- Finnigan, W.; Citoler, J.; Cosgrove, S.C.; Turner, N.J. Rapid Model-Based Optimization of a Two-Enzyme System for Continuous Reductive Amination in Flow. Org. Process Res. Dev. 2020, 24, 1969–1977. [Google Scholar] [CrossRef]
- Peschel, A.; Jörke, A.; Sundmacher, K.; Freund, H. Optimal reaction concept and plant wide optimization of the ethylene oxide process. Chem. Eng. J. 2012, 207–208, 656–674. [Google Scholar] [CrossRef]
- Freund, H.; Sundmacher, K. Towards a methodology for the systematic analysis and design of efficient chemical processes. Chem. Eng. Process. Process Intensif. 2008, 47, 2051–2060. [Google Scholar] [CrossRef]
- Maußner, J.; Dreiser, C.; Wachsen, O.; Freund, H. Systematic model-based design of tolerant chemical reactors. JNL Adv. Manuf. Process. 2019, 1, 1. [Google Scholar] [CrossRef]
- Xie, M.; Freund, H. Optimal reactor design and operation taking catalyst deactivation into account. Chem. Eng. Sci. 2018, 175, 405–415. [Google Scholar] [CrossRef]
- Kaiser, M.; Freund, H. A multimodular pseudoheterogeneous model framework for optimal design of catalytic reactors exemplified by methanol synthesis. Chem. Eng. Sci. 2019, 206, 401–423. [Google Scholar] [CrossRef]
- Emenike, V.N.; Schenkendorf, R.; Krewer, U. Model-based optimization of biopharmaceutical manufacturing in Pichia pastoris based on dynamic flux balance analysis. Comput. Chem. Eng. 2018, 118, 1–13. [Google Scholar] [CrossRef]
- Rozzell, J.D. Commercial scale biocatalysis: Myths and realities. Bioorgan. Med. Chem. 1999, 7, 2253–2261. [Google Scholar] [CrossRef]
- Peschke, T.; Skoupi, M.; Burgahn, T.; Gallus, S.; Ahmed, I.; Rabe, K.S.; Niemeyer, C.M. Self-Immobilizing Fusion Enzymes for Compartmentalized Biocatalysis. ACS Catal. 2017, 7, 7866–7872. [Google Scholar] [CrossRef]
- Burgahn, T.; Pietrek, P.; Dittmeyer, R.; Rabe, K.S.; Niemeyer, C.M. Evaluation of a Microreactor for Flow Biocatalysis by Combined Theory and Experiment. ChemCatChem 2020, 12, 2452–2460. [Google Scholar] [CrossRef]
- Skoupi, M.; Vaxelaire, C.; Strohmann, C.; Christmann, M.; Niemeyer, C.M. Enantiogroup-differentiating biocatalytic reductions of prochiral Cs -symmetrical dicarbonyl compounds to meso compounds. Chemistry 2015, 21, 8701–8705. [Google Scholar] [CrossRef]
- Liebermeister, W.; Uhlendorf, J.; Klipp, E. Modular rate laws for enzymatic reactions: Thermodynamics, elasticities and implementation. Bioinformatics 2010, 26, 1528–1534. [Google Scholar] [CrossRef] [PubMed]
- Freund, H.; Peschel, A.; Sundmacher, K. Modellgestützter Reaktorentwurf auf Basis der optimalen Reaktionsführung. Chem. Ing. Tech. 2011, 83, 420–426. [Google Scholar] [CrossRef]
- Freund, H.; Maußner, J.; Kaiser, M.; Xie, M. Process intensification by model-based design of tailor-made reactors. Curr. Opin. Chem. Eng. 2019, 26, 46–57. [Google Scholar] [CrossRef]
- Tufvesson, P.; Lima-Ramos, J.; Nordblad, M.; Woodley, J.M. Guidelines and Cost Analysis for Catalyst Production in Biocatalytic Processes. Org. Process Res. Dev. 2011, 15, 266–274. [Google Scholar] [CrossRef]
- Thermo Fischer. Dynabeads Magnetic Bead Technology. Available online: https://www.thermofisher.com/de/de/home/brands/product-brand/dynal.html (accessed on 14 December 2020).
- Sigma Aldrich. NADPH Tetrasodium Salt. Available online: https://www.sigmaaldrich.com/catalog/product/roche/nadphro (accessed on 14 December 2020).
- Sigma Aldrich. NADP Disodium Salt. Available online: https://www.sigmaaldrich.com/catalog/product/roche/nadpro (accessed on 14 December 2020).
- Pashchenko, D. Effect of the geometric dimensionality of computational domain on the results of CFD-modeling of steam methane reforming. Int. J. Hydrogen Energy 2018, 43, 8662–8673. [Google Scholar] [CrossRef]
- The MathWorks, Inc. MATLAB Optimization Toolbox; MathWorks: Natick, MA, USA, 2020; Available online: https://www.mathworks.com/help/symbolic/ (accessed on 10 December 2020).
- Baumer, B.; Classen, T.; Pohl, M.; Pietruszka, J. Efficient Nicotinamide Adenine Dinucleotide Phosphate [NADP(H)] Recycling in Closed-Loop Continuous Flow Biocatalysis. Adv. Synth. Catal. 2020, 362, 2894–2901. [Google Scholar] [CrossRef] [Green Version]
- Subramani, H.; Kurup, A. Micro-simulated moving bed (μSMB) systems: A numerical study. Chem. Eng. J. 2006, 120, 169–179. [Google Scholar] [CrossRef]
- Hessel, V.; Renken, A.; Schouten, J.C.; Yoshida, J.-I. Micro Process Engineering, 3 Volume Set: A Comprehensive Handbook; John Wiley & Sons: Hoboken, NJ, USA, 2005; ISBN 3527315500. [Google Scholar]





Basic Model | Model F2D | Model F3D | |
|---|---|---|---|
| Length | 50 mm | 2 mm | 1 mm |
| Number of cells | 35,000 | 0.75 million | 8 million |
| Computing time | 4 min | 7 days | 7 days |
| Deviation | ±3.5% | ±0.1% | reference |
| STY | Flow Rate | Enzyme Utilization (EU) [-] | CapEx | OpEx | Cost | Productivity | TEP [-] | |
|---|---|---|---|---|---|---|---|---|
| GDH aq. | 96.25 | 0.47 | 0.74 | 85.83 | 0.025 | 20,330 | 155.9 | 1.00 |
| GDH imm. | 96.26 | 0.47 | 0.89 | 59.56 | 0.009 | 15,091 | 263.5 | 2.28 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pietrek, P.; Kraut, M.; Dittmeyer, R. Towards a Novel Computer-Aided Optimization of Microreactors: Techno-Economic Evaluation of an Immobilized Enzyme System. Symmetry 2021, 13, 524. https://doi.org/10.3390/sym13030524
Pietrek P, Kraut M, Dittmeyer R. Towards a Novel Computer-Aided Optimization of Microreactors: Techno-Economic Evaluation of an Immobilized Enzyme System. Symmetry. 2021; 13(3):524. https://doi.org/10.3390/sym13030524
Chicago/Turabian StylePietrek, Philip, Manfred Kraut, and Roland Dittmeyer. 2021. "Towards a Novel Computer-Aided Optimization of Microreactors: Techno-Economic Evaluation of an Immobilized Enzyme System" Symmetry 13, no. 3: 524. https://doi.org/10.3390/sym13030524
APA StylePietrek, P., Kraut, M., & Dittmeyer, R. (2021). Towards a Novel Computer-Aided Optimization of Microreactors: Techno-Economic Evaluation of an Immobilized Enzyme System. Symmetry, 13(3), 524. https://doi.org/10.3390/sym13030524







