Laser Assisted Dirac Electron in a Magnetized Annulus
Abstract
:1. Introduction
2. Theory
2.1. Field Free Case
2.1.1. Time Evolution of the Operators
2.1.2. The Charge’s States
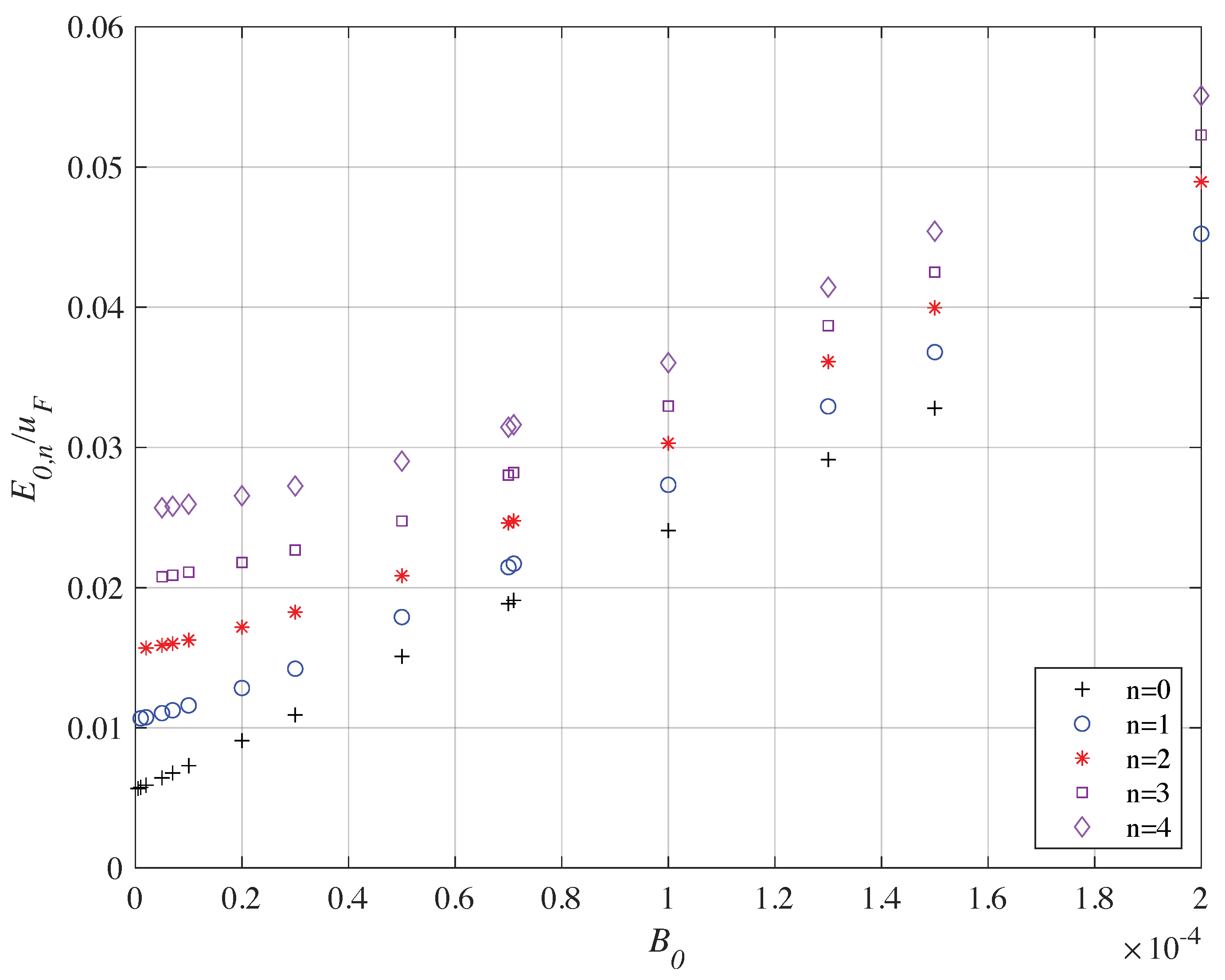
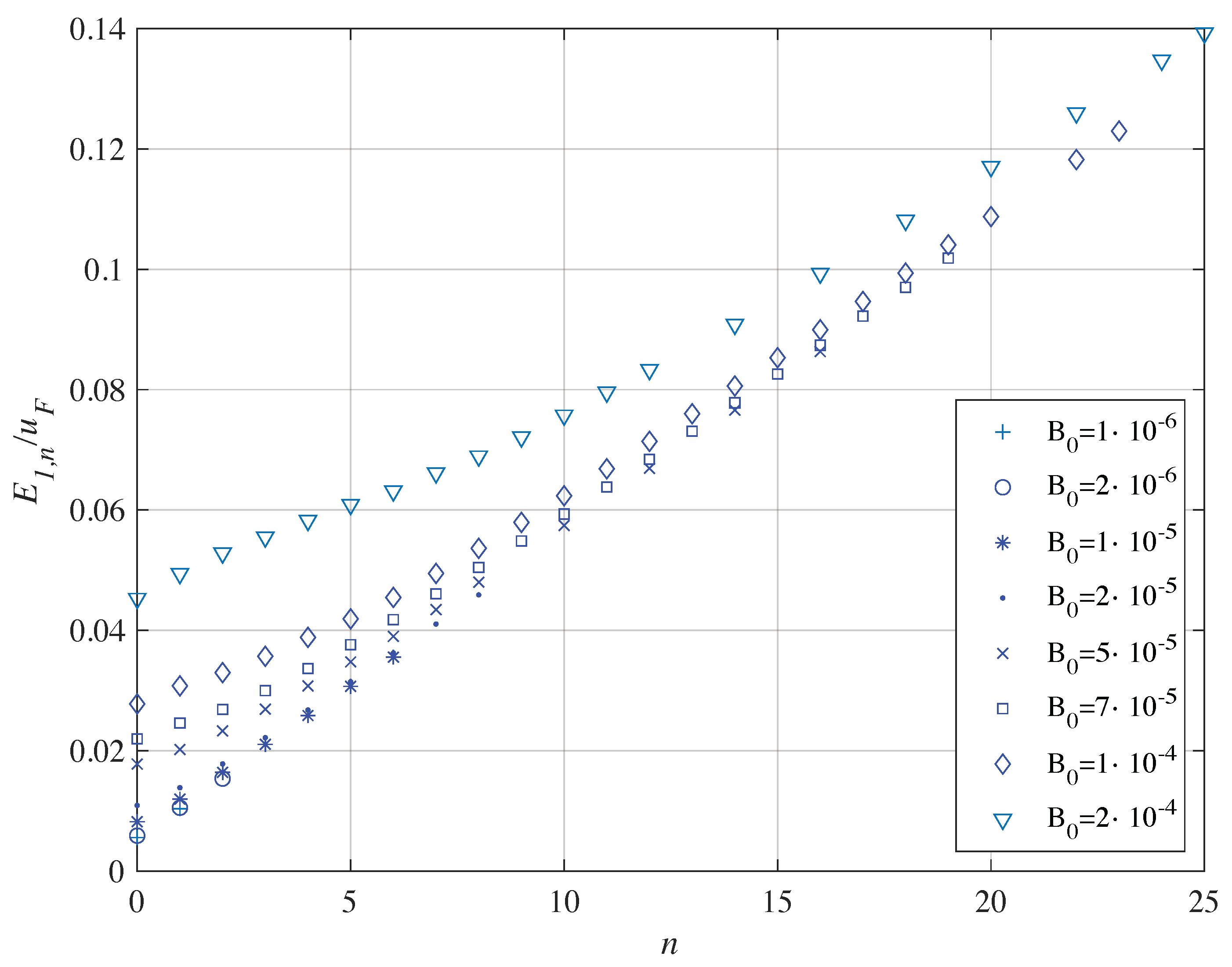
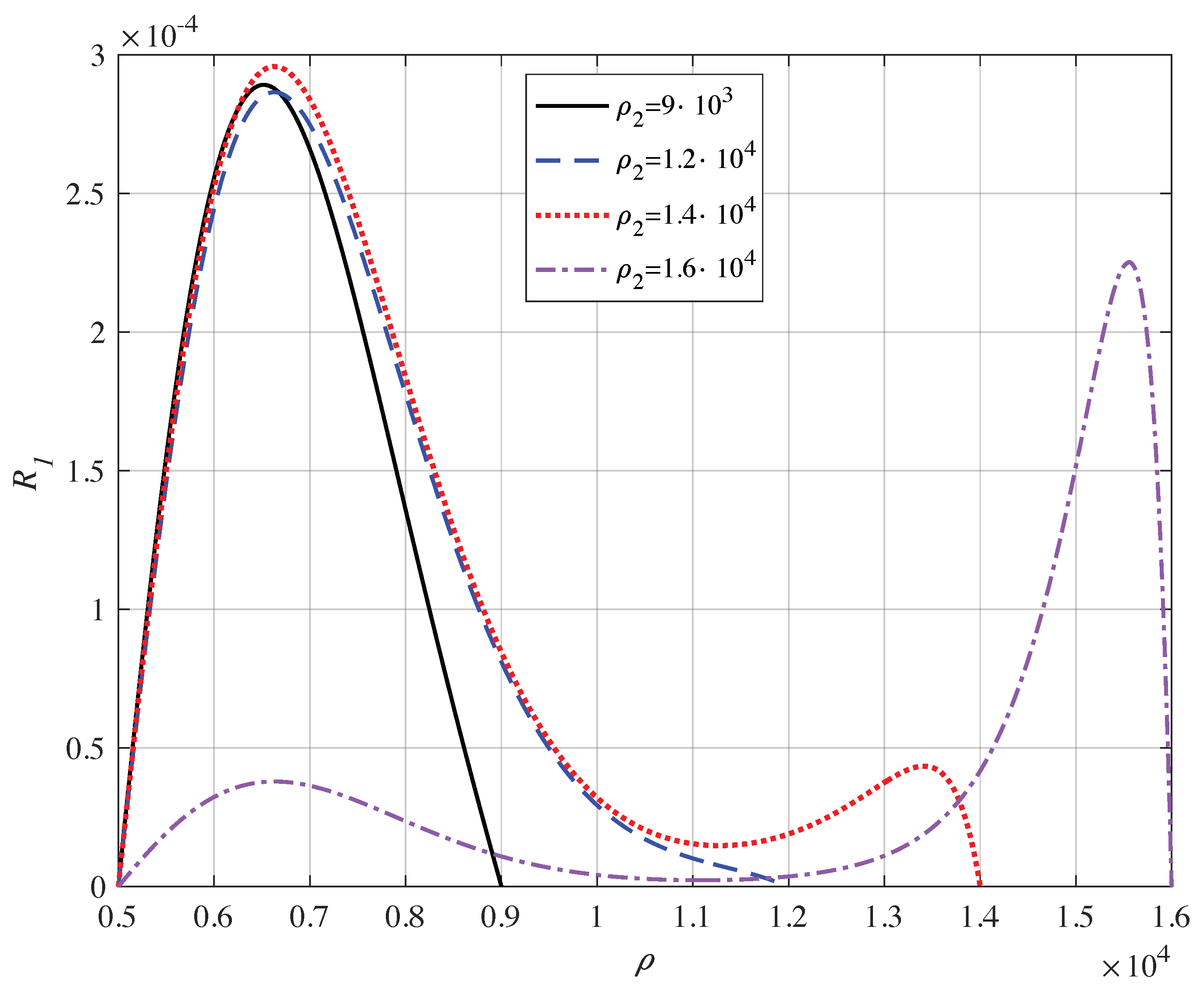
3. Static Magnetic Field
Solution
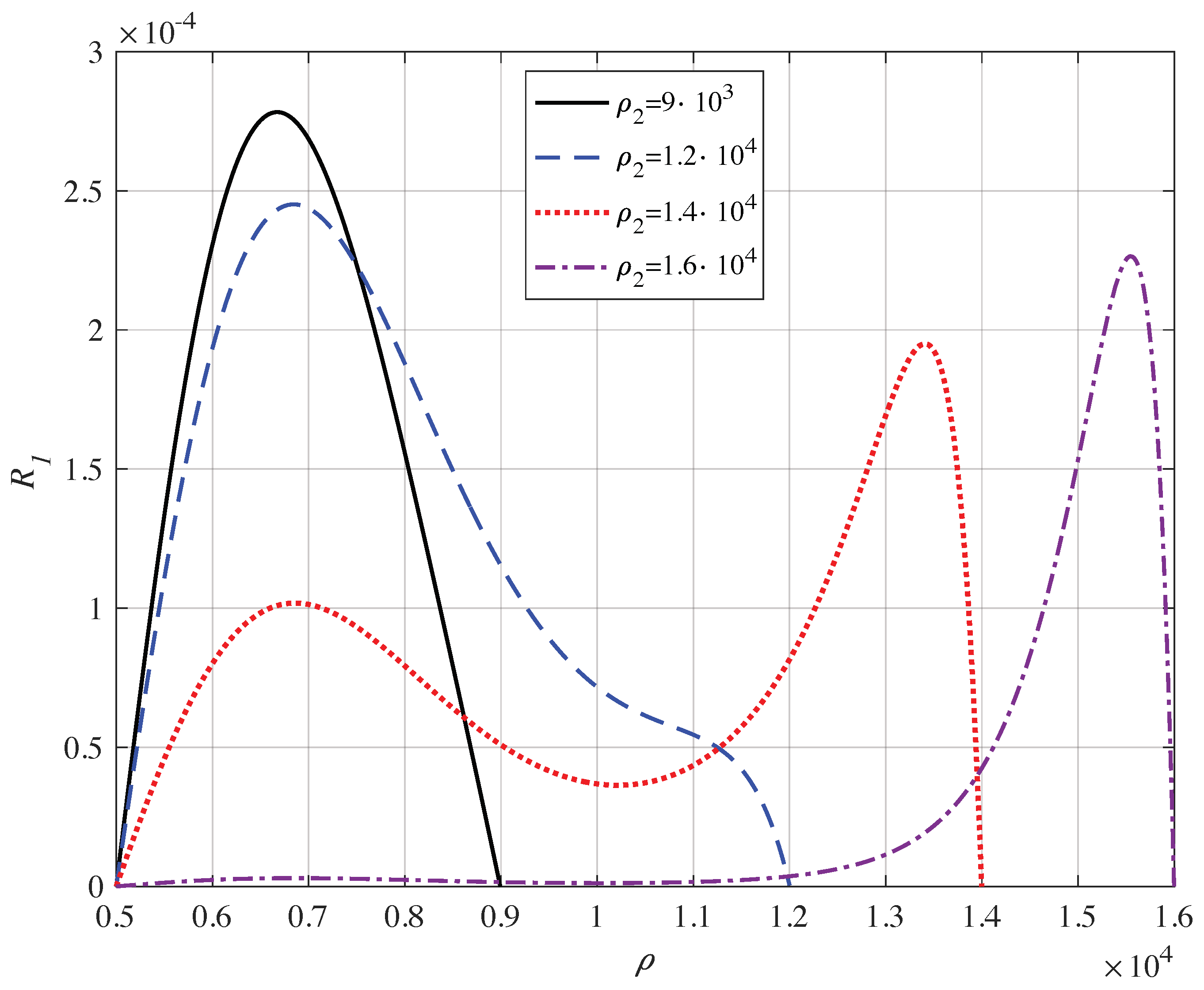
4. Adding a Laser
5. Conclusions and Comments
Funding
Conflicts of Interest
References
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2001. [Google Scholar]
- Maggiore, M. A Modern Introduction to Quantum Field Theory; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Sadowski, M.L.; Martinez, G.; Potemski, M.; Berger, C.; de Heer, W.A. Landau level spectroscopy of ultrathin graphite layers. Phys. Rev. Lett. 2006, 97, 266405. [Google Scholar] [CrossRef] [Green Version]
- Neto, A.H.C.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef] [Green Version]
- Goerbig, M.O. Electronic properties of graphene in a strong magnetic field. Rev. Mod. Phys. 2011, 83, 1193. [Google Scholar] [CrossRef] [Green Version]
- Martino, A.D.; Dell’Anna, L.; Egger, R. Magnetic confinement of massless Dirac fermions in graphene. Phys. Rev. Lett. 2007, 98, 066802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eshghi, M.; Mehraban, H.; Azar, I.A. Eigenspectra and wave functions of the massless Dirac fermions under the nonuniform magnetic fields in graphene. Physica E 2017, 94, 106. [Google Scholar] [CrossRef]
- Hartmann, R.R.; Portnoi, M.E. Quasi-exact solution to the Dirac equation for the hyperbolic-secant potential. Phys. Rev. A 2014, 89, 012101. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Nurbawono, A.; Guo, N.; Zhang, C. Massless Dirac fermions in graphene under an external periodic magnetic field. J. Phys. Cond. Mat. 2013, 25, 395302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peres, N.M.R.; Rodrigues, J.N.B.; Stauber, T.; Dos Santos, J.L. Dirac electrons in graphene-based quantum wires and quantum dots. J. Phys. Cond. Mat. 2009, 21, 344202. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Masir, M.R.; Vasilopoulos, P.; Peeters, F.M. Magnetic Kronig–Penney model for Dirac electrons in single-layer graphene. New J. Phys. 2009, 11, 095009. [Google Scholar] [CrossRef]
- Cricchio, D.; Corso, P.P.; Fiordilino, E.; Orlando, G.; Persico, F. A paradigm of fullerene. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 085404. [Google Scholar] [CrossRef]
- Cricchio, D.; Fiordilino, E.; Persico, F. Electrons on a spherical surface: Physical properties and hollow spherical clusters. Phys. Rev. A 2012, 86, 013201. [Google Scholar] [CrossRef] [Green Version]
- Ganeev, R.A.; Hutchison, C.; Witting, T.; Frank, F.; Weber, S.; Okell, W.A.; Fiordilino, E.; Cricchio, D.; Persico, F.; Zaïr, A.; et al. High-order harmonic generation in fullerenes using few-and multi-cycle pulses of different wavelengths. JOSA B 2013, 30, 7. [Google Scholar] [CrossRef] [Green Version]
- Castiglia, G.; Corso, P.P.; Cricchio, D.; Daniele, R.; Fiordilino, E.; Morales, F.; Persico, F. High-order-harmonic generation in dimensionally reduced systems. Phys. Rev. A 2013, 88, 033837. [Google Scholar] [CrossRef]
- Sakurai, J.J. Advanced Quantum Mechanics; Addison-Wesley Series in Advanced Physics; 1967; Available online: https://www.fisica.net/ebooks/quantica/Advanced%20Quantum%20Mechanics.pdf (accessed on 15 March 2021).
- Chen, H.-Y.; Apalkov, V.; Chakraborty, T. Fock-Darwin states of Dirac electrons in graphene-based artificial atoms. Phys. Rev. Lett. 2007, 98, 186803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Downing, C.A.; Pearce, A.R.; Churchill, R.J.; Portnoi, M.E. Optimal traps in graphene. Phys. Rev. B 2015, 92, 165401. [Google Scholar] [CrossRef] [Green Version]
- Downing, C.A.; Portnoi, M.E. Massless Dirac fermions in two dimensions: Confinement in nonuniform magnetic fields. Phys. Rev. B 2016, 94, 165407. [Google Scholar] [CrossRef] [Green Version]
- Mailly, D.; Chapelier, C.; Benoit, A. Experimental observation of persistent currents in GaAs-AlGaAs single loop. Phys. Rev. Lett. 1993, 70, 2020. [Google Scholar] [CrossRef] [PubMed]
- Bauer, D.; Ceccherini, F. A numerical ab initio study of harmonic generation from a ring-shaped model molecule in laser fields. Laser Part. Beams 2001, 19, 85. [Google Scholar] [CrossRef] [Green Version]
- Barth, I.; Manz, J.; Shigeta, Y.; Yagi, K. Unidirectional electronic ring current driven by a few cycle circularly polarized laser pulse: Quantum model simulations for Mg-Porphyrin. J. Am. Chem. Soc. 2006, 128, 7043. [Google Scholar] [CrossRef]
- Moskalenko, A.S.; Matos-Abiague, A.; Berakdar, J. Nonequilibrium charge dynamics of light-driven rings threaded by a magnetic flux. Europhys. Lett. 2007, 78, 57001. [Google Scholar] [CrossRef]
- Zhu, Z.-G.; Berakdar, J. Photoinduced nonequilibrium spin and charge polarization in quantum rings. Phys. Rev. B 2008, 77, 235438. [Google Scholar] [CrossRef] [Green Version]
- Hinsche, N.F.; Moskalenko, A.S.; Berakdar, J. High-order harmonic generation by a driven mesoscopic ring with a localized impurity. Phys. Rev. A 2009, 79, 023822. [Google Scholar] [CrossRef]
- Fuhrer, A.; Lüscher, S.; Ihn, T.; Heinzel, T.; Ensslin, K.; Wegscheider, W.; Bichler, M. Energy spectra of quantum rings. Nature 2001, 413, 822. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Castiglia, G.; Corso, P.P.; Giovannini, U.D.; Fiordilino, E.; Frusteri, B. Laser driven structured quantum rings. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 115401. [Google Scholar] [CrossRef] [Green Version]
- Castiglia, G.; Corso, P.P.; Cricchio, D.; Giovannini, U.D.; Frusteri, B.; Fiordilino, E. Classical chaos and harmonic generation in laser driven nanorings. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 245601. [Google Scholar] [CrossRef]
- Khanzadi, H.; Salehani, H.K. Design of basic logic gates by triple quantum rings. J. Nanosci. Tech. 2016, 2, 119. [Google Scholar]
- Batra, K.; Joshi, H.; Prasad, V. Quantum ring states in magnetic field and delayed half-cycle pulses. Pramana 2016, 87, 29. [Google Scholar] [CrossRef]
- L-Badry, L.F.A. The electronic properties of concentric double quantum ring and possibility designing xor gate. Sol. St. Comm. 2017, 254, 15. [Google Scholar] [CrossRef]
- Fiordilino, E.; Frusteri, B. Defects in quantum ring to control high-harmonic spectrum. Laser Part. Beams 2017, 35, 126. [Google Scholar] [CrossRef]
- Wätzel, J.; Berakdar, J. Tunable high harmonic pulses from nanorings swirled by optical vortices. Opt. Express 2017, 25, 27857–27873. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cricchio, D.; Fiordilino, E. Laser driven quantum rings: One byte logic gate implementation. RSC Adv. 2018, 8, 3493. [Google Scholar] [CrossRef] [Green Version]
- Cricchio, D.; Fiordilino, E. Quantum ring in a magnetic field: High harmonic generation and not logic gate. Adv. Theory Simul. 2020, 2020, 2000070. [Google Scholar] [CrossRef]
- Riley, K.F.; Hobson, M.P.; Bence, S.J. Mathematical Methods for Physics and Engineering, 3rd ed.; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Matos-Abiague, A.; Berakdar, J. Emission spectrum of a mesoscopic ring driven by fast unipolar pulses. Phys. Lett. A 2004, 330, 113. [Google Scholar] [CrossRef]
- Moskalenko, A.S.; Matos-Abiague, A.; Berakdar, J. Revivals, collapses, and magnetic-pulse generation in quantum rings. Phys. Rev. B 2006, 74, 161303. [Google Scholar] [CrossRef] [Green Version]
- Maiti, S.K. NAND gate response in a mesoscopic ring: An exact result. Phys. Scr. 2009, 80, 055704. [Google Scholar] [CrossRef] [Green Version]
- Tian, Y.; Zhang, L.; Ji, R.; Yang, L.; Zhou, P.; Chen, H.; Ding, J.; Zhu, W.; Lu, Y.; Jia, L.; et al. Proof of concept of directed or/nor and and/nand logic circuit consisting of two parallel microring resonators. Opt. Lett. 2011, 36, 1650. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Zhang, L.; Yang, L. Electro-optic directed AND/NAND logic circuit based on two parallel microring resonators. Opt. Express 2012, 20, 16794. [Google Scholar] [CrossRef]
- Cricchio, D.; Fiordilino, E. Wavelet analysis and HHG in nanorings: Their applications in logic gates and memory mass devices. Nanoscale 2016, 8, 1968. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barth, I.; Manz, J. Electric ring currents in atomic orbitals and magnetic fields induced by short intense circularly polarized π laser pulses. Phys. Rev. A 2007, 75, 012510. [Google Scholar] [CrossRef]
- Cricchio, D.; Fiordilino, E. Harmonic generation from nanorings driven by a two-color laser field. Laser Phys. Lett. 2014, 11, 066002. [Google Scholar] [CrossRef]


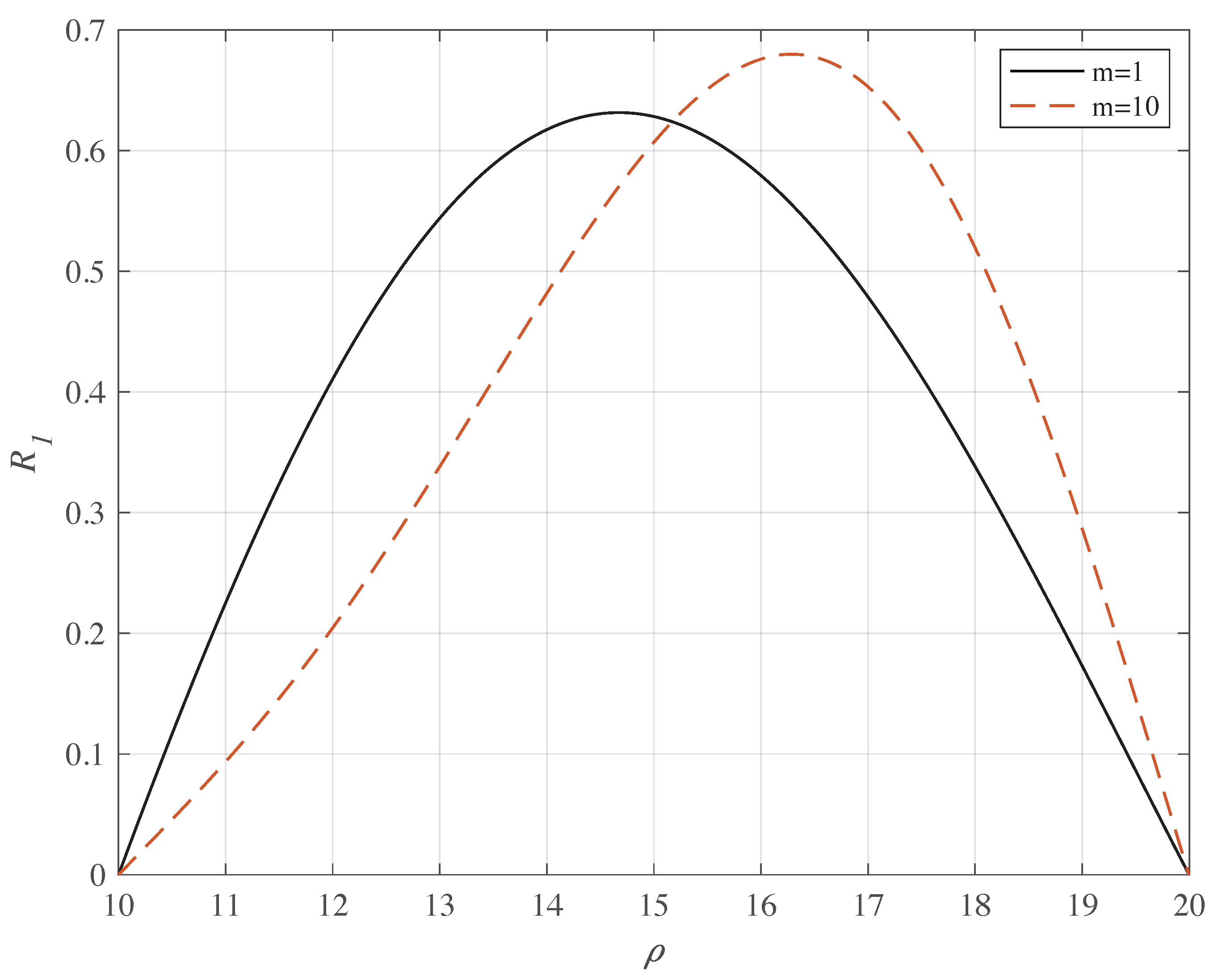

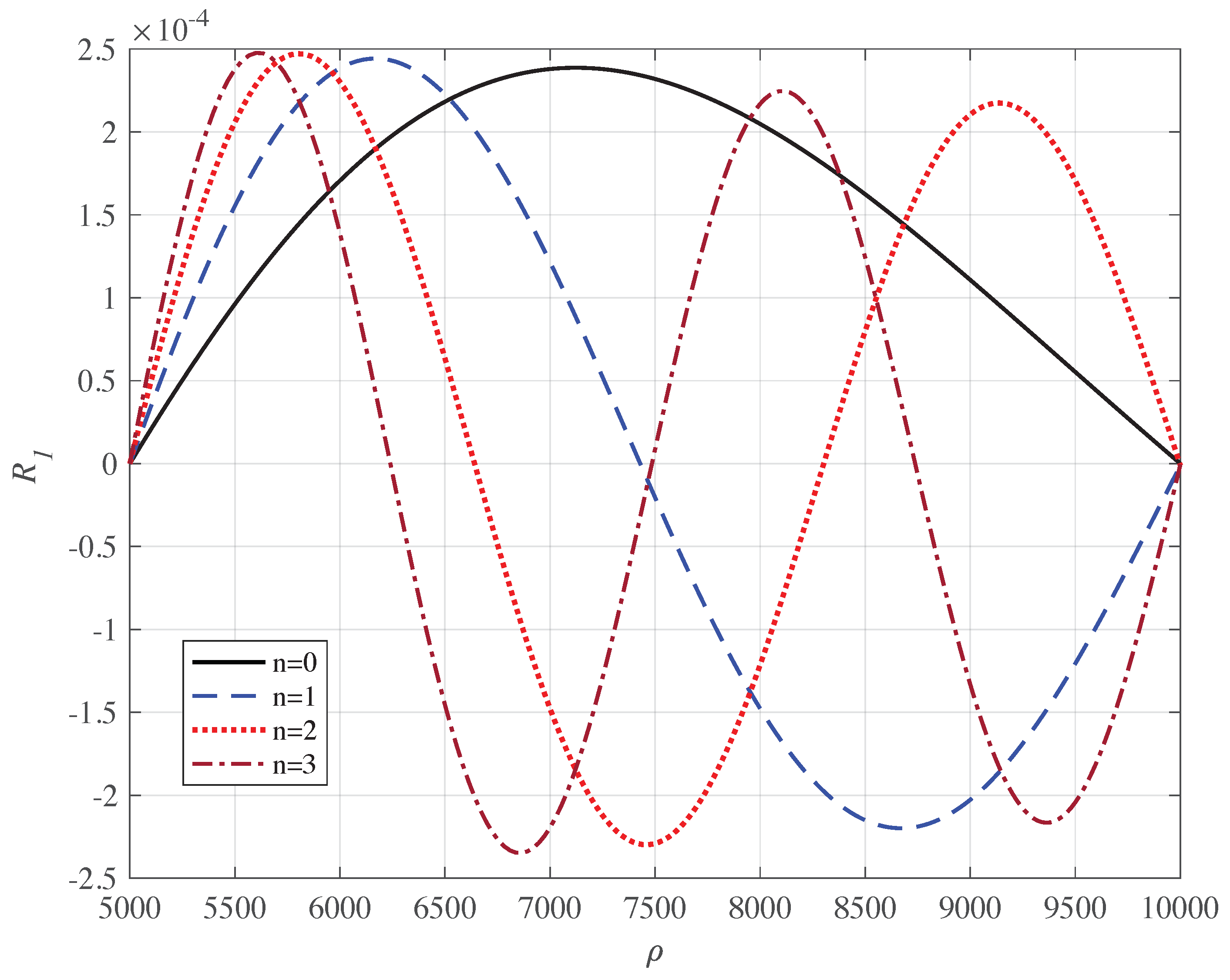
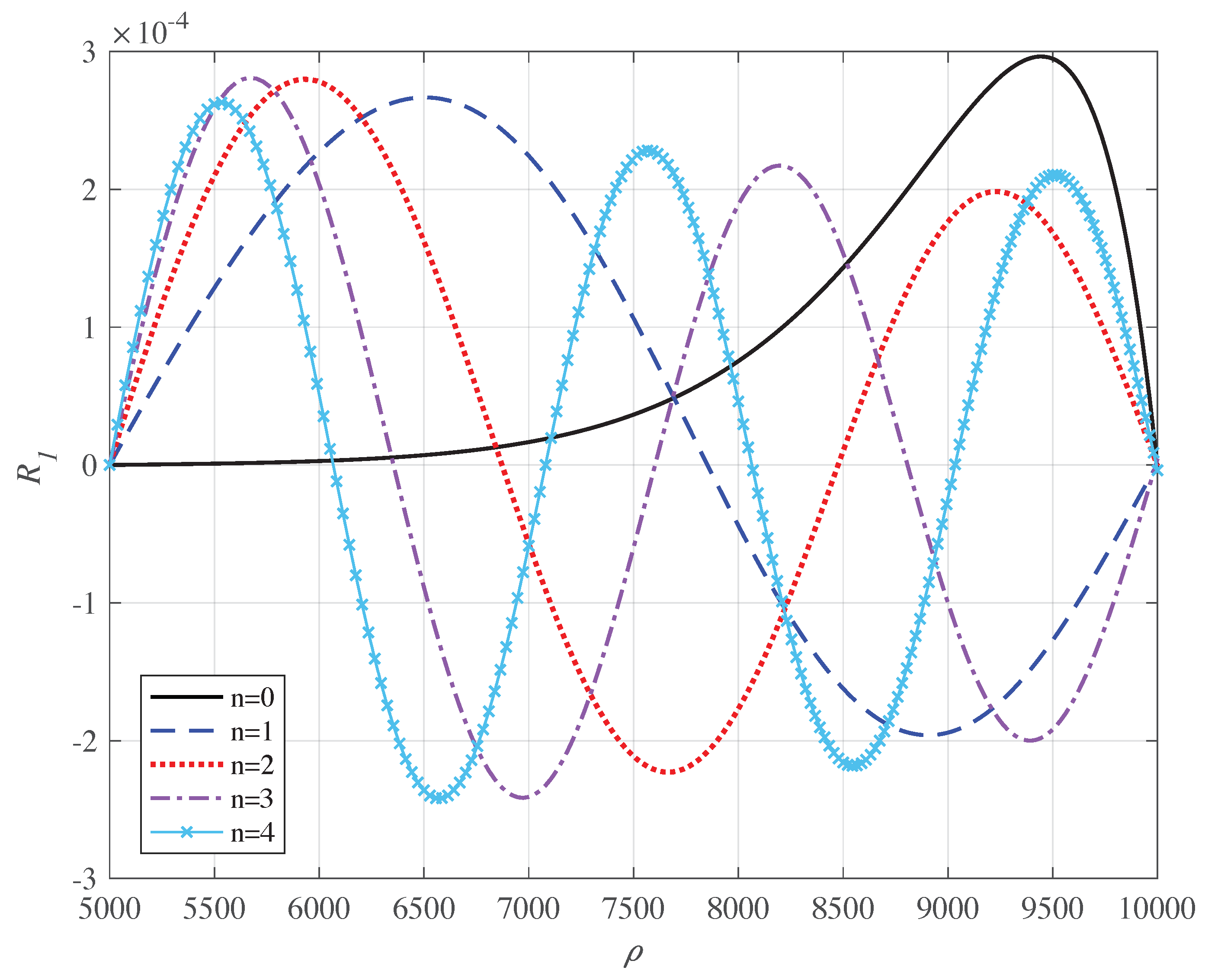
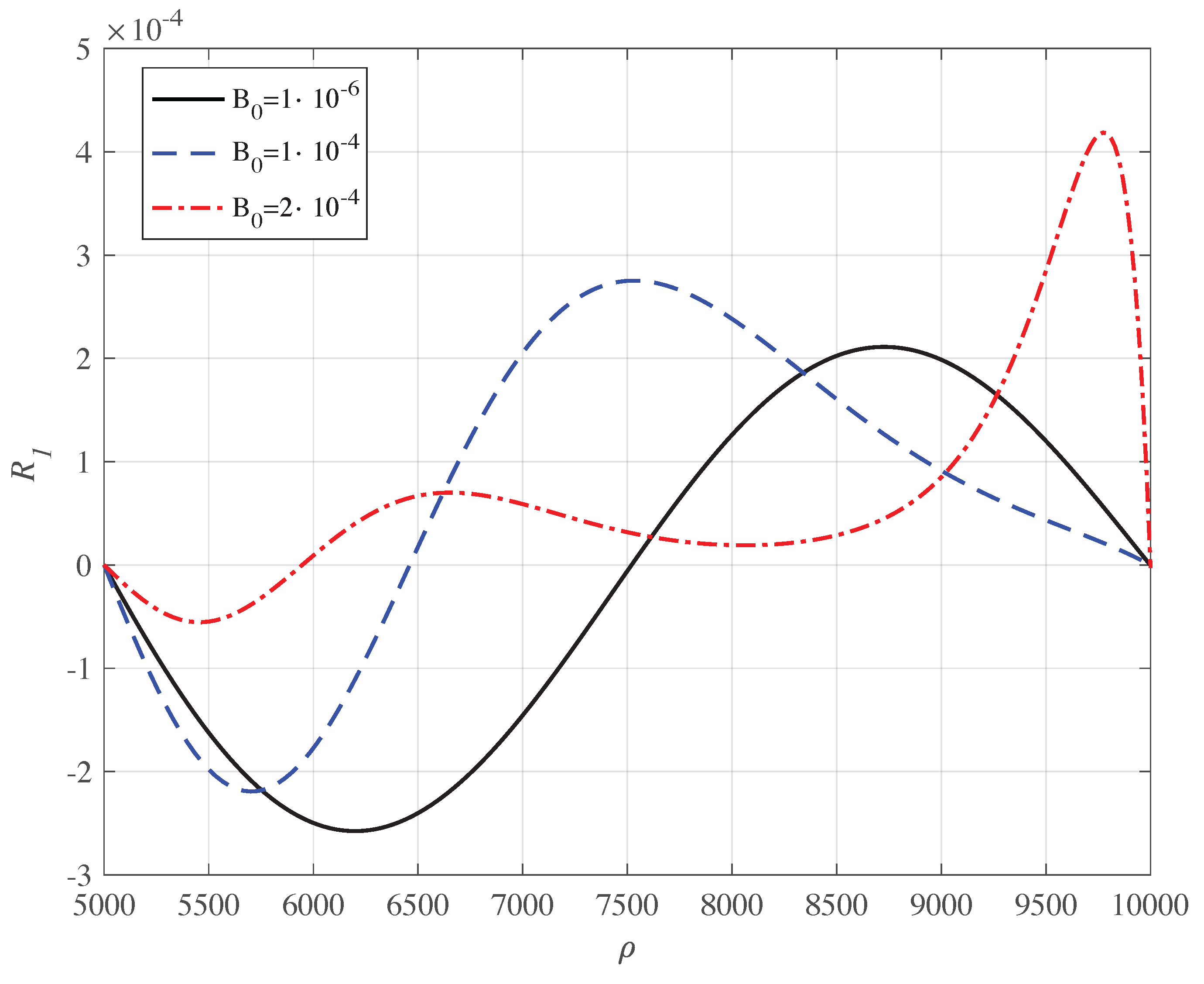
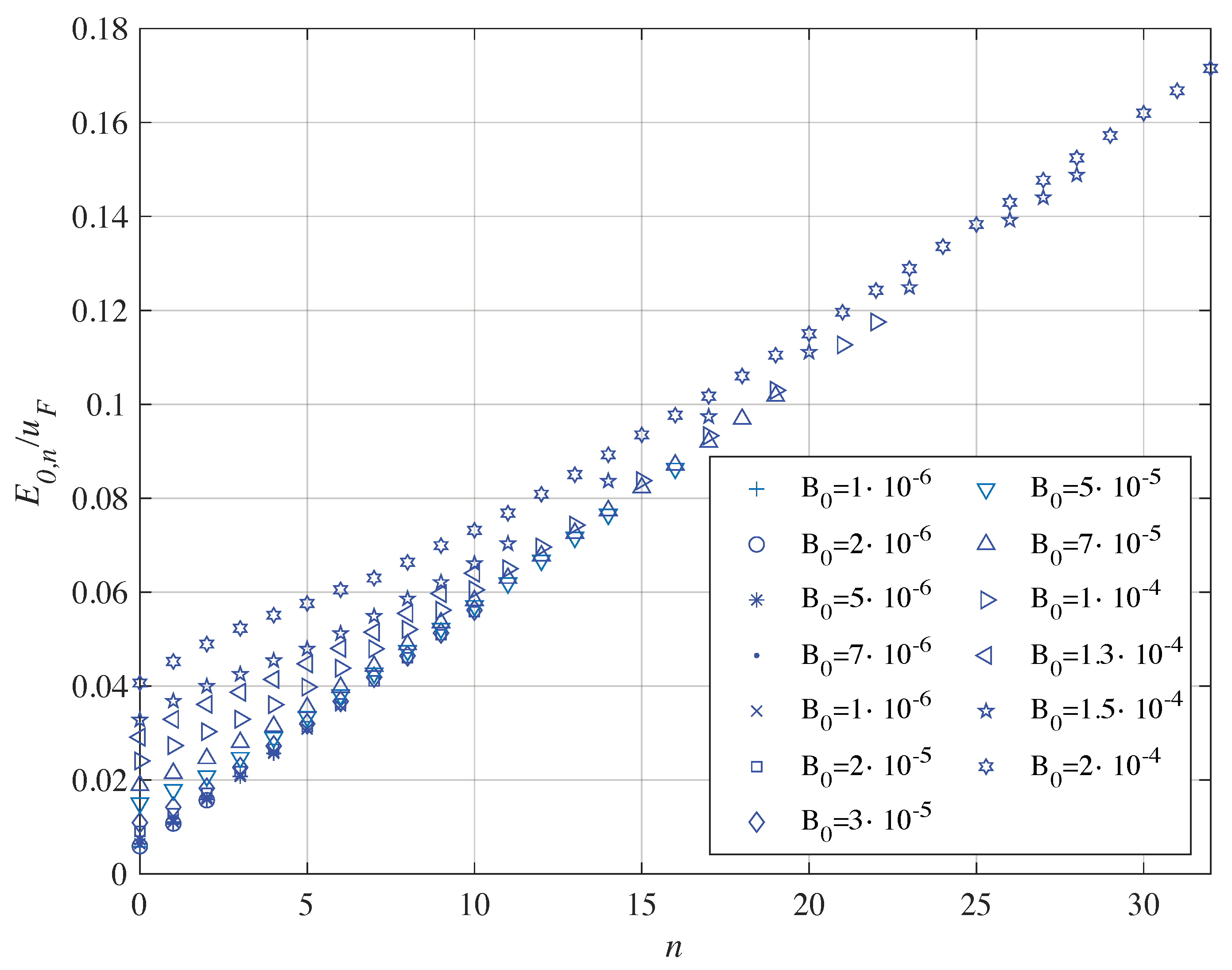
| n | ||
|---|---|---|
| 0 | 0.3197 | 0.7253 |
| 1 | 0.6315 | 0.9416 |
| 2 | 0.9451 | 1.1790 |
| 3 | 1.2578 | 1.4422 |
| 4 | 1.5714 | 1.7230 |
| 5 | 1.8865 | 2.0129 |
| 6 | 2.2001 | – |
| m | |||
|---|---|---|---|
| 0 | 2.988 | 3.355 | 3.836 |
| 1 | 3.258 | 3.627 | 4.046 |
| 2 | 3.551 | 3.864 | 4.289 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fiordilino, E. Laser Assisted Dirac Electron in a Magnetized Annulus. Symmetry 2021, 13, 642. https://doi.org/10.3390/sym13040642
Fiordilino E. Laser Assisted Dirac Electron in a Magnetized Annulus. Symmetry. 2021; 13(4):642. https://doi.org/10.3390/sym13040642
Chicago/Turabian StyleFiordilino, Emilio. 2021. "Laser Assisted Dirac Electron in a Magnetized Annulus" Symmetry 13, no. 4: 642. https://doi.org/10.3390/sym13040642






