Computing Expectiles Using k-Nearest Neighbours Approach

Abstract

Expectiles have gained considerable attention in recent years due to wide applications in many areas. In this study, the k-nearest neighbours approach, together with the asymmetric least squares loss function, called ex-$kNN$, is proposed for computing expectiles. Firstly, the effect of various distance measures on ex-$kNN$ in terms of test error and computational time is evaluated. It is found that Canberra, Lorentzian, and Soergel distance measures lead to minimum test error, whereas Euclidean, Canberra, and Average of $(L_1,L_{\infty })$ lead to a low computational cost. Secondly, the performance of ex-$kNN$ is compared with existing packages er-boost and ex-svm for computing expectiles that are based on nine real life examples. Depending on the nature of data, the ex-$kNN$ showed two to 10 times better performance than er-boost and comparable performance with ex-svm regarding test error. Computationally, the ex-$kNN$ is found two to five times faster than ex-svm and much faster than er-boost, particularly, in the case of high dimensional data.

1. Introduction

Given independent data $D_n:=((x_1,y_1),\dots ,(x_n,y_n))$ that were drawn from unknown probability distribution $\mathrm{P}$ on $X\times Y$, where $X\subset {\mathbb{R}}^d$ and $Y\subset \mathbb{R}$, the symmetric loss functions, such as least absolute deviation loss or least squares loss lead to study the center of the conditional distribution $\mathrm{P}\left(Y\right|X=x)$ by estimating the conditional median $\mathrm{med}\left(Y\right|X=x)$ or the conditional mean $\mathbb{E}\left(Y\right|X=x)$, respectively. To investigate $\mathrm{P}(·|x)$ beyond the center, one well-known approach is computing quantiles that were proposed by Koenker and Bassett Jr. [1]. If $\mathrm{P}(·|x)$ has strictly positive Lebesgue density, the conditional τ-quantile $q_{\tau }$, $\tau \in (0,1)$ of Y given $x\in X$ is the solution of

$$\begin{array}{c}\hfill \mathrm{P}(Y\le q_{\tau }|X=x)=\tau .\end{array}$$

Another approach is computing expectiles proposed by Newey and Powell [2] and it has gained considerable attention recently. Assume that $Q:=\mathrm{P}\left(Y\right|x)$ such that ${\left|Q\right|}_1:={\int }_{Y}ydQ\left(y\right)<\infty$, then the conditional τ-expectile ${\mu }_{\tau }$ for each $\tau \in (0,1)$ is the unique solution of

$$\begin{array}{c}\hfill \tau {\int }_{{\mu }_{\tau }}^{\infty }(y-{\mu }_{\tau })dQ\left(y\right)=(1-\tau ){\int }_{-\infty }^{{\mu }_{\tau }}({\mu }_{\tau }-y)dQ\left(y\right).\end{array}$$

It is well-known that quantiles or expectiles can be computed algorithmically, see, for example, Efron [3] and Abdous and Remillard [4]. To be more precise, for all $t\in \mathbb{R}$ and a fixed $\tau \in (0,1)$, one needs to solve the optimization problem

$$\begin{array}{c}\hfill {\eta }_{\tau }:=arg\underset{t\in \mathbb{R}}{min}{\mathbb{E}}_{y\sim Q}{L}_{\tau }(y,t),\end{array}$$

(1)

where L_τ is the asymmetric loss function, which, for $p\ge 1$, is defined by

$$\begin{array}{c}\hfill L_{\tau }(y,t)=\left\{\begin{array}{cc}{(1-\tau )\left|y-t\right|}^p,\hfill & \mathrm{if}y<t,\hfill \\ \tau {\left|y-t\right|}^p,\hfill & \mathrm{if}y⩾t.\hfill \end{array}\right.\end{array}$$

(2)

For $p=1$, we reach the asymmetric least absolute deviation (ALAD) loss function from (2) and, consequently, conditional quantiles $q_{\tau }={\eta }_{\tau }$ from (1). Analogously, for $p=2$, L_τ from (2) is the asymmetric least squares (ALS) loss and, thus, (1) produces conditional expectiles ${\mu }_{\tau }={\eta }_{\tau }$.

In general, for fixed τ, expectiles do not coincide with quantiles. The decision of computing either expectiles or quantiles depends on the applications at hand. For example, if one is interested to compute the threshold below which τ-fraction of observations lies, then τ-quantile is the right choice. On the other hand, to compute the thresholds, such that the ratio of gain (average deviations above threshold) and loss (average deviations below threshold) is equal to k where $k:=\frac{1-\tau }{\tau }$, then τ-expectile is the right choice. Broadly speaking, quantiles are the tail probabilities, while expectiles are considered tail expectations. This distinction of expectiles from quantiles made expectiles applicable in the fields of, for example, demography [5], education [6], and extensively in finance (see, e.g., Wang et al. [7] and Kim and Lee [8]). In fact, expectiles are the only risk measures that satisfy the well-known properties of coherence and elicitability (see, e.g., Bellini et al. [9]), and they are are proved to be better alternative to quantile-based value-at-risk (VaR). Furthermore, one can immediately realized the well-known performance measure in portfolio management known as gain-loss ratio or $\Omega$-ratio by τ-expectile for any $\tau \in (0,1)$, see Keating and Shadwick [10] for more details.

Different semiparametric and non-parametric approaches have been proposed in the literature for estimating expectiles. For example, Schnabel and Eilers [11] proposed an algorithm using P-splines, which is found to be difficult to implement on the problems involving multiple predictors. Another algorithm that is based on gradient boosting is proposed by [12] and Yang and Zou [13]. It is observed by Farooq and Steinwart [14] through experiments that boosting-based algorithm becomes computationally expensive when the dimensions of input space increases. Recently, Farooq and Steinwart [14] developed an SVM-like solver while considering sequential minimal optimization. Although the solver is found to be efficient when compared with an R-package er-boost developed by Yang and Zou [13], but SVM-based solver is found time-sensitive to the training set size.

It is important to note that the aforementioned algorithms are required to select an appropriate nonlinear function. To estimate conditional expectiles directly, Yao and Tong [15] used the kernelized iteratively reweighted approach, where kernel is used to assign higher weights to the points that are closer to the query point. However, choosing the right kernel for a problem at hand is tricky. Moreover, this method leads to the curse of dimensionality issue. Another simple, yet very popular, approach for estimating conditional quantities is the k-nearest neighbours that has competed with the advanced complex machine learning approaches when it comes to dealing with complex problems. Since the introduction of $kNN$ in 1967, it has been applied in many applications regarding classification, regression, and missing value imputation, such as pattern recognition, economic forecasting, data compression, outlier detection, and genetics, etc., see [16]. One key advantage of the $kNN$ approach is that it does not require a smoothness assumption of functions, which is, in general, necessary in advanced techniques of classification and regression. With these advantages, we use $kNN$ together with the ALS loss function to compute expectiles and named the algorithm ex-$kNN$. We then compare the ex-$kNN$ with and R-package, called er-boost proposed by Yang and Zou [13], and show, numerically, that ex-$kNN$ not only better performs in terms of accuracy and computational cost, but is also less sensitive to the dimensions of input space as compared to er-boost. In addition, we show that the performance of ex-$kNN$ is comparable with an SVM-like solver ex-svm proposed by [14]. Moreover, ex-$kNN$ is found to be less sensitive to the training set size as compared to ex-svm.

This paper is organized, as follows: Section 2 gives a brief overview of the $kNN$ approach in the context of computing expectiles. This also includes a concise introduction of different distance measures (Section 2.1) and the procedure of choosing the best value for k (Section 2.2)—two aspects of $kNN$ that greatly influence its performance. Section 3 covers the experiments while considering nine real life datasets in order to evaluate the effect of various distance measures on the performance of ex-$kNN$ as well as comparing the results with existing packages for computing expectiles, like er-boost and ex-svm. Section 4 provides the concluding remarks.

2. K-Nearest Neighbours Expectile Regression

The $kNN$ approach to computing expectiles is explained in this section. Because the performance of $kNN$ depends on the selection of suitable distance measures and the best value of k-neighbours, a detailed discussion on these two aspects is given in Section 2.1 and Section 2.2, respectively. To this end, let ${\mathbf{x}}_q\in X$ be a query point and $R:=\{{\mathbf{x}}_1,\dots ,{\mathbf{x}}_r\}\in X$ be a set of reference points. Subsequently, the $kNN$ approach searches the k nearest neighbours for query point ${\mathbf{x}}_q$ in the reference set R based on a specified distance measure, and then uses the set $\{y_1,\dots ,y_k\}$ that corresponds to the k nearest neighbours for classification or regression.

Once the set $\{y_1,\dots ,y_k\}$ corresponding to k-nearest neighbours is achieved, expectiles can be computed by solving the empirical version of (1), which is, for $p=2$, we solve the optimization problem

$${\widehat{\mu }}_{\tau }:=arg\underset{t\in \mathbb{R}}{min}\sum _{i=1}^k{L}_{\tau }(y_i,t_i).$$

(3)

Because the loss function used in (3) is quadratic in nature, the problem (3) can be solved by using iterative reweighted least squares (IRLS) algorithm. To be more precise, we assume an initial estimate of the expectile e_τ and generate a sequence of weights τ (when $y_i<e_{\tau }$) and $1-\tau$ (when $y_i\ge e_{\tau }$) for all $i=1,2,\dots ,k$. Subsequently, we update the estimate of e_τ by

$$e_{\tau }:=\frac{(1-\tau )\left({\sum }_{i=1}^k{y}_i|y<e_{\tau }\right)+\tau \left({\sum }_{i=1}^k{y}_i|y\ge e_{\tau }\right)}{{\sum }_{i=1}^k(1-\tau )|y<e_{\tau }+{\sum }_{i=1}^k\tau |y<e_{\tau }}.$$

(4)

and, hence, the corresponding weights, repeatedly, until convergence is achieved. Note that one may initialize e_τ by the average value of $\{y_1,\dots ,y_k\}$. Following [11], Procedure 1 presents the pseudo code for computing expectiles using IRLS.

Procedure 1 Computing Expectiles

Input: response variable y, $\tau \in (0,1)$, stopping criteria $T\leftarrow T_0$  Initialize: $e_{\tau }^{\ast }\leftarrow \frac{1}{k}{\sum }_{i=1}^k{y}_i$, $g\leftarrow g_0$  while $(g<T)$ do   $w\leftarrow \left\{(1-\tau )\right|y_i<e_{\tau }^{\ast }\}\cup \left\{\tau \right|y_i\ge e_{\tau }^{\ast }\}$ for all $i=1=1,2,\dots ,k$   $e_{\tau }\leftarrow \frac{1}{{\sum }_{i=1}^k{w}_i}{\sum }_{i=1}^k{w}_i{y}_i$   $g\leftarrow |e_{\tau }-e_{\tau }^{\ast }|$   $e_{\tau }^{\ast }\leftarrow e_{\tau }$  end while  return $e_{\tau }^{\ast }$

Here, g is the margin of error achieved in an iteration and T is the stopping criterion. Fast convergence can be achieved by making good choice of T and initialization of $e_{\tau }^{\ast }$. Moreover, in the case when $\tau =0$ or $\tau =1$, the τ-expectile can be considered to be the minimum or maximum value of the set $\{y_1,\dots ,y_k\}$, respectively.

2.1. Distance Measures

As mentioned above, one of the aspects that influences the performance of $kNN$ algorithm is the distance measure that is used to identify the closest neighbours in the training data. The Euclidean is a commonly used distance measure while implementing $kNN$. However, to our knowledge, there is no study indicating that it is the best suitable choice with $kNN$ in all cases. Therefore, several studies have been dedicated to exploring the suitable distance measure with $kNN$ for the given problem at hand. For instance, Mulak and Talhar [17] evaluated the performance of $kNN$ with four distance measures on the KDD data set and found that the Manhattan distance measure is the best in terms of classification accuracy. Lopes and Ribeiro [18] investigated the impact of five distance measures, such as Euclidean, Manhattan, Canberra, Chebychev, and Minkowsky, for various small datasets and found that Euclidean and Manhattan perform better for most of the datasets. Extending the investigation, Kittipong et al. [19] investigated the performance of $kNN$ with eleven distance measures and determined that Manhattan, Minkowsky, and Chebychev lead to better performance. Analogously, Todeschini et al. [20] considered eighteen distance measures and sorted out the best five distance measures leading to better performance.

A more detailed investigation in this regard has been done by [21], where they have considered 54 different distance measures from seven families of distances and shown that no single distance metric can be considered to be good enough for all types of datasets. In other words, the choice of the distance measures with $kNN$ depends on many factors, such as nature of input variables, number of dimensions, and size of datasets. This raises the need of also considering different distance measures in our study for computing expectiles using $kNN$ and to identify the one that leads to the best performance in our case for a specified dataset. For this purpose, we consider a set of distance measures that have been found to be the best in the aforementioned studies for various datasets. This set includes the Euclidean distance, Manhattan distance, Chebychev distance, Canberra distance, Soergel distance, Lorentzian distance, Cosine distance, Contracted JT distance, Clark distance Squared Chi-Squared distance, Average $(L_1,L_{\infty })$ distance, Divergence distance, Hassanat distance, and Whittaker’s Index association. A brief description of these distance measures is given in the following. We refer to [21] for more details on these and other lists of distance measures. To this end, we assume that ${\mathbf{x}}_i=\{x_{i1},\dots ,x_{ip}\}$ and ${\mathbf{x}}_j=\{x_{j1},\dots ,x_{jp}\}$ are the p-dimensional ith and jth data points in $X^p$.

•

Euclidean Distance (ED) is also called $L_2$ norm or Ruler distance and defined by

$$d_E({\mathbf{x}}_i,{\mathbf{x}}_j):=\sqrt{\sum _{l=1}^p{(x_{il}-x_{jl})}^2}.$$

(5)

•

Manhattan Distance (MD) is also known as $L_1$ distance, and defined as the sum of absolute difference of elements of ${\mathbf{x}}_i$ and ${\mathbf{x}}_j$ for $i=j=1,2,\dots ,p$, which is,

$$d_{MD}({\mathbf{x}}_i,{\mathbf{x}}_j):=\sum _{l=1}^p\left|x_{il}-x_{jl}\right|.$$

(6)

•

Chebychev Distance (CbD) is the maximum value distance and specified by

$$d_{CbD}({\mathbf{x}}_i,{\mathbf{x}}_j):=\underset{l}{max}\left|x_{il}-x_{jl}\right|.$$

(7)

•

Canberra Distance (CD) is a weighted version of Manhattan distance measure and defined by

$$d_{CD}({\mathbf{x}}_i,{\mathbf{x}}_j):=\sum _{l=1}^p\frac{|x_{il}-x_{jl}|}{|x_{il}|+|x_{jl}|}.$$

(8)

Note that (8) is sensitive to small changes when both ${\mathbf{x}}_i$ and ${\mathbf{x}}_j$ are close to zero.

•

Soergel Distance (SoD) is widely used for calculating the evolutionary distance and obeying all four properties of a valid distance measure. It is listed by

$$d_{SoD}({\mathbf{x}}_i,{\mathbf{x}}_j):=\frac{{\sum }_{l=1}^p\left|x_{il}-x_{jl}\right|}{{\sum }_{l=1}^p(x_{il}+x_{jl})}.$$

(9)

•

Lorentzain Distance (LD) is defined as a natural log of absolute distance between vector ${\mathbf{x}}_i$ and ${\mathbf{x}}_j$, that is

$$d_{LD}({\mathbf{x}}_i,{\mathbf{x}}_j):=\sum _{l=1}^{p}ln(1+|x_{il}-x_{jl}\left|\right),$$

(10)

where one is added to avoid the log of zero and to ensure non-negative property of a distance metric.

•

Cosine Distance is derived from a cosine similarity that measures the angle between two vectors. It is specified by

$$d_{CosD}({\mathbf{x}}_i,{\mathbf{x}}_j):=1-\frac{{\sum }_{l=1}^p{x}_{il}{y}_{jl}}{\sqrt{{\sum }_{l=1}^p{x}_{il}^2{\sum }_{l=1}^p{x}_{jl}^2}}.$$

(11)

•

Jaccard Distance (JacD) measures dissimilarity between two vectors. It is defined by

$$d_{JacD}({\mathbf{x}}_i,{\mathbf{x}}_j)=\frac{{\sum }_{l=1}^p{(x_{il}-xjl)}^2}{{\sum }_{l=1}^p{x}_{il}^2+{\sum }_{l=1}^p{x}_{jl}^2-{\sum }_{l=1}^p{x}_{il}{x}_{jl}}.$$

(12)

•

Clark Distance is also called the coefficient of divergence. It is the square root of half of divergence distance. It is defined by

$$d_{DivD}({\mathbf{x}}_i,{\mathbf{x}}_j):=\sqrt{\sum _{l=1}^p\frac{{(x_{il}-x_{jl})}^2}{{(x_{il}+x_{jl})}^2}}.$$

(13)

•

Squared Chi-Squared Distance belongs to the family of $L_2$ and it is defined by

$$d_{SCSD}({\mathbf{x}}_i,{\mathbf{x}}_j):=\sum _{l=1}^p\frac{{(x_{il}-x_{jl})}^2}{|x_{il}+x_{jl}|}.$$

(14)

•

Average $(L_1,L_{\infty })$ Distance is the average of Manhattan distance and Chebyshev distance. It is defined by

$$d_{AvgD}({\mathbf{x}}_i,{\mathbf{x}}_j):=\frac{{\sum }_{l=1}^p|x_{il}-x_{jl}|+max|x_{il}-x_{jl}|}{2}.$$

(15)

•

Divergence Distance is defined by

$$d_{ClaD}({\mathbf{x}}_i,{\mathbf{x}}_j):=2\sum _{l=1}^p\frac{{(x_{il}-x_{jl})}^2}{{(x_{il}+x_{jl})}^2}.$$

(16)

•

Hassanat Distance (HasD) is defined by

$$d_{Has}({\mathbf{x}}_i,{\mathbf{x}}_j):=\sum _{l=1}^{p}D(x_{il},x_{jl}),$$

(17)

where for $l=1,2,\dots ,p$

$$\begin{array}{c}\hfill D(x_{il},x_{jl}):=\left\{\begin{array}{cc}{\displaystyle 1-\frac{1-min(x_{il},x_{jl})}{max(x_{il},x_{jl})},}\hfill & \mathrm{if}min(x_{il},x_{jl})\ge 0,\hfill \\ {\displaystyle 1-\frac{1-min(x_{il},x_{jl})+\left|min(x_{il},x_{jl})\right|}{max(x_{il},x_{jl})+\left|min(x_{il},x_{jl})\right|},}\hfill & \mathrm{if}min(x_{il},x_{jl})<0.\hfill \end{array}\right.\end{array}$$

It is important to note that (17) is invariant to different scale, noise, and outlier, and it is always bounded by $[0,1[$. Contrary to other distances measures, $HasD(.,.)$ shows high similarity between points ${\mathbf{x}}_i$ and ${\mathbf{x}}_j$ when it approaches zero where as it shows high dissimilarity when it approaches one. Moreover, it can only achieve limiting value one if $max(x_{il},x_{jl})\to +\infty$ or $min(x_{il},x_{jl})\to -\infty$.

•

Whittaker’s Index of Association Distance

$$d_{WIAD}({\mathbf{x}}_i,{\mathbf{x}}_j):=\frac{1}{2}\sum _{l=1}^p\left|\frac{x_{il}}{{\sum }_{l=1}^p{x}_{il}}-\frac{x_{jl}}{{\sum }_{l=1}^p{x}_{jl}}\right|.$$

(18)

2.2. Selecting Best k

The selection of an appropriate value for k plays a key role in determining the performance of $kNN$. A lot of work has been done so far in the context of classification, regression, and missing data imputation in order to deal with this issue. For example, Lall and Sharma [22] suggested choosing the fixed optimal $k=\sqrt{n}$ for training a dataset when the sample size $n>100$. However, this approach has been criticised due to lack of theoretical guarantee. Many more advanced approaches to determine k-value have been proposed. For example, the kTree method is used to learn different k-value for different test sample [23], sparse-based $kNN$ method [24], and using reconstruction framework [25]. For more details, we refer the readers to [23], and the references therein.

The cross-validation is one of the approaches that has gained popularity in machine learning applications to tune the hyperparameters and that has also been considered in $kNN$. Recall that the cross-validation splits the data into two folds, where one fold is used to train the model by learning suitable values for the hyperparameters and the other fold is used to validate the model. The m-fold cross-validation method extends this approach by randomly dividing data into m equally (or nearly equally) folds. In other words, the process of cross-validation is repeated m times, such that in the each iteration a different fold is held-out for model validation and the remaining m-1 folds are used to learn the hyperparameters.

Note that the algorithms, such as er-boost and ex-svm, use cross-validation approach to tune the hyperparameters. We consider the same approach in this study to select the best value of k, despite the existence of advanced strategies so that a fair comparison of ex-$kNN$ with these algorithms can be made in terms of training time. Procedure 2 provides the pseudo code of selecting best k value by cross-validation.

Procedure 2 Computing Best k

Input: $\tau \in (0,1)$, $k_{max}$, data  split data into m-folds  for $i=1$ to $k_{max}$ do   for $j=1$ to m do    Obtain $k=i$ neighbours against each query point of j-th fold using distance measure $d(·,·)$    Compute expectiles from $k=i$ neighbours using Procedure 1    Compute error for j-th fold using $L_{\tau }$   end for   For each $k=i$ choose minimum error from all folds  end for  Choose k with minimum cross-validation error  return Best k

2.3. The ex-$kNN$ Algorithm

After considering a distance measures from the list that is given in Section 2.1, the best k-value for the training part of the data is attained using cross-validation approach following Procedure 2. The selected best k-value is used in testing part of data to compute the test error. The whole procedure of implementing the ex-$kNN$ is described in the following Algorithm 1.

Algorithm 1 Compute test error

Training Phase:  Input: $\tau \in (0,1)$, $k_{max}$, train data  split data into m-folds  Compute best k-value using Procedure 2  Testing Phase:  Input: $\tau \in (0,1)$, best k, test data  Compute expectiles using Procedure 1  Compute test error using $L_{\tau }$

3. Experimental Results

In this section, we conduct experiments using different datasets to compare the performance of ex-$kNN$ with the existing algorithms of computing expectiles, like er-boost and ex-svm, in terms of training time and test error. All of the experiments have been performed on INTEL CORE i3-4010U (1.70 GHz) 4 GB RAM system under 64 bit version of WINDOWS 8. The run time during experiments is computed by using single core, whereas the running of other processes were minimized.

Recall that [14] have considered nine datasets in their study to compare the performance of ex-svm with er-boost. To make a fair comparison of ex-$kNN$ with ex-svm and er-boost, we have downloaded the same datasets following the details that are given by [14]. That is, the data sets concrete-comp, updrs-motor, cycle-pp, airfoil-noise, and hour have been downloaded from UCI repository. Three data sets—nc-crime, head-circum, and cal-housing—were extracted from R packages Ecdat, AGD and StatLib repository, respectively. Finally, one data set munich-rent was downloaded from the data archive of Institute of Statistics, Ludwig-Maximilians-University. These datasets were scaled componentwise, such that all of the variables, including the response variable, lie in ${[-1,1]}^{d+1}$, where d denotes the dimension of the data. Table 1 describes the characteristics of the considered data sets. All of the datasets were randomly divided into training and testing samples comprising $70\%$ and $30\%$, respectively. The training sample is further divided into m-folds with randomly generated folds to implement cross-validation approach for determining the best k-value.

Table 1. Characteristics of data sets together with the training sizes and the test sizes that refer to the splits used in the run time experiments.

Data	Sample Sizes	Training Size	Test Size	Categorical	Features Continuous	Total
nc-crime	630	441	189	3	16	19
concrete-comp	1030	721	309	0	8	8
airfoil-noise	1503	1052	451	1	4	5
munich-rent	2053	1437	616	8	4	12
updrs-motor	5875	4112	1763	1	18	19
head-circum	7020	4914	2106	0	4	5
cycle-pp	9568	6697	2871	0	5	5
hour	17,379	12,165	5214	7	5	12
cal-housing	20,639	14,447	6192	0	8	8

It is important to note that the algorithms er-boost and ex-svm are implemented in C⁺⁺ to gain the computational advantages. For fair comparison regarding computational cost, we have implemented ex-$kNN$ in the R 3.6.1 package using the libraries Rcpp [26] and ArmadilloRcpp [27]. The library Rcpp provides seamless integration of R and C⁺⁺, whereas ArmadilloRcpp is the templated C⁺⁺ linear algebra library. The use of these libraries makes the implementation of ex-$kNN$ algorithm close to the implementation of er-boost and ex-svm algorithms.

Firstly, we evaluate the effect of different distance measures that were considered in Section 2.1 on the performance of ex-$kNN$ for computing expectiles. Note that the performance is measured in terms of test error and computational time, and the distance measure that leads to the minimum on these two evaluation factors is considered to be the best distance measure. In this context, for $\tau =0.25,0.50,0.75$, the test error and computational time of ex-$kNN$ is computed and presented in Table A1, Table A2, Table A3, Table A4, Table A5 and Table A6 in Appendix A. By giving rank to the test error and computation time of ex-$kNN$ for each distance measure in each dataset, we observe that there is no single distance measure that performs well on all data sets in terms of test error and computational cost. For instance, by looking in Table A1 of test error for $\tau =0.25$, we see that, for the dataset hour, the Euclidean distance provides the minimum test error, whereas the same distance measure behaves entirely opposite for dataset munich-rent. This leads us to conclude that the distance measure that plays vital role on the performance of ex-$kNN$ depends on the characteristics of datasets. This observation is also noted by [21] in their investigation. Therefore, one need to consider the nature of datasets while choosing a distance measure for $kNN$-type methods.

In order to determine the overall performance of a distance measure on all datasets, we have computed the average of ranks assigned to individual distance measures on different datasets, see Table A1, Table A2, Table A3, Table A4, Table A5 and Table A6 in Appendix A. Clearly, the distance measures Canberra, Lorentzian, and Soergel can be labelled as the best three distance measures when the goal is to achieve the high accuracy of the results. However, on the other hand, when the objective is to attain a low computational cost of ex-$kNN$, the Euclidean, Canberra, and Average $(L_1,L_{\infty })$ distance measures are ranked as the top three. Furthermore, these best three distance measures regarding test error and computational cost does not hold the said order for $\tau =0.25,0.5$ and $0.75$. This indicates that the distance measure for the same data set behaves differently for different $\tau$-level. To be more elaborative, we see, in Table A2 and Table A3, that the Canberra distance measure that holds top position in providing minimum distance measure in most of the datasets when computing expectiles for $\tau =0.50,0.75$ attains third position for $\tau =0.25$. Similar is the situation with other distance measures. It is interesting to note from the results of our experiments based on the considered datasets that no single distance measure can lead the ex-$kNN$ towards achieving both goals of high accuracy and low computational cost at the same time. In other words, the choice of a distance measures with ex-$kNN$ not only depends on the data set, but also the objective. It is also important to note that the Euclidean distance that has been considered more often with $kNN$ in the literature shows poor performance in general when the goal is to achieve highly accurate predictions.

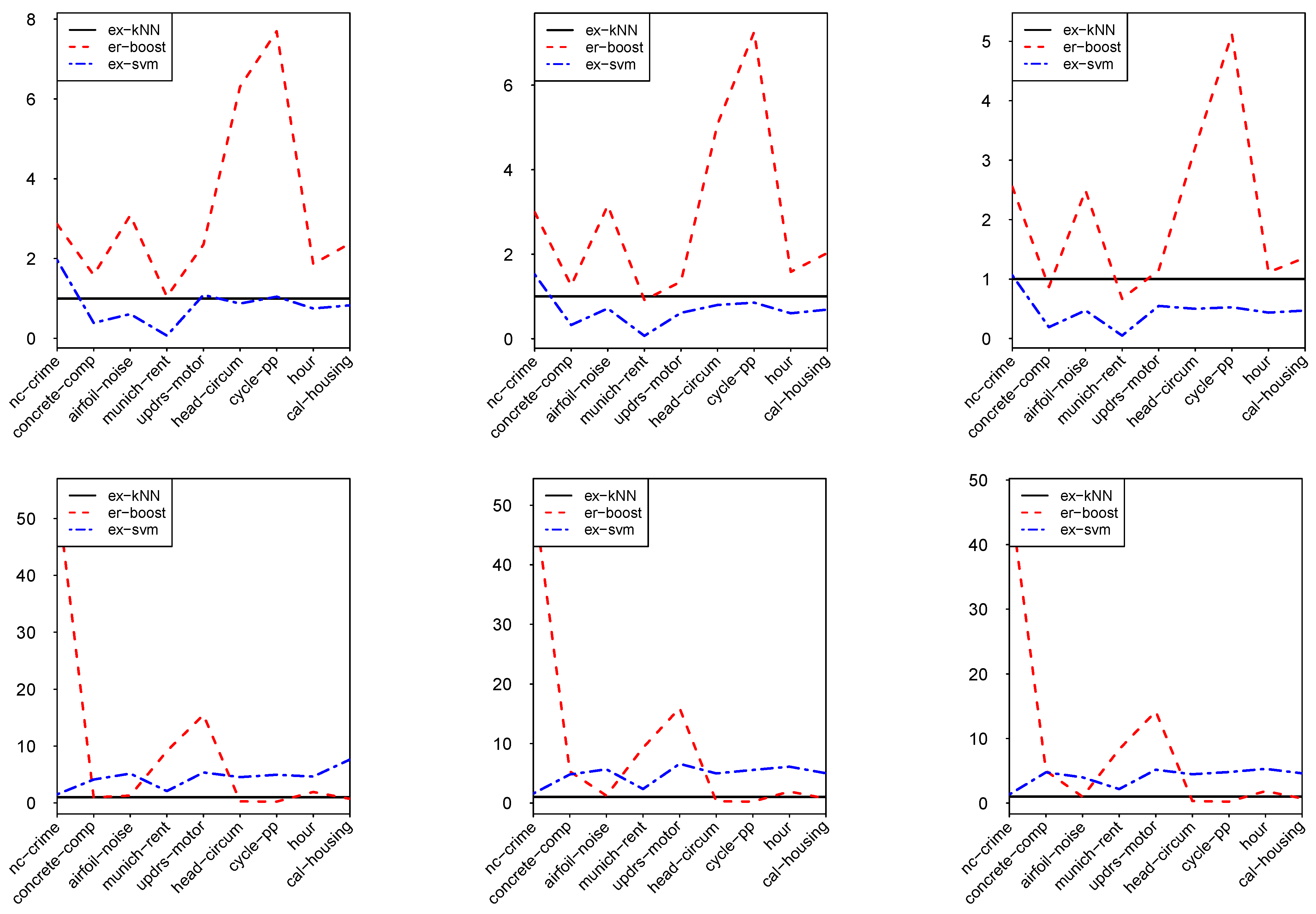
Finally, we compare the performance of ex-$kNN$ with the existing packages of computing expectiles, like er-boost and ex-svm, with respect to the test error and computational cost. To perform experiments by er-boost, we set the default value of boosting steps ($M=10$) and use 5-fold cross-validation to choose the best value of interaction (L) between variables. For more details regarding experimental setting with er-boost, we refer the interested readers to [28]. To perform the ex-svm, which is the part of package liquidSVM, we downloaded the terminal version of liquidSVM for Windows 64 bit. The default setting of 10 by 10 grid search of hyperparameters together with 5-fold cross validation is used to tune these hyperparameters. For more details on ex-svm and liquidSVM, we refer the readers to [14,29], respectively. Finally, to compute the test error and computation cost for ex-$kNN$ we consider the distance measures that attain the top average rank for $\tau$-expectile, which is, Canberra distance for test error and Euclidean distance for computational time. Furthermore, we also use five-fold cross-validation to determine the best k-value. Based on the aforementioned settings, the results for test error and computational cost of ex-$kNN$, er-boost, and ex-svm for different datasets are presented in Table 2 and Table 3. By comparing ex-$kNN$ with er-boost regarding test error at $\tau =0.25,0.50$, and $0.75$, we see that ex-$kNN$, depending on the nature of the data, shows between two to eight times better performance, see Figure 1. On the other hand, the performance of ex-$kNN$ in terms of test error is comparable with ex-svm on some examples. Regarding computational cost, similar to the findings of [14] for ex-svm, we observe that ex-$kNN$ is also more sensitive to the training set size and less sensitive to data dimensions. However, it is interesting to note that ex-$kNN$, based on the datasets, is up to five times more efficient on some examples than ex-svm. Moreover, ex-$kNN$ is found to be considerably time efficient on the datasets, particularly when the data sets are high dimensional, as we see in Figure 1.

Table 2. Test error obtained by performing ex-$kNN$, er-boost, and ex-svm while computing expectiles for $\tau =0.25,0.50,0.75$.

Data Set	$\mathit{\tau }=0.25$			$\mathit{\tau }=0.50$			$\mathit{\tau }=0.75$
	ex-$\mathit{kNN}$	er-boost	ex-svm	ex-$\mathit{kNN}$	er-boost	ex-svm	ex-$\mathit{kNN}$	er-boost	ex-svm
NC-CRIME	0.0029	0.0083	0.0057	0.0040	0.0120	0.0061	0.0047	0.0120	0.0050
CONCRETE-COMP	0.0250	0.0397	0.0097	0.0389	0.0490	0.0127	0.0522	0.0452	0.0100
AIRFOIL-NOISE	0.0130	0.0401	0.0079	0.0149	0.047	0.0107	0.0169	0.0462	0.0080
MUNICH-RENT	0.0131	0.0137	0.0009	0.0172	0.0158	0.0012	0.0202	0.0135	0.0010
UPDRS-MOTO	0.0229	0.0538	0.0249	0.0474	0.0640	0.0291	0.0474	0.0545	0.026
HEAD-CIRCUM	0.0039	0.0246	0.0034	0.00500	0.0254	0.0040	0.0060	0.0193	0.0030
CYCLE-PP	0.0046	0.0354	0.0048	0.0062	0.0450	0.0053	0.0076	0.0389	0.0040
HOUR	0.0155	0.0289	0.0116	0.0252	0.0399	0.0152	0.0344	0.0383	0.0150
CAL-HOUSING	0.0231	0.0549	0.0191	0.0375	0.0761	0.0259	0.0552	0.0751	0.0260

Table 3. Train time (in seconds) obtained by performing ex-$kNN$, er-boost and ex-svm while computing expectiles for $\tau =0.25,0.50,0.75$.

Data Set	$\mathit{\tau }=0.25$			$\mathit{\tau }=0.50$			$\mathit{\tau }=0.75$
	ex-$\mathit{kNN}$	er-boost	ex-svm	ex-$\mathit{kNN}$	er-boost	ex-svm	ex-$\mathit{kNN}$	er-boost	ex-svm
NC-CRIME	0.545	29.790	0.900	0.571	29.819	0.830	0.617	29.730	0.820
CONCRETE-COMP	0.584	2.924	2.740	0.572	3.032	2.740	0.575	2.867	2.410
AIRFOIL-NOISE	0.132	1.091	5.060	0.893	1.105	4.510	1.130	1.072	4.510
MUNICH-RENT	1.619	14.760	3.82	1.619	15.026	4.070	1.872	15.604	3.380
UPDRS-MOTO	10.524	163.30	6.91	10.495	167.24	59.52	11.516	163.63	56.49
HEAD-CIRCUM	9.064	2.512	44.320	8.908	2.664	39.43	8.821	2.819	41.20
CYCLE-PP	16.163	3.833	88.670	15.961	3.728	77.06	16.018	3.680	80.250
HOUR	65.435	126.30	386.160	63.252	121.820	343.23	64.775	120.270	303.550
CAL-HOUSING	75.757	54.780	381.12	76.221	57.433	342.99	74.301	53.620	340.69

Figure 1. Test error ratio of er-boost and ex-svm to ex-$kNN$(top) and computational time ratio of er-boost and ex-svm to ex-$kNN$ (bottom). The graphs comprise of $\tau =0.25$ (left), $\tau =0.50$ (middle) and $\tau =0.75$ (right).

4. Conclusions

In this study, an algorithm, called ex-$kNN$, is proposed by combining the idea of the k-nearest neighbours approach and the asymmetric least squares loss function in order to compute expectiles. Because the performance of ex-$kNN$ depends on the distance measure used to determine the neighbourhood of the query point, various distance measures are considered and their impact is evaluated in terms of test error and computational time. It is observed that there exists no single distance measures that can be associated with ex-$kNN$ to achieve high performance for different kinds of datasets. To be more precise, it is found from the list of considered distance measures that Canberra, Lorentzian, and Soergel lead to minimum test error, whereas Euclidean, Canberra, and Average of $(L_1,L_{\infty })$ provide a low computational cost of ex-$kNN$. Furthermore, using nine real-world datasets, the performance of ex-$kNN$ is compared with existing packages for computing expectiles, namely er-boost and ex-svm. The results showed that the ex-$kNN$, depending on the nature of data, performs between two to eight times better than ex-$kNN$ in terms of test error and it showed comparable performance with ex-svm on some datasets. Regarding computational cost, it is found that ex-svm is up to five times more efficient than ex-svmm and much more efficient than er-boost.

To make a fair comparison of ex-$kNN$ with existing packages, this study is limited to using the cross-validation approach with ex-$kNN$ to select the best value of k-neighbours. However, more advanced and efficient approaches for this purpose can be considered with ex-$kNN$ for a further reduction of computational cost. Moreover, some other loss functions to compute expectiles can be investigated, with the results compared to the one considered in this study.