On the Conservation Laws and Exact Solutions to the (3+1)-Dimensional Modified KdV-Zakharov-Kuznetsov Equation
Abstract
:1. Introduction
2. Fundamental Definitions and Mathematical Concepts
2.1. Information About Conservation Theorem
2.2. Description of the ()-Expansion Method
3. Applications
3.1. Conservation Laws
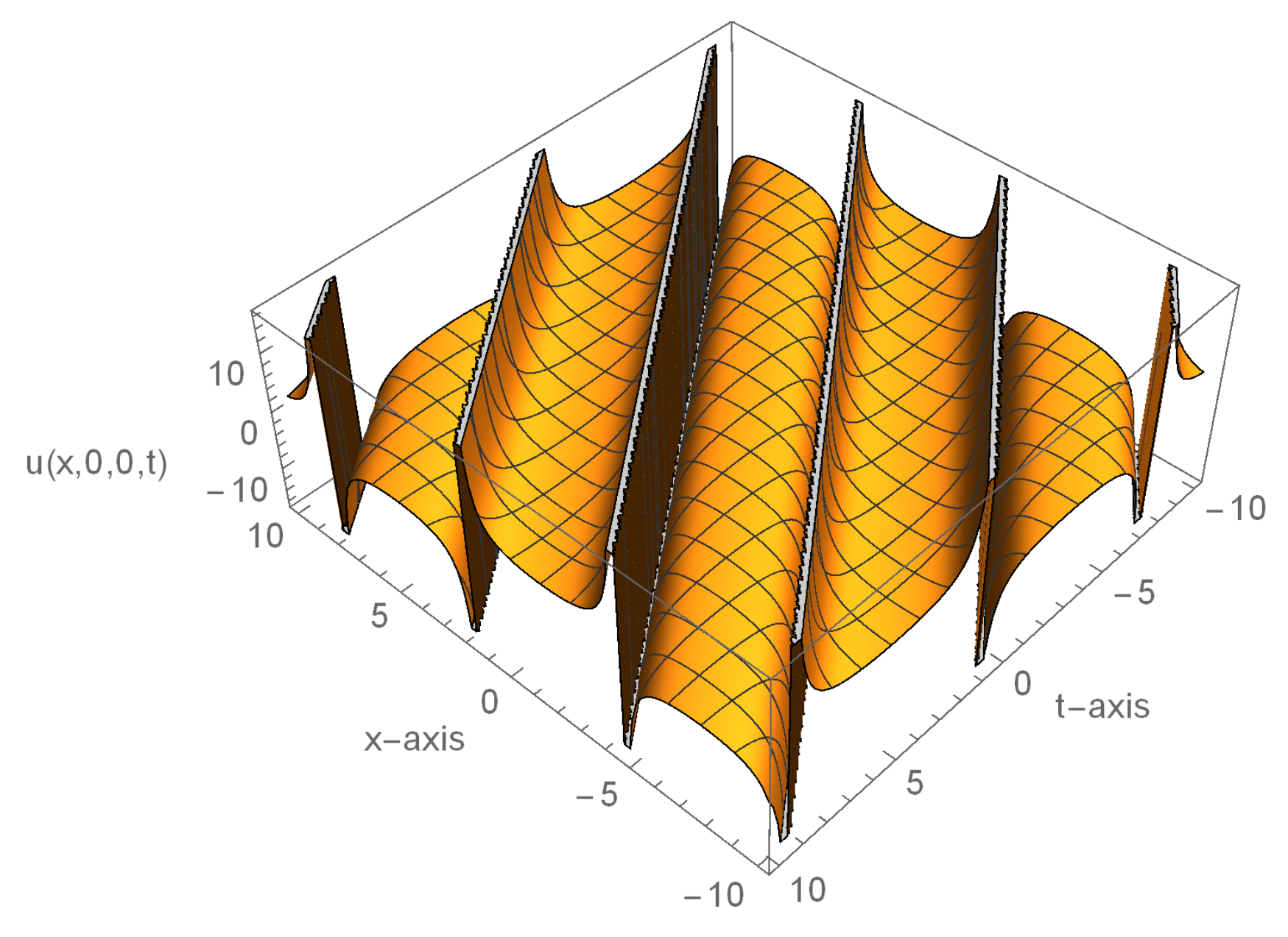
3.2. Exact Solutions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Osman, M.S.; Rezazadeh, H.; Eslami, M.; Neirameh, A.; Mirzazadeh, M. Analytical study of solitons to benjamin-bona-mahony-peregrine equation with power law nonlinearity by using three methods. U. Politeh. Buch. Ser. A 2018, 80, 267–278. [Google Scholar]
- Ali, K.K.; Cattani, C.; Gómez-Aguilar, J.F.; Baleanu, D.; Osman, M.S. Analytical and numerical study of the DNA dynamics arising in oscillator-chain of Peyrard-Bishop model. Chaos Soliton. Fract. 2020, 139, 110089. [Google Scholar] [CrossRef]
- Liu, J.G.; Osman, M.S.; Wazwaz, A.M. A variety of nonautonomous complex wave solutions for the (2+1)-dimensional nonlinear Schrödinger equation with variable coefficients in nonlinear optical fibers. Optik 2019, 180, 917–923. [Google Scholar] [CrossRef]
- Osman, M.S. Multi-soliton rational solutions for quantum Zakharov-Kuznetsov equation in quantum magnetoplasmas. Waves Random Complex Media 2016, 26, 434–443. [Google Scholar] [CrossRef]
- Hirota, R. Direct Method of Finding Exact Solutions of Nonlinear Evolution Equations; Bullough, R., Caudrey, P., Eds.; Backlund Transformations; Springer: Berlin, Germany, 1980. [Google Scholar]
- Osman, M.S.; Inc, M.; Liu, J.G.; Hosseini, K.; Yusuf, A. Different wave structures and stability analysis for the generalized (2+1)-dimensional Camassa-Holm-Kadomtsev-Petviashvili equation. Phys. Scr. 2020, 95, 035229. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Multiple soliton solutions for (2+1)-dimensional Sawada-Kotera and Caudrey-Dodd-Gibbon equations. Math. Meth. Appl. Sci. 2011, 34, 1580–1586. [Google Scholar] [CrossRef]
- Liu, J.G.; Zhu, W.H.; Osman, M.S.; Ma, W.X. An explicit plethora of different classes of interactive lump solutions for an extension form of 3D-Jimbo—Miwa model. Eur. Phys. J. Plus 2020, 135, 412. [Google Scholar] [CrossRef]
- Yusufoğlu, E.; Bekir, A. Exact solutions of coupled nonlinear evolution equations. Chaos Solitons Fractals 2008, 37, 842–848. [Google Scholar] [CrossRef]
- Misirli, E.; Gurefe, Y. Exp-function method to solve the generalized Burgers-Fisher equation. Nonlinear Sci. Lett. A 2010, 13, 323–328. [Google Scholar]
- Zhang, S. Application of Exp-function method to a KdV equation with variable coefficients. Phys. Lett. A 2007, 365, 448–453. [Google Scholar] [CrossRef]
- Naher, H. New approach of (G′/G)-expansion method and new approach of generalized (G′/G)-expansion method for ZKBBM equation. J. Egypt. Math. Soc. 2015, 23, 42–48. [Google Scholar] [CrossRef] [Green Version]
- Ding, Y.; Osman, M.S.; Wazwaz, A.M. Abundant complex wave solutions for the nonautonomous FokasLenells equation in presence of perturbation terms. Optik 2019, 181, 503–513. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Al-Joudi, S. Applications of an Extended (G′/G)-Expansion Method to Find Exact Solutions of Nonlinear PDEs in Mathematical Physics. Math. Probl. Eng. 2010, 2010, 19. [Google Scholar] [CrossRef]
- Alam, M.N.; Bonyah, E.; Fayz-Al-Asad, M.; Osman, M.S.; Abualnaja, K.M. Stable and functional solutions of the Klein-Fock-Gordon equation with nonlinear physical phenomena. Phys. Scr. 2021, 96, 055207. [Google Scholar] [CrossRef]
- Gurefe, Y.; Misirli, E.; Sonmezoglu, A.; Ekici, M. Extended trial equation method to generalized partial differential equations. Appl. Math. Comput. 2013, 219, 5253–5260. [Google Scholar] [CrossRef]
- Tascan, F.; Bekir, A.; Koparan, M. Travelling wave solutions of nonlinear evolution equations by using the first integral method. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1810–1815. [Google Scholar] [CrossRef]
- Wazwaz, A.M. A sine-cosine method for handling nonlinear wave equations. Math. Comput. Model. 2004, 40, 499–508. [Google Scholar] [CrossRef]
- Kaplan, M.; Akbulut, A.; Bekir, A. Exact travelling wave solutions of the nonlinear evolution equations by auxiliary equation method. Z. Naturforsch. A 2015, 70, 969–974. [Google Scholar] [CrossRef]
- Naz, R.; Mahomed, F.M.; Mason, D.P. Conservation laws via the partial Lagrangian and invariant solutions for radial and two-dimensional free jets. Nonlinear Anal. Real World Appl. 2009, 10, 3457–3465. [Google Scholar] [CrossRef]
- Bluman, G.W.; Kumei, S. Symmetries and Differential Equations with 21 Illustrations; Springer: New York, NY, USA, 1989. [Google Scholar]
- Ibragimov, N.H.; Khamitova, R.; Avdonina, E.D.; Galiakberova, L.R. Conservation laws and solutions of a quantum drift-diffusion model for semiconductors. Int. J. Non-Linear Mech. 2015, 77, 69–73. [Google Scholar] [CrossRef]
- Olver, P.J. Application of Lie Groups to Differential Equations; Springer: New York, NY, USA, 1993. [Google Scholar]
- Ibragimov, N.H. A new conservation theorem. J. Math. Anal. Appl. 2007, 333, 311–328. [Google Scholar] [CrossRef] [Green Version]
- Anco, S.C.; Bluman, G.W. Direct construction method for conservation laws of partial differential equations. Part II: General treatment. Eur. J. Appl. Math. 2002, 9, 567–585. [Google Scholar] [CrossRef] [Green Version]
- Gandarias, M.L. Conservation laws for some equations that admit compacton solutions induced by a non-convex convection. J. Math. Anal. Appl. 2015, 430, 695–702. [Google Scholar] [CrossRef]
- Tutueva, A.; Karimov, T.; Butusov, D. Semi-Implicit and Semi-Explicit Adams-Bashforth-Moulton Methods. Mathematics 2020, 8, 780. [Google Scholar] [CrossRef]
- Kress, W.; Lötstedt, P. Time step restrictions using semi-explicit methods for the incompressible Navier—Stokes equations. Comput. Method Appl. Mech. Eng. 2006, 195, 4433–4447. [Google Scholar] [CrossRef]
- Bürger, R.; Gavilán, E.; Inzunza, D.; Mulet, P.; Villada, L.M. Implicit-explicit methods for a convection-diffusion-reaction model of the propagation of forest fires. Mathematics 2020, 8, 1034. [Google Scholar] [CrossRef]
- Ibragimov, N.H.; Kolsrud, T. Lagrangian Approach to Evolution Equations: Symmetries and Conservation Laws. Nonlinear Dyn. 2004, 36, 29–40. [Google Scholar] [CrossRef]
- Buhe, E.; Bluman, G.; Kara, A.H. Conservation laws for some systems of nonlinear PDEs via the symmetry/adjoint symmetry pair method. J. Math. Anal. Appl. 2016, 436, 94–103. [Google Scholar] [CrossRef]
- Xin, X.; Liu, Y.; Liu, X. Nonlocal symmetries, exact solutions and conservation laws of the coupled Hirota equations. Appl. Math. Lett. 2016, 55, 63–71. [Google Scholar] [CrossRef]
- Gandarias, M.L.; Khalique, C.M. Symmetries, solutions and conservation laws of a class of nonlinear dispersive wave equations. Commun. Nonlinear Sci. Numer. Simul. 2016, 32, 114–121. [Google Scholar] [CrossRef]
- Osman, M.S.; Baleanu, D.; Adem, A.R.; Hosseini, K.; Mirzazadeh, M.; Eslami, M. Double-wave solutions and Lie symmetry analysis to the (2+1)-dimensional coupled Burgers equations. Chin. J. Phys. 2020, 63, 122–129. [Google Scholar] [CrossRef]
- Kumar, S.; Kour, B.; Yao, S.W.; Inc, M.; Osman, M.S. Invariance Analysis, Exact Solution and Conservation Laws of (2+1) Dim Fractional Kadomtsev-Petviashvili (KP) System. Symmetry 2021, 13, 477. [Google Scholar] [CrossRef]
- Tascan, F.; Yakut, A. Conservation Laws and Exact Solutions with Symmetry Reduction of Nonlinear Reaction Diffusion Equations. Int. J. Nonlinear Sci. Numer. Simul. 2015, 16, 191–196. [Google Scholar] [CrossRef]
- Yakut, A. Consevation Laws for Partial Differential Equations. Master’s Thesis, Eskişehir Osmangazi University, Eskişehir, Turkey, 2012. [Google Scholar]
- Yaşar, E. Conservation laws for a class of soil water equations. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 3193–3200. [Google Scholar] [CrossRef]
- Li, L.X.; Li, E.Q.; Wang, M.L. The (G′/G, 1/G)-expansion method and its application to travelling wave solutions of the Zakharov equations. Appl. Math. J. Chin. Univ. 2010, 25, 454–462. [Google Scholar] [CrossRef]
- Kaplan, M. Exact Solutions of Nonlinear Schrödinger Equation. Master’s Thesis, Eskişehir Osmangazi University, Eskişehir, Turkey, 2013. [Google Scholar]
- Akbulut, A.; Kaplan, M.; Taşcan, F. Conservation laws and Exact Solutions of Phi-Four (Phi-4) Equation via the (G′/G,1/G)-Expansion Method. Z. Naturforsch. A 2016, 71, 439–446. [Google Scholar] [CrossRef] [Green Version]
- Alam, M.N.; Hafez, M.G.; Akbar, M.A.; Roshid, H.O. Exact traveling wave solutions to the (3+1)-dimensional mKdV-ZK and the (2+1)-dimensional Burgers equations via exp(-Φ(η))-expansion method. Alex. Eng. J. 2015, 54, 635–644. [Google Scholar] [CrossRef] [Green Version]
- Khan, K.; Akbar, M.A. Exact and solitary wave solutions for the Tzitzeica-Dodd-Bullough and the modified KdV-Zakharov-Kuznetsov equations using the modified simple equation method. Ain Shams Eng. J. 2014, 4, 903–909. [Google Scholar] [CrossRef] [Green Version]
- Islam, M.H.; Khan, K.; Akbar, M.A.; Salam, M.A. Exact traveling wave solutions of modified KdV-Zakharov-Kuznetsov equation and viscous Burgers equation. SpringerPlus 2014, 3, 105. [Google Scholar]
- Naher, H.; Abdullah, F.A.; Akbar, M.A. Generalized and Improved (G′/G)-Expansion Method for (3+1)-Dimensional Modified KdV-Zakharov-Kuznetsov Equation. PLoS ONE 2013, 8, e64618. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akbulut, A.; Almusawa, H.; Kaplan, M.; Osman, M.S. On the Conservation Laws and Exact Solutions to the (3+1)-Dimensional Modified KdV-Zakharov-Kuznetsov Equation. Symmetry 2021, 13, 765. https://doi.org/10.3390/sym13050765
Akbulut A, Almusawa H, Kaplan M, Osman MS. On the Conservation Laws and Exact Solutions to the (3+1)-Dimensional Modified KdV-Zakharov-Kuznetsov Equation. Symmetry. 2021; 13(5):765. https://doi.org/10.3390/sym13050765
Chicago/Turabian StyleAkbulut, Arzu, Hassan Almusawa, Melike Kaplan, and Mohamed S. Osman. 2021. "On the Conservation Laws and Exact Solutions to the (3+1)-Dimensional Modified KdV-Zakharov-Kuznetsov Equation" Symmetry 13, no. 5: 765. https://doi.org/10.3390/sym13050765





