Spherically Symmetric Tensor Fields and Their Application in Nonlinear Theory of Dislocations
Abstract
:1. Introduction
2. Input Relations of the Theory of Dislocations
3. Spherically Symmetric Tensor Fields
4. Spherically Symmetric State of Elastic Hollow Sphere with Distributed Dislocations in Radial Direction
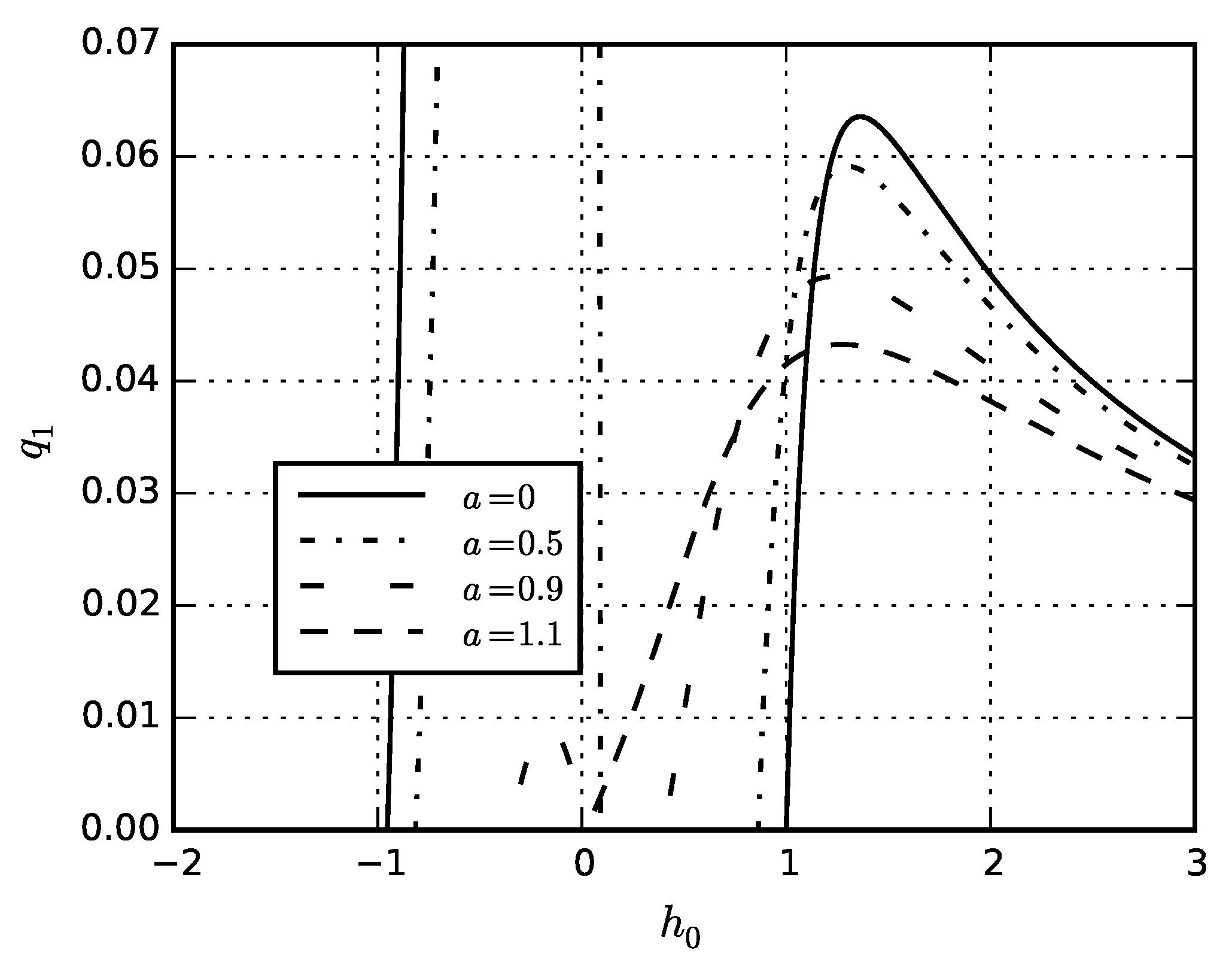
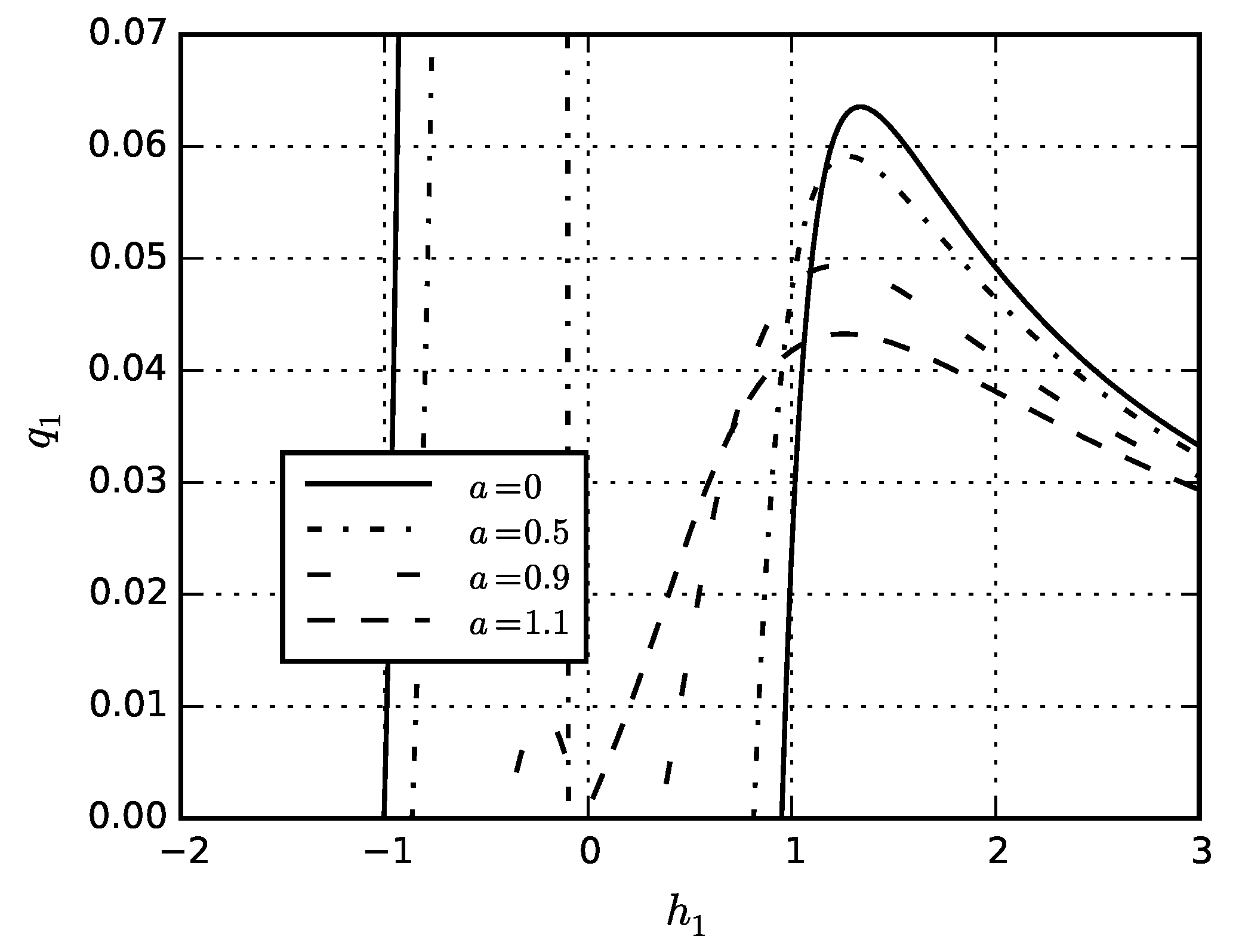
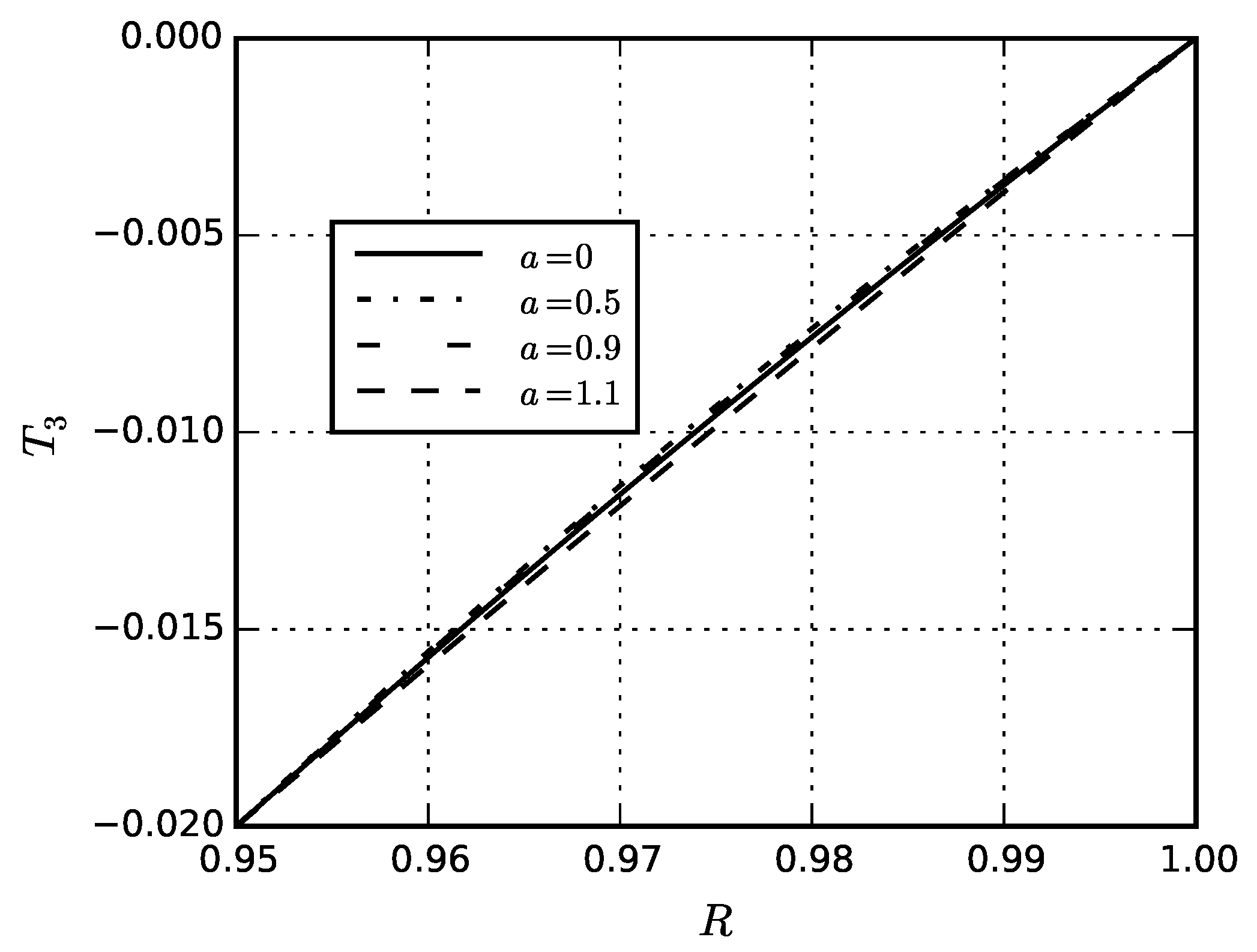
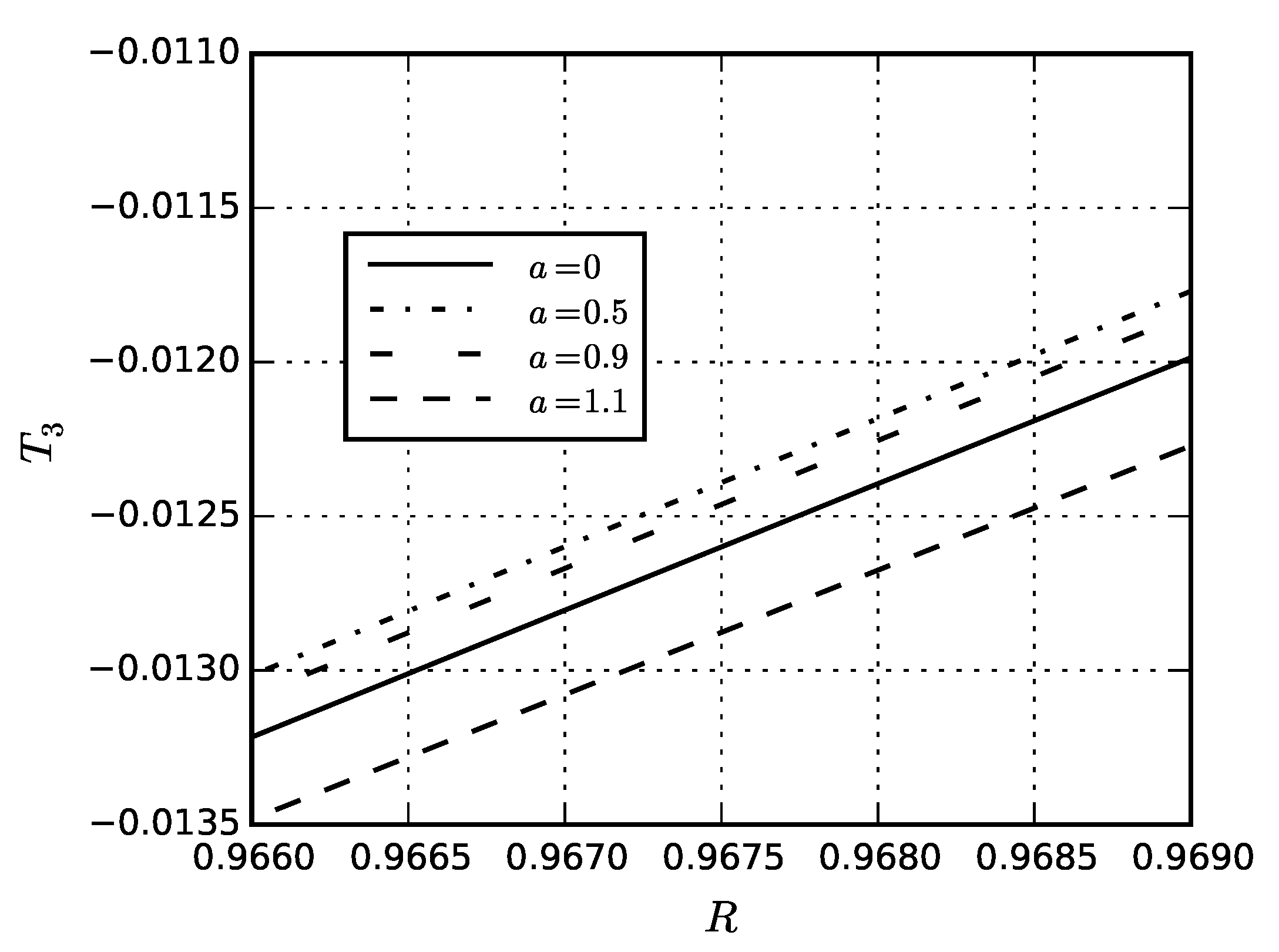
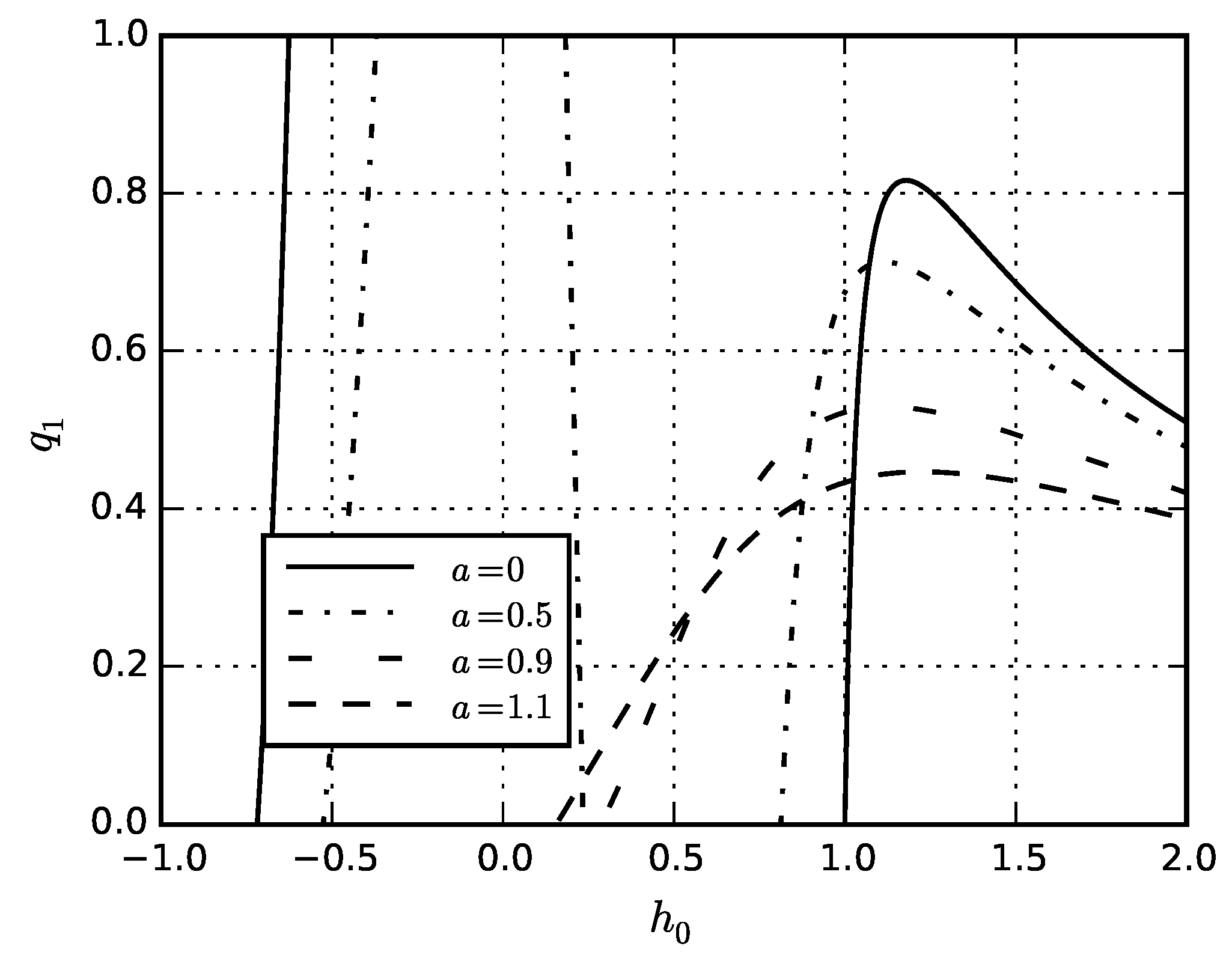
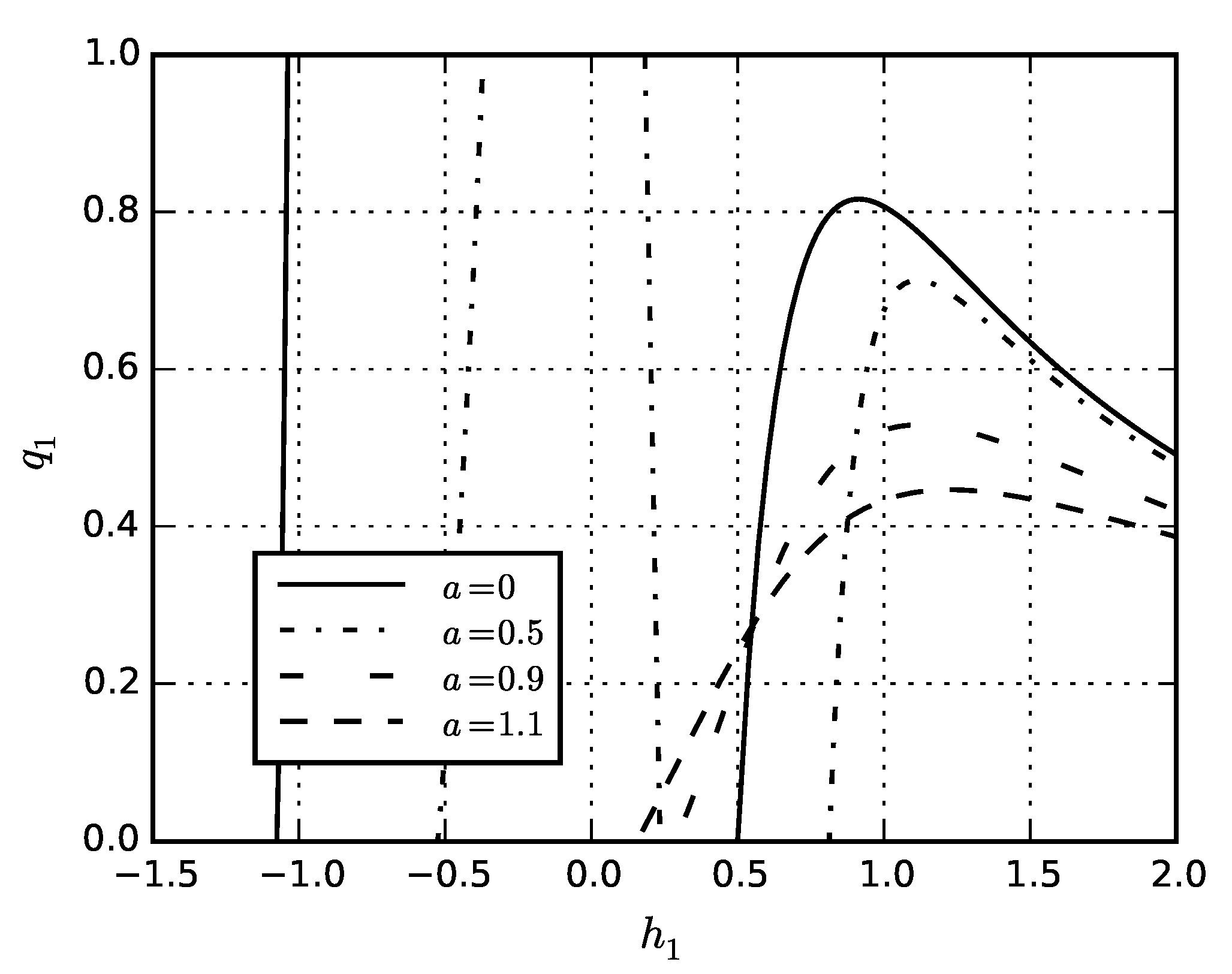
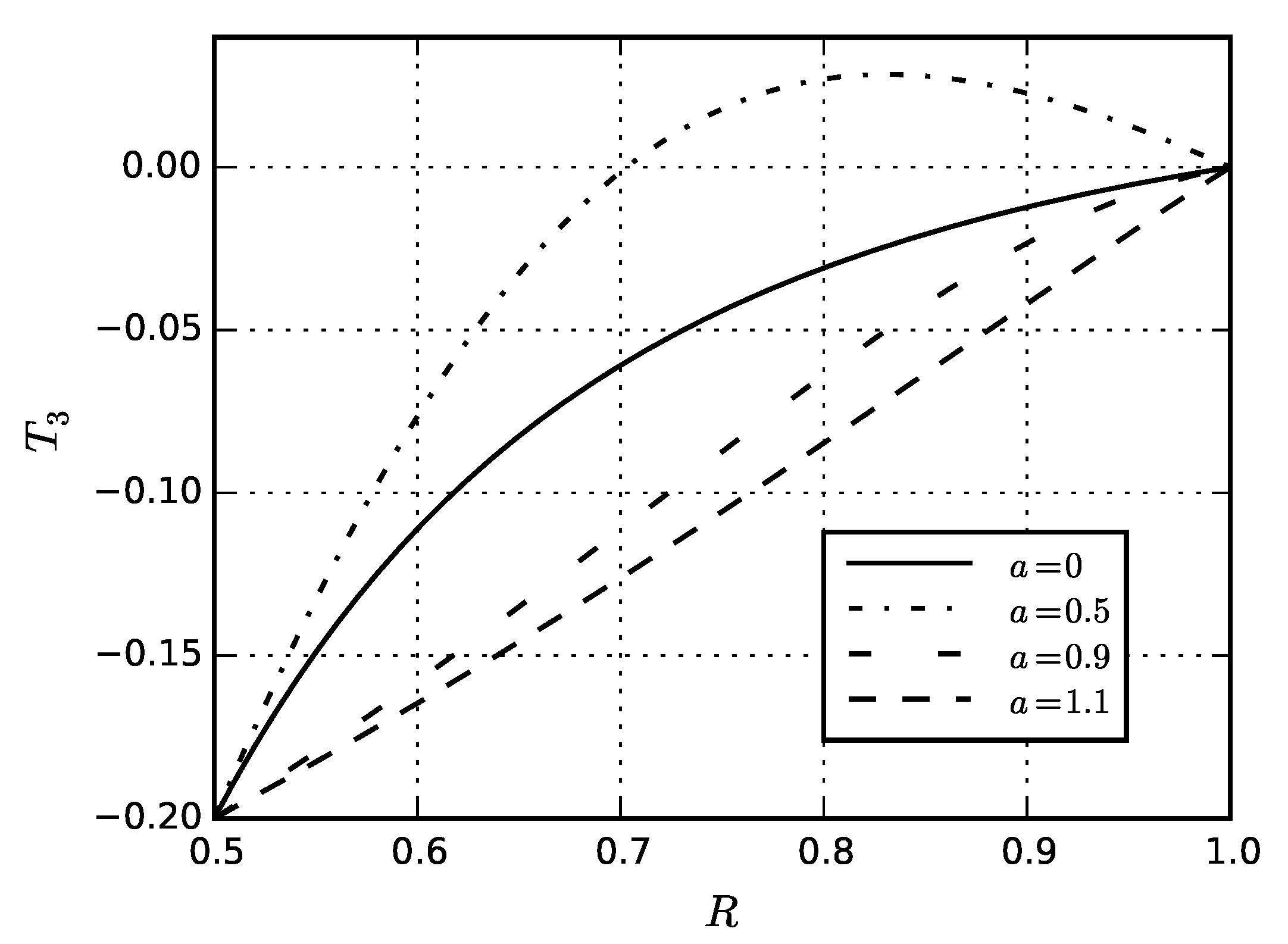
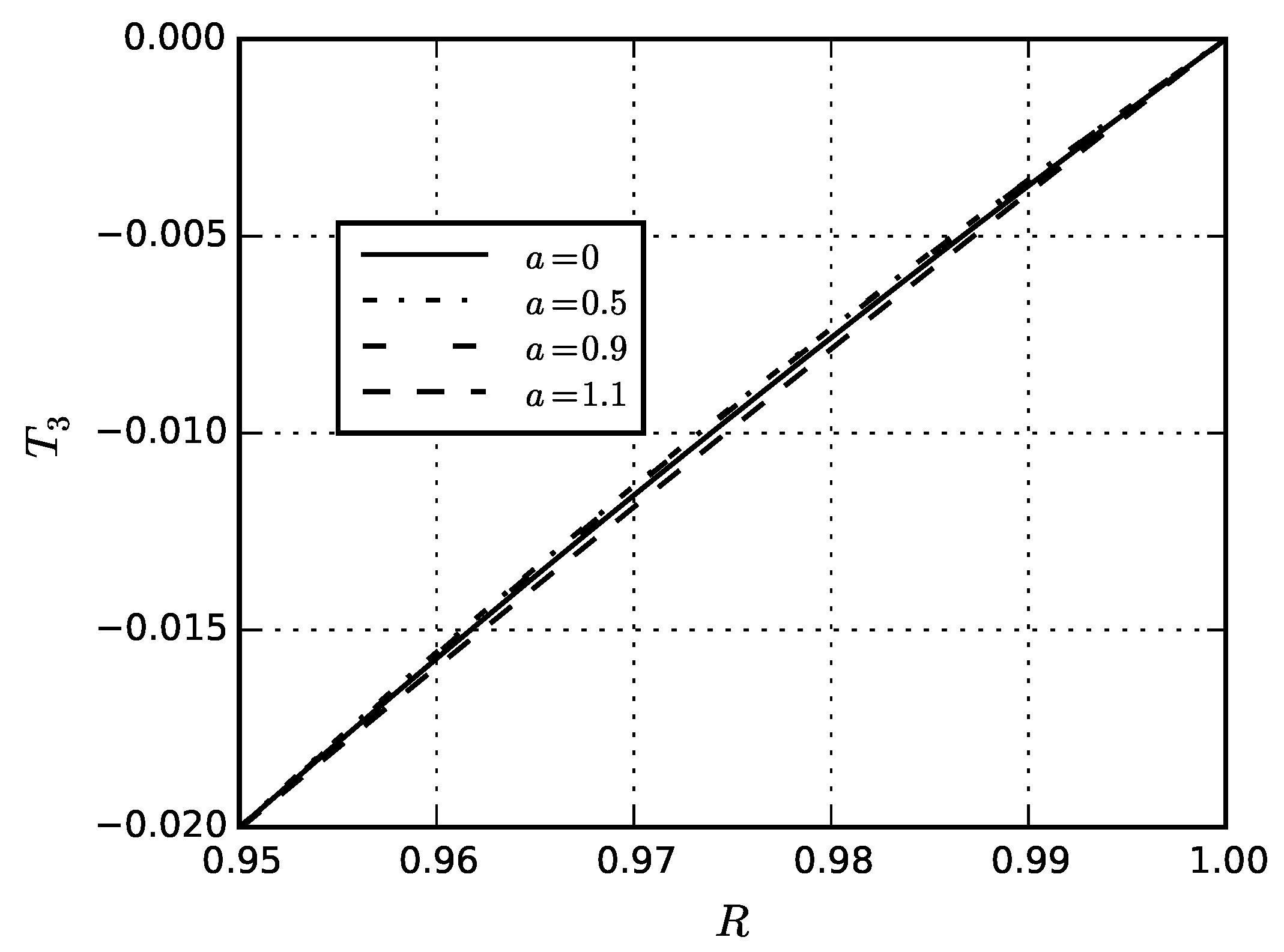
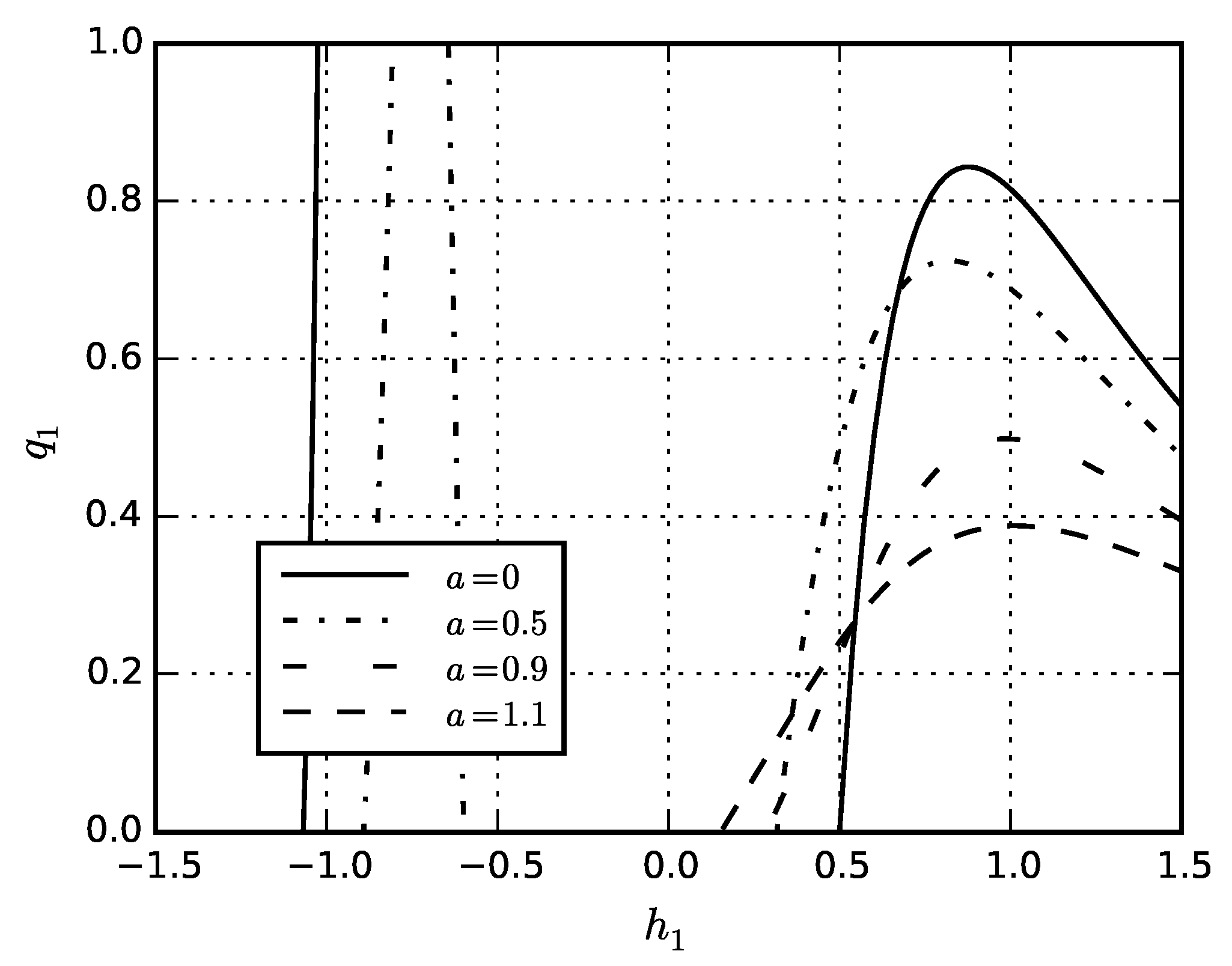
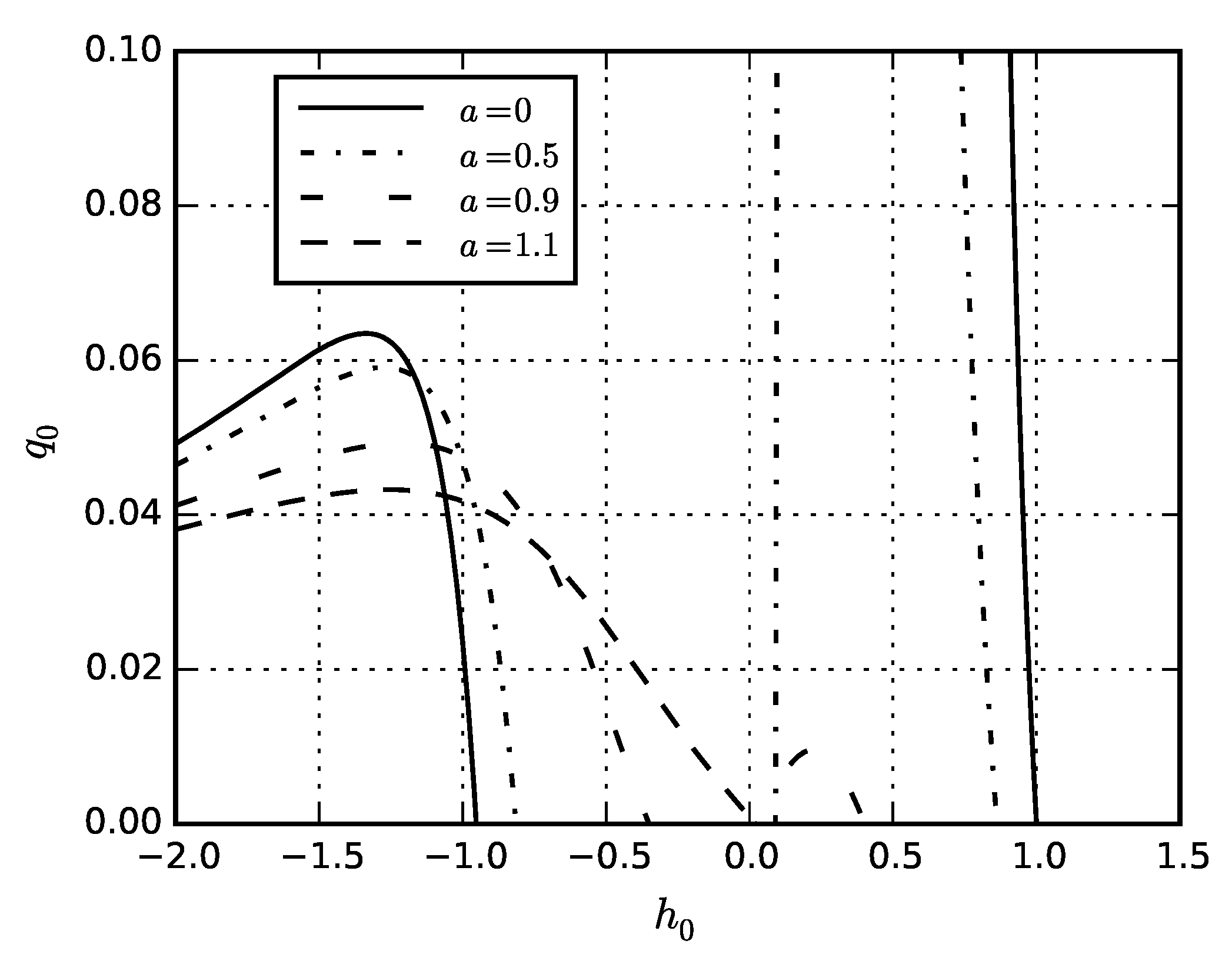
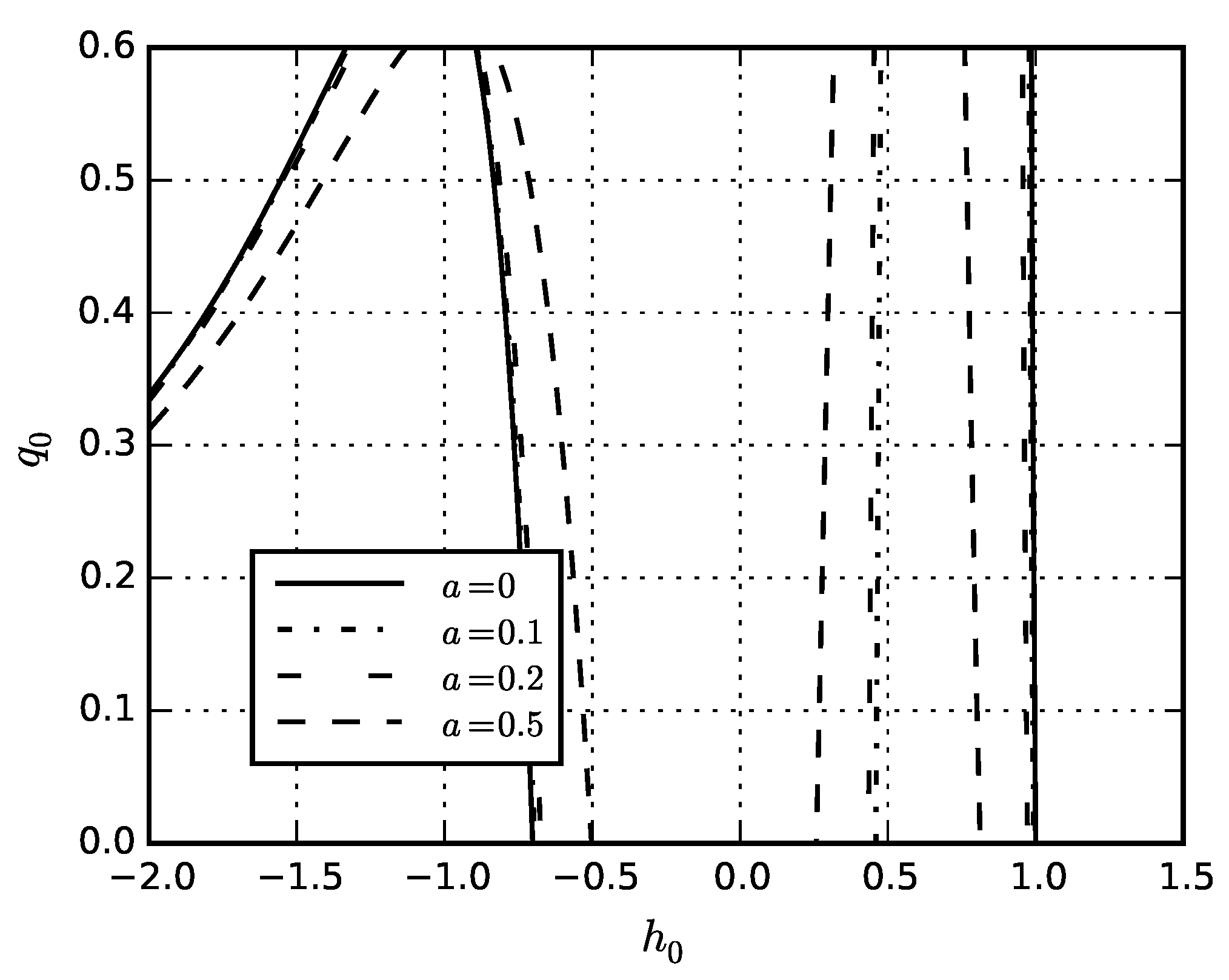
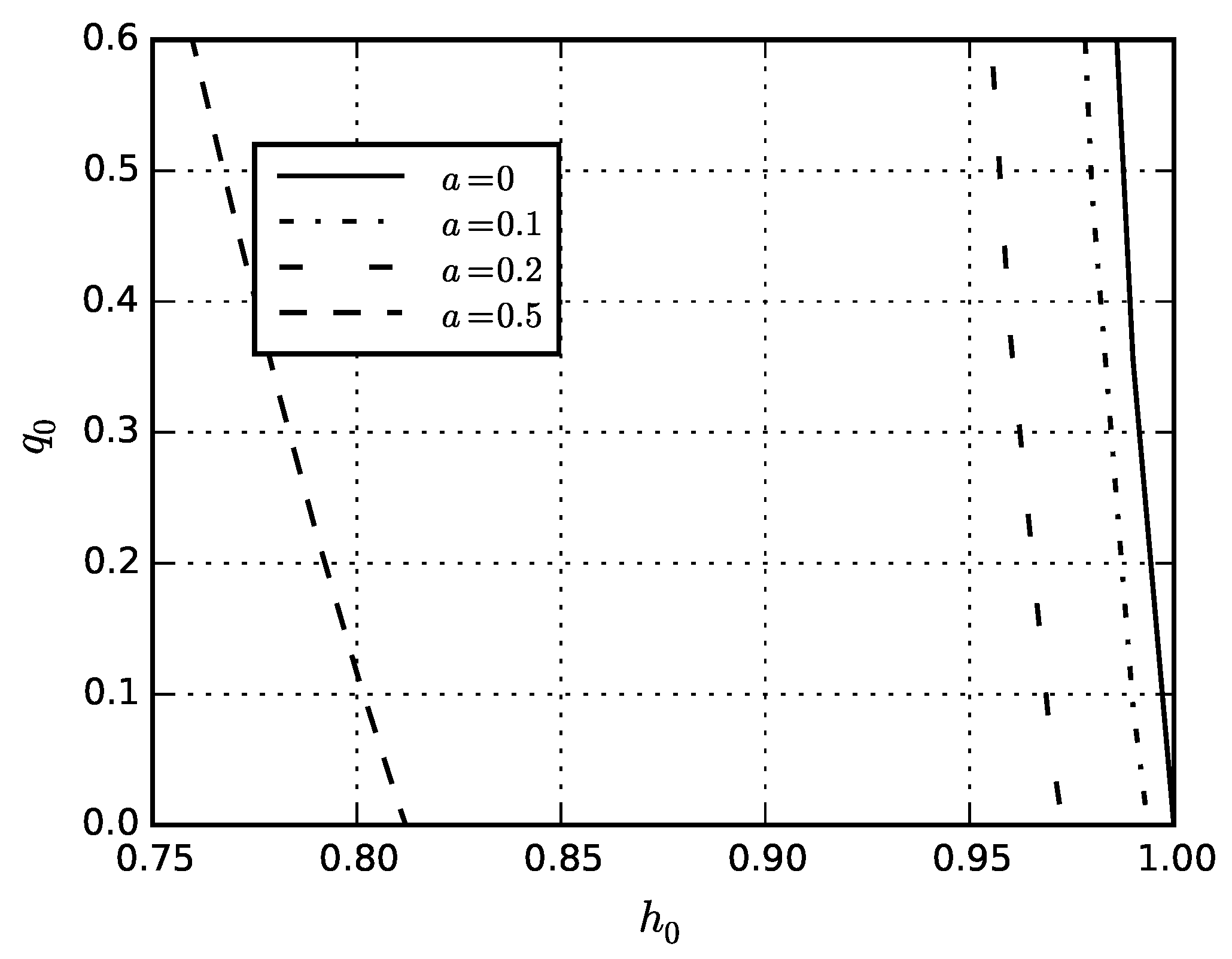
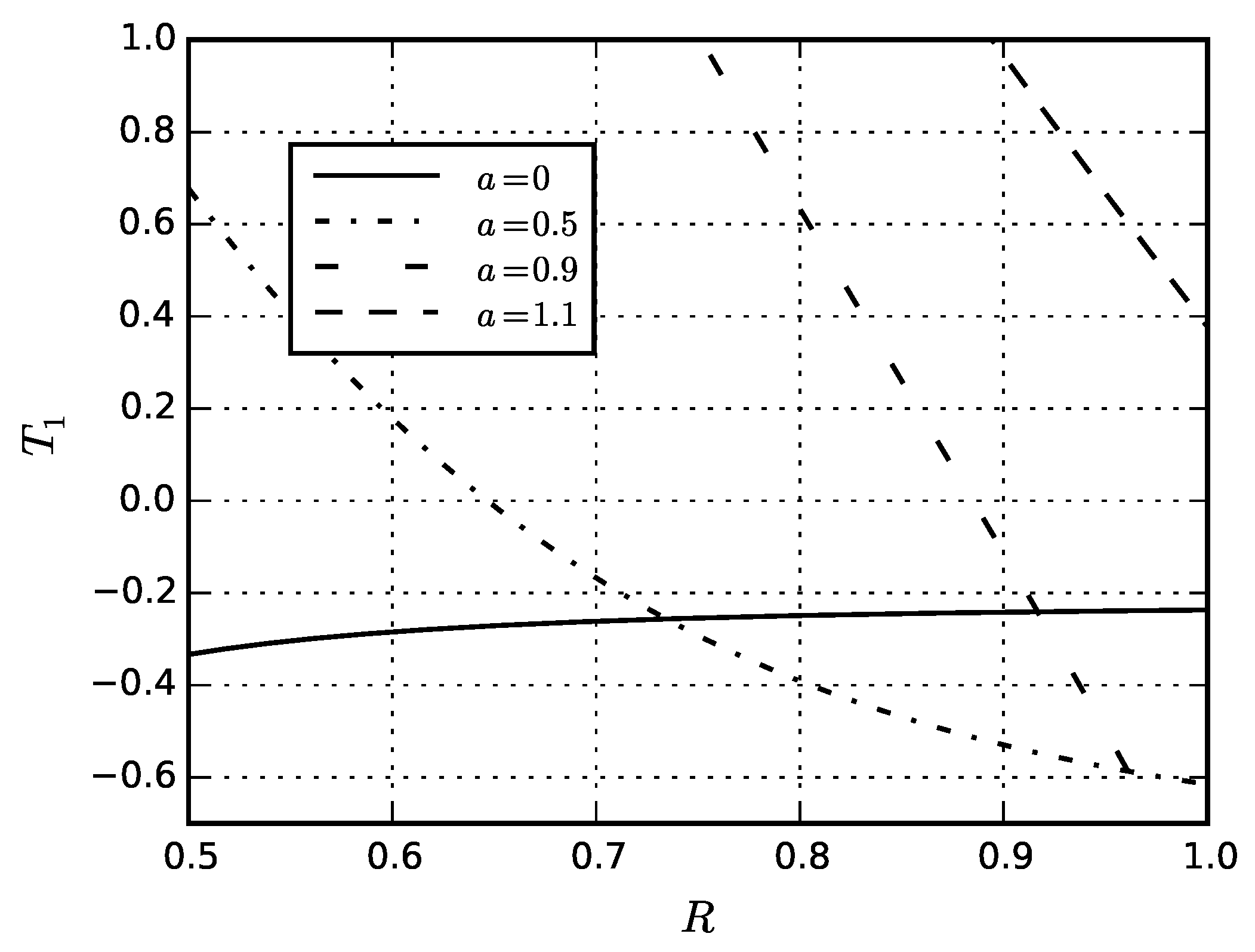
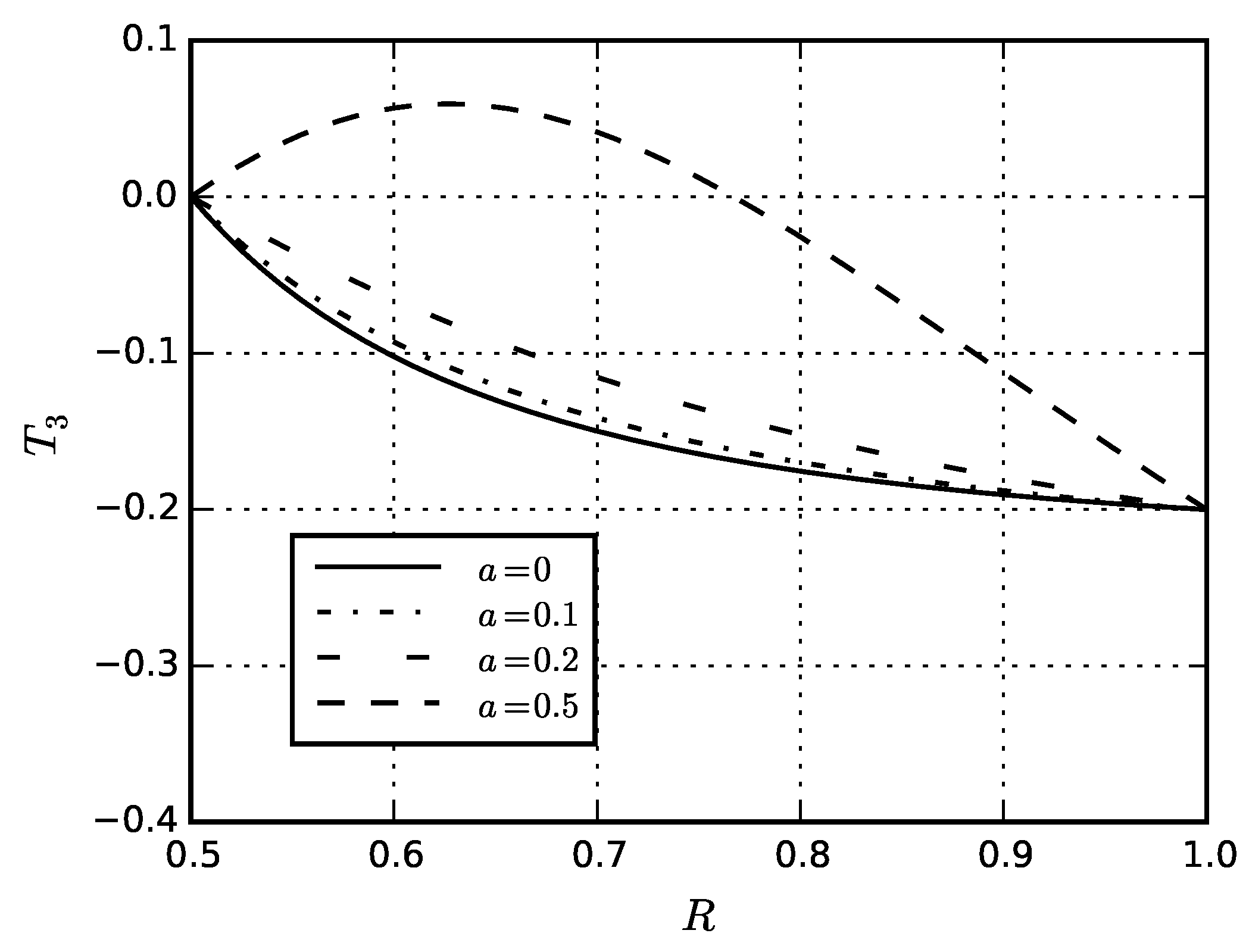
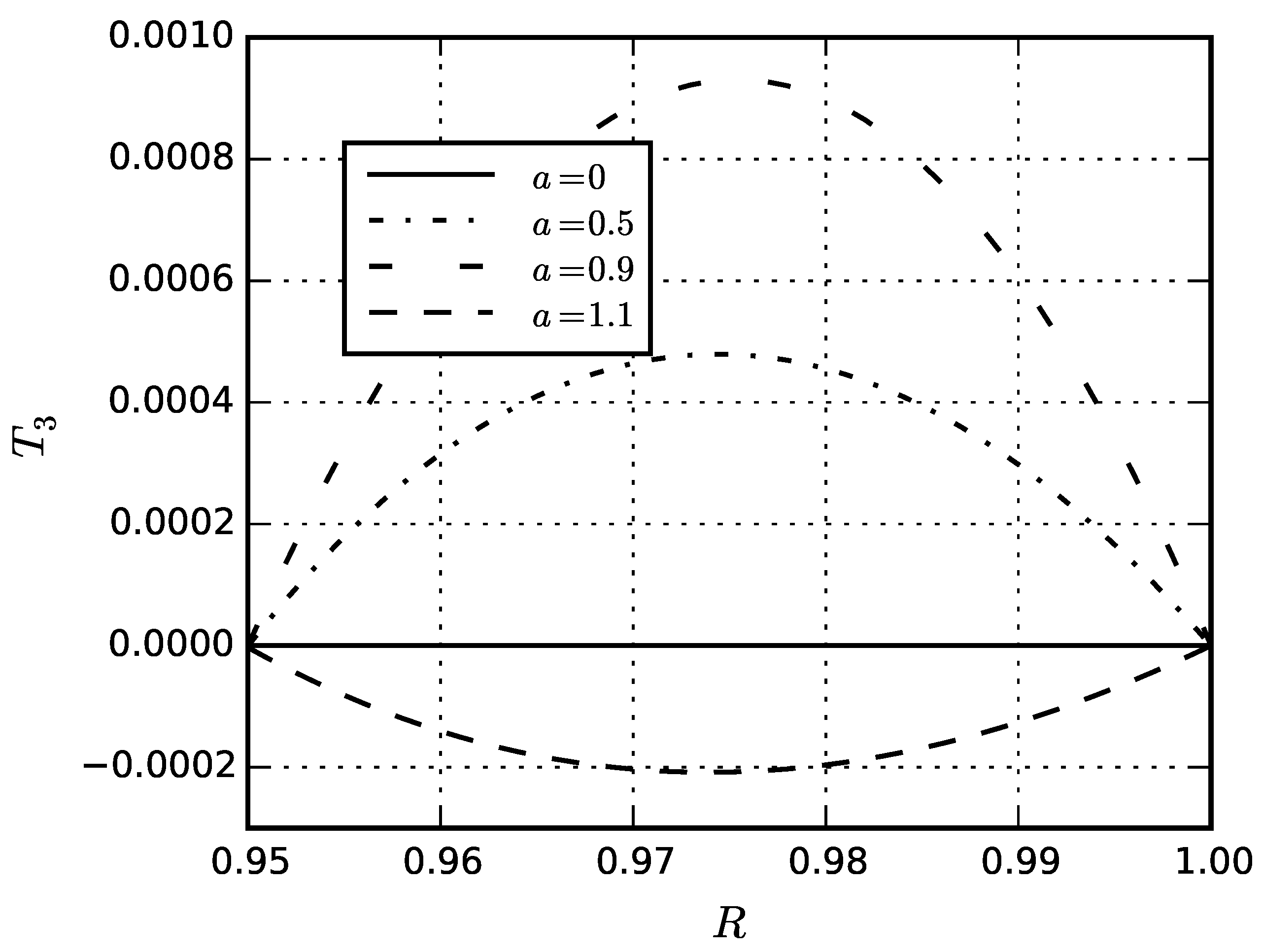
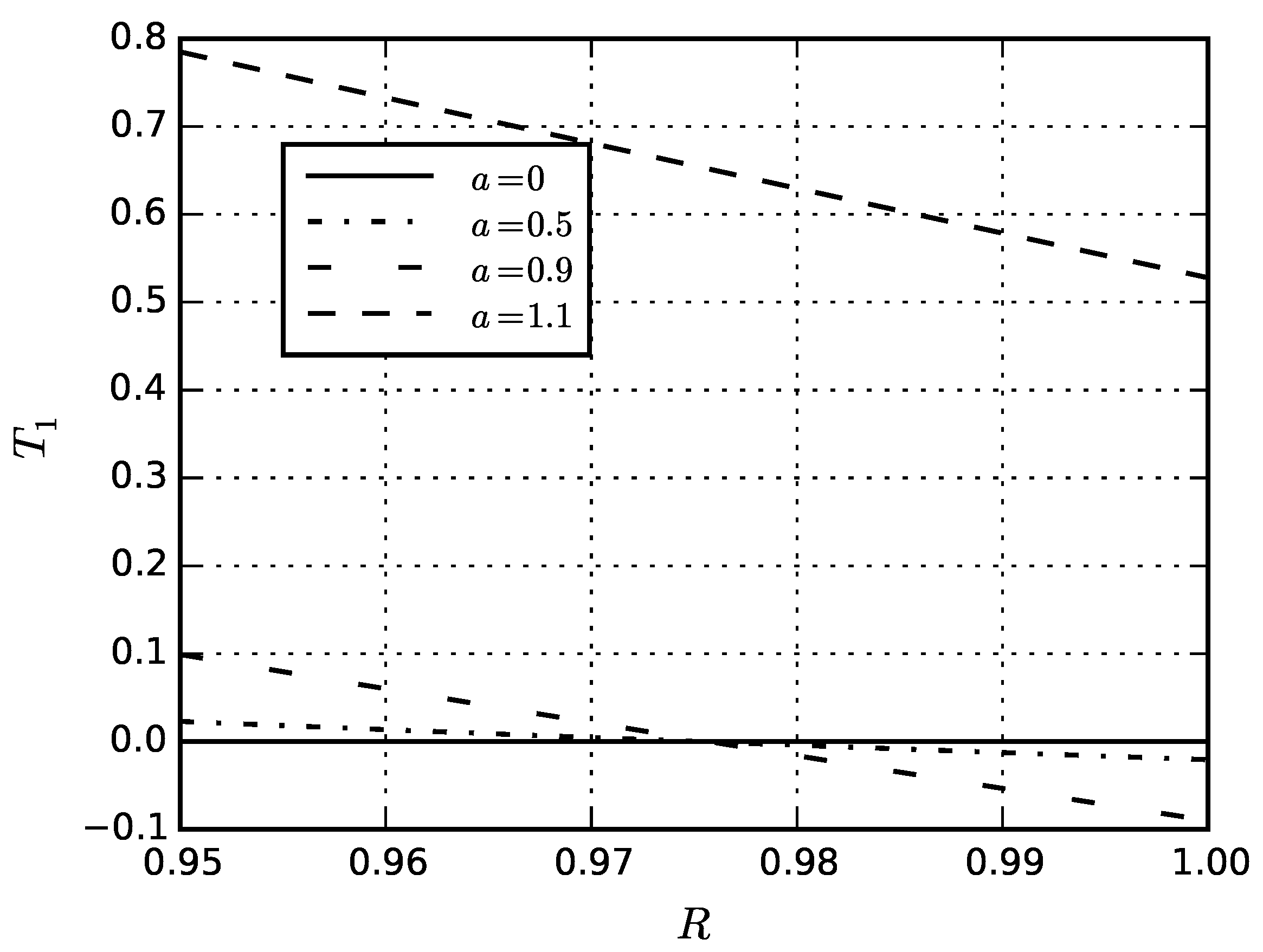
5. Numerical Results
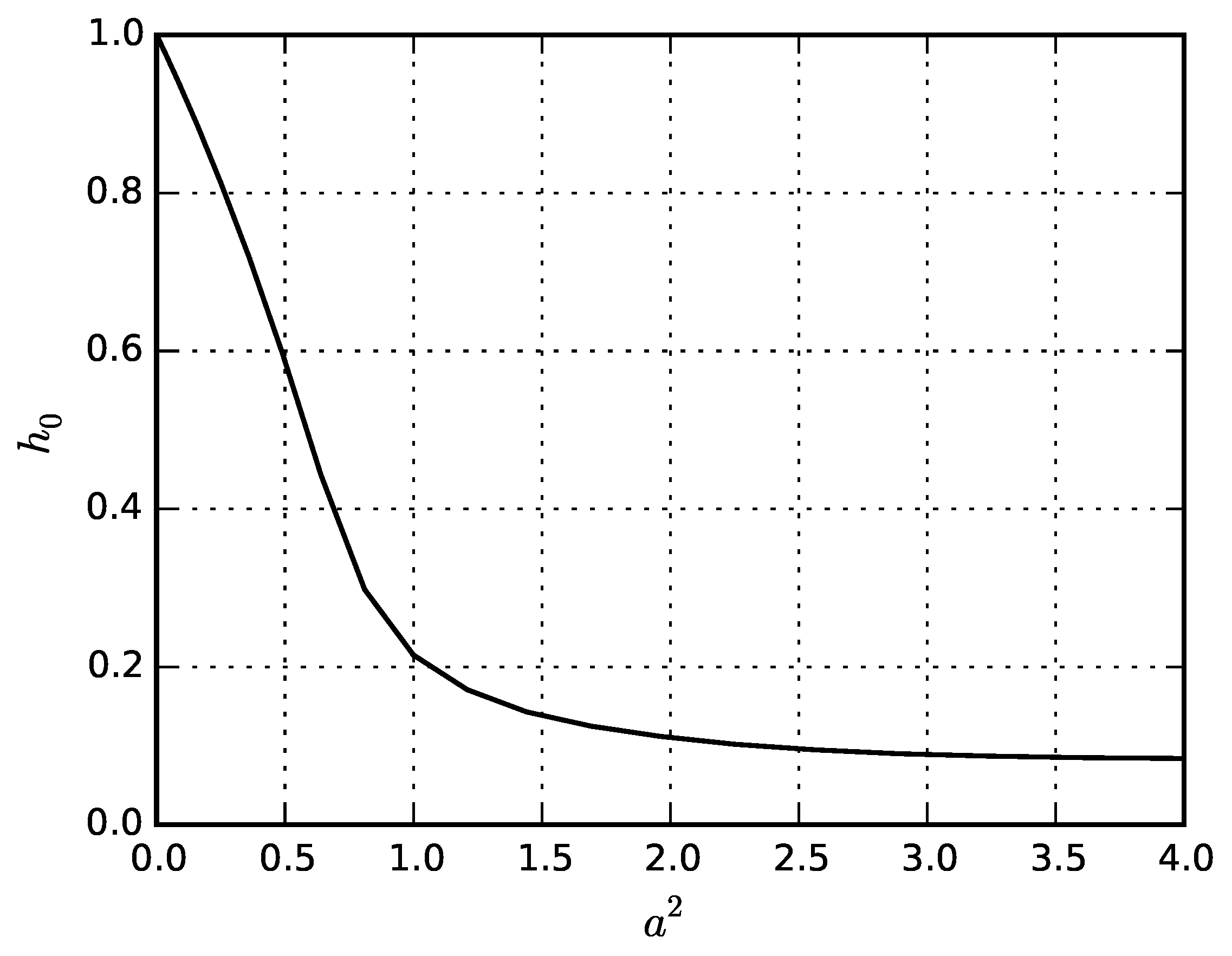
5.1. Problem for Solid Sphere
5.2. Inflation of Sphere
5.3. Compression of Sphere by Hydrostatic Pressure
5.4. Eigenstresses in Sphere
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sedov, L.I. Propagation of strong shock waves. J. Appl. Math. Mech. 1946, 10, 241–250. [Google Scholar]
- SenGupta, S.; Sur, S. Spherically symmetric solutions of gravitational field equations in Kalb-Ramond background. Phys. Lett. B 2001, 521, 350–356. [Google Scholar] [CrossRef] [Green Version]
- Garcia-Diaz, A.A.; Gutierrez-Cano, G. Regularity conditions for spherically symmetric solutions of Einstein-nonlinear electrodynamics equations. Ann. Phys. 2020, 422, 168323. [Google Scholar] [CrossRef]
- Künzle, H.P.; Oliynyk, T.A. Spherically symmetric Einstein–Yang–Mills–Higgs fields for general compact gauge groups. Nonlinear Anal. 2005, 63, 473–480. [Google Scholar] [CrossRef]
- Baekler, P. Spherically symmetric solutions of the Poincaré gauge field theory. Phys. Lett. 1983, 96A, 279–282. [Google Scholar] [CrossRef]
- Dymnikova, I.G. The algebraic structure of a cosmological term in spherically symmetric solutions. Phys. Lett. B 2000, 472, 33–38. [Google Scholar] [CrossRef] [Green Version]
- Wheeler, J.T. Symmetric solutions to the maximally Gauss – Bonnet extended Einstein equations. Nuclear Phys. 1986, B273, 732–748. [Google Scholar] [CrossRef] [Green Version]
- Kondo, K. On the geometrical and physical foundations in the theory of yielding. In Proceedings of the 2nd Japan National Congress of Applied Mechanics, Istanbul, Turkey, 20–28 August 1952; pp. 41–47. [Google Scholar]
- Bilby, B.A.; Bullough, R.; Smith, E. Continuous distributions of dislocations: A new application of the methods of non-Riemannian geometry. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1955, A231, 263–273. [Google Scholar]
- Kröner, E. Allgemeine Kontinuumstheorie der Versetzungen und Eigenspannungen. Arch. Ration. Mech. Anal. 1960, 4, 273–334. [Google Scholar] [CrossRef]
- Zorski, H. Statistical theory of dislocations. Int. J. Solids Struct. 1968, 4, 959–974. [Google Scholar] [CrossRef]
- Mossakowska, Z. Displacement description of dislocation lines. I. Cyclic functions. Arch. Mech. 1979, 31, 533–545. [Google Scholar]
- Zubov, L.M. Nonlinear Theory of Dislocations and Disclinations in Elastic Bodies; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Derezin, S.V.; Zubov, L.M. Equations of a nonlinear elastic medium with continuously distributed dislocations and disclinations. Dokl. Phys. 1999, 44, 391–394. [Google Scholar]
- Derezin, S.V.; Zubov, L.M. Disclinations in nonlinear elasticity. Ztsch. Angew. Math. Mech. 2011, 91, 433–442. [Google Scholar] [CrossRef]
- Yavary, A.; Goriely, A. Riemann—Cartan geometry of nonlinear dislocation mechanics. Arch. Ration. Mech. Anal. 2012, 205, 59–118. [Google Scholar] [CrossRef]
- Zelenina, A.A.; Zubov, L.M. Bending and twisting of nonlinear elastic bodies with continuously distributed dislocations. Vestn. Yuzhn. Nauchn. Tsentr. RAN 2009, 3, 15–22. [Google Scholar]
- Zubov, L.M. Spherically symmetric solutions in the nonlinear theory of dislocations. Dokl. Phys. 2014, 59, 419–422. [Google Scholar] [CrossRef]
- Zelenina, A.A.; Zubov, L.M. Nonlinear effects during the tension, bend, and torsion of elastic bodies with distributed dislocations. Dokl. Phys. 2013, 58, 354–357. [Google Scholar] [CrossRef]
- Zhbanova, E.V.; Zubov, L.M. The Influence of Distributed Dislocations on Large Deformations of an Elastic Sphere. In Advanced Methods of Continuum Mechanics for Materials and Structures; Advanced Structured Materials; Naumenko, K., Aßmus, M., Eds.; Springer: Singapore, 2016; Volume 60, pp. 61–76. [Google Scholar]
- Goloveshkina, E.V.; Zubov, L.M. Universal spherically symmetric solution of nonlinear dislocation theory for incompressible isotropic elastic medium. Arch. Appl. Mech. 2019, 89, 409–424. [Google Scholar] [CrossRef]
- Goloveshkina, E.V.; Zubov, L.M. Eigenstresses in a Nonlinearly Elastic Sphere with Distributed Dislocations. In New Achievements in Continuum Mechanics and Thermodynamics; Advanced Structured Materials; Abali, B., Altenbach, H., dell’Isola, F., Eremeyev, V., Öchsner, A., Eds.; Springer International Publishing: Cham, Switzerland, 2019; Volume 108, pp. 137–155. [Google Scholar]
- Zelenina, A.A.; Zubov, L.M. Spherically Symmetric Deformations of Micropolar Elastic Medium with Distributed Dislocations and Disclinations. In Advances in Mechanics of Microstructured Media and Structures; dell’Isola, F., Eremeyev, V.A., Porubov, A., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 357–369. [Google Scholar]
- Lurie, A.I. Nonlinear Theory of Elasticity; North-Holland: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Rivlin, R. Large Elastic Deformations of Isotropic Materials. IV. Further Developments of the General Theory. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 1948, 241, 379–397. [Google Scholar]
- Truesdell, C.; Noll, W. The Non-Linear Field Theories of Mechanics. In Handbuch der Physik; Flügge, S., Ed.; Springer: Berlin, Germany, 1965; Volume 3, pp. 1–602. [Google Scholar]
- Rivlin, R. Large elastic deformations of isotropic materials. V. The problem of flexure. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1949, 195, 463–473. [Google Scholar]
- Rivlin, R. Large elastic deformations of isotropic materials. VI. Further results in the theory of torsion, shear and flexure. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 1949, 242, 173–195. [Google Scholar]
- Ericksen, J.L. Deformations possible in every isotropic, incompressible, perfectly elastic body. Z. Angew. Math. Phys. ZAMP 1954, 5, 466–489. [Google Scholar] [CrossRef]
- Klingbeil, W.W.; Shield, R.T. On a class of solutions in plane finite elasticity. Z. Angew. Math. Phys. ZAMP 1966, 17, 489–511. [Google Scholar] [CrossRef]
- Truesdell, C. A First Course in Rational Continuum Mechanics; Academic Press: New York, NY, USA, 1977. [Google Scholar]
- Ogden, R.W. Non-Linear Elastic Deformations; Dover: New York, NY, USA, 1997. [Google Scholar]
- Pucci, E.; Saccomandi, G. Universal motions for constrained simple materials. Int. J. Non-Linear Mech. 1998, 34, 469–484. [Google Scholar] [CrossRef]
- Saccomandi, G. Universal Results in Finite Elasticity. Non-linear Elasticity: Theory and Applications. Lond. Math. Soc. Lect. Note Ser. 2001, 283, 97–134. [Google Scholar]
- Saccomandi, G.; Beatty, M.F. Universal Relations for Fiber-Reinforced Elastic Materials. Math. Mech. Solids 2002, 7, 95–110. [Google Scholar] [CrossRef]
- Eremeyev, V.; Lebedev, L.P.; Altenbach, H. Foundations of Micropolar Mechanics; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Lurie, K.A. The problem of effective parameters of a mixture of two isotropic dielectrics distributed in space-time and the conservation law for wave impedance in one-dimensional wave propagation. Proc. R. Soc. A Math., Phys. Eng. Sci. 1998, A454, 1767–1779. [Google Scholar] [CrossRef]
- Lurie, K.A. An Introduction to the Mathematical Theory of Dynamic Materials. In Advances in Mechanics and Mathematics; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2007; Volume 15. [Google Scholar]
- Maugin, G.A. Continuum Mechanics Through the Twentieth Century; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Dorfmann, A.; Ogden, R.W.; Saccomandi, G. Universal relations for non-linear magnetoelastic solids. Int. J. Non-Linear Mech. 2004, 39, 1699–1708. [Google Scholar] [CrossRef]
- Zubov, L.M. Universal deformations of micropolar isotropic elastic solids. Math. Mech. Solids 2016, 21, 152–167. [Google Scholar] [CrossRef]
- Zubov, L.M. Universal Solutions of Nonlinear Dislocation Theory for Elastic Cylinder. Mech. Solids 2020, 55, 701–709. [Google Scholar] [CrossRef]
- Nye, J.F. Some geometrical relations in dislocated crystals. Acta Met. 1953, 1, 153–162. [Google Scholar] [CrossRef]
- Eshelby, J.D. The continuum theory of Lattice Defects. In Solid State Physics; Seitz, F., Turnbul, D., Eds.; Academic Press: New York, NY, USA, 1956; Volume 3, pp. 79–144. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity; Theoretical Physics; Pergamon: Oxford, UK, 1975; Volume 7. [Google Scholar]
- Vakulenko, A.A. The relationship of micro- and macroproperties in elastic-plastic media. Itogi Nauk. Tekh. Ser. Mekh. Deform. Tverd. Tela 1991, 22, 3–54. [Google Scholar]
- Zubov, L.M.; Karyakin, M.I. Tensor Calculus; Vuzovskaya kniga: Moscow, Russia, 2006. (In Russian) [Google Scholar]
- Eremeyev, V.A.; Cloud, M.J.; Lebedev, L.P. Applications of Tensor Analysis in Continuum Mechanics; World Scientific: Hackensack, NJ, USA, 2018. [Google Scholar]
- Goloveshkina, E.V.; Zubov, L.M. Equilibrium stability of nonlinear elastic sphere with distributed dislocations. Contin. Mech. Therm. 2020, 32, 1713–1725. [Google Scholar] [CrossRef]
- Teodosiu, C. Elastic Models of Crystal Defects; Springer: Berlin/Heidelberg, Germany, 1982. [Google Scholar]


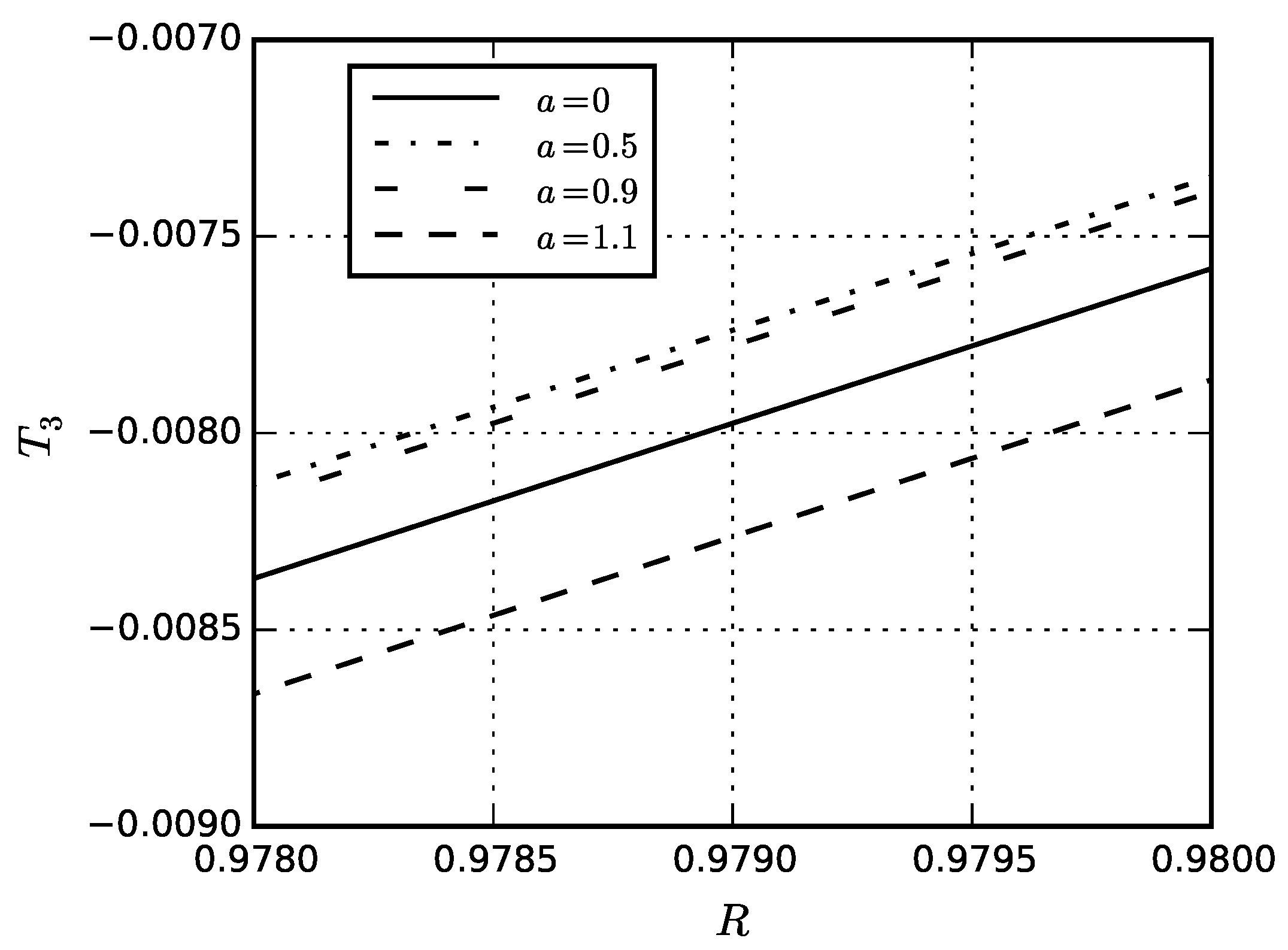


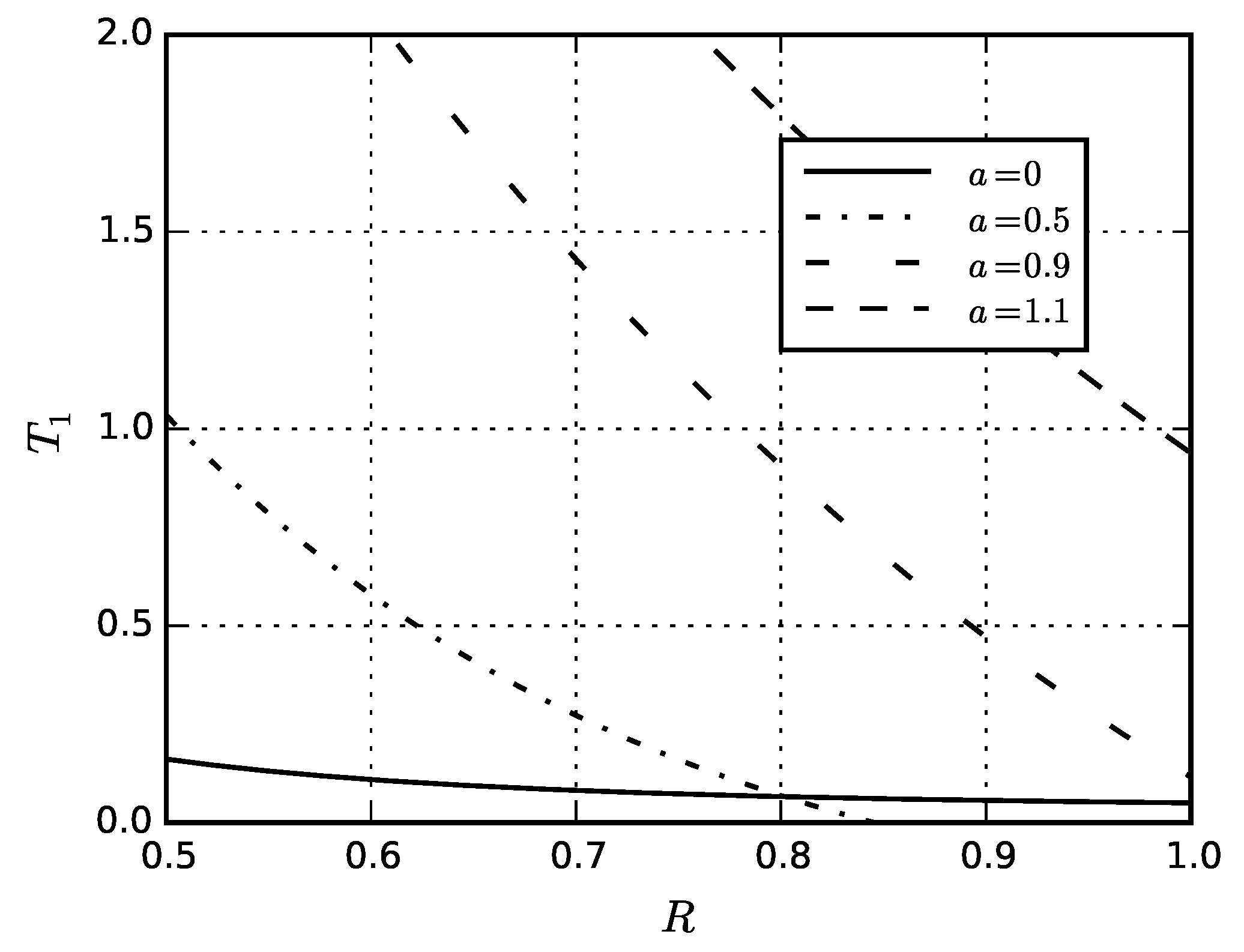
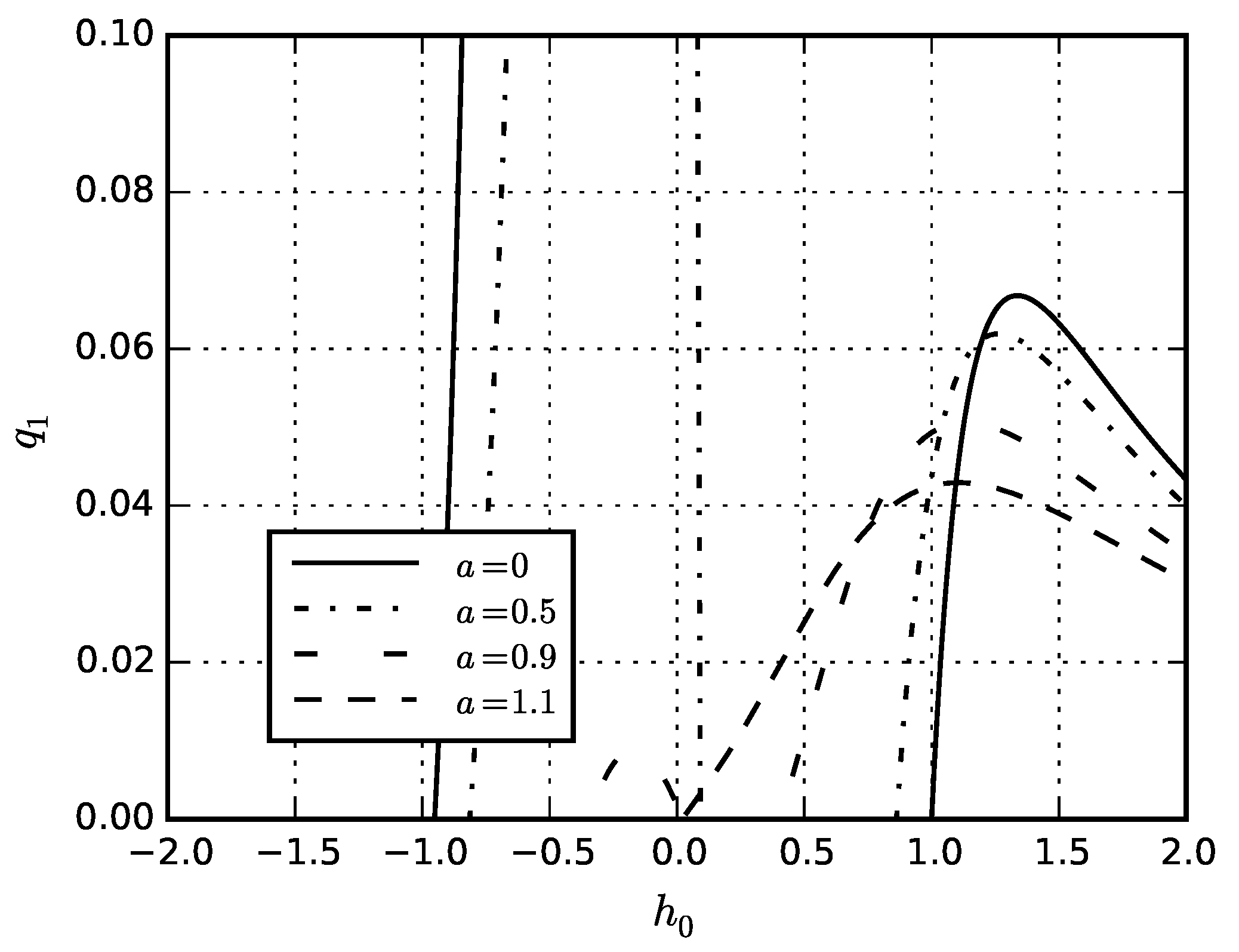
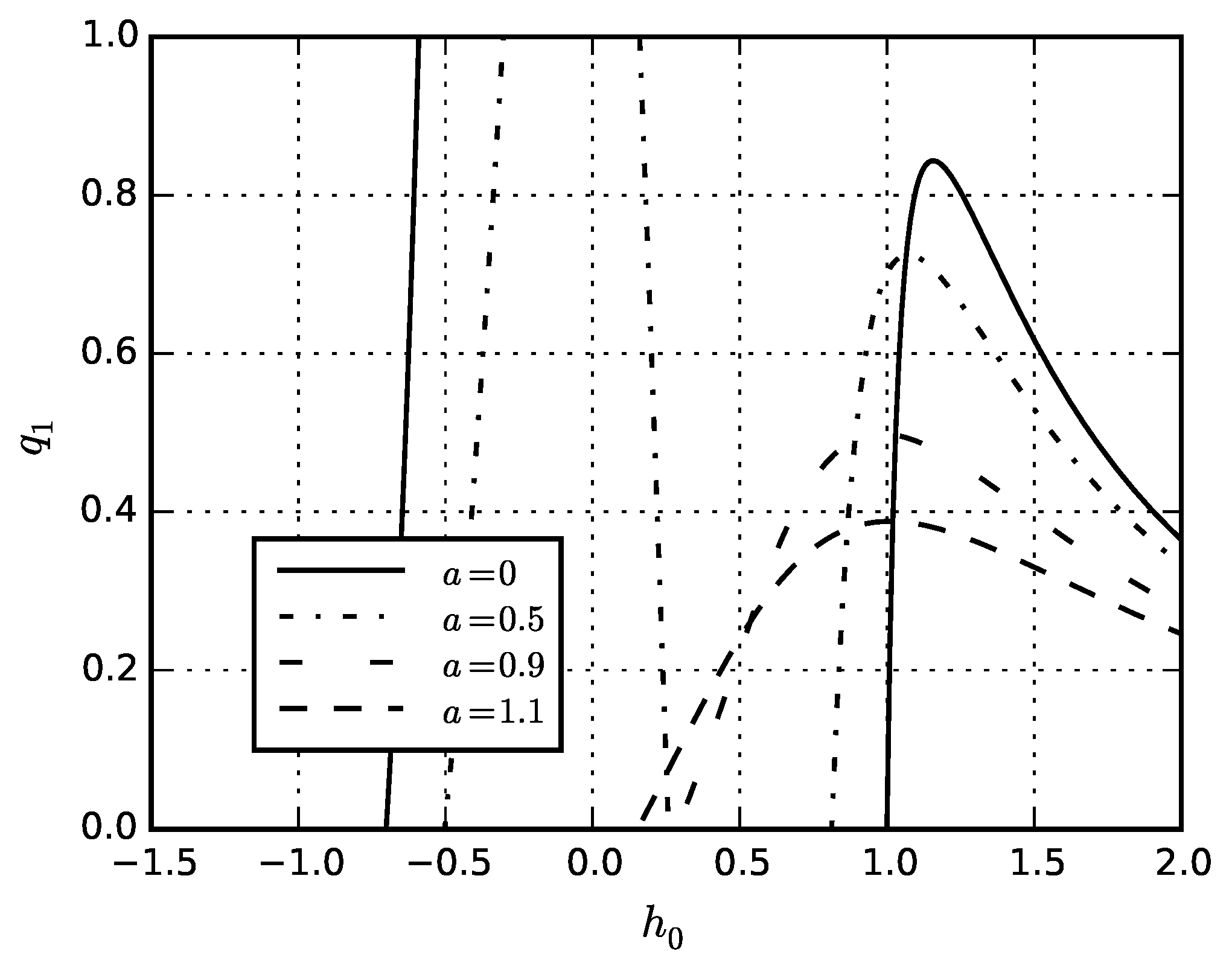




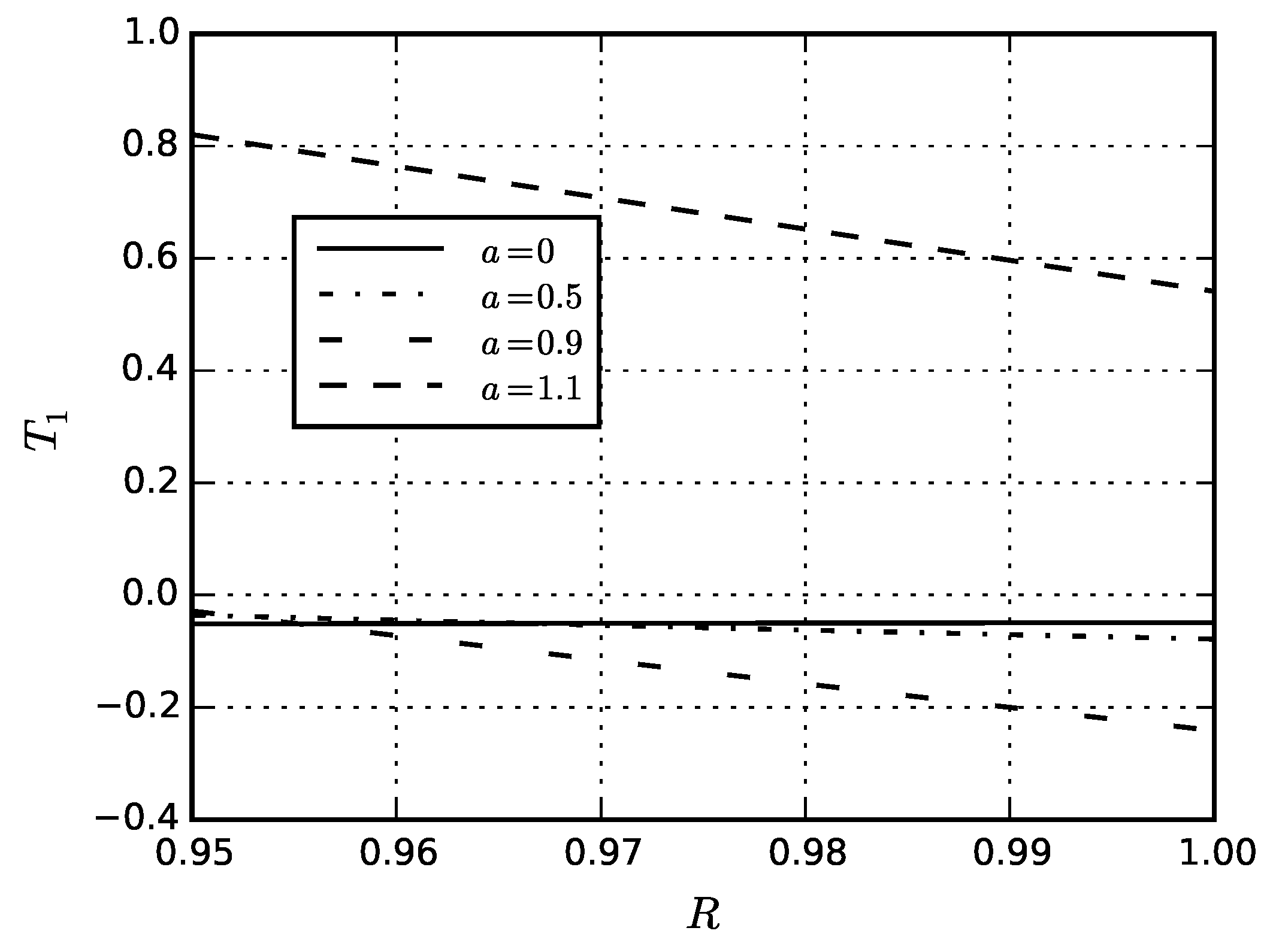
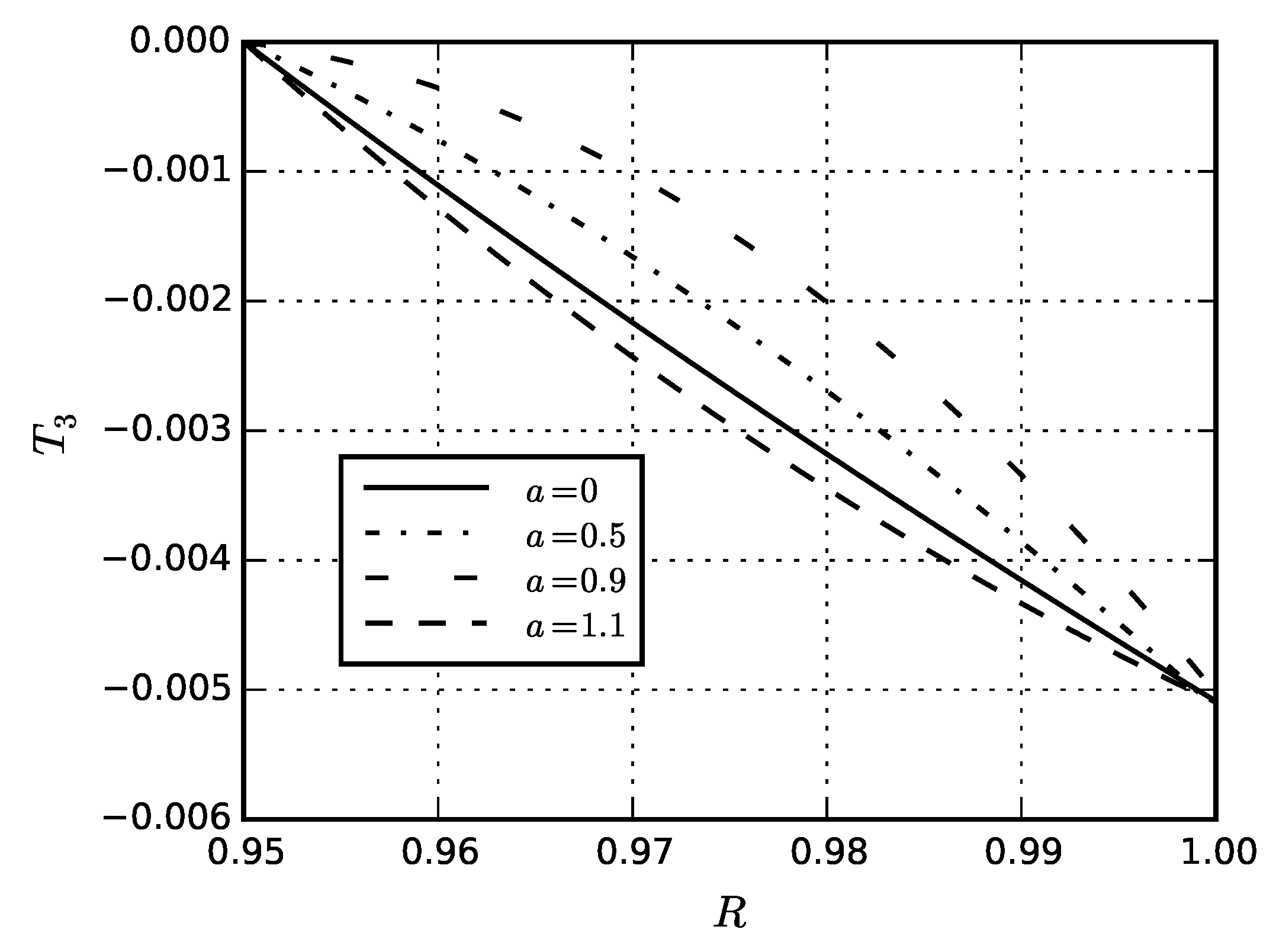
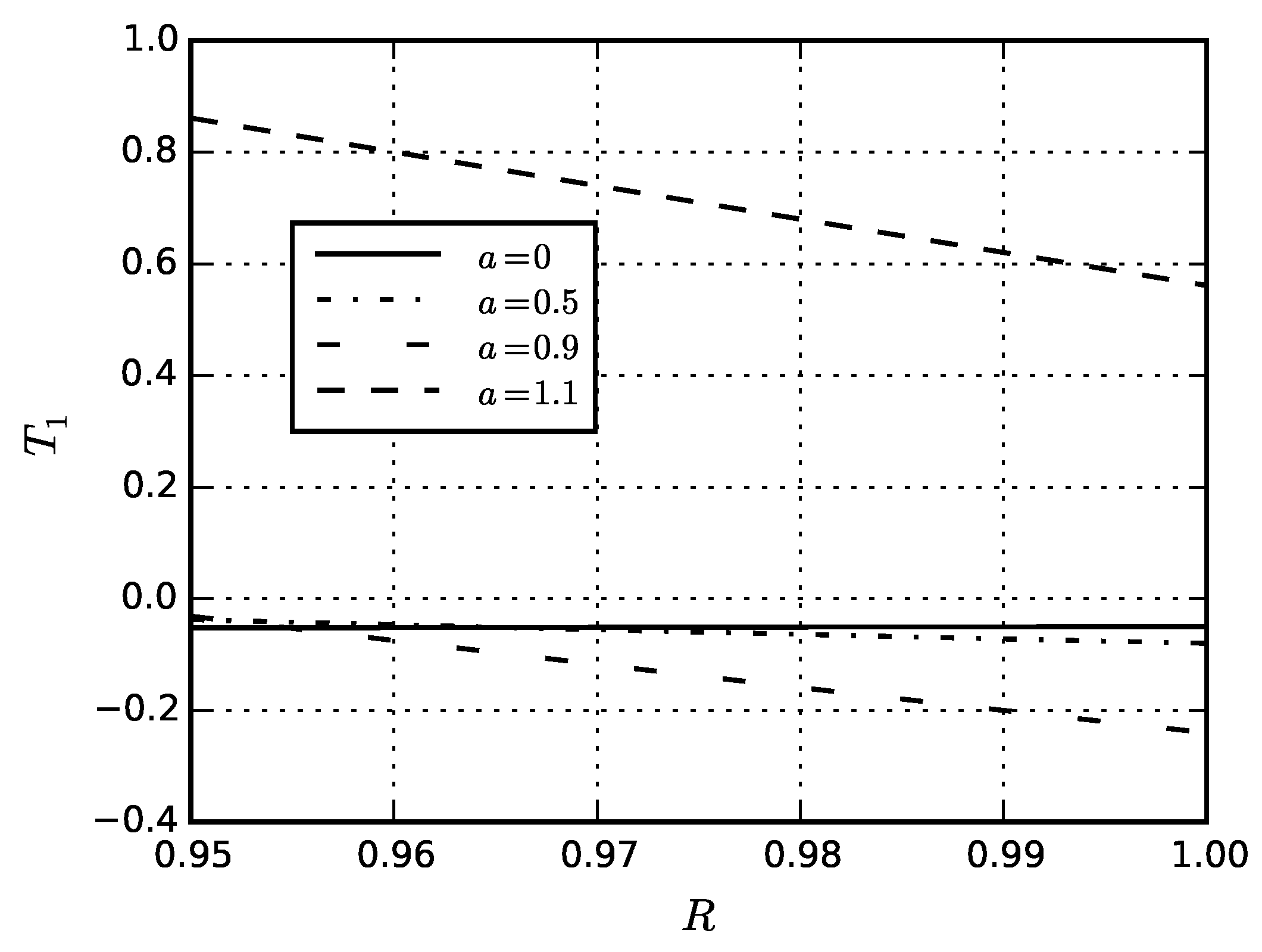
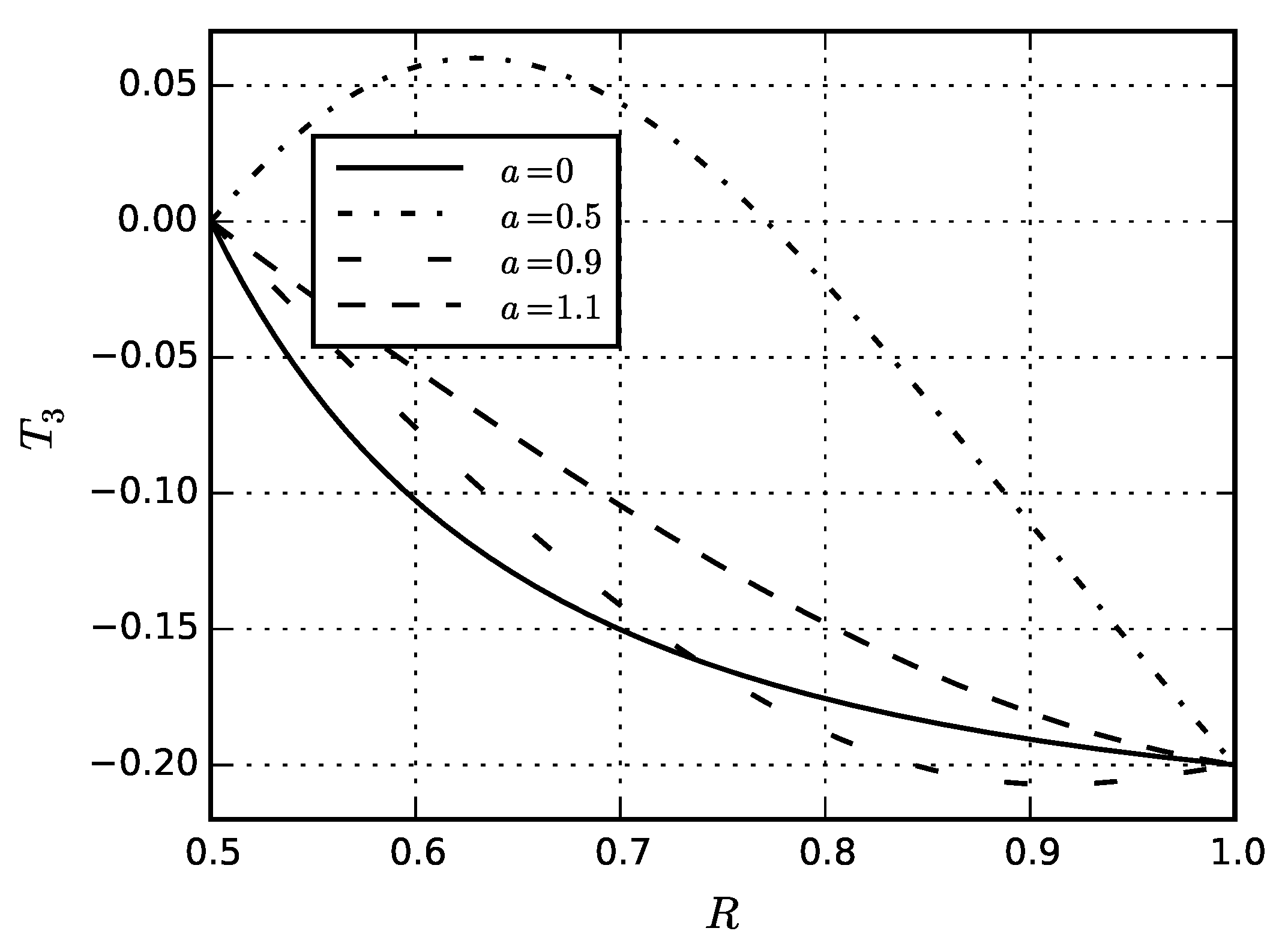

| Material | Thin Shell | Thick Shell |
|---|---|---|
| neo-Hookean Bartenev–Khazanovich | , | , |
| a | ||||
|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 |
| 0 | ||||
| 1 | 0 | |||
| 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goloveshkina, E.V.; Zubov, L.M. Spherically Symmetric Tensor Fields and Their Application in Nonlinear Theory of Dislocations. Symmetry 2021, 13, 830. https://doi.org/10.3390/sym13050830
Goloveshkina EV, Zubov LM. Spherically Symmetric Tensor Fields and Their Application in Nonlinear Theory of Dislocations. Symmetry. 2021; 13(5):830. https://doi.org/10.3390/sym13050830
Chicago/Turabian StyleGoloveshkina, Evgeniya V., and Leonid M. Zubov. 2021. "Spherically Symmetric Tensor Fields and Their Application in Nonlinear Theory of Dislocations" Symmetry 13, no. 5: 830. https://doi.org/10.3390/sym13050830






