1. Introduction
The purpose of this study is to numerically analyze design of manga characters, which are widely used in entertainment field, and to critically review the symbol constructivism model. Currently, virtual agents have been employed for various purposes, such as recommending online shopping sites [
1], providing lifestyle support for patients with dementia [
2], counseling post-traumatic stress disorder patients [
3], and performing music shows as an entertainer [
4]. The fact that the majority of virtual agents have been designed based on Japanese manga and animation is self-evident. However, little research on design features of virtual agents, considering their acceptance level for a particular application, has been conducted. Furthermore, in traditional systems and services, fixed character design is adopted; therefore, users are not allowed to perform customization and their preferences are neglected. In the future, video advertisements created using computer graphics and systems that automatically customize appearances of characters based on preferences of users may become commonly used. In this case, a model that generates character images that match preferences of users would be required.
The database theory derived by Hiroki Azuma, which assumes that grouping elements of a character, such as eyes and ears, are related to their internal characteristics, is widely used as a character configuration model [
5]. Azuma suggested that a character may be created by assembling different grouping elements collected from a database composed of elements of already designed characters, independently of the creativity of the creator or history of the product. To complement this theory, the concepts of “chara,” which are external elements of the character, and “character,” which refers to the biology and otherness generated from the “chara” while considering the product, are introduced [
6]. In this work, these concepts are considered to be completely separable and arbitrarily combinable, and the acceptance of the “chara” by a user occurs when the features of a character are rightly combined. This assumes that no individual aspect in external image of a virtual agent, which is created based on a text, is significant. Komatsu et. al performed an experiment where users estimated internal aspects of virtual agents based on the shapes of their eyes. Consequently, it was shown that most participants could estimate similar internal aspects, partially corroborating the theory derived by Azuma [
7].
In this work, the Azuma hypothesis and Ito et al. models, which assume that the constituent elements of a character are directly related to its internal traits and that the internal image of a character is the sum of the images of its external constituent elements, are also considered, as indicated in
Figure 1. In symbol constructivism, the complexity of the image of a character is only related to the complexity of the combination of elements. Furthermore, the creativity of a creator is defined as the decision process to adopt or reject a combination of elements.
However, Otsuka criticized the theory proposed by Azuma, regarding the creativity definition, by suggesting a structural principle of the external image that was not solely influenced by the complexity of the combinations of elements [
8]. In this paper, based on the hypothesis derived by Otsuka, we attempt to numerically elucidate this principle using the rough set induction bundles method, thereby providing a counter-argument against the symbol constructivism theory.
Currently, personified agents are often designed based on rules of thumb; therefore, firm logical grounds have not been proposed. Verification of the symbol constructivism theory would be important considering entertainment computing because a theory related to the design of virtual personified agents, which are often used as interfaces in this field, would be achieved. This logic could be applied to construct a dynamic casting system in which the design of the virtual agent would be automatically generated based on the preferences of the user. Furthermore, by clarifying the character structure principles in animation and manga, which are closely related to entertainment computing, new potential collaborations between these industries can be developed.
In this work, therefore, we analyzed the relationship between the external image, comprising text information, and the internal image. Visual images (i.e., mental images) generated from text have already been discussed in the field of psychology since the 70s, when the image controversy debate occurred between those on the side of it being a homologous picture with things in the outside world and those considering things in the outside world to be a set of coded propositions.
The theory that suggested that images could be comprehended as picture metaphors was supported by experiments in which three-dimensional figures inside an image were rotated [
9]. This phenomenon could also be explained by the proposition model [
10]. In contrast, based on the dual coding theory, which is related to the mechanism of long-term memory, language and visual images are closely related and are responsible for generating memories, thereby partially supporting both the picture and proposition models [
11].
Considering experiments conducted on images of human faces, Bower and Karlin [
12] showed that memories are more clearly remembered when internal characteristics, which could be felt through a picture, occur than when considering external characteristics. Therefore, it is suggested, at least in case of remembering human faces, that an image may be more clearly remembered with both propositional and language information than with only visual information. The present study considers visual images of characters that appear in text, with picture and propositional qualities related to the imagined internal aspects. These two related qualities that form the image are, thereafter, investigated. Afterwards, we provide an overview of preceding research on characters (virtual personified agents).
Gray et al. proposed a two-dimensional model generated from applying factor analysis to the results of questionnaires for the image held by users about statements explaining humans, animals, and robots [
13]. With this model, the existence of “Agency” and “Experience” axes was espoused. In the case of a human agent, it was concluded, both Agency and Experience values were high. This model and question sheet have been used in various studies, such as analysis of images of individuals by psychiatric patients [
14] and analysis of robot agents regarding human and robot interaction (HRI) and human and agent interaction (HAI) [
15,
16,
17]. Moreover, Takahashi et al. suggested a similar method to propose a biaxial model of “Emotion” and “Intelligence” [
18]. In these studies, agent images generated from text were discussed considerably. However, to the best of our knowledge, no study focusing solely on the human-type agent without considering the external appearance has been conducted.
Matsui and Yamada, in an attempt to create a similar biaxial model, which focus on human-type virtual agents, discussed the importance of the “Reality” and “Familiarity” axes for evaluating impression of a virtual agent [
19].
Several studies have been recently conducted in the HAI field to evaluate the impact on users caused by differences in external appearances of personified agents. Among these studies, gender choice based on the external appearance of the agent has been a focused topic. However, Payne et al. have demonstrated that female users prefer interacting with agents of the same gender whereas male users choose agents of a different gender [
20]. In contrast, Guadagno has shown that each user prefers agents of their own gender [
21]. Meanwhile, Kim et al. revealed that users had an impression of male personified agents being closer to humans than female personified agents [
22]. These discrepancies, in addition to differences in cultural backgrounds, might be affected by the context and text information used by the agent. Moreover, Rossen et al. have shown that skin color is an effective parameter to express racial differences as users apply racial biases toward both actual humans and agents [
23].
These prior works always focused on the appearance itself and considered that whole impression of virtual agent was mere sums of impressions of elements. In this paper, we aimed to focused on the combinations of the elements and show that whole impression of virtual agent/manga character is not mere sums of impressions of elements.
2. Rough Set Induction Bundles
In this study, we use rough set induction bundles, which is a concept advocated by Gunji and Haruna [
24] to explore human cognitive characteristics, to analyze the visual images. Furthermore, this model has already been used for analyzing the cognition of characters appearing in literary works [
25] and ambiguous figures [
26].
Rough set is the set that is described by a pair of sets which give the lower and the upper approximation that are derived by the original set [
27]. This can describe the non-numeric data and inconsistent data. We will describe the mathematical definition in
Appendix A.
The basic properties and numerical definition of bundles and rough sets are discussed in the
Appendix A and source text [
24]. In this method, for a certain set
U, two types of equivalent relationships
R and
K are available. As a result, at first, various bundles, which are not limited to Boolean algebra, and various logical structures occur. These logical structures can be influenced by the world view of the analyst.
Assuming that U is composed of different types of animals, including lions, tigers, artic wolves, pandas, polar bears, and sea otters, a set that captures mapping relationships was desired.
First, we considered a classification composed of the taxonomy of cats, dogs, bears, and weasels, and linked the elements of set U to these elements. Therefore, they could be separated as {lions, tigers}, {Arctic wolf}, {pandas, polar bears}, and {sea otters}. This taxonomy was used to induce an equivalence relationship, R, that could evaluate the similarities of lions with tigers, and pandas with polar bears; therefore, [panda] = {panda, polar bear} = [polar bear] = bears are R’s equivalent class.
Moreover, we can derive a classification model based on habitations, such as {grassland, forest, polar regions, ocean}, and apply these elements to subsets {lion}{tigers, pandas}, {Arctic wolf, polar bears}{sea otters} of set U. Therefore, these elements would be separated based on their habitation induced by the equivalence relationship, K. We can say, therefore, that there is an equivalence relationship K defined as [panda] = {tiger, panda} = [tiger] = forest.
The Boolean algebra obtained from Supplementary Theorem A1 in the
Appendix A has an effect such that, if we fix the equivalence class or lattice elements (structural units for interpreting the world), this equivalence class will be an atom. For example, in relation to
K, this becomes
({lion, tiger}) = {lion, tiger, panda}, and although {lion, tiger} does not becomes an
X satisfying
(
X) =
X, the equivalence class {tiger, panda} is satisfied by
({tiger, panda}) = {tiger, panda}, and this becomes a lattice element.
Hence, we can consider these two equivalence classes as two different interpretations of the world according to the interpreters (set U). Neither of these interpretations is more important, and they have the same significance in understanding the world. Therefore, rather than choosing and considering the lattice, we consider it more appropriate to use these two equivalence classes and take the fixed point related to approximation. This is how Theorem 1 is obtained.
Theorem 1. Let set U be given. There are two equivalence relations R and K on U. Then,are all lattices. These are all the same lattice types and have the same structure (proof by Gunji and Haruna [24]). For example, let us calculate the lattice elements in Formula (
4). As
({sea otter, Arctic wolf}) =
{sea otter, Arctic wolf, polar bear} = {sea otter, Arctic wolf}, {sea otter, Arctic wolf} is a set of lattice elements. Moreover, as
({lion, tiger, panda}) =
{lion, tiger}, the set {lions, tigers} contains lattice elements. In Boolean algebra, the union of two lattice elements also becomes a lattice element. By taking the union of {sea otter, Arctic wolf} and {lions, tiger}, and testing whether it({sea otter, Arctic wolf, lion, tiger}) satisfies the formula, we observe that
({sea otter, Arctic wolf, lion, tiger}) =
{sea otter, Arctic wolf, polar bear, panda, lion, tiger} = {sea otter, Arctic wolf, polar bear, panda, lion, tiger}, and that this is not satisfied.
In this manner, if we calculate the fixed point (unit for interpreting the world) related to approximation based on both interpretations, we observe that generally not all combinations will appear, and the lattice cannot become Boolean algebra.
If we inquire as to whether this is a stable interpretation unit for the two interpretations, we observe that this contradicts the fact that the possible combinations can be used for either interpretation, and that implies that this is excluded. In the case of the previously-described example using animals, let us suppose that you are the head of a zoo, and that you are allocating cages considering taxonomy and habitat. Both {sea otter, Arctic wolf} and {lion, tiger} are interpretation units, and we can summarize and name their zones as oceans, polar regions, or grasslands. However, as all animals come within the zones of oceans, polar regions, or grasslands, in the end we cannot accept the proposal of summarizing as {sea otter, Arctic wolf} and {lion, tiger}.
As shown here, under two interpretations (two same-valued interpretations), several interpretation units are discarded (information is discarded) and the resulting picture of the world is no longer understandable in combination. More specifically, this is exemplified by whether it is possible to see what kind of relationship the lattice properties of the two interpretations have. In a case in which the two interpretations match, as in
Figure 2, i.e., only one type of interpretation can be applied, the resulting lattice becomes a linear lattice (lattice in which an order between all dimensions can be defined). Conversely, applying two different interpretations, as in
Figure 3, results in a nonlinear lattice (lattice including a dimension for which an order cannot be defined). In the latter case, defining an order between dimensions {A} and {C} is not possible. Therefore, observing the obtained lattice shape enables us to evaluate the relationship between the two interpretations.
In the present study, two of either the external appearance or social attributes of the virtual agent generated from the text are defined as two interpretations for the text to derive rough set induction lattices. In other words, we applied two different interpretations to “text sets.”
A lattice obtained in this manner is a lattice for expressing how concepts are merged within human cognition. A lattice with concept sets as elements (different from the “concept lattice” in a lattice theory) is shown in
Figure 4. In this figure, an order between the dimensions surrounded by blue lines can be defined, but an order between the dimensions surrounded by red lines cannot.
This rough set induction lattice has been used to analyze the figure and ground relationships and ambiguity in human recognition. Kitamura et al. [
25] analyzed the figure and ground relationships of characters appearing in literary works using rough set induction lattices. In the present study, to determine the figure and ground relationships in one scene of a literary work, we applied the two interpretations of “appearing character” and “verb” in relation to the text to derive the lattice. Then, in scenes that became turning points in the story, the figure and ground relationships became more stratified. In other words, uniquely determining whether specific characters are “figure” or “ground” is not possible. In Sonoda et al. [
26], the cognition mechanism for ambiguous figures is analyzed using a rough set induction lattice. In the present work, to interpret each of the sections of an ambiguous figure, we derived lattices that provided two interpretations. Consequently, despite the fact that multiple interpretations of an ambiguous figure are possible, a quantifiable relationship can be uniquely determined according to the lattice.
In these preceding studies, properties of the rough set induction lattices derived from the two interpretations are quantified by calculating the “complementarity” and “non-distribution rate.” In a lattice, the upper limit is the maximum whereas the lower limit is the minimum dimension in the lattice, and these two dimensions are defined as having a “complementary relationship.” The total number of dimensions in a complementary relationship and the negative of the total number of dimensions within a lattice are called complementarity, and the negative of the total number of complements and total number of dimensions with complements is called the non-distribution rate [
28]. Using these two notions, the structure of the lattice can be evaluated quantitatively; however, as the number of dimensions increases, these values increase regardless of the structure of the lattice. For this reason, these properties are inappropriate for comparing lattices that have a high number of dimensions. Therefore, in the present study we introduce direct product decomposition as a method of analyzing lattices numerically to evaluate the nature of lattices with a high number of dimensions.
As the numerical definition of direct product decomposition will be described hereinafter, here we provide an intuitive explanation of what we can elucidate using direct product decomposition. In the case of complex lattices, such as that on the left of
Figure 5, information regarding their nature based on complementarity and non-distribution rate is limited. Consequently, we break this lattice down into two or more mutually-independent lattices after saving the order relation. This operation is the direct sum decomposition. In cases in which a lattice can be decomposed into multiple lattices with a single structure, the complexity of a lattice can bring about a large number of elements, but this is nothing more than an appearance issue. Conversely, we can observe that, in cases in which we cannot break down a lattice into lattices having simple structures, as in
Figure 5, this is caused by the existence of dimensions for which the order relation cannot be defined. The fact that order relations cannot be defined for certain dimensions indicates that some element sets are present that cannot be combined. For example, if elements
a and
b cannot be combined in any case,
a and
b constitute dimensions on their own, and as an order relationship cannot be defined between these two dimensions, the lattice is a nonlinear lattice. In other words, performing direct sum decomposition on the lattice enables us to determine what is causing the complexity of the lattice structure.
In the present study, we verify symbol constructivism using this property. As shown provisionally in
Figure 1, it is clear from the discussion thus far that, if symbol constructivism is applied, then there being a one-to-one correspondence between external and internal elements, and these external elements being arbitrarily combined enable us to derive rough set induction lattices from the two interpretations of “external elements” and “internal elements” in relation to manga character mental images; thus, when a direct sum decomposition is performed, only linear lattices can be obtained. Conversely, this shows that, if nonlinear lattices are included in the rough set induction lattices after direct decomposition, “external elements” and “internal elements” cannot be arbitrarily combined, or, in other words, symbol constructivism cannot be performed.
3. Experiment
3.1. Procedure
The experiment was performed in a laboratory with text and images provided on a PC screen. The 30 participants were Japanese, 22 males and 8 females. Their ages were between 18 and 31 years old. The authors obtained informed consent from all participants at the time of the experiment.
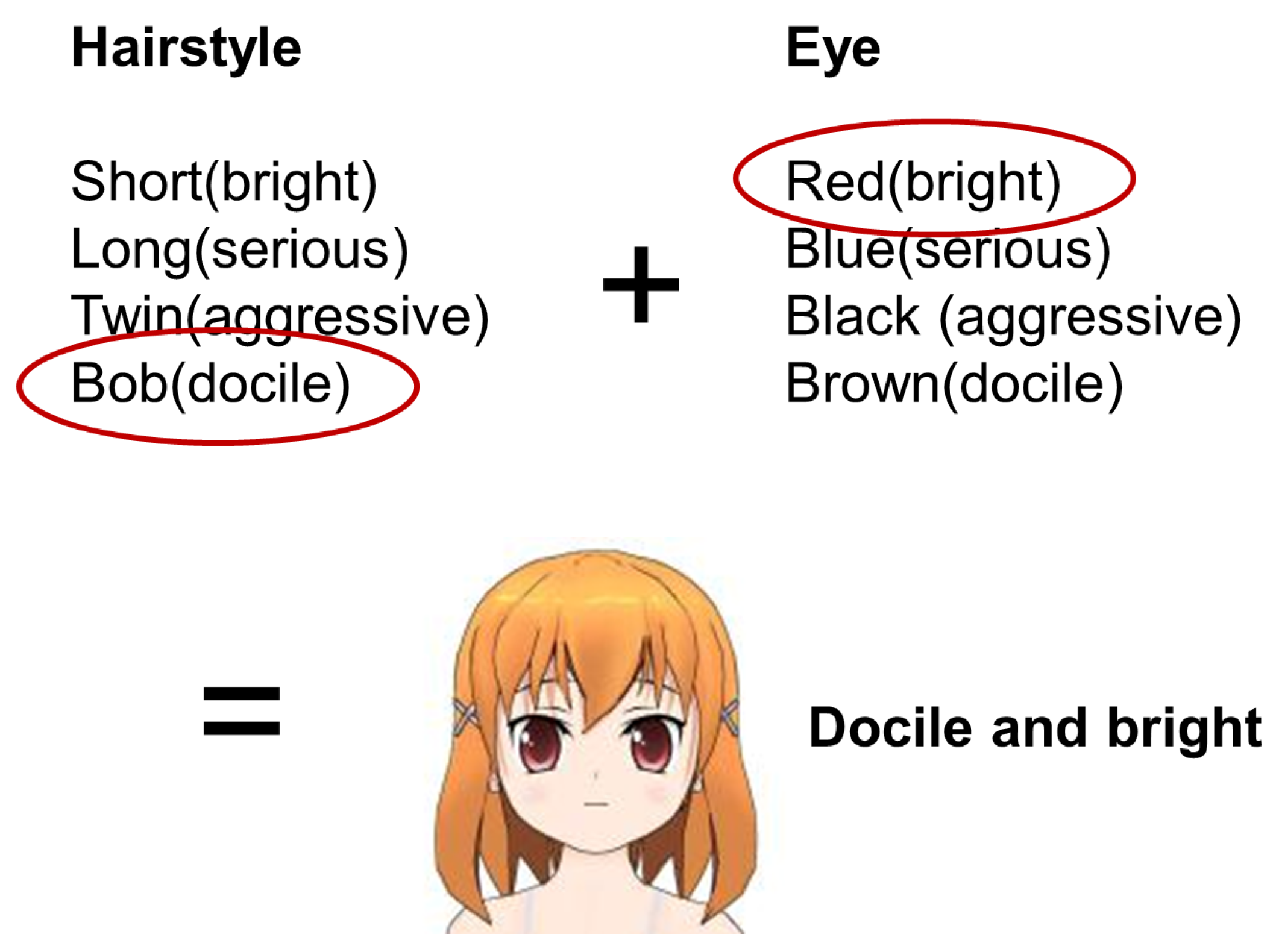
The character pictures used in the experiment were all created using the Web Technology software “Comi Po!” This software enables you to create manga even if you cannot draw pictures, and, by combining parts, such as hair and eyes, for which several varieties were prepared in advance, you can create many characters.
Using this software, we created 40 character pictures. These pictures differed only based on hair style, eyes, and head area accessories and were otherwise the same. The four hair types were short hair, long hair, twin tail, and bob cut. The four eyes types were blue eyes with corners slanting up, blue eyes with corners slanting down, red eyes with corners slanting up, and red eyes with corners slanting down. For head accessories, the four types were having nothing, a ribbon, a headband, and glasses.
Previous research had shown that eyes were perceived to have a deep connection to the internal aspects of a character [
7], and that hair style and accessories were also often used to characterize characters in manga. For this reason, when reviewing the internal aspects conjured up from the external aspects of the character, we considered it appropriate to use these elements.
From the character pictures created by combining the aforementioned parts, we chose four to create one set. At that time, the character pictures included in the same group were chosen to have mutually different hair types, eyes, or accessories. An example of a set created in this manner is shown in
Figure 6. We created ten such sets.
Separately from this, we created ten sections of text depicting fictitious characters. These sections described a short episode involving the character and subjects at which the character excelled, as well as the character’s favorite animal, food, and hobby.
The participants were told that the characters were junior-high school students. A sample of the text is shown below.
Favorite subject: social studies.
Favorite animal: dog.
Favorite food: shortcake.
Hobby: reading.
Even during break time, she reads a book at her own desk and has a quiet personality. However, she clearly has her own personality. She is interested in social issues, and this often makes her angry.
The participants read the text displayed on the PC screen and chose the picture closest to the external image of the manga character conjured up by the text. Next, they chose the club activities that they imagined the character to be participating in, including archery, soccer, art, brass band, or no club. In this way, one picture and club activity was selected for each text. This task was conducted ten times by each participant. As a result, we could prepare different interpretations of pictures and club activities for ten sections of the text.
The purpose of this study was to verify whether through images of characters obtained from arbitrary text, symbol constructivism can be achieved. The content of the text does not necessarily affect the analysis results. Therefore, we just ensured the need for the content of the text to be such that the participant could easily conjure up an image. In the same manner, as the main focus was on verifying the properties of the lattice in the event that rough set induction lattices can be obtained from arbitrary external and internal elements, when setting such elements, we chose attributes and types often seen in animation and manga culture. These selections did not necessarily affect the analysis results.
3.2. Creation of Rough Set Induction Lattices and Direct Sum Decomposition
We created the rough set induction lattices based on these results.
We define multiple interpretations to create lattices, but we first use club activities as interpretations that are strongly linked to the internal elements of the character. Interpretations related to the picture are defined as one interpretation combining three of the above elements. In other words, “combination of hair style and eyes,” “combination of hair style and accessory,” or “combination of eyes and accessory.” Defining the interpretation related to the picture in this manner, considering the diversity of virtual characters makes it self-evident that different external elements, such as “eyes” and “hair style,” can be combined arbitrarily. Therefore, in the present study, we can see the combination of two external elements as one interpretation and verify whether an arbitrary combination is possible. At the same time, we verify differences in the nature of lattices derived in this manner and lattices derived from the two interpretations of club activities and combination with external elements. By selecting two of the four prepared interpretations, we can create one lattice.
Below, we describe the actual method of creating a lattice and method of analysis.
Figure 7 schematically demonstrates the method of creating a lattice in accordance with the interpretation of “club activities” and “hair style and eyes combination” in the experimental results for Participant 1. We show the various text sections from A through J. For convenience, the letters “a” through “e” are assigned to club activities and “f” through “l” to the combinations of hair style and eyes. We have omitted combinations for which not even one character in that combination was selected. Based on this figure, we created the table shown in
Figure 8. In this table, the squares are filled with red, with text that is classified by club activity shown vertically and text that is classified by combination of hair style and eyes shown horizontally.
From this table, we derived the lattices in accordance with the method described in the previous section. Lattices created in this manner have many dimensions, and, as it is difficult to evaluate their nature in this state quantitatively, we performed direct sum decomposition on the mutually-independent lattices, as shown below.
Definition 1.M, N, G, and H are defined as follows: For all , if . For all , if . H, and N are defined in the same manner. This is the two-term direct sum decomposition. The respective lattices are derived from each section resulting from this decomposition. Then, the lattice derived from the table before the separation and each lattice derived from each part after the separation satisfy the following formula. The lattice before separation is the direct product of each lattice after separation.
The two-term relation in the table is divided into multiple parts to satisfy the following formula. Consequently, the direct sum of each decomposed part is the dimension table.
Theorem 2. If the rough set induction lattices derived from each part in Figure 5 are , , and , respectively, they satisfy the relationship,where × indicates the direct product. Here, a, b, that satisfy , , satisfy the Formulas below (+ is the direct sum). Consequently, if the lattice obtained through analysis is not a linear lattice (lattice for which order can be defined between all dimensions) but rather a nonlinear lattice with sets of dimensions for which the order cannot be defined, then elements that cannot be combined within perception are present. Obtaining this kind of lattice demonstrates that the character image can comprise arbitrary combinations.
In other words, this direct sum/direct product decomposition is a process for extracting only mutually related concepts. We showed that, if we can only decompose linear lattices, we can arbitrarily combine elements within each decomposed lattice, and that the decomposed lattice can also be arbitrarily combined. If nonlinear lattices are included in the decomposed lattice, then there will be elements that cannot be arbitrarily combined. Incidentally, Boolean algebra, in which everything can be reduced to atoms, involves a direct product lattice of the simplest linear logic for {0, 1}.
In
Figure 9, using the method described in
Figure 8, we show the method for decomposing the two parts of
) +
) and deriving a lattice from each part. The two lattices on the left of this figure are equivalent to the direct product decomposition, using the above method, of the lattice in
Figure 10, which is the lattice derived from
Figure 8. The elements of the lattice
L) =
L) ×
L) in
Figure 10 are the direct sum of all elements of lattices
L) and
L) in
Figure 9. For example, the relationships in the Formulas (16)–(18) are formed between the element {
a} in the lattice
L) and the element {
c} in the lattice
L) in
Figure 9, and the elements {
a,
c} of the lattice
L) =
L) ×
L) in
Figure 10.
We used visual c++ to construct and describe lattice because this language is suitable for describing Hasse diagram.
5. Observations
Table 1 shows that depending on the combination of text and external elements, a significant bias is shown in the images conjured up from the text for specific patterns. From this, it is clear that the combination of the text and external image conjured up by this is not arbitrary.
According to
Figure 11 and
Figure 12, deriving and decomposing lattices from two interpretations of “club activities” and any of the physical elements results in the ratio of nonlinear lattices included after decomposition being significantly greater than when creating lattices based on two interpretations involving physical elements. Lattices that are not linear include elements for which an order relationship cannot be defined. These results show that for lattices derived from club activities and physical elements, there is a strong possibility that elements for which order relationships cannot be defined even after decomposition will be included. In other words, the complexity of these lattices is not caused solely by the large number of element combinations but results from their having a non-restorable original structure.
This result suggests that “it is possible for the combination of physical elements to be arbitrary, but social attributes, such as club activities, cannot be combined in an arbitrary way.” In other words, when conjuring up an image of the characters from the text, the external and internal images are not independent but restrict each other. This result suggests that the image of the appearing character relies on internal rather than social aspects, and that there is an affinity with propositionalism in the image debate.
It is difficult to say that these results are consistent with the symbol constructivism of Azuma [
5] and Ito [
6], in which the external appearance of the manga character is independently and arbitrarily configurable from the text.
According to the database theory, the elements comprising a character can be combined arbitrarily. Considering this, it should be possible to decompose all of the lattices obtained in this study as linear lattices. However, in reality, lattices which were created from the two interpretations of “club activities” and “physical elements,” we observed a trend for nonlinear lattices with complex structures to remain after decomposition. The result that a lattice cannot be reduced as a consequence of having a large number of element combinations provides counterevidence to the database theory. In contrast, according to the chara/character model, the “chara,” which is the set of physical elements, and the “character,” known by the user based on the activities during creation, are independent. This theory predicts that, in “chara,” the question of how the physical image is linked to club activities can be determined arbitrarily. However, in the present study, we show that lattices cannot be combined freely when they are derived from a physical image and club activities. These results cast doubt on traditional character theory and also provide an important perspective on the process of forming visual images.
This method seems to be able to implement by artificial neural networks and will be able to construct more suitable manga characters automatically.
However, this experiment has some issues. The content of the text used in the experiment was created arbitrarily, and the club activities and physical elements, introduced as interpretations for creating rough set induction lattices, were also selected arbitrarily. Therefore, there might be restrictions in terms of the generality of the results. However, as described in the experiment section, the aim of the experiment was to test whether the mental image of manga characters is not formed by an arbitrary combination of physical elements and social attributes. Based on this objective, the text content, physical elements, and social attributes used for conjuring up the mental image are not the essential problem. As a result, we assume that the results of this experiment are sufficiently general.