Recursively Divided Pancake Graphs with a Small Network Cost

Abstract

Graphs are often used as models to solve problems in computer science, mathematics, and biology. A pancake sorting problem is modeled using a pancake graph whose classes include burnt pancake graphs, signed permutation graphs, and restricted pancake graphs. The network cost is degree × diameter. Finding a graph with a small network cost is like finding a good sorting algorithm. We propose a novel recursively divided pancake (RDP) graph that has a smaller network cost than other pancake-like graphs. In the pancake graph P_n, the number of nodes is n!, the degree is n − 1, and the network cost is O(n²). In an RDP_n, the number of nodes is n!, the degree is 2log₂n − 1, and the network cost is O(n(log₂n)³). Because O(n(log₂n)³) < O(n²), the RDP is superior to other pancake-like graphs. In this paper, we propose an RDP_n and analyze its basic topological properties. Second, we show that the RDP_n is recursive and symmetric. Third, a sorting algorithm is proposed, and the degree and diameter are derived. Finally, the network cost is compared between the RDP graph and other classes of pancake graphs.

1. Introduction

The pancake graphs originated with pancake sorting problems. An n-pancake sorting problem refers to the task of sorting n pancakes of varied sizes piled on a stack. The stacked states are represented as permutations of the set {1, …, n}. The operation of reversing the positions of the pancakes from the top to the k-th pancake is called prefix reversal (flip hereinafter). A flip, therefore, changes the positions of the first k (1 < k ≤ n) pancakes. When sorting is finished, symbol 1 is positioned at the top, and symbol n at the bottom [1]. The solution to this problem is as follows. First, put the largest pancake on the top, and then take it down to the bottom, then repeat this iteration with the rest of the pancakes n − 2 times. Simply put, the number of flips in order to complete the sort in the worst time complexity is 2n − 3. W. Gates suggests a method in which the number of required flips is ≒1.6666n and the lower bound is proved to be ≒1.0625n (n≡0(mod 16)) [2], while B. Chitturi suggests a method in which the number of flips is ≒1.6363n and the lower bound is proved to be ≒1.071n (n ≡ 0(mod 16)) [3].

The n-pancake sorting problem can be represented by the pancake graph P_n. The permutations are mapped to the nodes and flips to the edges. The number of nodes in P_n is n, and the degree is n − 1. The operation that flips the kth pancake is flip_k. In graph theory, the degree of a node is the number of edges incident with the node. The degree of a graph represents the maximum degree of all nodes. The distance between two nodes, u and v, is the number of edges of the shortest path between u and v. The diameter is the maximum distance between all pairs of nodes [4].

Time complexity is a measure used to evaluate sorting algorithms. It refers to the number of times the main operations are performed so that the algorithm can terminate. There are three main operations for sorting the permutations, as is the case for the classes of star or pancake graphs: reversals (flips) that flip the order of symbols, transpositions that move the symbols to other positions, and translocations that exchange two symbols with each other.

Direct comparison of sorting algorithms using these three operations is difficult, because the given main operations all differ. Suppose we are given an arbitrary node, S = s₁s₂s₃ … s_n−2s_n−1s_n. Then, the main operation of a star graph exchanges s₁ and s_k (1 < k ≤ n). However, the main operation of a pancake graph is the flip. The sorting time complexity of a star graph S_n is ≒1.5n, and that of a pancake graph P_n is ≒1.67n [5]. Thus, it is not reasonable to simply compare the time complexities of these algorithms. In an extreme case, if there is a graph wherein all symbols can move to all positions, the time complexity is n − 1. However, it cannot be said that this sorting algorithm is effective. When evaluating time complexity, the number of main operations must also be evaluated.

When a sorting problem is expressed as a graph, the number of main operations is mapped to the degree and the worst time complexity to the diameter. The network cost is degree × diameter. The network cost is the sorting cost of the sorting algorithm. If an edge is added to the graph, the degree increases, and the diameter decreases. Conversely, if an edge is removed, the degree decreases and the diameter increases. These two factors provide a trade-off. Therefore, it is difficult to reduce network costs [6]. The degree of a pancake graph is n − 1, and the network cost is O(n²). We propose an RDP that reduces the degree to O(log₂n) and the network cost to O(log₂n³) by using recursively divided edges.

Pancake-like graphs have been studied for sorting problems [2,3,7,8,9,10], interconnection networks in computer science [11,12,13,14,15,16], and DNA computing models in biology [17,18,19,20,21]. Finding a graph with a small network cost is like a high-performance interconnection network and a good sorting algorithm [22]. The burnt pancake problem involves the sorting of pancakes that are burnt on one side in order of their size. W. Gates proved that the lower bound for the number of flips is 1.5n and the upper bound is 2n + 3 in the sorting of n burnt pancakes [2]. D. Cohen proved that the lower bound for the number of flips (n ≥ 10) is 1.5n and the upper bound is 2n − 2 [23]. V. Bafna introduced research on the sorting permutations to the genes of animals and plants in order to translate between two permutations [24]. P. Berman proposed an algorithm that completes a sort ≒ 1.375n number of flips [17]. A signed permutation by reversal (SBR) is a problem that involves the sorting of permutations that consist of an integer between −n and n, excluding 0. S. Hannenhalli proposed an algorithm in which the upper bound of the number of flips is O(n²) [18]. The result of the research in this paragraph is introduced in [6].

In this paper, we propose an RDP graph that has a lower network cost than pancake-like graphs. In Section 2, the notations used throughout the paper are described, and the RDP is defined. In Section 3, we analyze the properties of the RDP. In Section 4, a sorting algorithm is introduced, and diameters and network costs are analyzed and compared. Finally, Section 5 presents the conclusions.

2. Preliminaries and Definition of Recursively Divided Pancake

This section provides the definitions used in this paper, and a recursively divided pancake RDP_n is described.

An RDP divides the symbols in half and performs a flip operation using edges. These edges are generated recursively. In flip_k, the pancake graph is 1 < k ≤ n. With an RDP, k = n, n/2 + 1, n/2, n/4 + 1, n/4, n/8 + 1, n/8, …, 3, 2. Thus, k divides n recursively.

For a node address of RDP_n, a permutation of natural numbers from 1 to n is used. Let an arbitrary node, S = s₁s₂s₃ … s_k−1s_ks_k+1 … s_n−2s_n−1s_n, exist. Definition 2 defines the flip operation and, in Definition 3, symbol s_k at the kth position is moved to the top. The symbols that should be carefully considered throughout this paper are written in blue.

Definition 1.

s_k is the kth symbol or position k symbol. |S| denotes the number of symbols.

Definition 2.

The flip operation forSis FO_k(S) = s_ks_k−1s_k−2 … s₃s₂s₁s_k+1 … s_n−2s_n−1s_n, k = n, n/2 + 1, n/2, n/4 + 1, n/4, n/8 + 1, n/8,…, 3, 2.

Definition 3.

The moving operation fors_kto thetopis MTF_k(S) =

MTF_k(S) {

 if (|S| == 1) then return

 if (|S|/2 < k) then {

  FO_n

  k = (n − k) + 1

 }

 MTF_k(s₁s₂s₃ … s_n./2)

}

The definition of a recursively divided pancake RDP_n is as follows:

RDP_n = (V, E) | n = 2^m, where m is the natural number.

node V = {s₁s₂s₃ … s_k−1s_ks_{k + 1} … s_n−2s_n−1s_n | 1 ≤ s_k ≤ n, 1 ≤ k ≤n}.

The edges of the RDP_n are defined as follows:

flip edge FE_k = (S, FO_k(S)).

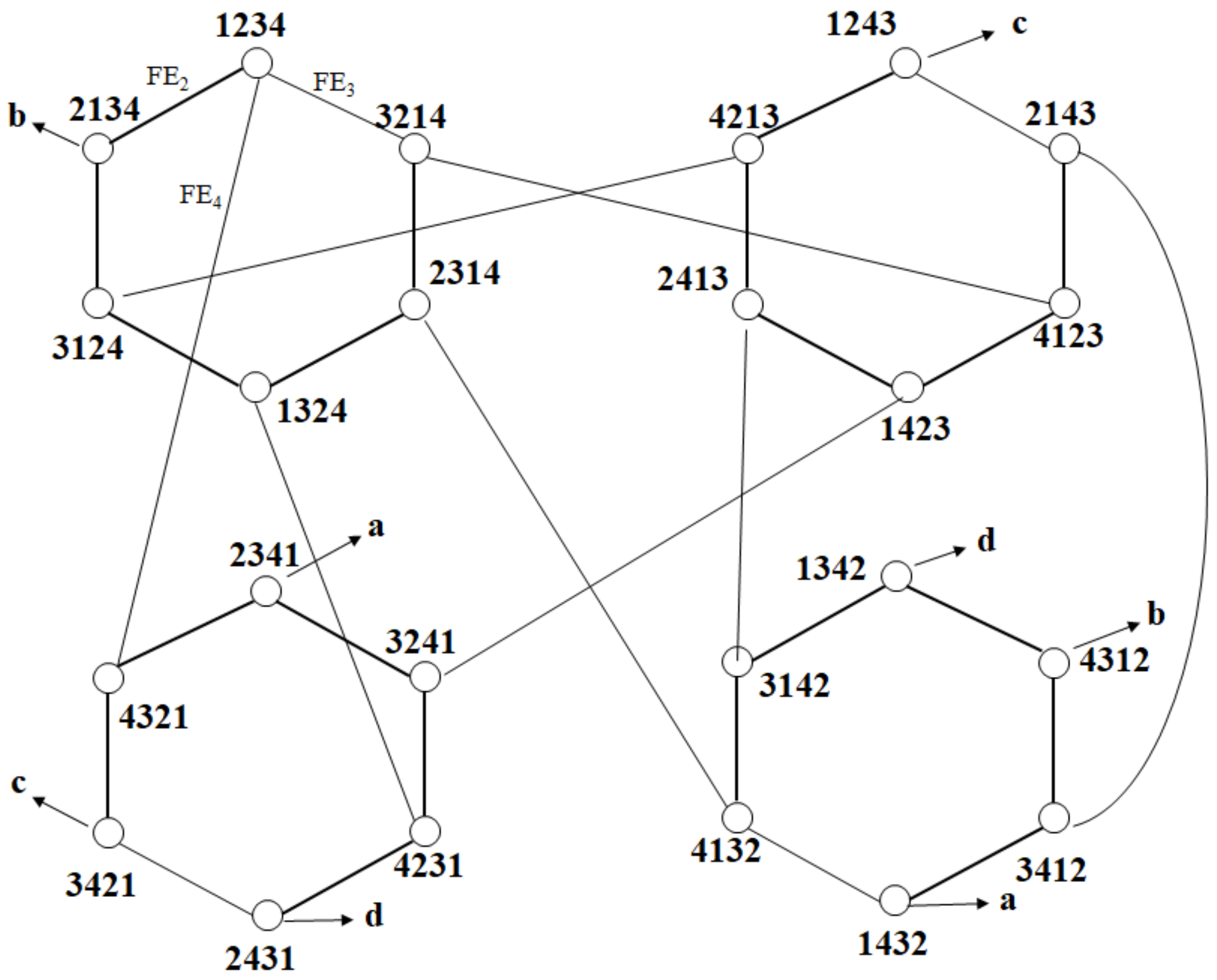
Figure 1 shows RDP₄. The solid lines forming a hexagon are FE₂ and FE₃, and the blue line connecting a hexagon and another hexagon is FE₄.

For example, in RDP₈, the (connecting edge, neighboring node) pairs for node 12345678 are as follows:

(FE₂, 21345678), (FE₃, 32145678), (FE₄, 43215678), (FE₅, 54321678), (FE₈, 87654321).

A path can be expressed as a node sequence from the start node to the destination node. Here, a neighboring node is connected by an edge. The paths are represented as follows:

Notation 1.

→ is used to indicate a path. For example, the paths between 1234, 2134, 3124, and 4213 in Figure 1 can be represented as follows:

1234 → 2134 → 3124 → 4213 or

1234 → FE₂ → 2134 → FE₃ → 3124 → FE₄ → 4213.

3. Topological Properties

In this section, the basic topological properties and the recursive expandability of the RDP are examined. Then, we prove that it is a connected graph.

Theorem 1.

RDP_n is a regular graph with a degree of 2log₂n − 1, and the number of nodes is n!. The number of edges is n!log₂n − 0.5n.

Proof. 

Because the node addresses of RDP_n are permutations of natural numbers from 1 to n, the total number of nodes is n!. The number of edges FE connected to an arbitrary node is 2log₂n − 1. Because every node has the same number of edges, RDP_n is regular, and the degree is 2log₂n − 1. Because it is an undirected graph, the total number of edges is (n! × (2log₂n − 1))/2 = n!log₂n − 0.5n!. □

For a graph to be expanded recursively, two conditions must be satisfied. First, the expansion rules must be consistent. Second, the graph of level n must contain a graph of level n − 1. Recursive graphs are favorable for sorting algorithms, broadcasting algorithms, and algorithms for path problems, because the algorithm at the n − 1 level is used the same way as in an algorithm at level n.

Theorem 2.

RDP_n expands recursively.

Proof. 

First, nodes are examined, after which the edges are explained. Here, |RDP_n| is the number of nodes in RDP_n. In RDP_n, the number of nodes increases as the level increases based on the following method: |RDP₂| = 2. |RDP₄| = |RDP₂| × 3 × 4. |RDP₈| = |RDP₄| × 5 × 6 × 7 × 8. |RDP_n| = |RDP_n/2| × (n/2) + 1 × (n/2) + 2 × (n/2) + 3 × ⋯ × n.

Therefore, |RDP_n| is defined recursively as follows:

|RDP_n| = |RDP_n/2| × (n/2) + 1 × (n/2) + 2 × (n/2) + 3 × ⋯ × n.

Let us now examine the edges. Figure 2 provides arrows to indicate the positions that can be flipped in the node addresses for RDP₂, RDP₄, RDP₈, and RDP₁₆ from left to right. See the red arrows. Even if the level increases, the flip position of the previous level remains intact. In other words, RDP_n maintains the edges of RDP_n−1 as they are. See the green arrows. As the level increases, edges are added at positions n/2 + 1 and n recursively. Therefore, RDP_n expands recursively. □

If all nodes are connected in a graph, it is a connected graph that has a path from an arbitrary node to every other node. A node address is comprised of permutations. If a symbol that forms a permutation can be moved to any position, then all permutations are connected to each other. If a symbol, s₁, can be moved to any other position, those of all positions can also be moved to s₁. This ensures that all symbols can be moved to any position.

Theorem 3. 

RDP_n is a connected graph.

Proof. 

RDP₄ and RDP₈ are examined sequentially, and the graph is generalized for RDP_n. Suppose S = s₁s₂s₃s₄ in RDP₄. s₁ can be moved to any position.

FO₂(S) = s₂s₁s₃s₄, FO₃(S) = s₃s₂s₁s₄, FO₄(S) = s₄s₃s₂s₁.

Therefore, RDP₄ is a connected graph. Suppose S = s₁s₂s₃s₄s₅s₆s₇s₈ in RDP₈. It was shown in RDP₄ that s₁ can move to positions 2, 3, and 4. Here, if FO₈ is added, s₁ moves to positions 5, 6, 7, and 8.

s₈s₇s₆s₅s₁s₂s₃s₄ = FO₈(FO₄(S)).

s₈s₇s₆s₅s₄s₁s₂s₃ = FO₈(FO₃(S)).

s₈s₇s₆s₅s₄s₃s₁s₂ = FO₈(FO₂(S)).

s₈s₇s₆s₅s₄s₃s₂s₁ = FO₈(S).

Therefore, RDP₈ is a connected graph. According to these results, s₁ can move to positions 2, 3, 4, ⋯, n/2 in RDP_n. Here, if FO_n is added, s₁ moves to positions n/2 + 1, n/2 + 2, ⋯, n. Therefore, RDP_n is a connected graph. □

It is well known that a permutation (e.g., a star graph) is a symmetry group [11]. Symmetry groups are automorphic. Because the nodes of RDP_n are permutations, the proof of node transitivity is omitted in the proof of Theorem 4.

Theorem 4.

RDP_n is a symmetric graph.

Proof. 

Only the edge transitivity is proved. Let an arbitrary node be s = s₁s₂s₃ … s_k … s_n−1s_n. The mapping function is f = s₁s₂s₃ … s_k … s_n−1s_n → s₁s₂s₃ … s_k … s_ns_n−1. The mapping function, f, is a bijection, which can be any function that exchanges symbols. The edge, FE_k, is denoted by (s, t). It is shown that f(s) and f(t) are connected to each other.

If s = s₁s₂s₃ … s_k-1s_ks_{k + 1} … s_n−2s_n−1s_n, then t = s_ks_k-1 … s₃s₂s₁s_{k + 1} … s_n−2s_n−1s_n. f(s) = s₁s₂s₃ … s_k-1s_ks_{k + 1} … s_n−2s_ns_n−1, and f(t) = s_ks_k-1 … s₃s₂s₁s_{k + 1} … s_n−2s_ns_n−1. Thus, f(s) and f(t) are connected to FE_k. Therefore, RDP_n is a node- and edge-transitive graph and is symmetric. □

4. Sorting Algorithm and Network Cost Comparison

In this section, we first present a sorting algorithm. Subsequently, the diameter is derived to calculate the network cost. Then, the network cost is compared to that of other pancake-like graphs.

Let us assume that a start node is u, and a destination node is v. A sorting algorithm is a rule that generates a sequence of nodes from u to v. In other words, it changes the address of the start node to that of the destination node by using the flip operator, FO_k. If the destination node v = 1234 … n, then it is a sorting algorithm.

A rough overview of sorting is as follows. First, the symbols of u are divided into two bundles, uf and ur, as shown in Figure 3. Then, symbols 5 and 6 in uf are exchanged with symbols 1 and 2 in ur. When this step is completed, uf and vf comprise the same symbols. This is also true for ur and vr. If the above process is repeated in uf and ur until the number of symbols becomes 1, u will be the same as v.

In the sorting algorithm, <pre-work> defines several factors. In particular, it defines the symbols that should be exchanged between uf and ur. In Figure 3, 56 and 12 are symbols that should be exchanged. Let the start node be u = u₁u₂u₃ … u_k-1u_ku_{k + 1} … u_n−2u_n−1u_n, and the destination node be v = v₁v₂v₃ … v_k-1v_kv_{k + 1} … v_n−2v_n−1v_n. <pre-work>.

In the address of node u, a set uf = {u₁,u₂,u₃, …, u_n/2} and a set ur = {u_n/2+1, … u_n}. In the case of node v, vf = {v₁,v₂,v₃, …, v_n/2} and vr = {v_n/2+1, … v_n}.

Set fdif = {uf} − {vf} and set rdif = {ur} − {vr}. There is a sequential order in fdif and rdif, and the m-th rdif element is written as rdif[m].

In Figure 3, for example, if u = 34561278 and v = 12345678, then uf = {3,4,5,6}, vf = {1,2,3,4}, ur = {1,2,7,8}, and vr = {5,6,7,8}. Here, fdif = {5,6}, rdif = {1,2}, |fdif| = |rdif| = 2, fdif[1] = 5, and fdif[2] = 6.

The sorting algorithm in Algorithm 1 is performed recursively until |uf| = |ur| = 1. The sorting algorithm is as follows: = = is an equality operator, and = is an assignment operator.

Algorithm 1. sorting(u) {

1: if (|u| = =1) return; 2: <pre-work > 3: if (|fdif| > n/4) { 4:  u = u → FOn/2; 5:  <pre-work > 6:  } 7:   exchange(u); 8:  sorting(uf, vf); 9:  u = u → FOn/2; 10:  sorting(uf, vr); 11:  u = u → FOn/2; 12: }

The function exchange() in Algorithm 2 exchanges fdif in uf with rdif in ur. If exchange() is executed once, then there is no additional symbol exchange with uf and ur.

Algorithm 2. exchange(u) {

1: for (m = 1; m ≤ |fdif|; m + +) { 2:   k = fdif[m]; 3:   MTFk(uf); 4:   FOn/2; 5:   FOn; 6:   k = rdif[m]; 7:   MTFk(uf); 8:   FO(n/2) + 1; 9:  } 10: if (|fdif| is odd) FOn; 11: }

The Algorithm 2 exchanges symbols based on the following method.

• Move the first symbol to be exchanged to u₁ via MTF().
• Flip a half through FO_n/2.
• Flip the whole thing through FO_n.
• Move the second symbol to be exchanged to u₁ via MTF().
• Exchange u₁ and u_{(n/2) + 1} with each other through FO_{n + 1}.

The diameter is the distance between the two farthest nodes in the graph. The diameter is an important measure for evaluating a graph, and, in the worst case, it is the sorting time complexity. It represents the software cost when the graph is implemented in a system.

Theorem 5.

The diameter of RDP_n is 0.5n(log₂n)² + nlog₂n.

Proof. 

The diameter analysis is substituted by finding the worst-case time complexity of the sorting algorithm. The number of calls, a, of sorting(u) is called recursively as follows: |u| and |v| are reduced by half each time the function is called, and the function is terminated when the size becomes one. Therefore, a = log₂n. In the worst case, the number of symbols exchanged is b = n/2 when the function is called once in the sorting algorithm. The operations required to exchange two symbols with each other are MTF() and FO, which are performed twice and thrice, respectively. If the number of exchanged symbols is odd, FO is required only once. The number of times MTF() is executed for a symbol is log₂n in the worst case. The number of operations required to exchange the two symbols is c = 2log₂n + 3 + 1.

The diameter, k = a × (bc)/2, where a is the number of times that sorting() is called, and (bc)/2 is the internal time complexity of sorting().

k = a · (bc)/2.
= log₂n · ((n/2 × (2log₂n + 4))/2).
= log₂n · n/4(2log₂n + 4).
= log₂n(0.5nlog₂n + n).
= 0.5n(log₂n)² + nlog₂n

. □

Network cost is an important measure for evaluating graphs.

Table 1. Comparison of network cost with other classes of pancake graphs.

Graph.		No. of Node	Degree	Diameter	Network Cost
pancake	[2]	n!	n − 1	O(5n/3)	≒1.67n2
	[9]			O(18n/11)	≒1.64n2
restricted	[6]	n!	n/2 + 1	O(3.5n)	≒1.7n2
pancake
burnt	[2]	2n × n!	n(n + 1)/2	O(3n/2)	≒0.75n3
pancake	[1]			O(23n/14)	≒0.82n3
restricted	[6]	2n × n!	n/2 + 2	O(4.5n)	≒2.25n2
burnt pancake
signed	[8]	2n × n!	n(n − 1)/2	O(n2)	≒0.5n4
permutation	[10]			O(n1.5)	≒0.5n3.5
RDP		n!	2log2n − 1	O(n(log2n)2)	≒2n(log2n)3

shows the network cost of RDP_n vs. various pancake-like graphs. The diameter and degree of pancake [2,10], restricted pancake [6], burnt pancake [1,2], restricted burnt pancake [6], and signed permutation [8,10] have been presented in a previous study [6]. The network cost is shown by the Big-O notation.

Because O((log₂n)³) < O(n²), RDP is superior to other pancake-like graphs as shown in Table 1 in terms of network cost.

5. Conclusions

Pancake-like graphs are used in various fields wherein network cost is an important evaluation measure. We have provided an RDP that has a smaller network cost than existing pancake-like graphs. In RDP_n, the number of nodes was n!, the degree was 2log₂n − 1, and the diameter was 0.5n(log₂n)² + nlog₂n. The network cost of RDP_n was O((log₂n)³). we propose an RDP that has a lower network cost than pancake-like graphs. The pancake-like graphs have been studied for sorting problems, interconnection networks, and DNA computing models. We hope that RDP will be used as a model to solve problems in various fields. We analyzed the topological properties of the RDP and connected graphs and proposed a more efficient sorting algorithm. It is expected that various algorithms, such as broadcasting, parallel path, spanning tree, and embedding algorithms, can be improved based on this graph in the future. Time complexity is a measure used to evaluate sorting algorithms. It refers to the number of times the main operations are performed so that the algorithm can terminate. I wonder if it is correct to compare sorting algorithms using only time complexity. I think the number of main operations can also be included in the evaluation. I think this idea needs more discussion.