Constraints on Newtonian Interplanetary Point-Mass Interactions in Multicomponent Systems from the Symmetry of Their Cycles
Abstract
1. Introduction and Background
1.1. Previous Theoretical Models of Planetary Interactions
1.2. Purpose and Organization
2. Physical Principles Governing Newtonian Interplanetary Point-Mass Interactions
2.1. Forces, Small and Large
2.2. Conservation Laws in a Frictionless System Involving Small Perturbing Forces
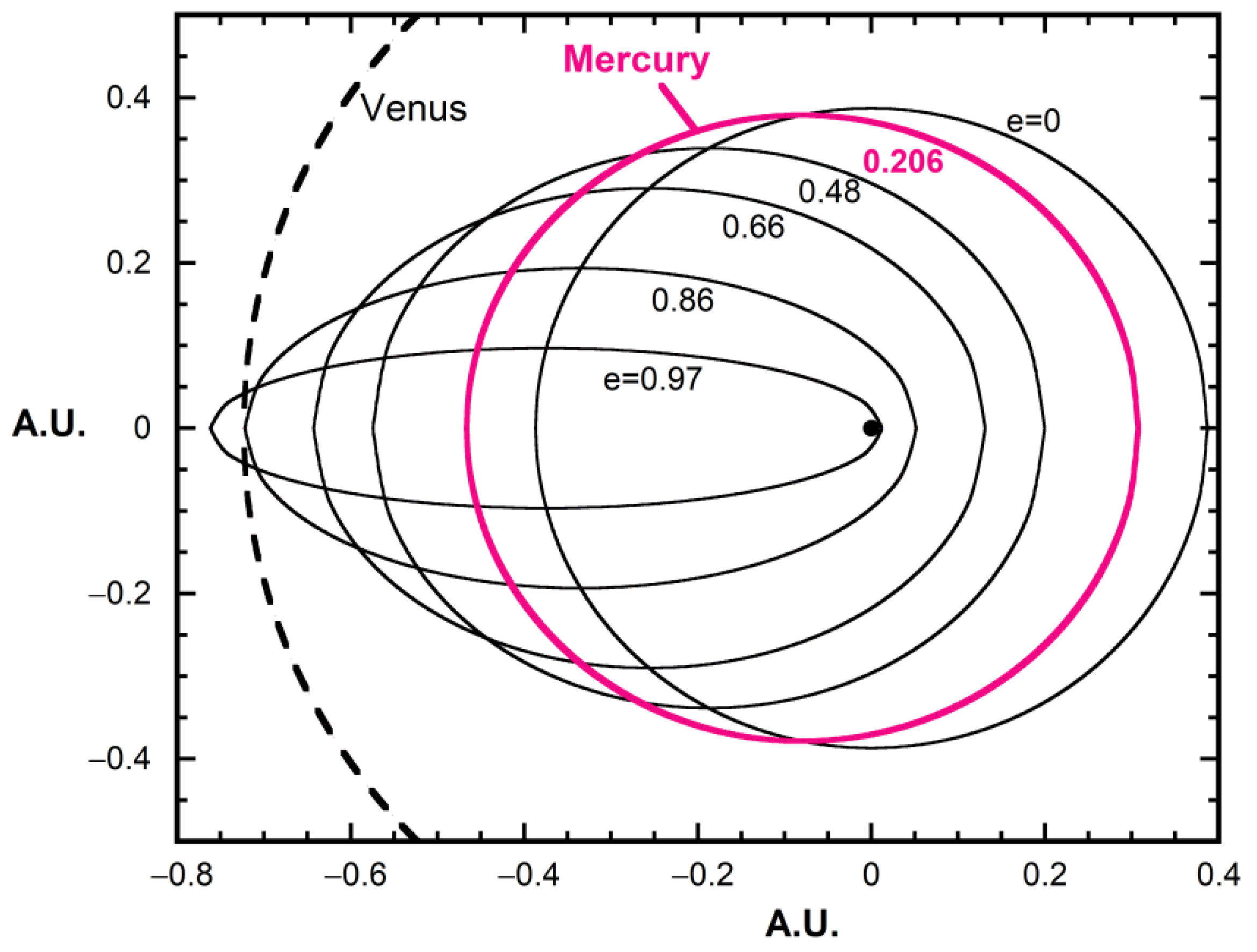
- Orbital eccentricity can change, even under the strong restriction of energy and angular momentum being conserved separately for each closed orbit. This is evident from Equation (4), which is based on the average radius. See [22] for further discussion. Figure 4 shows various possibilities for Mercury.
- Inclinations changing do not affect angular momentum magnitude or energy as this parameter does not enter into the equations for the orbits (Section 2.1). Additionally, any inclination is permitted about the Sun in the Keplerian formulation.
3. Symmetry Constraints on Orbital Evolution Due to Paired Point-Mass Interactions
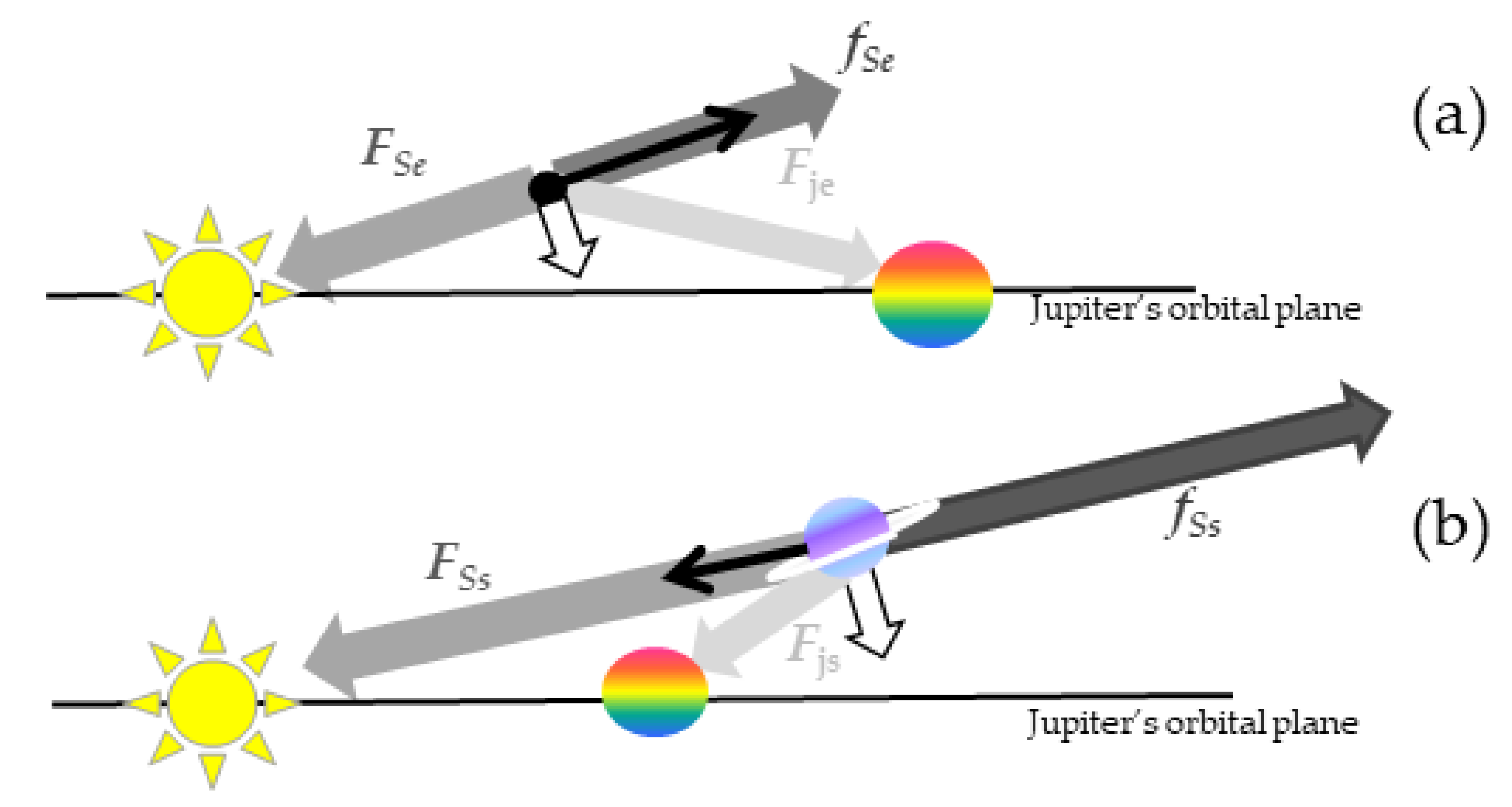
3.1. Motions Induced by Symmetrical, Small Forces during an Interaction Cycle
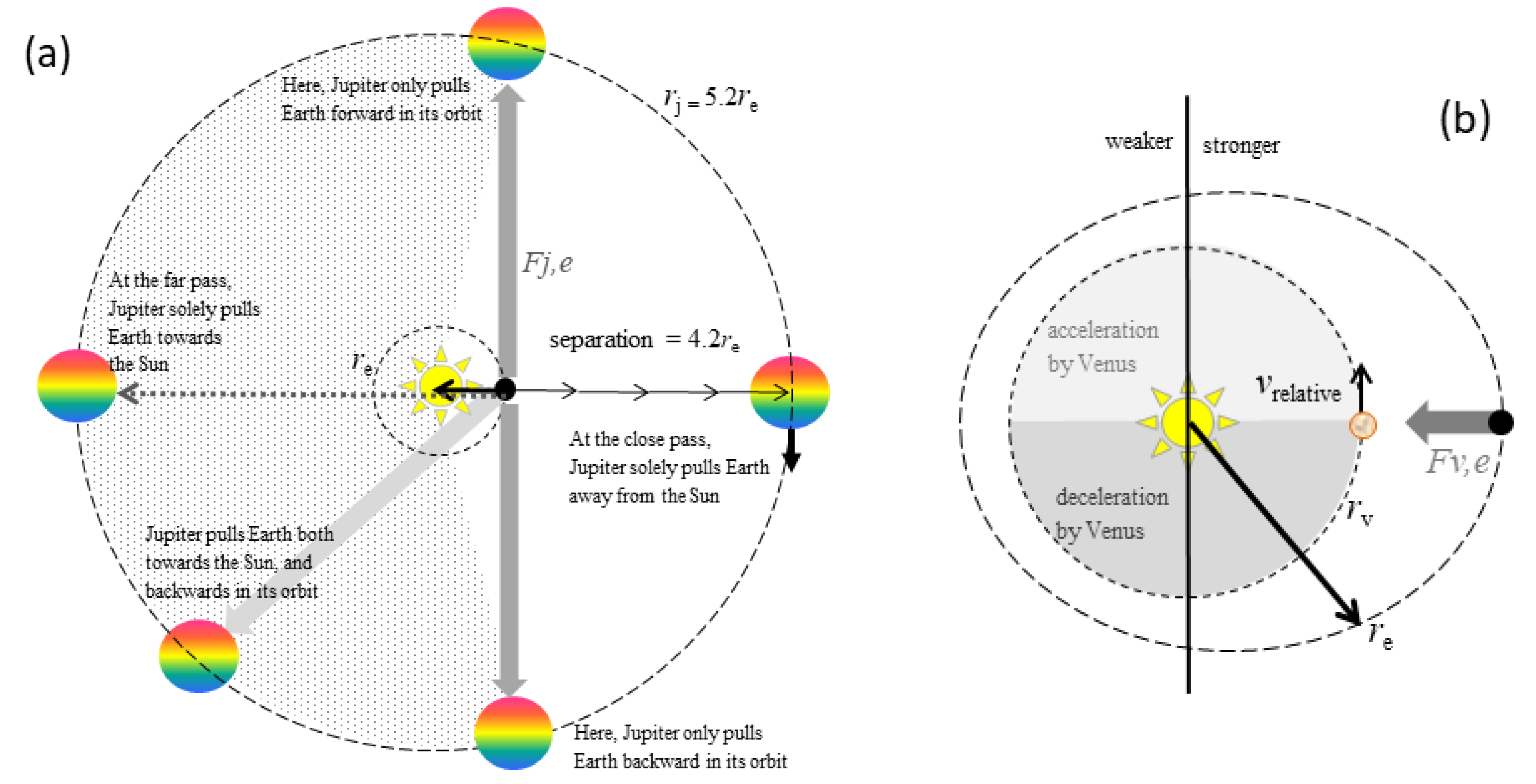
- On average (i.e., over the cycle), the inboard planet of a pair pulls its outboard partner towards the center. Taken at face value, the outboard planet’s orbital radius could contract over the cycle, and conversely the inboard planet’s radius could expand, in accordance with Newton’s third law. However, these radius changes are inferred in view of introducing a perturbing planet (PP). As the Solar System formed essentially simultaneously, the radius of any given planet already accounts for the presence of inboard and outboard mass. Moreover, the conservation requirements of Section 2.2 cannot be met during radius changes of the pair.
- From the symmetry of circular orbits, the faster inboard planet pulls the slower outboard planet forward, and conversely, but only during one half of the interaction cycle (Figure 5b). The converse holds for the other half cycle. As such, tangential forces should sum to zero over an interaction cycle.
- With small forces, the net change in angular momentum over the cycle is null, i.e., angular momentum should be conserved to first order over the interaction cycle. Precession is thus a second-order term in our analytical perturbation model.
- Because angular momentum is a function of Iω, and energy is a function of Iω2, it is not possible to change the energy of an orbit without changing the angular momentum (Iω). Because our model considers only symmetrical perturbations by point-mass interactions, no angular momentum change occurs.
- Changes in eccentricity and inclination angle are permitted (Section 2.2) and thus are the dominant changes.
3.2. Changes in Eccentricity from NIPI and the Effect of Eccentricity on Interactions
3.3. Tilted Orbits Are Continually Torqued
3.4. Summary
4. Numerical Models of Newtonian Interplanetary Point-Mass Interactions
4.1. Numerical Methods
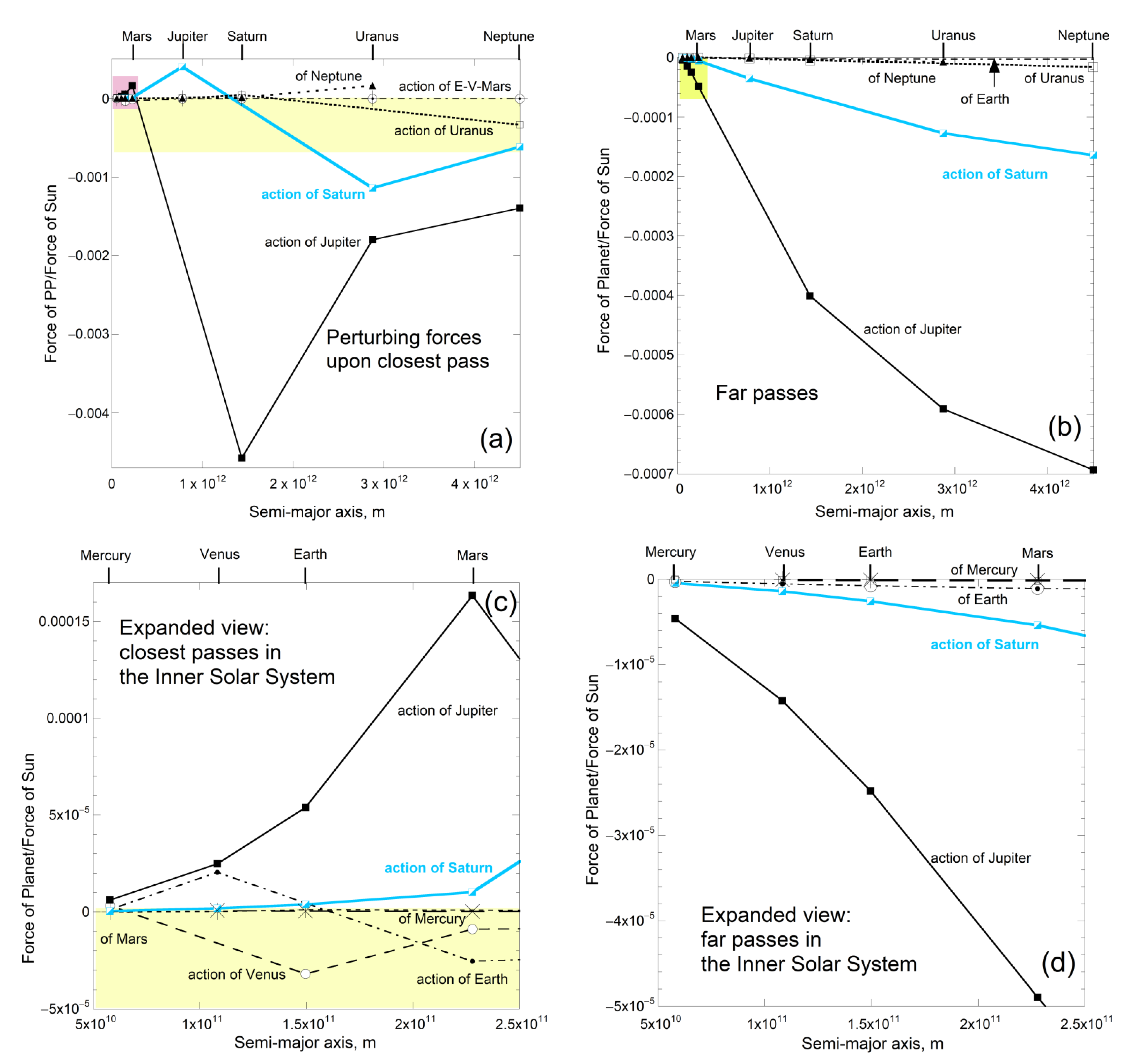
4.2. Perturbation of Mercury by Outboard Planets in Circular Orbits
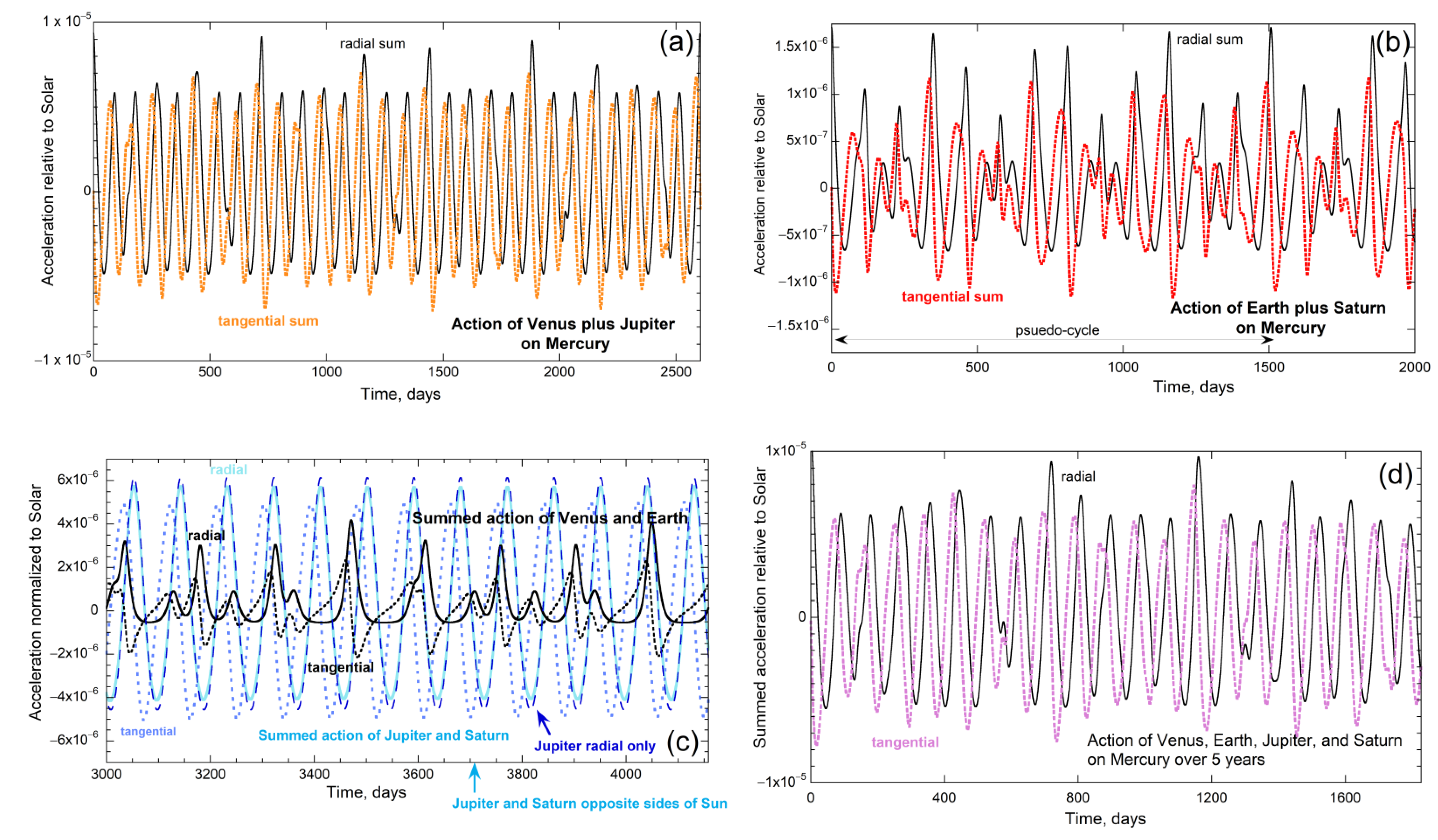
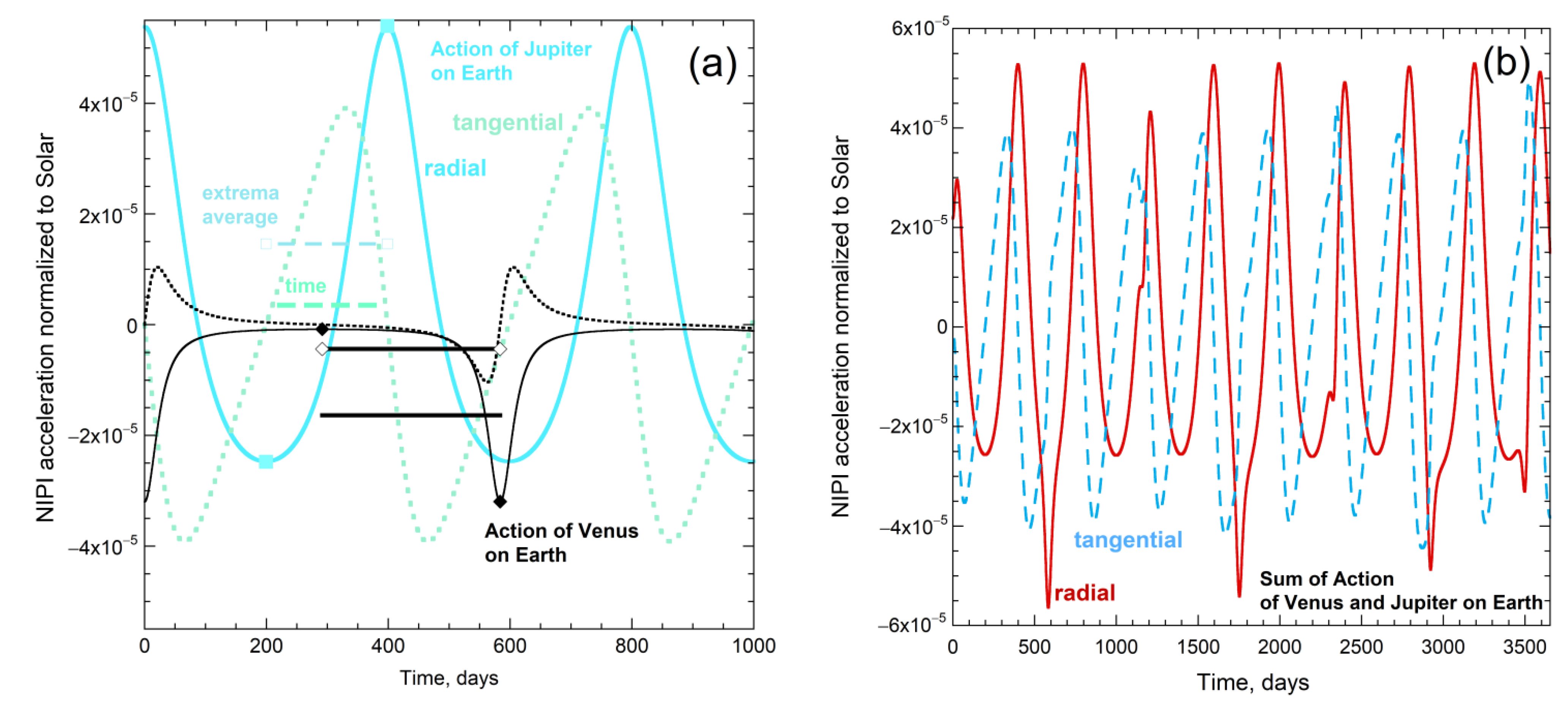
4.3. Sums of NIPI for Mercury Reveal Beat Patterns
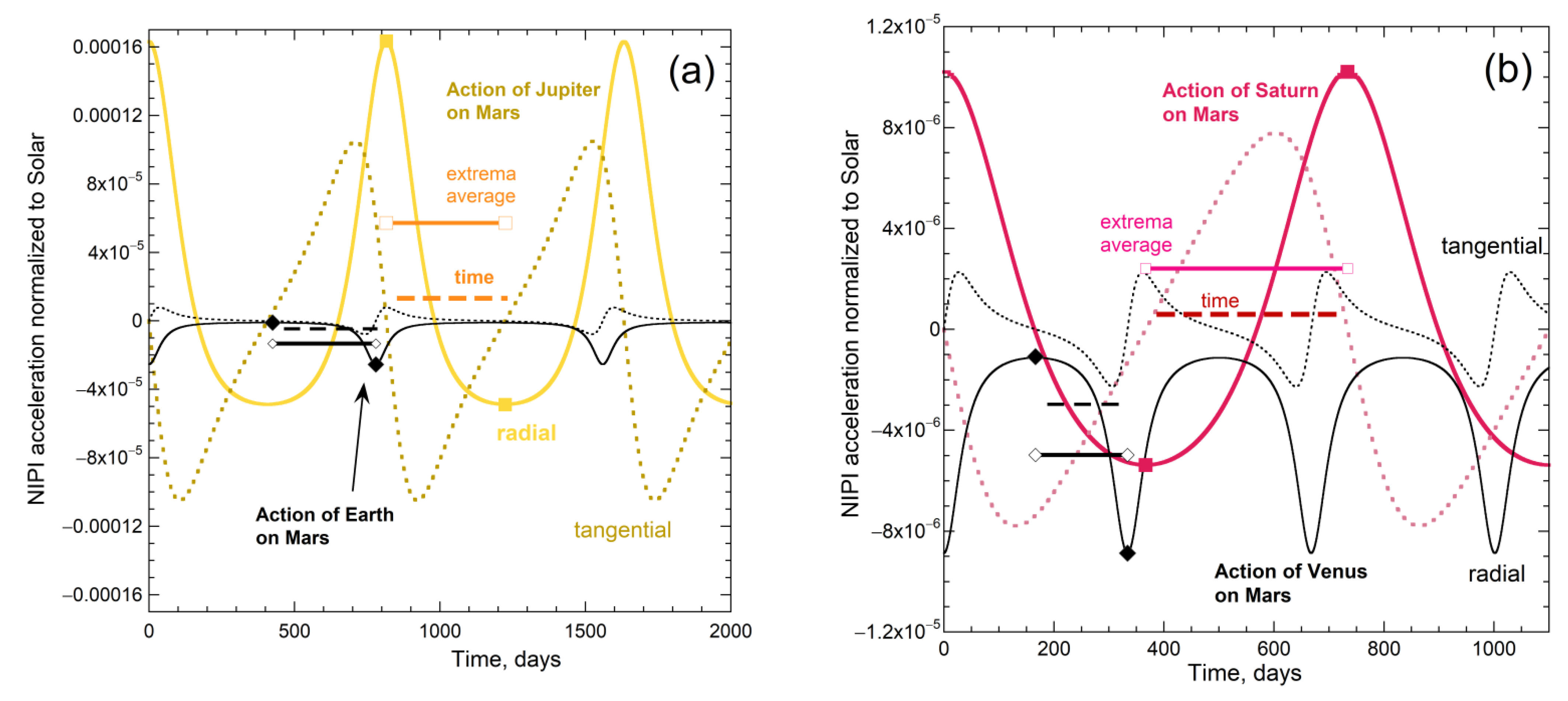
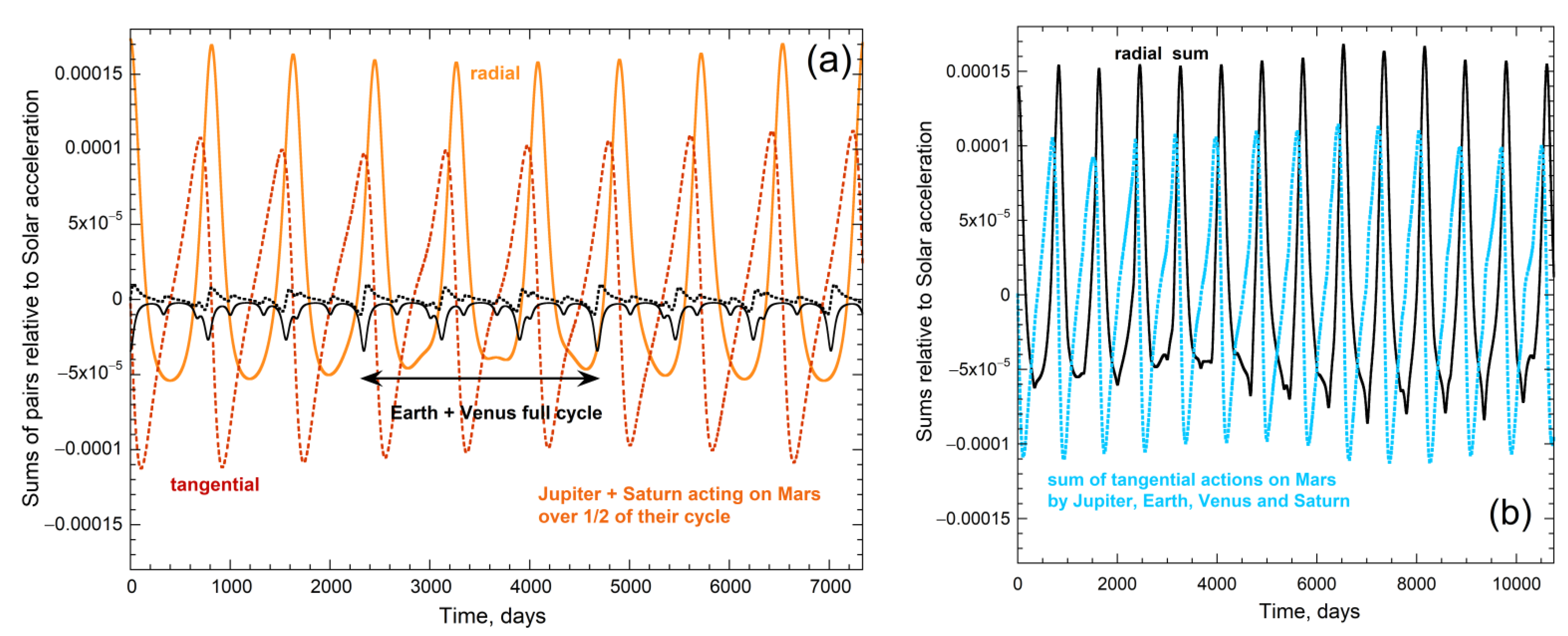
4.4. Competition of Inboard vs. Outboard PP Actions on Mars and on Earth
4.5. Sums Involving Inboard and Outboard PP
5. Discussion
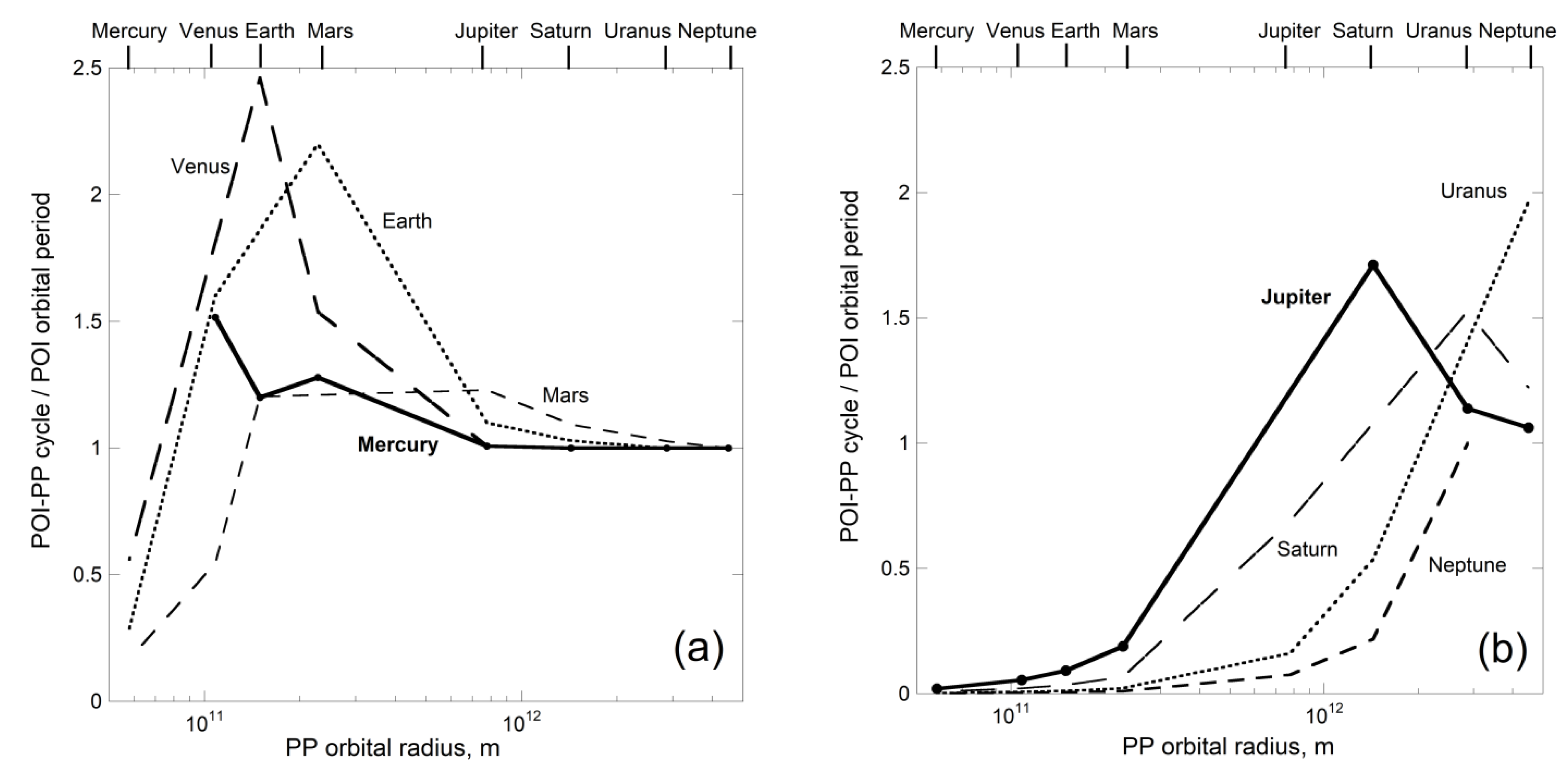
5.1. Consistency of Numerical Results for Accelerations with Geometrical Analyses
- The existence of a perturbing planet changes the perpetual balance of radial pull with centrifugal acceleration of the two-body solution for the POI to a balance over its interaction cycle with the PP.
5.2. Permissible Changes in Orbital Parameters
5.3. Comparison of Model Results with Deduced Basic Orbital Parameters
5.4. Inclinations and Evolution
5.5. Eccentricity and Evolution
- If the pair is composed of a very heavy and a very light planet, the light planet is displaced far more during the elongation.
- If the masses are equal, no elongation is expected. Rather, the planets approach and recede from their center of mass in a balanced fashion.
- From the patterns of radial acceleration (Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12) for a greatly separated pair, the action of the outboard PP approaches sinusoidal, so the inboard POI oscillates in its orbit, rather than elongation occurring. Due to symmetry, the same holds for its partner.
5.6. Precession of the Spinning Earth
6. Conclusions and Implications
- Hill’s steady-state ring model is inapplicable.
- Observational data are not only influenced by the geocenter’s peculiar orbital path around the Sun, but more importantly represent incomplete cycles of interplanetary interactions.
- Mercury’s orbit is Keplerian, within the uncertainties of short-term observational data. Adding a relativistic correction is not supported by the existing data. Such corrections should be applied only after observational data are corrected for Earth’s non-Keplerian orbit, and precession models based on transient planetary interactions are considered.
- Conservation laws and the Virial theorem set stringent limits on the evolutionary behavior of the eight planets. Only eccentricity and inclination can change, as long as the interplanetary forces are small compared with Solar (<2%), which is met today.
- The pair Jupiter–Saturn merits closer examination, as these are the most strongly interacting planets.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Simon, J.L.; Bretagnon, P.; Chapront, J.; Chapront-Touze, M.; Francou, G.; Laskar, J. Numerical expressions for precession formulae and mean elements for the Moon and the planets. Astron. Astrophys. 1994, 282, 663–683. [Google Scholar]
- Chapront, M.; Chapront-Touzé, M.; Francou, G. A new determination of lunar orbital parameters, precession constant and tidal acceleration from LLR measurements. Astron. Astrophys. 2002, 387, 700–709. [Google Scholar] [CrossRef]
- Ford, D. Solar System Orrery. Available online: https://in-the-sky.org/solarsystem.php (accessed on 15 July 2018).
- Hofmeister, A.M.; Criss, R.E.; Criss, E.M. Link of Planetary Energetics to Moon Size, Orbit, and Planet Spin: A New Mechanism for Plate Tectonics. In In the Footsteps of Warren B. Hamilton: New Ideas in Earth Science (Geological Society of America Special Paper 553); Foulger, G.F., Jurdy, D.M., Stein, C.A., Hamilton, L.C., Howard, K., Stein, S., Eds.; Geological Society of America: Boulder, CO, USA, 2021; in press. [Google Scholar] [CrossRef]
- Price, M.P.; Rush, W.F. Nonrelativistic contribution to Mercury’s perihelion precession. Am. J. Phys. 1979, 47, 531–534. [Google Scholar] [CrossRef]
- Hofmeister, A.M.; Criss, R.E.; Criss, E.M. Verified solutions for the gravitational attraction to an oblate spheroid: Implications for planet mass and satellite orbits. Planets Space Sci. 2018, 152, 68–81. [Google Scholar] [CrossRef]
- Gauss, C.F. Determinatio Attractionis Quam in Punctum Quodvis Positionis Datae ejus Massa per Totam Orbitam Ratione Temporis quo Singulae Partes Describuntur Esset Dispertita. In Werke; Königlichen Gesellschaft der Wissenschaften: Göttingen, Germany, 1866; Volume 3, pp. 331–357. Available online: http://resolver.sub.uni-goettingen.de/purl?PPN235999628 (accessed on 7 May 2021). (In Latin)
- Hill, G.W. On Gauss’s method of computing secular perturbations, with an application to the action of Venus on Mercury. Astron. Pap. Am. Eph. Naut. Alm. 1882, 1, 315–362. [Google Scholar]
- Hill, G.W. The secular perturbations of the planets. Am. J. Math. 1901, 23, 317–336. [Google Scholar] [CrossRef]
- Doolittle, E. The secular variations of the elements of the orbits of the four inner planets computed for the epoch 1850.0 G.M.T. Trans. Am. Philic Philos. Soc. 1912, 22, 37–189. [Google Scholar] [CrossRef]
- Clemence, G.M. The relativity effect in planetary motions. Rev. Mod. Phys. 1947, 19, 361–364. [Google Scholar] [CrossRef]
- Park, R.S.; Folkner, W.M.; Konopliv, A.S.; Williams, J.G.; Smith, D.E.; Zuber, M.T. Precession of Mercury’s perihelion from ranging to the MESSENGER spacecraft. Astron. J. 2017, 153, 121. [Google Scholar] [CrossRef]
- Kellogg, O.D. Foundations of Potential Theory; Dover Publications: New York, NY, USA, 1953. [Google Scholar]
- Criss, R.E.; Hofmeister, A.M. Density profiles of 51 galaxies from parameter-free inverse models of their measured rotation curves. Galaxies 2020, 8, 19. [Google Scholar] [CrossRef]
- Planetary Factsheets. Available online: https://nssdc.gsfc.nasa.gov (accessed on 1 July 2018).
- Cornbleet, S. Elementary derivation of the advance of the perihelion of a planetary orbit. Am. J. Phys. 1993, 61, 650–651. [Google Scholar] [CrossRef]
- Stewart, M.G. Precession of the perihelion of Mercury’s orbit. Am. J. Phys. 2005, 73, 730–734. [Google Scholar] [CrossRef]
- Lo, K.-H.; Young, K.; Lee, B.Y.P. Advance of perihelion. Am. J. Phys. 2013, 81, 695–702. [Google Scholar] [CrossRef]
- Treschman, K.J. Recent astronomical tests of general relativity. Int. J. Phys. Sci. 2015, 10, 90–105. [Google Scholar]
- Friedman, Y.; Steiner, J.M. Predicting Mercury’s precession using simple relativistic Newtonian dynamics. Eur. Phys. Lett. 2016, 113, 39001. [Google Scholar] [CrossRef][Green Version]
- Hofmeister, A.M.; Criss, R.E. Spatial and symmetry constraints as the basis of the virial theorem and astrophysical implications. Can. J. Phys. 2016, 94, 380–388. [Google Scholar] [CrossRef]
- Hofmeister, A.M.; Criss, R.E. Origin of HED meteorites from the spalling of Mercury: Implications for the formation and composition of the inner planets. In New Achievements in Geoscience; Hwee-San, L., Ed.; InTech: London, UK, 2012; pp. 153–178. Available online: http://www.intechopen.com/articles/show/title/the-case-for-hed-meteorites-originating-in-deep-spalling-of-mercury-implications-for-composition-and (accessed on 7 May 2021).
- Newcomb, S. Secular variations of the orbits of the four inner planets. Astron. Pap. Amer. Ephemer. 1895, 5, 98–297. [Google Scholar]
- Clemence, G.M. The motion of Mercury 1765–1937. Astron. Pap. Am. Ephemer. 1943, 11, 1–224. Available online: https://catalog.hathitrust.org/Record/000068403 (accessed on 9 July 2018). [CrossRef]
- Standish, E.M., Jr. The observational basis for JPL’s DE 200, the planetary ephemerides of the Astronomical Almanac. Astron. Astrophys. 1990, 233, 255–271. [Google Scholar]
- Morgan, H.R. The Earth’s perihelion motion. Astron. J. 1945, 51, 127–129. [Google Scholar] [CrossRef]
- Sobchak, P. Schematic of the Lunar Plane. Available online: https://commons.wikimedia.org/wiki/File:Lunar_Orbit_and_Orientation_with_respect_to_the_Ecliptic.tif (accessed on 5 July 2018).
- van den Bergh, G. Periodicity and Variation of Solar (and Lunar) Eclipses; H.D.·Tjeenk Willink and Zoon N.V.: Haarlem, The Netherlands, 1955. [Google Scholar]
- van Ghent, P. A catalogue of Eclipse Cycles. Available online: http://www.staff.science.uu.nl/~gent0113/eclipse/eclipsecycles.htm (accessed on 6 August 2018).
- Espenak, F. Eclipses and the Saros. Available online: https://eclipse.gsfc.nasa.gov/SEsaros/SEsaros.html (accessed on 6 August 2018).
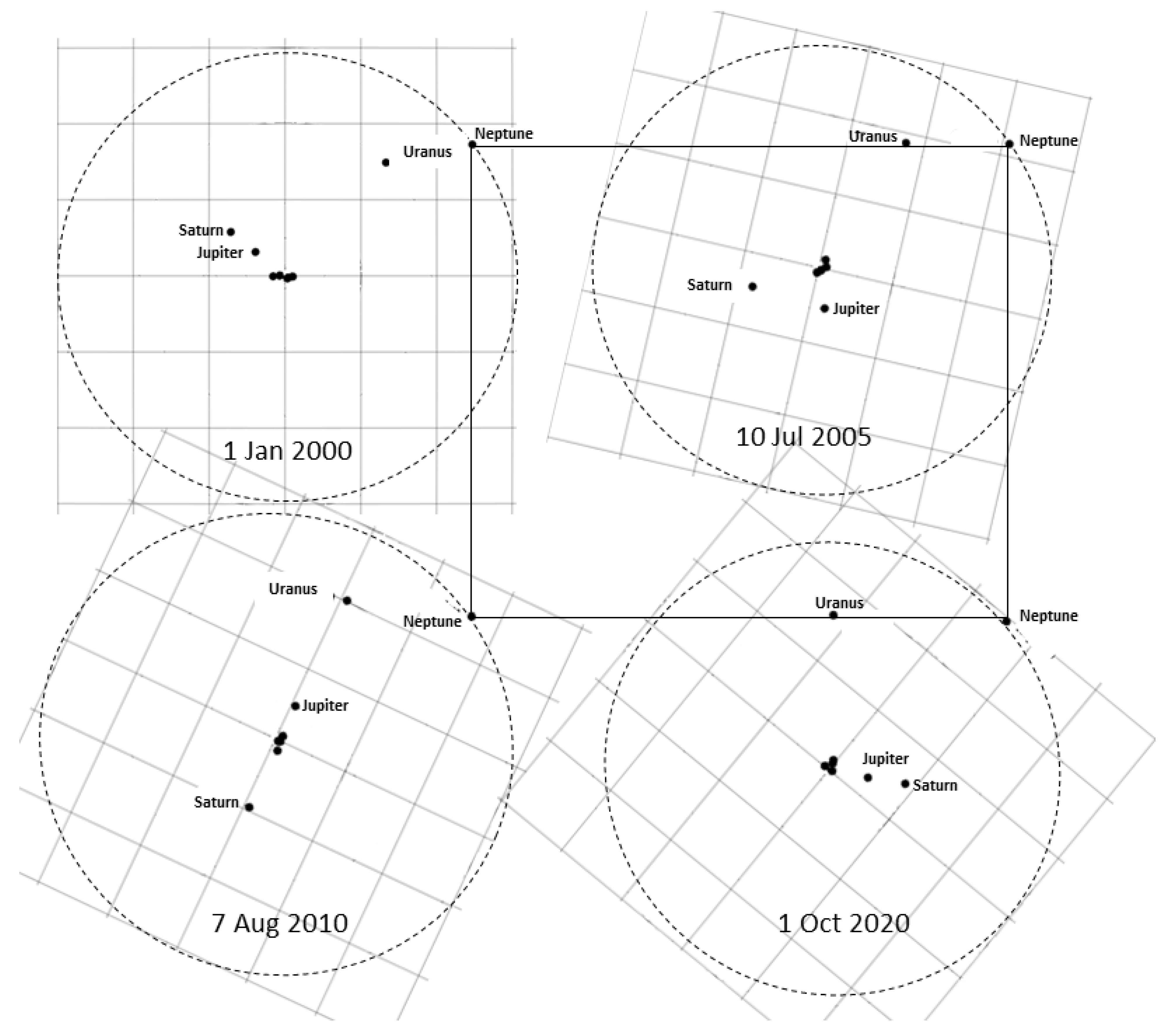


| Pair | Interval | Pair | Interval | Pair | Interval |
|---|---|---|---|---|---|
| Mercury–Jupiter | 0.242 | Mercury–Saturn | 0.24 | Mercury–Mars | 0.307 |
| Venus–Jupiter | 0.655 | Venus–Saturn | 0.65 | Venus–Mars | 1.0 |
| Earth–Jupiter | 1.1 | Earth–Saturn | 1.03 | Earth–Mars | 2.2 |
| Mars–Jupiter | 2.25 | Mars–Saturn | 2.0 | Uranus–Mars | 1.9 |
| Saturn–Jupiter | 20.3 | Uranus’ orbit | 83.8 | Neptune–Mars | 1.88 |
| Uranus–Jupiter | 13.5 | Uranus–Saturn | ~45 | Mars’ orbit | 1.88 |
| Neptune–Jupiter | 12.6 | Neptune–Saturn | ~36 | Neptune–Uranus | ~164 |
| Jupiter’s orbit | 11.86 | Saturn’s orbit | 29.46 | Neptune’s orbit | 163.7 |
| Mercury–Venus | 0.364 | Mercury–Earth | 0.288 | Venus–Earth | 1.6 |
| Perturbers | Interval Days | Significance | No. Orbits | Average Acceleration Ratios | |
|---|---|---|---|---|---|
| Radial * | Tangential | ||||
| Venus + Jupiter | 2604 | pseudo-cycle † | 29.6 | 4.6985 × 10−7 | −1.60 × 10−10 |
| 3652.5 | 10 Julian years | 41.5 | 4.5812 × 10−7 | −4.23 × 10−8 | |
| 7305 | 20 Julian years | 83.0 | 4.7779 × 10−7 | −2.35 × 10−8 | |
| 8529.3 | complete cycle | 96.9 | 4.6986 × 10−7 | −2.26 × 10−11 ‡ | |
| Earth + Saturn | 1507 | pseudo-cycle † | 15.7 | 1.1422 × 10−7 | −2.15 × 10−11 |
| 3652.5 | 10 Julian years | 41.5 | 1.1483 × 10−7 | −5.11 × 10−9 | |
| 7305 | 20 Julian years | 83.0 | 1.1529 × 10−7 | −1.67 × 10−9 | |
| 7184.3 | complete cycle | 81.6 | 1.1395 × 10−7 | −6.89 × 10−13 ‡ | |
| All § | 3652.5 | 10 Julian years | 41.5 | 5.741 × 10−7 | −4.934 × 10−8 § |
| 7305 | 20 Julian years | 83.0 | 5.930 × 10−7 | −2.522 × 10−8 § | |
| POI | PP | Time Average * | Extrema Average * | Ratio |
|---|---|---|---|---|
| Mercury | Venus | 0.2735 | 1.473 | 5.38 |
| Earth | 0.1047 | 0.483 | 4.61 | |
| Jupiter | 0.1967 | 0.794 | 4.40 | |
| Saturn | 0.00832 | 0.0375 | 4.50 | |
| Sum ‡ | 0.583 | 2.79 | 4.8 | |
| Venus | Mercury | −0.065 | −0.419 | 6.4 |
| Earth | 2.81 | 9.99 | 3.56 | |
| Mars | 0.088 | 0.111 | 1.26 | |
| Jupiter | 1.3 § | 5.33 | 4.3 § | |
| Saturn | 0.057 § | 0.25 | 4.3 § | |
| Sum ‡ | est.5.5 | 15.26 | est. 2.8 | |
| Earth | Mercury | −0.038 | −0.18 | 4.66 |
| Venus | −4.38 | −16.4 | 3.74 | |
| Mars | 0.215 | 0.540 | 2.50 | |
| Jupiter | 3.52 | 14.6 | 4.14 | |
| Saturn | 0.15 ‖ | 0.665 | 4.4 ‖ | |
| Sum ‡ | −0.86 | −1.80 | 2.1 | |
| Mars | Venus | −2.97 | −4.98 | 1.68 |
| Earth | −4.65 | −13.3 | 2.86 | |
| Jupiter | 13.2 | 57.2 | 4.3 | |
| Saturn | 0.591 | 2.42 | 4.1 | |
| Sum ‡ | 6.17 | 41.3 | 6.7 |
| Inner Planets | Maximum de/dt (Century−1) | Outer Planets | Maximum de/dt (Century−1) |
|---|---|---|---|
| Mercury | 4.5256 × 10−9 | Jupiter | 1.0764 × 10−9 |
| Venus | 1.4748 × 10−10 | Saturn | 1.2437 × 10−9 |
| Earth | 3.6760 × 10−10 | Uranus | 1.0280 × 10−9 |
| Mars | 2.0581 × 10−9 | Neptune | 2.4873 × 10−10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hofmeister, A.M.; Criss, E.M. Constraints on Newtonian Interplanetary Point-Mass Interactions in Multicomponent Systems from the Symmetry of Their Cycles. Symmetry 2021, 13, 846. https://doi.org/10.3390/sym13050846
Hofmeister AM, Criss EM. Constraints on Newtonian Interplanetary Point-Mass Interactions in Multicomponent Systems from the Symmetry of Their Cycles. Symmetry. 2021; 13(5):846. https://doi.org/10.3390/sym13050846
Chicago/Turabian StyleHofmeister, Anne M., and Everett M. Criss. 2021. "Constraints on Newtonian Interplanetary Point-Mass Interactions in Multicomponent Systems from the Symmetry of Their Cycles" Symmetry 13, no. 5: 846. https://doi.org/10.3390/sym13050846
APA StyleHofmeister, A. M., & Criss, E. M. (2021). Constraints on Newtonian Interplanetary Point-Mass Interactions in Multicomponent Systems from the Symmetry of Their Cycles. Symmetry, 13(5), 846. https://doi.org/10.3390/sym13050846






