The Problem of the Non-Uniqueness of the Solution to the Inverse Problem of Recovering the Symmetric States of a Bistable Medium with Data on the Position of an Autowave Front
Abstract
:1. Introduction
2. Statement of the Inverse Problem
3. Construction of the Reduced Statement of the Inverse Problem Using the Asymptotic Analysis Methods
- are the regular part functions describing the behavior of the solution far from the points ;
- are the transition layer functions describing the solution near the localization point of the transition layer at each time and depending on the stretched variable ;
- is a boundary function describing the solution near the point and depending on the stretched variable ;
- is a boundary function describing the behavior of the solution near the point and depending on the stretched variable ; note that the boundary functions exponentially decrease with distance from the points and [24].
4. The Problem of the Non-Uniqueness of the Solution to the Inverse Problem and a Proposal to Resolve this Issue
- (1)
- The unknown coefficient can be recovered only in the region , where the autowave front passed through during its experimental observation.
- (2)
4.1. Numerical Study of the Non-Uniqueness of the Solution to the Inverse Problem with a Fixed Value of the Small Parameter
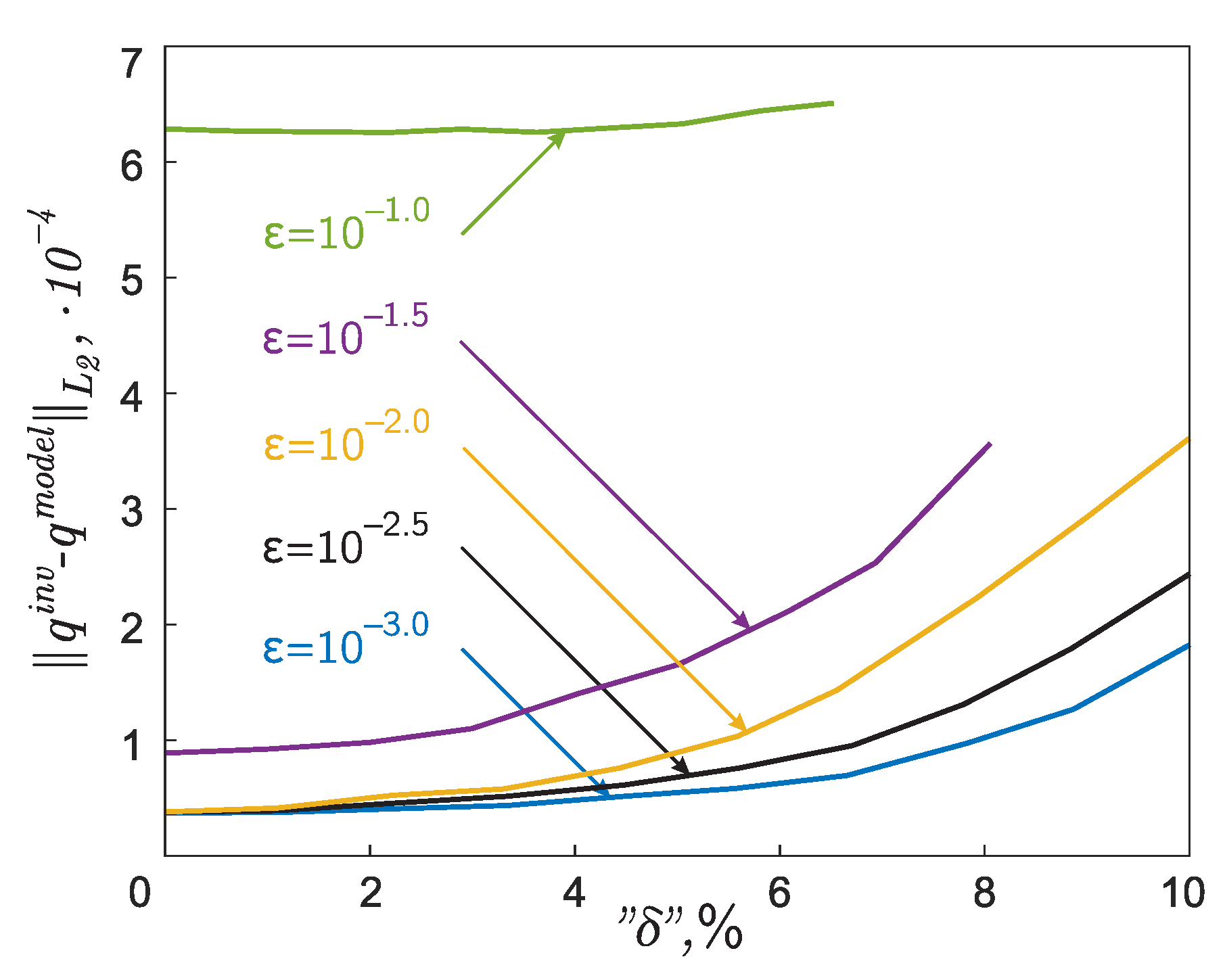
4.2. Numerical Study of the Small Parameter Value Influence on the Quality of the Function Recovered from the Reduced Statement of the Problem with Additional Information
5. Discussion
- (1)
- The problem of the non-uniqueness of the solution to the inverse problem was revealed in the case of the presence of symmetric stable states of a bistable medium. In the case of asymmetric stable states, the result would be different.
- (2)
- In previous works (see, for example, [20,21,27]), the authors dealt with the problems in which the recovery of the unknown coefficient was successful using only the information about the front position . This was due to the fact that the reduced statements were algebraic [21,27] or integral [20] equations with respect to .
- (3)
- Information about the value , , can be used as additional data for the inverse problem statement. In this case, it is possible (1) to construct an algorithm for solving the problem (1) and (2) in the full statement using the gradient method of minimizing the cost functional (see, for example, [20,28]) and (2) to use some recent results concerning features of solving nonlinear inverse problems (see, for example, [29,30,31,32,33,34,35,36,37,38,39]), including error estimation (see, for example, [40,41,42,43,44,45]). However, as already noted, applying this approach will require additional information about the function , which can be difficult to measure experimentally.
- (4)
- The proposed way of using the additional information allows recovering the function only at the points the autowave front passed through during experimental observation.
- (5)
- In some cases, autowave equations have exact solutions [1,46,47]. For example, in [46], for an equation of the form (1) with : (1) families of the traveling wave solutions and two-shock wave solutions and (2) the explicit formulae determining their velocities were obtained. Let us set the problem (1) with the initial condition and the boundary conditions , . The boundary and initial conditions specify the unique autowave solution with zero velocity of the family. It is easy to check (see [46]) that the function is an exact solution to the problem (1). Thus, . This result has a clear physical meaning, as there is no reason for the autowave front motion in a homogeneous medium with balanced nonlinearity.It would seem that when solving the inverse problem (1) and (2), it is possible to use the reduced formulation (18) for the obtained function . Equation (18) gives . Using for any , we obtained that . However, the obtained function is defined only at one point because (see the previous Discussion point). Thus, it is difficult to construct an example with an exact known solution for this type of problem. This is the reason why we constructed the model function for the known exact solution numerically (see Section 4.2 and Figure 4).
- (6)
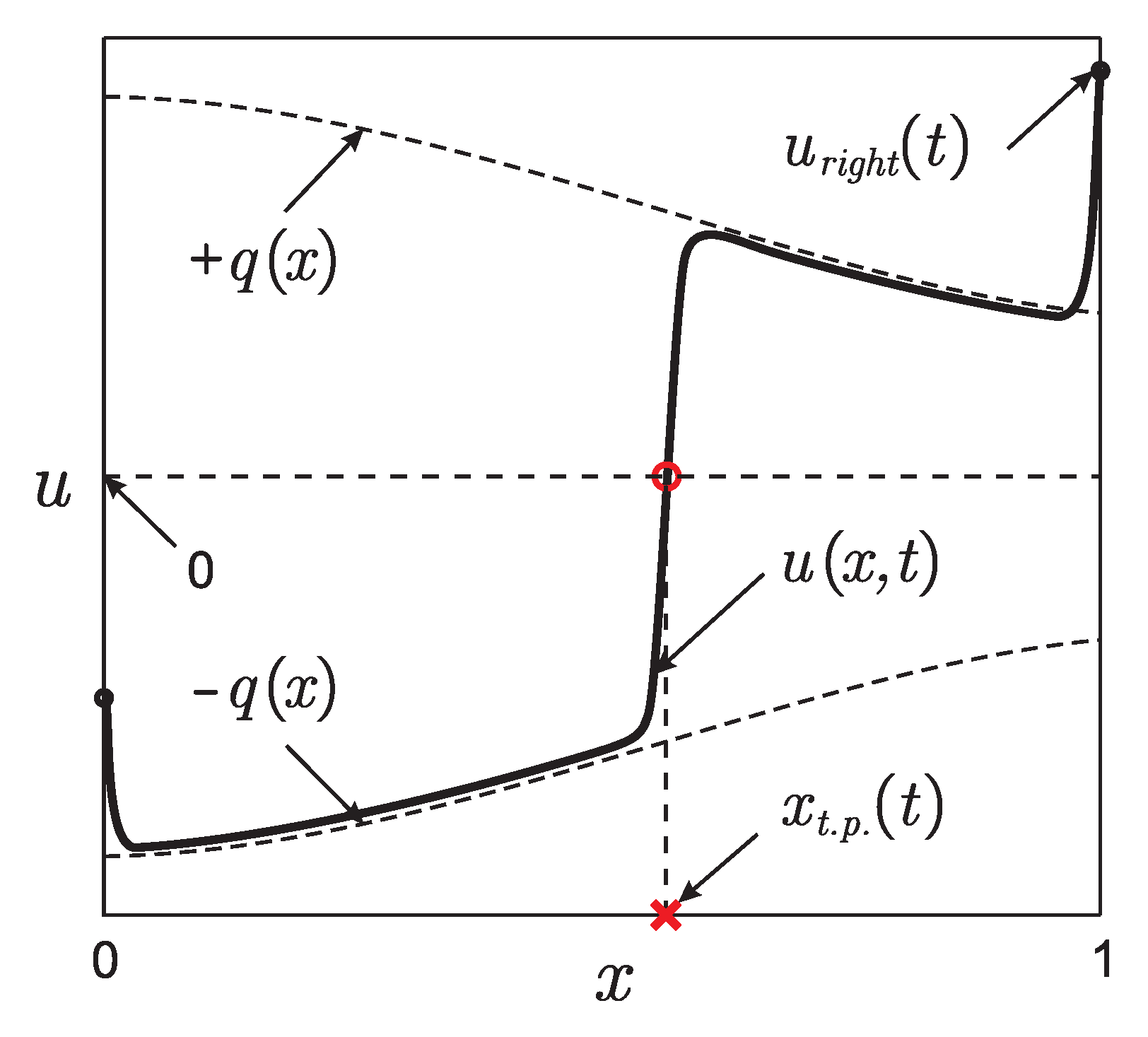
- The boundary conditions and cannot be used as the initial condition for solving the reduced problem (19) and (20) even if it does not depend on t. This is due to the fact that unknown function is defined by (19) only on the segment the autowave front passed through the experimental observation (see Figure 4). Thus, (in other words, or ) when we observe the moving autowave front in the experiment.
- (7)
- There is no need to state and check the conditions for the existence of a front-type solution in the direct problem (1). We solved the inverse problem. Therefore, if we observe a moving autowave front, this means that the conditions for the existence of a solution of the front type are satisfied (whatever they may be).
- (8)
- The non-uniqueness of the solution to the inverse problem (1) and (2) is theoretically justified only if . Having a fixed value of when solving a practical inverse problem, the non-uniqueness of the solution can only occur if the error of the input data is sufficiently large. The question raised in Section 4.1 about the dependence , when the inverse problem (1) and (2) has a unique solution, remains open. This issue is of significant interest and may be the topic of separate work.
- (9)
- The recovered functions coincide with at any fixed time moment outside a small neighborhood of the autowave front localization point (see Figure 1). However, the values of the function at a fixed-time instant can be much more difficult to observe experimentally than a clearly distinguishable contrast structure that determines the position of the interior layer (autowave front).
- (10)
- As was mentioned in the Introduction, the work was motivated by the example of flame propagation modeling in combustion theory [1] and the problem of modeling of habitat area movement in biophysics [2]. However, equations similar to the one considered in the work can occur in gas dynamics [48], chemical kinetics [49,50,51,52,53,54], nonlinear wave theory [3], biophysics [55,56,57,58], medicine [59,60,61,62], finance [63], and other fields of science [64].
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Zeldovich, Y.; Barenblatt, G.; Librovich, V.; Makhviladze, G. The Mathematical Theory of Combustion and Explosions; Plenum: New York, NY, USA, 1985. [Google Scholar]
- Murray, J. Mathematical Biology. I. An Introduction; Springer: New York, NY, USA, 2002. [Google Scholar] [CrossRef]
- Volpert, A.; Volpert, V.; Volpert, V. Traveling Wave Solutions of Parabolic Systems; American Mathematical Society: Providence, RI, USA, 2000. [Google Scholar]
- Nefedov, N.; Nikulin, E. Existence and stability of periodic contrast structures in the reaction-advection-diffusion problem in the case of a balanced nonlinearity. Differ. Equ. 2017, 53, 516–529. [Google Scholar] [CrossRef]
- Davydova, M.; Nefedov, N. Multidimensional singularly perturbed reaction-diffusion-advection problems with a balanced nonlinearity and their applications in the theory of nonlinear heat conductivity. J. Physics Conf. Ser. 2019, 1205, 012011. [Google Scholar] [CrossRef]
- Sidorova, A.; Levashova, N.; Garaeva, A.; Tverdislov, V. A percolation model of natural selection. BioSystems 2020, 193, 104120. [Google Scholar] [CrossRef] [PubMed]
- Garaeva, A.; Sidorova, A.; Tverdislov, V.; Levashova, N. A model of speciation preconditions in terms of percolation and self-organized criticality theories. Biophysics 2020, 65, 795–809. [Google Scholar] [CrossRef]
- Cannon, J.; DuChateau, P. An Inverse problem for a nonlinear diffusion equation. SIAM J. Appl. Math. 1980, 39, 272–289. [Google Scholar] [CrossRef]
- DuChateau, P.; Rundell, W. Unicity in an inverse problem for an unknown reaction term in a reaction-diffusion equation. J. Differ. Equ. 1985, 59, 155–164. [Google Scholar] [CrossRef] [Green Version]
- Pilant, M.; Rundell, W. An inverse problem for a nonlinear parabolic equation. Commun. Partial. Differ. Equ. 1986, 11, 445–457. [Google Scholar] [CrossRef]
- Kabanikhin, S. Definitions and examples of inverse and ill-posed problems. J. Inverse Ill-Posed Probl. 2008, 16, 317–357. [Google Scholar] [CrossRef]
- Kabanikhin, S. Inverse and Ill-Posed Problems Theory and Applications; de Gruyter: Berlin, Germany, 2011. [Google Scholar]
- Jin, B.; Rundell, W. A tutorial on inverse problems for anomalous diffusion processes. Inverse Probl. 2015, 31, 035003. [Google Scholar] [CrossRef] [Green Version]
- Belonosov, A.; Shishlenin, M. Regularization methods of the continuation problem for the parabolic equation. Lect. Notes Comput. Sci. 2017, 10187, 220–226. [Google Scholar]
- Kaltenbacher, B.; Rundell, W. On the identification of a nonlinear term in a reaction-diffusion equation. Inverse Probl. 2019, 35, 115007. [Google Scholar] [CrossRef] [Green Version]
- Belonosov, A.; Shishlenin, M.; Klyuchinskiy, D. A comparative analysis of numerical methods of solving the continuation problem for 1D parabolic equation with the data given on the part of the boundary. Adv. Comput. Math. 2019, 45, 735–755. [Google Scholar] [CrossRef]
- Kaltenbacher, B.; Rundell, W. The inverse problem of reconstructing reaction-diffusion systems. Inverse Probl. 2020, 36, 065011. [Google Scholar] [CrossRef]
- Lukyanenko, D.; Shishlenin, M.; Volkov, V. Solving of the coefficient inverse problems for a nonlinear singularly perturbed reaction-diffusion-advection equation with the final time data. Commun. Nonlinear Sci. Numer. Simul. 2018, 54, 233–247. [Google Scholar] [CrossRef]
- Lukyanenko, D.; Prigorniy, I.; Shishlenin, M. Some features of solving an inverse backward problem for a generalized Burgers’ equation. J. Inverse Ill-Posed Probl. 2020, 28, 641–649. [Google Scholar] [CrossRef]
- Lukyanenko, D.; Borzunov, A.; Shishlenin, M. Solving coefficient inverse problems for nonlinear singularly perturbed equations of the reaction-diffusion-advection type with data on the position of a reaction front. Commun. Nonlinear Sci. Numer. Simul. 2021, 99, 105824. [Google Scholar] [CrossRef]
- Lukyanenko, D.; Grigorev, V.; Volkov, V.; Shishlenin, M. Solving of the coefficient inverse problem for a nonlinear singularly perturbed two-dimensional reaction-diffusion equation with the location of moving front data. Comput. Math. Appl. 2019, 77, 1245–1254. [Google Scholar] [CrossRef]
- Butuzov, V.; Vasilieva, A. Singularly perturbed problems with boundary and interior layers: Theory and applications. Adv. Chem. Phys. 1997, 97, 47–179. [Google Scholar]
- Vasilieva, A.; Butuzov, V.; Nefedov, N. Singularly perturbed problems with boundary and internal layers. Proc. Steklov Inst. Math. 2010, 268, 258–273. [Google Scholar] [CrossRef]
- Vasilieva, A.; Butuzov, V.; Kalachev, L. The Boundary Function Method for Singular Perturbation Problems; SIAM: Philadelphia, PA, USA, 1995. [Google Scholar]
- Fife, P.; McLeod, J. The approach of solutions of nonlinear diffusion. Equations to travelling front solutions. Arch. Ration. Mech. Anal. 1977, 65, 335–361. [Google Scholar] [CrossRef]
- Tikhonov, A.N.; Goncharsky, A.V.; Stepanov, V.V.; Yagola, A.G. Numerical Methods for the Solution of Ill-Posed Problems; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1995. [Google Scholar]
- Lukyanenko, D.; Shishlenin, M.; Volkov, V. Asymptotic analysis of solving an inverse boundary value problem for a nonlinear singularly perturbed time-periodic reaction-diffusion-advection equation. J. Inverse Ill-Posed Probl. 2019, 27, 745–758. [Google Scholar] [CrossRef]
- Lukyanenko, D.; Yeleskina, T.; Prigorniy, I.; Isaev, T.; Borzunov, A.; Shishlenin, M. Inverse problem of recovering the initial condition for a nonlinear equation of the reaction-diffusion-advection type by data given on the position of a reaction front with a time delay. Mathematics 2021, 9, 342. [Google Scholar] [CrossRef]
- Klibanov, M.; Li, J.; Zhang, W. Convexification for an inverse parabolic problem. Inverse Probl. 2020, 36, 085008. [Google Scholar] [CrossRef]
- Klibanov, M.; Nguyen, D.L. Convergence of a series associated with the convexification method for coefficient inverse problems. J. Inverse -Ill-Posed Probl. 2020. [Google Scholar] [CrossRef]
- Leonov, A. Extra-Optimal Methods for Solving Ill-Posed Problems: Survey of Theory and Examples. Comput. Math. Math. Phys. 2020, 60, 960–986. [Google Scholar] [CrossRef]
- Bakushinskii, A.; Kokurin, M.; Kokurin, M. Direct and Converse Theorems for Iterative Methods of Solving Irregular Operator Equations and Finite Difference Methods for Solving Ill-Posed Cauchy Problems. Comput. Math. Math. Phys. 2020, 60, 915–937. [Google Scholar] [CrossRef]
- Kokurin, M. A posteriori choice of time-discretization step in finite difference methods for solving ill-posed Cauchy problems in Hilbert space. J. Inverse Ill-Posed Probl. 2021. [Google Scholar] [CrossRef]
- Lin, G.; Cheng, X.; Zhang, Y. A parametric level set based collage method for an inverse problem in elliptic partial differential equations. J. Comput. Appl. Math. 2018, 340, 101–121. [Google Scholar] [CrossRef] [Green Version]
- Gulliksson, M.; Holmbom, A.; Persson, J.; Zhang, Y. A separating oscillation method of recovering the G-limit in standard and non-standard homogenization problems. Inverse Probl. 2016, 32, 025005. [Google Scholar] [CrossRef]
- Egger, H.; Engl, H.; Klibanov, M. Global uniqueness and Holder stability for recovering a nonlinear source term in a parabolic equation. Inverse Probl. 2005, 21, 271–290. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, R. Second order asymptotical regularization methods for inverse problems in partial differential equations. J. Comput. Appl. Math. 2020, 375, 112798. [Google Scholar] [CrossRef] [Green Version]
- Gavalec, M.; Plavka, J.; Ponce, D. Strong, Strongly Universal and Weak Interval Eigenvectors in Max-Plus Algebra. Mathematics 2020, 8, 1348. [Google Scholar] [CrossRef]
- Angiulli, G.; Versaci, M.; Calcagno, S. Computation of the Cutoff Wavenumbers of Metallic Waveguides with Symmetries by Using a Nonlinear Eigenproblem Formulation: A Group Theoretical Approach. Mathematics 2020, 8, 489. [Google Scholar] [CrossRef] [Green Version]
- Yagola, A.; Leonov, A.; Titarenko, V. Data errors and an error estimation for ill-posed problems. Inverse Probl. Eng. 2002, 10, 117–129. [Google Scholar] [CrossRef]
- Titarenko, V.; Yagola, A. Error estimation for ill-posed problems on piecewise convex functions and sourcewise represented sets. J. Inverse -Ill-Posed Probl. 2008, 16, 625–638. [Google Scholar] [CrossRef]
- Leonov, A. Which of inverse problems can have a priori approximate solution accuracy estimates comparable in order with the data accuracy. Numer. Anal. Appl. 2014, 7, 284–292. [Google Scholar] [CrossRef]
- Leonov, A. A posteriori accuracy estimations of solutions to ill-posed inverse problems and extra-optimal regularizing algorithms for their solution. Numer. Anal. Appl. 2012, 5, 68–83. [Google Scholar] [CrossRef]
- Kokurin, M. Accuracy estimates of regularization methods and conditional well-posedness of nonlinear optimization problems. J. Inverse Ill-Posed Probl. 2018, 26, 789–797. [Google Scholar] [CrossRef]
- Kokurin, M. Ill-Posed Nonlinear Optimization Problems and Uniform Accuracy Estimates of Regularization Methods. Numer. Funct. Anal. Optim. 2020, 41, 1887–1900. [Google Scholar] [CrossRef]
- Cherniha, R. New Q-conditional symmetries and exact solutions of some reaction–diffusion–convection equations arising in mathematical biology. J. Math. Anal. Appl. 2007, 326, 783–799. [Google Scholar] [CrossRef] [Green Version]
- Cherniha, R.; Pliukhin, O. New conditional symmetries and exact solutions of nonlinear reaction-diffusion-convection equations. J. Phys. Math. Theor. 2007, 40, 10049–10070. [Google Scholar] [CrossRef] [Green Version]
- Danilov, V.; Maslov, V.; Volosov, K. Mathematical Modelling of Heat and Mass Transfer Processes; Kluwer: Dordrecht, The Netherlands, 1995. [Google Scholar]
- Liu, Z.; Liu, Q.; Lin, H.C.; Schwartz, C.; Lee, Y.H.; Wang, T. Three-dimensional variational assimilation of MODIS aerosol optical depth: Implementation and application to a dust storm over East Asia. J. Geophys. Res. Atmos. 2010, 116. [Google Scholar] [CrossRef] [Green Version]
- Egger, H.; Fellner, K.; Pietschmann, J.F.; Tang, B.Q. Analysis and numerical solution of coupled volume-surface reaction-diffusion systems with application to cell biology. Appl. Math. Comput. 2018, 336, 351–367. [Google Scholar] [CrossRef] [Green Version]
- Yaparova, N. Method for determining particle growth dynamics in a two-component alloy. Steel Transl. 2020, 50, 95–99. [Google Scholar] [CrossRef]
- Wu, X.; Ni, M. Existence and stability of periodic contrast structure in reaction-advection-diffusion equation with discontinuous reactive and convective terms. Commun. Nonlinear Sci. Numer. Simul. 2020, 91, 105457. [Google Scholar] [CrossRef]
- Lin, G.; Zhang, Y.; Cheng, X.; Gulliksson, M.; Forssén, P.; Fornstedt, T. A regularizing Kohn–Vogelius formulation for the model-free adsorption isotherm estimation problem in chromatography. Appl. Anal. 2018, 97, 13–40. [Google Scholar] [CrossRef]
- Zhang, Y.; Lin, G.; Gulliksson, M.; Forssén, P.; Fornstedt, T.; Cheng, X. An adjoint method in inverse problems of chromatography. Inverse Probl. Sci. Eng. 2017, 25, 1112–1137. [Google Scholar] [CrossRef]
- Meinhardt, H. Models of Biological Pattern Formation; Academic Press: London, UK, 1982. [Google Scholar]
- FitzHugh, R. Impulses and physiological states in theoretical model of nerve membrane. Biophys. J. 1961, 1, 445–466. [Google Scholar] [CrossRef] [Green Version]
- Egger, H.; Pietschmann, J.F.; Schlottbom, M. Identification of nonlinear heat conduction laws. J. Inverse Ill-Posed Probl. 2015, 23, 429–437. [Google Scholar] [CrossRef] [Green Version]
- Gholami, A.; Mang, A.; Biros, G. An inverse problem formulation for parameter estimation of a reaction-diffusion model of low grade gliomas. J. Math. Biol. 2016, 72, 409–433. [Google Scholar] [CrossRef] [Green Version]
- Aliev, R.; Panfilov, A. A simple two-variable model of cardiac excitation. Chaos Solitons Fractals 1996, 7, 293–301. [Google Scholar] [CrossRef]
- Generalov, E.; Levashova, N.; Sidorova, A.; Chumankov, P.; Yakovenko, L. An autowave model of the bifurcation behavior of transformed cells in response to polysaccharide. Biophysics 2017, 62, 876–881. [Google Scholar] [CrossRef]
- Mang, A.; Gholami, A.; Davatzikos, C.; Biros, G. PDE-constrained optimization in medical image analysis. Optim. Eng. 2018, 19, 765–812. [Google Scholar] [CrossRef] [Green Version]
- Kabanikhin, S.; Shishlenin, M. Recovering a Time-Dependent Diffusion Coefficient from Nonlocal Data. Numer. Anal. Appl. 2018, 11, 38–44. [Google Scholar] [CrossRef]
- Isakov, V.; Kabanikhin, S.; Shananin, A.; Shishlenin, M.; Zhang, S. Algorithm for determining the volatility function in the Black-Scholes model. Comput. Math. Math. Phys. 2019, 59, 1753–1758. [Google Scholar] [CrossRef]
- Kadalbajoo, M.; Gupta, V. A brief survey on numerical methods for solving singularly perturbed problems. Appl. Math. Comput. 2010, 217, 3641–3716. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Levashova, N.; Gorbachev, A.; Argun, R.; Lukyanenko, D. The Problem of the Non-Uniqueness of the Solution to the Inverse Problem of Recovering the Symmetric States of a Bistable Medium with Data on the Position of an Autowave Front. Symmetry 2021, 13, 860. https://doi.org/10.3390/sym13050860
Levashova N, Gorbachev A, Argun R, Lukyanenko D. The Problem of the Non-Uniqueness of the Solution to the Inverse Problem of Recovering the Symmetric States of a Bistable Medium with Data on the Position of an Autowave Front. Symmetry. 2021; 13(5):860. https://doi.org/10.3390/sym13050860
Chicago/Turabian StyleLevashova, Natalia, Alexandr Gorbachev, Raul Argun, and Dmitry Lukyanenko. 2021. "The Problem of the Non-Uniqueness of the Solution to the Inverse Problem of Recovering the Symmetric States of a Bistable Medium with Data on the Position of an Autowave Front" Symmetry 13, no. 5: 860. https://doi.org/10.3390/sym13050860
APA StyleLevashova, N., Gorbachev, A., Argun, R., & Lukyanenko, D. (2021). The Problem of the Non-Uniqueness of the Solution to the Inverse Problem of Recovering the Symmetric States of a Bistable Medium with Data on the Position of an Autowave Front. Symmetry, 13(5), 860. https://doi.org/10.3390/sym13050860






