Production of the Doubly Charged Higgs Boson in Association with the SM Gauge Bosons and/or Other HTM Scalars at Hadron Colliders
Abstract
:1. Introduction
2. The Higgs Triplet Model Phenomenological Constraints
3. Results
- to maximize the signal: (inverted neutrino mass hierarchy), , ,
- to maximize the signal: eV (normal neutrino mass hierarchy), , ,
- Lepton identification criteria: transverse momentum GeV, pseudorapidity ;
- Hard cuts: GeV, GeV, GeV;
- Detector efficiency for electron (muon): 70% (90%);
- Lepton–lepton separation: ;
- Z-veto—the invariant mass of any same flavour and opposite charge lepton should satisfy the condition: .
4. Summary and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BSM | Beyond Standard Model |
| HTM | Higgs Triplet Model |
| LFV | Lepton Flavour Violation |
| LNV | Lepton Number Violation |
| SM | Standard Model |
| VEV | Vacuum Expectation Value |
Appendix A
Appendix A.1. The Scalar Potential of the Model
Appendix A.2. Scalar-Leptons Couplings
Appendix A.3. Feynman Diagrams
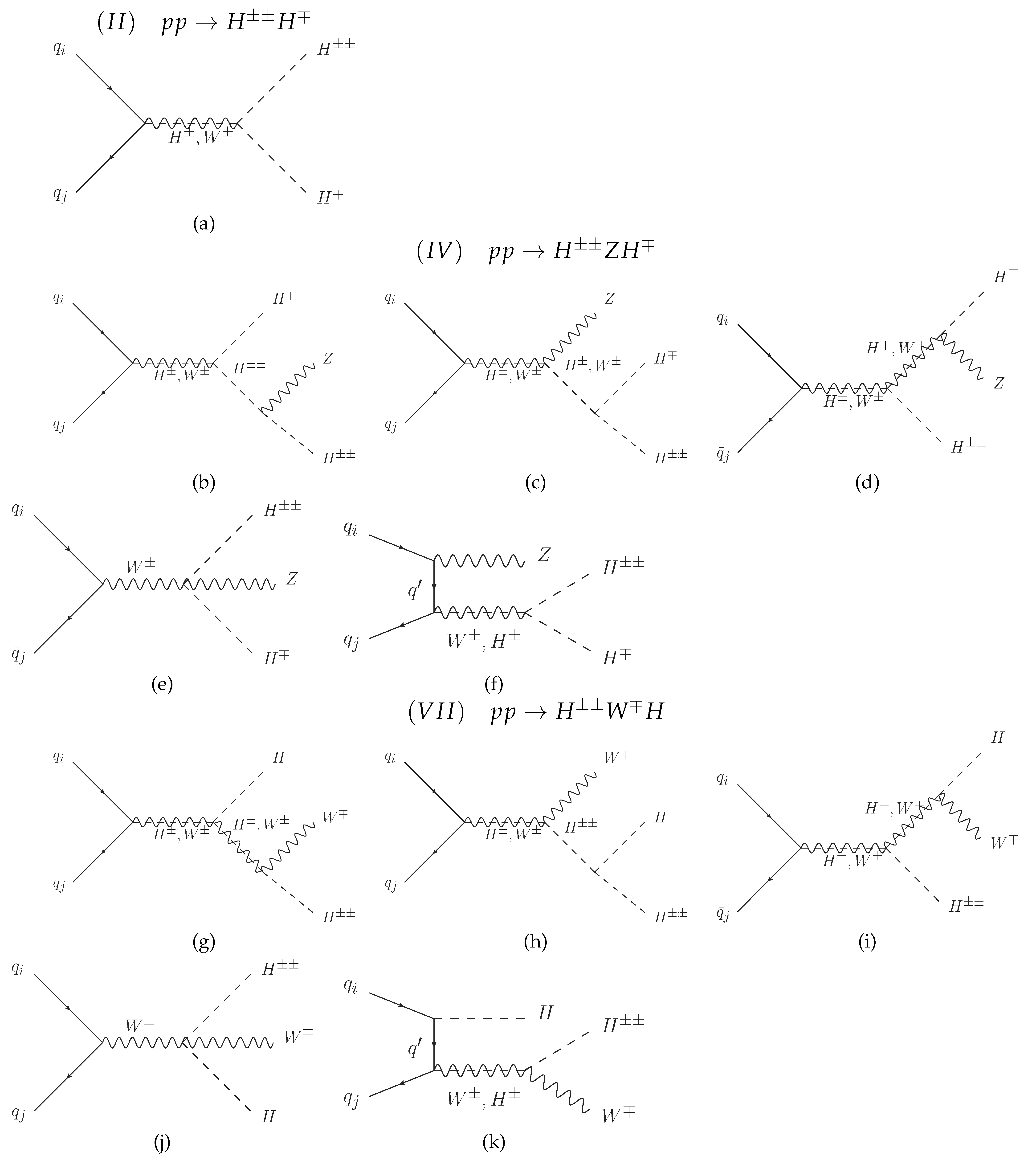
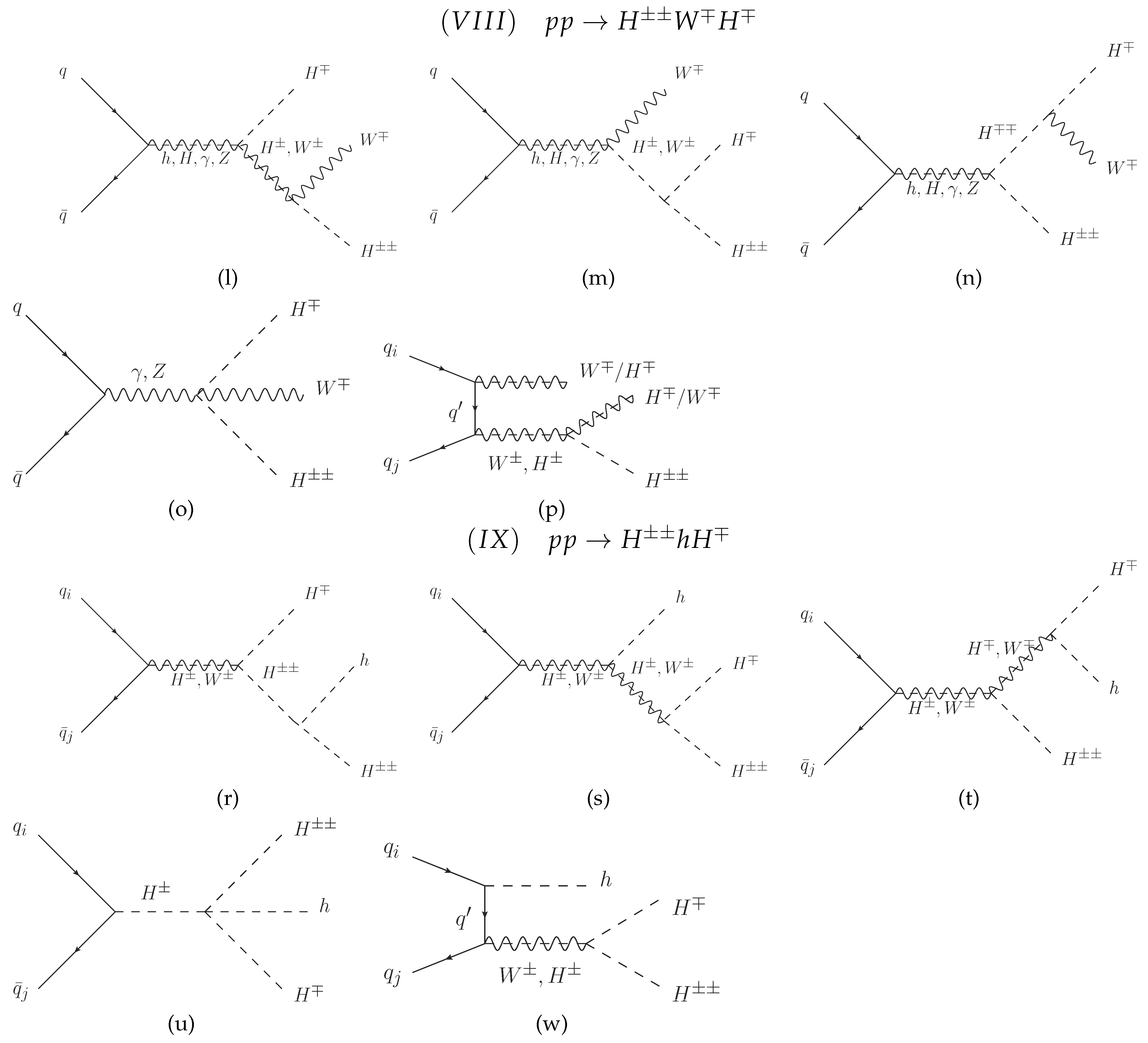
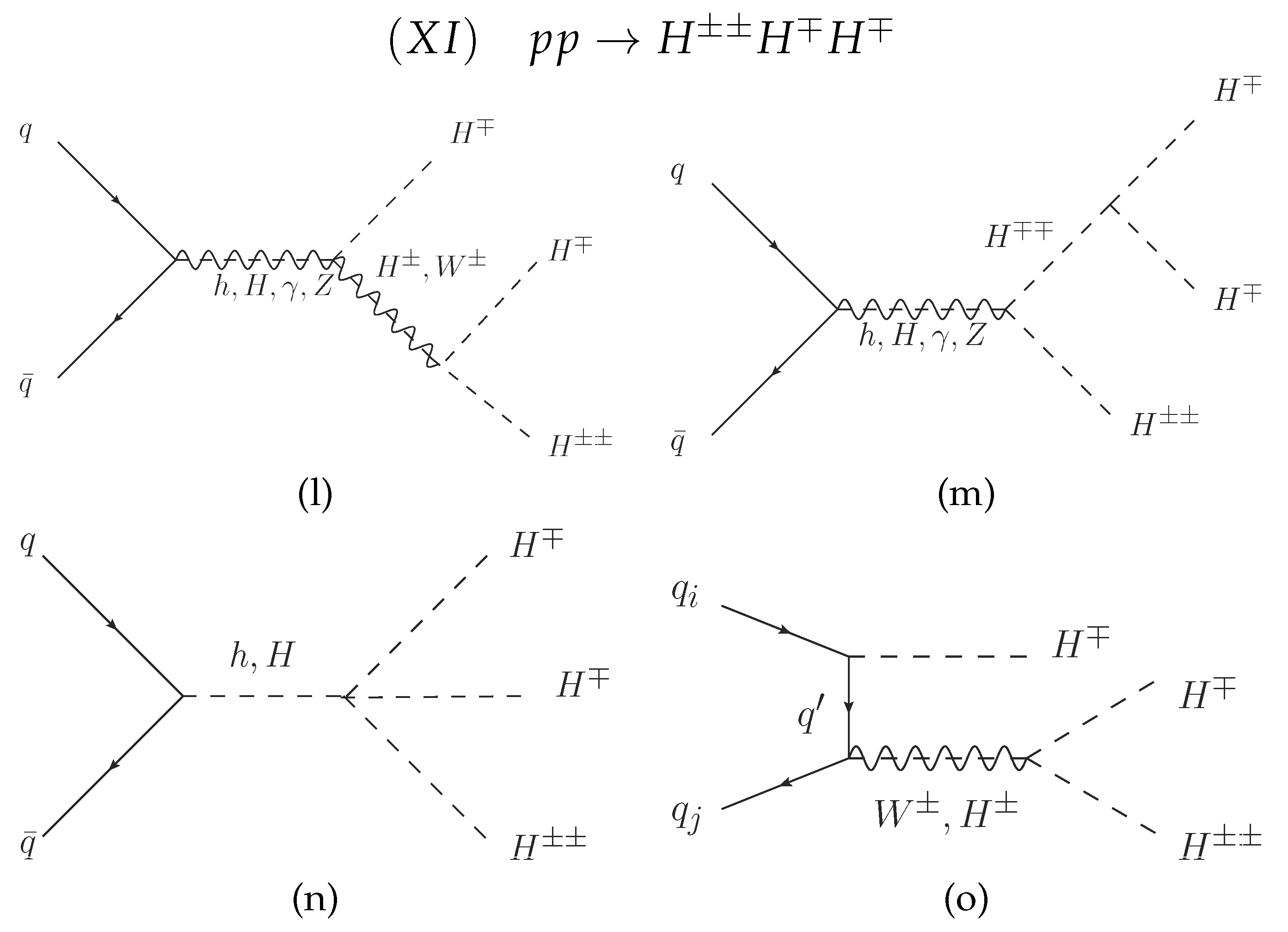
References
- Aad, G.; Abajyan, T.; Abbott, B.; Abdallah, J.; Khalek, S.A.; Abdelalim, A.A.; Aben, R.; Abi, B.; Abolins, M.; AbouZeid, O.S.; et al. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. 2012, B716, 1–29. [Google Scholar] [CrossRef]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Aguilo, E.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; et al. Observation of a New Boson at a Mass of 125 GeV with the CMS Experiment at the LHC. Phys. Lett. 2012, B716, 30–61. [Google Scholar] [CrossRef]
- Mohapatra, R.N.; Pati, J.C. A Natural Left-Right Symmetry. Phys. Rev. 1975, D11, 2558. [Google Scholar] [CrossRef]
- Senjanovic, G.; Mohapatra, R.N. Exact Left-Right Symmetry and Spontaneous Violation of Parity. Phys. Rev. 1975, D12, 1502. [Google Scholar] [CrossRef]
- Mohapatra, R.N.; Senjanović, G. Neutrino Mass and Spontaneous Parity Nonconservation. Phys. Rev. Lett. 1980, 44, 912–915. [Google Scholar] [CrossRef] [Green Version]
- Deshpande, N.G.; Gunion, J.F.; Kayser, B.; Olness, F. Left-right-symmetric electroweak models with triplet Higgs field. Phys. Rev. D 1991, 44, 837–858. [Google Scholar] [CrossRef] [PubMed]
- Duka, P.; Gluza, J.; Zralek, M. Quantization and renormalization of the manifest left-right symmetric model of electroweak interactions. Ann. Phys. 2000, 280, 336–408. [Google Scholar] [CrossRef] [Green Version]
- Barenboim, G.; Gorbahn, M.; Nierste, U.; Raidal, M. Higgs sector of the minimal left-right symmetric model. Phys. Rev. 2002, D65, 095003. [Google Scholar] [CrossRef] [Green Version]
- Gunion, J.F.; Haber, H.E.; Kane, G.L.; Dawson, S. The Higgs Hunter’s Guide; CRC Press: Boca Raton, FL, USA, 2000; Volume 80. [Google Scholar]
- Chun, E.J.; Lee, K.Y.; Park, S.C. Testing Higgs triplet model and neutrino mass patterns. Phys. Lett. 2003, B566, 142–151. [Google Scholar] [CrossRef] [Green Version]
- Pati, J.C.; Salam, A. Lepton Number as the Fourth Color. Phys. Rev. D 1974, 10, 275–289, Erratum in 1975, 11, 703. [Google Scholar] [CrossRef] [Green Version]
- Georgi, H.; Machacek, M. Doubly charged Higgs bosons. Nucl. Phys. B 1985, 262, 463–477. [Google Scholar] [CrossRef]
- Gunion, J.F.; Vega, R.; Wudka, J. Higgs triplets in the standard model. Phys. Rev. D 1990, 42, 1673–1691. [Google Scholar] [CrossRef] [PubMed]
- Gunion, J.F.; Grifols, J.; Mendez, A.; Kayser, B.; Olness, F. Higgs bosons in left-right-symmetric models. Phys. Rev. D 1989, 40, 1546–1561. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vega, R.; Dicus, D.A. Doubly charged Higgs and W+W+ production. Nucl. Phys. B 1990, 329, 533–546. [Google Scholar] [CrossRef]
- Huitu, K.; Maalampi, J.; Pietila, A.; Raidal, M. Doubly charged Higgs at LHC. Nucl. Phys. 1997, B487, 27–42. [Google Scholar] [CrossRef] [Green Version]
- Barger, V.D.; Baer, H.; Keung, W.Y.; Phillips, R.J.N. Decays of Weak Vector Bosons and T Quarks Into Doubly Charged Higgs Scalars. Phys. Rev. D 1982, 26, 218. [Google Scholar] [CrossRef]
- Muhlleitner, M.; Spira, M. A Note on doubly charged Higgs pair production at hadron colliders. Phys. Rev. D 2003, 68, 117701. [Google Scholar] [CrossRef] [Green Version]
- Primulando, R.; Julio, J.; Uttayarat, P. Scalar phenomenology in type-II seesaw model. JHEP 2019, 8, 24. [Google Scholar] [CrossRef] [Green Version]
- Dutta, B.; Eusebi, R.; Gao, Y.; Ghosh, T.; Kamon, T. Exploring the doubly charged Higgs boson of the left-right symmetric model using vector boson fusionlike events at the LHC. Phys. Rev. D 2014, 90, 055015. [Google Scholar] [CrossRef] [Green Version]
- Bambhaniya, G.; Chakrabortty, J.; Gluza, J.; Jelinski, T.; Szafron, R. Search for doubly charged Higgs bosons through vector boson fusion at the LHC and beyond. Phys. Rev. D 2015, 92, 015016. [Google Scholar] [CrossRef]
- Hessler, A.G.; Ibarra, A.; Molinaro, E.; Vogl, S. Impact of the Higgs boson on the production of exotic particles at the LHC. Phys. Rev. D 2015, 91, 115004. [Google Scholar] [CrossRef] [Green Version]
- Han, T.; Mukhopadhyaya, B.; Si, Z.; Wang, K. Pair production of doubly-charged scalars: Neutrino mass constraints and signals at the LHC. Phys. Rev. D 2007, 76, 075013. [Google Scholar] [CrossRef] [Green Version]
- Drees, M.; Godbole, R.M.; Nowakowski, M.; Rindani, S.D. gamma gamma processes at high-energy p p colliders. Phys. Rev. D 1994, 50, 2335–2338. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Akeroyd, A.G.; Aoki, M. Single and pair production of doubly charged Higgs bosons at hadron colliders. Phys. Rev. D 2005, 72, 035011. [Google Scholar] [CrossRef] [Green Version]
- Akeroyd, A.G.; Aoki, M.; Sugiyama, H. Probing Majorana Phases and Neutrino Mass Spectrum in the Higgs Triplet Model at the CERN LHC. Phys. Rev. D 2008, 77, 075010. [Google Scholar] [CrossRef] [Green Version]
- Akeroyd, A.G.; Sugiyama, H. Production of doubly charged scalars from the decay of singly charged scalars in the Higgs Triplet Model. Phys. Rev. D 2011, 84, 035010. [Google Scholar] [CrossRef] [Green Version]
- Alloul, A.; Frank, M.; Fuks, B.; Rausch de Traubenberg, M. Doubly-charged particles at the Large Hadron Collider. Phys. Rev. D 2013, 88, 075004. [Google Scholar] [CrossRef] [Green Version]
- Li, T. Type II Seesaw and tau lepton at the HL-LHC, HE-LHC and FCC-hh. JHEP 2018, 9, 79. [Google Scholar] [CrossRef] [Green Version]
- Dev, P.S.B.; Ramsey-Musolf, M.J.; Zhang, Y. Doubly-Charged Scalars in the Type-II Seesaw Mechanism: Fundamental Symmetry Tests and High-Energy Searches. Phys. Rev. 2018, D98, 055013. [Google Scholar] [CrossRef] [Green Version]
- Crivellin, A.; Ghezzi, M.; Panizzi, L.; Pruna, G.M.; Signer, A. Low- and high-energy phenomenology of a doubly charged scalar. Phys. Rev. D 2019, 99, 035004. [Google Scholar] [CrossRef] [Green Version]
- Du, Y.; Dunbrack, A.; Ramsey-Musolf, M.J.; Yu, J.H. Type-II Seesaw Scalar Triplet Model at a 100 TeV pp Collider: Discovery and Higgs Portal Coupling Determination. JHEP 2019, 1, 101. [Google Scholar] [CrossRef] [Green Version]
- Antusch, S.; Fischer, O.; Hammad, A.; Scherb, C. Low scale type II seesaw: Present constraints and prospects for displaced vertex searches. JHEP 2019, 2, 157. [Google Scholar] [CrossRef] [Green Version]
- de Melo, T.B.; Queiroz, F.S.; Villamizar, Y. Doubly Charged Scalar at the High-Luminosity and High-Energy LHC. Int. J. Mod. Phys. A 2019, 34, 1950157. [Google Scholar] [CrossRef]
- Padhan, R.; Das, D.; Mitra, M.; Kumar Nayak, A. Probing doubly and singly charged Higgs bosons at the pp collider HE-LHC. Phys. Rev. D 2020, 101, 075050. [Google Scholar] [CrossRef]
- Fuks, B.; Nemevsek, M.; Ruiz, R. Doubly Charged Higgs Boson Production at Hadron Colliders. Phys. Rev. D 2020, 101, 075022. [Google Scholar] [CrossRef] [Green Version]
- Gluza, J.; Kordiaczyńska, M.; Srivastava, T. Discriminating the HTM and MLRSM models in collider studies via doubly charged Higgs boson pair production and the subsequent leptonic decays. Chin. Phys. C 2021. accept. [Google Scholar]
- Yang, X.H.; Yang, Z.J. Doubly Charged Higgs Production at Future ep Colliders. arXiv 2021, arXiv:2103.11412. [Google Scholar]
- Aaboud, M.; Aad, G.; Abbott, B.; Abeloos, B.; Abidi, S.H.; AbouZeid, O.S.; Abraham, N.L.; Abramowicz, H.; Abreu, H.; Abreu, R.; et al. Search for doubly charged Higgs boson production in multi-lepton final states with the ATLAS detector using proton-proton collisions at . arXiv 2017, arXiv:1710.09748. [Google Scholar] [CrossRef] [Green Version]
- Aad, G.; Abbott, B.; Abbott, D.C.; Abud, A.A.; Abeling, K.; Abhayasinghe, D.K.; Abidi, S.H.; Abouzeid, O.; Abraham, N.; Abramowicz, H.; et al. Search for doubly and singly charged Higgs bosons decaying into vector bosons in multi-lepton final states with the ATLAS detector using proton-proton collisions at . arXiv 2021, arXiv:2101.11961. [Google Scholar]
- A Search for Doubly-Charged Higgs Boson Production in Three and Four Lepton Final States at . 2017. Available online: http://cds.cern.ch/record/2242956 (accessed on 2 July 2021).
- High-Luminosity LHC, CERN. Available online: https://home.cern/science/accelerators/high-luminosity-lhc (accessed on 2 July 2021).
- Ellis, R.K.; Sozzi, M.; Nisati, A.; D’Onofrio, M.; Siklér, F.; Schulte, D.; D’Hondt, J.; Jaeckel, J.; McCullough, M.; Wiedemann, U.; et al. Physics Briefing Book: Input for the European Strategy for Particle Physics Update 2020. arXiv 2019, arXiv:1910.11775. [Google Scholar]
- Contino, R.; Curtin, D.; Katz, A.; Mangano, M.L.; Panico, G.; Ramsey-Musolf, M.J.; Zanderighi, G.; Anastasiou, C.; Astill, W.; Bambhaniya, G.; et al. Physics at a 100 TeV pp collider: Higgs and EW symmetry breaking studies. CERN Yellow Rep. 2017, 3, 255–440. [Google Scholar] [CrossRef]
- Contino, R.; Curtin, D.; Katz, A.; Mangano, M.L.; Panico, G.; Ramsey-Musolf, M.J.; Zanderighi, G.; Anastasiou, C.; Astill, W.; Bambhaniya, G.; et al. Physics at a 100 TeV pp collider: Beyond the Standard Model phenomena. CERN Yellow Rep. 2017, 3, 441–634. [Google Scholar] [CrossRef]
- Abada, A.; Abbrescia, M.; AbdusSalam, S.S.; Abdyukhanov, I.; Fernandez, J.A.; Abramov, A.; Aburaia, M.; Acar, A.O.; Adzic, P.R.; Agrawal, P.; et al. FCC Physics Opportunities. Eur. Phys. J. 2019, C79, 474. [Google Scholar] [CrossRef] [Green Version]
- FCC Collaboration. FCC-hh: The Hadron Collider: Future Circular Collider Conceptual Design Report Volume 3. Eur. Phys. J. ST 2019, 228, 755–1107. [Google Scholar] [CrossRef]
- FCC—Future Circular Collider, Conceptual Design Report. Available online: https://fcc-cdr.web.cern.ch/ (accessed on 2 July 2021).
- Arhrib, A.; Benbrik, R.; Chabab, M.; Moultaka, G.; Peyranere, M.C.; Rahili, L.; Ramadan, J. The Higgs Potential in the Type II Seesaw Model. Phys. Rev. 2011, D84, 095005. [Google Scholar] [CrossRef] [Green Version]
- Akeroyd, A.G.; Moretti, S. Enhancement of H to gamma gamma from doubly charged scalars in the Higgs Triplet Model. Phys. Rev. 2012, D86, 035015. [Google Scholar] [CrossRef] [Green Version]
- Chun, E.J.; Lee, H.M.; Sharma, P. Vacuum Stability, Perturbativity, EWPD and Higgs-to-diphoton rate in Type II Seesaw Models. JHEP 2012, 11, 106. [Google Scholar] [CrossRef] [Green Version]
- Gluza, J.; Kordiaczyńska, M.; Srivastava, T. Doubly Charged Higgs Bosons and Spontaneous Symmetry Breaking at eV and TeV Scales. Symmetry 2020, 12, 153. [Google Scholar] [CrossRef] [Green Version]
- Das, D.; Santamaria, A. Updated scalar sector constraints in Higgs triplet model. Phys. Rev. 2016, D94, 015015. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Han, T.; Li, T.; Ruiz, R. Lepton Number Violation: Seesaw Models and Their Collider Tests. Front. Phys. 2018, 6, 40. [Google Scholar] [CrossRef] [Green Version]
- Pumplin, J.; Stump, D.R.; Huston, J.; Lai, H.L.; Nadolsky, P.; Tung, W.K. New generation of parton distributions with uncertainties from global QCD analysis. JHEP 2002, 7, 012. [Google Scholar] [CrossRef]
- Hou, T.J.; Gao, J.; Hobbs, T.J.; Xie, K.; Dulat, S.; Guzzi, M.; Huston, J.; Nadolsky, P.; Pumplin, J.; Schmidt, C.; et al. New CTEQ global analysis of quantum chromodynamics with high-precision data from the LHC. arXiv 2019, arXiv:1912.10053. [Google Scholar]
- Alwall, J.; Frederix, R.; Frixione, S.; Hirschi, V.; Maltoni, F.; Mattelaer, O.; Shao, H.-S.; Stelzer, T.; Torrielli, P.; Zaro, M. The automated computation of tree-level and next-to-leading order differential cross section, and their maching to parton shower simulations. JHEP 2014, 7, 79. [Google Scholar] [CrossRef] [Green Version]
- Sjostrand, T.; Mrenna, S.; Skands, P.Z. A Brief Introduction to PYTHIA 8.1. Comput. Phys. Commun. 2008, 178, 852–867. [Google Scholar] [CrossRef] [Green Version]
- Sjostrand, T.; Mrenna, S.; Skands, P.Z. PYTHIA 6.4 Physics and Manual. JHEP 2006, 5, 26. [Google Scholar] [CrossRef]
- Alloul, A.; Christensen, N.D.; Degrange, C.; Duhr, C.; Fuks, B. FeynRules 2.0—A complete toolbox for tree-level phenomenology. Comput. Phys. Commun. 2014, 185, 2250–2300. [Google Scholar] [CrossRef] [Green Version]
- Gluza, J.; Zralek, M. Feynman rules for Majorana neutrino interactions. Phys. Rev. D 1992, 45, 1693–1700. [Google Scholar] [CrossRef] [PubMed]
- Esteban, I.; Gonzalez-Garcia, M.C.; Hernandez-Cabezudo, A.; Maltoni, M.; Schwetz, T. Global analysis of three-flavour neutrino oscillations: Synergies and tensions in the determination of θ23, δCP, and the mass ordering. JHEP 2019, 1, 106. [Google Scholar] [CrossRef]
- Chakrabortty, J.; Gluza, J.; Sevillano, R.; Szafron, R. Left-Right Symmetry at LHC and Precise 1-Loop Low Energy Data. JHEP 2012, 7, 38. [Google Scholar] [CrossRef] [Green Version]
- Bambhaniya, G.; Chakrabortty, J.; Gluza, J.; Kordiaczyńska, M.; Szafron, R. Left-Right Symmetry and the Charged Higgs Bosons at the LHC. JHEP 2014, 5, 33. [Google Scholar] [CrossRef] [Green Version]
- Bambhaniya, G.; Chakrabortty, J.; Gluza, J.; Jeliński, T.; Kordiaczynska, M. Lowest limits on the doubly charged Higgs boson masses in the minimal left-right symmetric model. Phys. Rev. 2014, D90, 095003. [Google Scholar] [CrossRef] [Green Version]
- Chakrabortty, J.; Gluza, J.; Jelinski, T.; Srivastava, T. Theoretical constraints on masses of heavy particles in Left-Right Symmetric Models. Phys. Lett. 2016, B759, 361–368. [Google Scholar] [CrossRef] [Green Version]
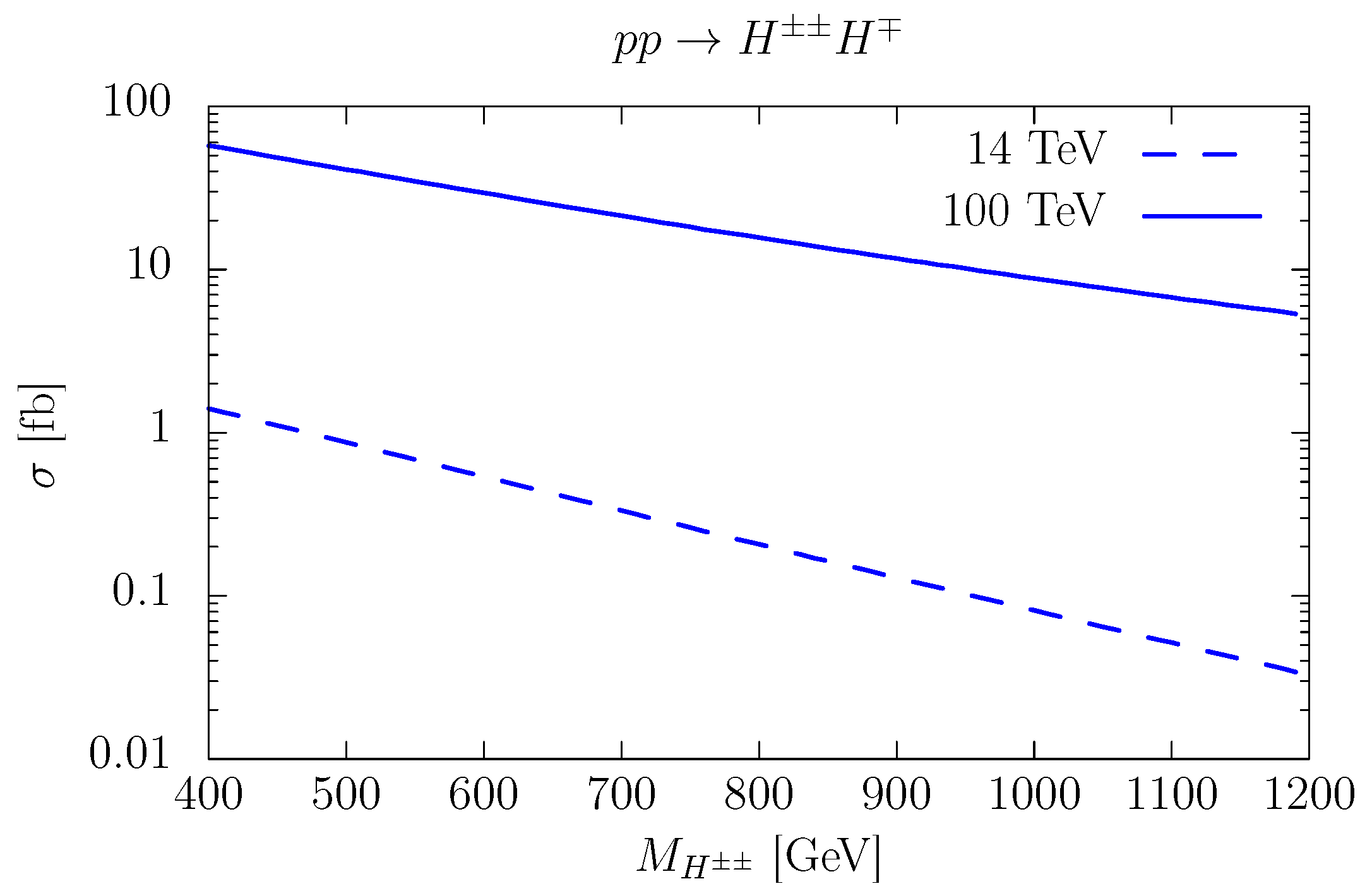
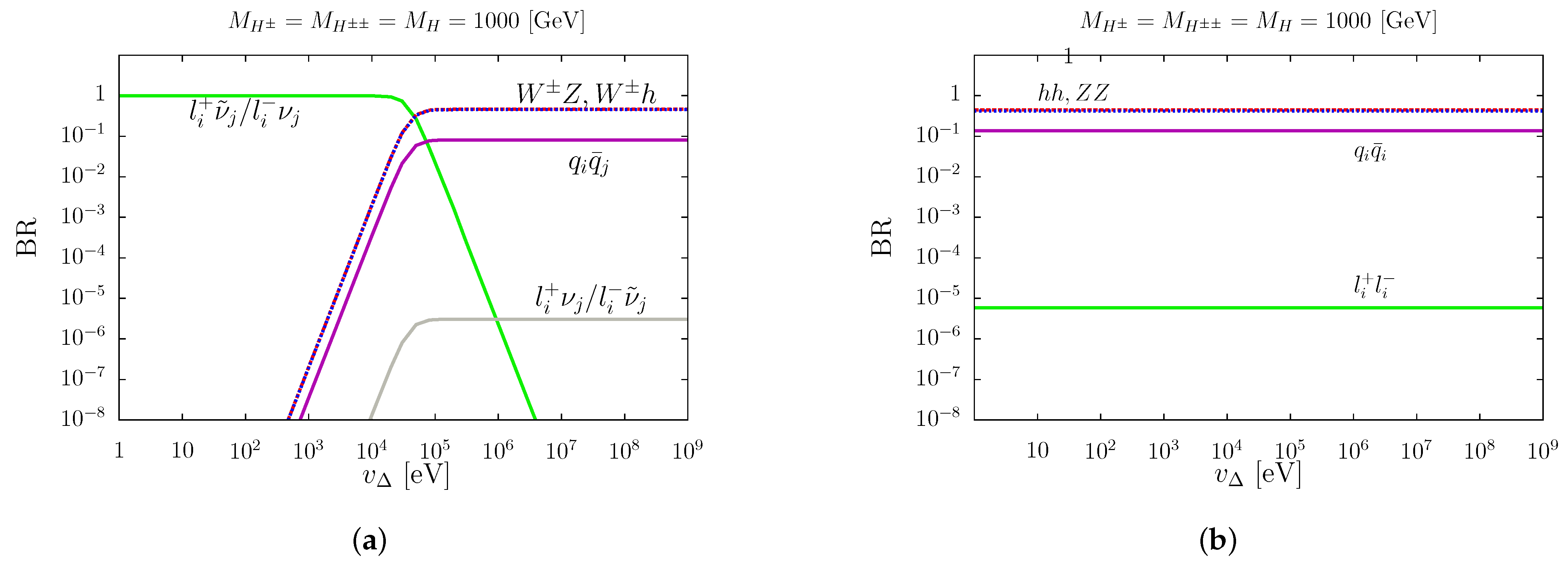
| Process | Cross Section [pb] | Process | Cross Section [pb] | ||
|---|---|---|---|---|---|
| ∼ | |||||
| (∼) | () | ||||
| ∼ | |||||
| () | () | ||||
| ∼ | ∼ | ||||
| () | () | ||||
| () | () | ||||
| ∼ | |||||
| () | (∼) | ||||
| ∼ | |||||
| (∼) | |||||
| Decay Channel | Coupling | Decay Channel | Coupling | Decay Channel | Coupling |
|---|---|---|---|---|---|
| ∼ | ∼ | ∼ | |||
| ∼ | ∼ | ∼ | |||
| ∼ | ∼ | ∼ | |||
| ∼ | ∼ |
| = 50 eV | → | → | ||||
| = 0.5 GeV | → | → | ||||
| Process: | Signal [pb]: | Background [pb]: | |||
|---|---|---|---|---|---|
| 50 eV | → | 1.79 × | 5.05 × | ||
| (2.00 × ) | (3.15 × ) | ||||
| 1.43 × | 5.05 × | ||||
| (1.55 × ) | (3.15 × ) | ||||
| 0.5 GeV | → | 3.62 × | 7.00 × | ||
| (3.93 × ) | (1.60 × | ||||
| 3.53 × | 6.19 × | ||||
| (3.84 × ) | (1.12 × ) | ||||
| 3.68 × | 3.09 × | ||||
| (4.01 × ) | (5.65) | ||||
| Process: | Signal: | Background: | ||
|---|---|---|---|---|
| Before Cuts [pb]: | After Cuts [fb]: | Before Cuts [pb]: | After Cuts [fb]: | |
| 1.79 × | 5.46 × | 5.05 × | 0.94 | |
| 1.43 × | 9.68 × | 5.05 × | 1.77 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dziewit, B.; Kordiaczyńska, M.; Srivastava, T. Production of the Doubly Charged Higgs Boson in Association with the SM Gauge Bosons and/or Other HTM Scalars at Hadron Colliders. Symmetry 2021, 13, 1240. https://doi.org/10.3390/sym13071240
Dziewit B, Kordiaczyńska M, Srivastava T. Production of the Doubly Charged Higgs Boson in Association with the SM Gauge Bosons and/or Other HTM Scalars at Hadron Colliders. Symmetry. 2021; 13(7):1240. https://doi.org/10.3390/sym13071240
Chicago/Turabian StyleDziewit, Bartosz, Magdalena Kordiaczyńska, and Tripurari Srivastava. 2021. "Production of the Doubly Charged Higgs Boson in Association with the SM Gauge Bosons and/or Other HTM Scalars at Hadron Colliders" Symmetry 13, no. 7: 1240. https://doi.org/10.3390/sym13071240
APA StyleDziewit, B., Kordiaczyńska, M., & Srivastava, T. (2021). Production of the Doubly Charged Higgs Boson in Association with the SM Gauge Bosons and/or Other HTM Scalars at Hadron Colliders. Symmetry, 13(7), 1240. https://doi.org/10.3390/sym13071240






