On Consensus Index of Triplex Star-like Networks: A Graph Spectra Approach
Abstract
:1. Introduction
- Several novel layered star-like networks with different linking structures but the same number of nodes have been constructed by applying graph operations.
- Graph spectra methods are applied to derive the Laplacian spectrums through the calculations of network coherence, and several new results on the asymptotic behavior have been acquired.
- This article gives the notion that some nodes with low degree, for instance, the leaf nodes, might only have connections within the same layer other than connections with the counterpart nodes in different layers.
2. Preliminaries
2.1. Graph Theory and Notations
- (i)
- Two multiplicity one eigenvalues for each eigenvalue of ;
- (ii)
- with multiplicity for every eigenvalue of .
2.2. Descriptions of Consensus Index with Laplacian Spectrum
- (i)
- First order case.
- (i)
- Second order case.
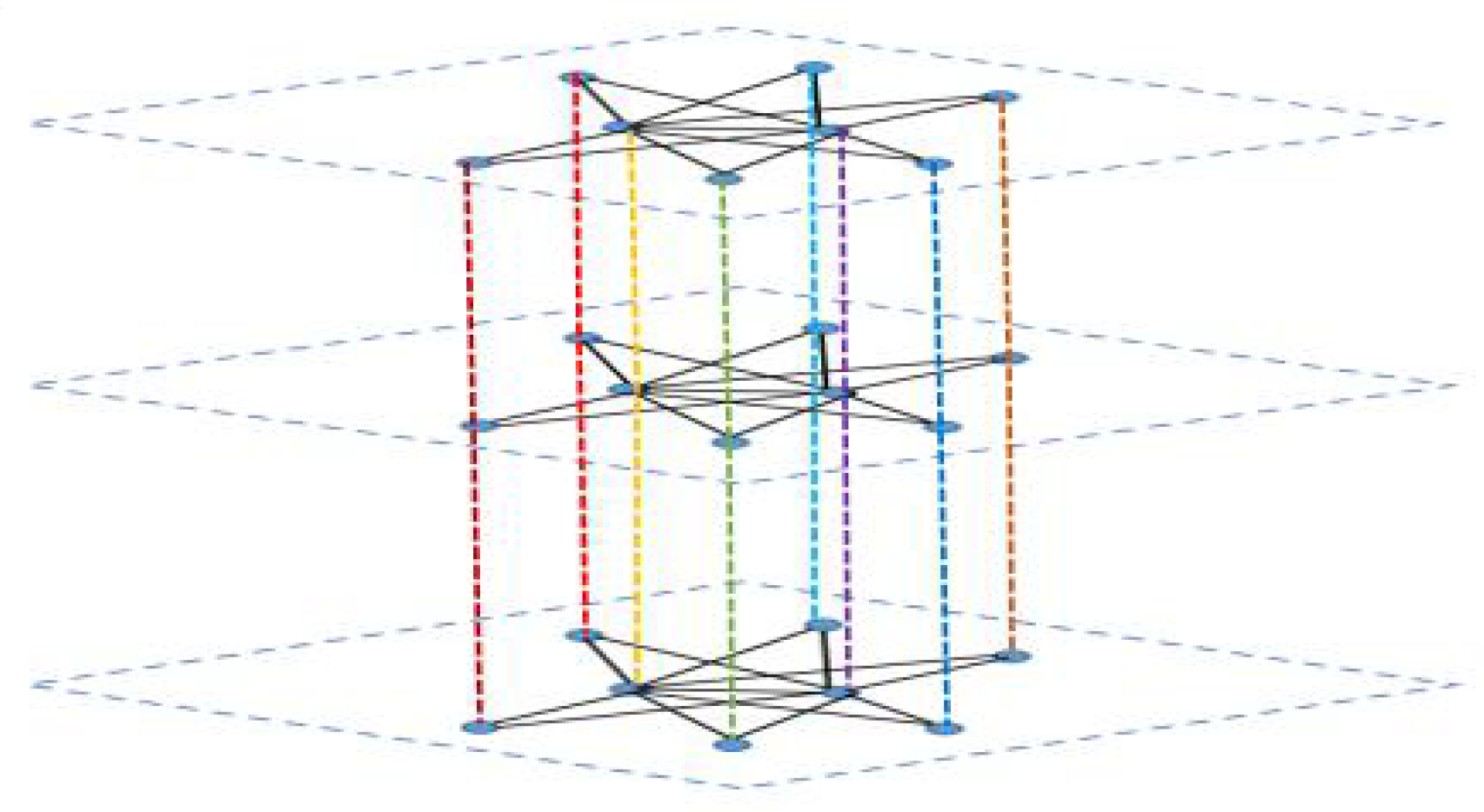
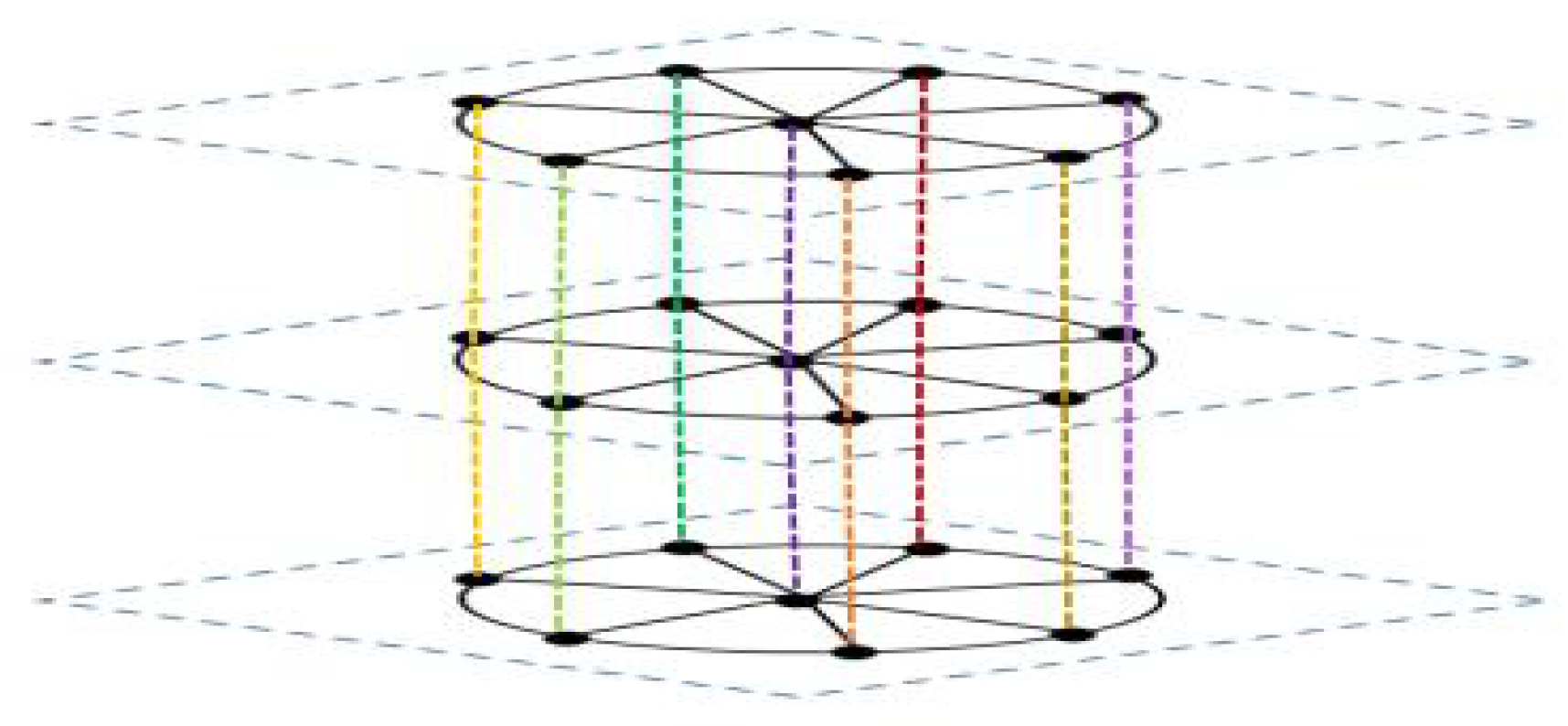
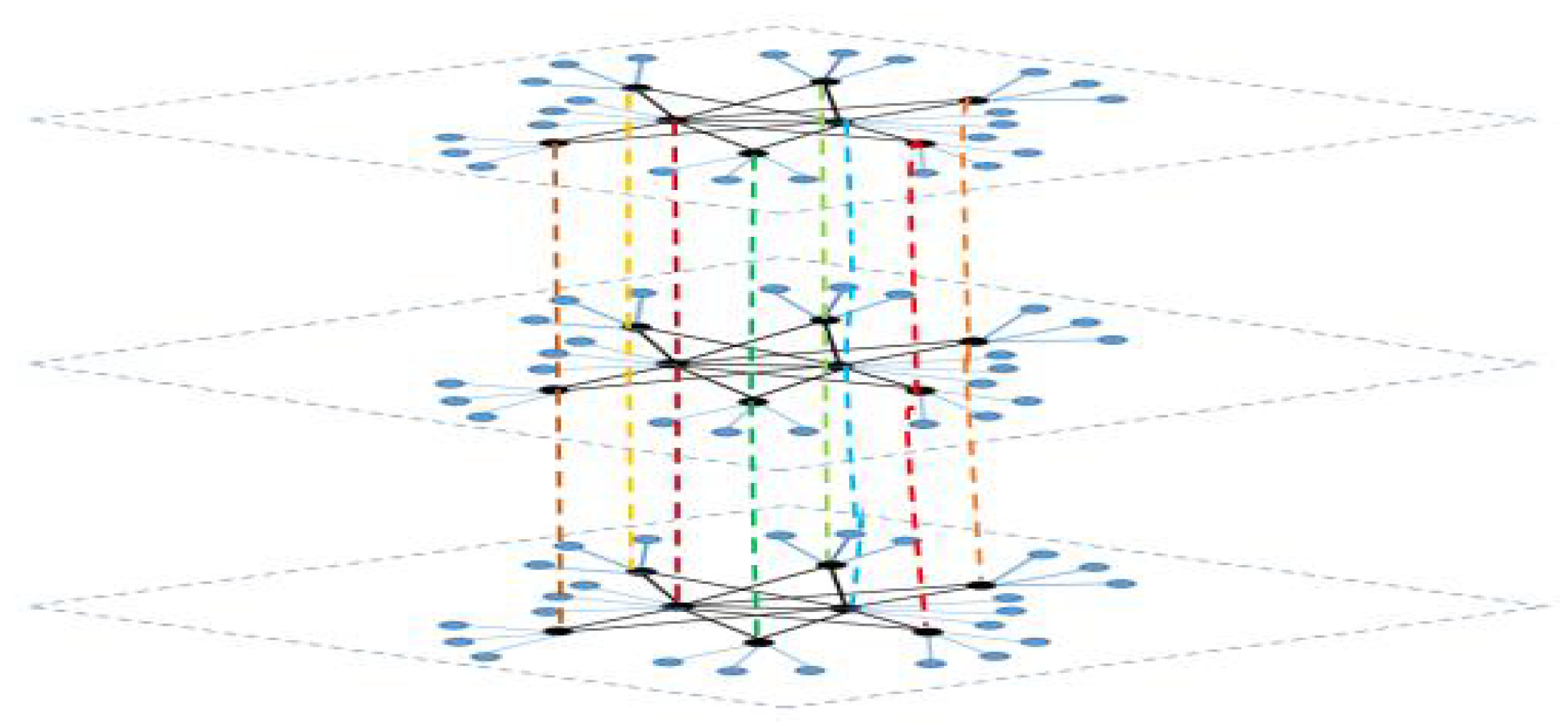
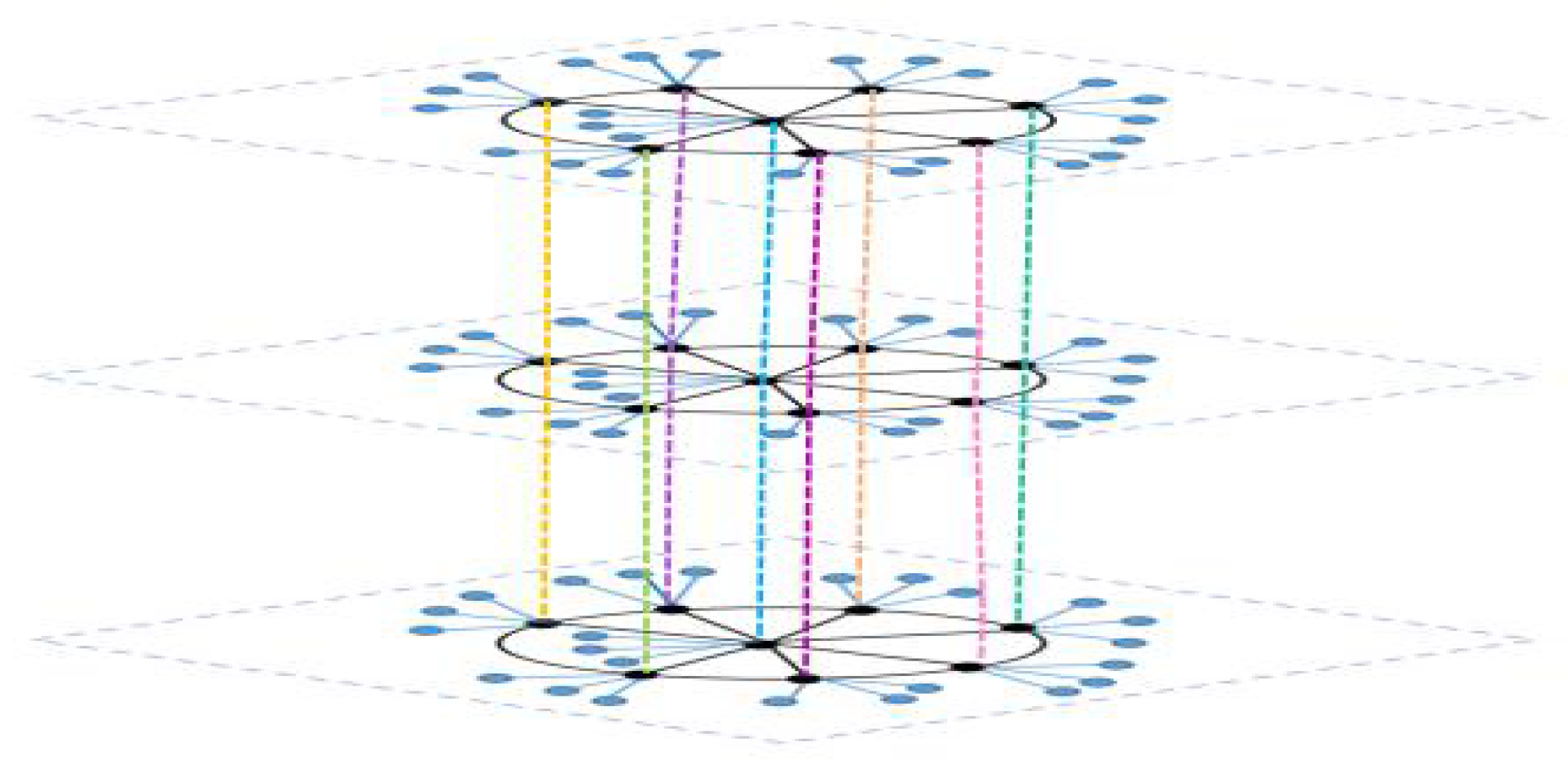
3. Model Description and Main Results
3.1. The Consensus Indices for Network Topology
3.2. The Consensus Indices for Network Topology
3.3. The Consensus Indices for Network Topology
- (1)
- and with multiplicity 1;
- (2)
- with multiplicity 1;
- (3)
- with multiplicity n;
- (4)
- with multiplicity 2;
- (5)
- with multiplicity 2;
- (6)
- with multiplicity ;
- (7)
- with multiplicity 2;
- (8)
- with multiplicity .
- (9)
- with multiplicity .
3.4. The Consensus Indices for Network Topology
- (1)
- with multiplicity 1;
- (2)
- with multiplicity 1;
- (3)
- with multiplicity 1;
- (4)
- with multiplicity 1, ;
- (5)
- with multiplicity 1;
- (6)
- with multiplicity 1;
- (7)
- with multiplicity 1, ;
- (8)
- with multiplicity 1;
- (9)
- with multiplicity 1, .
- (10)
- with multiplicity .
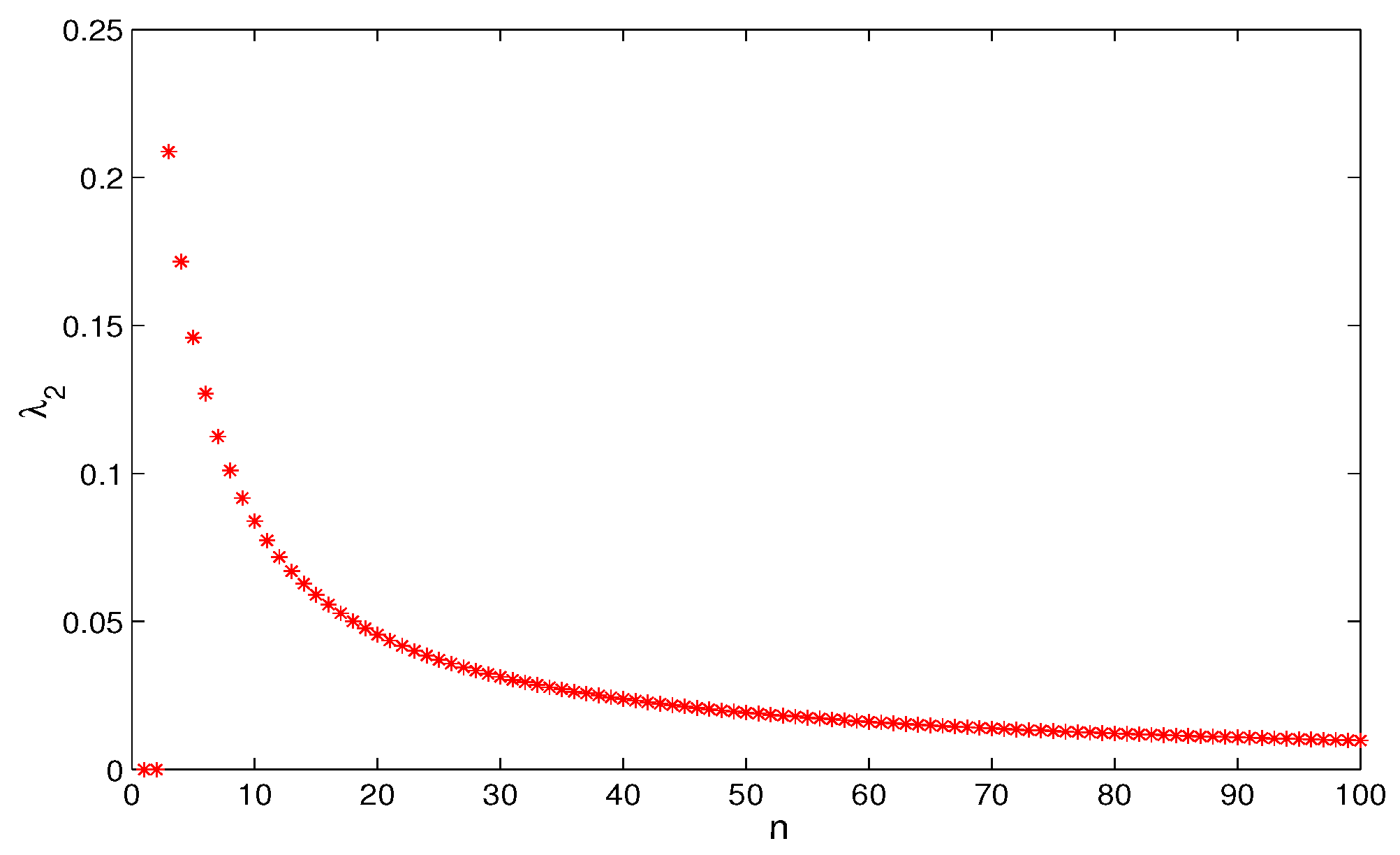
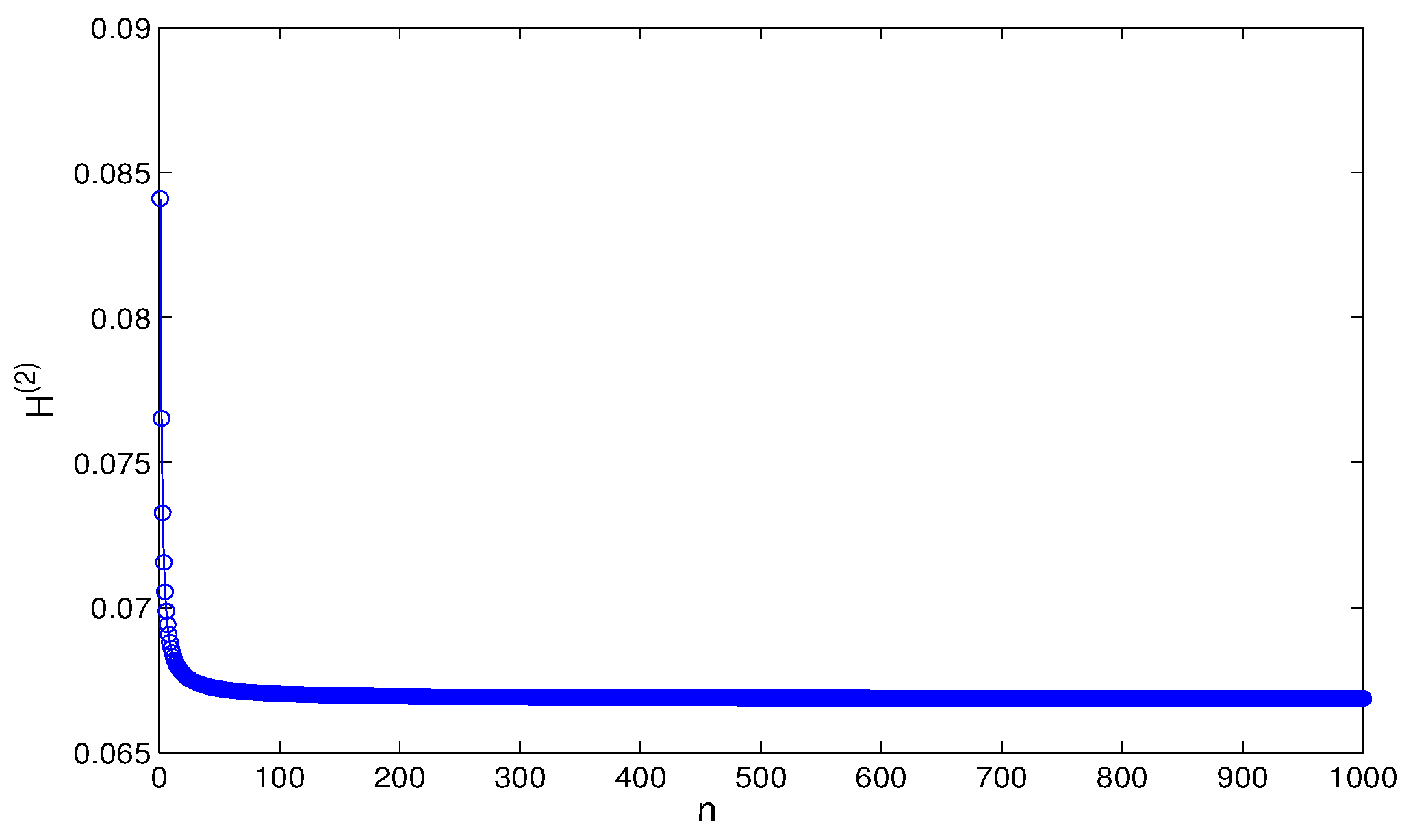
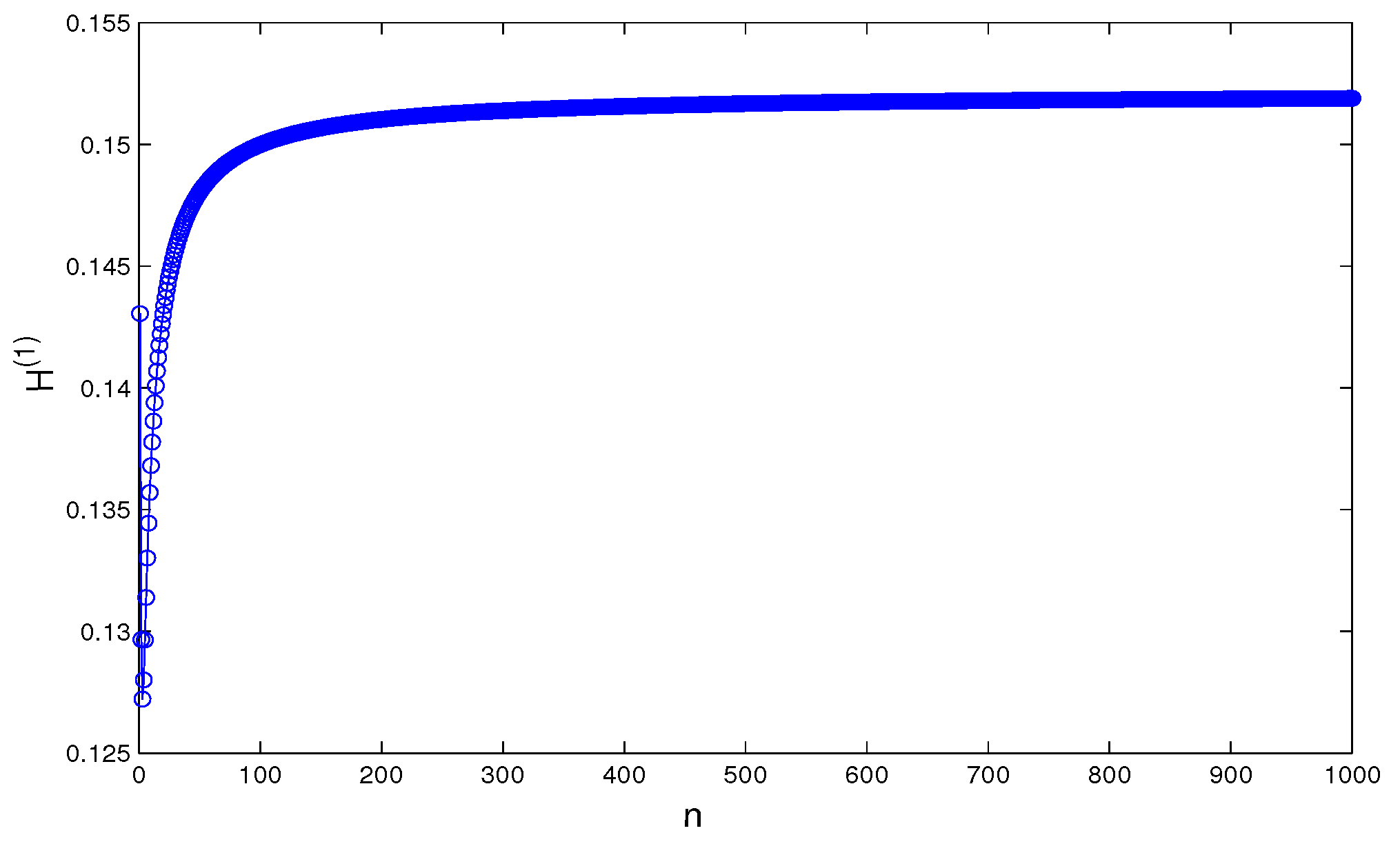
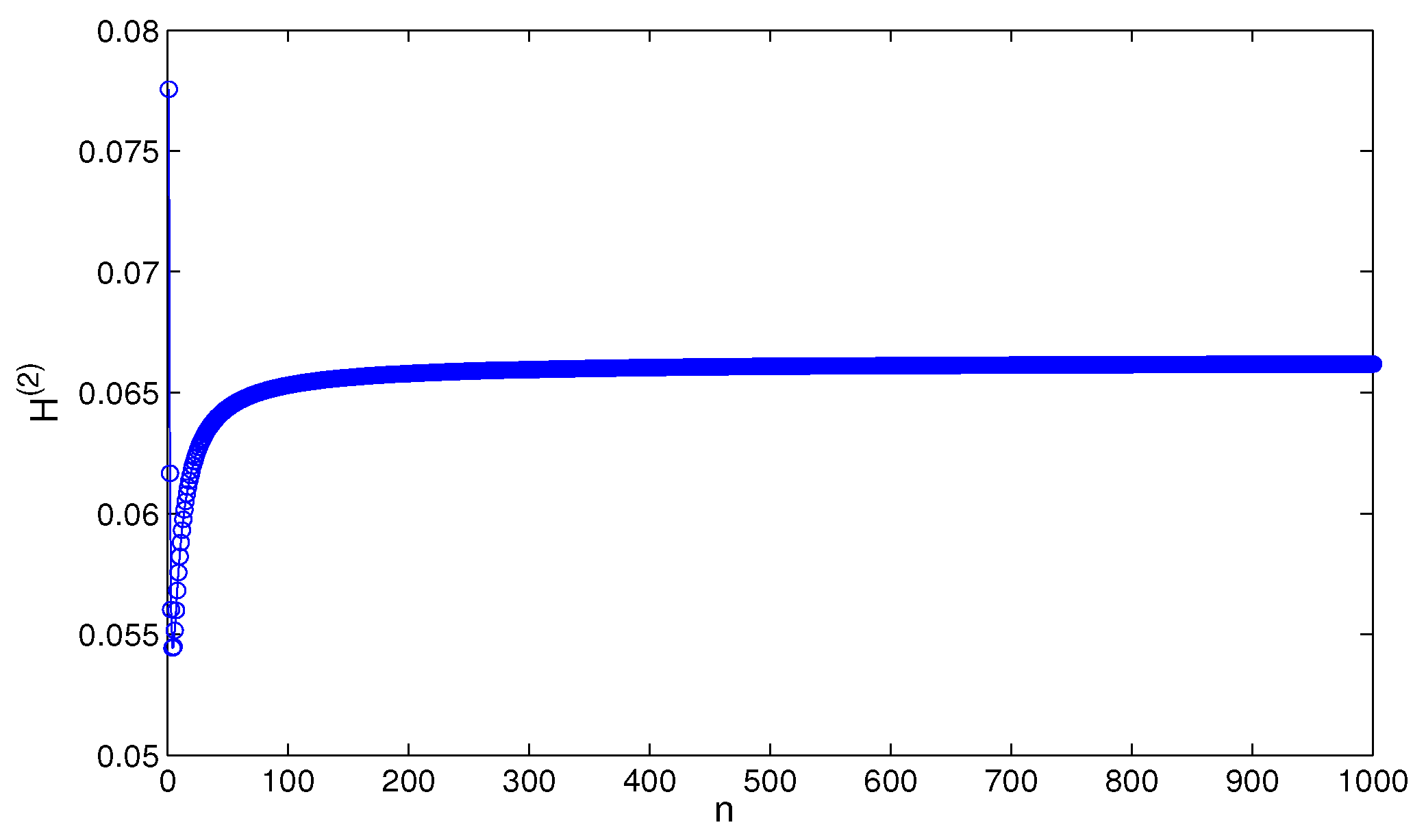
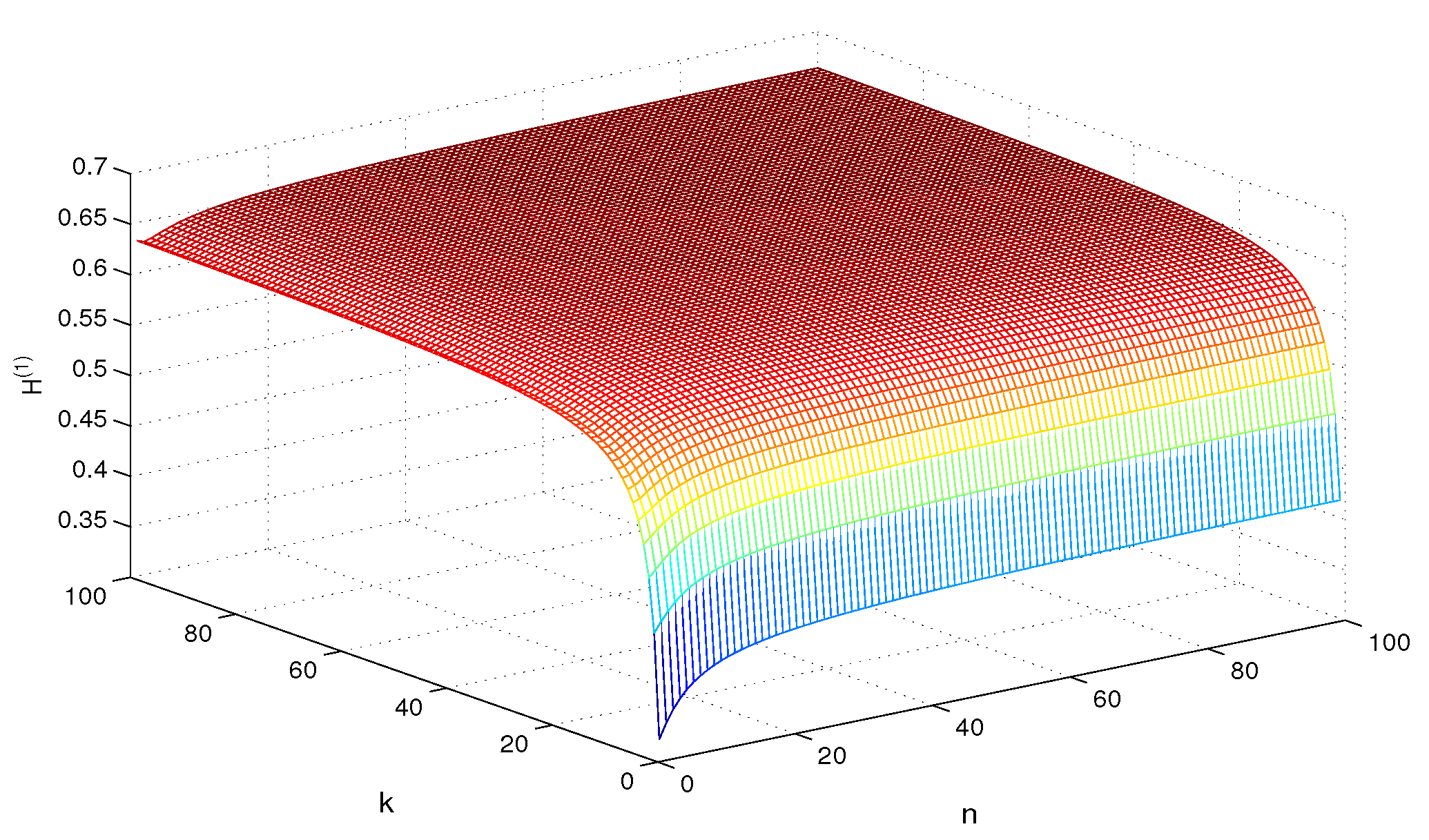
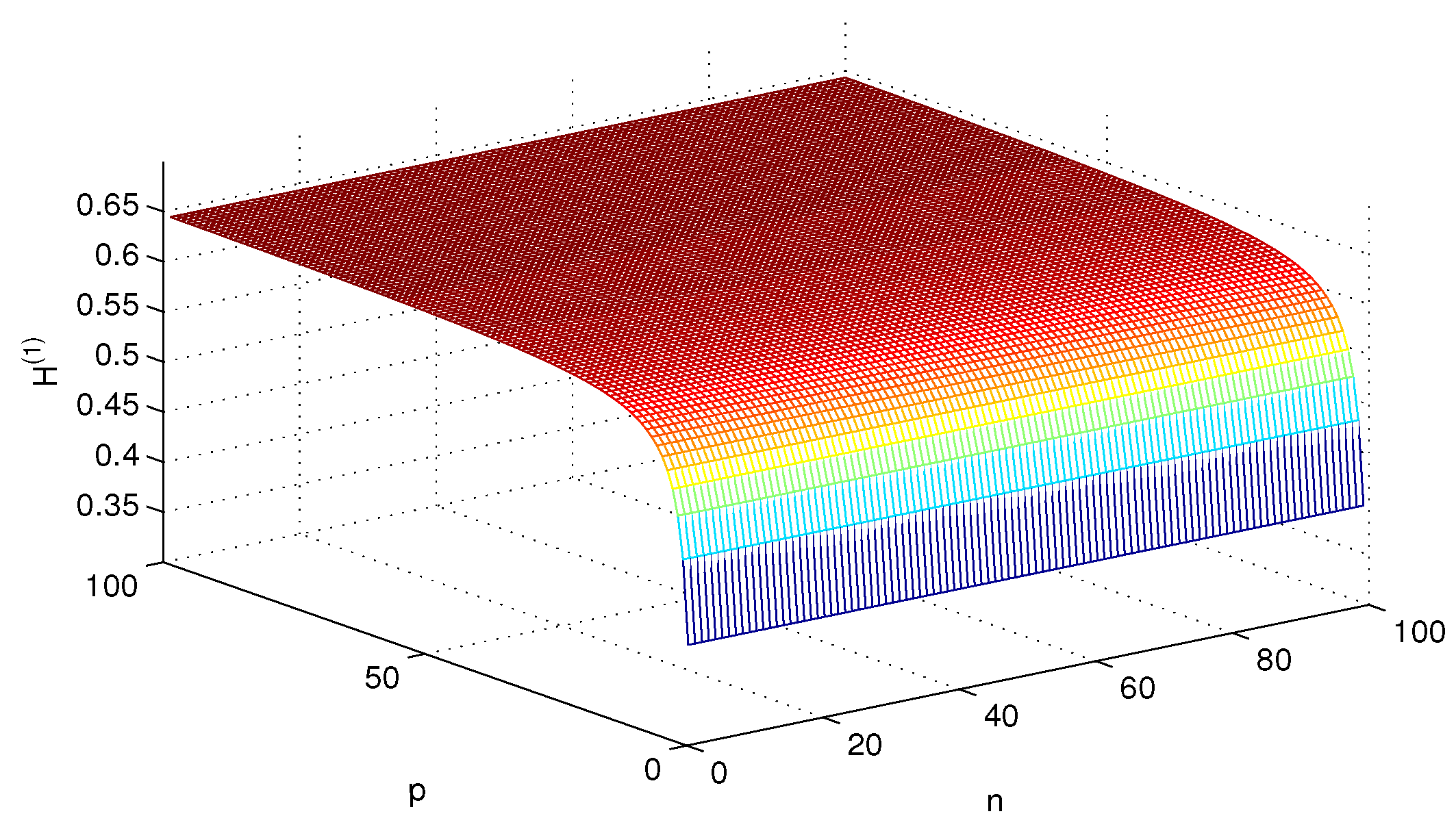
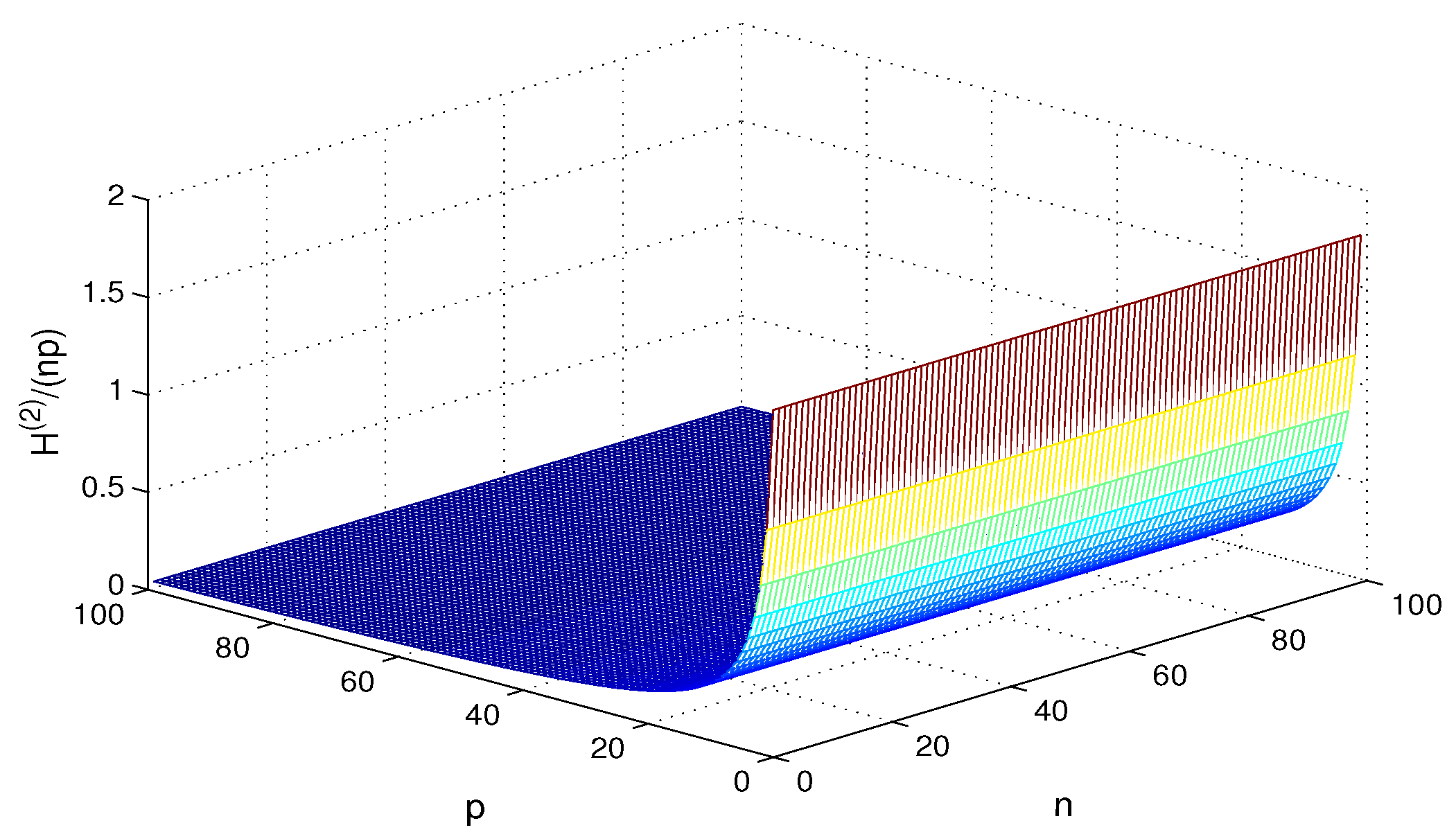
4. Simulation and Comparison
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.; Tian, Y.-P. Consensus tracking in sensor networks with periodic sensing and switching connected topologies. Syst. Control Lett. 2015, 84, 44–51. [Google Scholar] [CrossRef]
- Wen, G.; Chen, C.L.P.; Liu, Y.-J.; Liu, Z. Neural Network-Based Adaptive Leader-Following Consensus Control for a Class of Nonlinear Multiagent State-Delay Systems. IEEE Trans. Cybern. 2016, 47, 2151–2160. [Google Scholar] [CrossRef]
- Liang, C.-D.; Wang, L.; Yao, X.-Y.; Liu, Z.-W.; Ge, M.-F. Multi-target tracking of networked heterogeneous collaborative robots in task space. Nonlinear Dyn. 2019, 97, 1159–1173. [Google Scholar] [CrossRef]
- Saber, O.; Murray, R. Consensus problems in Networks of Agents With Switching Topology and Time-Delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef] [Green Version]
- Ren, W. On consensus algorithms for double-integrator dynamics. IEEE Trans. Autom. Control 2008, 53, 1503–1509. [Google Scholar] [CrossRef]
- Yu, W.; Chen, G.; Cao, M.; Kurths, J. Second-order consensus for multiagent systems with directed topologies and nonlinear dynamics. IEEE Trans. Syst. Man Cybern.-Part Cybern. 2010, 40, 881–891. [Google Scholar]
- Wen, G.; Duan, Z.; Yu, W.; Chen, G. Consensus of second-order multi-agent systems with delayed nonlinear dynamics and intermittent communications. Int. J. Control 2013, 86, 322–331. [Google Scholar] [CrossRef]
- Ma, J.; Zheng, Y.; Wang, L. LQR-based optimal topology of leader-following consensus. Int. J. Robust Nonlinear Control 2014, 25, 3404–3421. [Google Scholar] [CrossRef]
- Li, J.; Feng, T.; Zhang, J.; Yan, F. Optimal distributed cooperative control for multi-agent systems with constrains on convergence speed and control input. Neurocomputing 2021, 426, 14–25. [Google Scholar] [CrossRef]
- Sun, Y.; Li, W.; Zhao, D. Convergence time and speed of multi-agent systems in noisy environments. Chaos Interdiscip. J. Nonlinear Sci. 2012, 22, 43126. [Google Scholar] [CrossRef] [PubMed]
- Young, G.F.; Scardovi, L.; Leonard, N.E. Robustness of noisy consensus dynamics with directed communication. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 6312–6317. [Google Scholar]
- Xiao, L.; Boyd, S.; Kim, S.-J. Distributed average consensus with least-mean-square deviation. J. Parallel Distrib. Comput. 2007, 67, 33–46. [Google Scholar] [CrossRef] [Green Version]
- Patterson, S.; Bamieh, B. Network coherence in fractal graphs. In Proceedings of the IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 6445–6450. [Google Scholar]
- Bamieh, B.; Jovanovi, M.R.; Mitra, P.; Patterson, S. Coherence in large-scale networks: Dimension-dependent limitations of local feedback. Trans. Autom. Control 2012, 57, 2235–2249. [Google Scholar] [CrossRef] [Green Version]
- Patterson, S.; Bamieh, B. Consensus and Coherence in Fractal Networks. IEEE Trans. Control Netw. Syst. 2014, 1, 338–348. [Google Scholar] [CrossRef]
- Yi, Y.; Zhang, Z.; Shan, L.; Chen, G. Robustness of First- and Second-Order Consensus Algorithms for a Noisy Scale-Free Small-World Koch Network. IEEE Trans. Control Syst. Technol. 2017, 25, 342–350. [Google Scholar] [CrossRef]
- Sun, W.; Ding, Q.; Zhang, J.; Chen, F. Coherence in a family of tree networks with an application of Laplacian spectrum. Chaos: Interdiscip. J. Nonlinear Sci. 2014, 24, 043112. [Google Scholar] [CrossRef]
- Sun, W.; Li, Y.; Liu, S. Noisy consensus dynamics in windmill-type graphs. Chaos: Interdiscip. J. Nonlinear Sci. 2020, 30, 123131. [Google Scholar] [CrossRef]
- Dai, M.; Zhu, J.; Huang, F.; Li, Y.; Zhu, L.; Su, W. Coherence analysis for iterated line graphs of multi-subdivision graph. Fractals 2020, 28. [Google Scholar] [CrossRef]
- Wang, X.; Xu, H.; Dai, M. First-order network coherence in 5-rose graphs. Physica 2019, 527, 121129. [Google Scholar] [CrossRef]
- Zhou, B.; Liao, X. Leader-following second-order consensus in multi-agent systems with sampled data via pinning control. Nonlinear Dyn. 2014, 78, 555–569. [Google Scholar] [CrossRef]
- Yu, Z.; Jiang, H.; Huang, D.; Hu, C. Consensus of nonlinear multi-agent systems with directed switching graphs: A directed spanning tree based error system approach. Nonlinear Anal. Hybrid Syst. 2018, 28, 123–140. [Google Scholar] [CrossRef]
- Yu, Z.; Huang, D.; Jiang, H.; Hu, C. Consensus of second-order multi-agent systems with nonlinear dynamics via edge-based distributed adaptive protocols. J. Frankl. Inst. 2016, 353, 4821–4844. [Google Scholar] [CrossRef]
- Hu, J.; Hong, Y.; Feng, G. Distributed dynamic control for leaderless multi-agent consensus with star-like topology. Asian J. Control 2008, 10, 233–237. [Google Scholar] [CrossRef]
- Abdolyousefi, M.N.; Mesbahi, M. On the Controllability Properties of Circulant Networks. IEEE Trans. Autom. Control 2013, 58, 3179–3184. [Google Scholar] [CrossRef]
- Wen, G.; Yu, W.; Wang, J.; Xu, D.; Cao, J. Distributed node-to-node consensus of multi-agent systems with time-varying pinning links. Neurocomputing 2015, 149, 1387–1395. [Google Scholar] [CrossRef]
- Li, H.-L.; Cao, J.; Jiang, H.; Alsaedi, A. Graph theory-based finite-time synchronization of fractional-order complex dynamical networks. J. Frankl. Inst. 2018, 355, 5771–5789. [Google Scholar] [CrossRef]
- Xu, M.; Lu, J.; Zhou, J. Synchronizability and eigenvalues of two-layer star networks. Acta Phys. Sin. 2016, 65, 028902. [Google Scholar]
- Liu, H.; Xu, J.; Li, Z.; Wang, X.; Lu, J.; Zeng, Z. Optimizing Synchronizability of Multilayer Networks Based on the Graph Comparison Method. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 1740–1751. [Google Scholar] [CrossRef]
- He, W.; Xu, Z.; Du, W.; Chen, G.; Kubota, N.; Qian, F. Synchronization control in multiplex networks of nonlinear multi-agent systems. Chaos: Interdiscip. J. Nonlinear Sci. 2017, 27, 123104. [Google Scholar] [CrossRef]
- Lu, R.; Yu, W.; Lu, J.; Xue, A. Synchronization on Complex Networks of Networks. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 2110–2118. [Google Scholar] [CrossRef]
- Hu, C.; Jiang, H. Cluster synchronization for directed community networks via pinning partial schemes. Chaos Solitons Fractals 2012, 45, 1368–1377. [Google Scholar] [CrossRef]
- Hu, C.; He, H.; Jiang, H. Synchronization of complex-valued dynamic networks with intermittently adaptive coupling: A direct error method. Automatica 2020, 112, 108675. [Google Scholar] [CrossRef]
- He, W.; Chen, G.; Han, Q.-L.; Du, W.; Cao, J.; Qian, F. Multiagent Systems on Multilayer Networks: Synchronization Analysis and Network Design. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1655–1667. [Google Scholar] [CrossRef]
- Wang, Z.; Xia, C.; Chen, Z.; Chen, G. Epidemic Propagation With Positive and Negative Preventive Information in Multiplex Networks. IEEE Trans. Cybern. 2021, 51, 1454–1462. [Google Scholar] [CrossRef]
- Kivelä, M.; Arenas, A.; Barthelemy, M.; Gleeson, J.P.; Moreno, Y.; Porter, M.A. Multilayer Networks. J. Complex Netw. 2014, 2, 203. [Google Scholar]
- Barik, S.; Pati, S.; Sarma, B.K. The Spectrum of the Corona of Two Graphs. SIAM J. Discret. Math. 2007, 21, 47–56. [Google Scholar] [CrossRef]
- Liu, Q. The Laplacian spectrum of corona of two graphs. Kragujev. J. Math. 2014, 38, 163–170. [Google Scholar] [CrossRef]
- Douglas, B. West, Introduction to Graph Theory, 2nd ed.; Pearson Education: Hong Kong, China, 2004. [Google Scholar]
- Huang, D.; Zhang, Z. On cyclic vertex-connectivity of Cartesian product digraphs. J. Comb. Optim. 2012, 24, 379–388. [Google Scholar] [CrossRef]
- Cvetkovic, D.; Rowlinson, P.; Simic, S. An Introduction to the Theory of Graph Spectra; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Zhang, H.; Yang, Y. Resistance distance and Kirchhoff index in circulant graphs. Int. J. Quantum Chem. 2007, 107, 330–339. [Google Scholar] [CrossRef]
- Xu, P.; Huang, Q. The Kirchhoff index of enhanced hypercubes. arXiv 2018, arXiv:1809.07189. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, D.; Zhu, J.; Yu, Z.; Jiang, H. On Consensus Index of Triplex Star-like Networks: A Graph Spectra Approach. Symmetry 2021, 13, 1248. https://doi.org/10.3390/sym13071248
Huang D, Zhu J, Yu Z, Jiang H. On Consensus Index of Triplex Star-like Networks: A Graph Spectra Approach. Symmetry. 2021; 13(7):1248. https://doi.org/10.3390/sym13071248
Chicago/Turabian StyleHuang, Da, Jian Zhu, Zhiyong Yu, and Haijun Jiang. 2021. "On Consensus Index of Triplex Star-like Networks: A Graph Spectra Approach" Symmetry 13, no. 7: 1248. https://doi.org/10.3390/sym13071248
APA StyleHuang, D., Zhu, J., Yu, Z., & Jiang, H. (2021). On Consensus Index of Triplex Star-like Networks: A Graph Spectra Approach. Symmetry, 13(7), 1248. https://doi.org/10.3390/sym13071248




