Atoms in Highly Symmetric Environments: H in Rhodium and Cobalt Cages, H in an Octahedral Hole in MgO, and Metal Atoms Ca-Zn in C20 Fullerenes
Abstract
:1. Introduction
1.1. Background
1.2. Hypercoordinated H Atom
“[We] discuss hydrogen as a substitutional impurity in the binary metal oxides ZnO and MgO. Contrary to expectations, hydrogen on a substitutional oxygen site forms genuine chemical bonds with all of its metal—atom nearest-neighbours, in a truly multicoordinated configuration.”
“hydrogen is equally bonded to all four Zn neighbours in ZnO, and to all six neighbours in MgO.”
1.3. Endohedral Atoms in Fullerenes
2. Systems Studied
2.1. H Atom Capture in Inorganic Vacancies
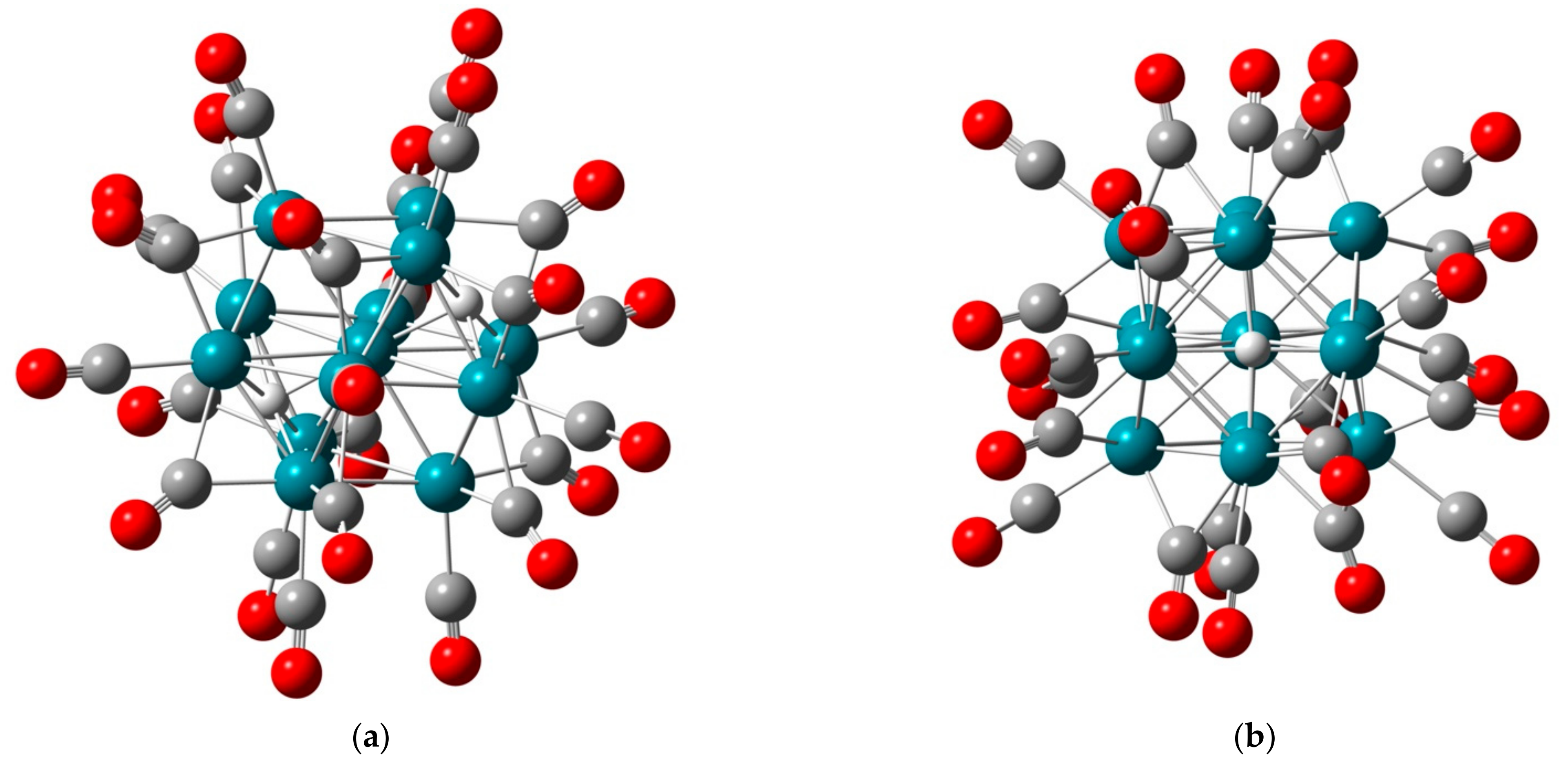
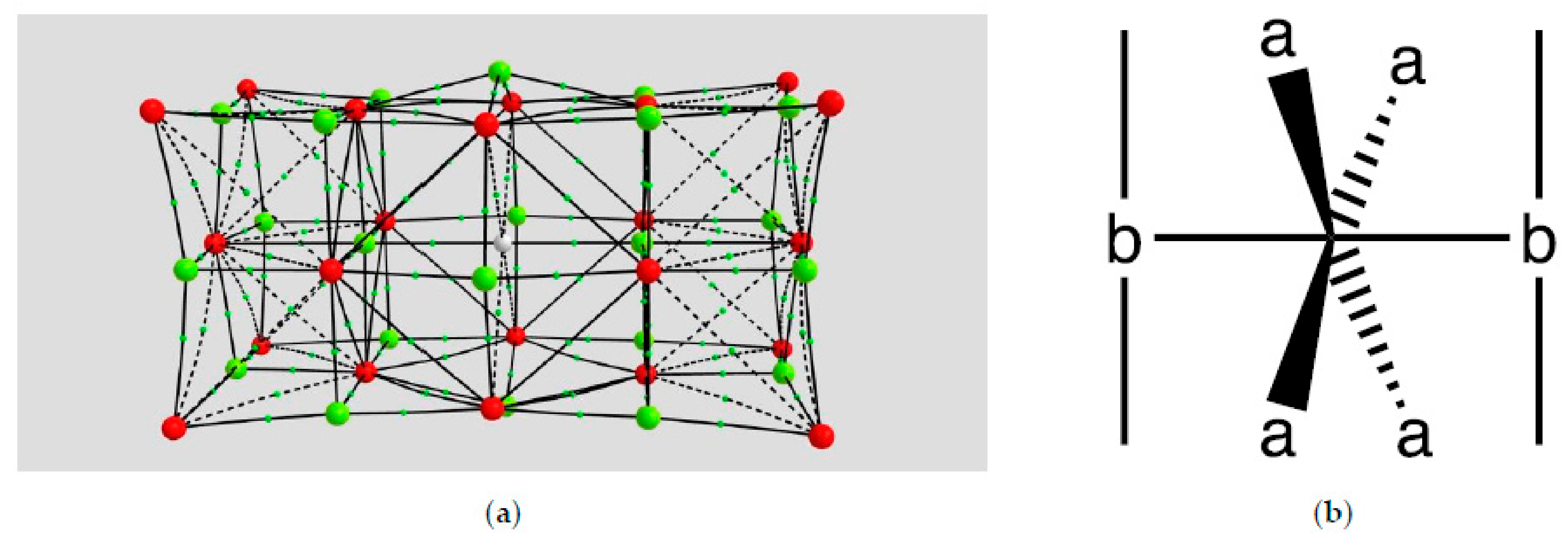
2.1.1. H Atoms in the Rhodium Square-Pyramidal Cages
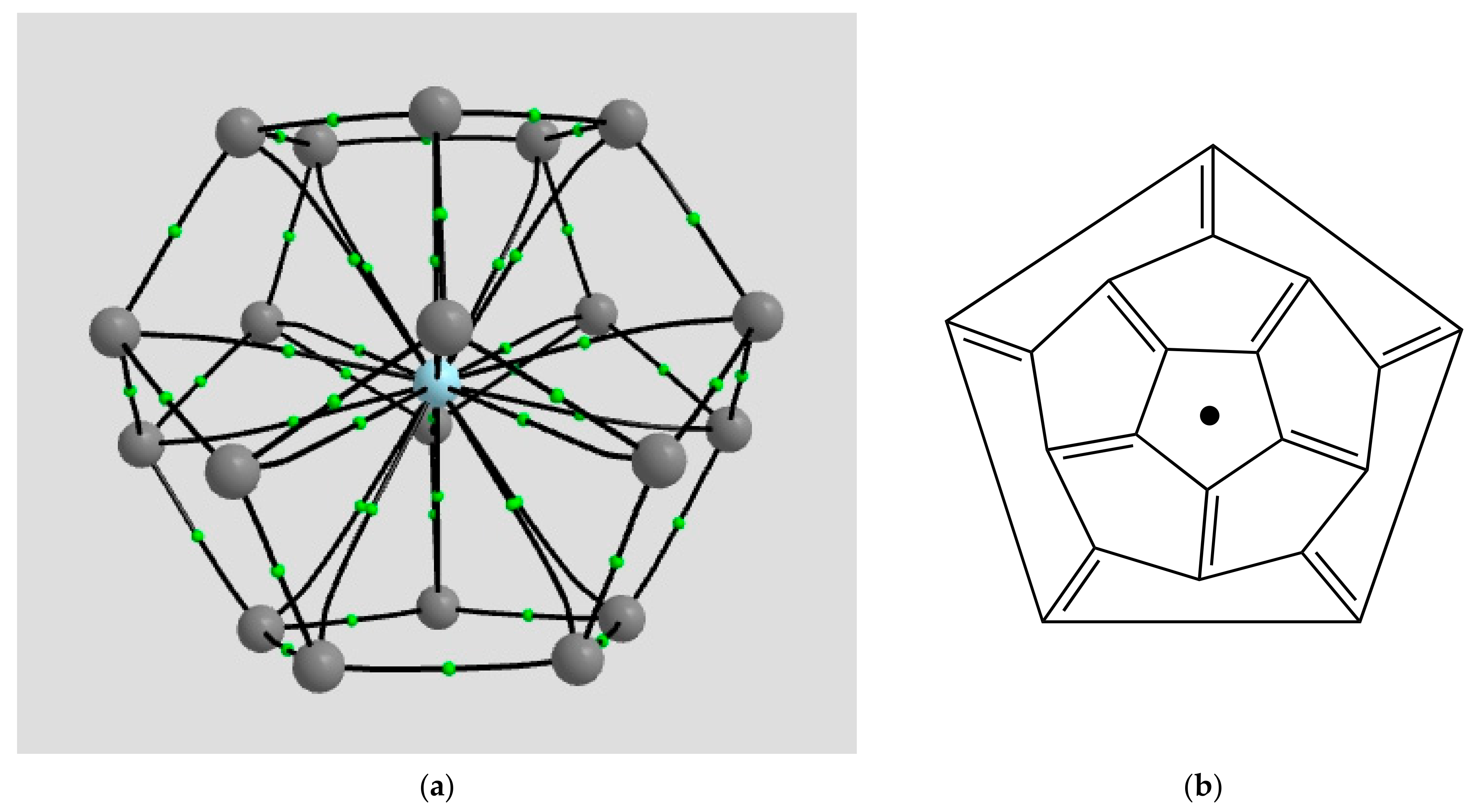
2.1.2. H Atom in a Cobalt Octahedral Cage
2.1.3. H Atom in a Magnesium Oxide Crystal Vacancy
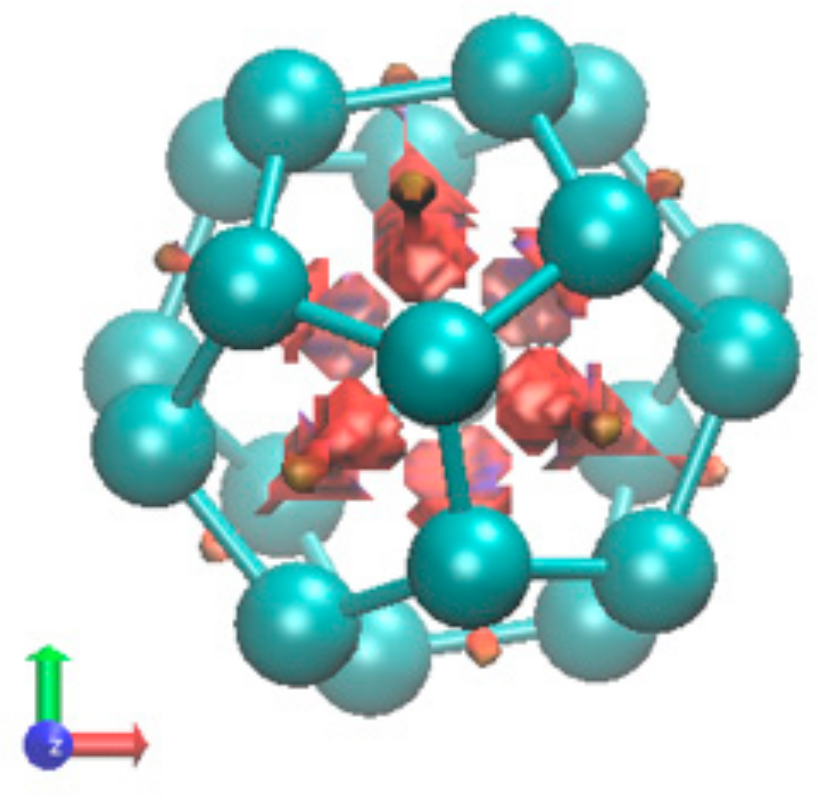
2.1.4. Endohedral M in C20 Fullerene
3. Methods and Software
4. Results
4.1. Captured H Atoms
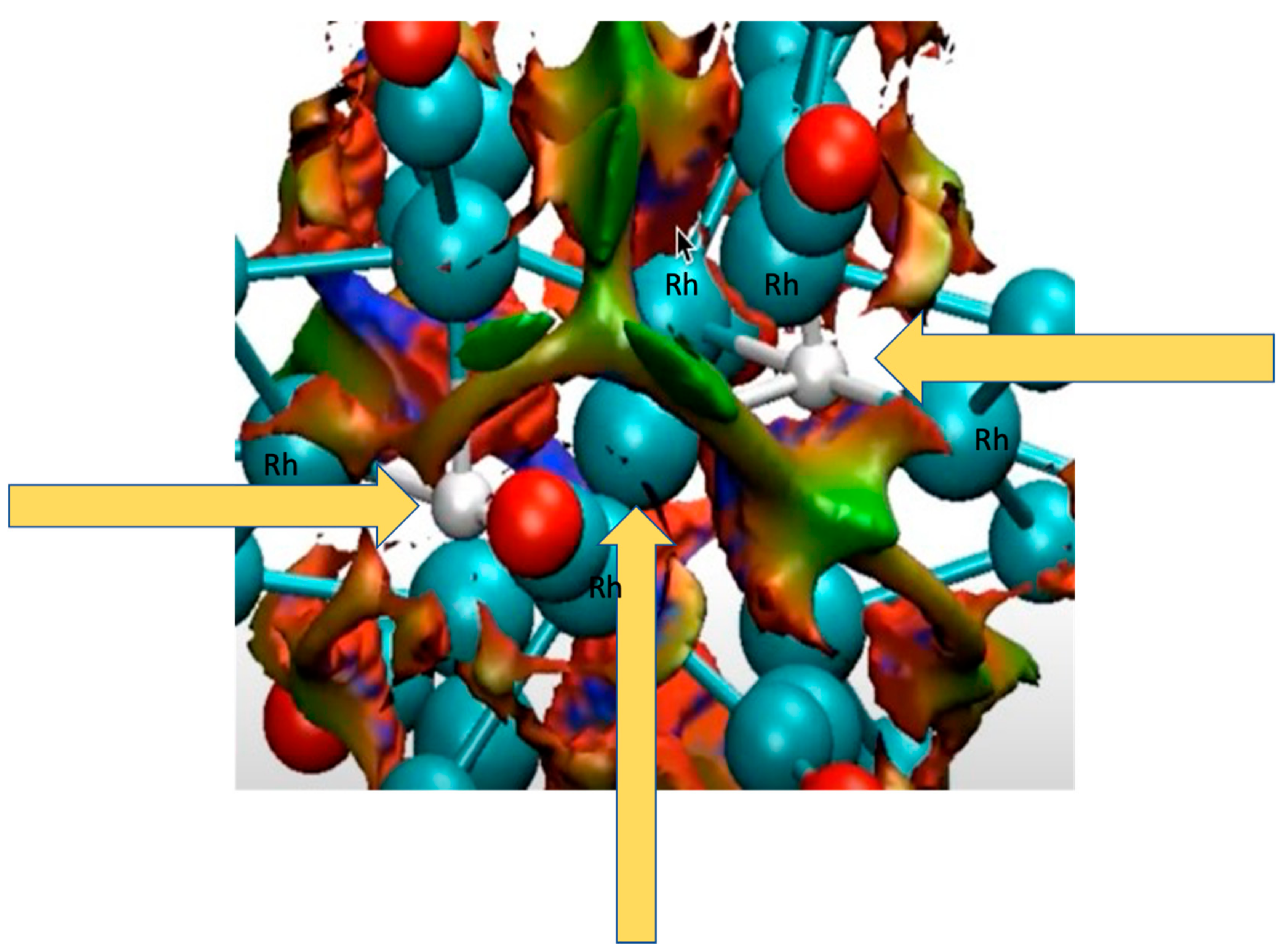
4.1.1. H Atoms in Rhodium Cages
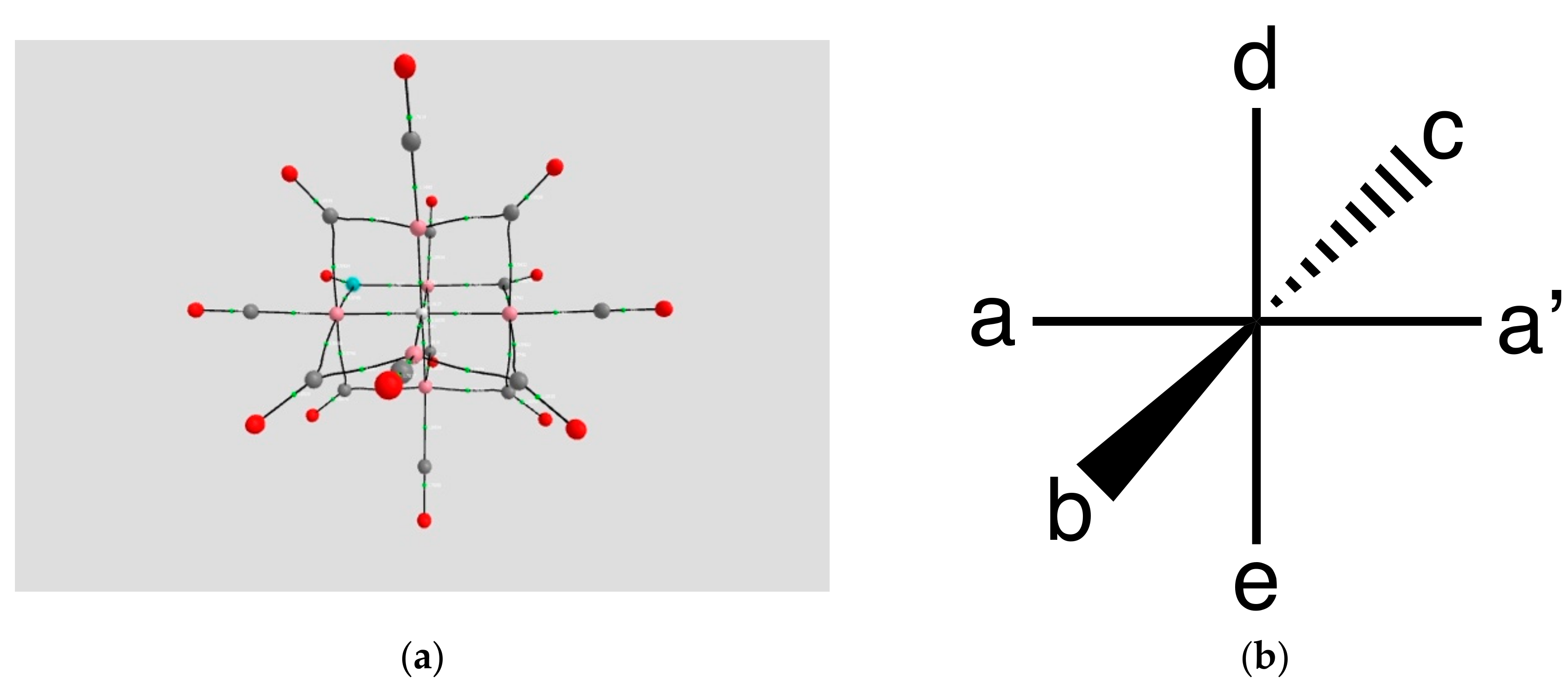
4.1.2. The H Atom Captured in a Six-Coordinate Cobalt Cage
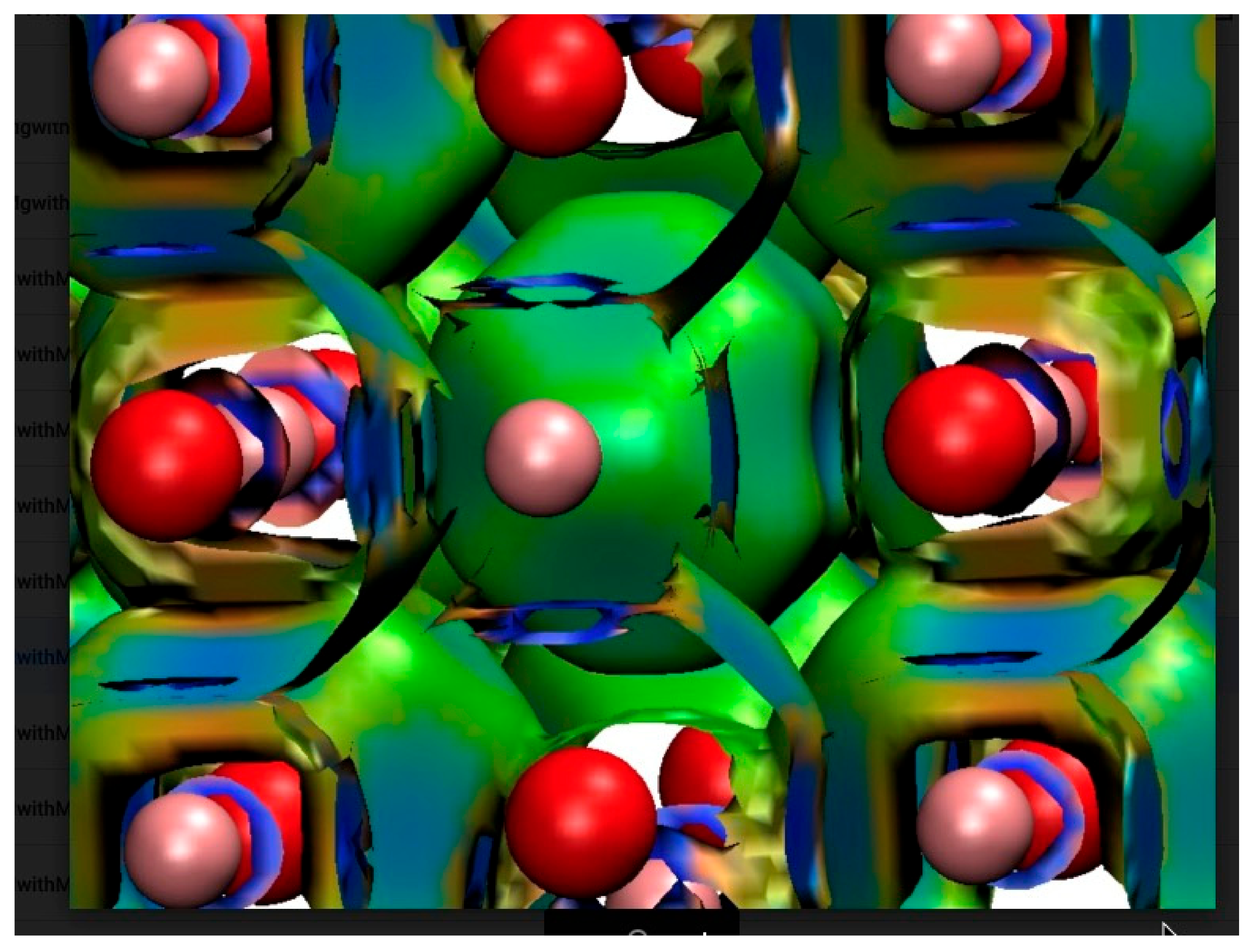
4.1.3. Hydrogen Atom in MgO
4.2. Neutral Metal Atoms in C20 Fullerene: Overview of Binding, QTAIM Interaction Ridges, and Non-Covalent Interactions
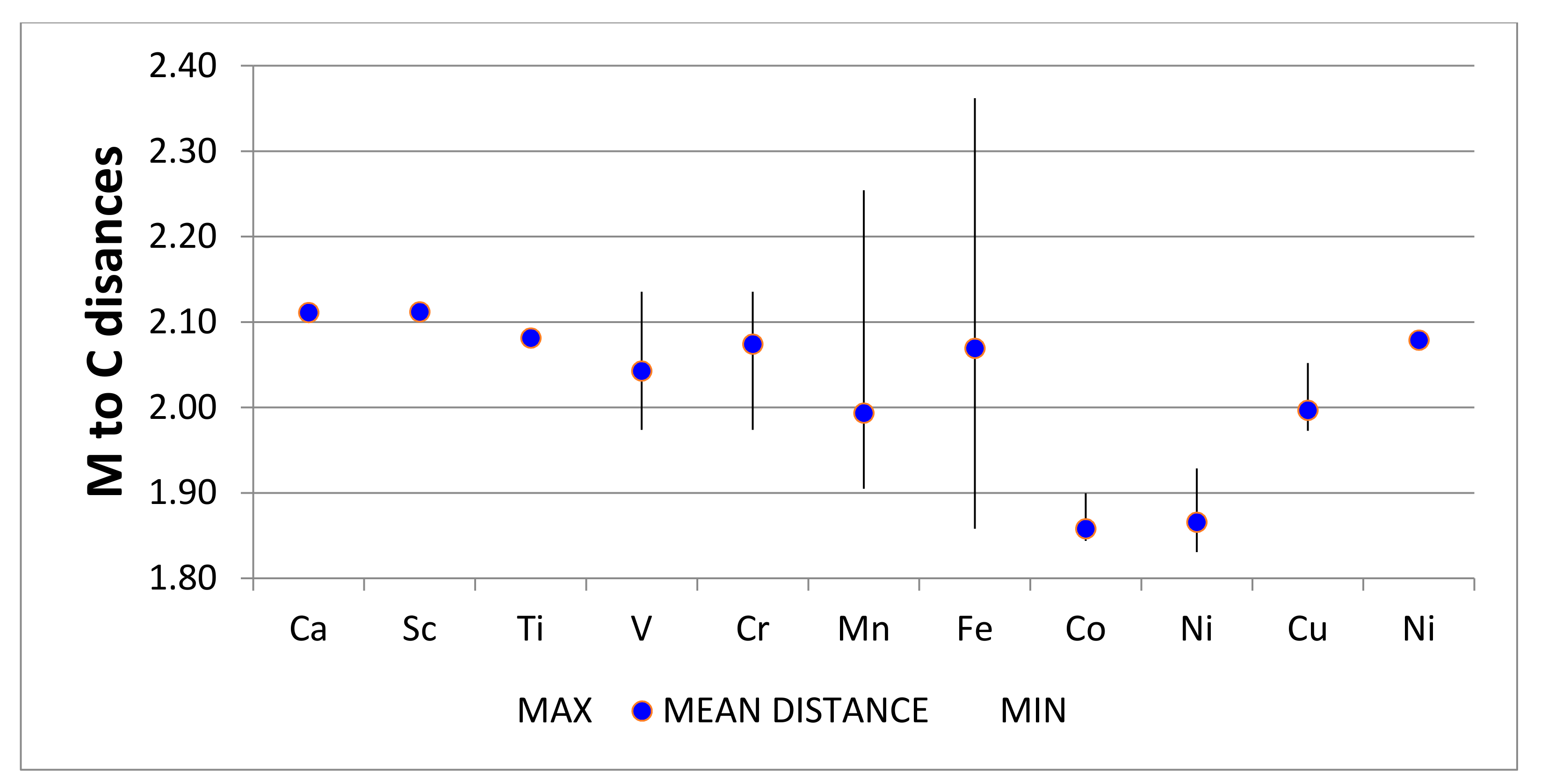
4.2.1. Energetics for M + C20 → M@C20 for the Series M = Ca-Zn
4.2.2. The Ne@C20 Reference System
4.2.3. QTAIM Analysis for Ca@C20 (d0 Spin Singlet)
4.2.4. Sc@C20 (d1 Spin Doublet)
4.2.5. Ti@C20 (d2 Spin Triplet)
4.2.6. V@C20 (d3 Spin Quartet)
4.2.7. Cr@C20 (d4 Spin Quintet)
4.2.8. Mn@C20 (d5 Spin Sextet)
4.2.9. Fe@C20 (d6 Spin Quintet)
4.2.10. Co@C20 (d7 Spin Quartet)
4.2.11. Ni@C20 (d8 Spin Triplet)
4.2.12. Cu@C20 (d9 Spin Doublet)
4.2.13. Zn@C20
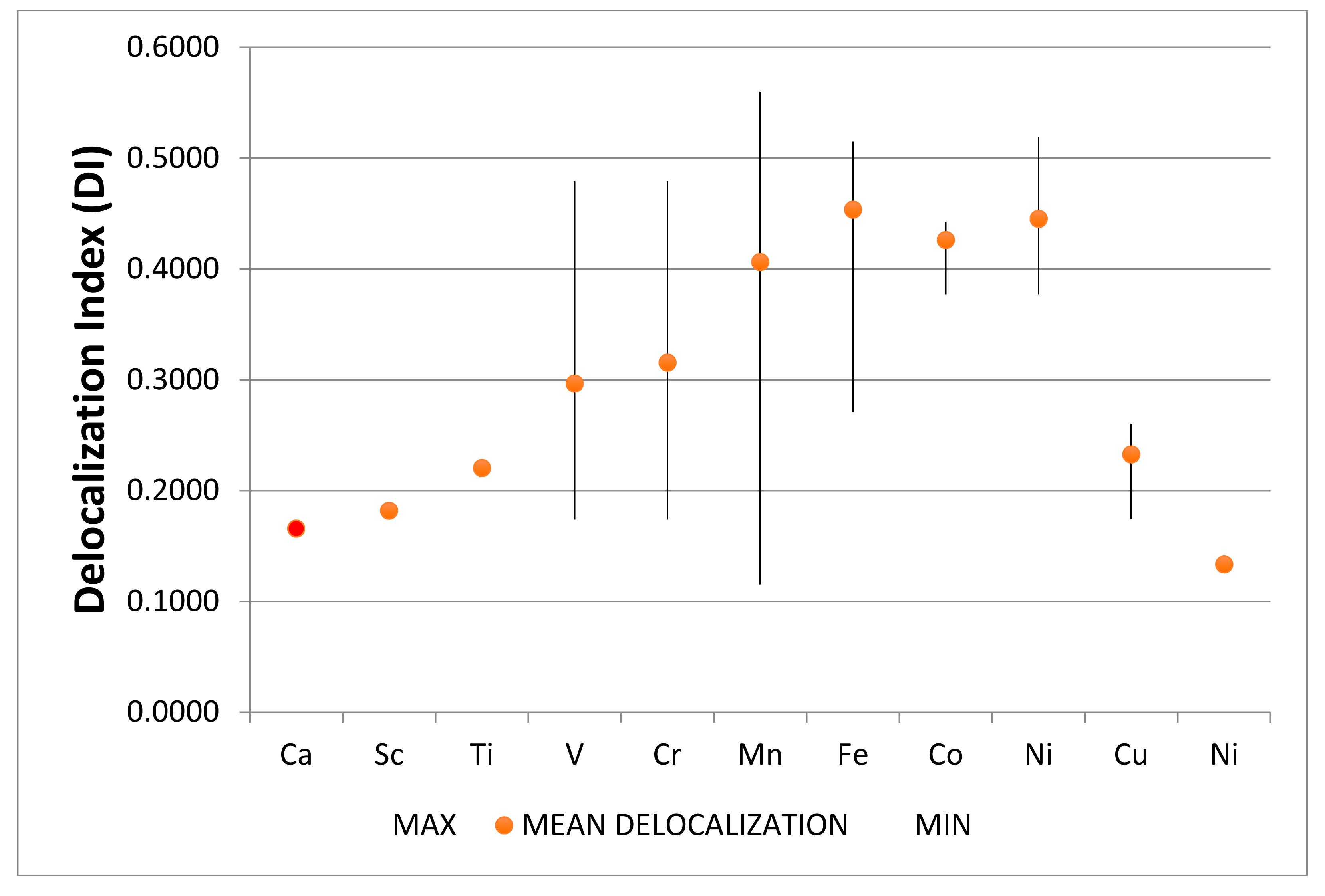
4.2.14. Summary Remarks on QTAIM Description of M@C20
4.2.15. Non-Covalent Interactions in M@C20
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Musher, J.I. The Chemistry of Hypervalent Molecules. Angew. Chem. Int. Ed. 1969, 8, 54–68. [Google Scholar] [CrossRef]
- Jensen, W.B. The Origin of the Term “Hypervalent”. J. Chem. Educ. 2006, 83, 1751. [Google Scholar] [CrossRef]
- Jackson, B.A.; Harshman, J.; Miliordos, E. Addressing the Hypervalent Model: A Straightforward Explanation of Traditionally Hypervalent Molecules. J. Chem. Educ. 2020, 97, 3638–3646. [Google Scholar] [CrossRef]
- Schleyer, P.V.R. LETTERS p4, 70. Chem. Eng. News 1984, 62. Available online: https://pubs.acs.org/toc/cenear/62/22 (accessed on 15 July 2021).
- Kühl, O. The coordination chemistry of the proton. Chem. Soc. Rev. 2011, 40, 1235–1246. [Google Scholar] [CrossRef] [PubMed]
- Yousufuddin, M.; Gutmann, M.J.; Baldamus, J.; Tardif, O.; Hou, Z.; Mason, S.A.; McIntyre, G.J.; Bau, R. Neutron Diffraction Studies on a 4-Coordinate Hydrogen Atom in an Yttrium Cluster. J. Am. Chem. Soc. 2008, 130, 3888–3891. [Google Scholar] [CrossRef] [PubMed]
- Bau, R.; Drabnis, M.H.; Garlaschelli, L.; Klooster, W.T.; Xie, Z.; Koetzle, T.F.; Martinengo, S. Five-Coordinate Hydrogen: Neutron Diffraction Analysis of the Hydrido Cluster Complex [H2Rh13(CO)24]3−. Science 1997, 275, 1099–1102. [Google Scholar] [CrossRef] [PubMed]
- Hart, D.W.; Teller, R.G.; Wei, C.-Y.; Bau, R.; Longoni, G.; Campanella, S.; Chini, P.; Koetzle, T.F. Six-Coordinate Hydrogen: Structure of [(Ph3P)2N]+[HCo6(C)O)15]- by Single-Crystal Neutron Diffraction Analysis. Angew. Chem Int. Ed. Engl. 1979, 18, 80–81. [Google Scholar] [CrossRef]
- Hart, D.W.; Teller, R.G.; Wei, C.-Y.; Bau, R.; Longoni, G.; Campanella, S.; Chini, P.; Koetzle, T.F. An Interstitial Hydrogen Atom in a Hexanuclear Metal Cluster: X-ray and Neutron Diffraction Analysis of [(Ph3P)2N]1+[HCo6(CO)15]1−. J. Am. Chem. Soc. 1981, 103, 1458–1466. [Google Scholar] [CrossRef]
- Janotti, A.; van der Walle, X. Hydrogen multicentre bonds. Nat. Mater. 2007, 6, 44–47. [Google Scholar] [CrossRef]
- Popov, A.A.; Yang, S.; Dunsch, L. Endohedral Fullerenes. Chem. Rev. 2013, 113, 5989–6113. [Google Scholar] [CrossRef] [PubMed]
- Bloodworth, S.; Sitinova, G.; Alom, S.; Vidal, S.; Bacanu, G.R.; Elliott, S.J.; Light, M.E.; Herniman, J.M.; Langley, G.J.; Levitt, M.H.; et al. First Synthesis and Characterization of CH4@C60. Angew. Chem. Int. Ed. 2019, 58, 5038–5043. [Google Scholar] [CrossRef] [Green Version]
- Mordkovich, V.Z.; Umnov, A.G.; Inoshita, T.; Endo, M. The Obserbation of multiwall fullerenes in thermally treated laser pyrolysis carbon blacks. Carbon 1999, 37, 1855–1858. [Google Scholar] [CrossRef]
- Cioslowski, J.; Fleishmannn, E.D. Endohedral complexes: Atoms and ions inside the C60 cage. J. Chem. Phys 1991, 94, 3730–3734. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules. A Quantum Theory; Clarendon: Oxford, UK, 1990. [Google Scholar]
- Bader, R.F.W. A Quantum Theory of Molecular Structure and its Applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
- Shahbazian, S. Why Bond Critical Points Are Not “Bond” Critical Points. Chem. Eur. J. 2018, 24, 5401–5405. [Google Scholar] [CrossRef]
- Jalife, S.; Arcudia, J.; Pan, S.; Merino, G. Noble gas endohedral fullerenes. Chem. Sci. 2020, 11, 6642–6652. [Google Scholar] [CrossRef] [PubMed]
- Morinaka, Y.; Sato, S.; Wakamiya, A.; Nikawa, N.; Mizorogi, N.; Tanabe, F.; Murata, M.; Komatsu, K.; Furukawa, K.; Kato, T.; et al. X-ray observation of a helium atom and placing a nitrogen atom inside He@C60 and He@C70. Nat. Commun. 2013, 4, 1554–1559. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yakigaya, K.; Takeda, A.; Yokoyama, Y.; Ito, S.; Miyazaki, T.; Suetsuna, T.; Shimotani, H.; Kakiuchi, T.; Sawa, H.; Takagi, T.; et al. Superconductivity of domed Ar@C60. New J. Chem. 2007, 31, 973–979. [Google Scholar] [CrossRef]
- Lee, H.M.; Olmstead, M.M.; Suetsuna, T.; Shimotani, H.; Dragoe, N.; Cross, R.J.; Kitazawa, K.; Balch, A.L. Crystallographi characterization of Kr@C60 in (0.09 Kr @ C60/0.91C60)∙{NiII)OEP)}∙2C6H6. Chem. Commun. 2002, 1352–1353. [Google Scholar] [CrossRef]
- Cerpa, E.; Krapp, A.; Vela, A.; Merino, G. The Implications of Symmetry of the External Potential on Bond Paths. Chem. Eur. J. 2008, 14, 10232–10234. [Google Scholar] [CrossRef]
- Popov, A.A.; Dunsch, L. Bonding in Endohedral Metallofullerenes as Studied by Quantum Theory of Atoms in Molecules. Chem. Eur. J. 2009, 15, 9707–9729. [Google Scholar] [CrossRef]
- Estrada-Salas, R.E.; Valladares, A.A. DFT calculations of the structure and electronic properties of late 3d transition metal atoms endohedrally doping C60. J. Mol. Struct. THEOCHEM 2008, 869, 1–5. [Google Scholar] [CrossRef]
- An, Y.-P.; Yang, C.-L.; Wang, M.-S.; Ma, X.-G.; Wang, D.-H. Geometrical and Electronic Properties of the Clusters of C20 Cage Doped with Alkali Metal Atoms. J. Cluster Sci. 2011, 22, 31–39. [Google Scholar] [CrossRef]
- Garg, I.; Sharma, H.; Kapila, N.; Dharamvir, K.; Jandal, V.K. Transition metal induced magnetism in smaller fullerenes (Cn for n ≤ 36. Nanoscale 2011, 3, 217–224. [Google Scholar] [CrossRef]
- Baei, M.T.; Soltani, A.; Torabi, P.; Hosseini, F. Formation and electronic structure of C20 fullerene transition metal clusters. Monatsch. Chem. 2014, 145, 1401–1405. [Google Scholar] [CrossRef]
- Gonzalez, M.; Lujan, S.; Beran, K.A. Investigation into the molecular structure, electronic properties, and energetic stability of endohedral (TM@C20) and exohedral (TM-C20) metallofullerene derivatives of C20: TM = Group 11 and 12 transition metal atoms/ions. Comp. Theoret. Chem. 2017, 1119, 32–44. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, Z.; Wang, Q. Density functional theory study on the transition metal atoms encapsulated C20 cage clusters Mater. Res. Express 2018, 5, 065605. [Google Scholar] [CrossRef]
- Sarkar, S.; Paul, S.; Misra, A. Spin-polarized electrical transport in transition metal encapsulated C20 fullerenes: A theoretical account. Chem. Phys. Impact 2020, 1, 100002. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [Green Version]
- Grimme, S. Semiempirical gga-type density functional constructed with a long-range dispersion correction. J. Comp. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Dunning, T.H., Jr. Gaussian-basis sets for use in correlated molecular calculations. 3. The atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358–1371. [Google Scholar] [CrossRef] [Green Version]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef] [PubMed]
- Bergner, A.; Dolg, M.; Kuechle, W.; Stoll, H.; Preuss, H. Ab-initio energy-adjusted pseudopotentials for elements of groups 13–17. Mol. Phys. 1993, 80, 1431–1441. [Google Scholar] [CrossRef]
- Pritchard, B.P.; Altarawy, D.; Didier, B.; Gibson, T.D.; Windus, T.L. A New Basis Set Exchange: An Open, Up-to-date Resource for the Molecular Sciences Community. J. Chem. Inf. Model. 2019, 59, 4814–4820. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B. Gaussian 09, Revision, E.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A. Gaussian 16, Revision, A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Outeiral, C.; Vincent, M.A.; Pendás, Á.M.; Popelier, P.L.A. Revitalizing the concept of bond order through delocalization measures in real space. Chem. Sci. 2018, 9, 5517–5529. [Google Scholar] [CrossRef] [Green Version]
- Johnson, E.R.; Keinan, S.; Mori-Sanchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef] [Green Version]
- Contreras-García, J.; Johnson, E.R.; Keinan, S.; Chaudret, R.; Piquemal, J.-P.; Beratan, D.N.; Yang, W. NCIPLOT: A Program for Plotting Noncovalent Interaction Regions. J. Chem. Theory Comput. 2011, 7, 625–632. [Google Scholar] [CrossRef]
- Available online: http://www.jcrystal.com/steffenweber/gallery/Fullerenes/Fullerenes.html (accessed on 27 June 2021).
- Todd, A.; Keith, T.K. AIMAll (Version 19.10.12), Gristmill Software; AIMAll: Overland Park, KS, USA, 2019; Available online: Aim.tkgristmill.com (accessed on 15 April 2021).
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Available online: http://sobereva.com/multiwfn (accessed on 15 June 2021).
- Popelier, P.L.A. The QTAIM Perspective of Chemical Bonding. In The Chemical Bond: Fundamental Aspects of Chemical Bonding; Frenking, G., Shaik, S., Eds.; Wiley-VCH Verlag GmbH & Co KGaA, Boschstr.: Weinheim, Germany, 2014; Chapter 8. [Google Scholar]
- Espinosa, E.; Espinosa, J.E.; Elguero, J. From weak to strong interactions: A comprehensive analysis of the topological and energetic properties of the electron density involving X-H···F-Y systems. J. Chem. Phys. 2002, 117, 5529–5542. [Google Scholar] [CrossRef]
- Espinosa, J.E.; Molins, E.; LeComte, C. Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities. Chem. Phys. Lett. 1998, 285, 170–173. [Google Scholar] [CrossRef]
- Mantina, M.; Chamberlin, A.C.; Valero, R.; Cramer, C.J.; Truhlar, D.G. Consistent van der Waals Radii for the Whole Main Group. J. Phys. Chem. 2009, 113, 5806–5812. [Google Scholar] [CrossRef] [PubMed] [Green Version]

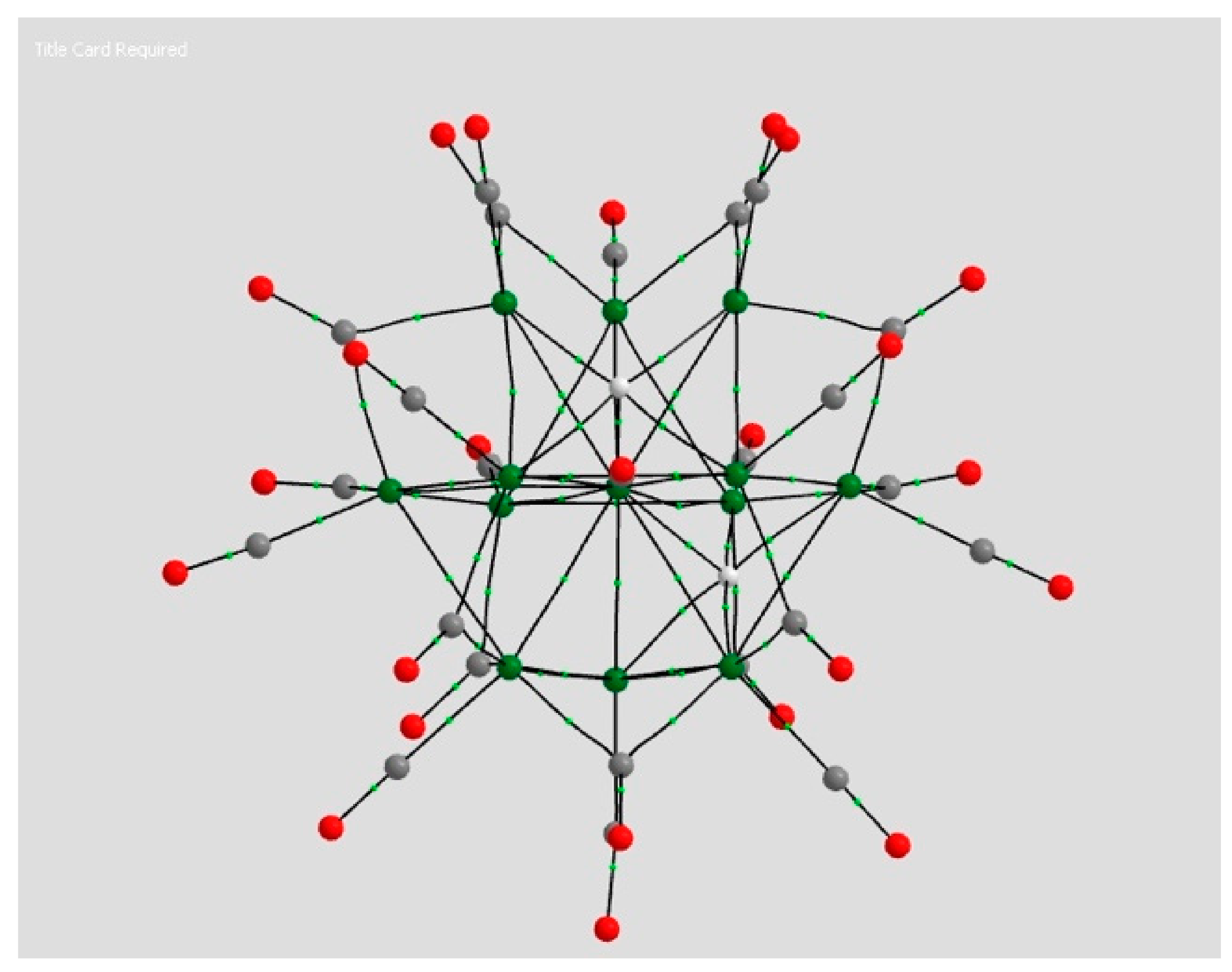
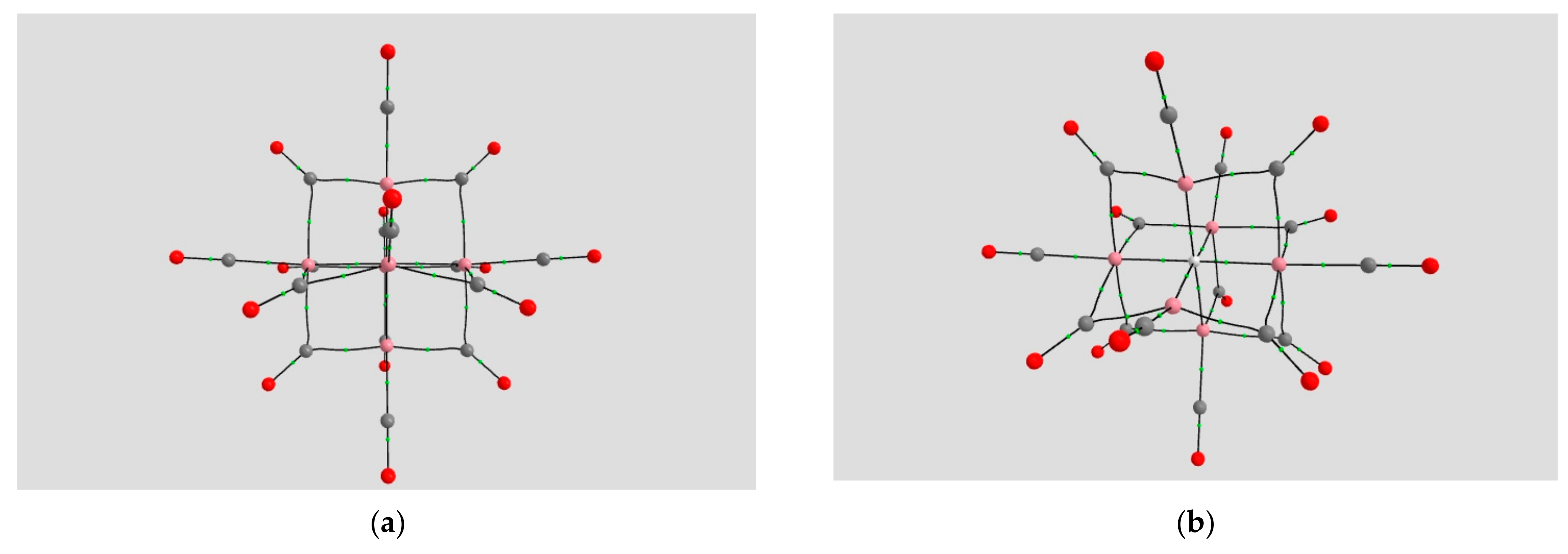
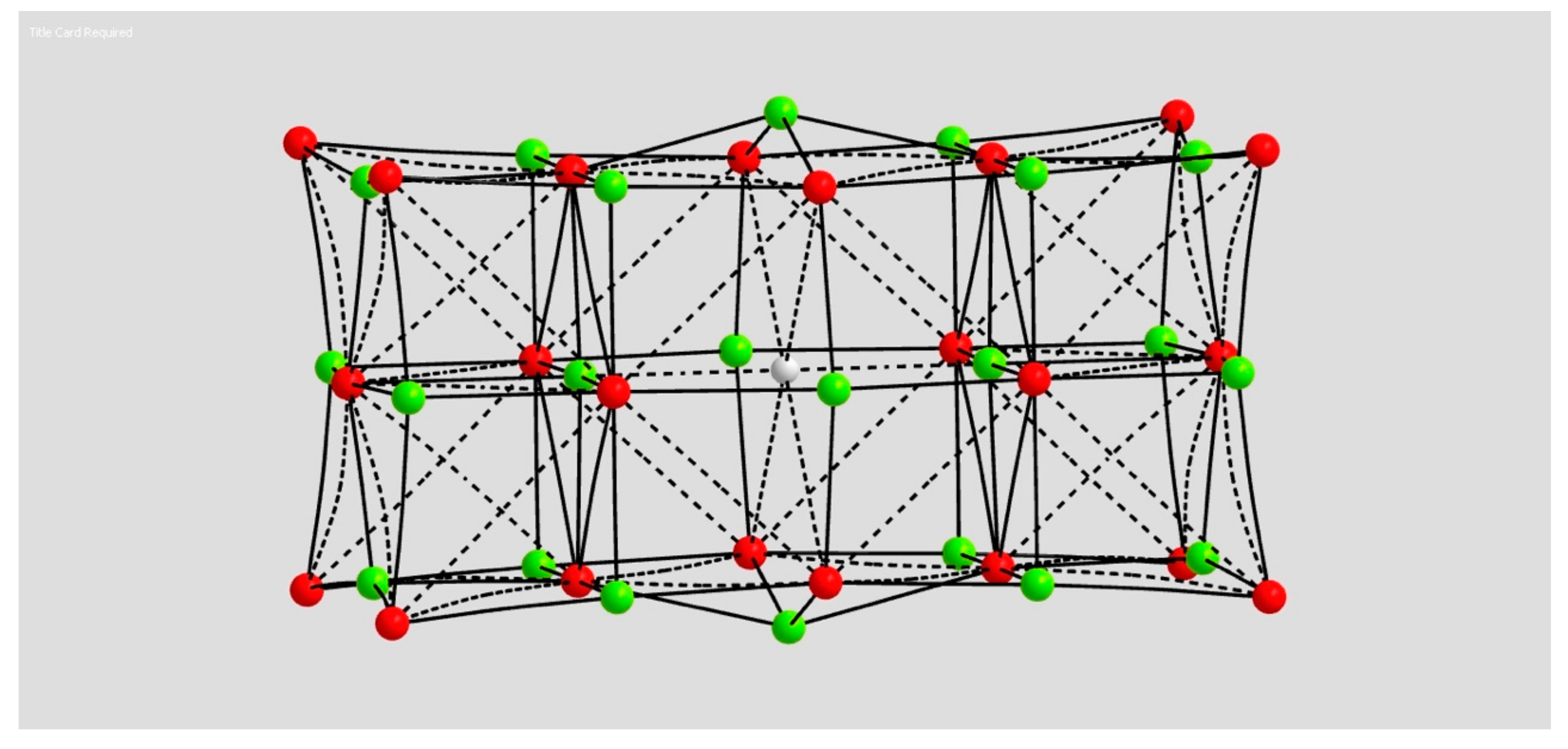
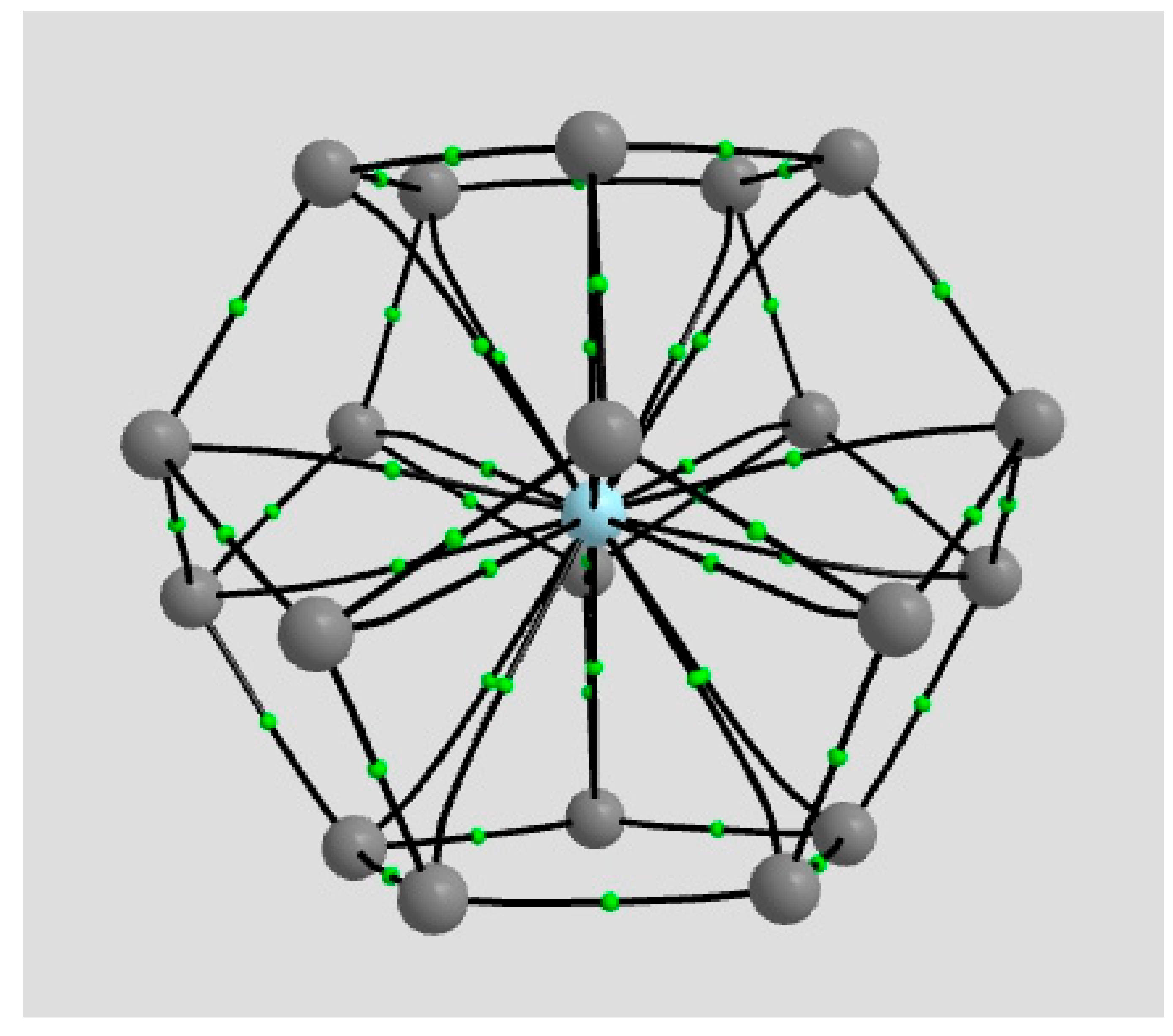
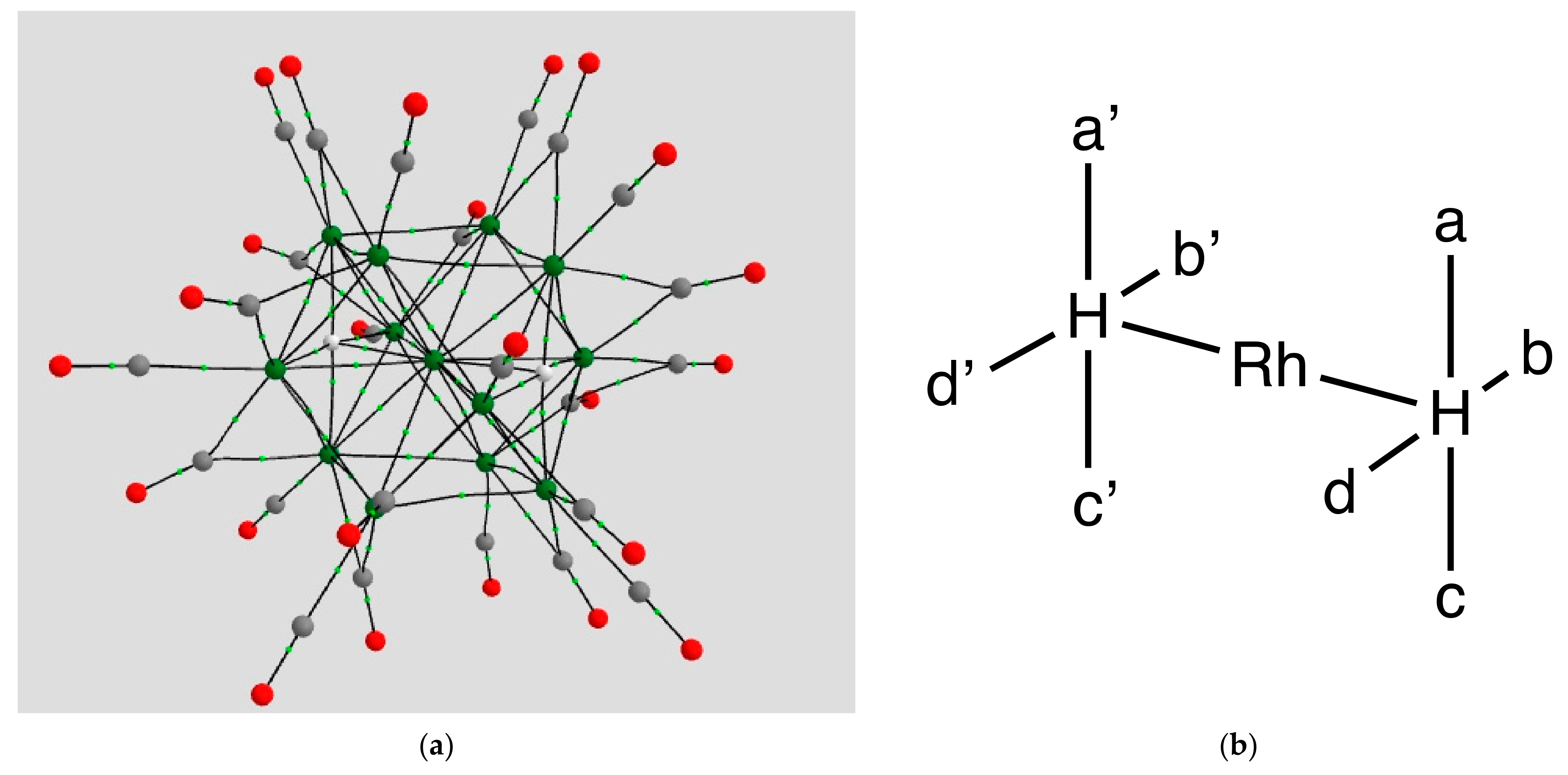

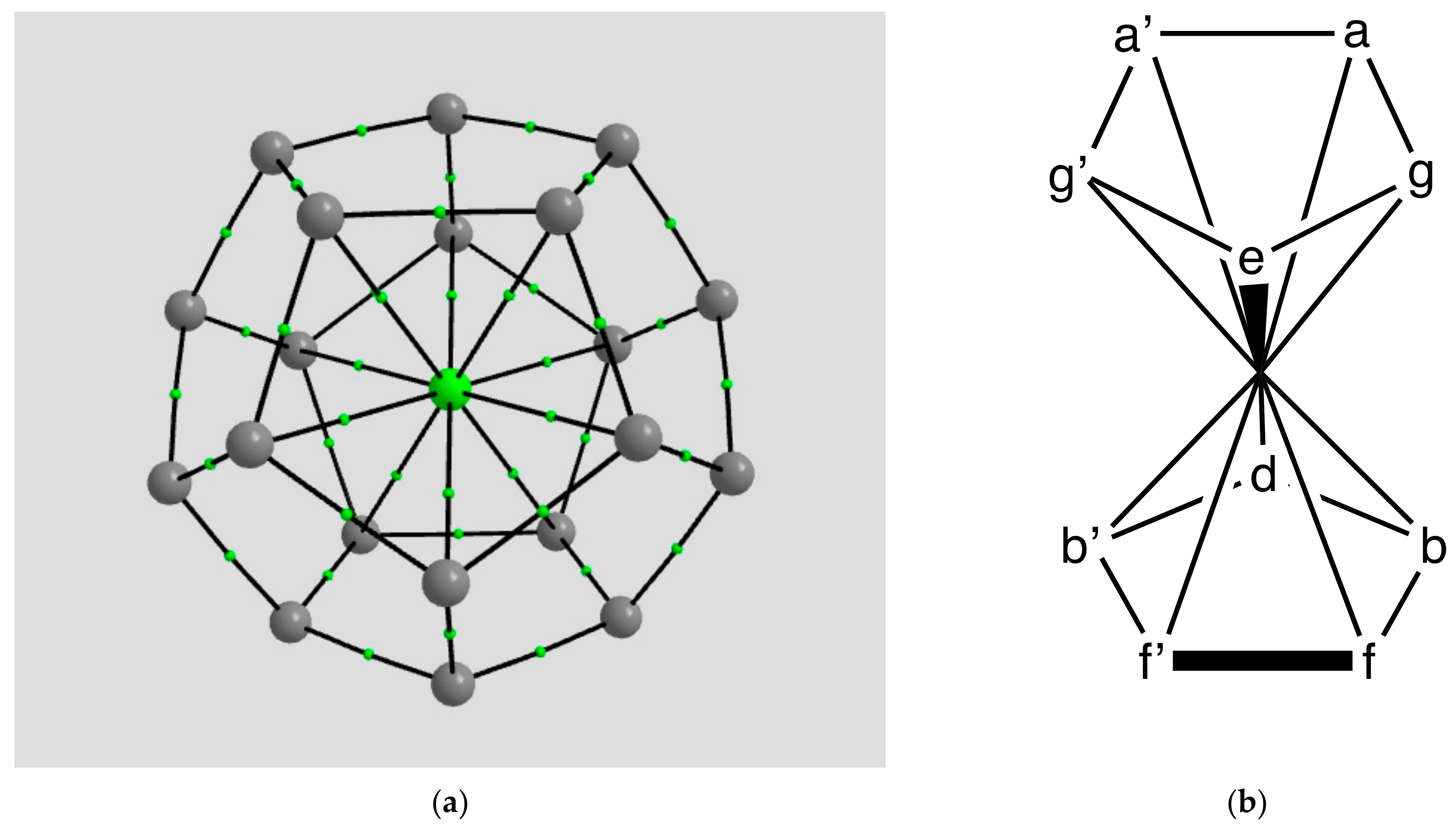
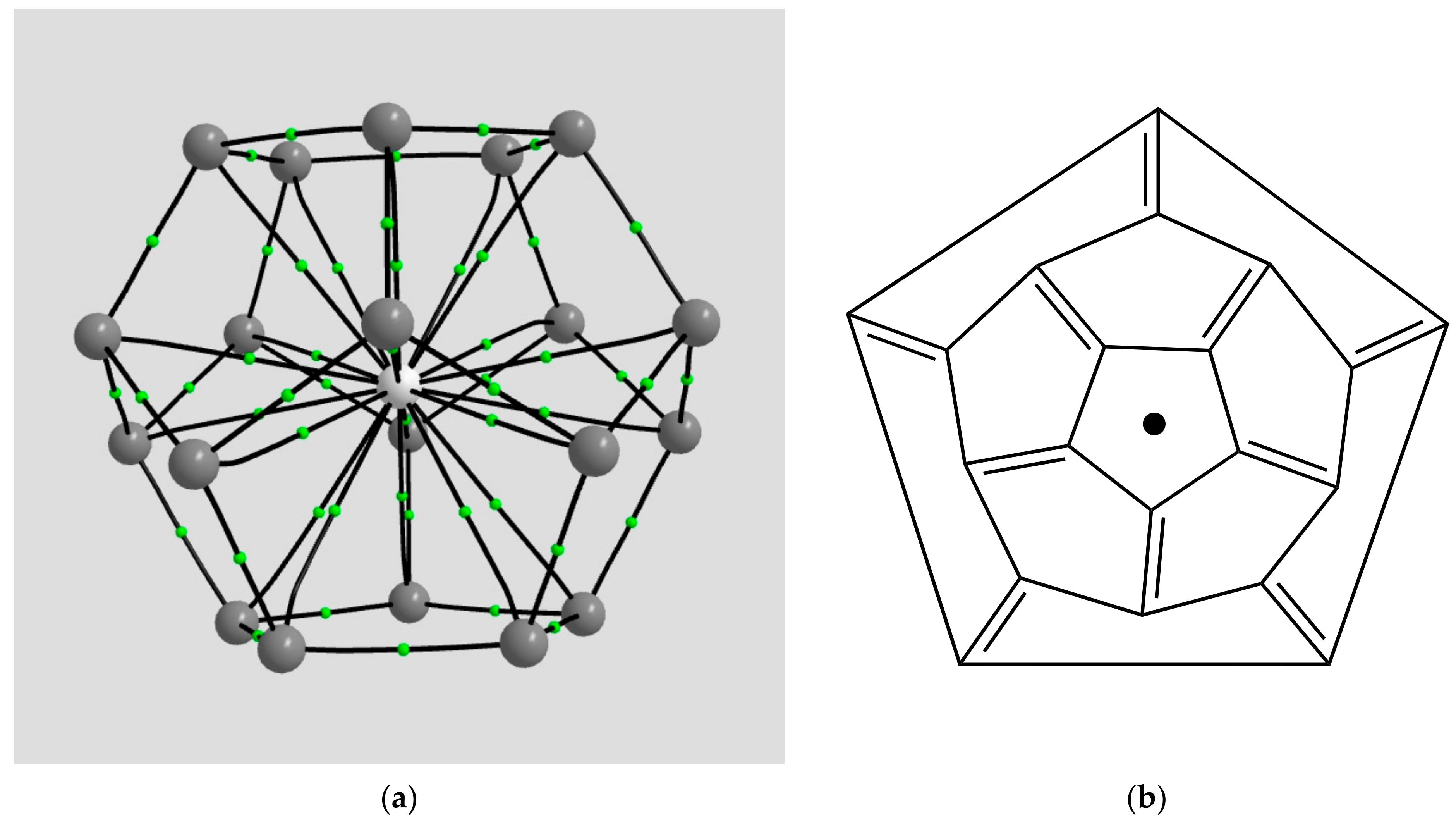
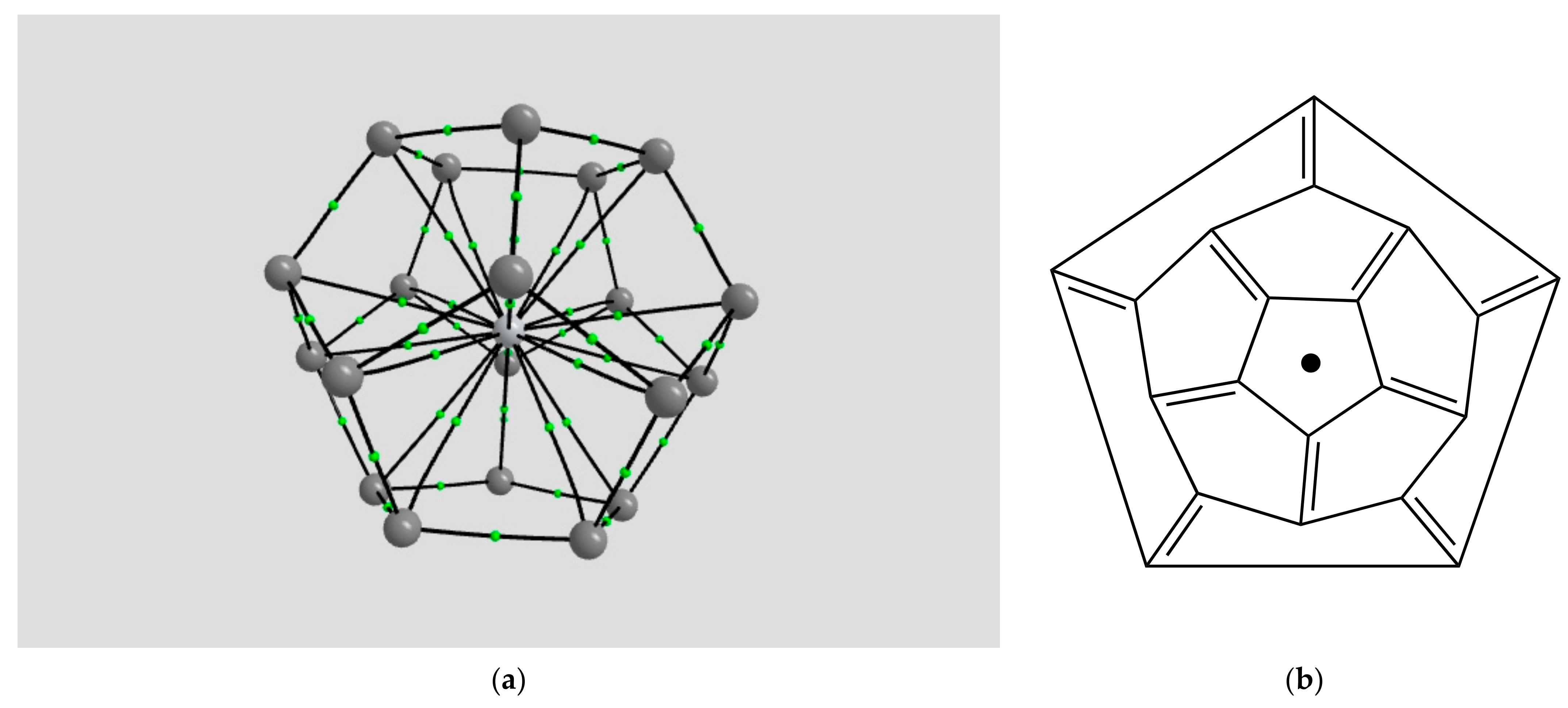

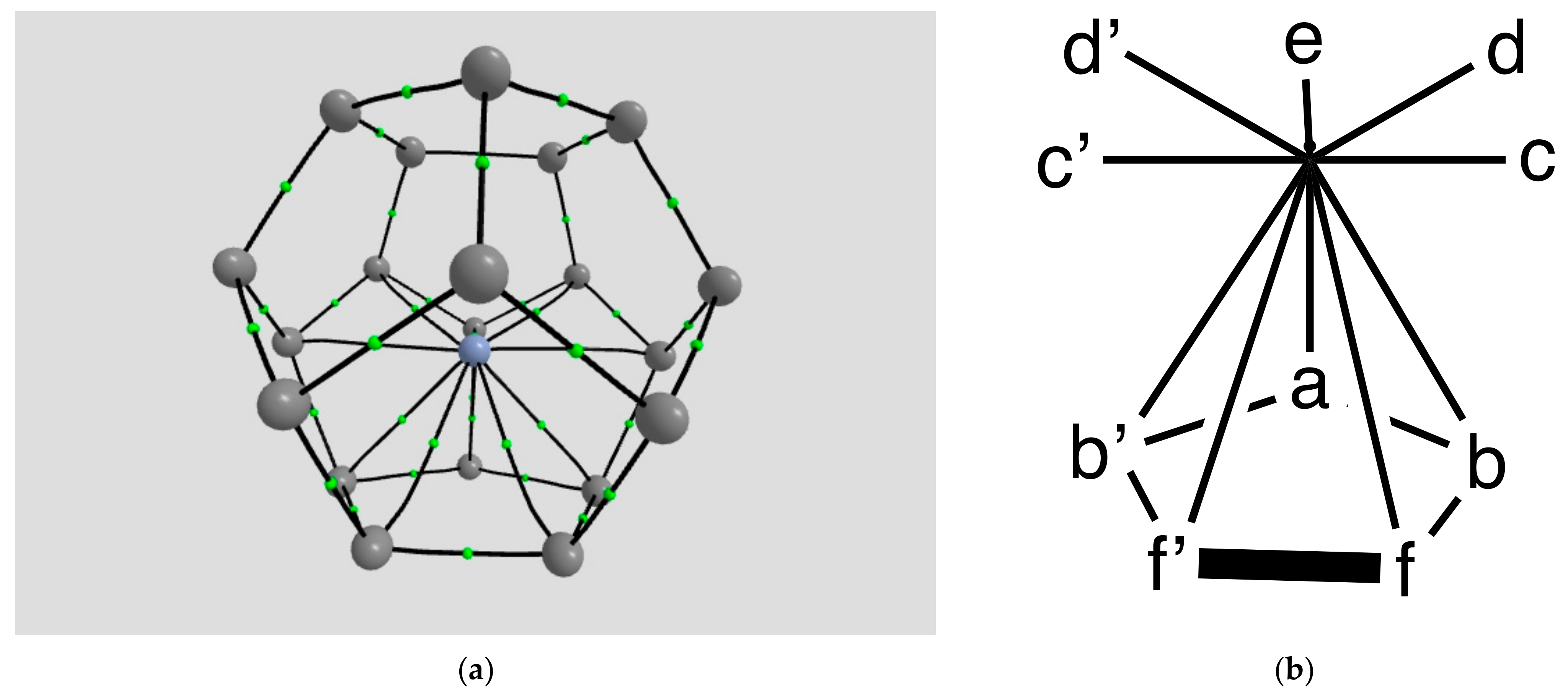

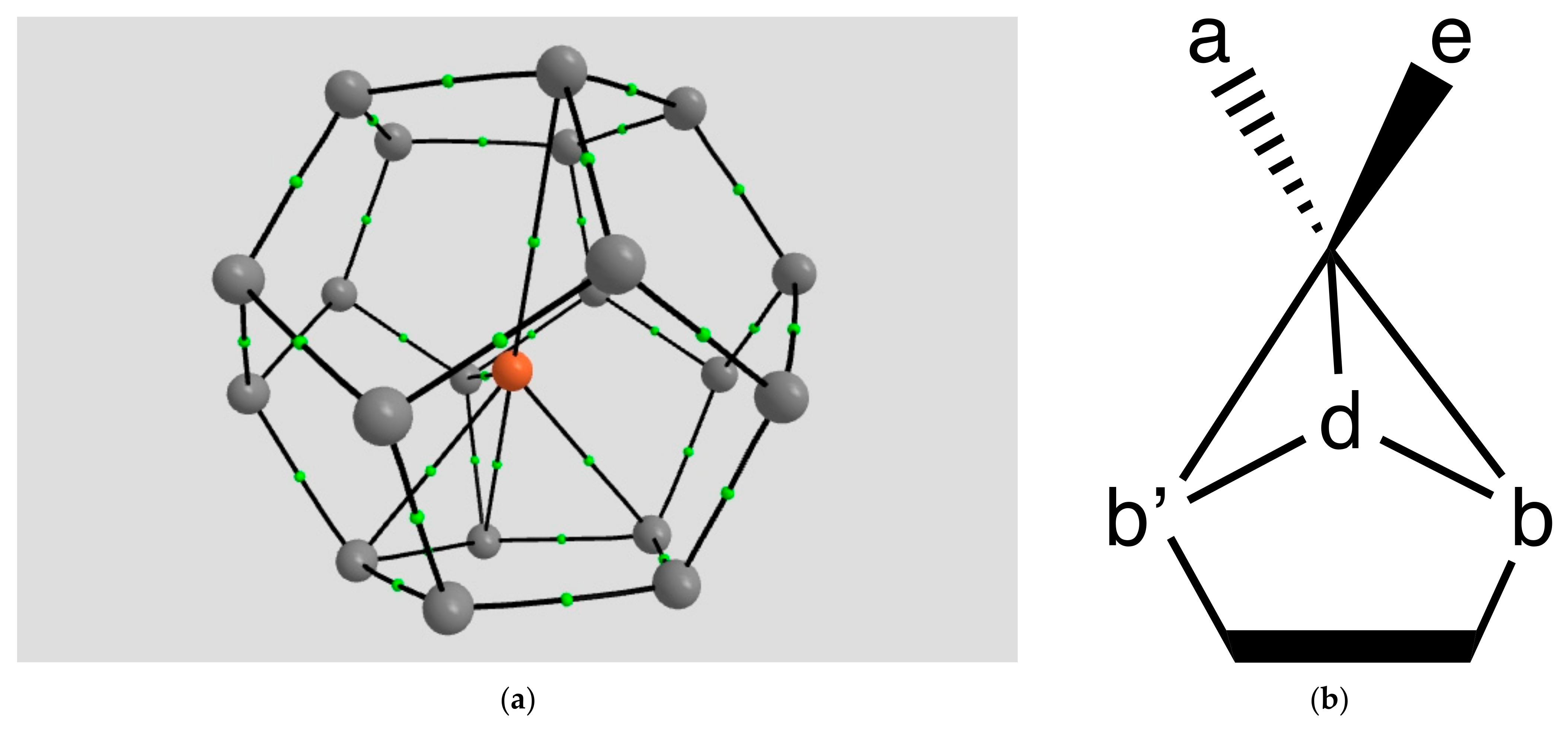

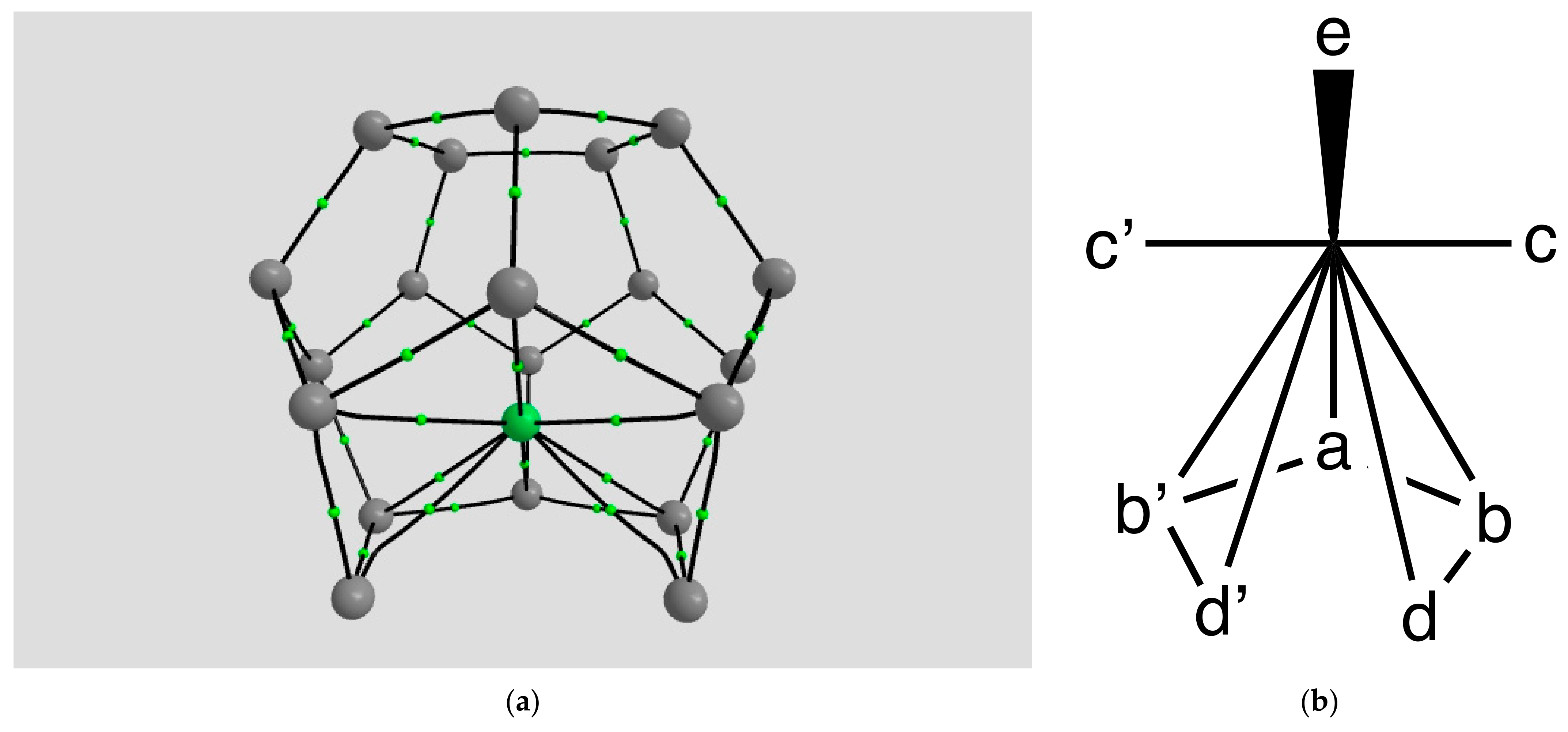

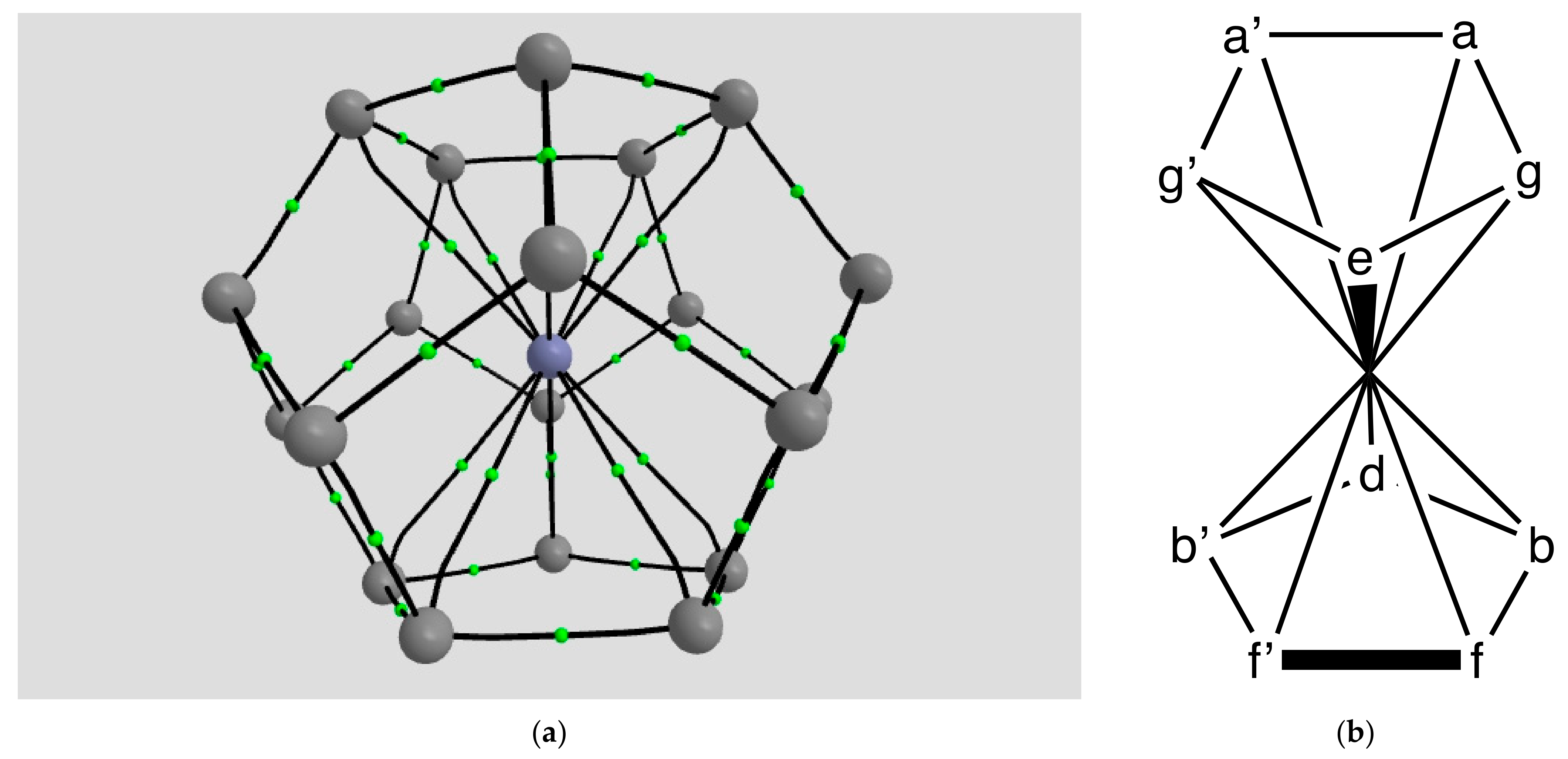


| Coordination | Length | Density ρ at LCP | ∇2ρ at LCP | DI | G | V | H |
|---|---|---|---|---|---|---|---|
| a, a’ | 1.5963, 1.6590 | 0.1271, 0.1114 | +0.2826, +0.2450 | 0.3734, 0.3075 | 0.1250, +0.1037 | −0.1799, −0.1465 | −0.0549, −0.0428 |
| b, b’ | 1.8013, 1.8155 | 0.0912, 0.0875 | +0.1998, +0.1902 | 0.2284, 0.2286 | 0.0812, 0.0767 | −0.1125, −0.1160 | −0.0313, −0.0393 |
| c, c’ | 1.7419, 1.7528 | 0.0963, 0.0913 | +0.2260, +0.2069 | 0.2694, 0.2622 | 0.0896, 0.0829 | −0.1229, −0.1142 | −0.0333, −0.0313 |
| d, d’ | 1.7949, 1.7832 | 0.0909, 0.0969 | +0.2150, 2221 | 0.2451, 0.2668 | 0.0845, 0.0893 | −0.1154, −0.1235 | −0.0309, −0.0342 |
| Rh-H | 1.8105,1.7836 | 0.0937, 0.0976 | +0.2353, +0.2356 | 0.2038, 0.2226 | 0.0914, 0.0942 | −0.1241, −0.1293 | −0.0327, −0.0351 |
| Coordination | Length | Density ρ at LCP | ∇2ρ at LCP | |
|---|---|---|---|---|
| a, a’ | 1.7933 | 0.0689 | +0.1267 | |
| b | 1.8158 | 0.0642 | +0.1376 | |
| d | 1.9129 | 0.0538 | +0.1337 | |
| c | 1.8158 | 0.0643 | +0.1376 | |
| e | 1.9130 | 0.0526 | +0.1338 | |
| Co a-a’ | 2.4666 | * 1 | * | |
| Co b-b’ | 2.4647 | * | * | |
| Co a-b (a’-b’) | 2.7959 | * | * | |
| DI | G | V | H | |
| a, a’ | 0.2731 | 0.0529 | −0.0741 | −0.0212 |
| b | 0.2341 | 0.0519 | −0.0694 | −0.0175 |
| d | 0.1971 | 0.0442 | −0.0580 | −0.0138 |
| c | 0.2341 | 0.0519 | −0.0694 | −0.0175 |
| e | 0.1918 | 0.0442 | −0.0551 | −0.0551 |
| Coordination | Length | Density ρ at LCP | ∇2ρ at LCP | DI | G | V | H |
|---|---|---|---|---|---|---|---|
| a (H…O) | 2.6108 | 0.0177 | +0.0399 | 0.0880 | 0.0107 | −0.0113 | −0.0006 |
| b (H…Mg) | 2.4025 | 0.0265 | +0.1241 | 0.0746 | 0.0286 | −0.0263 | +0.0023 |
| x (MgO) | 1.9109 | 0.0556 | +0.2731 | 0.1440 | 0.0583 | −0.0483 | −0.0100 |
| Atom M | LN | E (M + C20) | E (M@C20) | BE (eV) | BE (eV) 1 |
|---|---|---|---|---|---|
| 1Ca d0 | 10 | −1438.799965 | −1438.515743 | +7.73a | |
| 2Sc d1 | 20 | −1521.861237 | −1521.890211 | −0.79a | |
| 3Ti d2 | 20 | −1610.588977 | −1610.724727 | −3.69a | 3.80b |
| 4V d3 | 12 | −1705.143352 | −1705.194267 | −1.39a | 1.93b |
| 5Cr d4 | 8 | −1805.655613 | −1805.591705 | +1.74a | −3.23b |
| 6Mn d5 | 4 | −1912.089623 | −1912.078599 | +0.30a | −6.31b |
| 5Fe d6 | 5 | −2024.881830 | −2024.791288 | +2.46a | −3.47b |
| 4Co d7 | 8 | −2144.000844 | −2143.843613 | +4.28a | −4.19b |
| 3Ni d8 | 8 | −2269.221160 | −2269.386339 | −4.49a | −4.75b |
| 2Cu d9 | 6 | −2401.807669 | −2401.507195 | +8.18a | −7.52b, −2.17c |
| 1Zn d10 | 10 | −2540.729908 | −2540.386014 | +9.36a | −4.31c |
| Coordination | Length | Density ρ at LCP | ∇2ρ at LCP | DI | G | V | H |
|---|---|---|---|---|---|---|---|
| a (to C along D3 axis) | 2.0183 | 0.0591 | +0.3438 | 0.0825 | 0.0870 | −0.0879 | −0.0009 |
| b (to a neighboring C) | 2.0336 | 0.0566 | +0.3227 | 0.0762 | 0.0822 | −0.0822 | +0.0023 |
| c (to a non-neighboring C) | 2.1047 | 0.0512 | +0.3042 | 0.0642 | 0.0746 | −0.0732 | +0.0014 |
| Coordination | Length | Density ρ | ∇2ρ | DI | G | V | H |
|---|---|---|---|---|---|---|---|
| Ca to C in polar 5-rings | 2.1112 | 0.0782 | +0.3418 | 0.1654 | 0.0992 | −0.1128 | −0.0136 |
| Coordination | Length | Density ρ | ∇2ρ | DI | G | V | H |
|---|---|---|---|---|---|---|---|
| Sc- C to a C5 ring | 2.118 to 2.106 | 0.0832 to 0.0810 | +0.3233 to +0.3158 | 0.1852 to 0.1784 | 0.1009 to 0.0842 | −0.1201 to −0.1172 | −0.03 to −0.02 |
| Coordination | Length | Density ρ | ∇2ρ | DI | G | V | H |
|---|---|---|---|---|---|---|---|
| Ti C square plane | 2.087 | 0.0851 | +0.3228 | 0.2230 | 0.1016 | −0.1225 | −0.0209 |
| Ti-C four triangles C4 | 2.101 | 0.0877 | +0.3190 | 0.2121 | 0.0901 | −0.1228 | −0.0327 |
| Ti-C four triangles S4 | 2.101 | 0.0874 | +0.3148 | 0.2233 | 0.0980 | −0.1173 | −0.0193 |
| Coordination | Length | Density ρ | ∇2ρ | DI | G | V | H |
|---|---|---|---|---|---|---|---|
| a, a’ | 2.1356 | 0.0719 | +0.2772 | 0.1737 | 0.0830 | −0.0967 | −0.0137 |
| b, b’ | 2.0790 | 0.0917 | +0.3026 | 0.3749 | 0.1272 | −0.1686 | −0.0414 |
| c | 1.9737 | 0.1214 | +0.3958 | 0.2337 | 0.1165 | −0.1686 | −0.0531 |
| d | 2.1088 | 0.0839 | +0.2454 | 0.4793 | 0.1141 | −0.1553 | −0.0412 |
| e, e’ | 1.9785 | 0.1135 | 0.3426 | 0.2814 | 0.1014 | −0.1272 | −0.0258 |
| f, f’ | 1.9915 | 0.1112 | 0.3179 | 0.3706 | 0.1196 | −0.1598 | −0.0402 |
| g, g’ | 2.0299 | 0.1036 | 0.2801 | 0.3550 | 0.1059 | −0.1419 | −0.0360 |
| Coordination | Length | Density ρ | ∇2ρ | DI | G | V | H |
|---|---|---|---|---|---|---|---|
| a | 2.0919 | 0.0928 | +0.1693 | 0.4136 | 0.0928 | −0.1108 | −0.0180 |
| b, b’ | 1.8910 | 0.1249 | +0.2496 | 0.3498 | 0.1249 | −0.1772 | −0.0523 |
| c, c’ | 1.9854 | 0.1165 | +0.2913 | 0.3903 | 0.1165 | −0.1686 | −0.0531 |
| d, d’ | 1.9880 | 0.1142 | +0.3196 | 0.3869 | 0.1142 | −0.1687 | −0.0545 |
| e | 1.9068 | 0.1221 | +0.2656 | 0.4725 | 0.1221 | −0.1765 | −0.0544 |
| f, f’ | 2.0248 | 0.1138 | +0.3373 | 0.3498 | 0.1138 | −0.1739 | −0.0601 |
| Coordination | Length | Density ρ | ∇2ρ | DI | G | V | H |
|---|---|---|---|---|---|---|---|
| a | 1.9048 | 0.1390 | +0.2419 | 0.5599 | 0.1269 | −0.1935 | −0.0666 |
| b, b’ | 1.9074 | 0.1259 | +0.2296 | 0.4752 | 0.1274 | −0.2022 | −0.0748 |
| e | 2.2543 | 0.0625 | +0.1928 | 0.1152 | 0.0475 | −0.0647 | −0.0172 |
| Coordination | Length | Density ρ | ∇2ρ | DI | G | V | H |
|---|---|---|---|---|---|---|---|
| a | 1.8598 | 0.1380 | +0.2087 | 0.5135 | 0.1269 | −0.1935 | −0.0666 |
| b, b’ | 1.8588 | 0.1376 | +0.2076 | 0.5150 | 0.1274 | −0.2025 | −0.0851 |
| d | 1.9874 | 0.1046 | +0.3675 | 0.2707 | 0.0693 | −0.1721 | −0.1028 |
| e | 2.3621 | 0.0453 | +0.1686 | 0.1059 | 0.0475 | −0.0529 | −0.0054 |
| Coordination | Length | Density ρ | ∇2ρ | DI | G | V | H |
|---|---|---|---|---|---|---|---|
| a | 1.8973 | 0.1336 | +0.3179 | 0.4173 | 0.1366 | −0.1935 | −0.0569 |
| b, b’ | 1.8438 | 0.1442 | +0.2913 | 0.4750 | 0.1442 | −0.2155 | −0.0713 |
| c, c’ | 1.8445 | 0.1444 | +0.2914 | 0.4725 | 0.1442 | −0.2156 | −0.0714 |
| d, d’ | 1.8374 | 0.1358 | +0.2370 | 0.5672 | 0.1360 | −0.2127 | −0.0767 |
| e | 1.8975 | 0.1336 | +0.3183 | 0.4184 | 0.1366 | −0.1938 | −0.0400 |
| Coordination | Length | Density ρ | ∇2ρ | DI | G | V | H |
|---|---|---|---|---|---|---|---|
| a | 1.9285 | 0.1137 | +0.2350 | 0.3770 | 0.1171 | −0.1571 | −0.0400 |
| b, b’ | 1.8518 | 0.1297 | +0.2836 | 0.4426 | 0.1369 | −0.2030 | −0.0661 |
| c, c’ | 1.8516 | 0.1297 | +0.2835 | 0.4427 | 0.1369 | −0.2030 | −0.0661 |
| d, d’ | 1.8306 | 0.1329 | +0.2347 | 0.5188 | 0.1289 | −0.1991 | −0.0702 |
| e | 1.9285 | 0.1137 | +0.2683 | 0.3770 | 0.1171 | −0.1571 | −0.0400 |
| Coordination | Length | Density ρ | ∇2ρ | DI | G | V | H |
|---|---|---|---|---|---|---|---|
| a, a’ | 2.0034 | 0.0785 | +0.3038 | 0.2454 | 0.1077 | −0.1395 | −0.0318 |
| b, b’ | 1.9726 | 0.0978 | +0.3177 | 0.2348 | 0.1155 | −0.1586 | −0.0475 |
| d | 1.9766 | 0.0967 | +0.3128 | 0.2604 | 0.0956 | −0.1475 | −0.0531 |
| e | 2.0520 | 0.0785 | +0.2960 | 0.1740 | 0.0642 | −0.1172 | −0.0530 |
| Coordination | Length | Density ρ | ∇2ρ | DI | G | V | H |
|---|---|---|---|---|---|---|---|
| a, a’ | 2.0792 | 0.0763 | +0.2898 | 0.1333 | 0.0950 | −0.1175 | −0.0225 |
| b, b’ | 2.0788 | 0.0763 | +0.2897 | 0.1332 | 0.0948 | −0.1172 | −0.0220 |
| d | 2.0792 | 0.0765 | +0.2901 | 0.1334 | 0.0964 | −0.1174 | −0.0110 |
| e | 2.0786 | 0.0761 | +0.2960 | 0.1334 | 0.0948 | −0.1173 | −0.0221 |
| f, f’ | 2.0775 | 0.0762 | +0.2891 | 0.1330 | 0.0947 | −0.1171 | −0.0218 |
| g, g’ | 2.0786 | 0.0762 | 0.2894 | 0.1333 | 0.0948 | −0.1173 | −0.0221 |
| M@C20 | Density M-C LCP | Laplacian M-C LCP | H (G-V) | −V/2 | Radius (C20) | vdW Radius 1 Q | Range of DI |
|---|---|---|---|---|---|---|---|
| Ne | 0.0591 | 0.344 | <0.010 | 0.044 | 2.034 | 154 | 0.082 |
| 0.0512 | 0.322 | 0.041 | 2.018 | −0.004 | 0.076 | ||
| Ca | 0.7840 | 0.340 | −0.014 | 0.056 | 2.111 | 194 | 0.165 |
| 1.028 | |||||||
| Sc | 0.0832 | 0.323 | −0.03 | 0.060 | 2.118 | 184 | 0.185 |
| 0.0810 | 0.316 | −0.02 | 0.058 | 2.106 | 1.474 | 0.178 | |
| Ti | 0.0874 | 0.3228 | −0.033 | −0.1227 | 2.0814 | 176 | 0.2223 |
| 0.0851 | 0.3150 | −0.019 | −0.1173 | 2.0814 | 1.732 | 0.2120 | |
| V | 0.1135 | 0.396 | −0.036 | 0.071 | 2.03 | 171 | 0.355 |
| 0.1036 | 0.280 | −0.0193 | 0.064 | 1.97 | 1.620 | 0.281 | |
| Cr | 0.1249 | +0.2496 | −0.060 | 0.089 | 1.891 | 166 | 0.472 |
| 0.1138 | 0.3373 | −0.052 | 0.084 | 2.025 | 1.432 | 0.350 | |
| Mn | 0.1350 | 0.2419 | −0.067 | 0.1011 | 2.10 | 161 | 0.560 |
| 0.1259 | 0.2296 | −0.075 | 0.0967 | 2.09 | 1.362 | 0.475 | |
| Fe | 0.1380 | 0.2076 | −0.067 | 0.0967 | 1.86 | 156 | 0.514 |
| 0.1046 | 0.3675 | −0.085 | 0.1012 | 1.99 | 1.298 | 0.377 | |
| Co | 0.1358 | 0.2370 | −0.040 | 0.0967 | 1.837 | 152 | 0.519 |
| 0.1444 | 0.3183 | −0.077 | 0.1077 | 1.897 | 0.920 | 0.377 | |
| Ni | 0.1329 | 0.2347 | −0.077 | 0.0995 | 1.831 | 149 | 0.519 |
| 0.1137 | 0.3183 | −0.040 | 0.0786 | 1.923 | 0.834 | 0.377 | |
| Cu | 0.0978 | 0.3177 | −0.053 | 0.0793 | 1.973 | 145 | 0.260 |
| 0.0785 | 0.3038 | −0.032 | 0.0698 | 2.003 | 0.999 | 0.245 | |
| Zn | 0.0762 | 0.2930 | −0.022 | 0.0586 | 2.079 | 142 | 0.133 |
| 1.404 | |||||||
| Ar | 0.1202 | 0.3305 | −0.052 | 0.0721 | 2.180 | 188 | 0.366 |
| 0.0742 | 0.1568 | −0.010 | 0.0516 | 1.968 | −0.051 | 0.156 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Altun, Z.; Bleda, E.A.; Trindle, C. Atoms in Highly Symmetric Environments: H in Rhodium and Cobalt Cages, H in an Octahedral Hole in MgO, and Metal Atoms Ca-Zn in C20 Fullerenes. Symmetry 2021, 13, 1281. https://doi.org/10.3390/sym13071281
Altun Z, Bleda EA, Trindle C. Atoms in Highly Symmetric Environments: H in Rhodium and Cobalt Cages, H in an Octahedral Hole in MgO, and Metal Atoms Ca-Zn in C20 Fullerenes. Symmetry. 2021; 13(7):1281. https://doi.org/10.3390/sym13071281
Chicago/Turabian StyleAltun, Zikri, Erdi Ata Bleda, and Carl Trindle. 2021. "Atoms in Highly Symmetric Environments: H in Rhodium and Cobalt Cages, H in an Octahedral Hole in MgO, and Metal Atoms Ca-Zn in C20 Fullerenes" Symmetry 13, no. 7: 1281. https://doi.org/10.3390/sym13071281
APA StyleAltun, Z., Bleda, E. A., & Trindle, C. (2021). Atoms in Highly Symmetric Environments: H in Rhodium and Cobalt Cages, H in an Octahedral Hole in MgO, and Metal Atoms Ca-Zn in C20 Fullerenes. Symmetry, 13(7), 1281. https://doi.org/10.3390/sym13071281







