Hotspot Temperature Prediction of Dry-Type Transformers Based on Particle Filter Optimization with Support Vector Regression
Abstract
:1. Introduction
2. Hotspot Temperature Prediction Model Based on the Particle Filter Support Vector Regression
2.1. The Input Parameters of the Prediction Model
- Load rate K: The copper loss generated by the primary and secondary windings during the operation of the dry-type transformer is the main heat source, and the winding resistance loss is proportional to the square of the load rate. When the load rate changes, the corresponding loss changes and consequently leads to temperature changes.
- Ambient temperature Ta: Based on the principle of heat convection, the iron core and windings of dry-type transformers are directly in contact with air, and thermal convection is the main heat dissipation method. The ambient temperature affects the temperature of the dry-type transformer winding and consequently affects the hotspot temperature of the transformer.
- Cooling fan status sf: When the temperature of the transformer exceeds a certain limit, the cooling fan will be started in order to aid heat dissipation. Forced air cooling has a better heat dissipation effect than natural air flow. The temperature increase rate will be reduced when the fan is turned on.
- Historical temperature Ts: The process of temperature variation has a time lagging characteristic. The current temperature is closely related to the temperature value of the previous period.
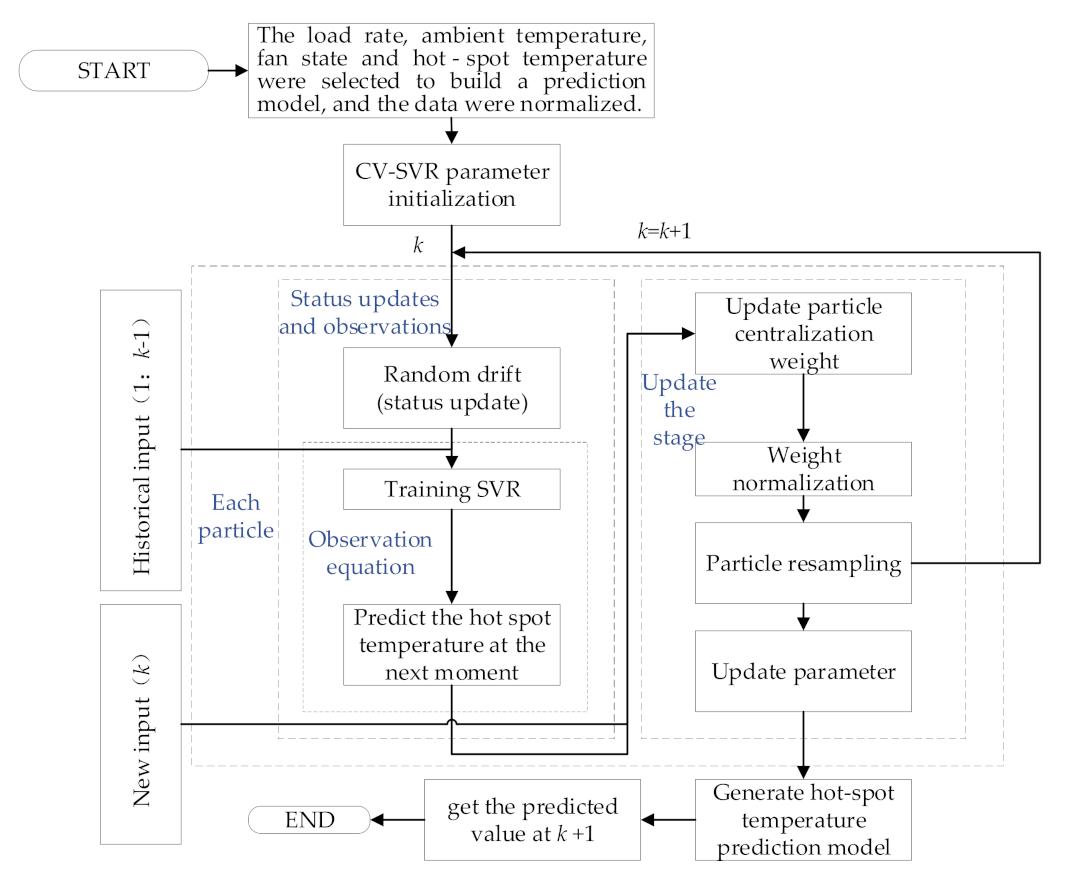
2.2. PF-SVR Hotspot Temperature Prediction Model
2.2.1. Support Vector Regression Principle
2.2.2. Particle Filter Principle
2.2.3. SVR Parameter Optimization
2.2.4. PF-SVR Optimization Method
- Particle initialization of the particle filter. The optimal SVR hyperparameters at the initial time are obtained through the cross-validation and the range of the number of particles Ns is set to be 300 to 500. The initial particle set is set to be .
- Prediction model updating. When k = 1, 2, …, the particle set is recorded as .
- Perform particle resampling and particle drift operation on the particle set in order to obtain a new particle set .
- Perform a small random drift for each particle as follows:
- Update the particle weight by measuring the possibility function value of zk and the predicted value of at each state as follows:
- Perform weight normalization as follows:
- Eliminate particles with lower weights, copy particles with higher weights, and regenerate new random particles as per .
- Output the prediction result and establish a prediction model based on each particle xki in the new particle set to obtain the prediction at time instant k + 1. The final prediction result is shown in Equation (20):
- Update the prediction model and return to step (2).
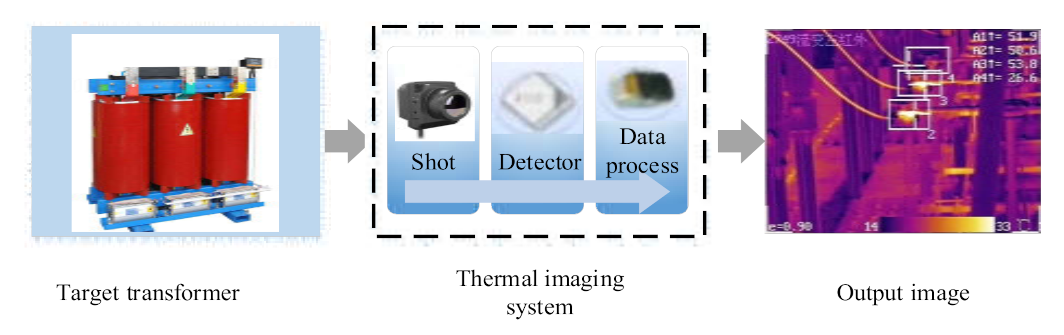
3. Dry-Type Transformer Temperature Online Monitoring
- Display and store the hotspot temperature of the three-phase winding and display and store the highest temperature in the monitoring area of the infrared thermal imager;
- an overheat alarm threshold is set to the initial value and can be adjusted;
- display the trend curve of historical temperature data and the initial value of historical time can be adjusted;
- the hotspot temperature can be combined with the historical temperature, load current, ambient temperature, fan status, and other characteristics to comprehensively judge the transformer temperature status.
- Any continuous temperature changes of the transformer can be monitored, which is helpful for the long-term statistics and overall status assessment of a dry-type transformer;
- From point detection to surface detection, the temperature images of the entire monitoring area can be obtained, and the hotspot temperature can be recorded;
- The non-contact temperature sensor can be combined with an existing embedded temperature sensor, which does not affect the normal operation of the transformer;
- Online temperature monitoring enables the measure of a large temperature range with a high monitoring accuracy. The temperature measurement range of infrared thermal imaging is generally −20 °C to 180 °C, and the monitoring error is typically ±2 °C.
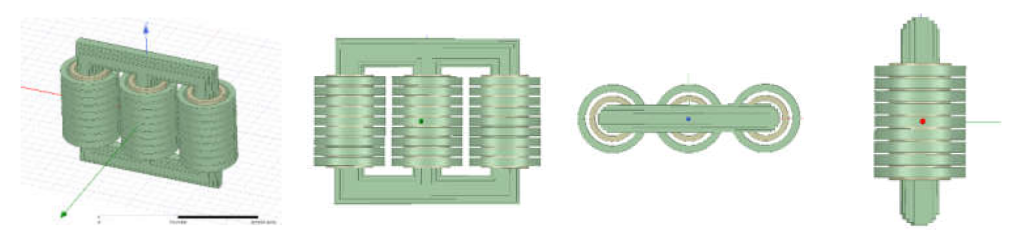
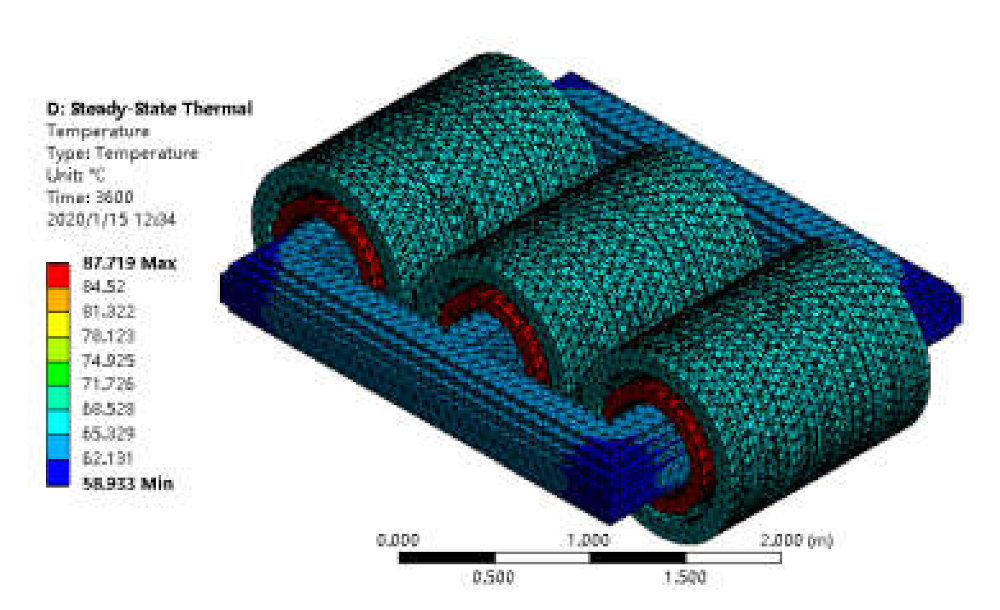
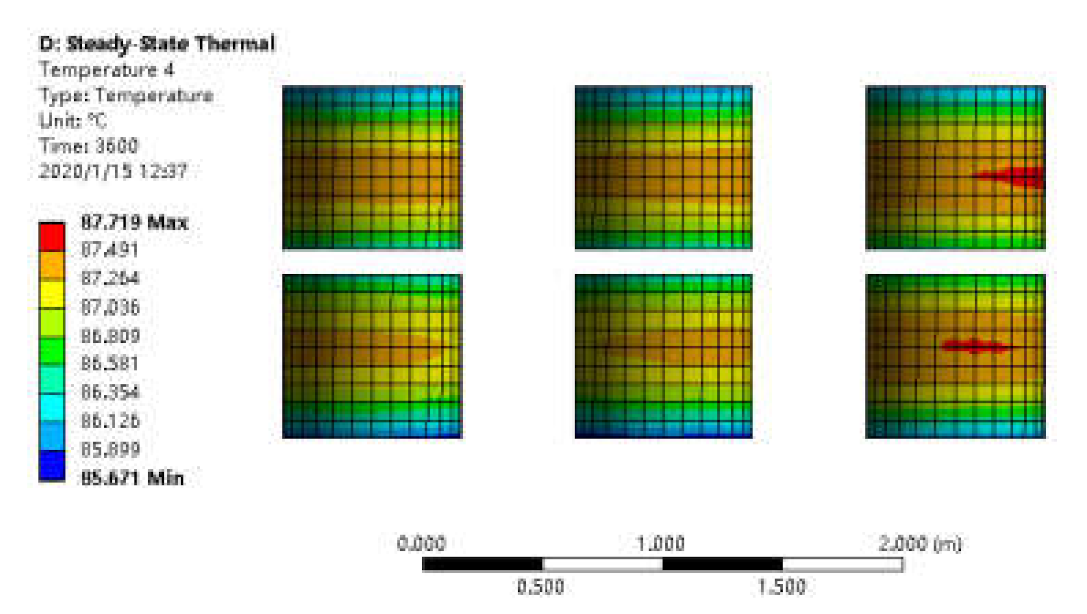
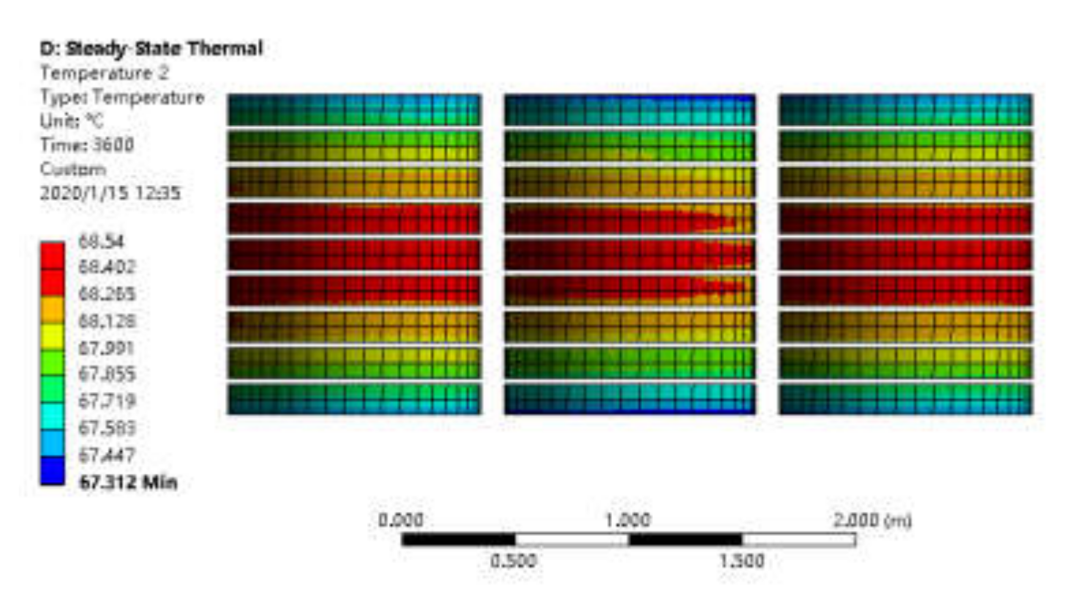
3.1. Analysis of Hotspot Temperature Location Based on Electromagnetic Thermal Coupled Model
- A field–circuit coupled finite element model is established where the electric and magnetic fields are coupled, and the core loss and winding loss may then be analyzed;
- The dry-type transformer losses obtained from the simulation are compared with theoretical values to verify the accuracy of the model;
- An indirect coupling method is used to couple the electromagnetic and temperature fields, in which the loss is used as the transmission medium to realize coupling and the distribution of the temperature field of each part is analyzed;
- Different load rates and ambient temperatures are set, and the transformer temperature distribution and hotspot locations in different states are analyzed;
- The temperature distribution is solved iteratively.
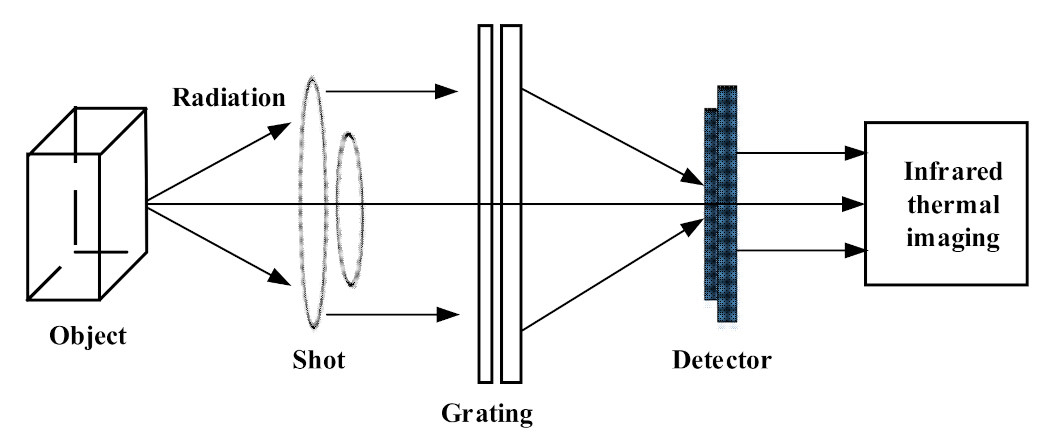
3.2. Temperature Monitoring Based on Infrared Thermal Imager
3.2.1. Principle of Infrared Thermal Imager
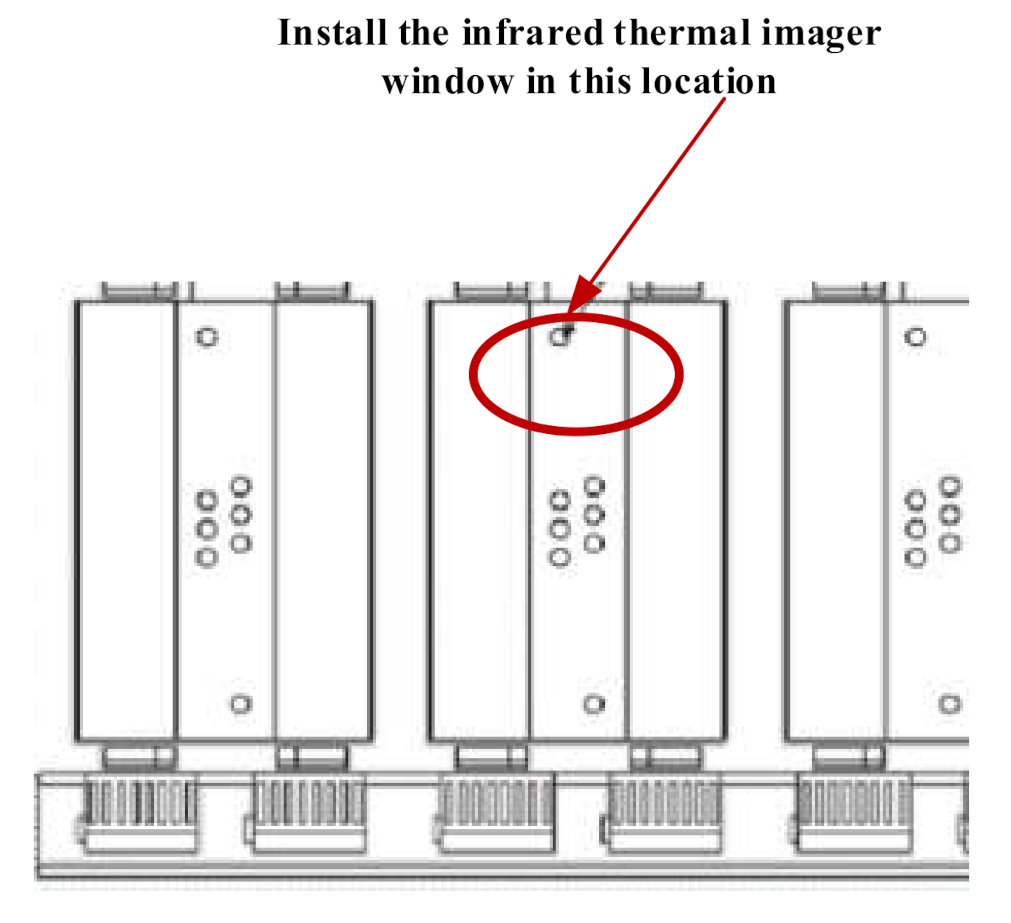
3.2.2. Design of the Thermal Monitoring System
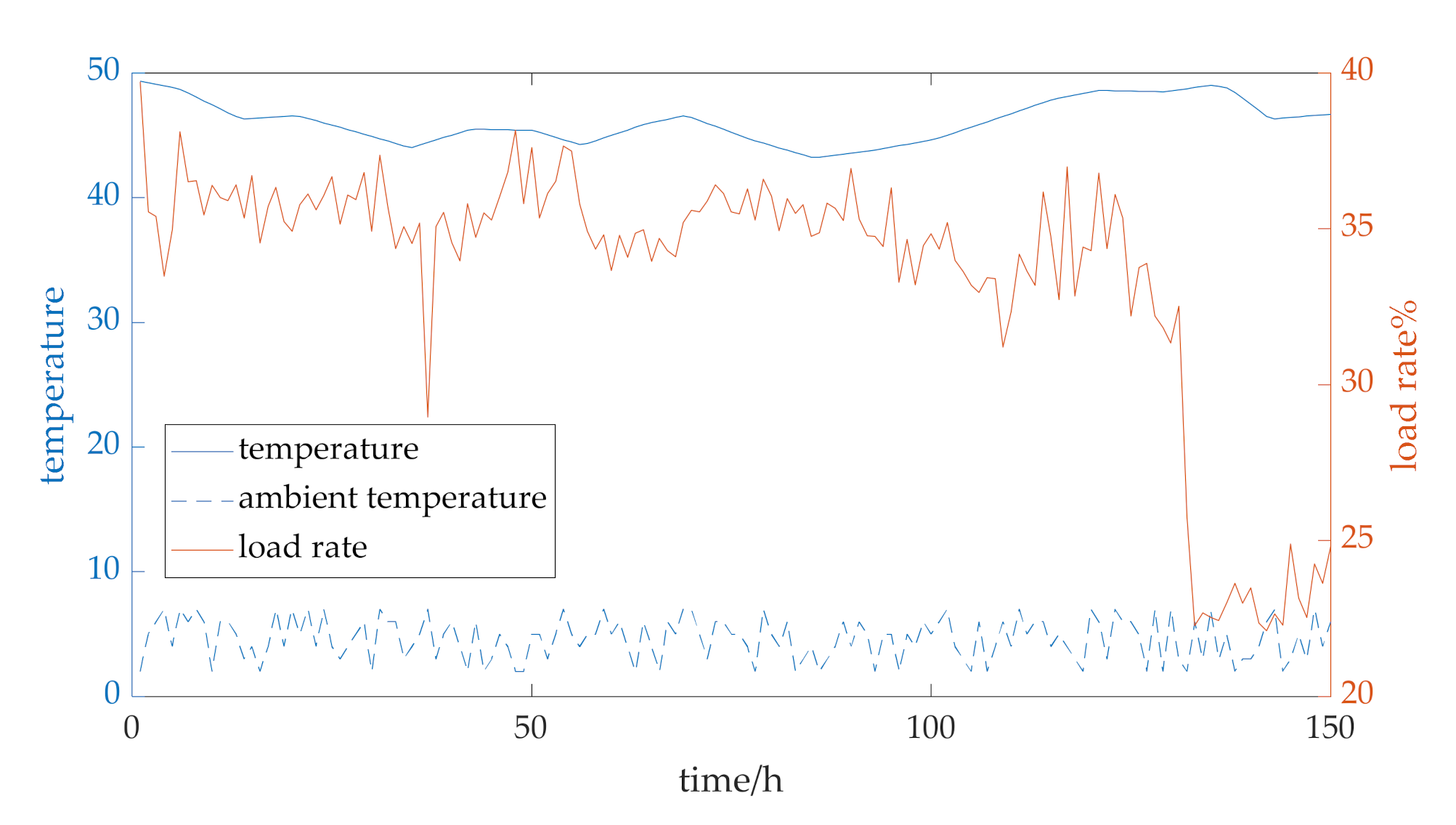
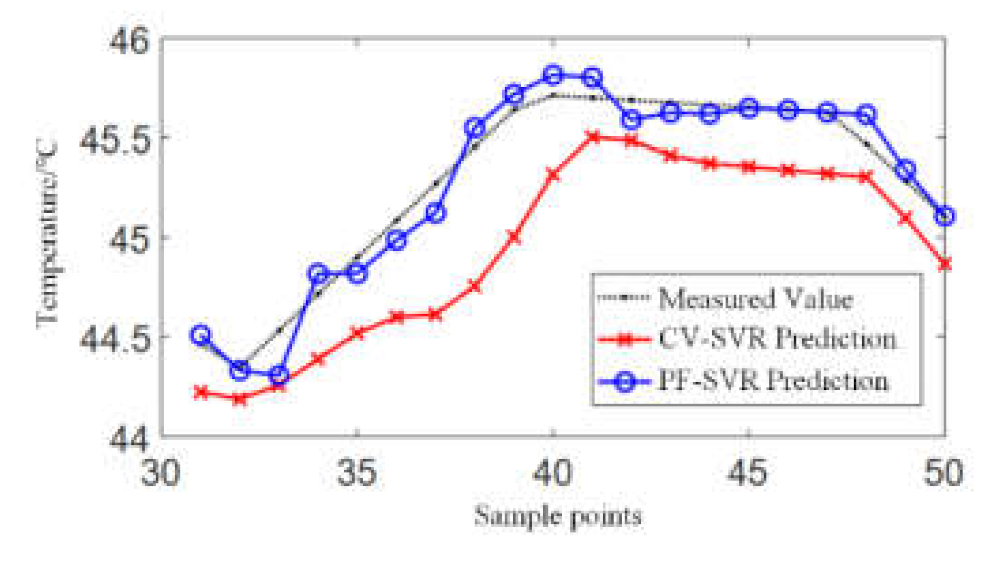
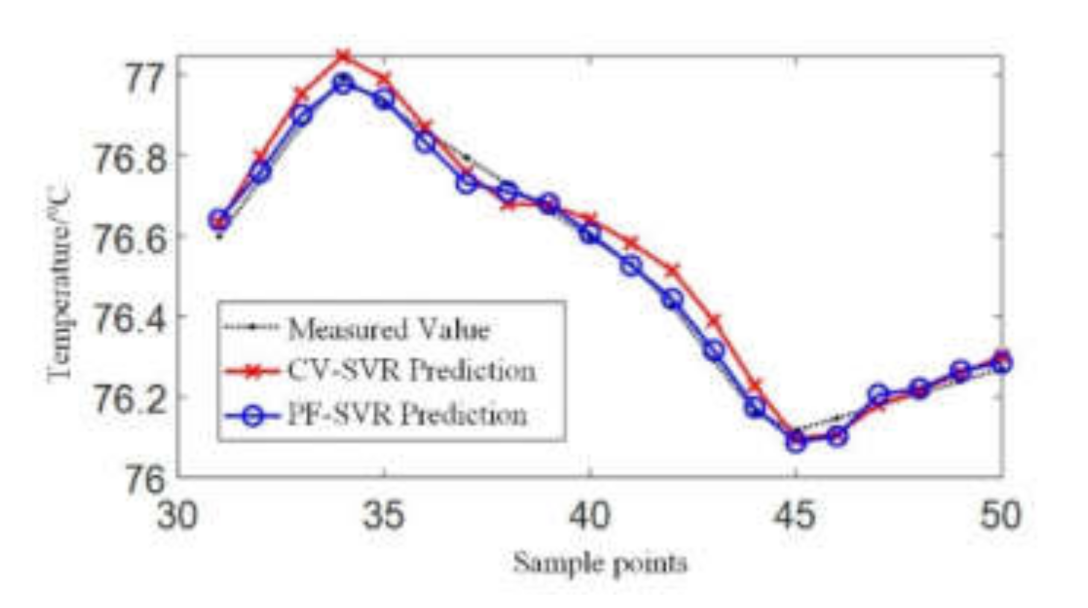
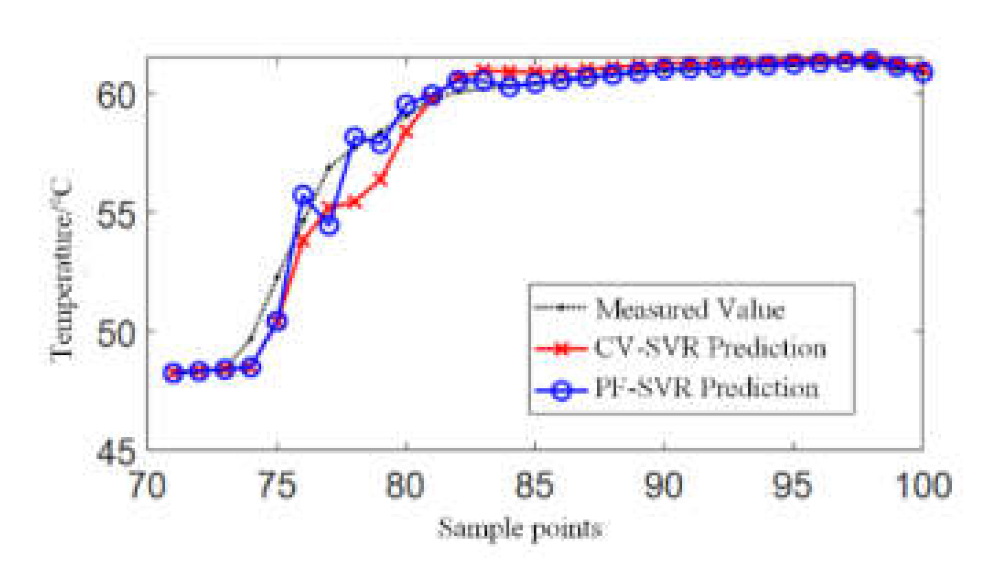
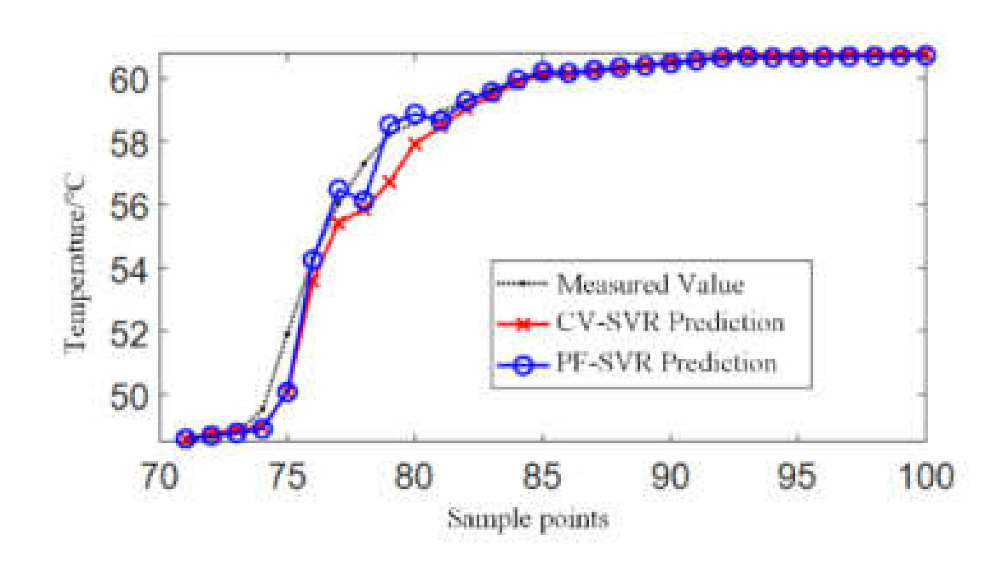
4. Results Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Eslamian, M.; Vahidi, B.; Eslamian, A. Thermal analysis of cast resin dry-type transformers. Energy Convers. Manag. 2011, 52, 2479–2488. [Google Scholar] [CrossRef]
- Rahimpour, E.; Azizian, D. Analysis of Temperature Distribution in Cast-resin Dry-type Transformers. Electr. Eng. 2007, 89, 301–309. [Google Scholar] [CrossRef]
- Cha, C.; Kim, J.K.; Kweon, K.Y. Investigation of the thermal head effect in a power transformer. In Proceedings of the 2009 Transmission & Distribution Conference & Exposition: Asia and Pacific, Seoul, Korea, 26–30 October 2009; Volume 67, pp. 1–4. [Google Scholar] [CrossRef]
- Wang, E.; Zhao, Z.; Cao, M. Multi Point Temperature Monitoring of Oil Immersed Transformer Based on Fiber Bragg Grating. High Volt. Eng. 2017, 43, 1543–1549. [Google Scholar] [CrossRef]
- Zhao, Z.; Jiang, F.; Li, Y. Air-cooled Thermal Circuit Model and FBG Temperature Measurement of Transformer Winding. High Volt. Eng. 2017, 43, 3938–3943. [Google Scholar] [CrossRef]
- Feng, D.; Wang, D.; Paul, J. Evaluation of Power Transformers’ Effective Hot-Spot Factors by Thermal Modeling of Scrapped Units. IEEE Trans. Power Deliv. 2014, 29, 2077–2085. [Google Scholar] [CrossRef]
- Swift, G.; Molinski, T.S.; Lehn, W. A fundamental approach to transformer thermal modeling-Part I: Theory and equivalent circuit. IEEE Trans. Power Deliv. 2001, 16, 171–175. [Google Scholar] [CrossRef]
- Susa, D.; Nordman, H. A Simple Model for Calculating Transformer Hot-Spot Temperature. IEEE Trans. Power Deliv. 2009, 24, 1257–1265. [Google Scholar] [CrossRef]
- Tang, W.; Wu, Q.; Richardson, Z.J. Equivalent heat circuit-based power transformer thermal model. Electr. Power Appl. IEEE Proc. 2002, 149, 87–92. [Google Scholar] [CrossRef]
- Li, Y.; Liu, N.; Liang, Y. A Model of Load Capacity Assessment for Oil-immersed Transformer by Using Temperature Rise Characteristics. Proc. CSEE 2018, 38, 6737–6746. [Google Scholar] [CrossRef]
- Elmoudi, A. Transformer windings hot spot temperature modeling and simulation. In Proceedings of the 2014 IEEE 27th Canadian Conference on Electrical and Computer Engineering (CCECE), Toronto, ON, Canada, 4–7 May 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Kang, Y.; Bai, B.; Guo, Y. Application of Field-Circuit Coupling Method of 3D Transient Finite Element Analysis for Large Power Transformers. Trans. China Electrotech. Soc. 2014, 29, 219–224. [Google Scholar] [CrossRef]
- Li, L. A Novel Approach to Investigate the Hot-Spot Temperature Rise in Power Transformers. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Santiseban, A.; Delgado, F.; Ortiz, A. Numerical Analysis of The Hot-Spot Temperature of a Power Transformer with Alternative Dielectric Liquids. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 3226–3235. [Google Scholar] [CrossRef] [Green Version]
- Liao, C.; Ruan, J.; Liu, C. 3-D Coupled Electromagnetic-Fluid-Thermal Analysis of Oil-Immersed Triangular Wound Core Transformer. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Ding, X.; Ning, W. Analysis of the Dry-type Transformer Temperature Field Based on Fluid-solid Coupling. In Proceedings of the 2012 Second International Conference on Instrumentation Measurement, Computer, Communication and Control, Harbin, China, 8–10 December 2012; pp. 520–523. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, F.; Qi, Y. Prediction of Winding Temperature in Power Transformers Based on Fluid Network. High Volt. Eng. 2017, 43, 1509–1517. [Google Scholar] [CrossRef]
- Yang, Z.; Zhou, Q.; Wu, X.; Zhao, Z. A Novel Measuring Method of Interfacial Tension of Transformer Oil Combined PSO Optimized SVM and Multi Frequency Ultrasonic Technology. IEEE Access 2019, 7, 182624–182631. [Google Scholar] [CrossRef]
- Cui, Y.; Ma, H.; Saha, T. Improvement of power transformer insulation diagnosis using oil characteristics data preprocessed by SMOTE Boost technique. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 2363–2373. [Google Scholar] [CrossRef]
- Lu, P. Real-Time Monitoring of Temperature Rises of Energized Transformer Cores with Distributed Optical Fiber Sensors. IEEE Trans. Power Deliv. 2019, 34, 1588–1598. [Google Scholar] [CrossRef]
- Khosravi, A.; Nahavandi, S.; Creighton, D.; Atiya, A.F. Comprehensive Review of Neural Network-Based Prediction Intervals and New Advances. IEEE Trans. Neural Netw. 2011, 22, 1341–1356. [Google Scholar] [CrossRef] [PubMed]
- Huang, G. An Insight into Extreme Learning Machines: Random Neurons, Random Features and Kernels. Cogn. Comput. 2014, 6, 376–390. [Google Scholar] [CrossRef]
- Li, K.; Qi, X.; Wei, B. Prediction of Transformer Top Oil Temperature Based on Kernel Extreme Learning Machine Error Prediction and Correction. High Volt. Eng. 2017, 43, 4045–4053. [Google Scholar] [CrossRef]
- Naseri, F.; Kazemi, Z.; Arefi, M. Fast Discrimination of Transformer Magnetizing Current from Internal Faults: An Extended Kalman Filter-Based Approach. IEEE Trans. Power Deliv. 2017, 33, 110–118. [Google Scholar] [CrossRef]
- Singh, A.K.; Pal, B.C. Rate of Change of Frequency Estimation for Power Systems Using Interpolated DFT and Kalman Filter. IEEE Trans. Power Syst. 2019, 34, 2509–2517. [Google Scholar] [CrossRef]
- Zhou, L. A Method for Hot-Spot Temperature Prediction and Thermal Capacity Estimation for Traction Transformers in High-Speed Railway Based on Genetic Programming. IEEE Trans. Transp. Electrif. 2019, 5, 1319–1328. [Google Scholar] [CrossRef]
- Zhao, W.; Tao, T.; Ding, Z. A dynamic particle filter-support vector regression method for reliability prediction. Reliab. Eng. Syst. Saf. 2013, 119, 109–116. [Google Scholar] [CrossRef]
- Pai, P. System reliability forecasting by support vector machines with genetic algorithms. Math. Comput. Model. 2006, 43, 262–274. [Google Scholar] [CrossRef]
- Lins, I.D. A Particle Swarm-optimized Support Vector Machine for Reliability Prediction. Qual. Reliab. Eng. Int. 2012, 28, 141–158. [Google Scholar] [CrossRef]





| Type | Value | Type | Value |
|---|---|---|---|
| Model | PSCZ10-8000/6.3/35 | Rated capacity | 8000 |
| Rated voltage/kV Phase number Group label Tapping range No-load loss/W | 6.3/35 3 YNd11 ±4 × 2.5% 12,100 | Rated current/A Rated frequency/Hz Insulation class Rated load loss/W | 733/132 50 F 40,400 (120 °C) |
| RMSE (°C) | NRMSE (°C1/2) | MAPE | |
|---|---|---|---|
| CV-SVR | 0.1147 | 0.1565 | 0.1645 |
| PF-SVR | 0.0812 | 0.1107 | 0.0876 |
| RMSE (°C) | NRMSE (°C1/2) | MAPE | |
|---|---|---|---|
| CV-SVR | 0.1152 | 0.1687 | 0.1614 |
| PF-SVR | 0.0530 | 0.0776 | 0.0675 |
| RMSE (°C) | NRMSE (°C1/2) | MAPE | |
|---|---|---|---|
| CV-SVR | 0.0632 | 0.1335 | 0.3035 |
| PF-SVR | 0.0338 | 0.0713 | 0.2635 |
| RMSE (°C) | NRMSE (°C1/2) | MAPE | |
|---|---|---|---|
| CV-SVR | 0.0993 | 0.1853 | 1.0505 |
| PF-SVR | 0.0739 | 0.1469 | 0.5669 |
| RMSE (°C) | NRMSE (°C1/2) | MAPE | |
|---|---|---|---|
| CV-SVR | 0.0993 | 0.1853 | 1.0505 |
| PF-SVR | 0.0739 | 0.1469 | 0.5669 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Xu, G.; Li, N.; Li, K.; Liang, Y.; Zhong, H.; Zhang, L.; Liu, P. Hotspot Temperature Prediction of Dry-Type Transformers Based on Particle Filter Optimization with Support Vector Regression. Symmetry 2021, 13, 1320. https://doi.org/10.3390/sym13081320
Sun Y, Xu G, Li N, Li K, Liang Y, Zhong H, Zhang L, Liu P. Hotspot Temperature Prediction of Dry-Type Transformers Based on Particle Filter Optimization with Support Vector Regression. Symmetry. 2021; 13(8):1320. https://doi.org/10.3390/sym13081320
Chicago/Turabian StyleSun, Yuanyuan, Gongde Xu, Na Li, Kejun Li, Yongliang Liang, Hui Zhong, Lina Zhang, and Ping Liu. 2021. "Hotspot Temperature Prediction of Dry-Type Transformers Based on Particle Filter Optimization with Support Vector Regression" Symmetry 13, no. 8: 1320. https://doi.org/10.3390/sym13081320
APA StyleSun, Y., Xu, G., Li, N., Li, K., Liang, Y., Zhong, H., Zhang, L., & Liu, P. (2021). Hotspot Temperature Prediction of Dry-Type Transformers Based on Particle Filter Optimization with Support Vector Regression. Symmetry, 13(8), 1320. https://doi.org/10.3390/sym13081320







