A Multivariate Flexible Skew-Symmetric-Normal Distribution: Scale-Shape Mixtures and Parameter Estimation via Selection Representation
Abstract
:1. Introduction
2. Methodology
2.1. The Family of SSMFSSN Distributions
2.2. Parameter Estimation via the ECME Algorithm
- CMQ-Step 1: Fixing and , we update via Proposition A2 by taking the partial derivative of (22) with respect to . Since the derivation cannot get a closed-form expression for its maximizer, the solution of is validated by numerically solving the root of the following equation:where the two terms and are nonlinear functions of with .
- CMQ-Step 2: Fixing and then updating by maximizing (22) over gives
- CMQ-Step 3: Fixing , we update via Proposition A3 by taking the partial derivative of (22) with respect to each, . Since their solutions cannot be isolated and set equal to zeros, we have the following equation for finding the nonlinear roots of :where is a nonlinear function of . After simplification, we can transform back to
- CML-Step: is updated by optimizing the following constrained log-likelihood function:
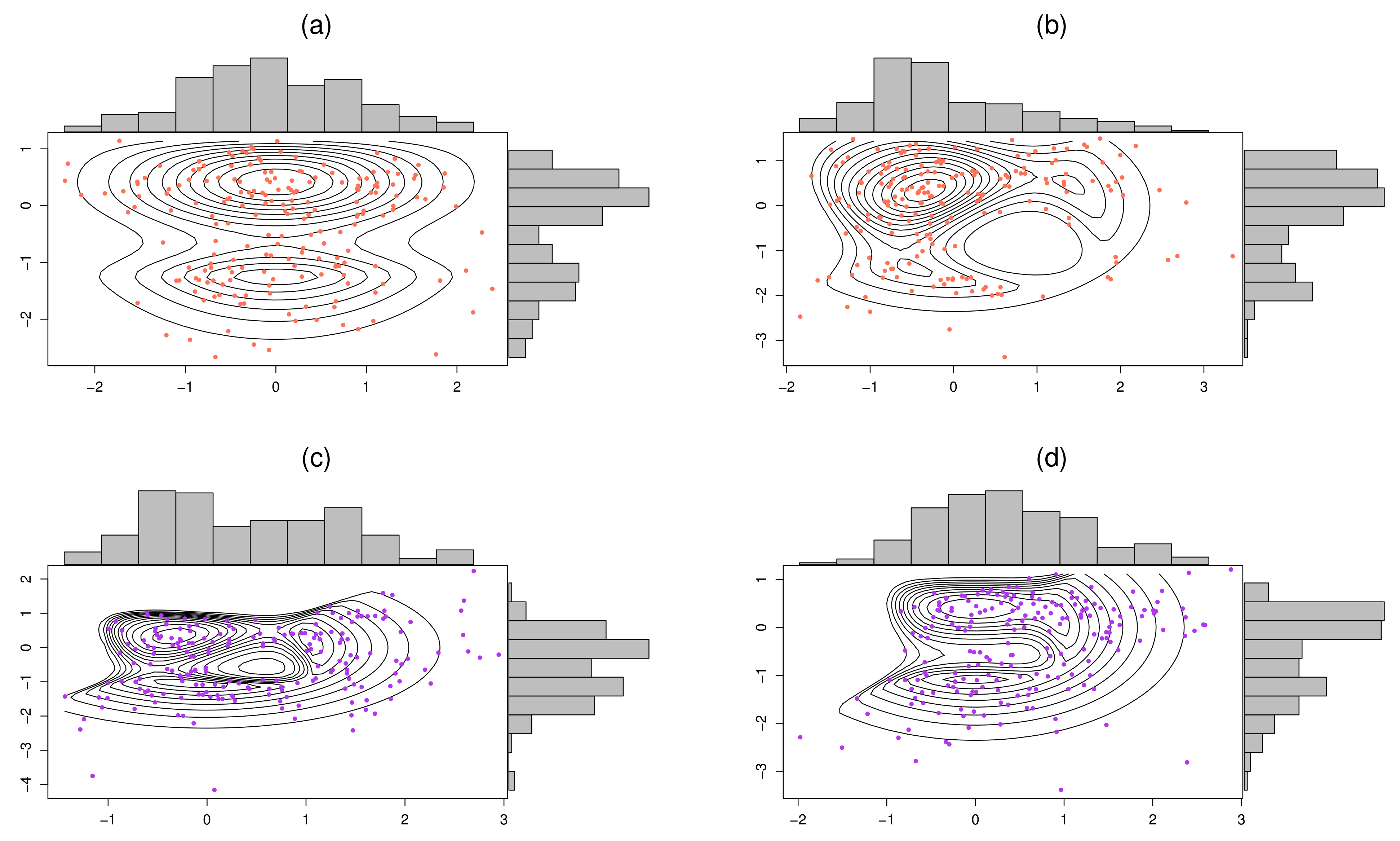
3. Examples of SSMFSSN Distributions
3.1. The Multivariate Flexible Skew-Symmetric-t-Normal Distribution
- CMQ-Step 4: is obtained by solving the root of the following equation:
3.2. The Multivariate Flexible Skew-Symmetric-Slash-Normal Distribution
- CMQ-Step 4:
3.3. The Multivariate Flexible Skew-Symmetric-Contaminated-Normal Distribution
3.4. The Multivariate Flexible Skew-Symmetric-t Distribution
3.5. The Multivariate Flexible Skew-Symmetric-t-t Distribution
- CMQ-Step 4: and are obtained by solving the roots of the following two equations:and
4. Simulation Studies
4.1. Recovery of the True Underlying Parameters
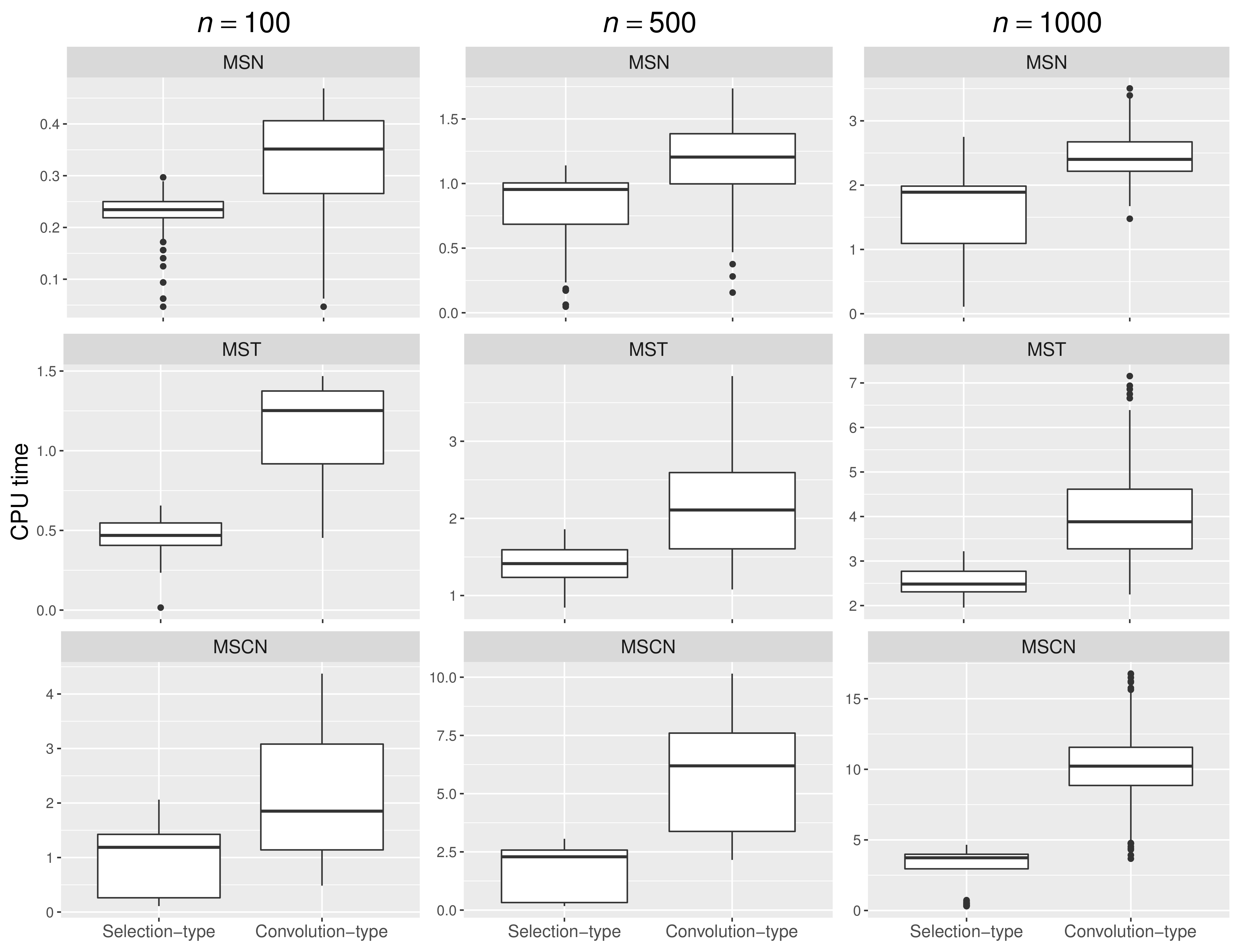
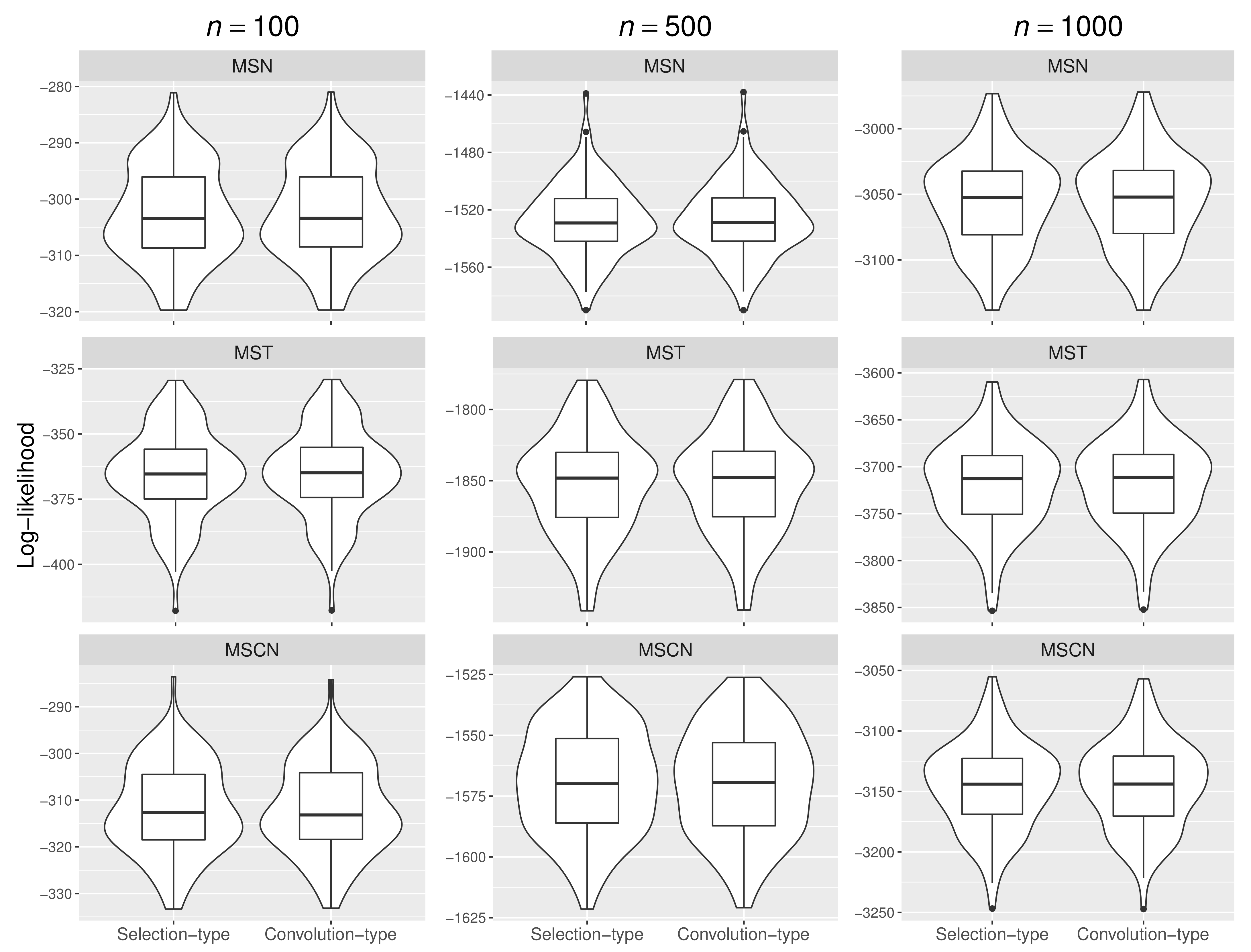
4.2. Comparing the Proposed Procedure with Convolution-Type EM Algorithms
- CMQ-Step 1: Fixing and , we obtain by
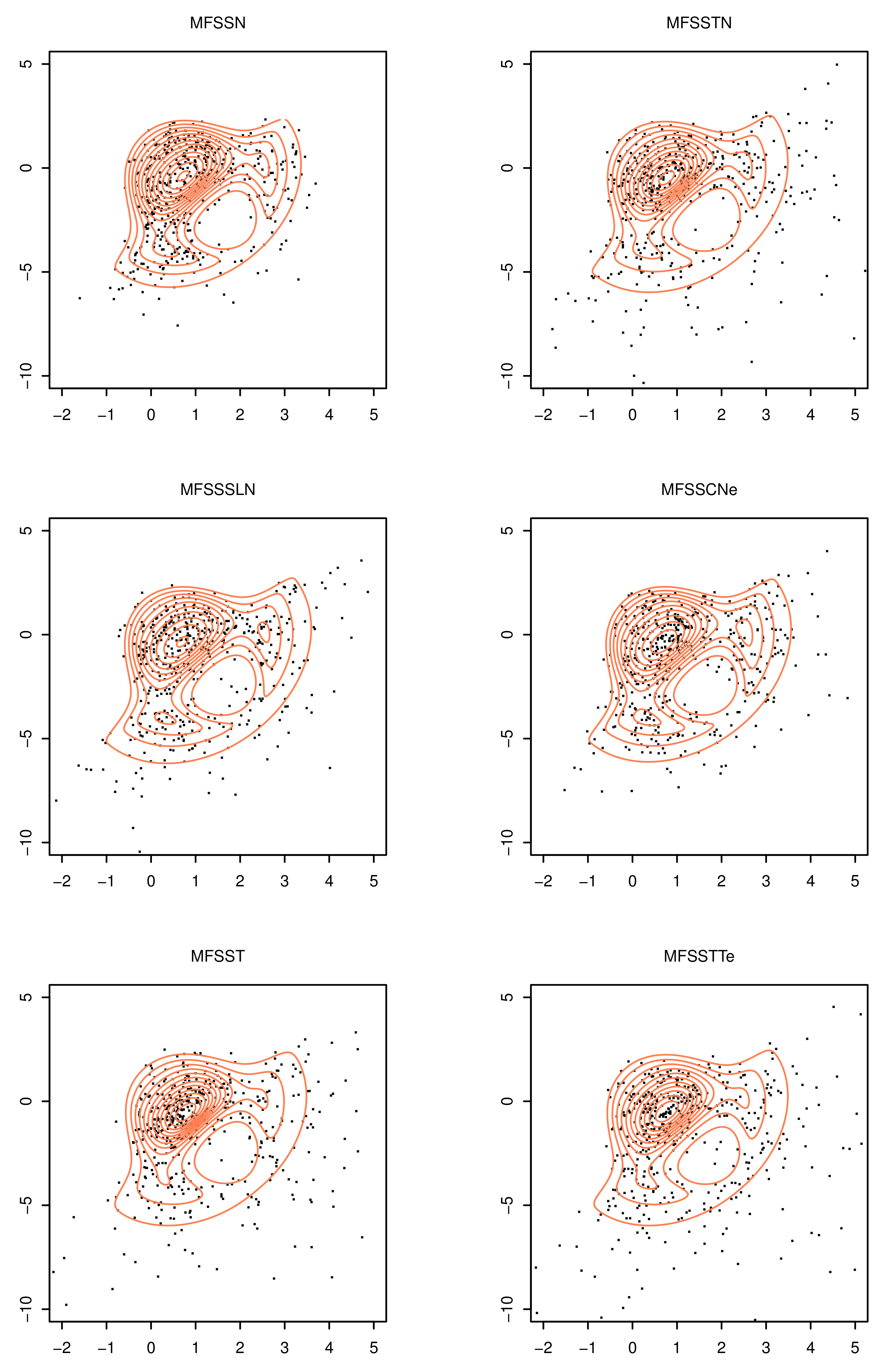
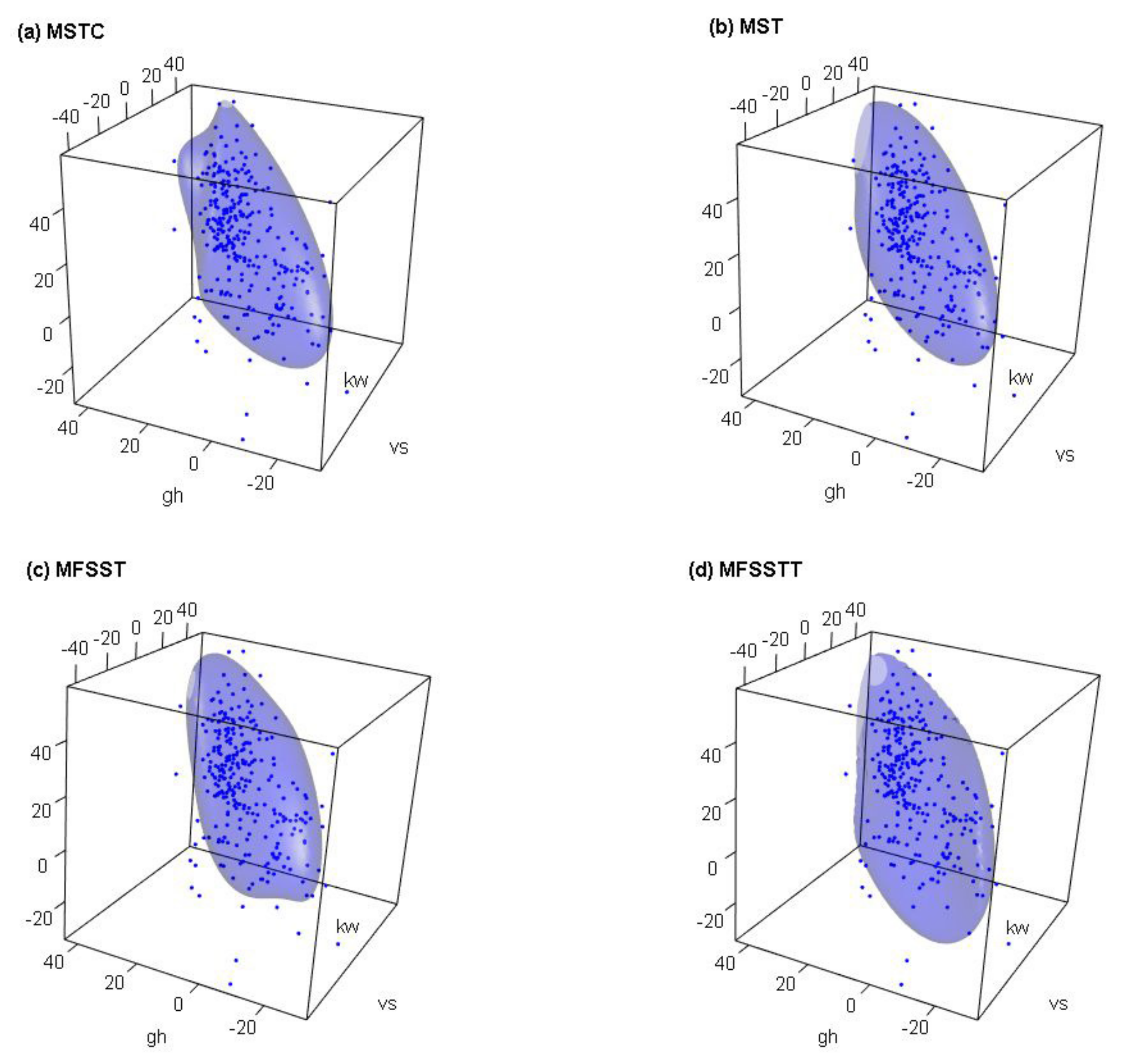
5. An Illustrative Example: The Wind Speed Data
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Hadamard Product
Appendix B. Proof of Equation (43)
References
- Branco, M.D.; Dey, D.K. A general class of multivariate skew-elliptical distributions. J. Multivar. Anal. 2001, 79, 99–113. [Google Scholar] [CrossRef] [Green Version]
- Azzalini, A.; Valle, A.D. The multivariate skew-normal distribution. Biometrika 1996, 83, 715–726. [Google Scholar] [CrossRef]
- Arellano-Valle, R.B.; Genton, M.G. On fundamental skew distributions. J. Multivar. Anal. 2005, 96, 93–116. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, C.S.; Lachos, V.H.; Bolfarine, H. Likelihood-based inference for multivariate skew scale mixtures of normal distributions. AStA Adv. Stat. Anal. 2016, 100, 421–441. [Google Scholar] [CrossRef]
- Arellano-Valle, R.B.; Ferreira, C.S.; Genton, M.G. Scale and shape mixtures of multivariate skew-normal distributions. J. Multivar. Anal. 2018, 166, 98–110. [Google Scholar] [CrossRef] [Green Version]
- Azzalini, A.; Capitanio, A. Distributions generated by perturbation of symmetry with emphasis on a multivariate skew t-distribution. J. R. Stat. Soc. Ser. B 2003, 65, 367–389. [Google Scholar] [CrossRef]
- Wang, J.; Boyer, J.; Genton, M.G. A skew-symmetric representation of multivariate distributions. Stat. Sin. 2004, 1259–1270. Available online: https://www.jstor.org/stable/24307231 (accessed on 5 January 2005).
- Ma, Y.; Genton, M.G. Flexible class of skew-symmetric distributions. Scand. J. Stat. 2004, 31, 459–468. [Google Scholar] [CrossRef] [Green Version]
- Styan, G.P. Hadamard products and multivariate statistical analysis. Linear Algebra Its Appl. 1973, 6, 217–240. [Google Scholar] [CrossRef] [Green Version]
- Mahdavi, A.; Amirzadeh, V.; Jamalizadeh, A.; Lin, T.I. Maximum likelihood estimation for scale-shape mixtures of flexible generalized skew normal distributions via selection representation. Comput. Stat. 2021, 36, 2201–2230. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B 1977, 39, 1–22. [Google Scholar]
- Meng, X.L.; Rubin, D.B. Maximum likelihood estimation via the ECM algorithm: A general framework. Biometrika 1993, 80, 267–278. [Google Scholar] [CrossRef]
- Liu, C.; Rubin, D.B. The ECME algorithm: A simple extension of EM and ECM with faster monotone convergence. Biometrika 1994, 81, 633–648. [Google Scholar] [CrossRef]
- Lin, T.I. Maximum likelihood estimation for multivariate skew normal mixture models. J. Multivar. Anal. 2009, 100, 257–265. [Google Scholar] [CrossRef] [Green Version]
- Lin, T.I. Robust mixture modeling using multivariate skew t distributions. Stat. Comp. 2010, 20, 343–356. [Google Scholar] [CrossRef]
- Lin, T.I.; Lee, J.C.; Yen, S.Y. Finite mixture modelling using the skew normal distribution. Stat. Sin. 2007, 909–927. Available online: https://www.jstor.org/stable/24307705 (accessed on 5 December 2007).
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020; Available online: http://www.R-project.org (accessed on 10 January 2021).
- Lin, T.I.; Ho, H.J.; Lee, C.-R. Flexible mixture modelling using the multivariate skew-t-normal distribution. Stat. Comp. 2014, 24, 531–546. [Google Scholar] [CrossRef]
- Wang, J.; Genton, M.G. The multivariate skew-slash distribution. J. Stat. Plan. Inference 2006, 136, 209–220. [Google Scholar] [CrossRef]
- Lin, T.I.; Lee, J.C.; Hsieh, W.J. Robust mixture modeling using the skew t distribution. Stat. Comp. 2007, 17, 81–92. [Google Scholar] [CrossRef]
- Wang, W.L.; Jamalizadeh, A.; Lin, T.I. Finite mixtures of multivariate scale-shape mixtures of skew-normal distributions. Stat. Pap. 2020, 61, 2643–2670. [Google Scholar] [CrossRef]
- Cabral, C.R.B.; Lachos, V.H.; Prates, M.O. Multivariate mixture modeling using skew-normal independent distributions. Comput. Stat. Data. Anal. 2012, 56, 126–142. [Google Scholar] [CrossRef]
- Prates, M.O.; Lachos, V.H.; Cabral, C.R.B. mixsmsn: Fitting finite mixture of scale mixture of skew-normal distributions. J. Stat. Softw. 2013, 54, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Azzalini, A.; Genton, M.G. Robust likelihood methods based on the skew-t and related distributions. Int. Stat. Rev. 2008, 76, 106–129. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE. Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R. Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy. Stat. Sci. 1986, 54–75. Available online: https://www.jstor.org/stable/2245500 (accessed on 22 May 2003). [CrossRef]
- Lin, T.I.; Wu, P.H.; McLachlan, G.J.; Lee, S.X. A robust factor analysis model using the restricted skew-t distribution. Test 2015, 24, 510–531. [Google Scholar] [CrossRef]
- Liu, M.; Lin, T. Skew-normal factor analysis models with incomplete data. J. Appl. Stat. 2015, 42, 789–805. [Google Scholar] [CrossRef]
- Wang, W.L.; Liu, M.; Lin, T.I. Robust skew-t factor analysis models for handling missing data. Stat. Methods. Appl. 2017, 26, 649–672. [Google Scholar] [CrossRef]
- Lin, T.I.; Wang, W.L.; McLachlan, G.J.; Lee, S.X. Robust mixtures of factor analysis models using the restricted multivariate skew-t distribution. Stat. Model. 2018, 28, 50–72. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.L.; Castro, L.M.; Lachos, V.H.; Lin, T.I. Model-based clustering of censored data via mixtures of factor analyzers. Comput. Stat. Data. Anal. 2019, 140, 104–121. [Google Scholar] [CrossRef]
- Wang, W.L.; Castro, L.M.; Hsieh, W.C.; Lin, T.I. Mixtures of factor analyzers with covariates formodeling multiply censored dependent variables. Stat. Pap. 2021. [Google Scholar]
- Wang, W.L.; Lin, T.I. Robust clustering of multiply censored data via mixtures of t factor analyzers. TEST 2021. [Google Scholar] [CrossRef]
- Wang, W.L.; Lin, T.I. Robust clustering via mixtures of t factor analyzers with incomplete data. Adv. Data Anal. Classif. 2021. [Google Scholar] [CrossRef]

| Model | Parameter | n = 100 | n = 250 | n = 500 | n = 1000 | ||||
|---|---|---|---|---|---|---|---|---|---|
| MAB | RMSE | MAB | RMSE | MAB | RMSE | MAB | RMSE | ||
| MFSSN | 0.090 | 0.122 | 0.057 | 0.074 | 0.037 | 0.048 | 0.027 | 0.033 | |
| 0.257 | 0.382 | 0.143 | 0.209 | 0.115 | 0.168 | 0.081 | 0.123 | ||
| 0.476 | 0.625 | 0.203 | 0.270 | 0.111 | 0.155 | 0.079 | 0.112 | ||
| 0.339 | 0.489 | 0.160 | 0.209 | 0.104 | 0.131 | 0.064 | 0.082 | ||
| MFSSTN | 0.095 | 0.127 | 0.062 | 0.086 | 0.040 | 0.053 | 0.028 | 0.036 | |
| 0.419 | 0.673 | 0.244 | 0.383 | 0.158 | 0.241 | 0.121 | 0.179 | ||
| 0.382 | 0.469 | 0.349 | 0.426 | 0.317 | 0.382 | 0.306 | 0.355 | ||
| 0.335 | 0.439 | 0.194 | 0.244 | 0.177 | 0.216 | 0.151 | 0.181 | ||
| 2.495 | 10.745 | 0.458 | 0.651 | 0.319 | 0.413 | 0.203 | 0.258 | ||
| MFSSSLN | 0.091 | 0.121 | 0.052 | 0.069 | 0.036 | 0.047 | 0.025 | 0.035 | |
| 0.424 | 0.641 | 0.306 | 0.489 | 0.190 | 0.314 | 0.127 | 0.200 | ||
| 0.458 | 0.588 | 0.267 | 0.347 | 0.216 | 0.269 | 0.174 | 0.206 | ||
| 0.470 | 0.614 | 0.259 | 0.378 | 0.174 | 0.227 | 0.114 | 0.138 | ||
| 6.530 | 11.849 | 3.425 | 8.206 | 1.191 | 3.251 | 0.481 | 0.721 | ||
| MFSSCNe | 0.087 | 0.117 | 0.048 | 0.064 | 0.036 | 0.047 | 0.026 | 0.034 | |
| 0.363 | 0.546 | 0.285 | 0.440 | 0.223 | 0.339 | 0.133 | 0.202 | ||
| 0.446 | 0.595 | 0.288 | 0.353 | 0.202 | 0.247 | 0.138 | 0.174 | ||
| 0.426 | 0.586 | 0.265 | 0.347 | 0.178 | 0.219 | 0.131 | 0.160 | ||
| 0.199 | 0.216 | 0.162 | 0.176 | 0.116 | 0.137 | 0.083 | 0.098 | ||
| MFSST | 0.114 | 0.152 | 0.069 | 0.091 | 0.042 | 0.055 | 0.032 | 0.040 | |
| 0.393 | 0.586 | 0.250 | 0.386 | 0.160 | 0.238 | 0.132 | 0.216 | ||
| 0.453 | 0.559 | 0.265 | 0.329 | 0.207 | 0.253 | 0.194 | 0.228 | ||
| 0.355 | 0.468 | 0.215 | 0.273 | 0.137 | 0.175 | 0.110 | 0.139 | ||
| 1.152 | 2.210 | 0.430 | 0.621 | 0.266 | 0.366 | 0.207 | 0.265 | ||
| MFSSTTe | 0.114 | 0.146 | 0.070 | 0.094 | 0.047 | 0.061 | 0.029 | 0.038 | |
| 0.400 | 0.654 | 0.213 | 0.323 | 0.165 | 0.255 | 0.115 | 0.188 | ||
| 0.437 | 0.546 | 0.411 | 0.476 | 0.406 | 0.453 | 0.414 | 0.438 | ||
| 0.313 | 0.409 | 0.216 | 0.260 | 0.183 | 0.217 | 0.167 | 0.193 | ||
| 1.332 | 2.733 | 0.424 | 0.573 | 0.300 | 0.408 | 0.210 | 0.279 | ||
| Family | Model | d | AIC | BIC | |
|---|---|---|---|---|---|
| MSTC | –3178.7 | 13 | 6383.4 | 6430.5 | |
| MSSMSN | MST | –3180.7 | 13 | 6387.5 | 6434.6 |
| MSTN | –3180.9 | 13 | 6387.8 | 6434.9 | |
| MFSSN | –3171.7 | 15 | 6373.4 | 6427.8 | |
| MFSSTN | –3145.6 | 16 | 6323.1 | 6381.2 | |
| SSMFSSN | MFSSSLN | –3147.1 | 16 | 6326.2 | 6384.2 |
| MFSSCN | –3145.6 | 16 | 6323.3 | 6381.3 | |
| MFSST | –3143.0 | 16 | 6318.1 | 6376.1 | |
| MFSSTT | –3138.2 | 17 | 6310.4 | 6372.1 |
| Parameter | MFSSN | MFSSTN | MFSSSLN | MFSSCN | MFSST | MFSSTT |
|---|---|---|---|---|---|---|
| 23.0(0.05) | 21.3 (0.09) | 21.1 (0.04) | 21.5 (0.07) | 19.9 (0.06) | 18.6 (0.08) | |
| 14.8 (0.04) | 15.6 (0.08) | 15.2 (0.04) | 15.0 (0.07) | 15.1 (0.04) | 15.0 (0.06) | |
| 14.6 (0.04) | 14.9 (0.06) | 14.8 (0.02) | 15.4 (0.04) | 13.4 (0.08) | 12.6 (0.09) | |
| 221.2 (0.26) | 122.9 (0.49) | 80.6 (0.24) | 115.8 (0.31) | 115.6 (0.21) | 115.6 (0.25) | |
| 138.8 (0.16) | 96.4 (0.36) | 64.6 (0.18) | 91.5 (0.24) | 92.8 (0.15) | 93.2 (0.17) | |
| 151.0 (0.13) | 104.8 (0.26) | 69.5 (0.13) | 99.1 (0.16) | 102.9 (0.18) | 106.0 (0.19) | |
| 181.3 (0.10) | 134.5 (0.27) | 90.3 (0.16) | 128.0 (0.18) | 131.2 (0.18) | 132.1 (0.20) | |
| 111.4 (0.07) | 80.8 (0.18) | 54.4 (0.09) | 79.6 (0.12) | 78.8 (0.15) | 79.1 (0.15) | |
| 296.4 (0.07) | 203.4 (0.19) | 134.0 (0.13) | 187.2 (0.09) | 204.4 (0.24) | 206.7 (0.27) | |
| –1.7 (0.01) | –0.4 (0.04) | –0.2 (0.01) | –0.3 (0.02) | 0.1 (0.02) | 1.0 (0.02) | |
| 1.6 (0.04) | 1.1 (0.04) | 1.0 (0.03) | 1.3 (0.04) | 1.3 (0.01) | 3.2 (0.01) | |
| 1.9 (0.04) | 1.4 (0.04) | 1.1 (0.02) | 1.3 (0.02) | 1.4 (0.01) | 2.8 (0.02) | |
| –0.7 (1.99) | –0.1 (2.36) | 0.0 (1.03) | –0.1 (1.53) | –0.2 (0.04) | 1.2 (0.32) | |
| –0.7 (0.05) | –0.4 (0.25) | –0.2 (0.05) | –0.4 (0.19) | –0.5 (0.01) | –1.6 (0.21) | |
| –0.1 (1.52) | –0.2 (1.98) | –0.1 (0.78) | –0.2 (1.18) | –0.1 (0.02) | –2.3 (0.17) | |
| – | 5.0 (0.18) | 1.5 (0.03) | 0.2 (0.04) | 4.7 (0.06) | 4.7 (0.08) | |
| – | – | – | 0.2 (0.54) | – | 1.0 (0.16) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahdavi, A.; Amirzadeh, V.; Jamalizadeh, A.; Lin, T.-I. A Multivariate Flexible Skew-Symmetric-Normal Distribution: Scale-Shape Mixtures and Parameter Estimation via Selection Representation. Symmetry 2021, 13, 1343. https://doi.org/10.3390/sym13081343
Mahdavi A, Amirzadeh V, Jamalizadeh A, Lin T-I. A Multivariate Flexible Skew-Symmetric-Normal Distribution: Scale-Shape Mixtures and Parameter Estimation via Selection Representation. Symmetry. 2021; 13(8):1343. https://doi.org/10.3390/sym13081343
Chicago/Turabian StyleMahdavi, Abbas, Vahid Amirzadeh, Ahad Jamalizadeh, and Tsung-I Lin. 2021. "A Multivariate Flexible Skew-Symmetric-Normal Distribution: Scale-Shape Mixtures and Parameter Estimation via Selection Representation" Symmetry 13, no. 8: 1343. https://doi.org/10.3390/sym13081343
APA StyleMahdavi, A., Amirzadeh, V., Jamalizadeh, A., & Lin, T.-I. (2021). A Multivariate Flexible Skew-Symmetric-Normal Distribution: Scale-Shape Mixtures and Parameter Estimation via Selection Representation. Symmetry, 13(8), 1343. https://doi.org/10.3390/sym13081343






