Evolution of Heavy Ion Beam Probing from the Origins to Study of Symmetric Structures in Fusion Plasmas
Abstract
:1. Preface
2. Introduction
2.1. Heavy Ion Beam Probe—A Tool for Measuring Electrical Potential and Plasma Turbulence
2.2. Physical Principles of HIBP Measurements
- Pass the beam through the existing vacuum vessel ports;
- Find the detector line from the core to the edge of the plasma;
- Find a detector grid covering the maximum part of the plasma cross section;
- Optimize the range of beam energies.
3. Mathematical Problems of Determining Plasma Parameters Using HIBP
3.1. Determination the Spatial Distribution of Electric Potential
3.2. Determination of the Spatial Distribution of Plasma Density
3.3. Determination of the Plasma Magnetic Potential (Field of Plasma Current)
4. Application of the HIBP to Fluctuation Measurements
5. Mathematical Problems of Experimental Data Processing for Fluctuations of Plasma Parameters
5.1. Spectral Fourier Analysis of Oscillations
5.2. Fourier Analysis of Coherency and Cross-Phase of Oscillations
5.3. Bispectral Fourier Analysis of Plasma Oscillations
6. Measurements by Several Spatial Channels
6.1. Measurement of Turbulent Particle Flux on the TJ-II Stellarator
6.2. Measurement of Turbulent Particle Flux in the T-10 Tokamak
6.3. Measurement of the GAM Poloidal Symmetry in the T-10 Tokamak
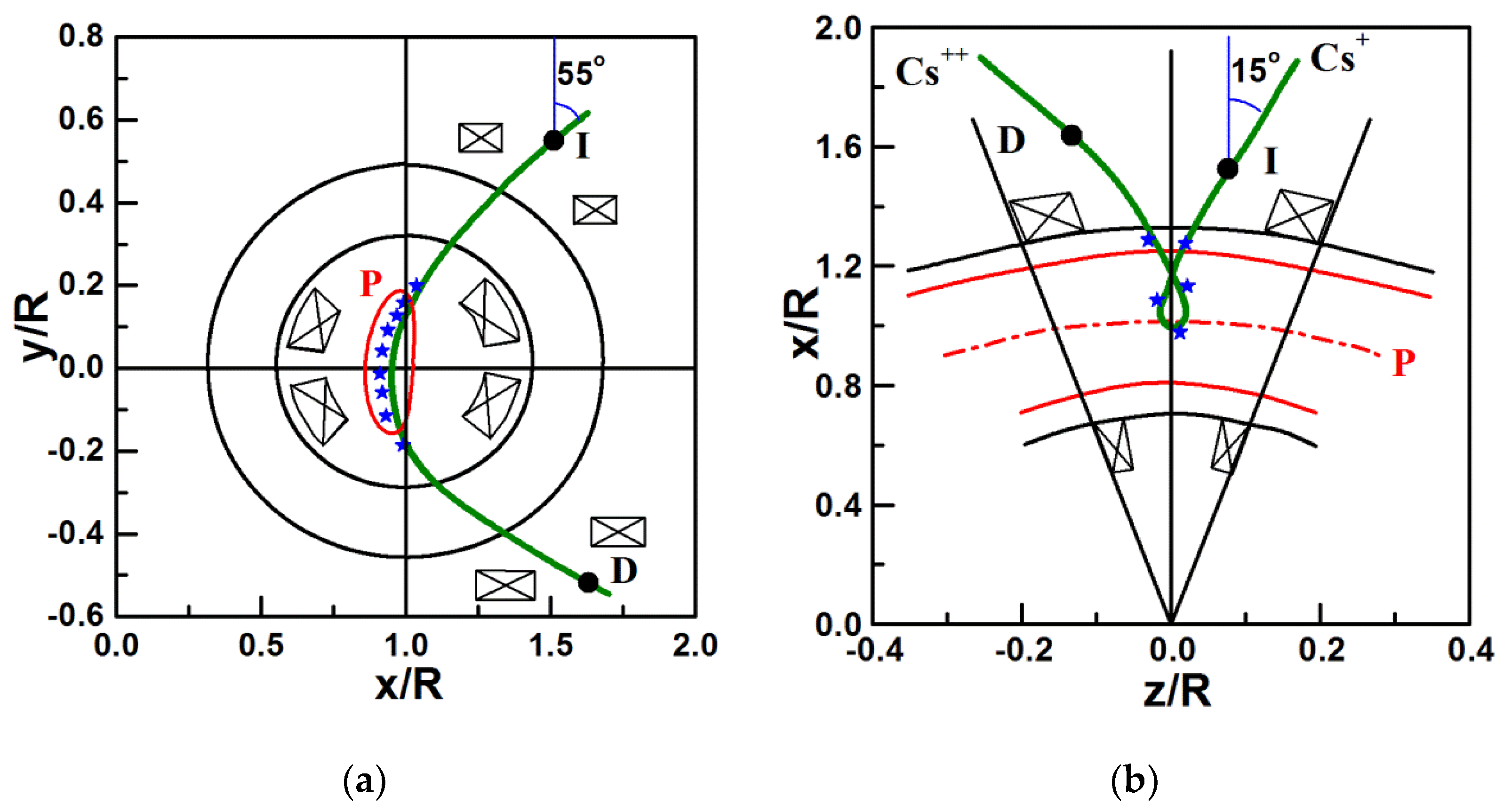
7. HIBP Diagnostics and Their Outcome for Plasma Symmetry Study
7.1. TM-4 HIBP
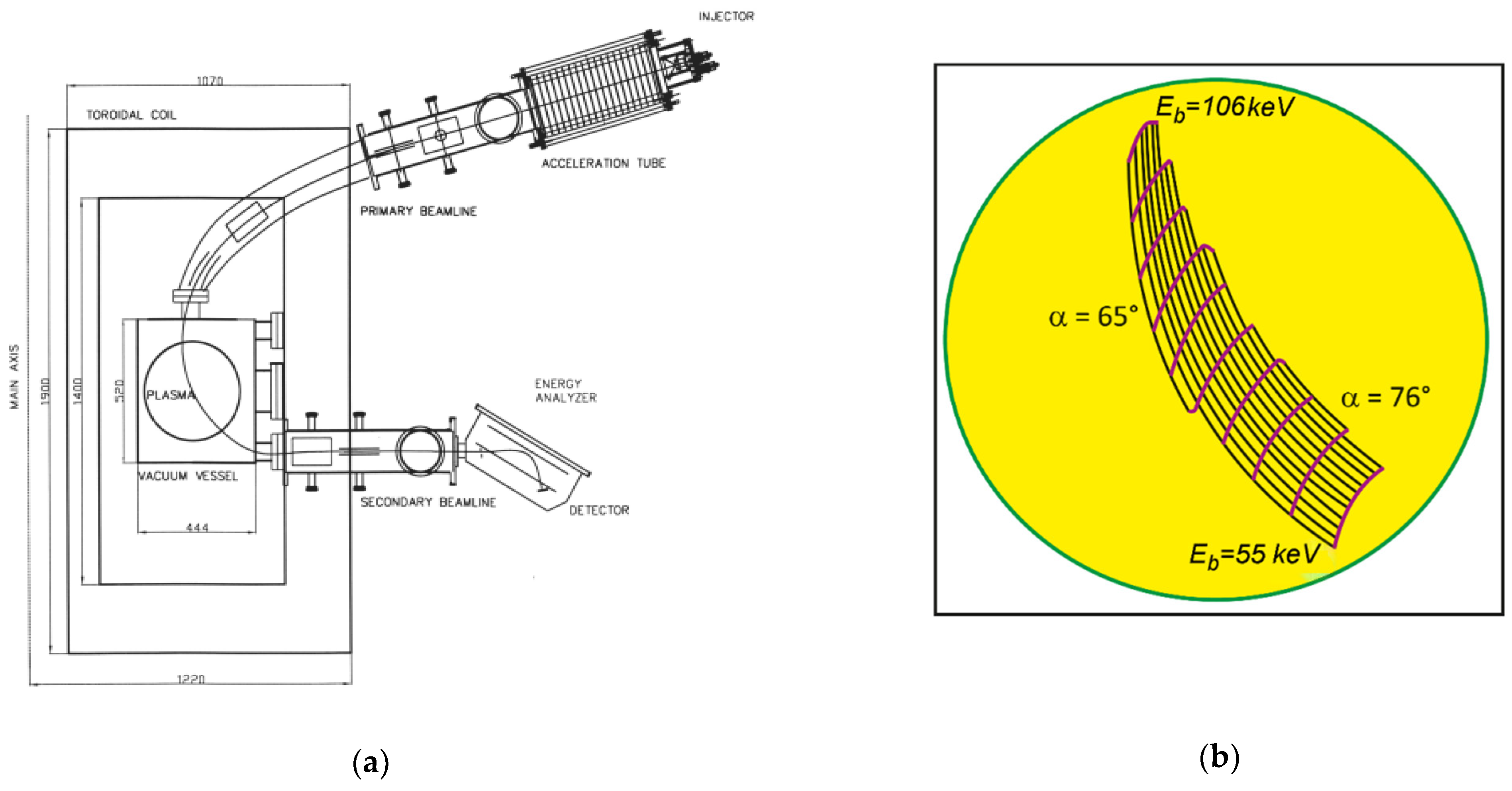
7.2. T-10 HIBP
- The Cs ions were replaced by heavier Tl ions. The energy range was consequently increased to 220, then to 280, 300, and finally to 330 kV. These changes allow to study discharges with microwave heating (ECRH) at 2.08 < Bt < 2.5 T. In discharges with Bt < 2.17 T, the radial region 0.2 < ρSV < 1 was investigated;
- The ion beamlines were modernized in the following way:
- Two serial pairs of steering plates were installed into the primary beamline. The first plates deflect the beam “counter-current” to the extreme toroidal position near the second plates. Thus, the beam approaches the second plates not axially, but maximally shifted. The second plates deflect the beam “co-current”. As a result, a zigzag trajectory is formed, and it became possible to use the full toroidal width of the port, not half of it, as in the axial injection of the beam, and maximize the toroidal correction angle β.
- The secondary beamline was significantly expanded. The toroidal correction plates were placed inside the vacuum chamber to increase the angle of toroidal correction of the secondary trajectories β3. Correcting plates were equipped with a continuous baking system that maintains their operating temperature at the level of 220–250 °C. This allows us to completely avoid the deposition of hydrocarbon films on the surface of the plates, and to exclude the appearance of high-voltage breakdowns between the plates or from the plate to the grounded T-10 wall. Immediately before the working shot of the tokamak, the baking was turned off and the baking circuit was disconnected in order to exclude the possibility of the interaction of the closed loop with the current and the confining magnetic fields of the machine. The electromagnetic forces resulting from this interaction could deform the plates, making it impossible for the secondary beam to pass into the analyzer. The described upgrades made it possible to expand the operational limits of measurements up to the operational limits of the tokamak 140 kA < Ipl < 330 kA.
- The technique of scanning the entry angle of the particle beam into the plasma was implemented. Additionally, the vertical correction plates for secondary trajectories were installed to optimize the particle entry angle into the analyzer. It allowed us to obtain fragments of the radial profile per discharge;
- A control system for the beam was created, which allows us to select a complete set of control voltages in the primary and secondary ion beamlines in each subsequent tokamak shot based on the analysis of the beam position in the previous shot (injection and sweeping angles in primary and secondary beamlines α1, α2, α3, β1, β2, β3). Its implementation radically simplified and accelerated the process of selecting control voltages, to significantly increase the accuracy of beam positioning, thereby providing systematic measurements both with a fixed SV position or with radial scan.Besides these two traditional HIBP operating modes, the developed system made it possible to operate in new non-standard modes. The most popular among them:
- Periodic variation of the SV between two spatial positions (“colon”),
- Periodic change of the SV between several positions (“multiple points”),
- Alternation of the scan and at point measurements during one shot (“scan + point”).
- A feedback for toroidal displacement was created, which adjust the toroidal correction voltage in the secondary beamline (toroidal angle β3), depending on the measured toroidal displacement in the detector ζd. This allows us to automate the selection of the toroidal correction voltage from shot to shot, as well as during one shot, especially in shots with changing plasma current (ramp-up, ramp-down) as well as the start of the plasma discharge with sharp increase of the plasma current. The feedback system for toroidal displacement is described in detail in the Reference [67].
- The initial single-channel energy analyzer was first replaced by a two-channel and then a five-channel one. As a result, we can carry out correlation measurements over several spatial channels. In particular, in the region of maximal beam penetration into the plasma, it became possible to measure the poloidal potential correlations or Ep, a turbulent particle flux ΓE×B, as well as the poloidal density correlations or rotation of turbulence. Closer to the plasma edge, it is possible to measure the velocity of radial correlations or the radial propagation of potential and density perturbations.
- An emitter-extractor unit has been developed, which makes it possible to significantly increase the primary beam current from 2–20 μA to 100–130 μA. Its use has expanded the allowable density limit for HIBP towards both high densities (plasma core) and also ultra-low densities at the plasma edge and in the scrape-off layer (SOL) [68].
7.3. TJ-I HIBP
7.4. TUMAN-3M HIBP
7.5. WEGA HIBP
7.6. URAGAN-2M HIBP
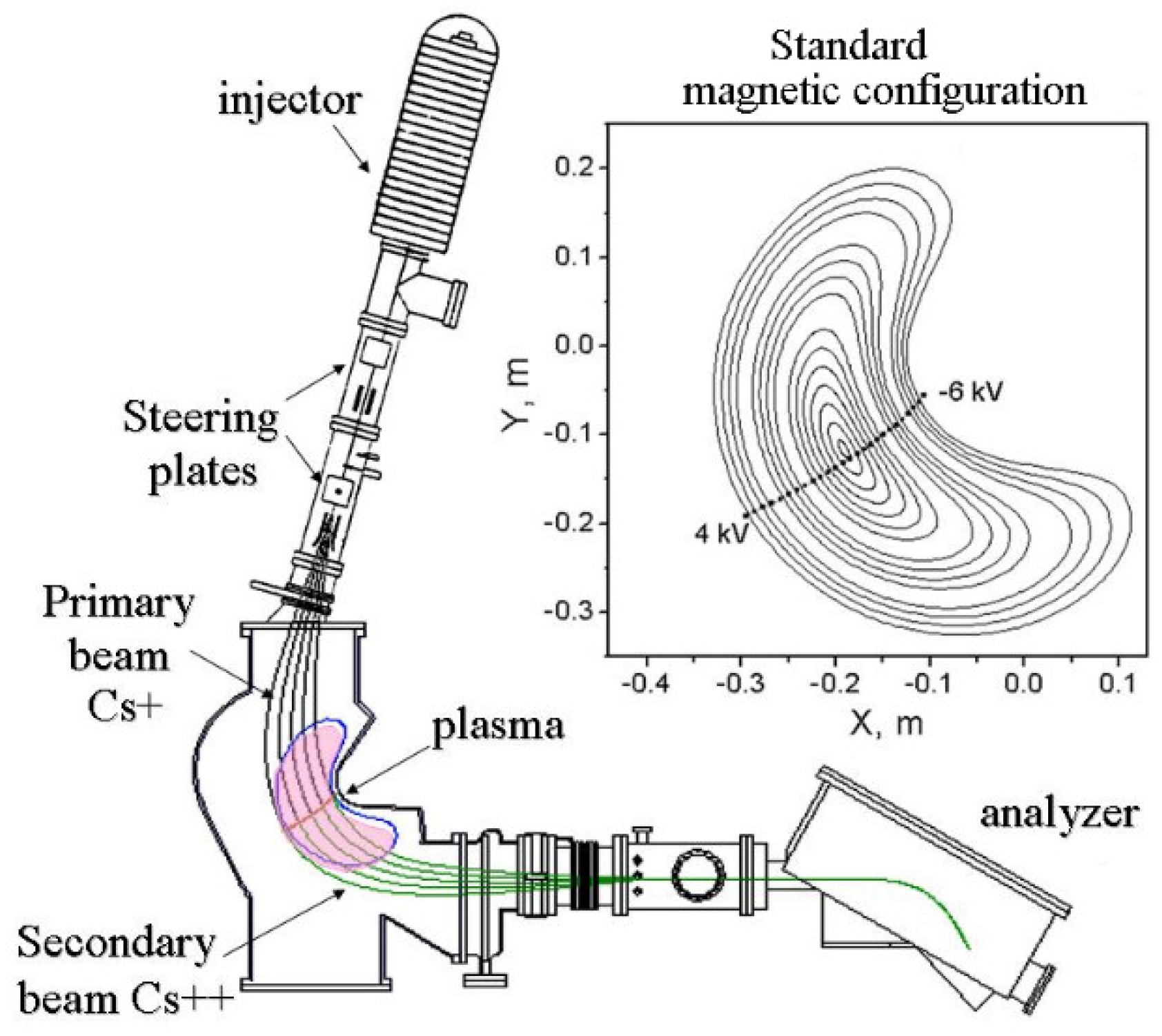
7.7. TJ-II HIBP—The Most Advanced Diagnostics to Study Plasma Symmetric Structures
8. Future Prospects to Study of Symmetric Structures in Toroidal Plasmas—Conceptual Design of the HIBP Diagnostics for Various Toroidal Devices
- (a)
- Simultaneous measurements of the all three signals for potential, density, magnetic oscillations for comprehensive analysis of the plasma phenomena, including turbulence;
- (b)
- Multichannel measurements for correlation studies, including plasma turbulence poloidal rotation and radial propagation, and turbulent particle flux;
- (c)
- Maximal extension of the detector grid for 2D mapping and study of the poloidal symmetry/symmetry braking;
- (d)
- Creation of the dual HIBP system for study of toroidal/helical symmetry.
8.1. HIBP Design for the TCABR Tokamak
8.2. HIBP Design for the Globus-M2 Tokamak
8.3. HIBP Design for the COMPASS Tokamak
8.4. HIBP Design for the TCV Tokamak
8.5. HIBP Design for the MAST Tokamak
8.6. HIBP Design for the T-15MD Tokamak
8.7. HIBP Design for the W7-X Stellarator
8.8. HIBP Design for the International Experimental Tokamak Reactor ITER
9. Summary
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tikhonov, A.N.; Arsenin, V.V. Solutions of Ill Posed Problems; John, F., Translator, V.H., Eds.; Winston and Sons: Silver Spring, MD, USA; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Dnestrovskij, Y.N.; Kostomarov, D.P.; Melnikov, A.V. Mathematical problems of active corpuscular diagnostics of plasmas. Proc. Moscov State Univ. Ser. 15 Appl. Math. Cybern. 1986, 3, 20–28. (In Russian) [Google Scholar]
- Melnikov, A.V. Applied and fundamental aspects of fusion science. Nat. Phys. 2016, 12, 386–390. [Google Scholar] [CrossRef]
- Van Oost, G.; Bulanin, V.V.; Donne, A.J.H.; Gusakov, E.; Kraemer-Flecken, A.; Krupnik, L.I.; Melnikov, A.; Nanobashvili, S.; Peleman, P.; A Razumova, K.; et al. Multi-machine studies of the role of turbulence and electric fields in the establishment of improved confinement in tokamak plasmas. Plasma Phys. Control. Fusion 2007, 49, A29–A44. [Google Scholar] [CrossRef]
- Kadomtsev, B.B. Collective Phenomena in Plasmas; Pergamon Press: Oxford, UK, 1982; ISBN 10-0080250182/13-978-0080250182. [Google Scholar]
- Burrell, K.H.; Carlstrom, T.N.; Doyle, E.J.; Finkenthal, D.; Gohil, P.; Groebner, R.J.; Hillis, D.L.; Kim, J.; Matsumoto, H.; Moyer, R.A.; et al. Physics of the L-mode to H-mode transition in tokamaks. Plasma Phys. Control. Fusion 1992, 34, 1859. [Google Scholar] [CrossRef]
- Tendler, M. Major achievements and challenges of fusion research. Phys. Scr. 2015, 90, 98002. [Google Scholar] [CrossRef]
- Melnikov, A.V. The study of electric potential of magnetically confined fusion plasmas. Comput. Nanotechnol. 2017, 2, 13–23. Available online: https://www.elibrary.ru/item.asp?id=29368049 (accessed on 1 January 2021). (In Russian).
- Melnikov, A.V. The evolution of the mathematical and technical aspects of heavy ion beam probe plasma diagnostics. Comput. Nanotechnol. 2018, 1, 31–57. Available online: https://www.elibrary.ru/item.asp?id=32775187n (accessed on 1 January 2021). (In Russian).
- Dnestrovskij, Y.; Melnikov, A.; Krupnik, L.; Nedzelskij, I. Development of heavy ion beam probe diagnostics. IEEE Trans. Plasma Sci. 1994, 22, 310–331. [Google Scholar] [CrossRef]
- Jobes, F.; Hickok, R. A direct measurement of plasma space potential. Nucl. Fusion 1970, 10, 195–197. [Google Scholar] [CrossRef]
- Bugarya, V.I.; Gorshkov, A.V.; Grashin, S.A.; Ivanov, I.V.; Krupin, V.A.; Krupnik, L.I.; Nedzel’skij, I.S.; Mel’nikov, A.V.; Razumova, K.A.; Sokolov, Y.A.; et al. Electric potential and toroidal and poloidal rotation velocities of a tokamak plasma. JETP Lett. 1983, 38, 404–408. [Google Scholar]
- Bugarya, V.; Gorshkov, A.; Grashin, S.; Ivanov, I.; Krupin, V.; Mel′nikov, A.; Razumova, K.; Sokolov, Y.; Trukhin, V.; Chankin, A.; et al. Measurements of plasma column rotation and potential in the TM-4 tokamak. Nucl. Fusion 1985, 25, 1707–1717. [Google Scholar] [CrossRef]
- Donné, A.J.H.; Melnikov, A.V.; Van Oost, G. Diagnostics for radial electric field measurements in hot magnetized plasmas. Czechoslov. J. Phys. 2002, 52, 1077–1096. [Google Scholar] [CrossRef]
- Melnikov, A.; Krupnik, L.; Eliseev, L.; Barcala, J.M.; Bravo, A.; Chmyga, A.; Deshko, G.; Drabinskij, M.; Hidalgo, C.; Khabanov, P.; et al. Heavy ion beam probing—diagnostics to study potential and turbulence in toroidal plasmas. Nucl. Fusion 2017, 57, 072004. [Google Scholar] [CrossRef]
- Askinazi, L.G.; Kornev, V.A.; Lebedev, S.V.; Tukachinsky, A.S.; Zhubr, N.A.; Dreval, N.B.; Krupnik, L.I. Heavy ion beam probe development for the plasma potential measurement on the TUMAN-3M tokamak. Rev. Sci. Instrum. 2004, 75, 3517–3519. [Google Scholar] [CrossRef]
- Cabral, J.A.C.; Malaquias, A.; Praxedes, A.; Van Toledo, W.; Varandas, C. The heavy ion beam diagnostic for the tokamak ISTTOK. IEEE Trans. Plasma Sci. 1994, 22, 350–358. [Google Scholar] [CrossRef]
- Bondarenko, I.S.; Gubarev, S.P.; Krupnik, L.I.; Mel’nikov, A.V.; Nedszel’skii, I.S.; Utkin, A.A.; Khrebtov, S.M. Plasma diagnostics using a heavy-ion beam in the T-10 tokamak. Sov. J. Plasma Phys. 1992, 18, 110. [Google Scholar]
- Fujisawa, A.; Iguchi, H.; Taniike, A.; Sasao, M.; Hamada, Y. A 6 MeV heavy ion beam probe for the Large Helical Device. IEEE Trans. Plasma Sci. 1994, 22, 395–402. [Google Scholar] [CrossRef] [Green Version]
- Ido, T.; Shimizu, A.; Nishiura, M.; Kato, S.; Nakano, H.; Ohshima, S.; Yokoyama, M.; Murakami, S.; Wakasa, A.; Nakamura, S.; et al. Development of 6-MeV Heavy Ion Beam Probe on LHD. Fusion Sci. Technol. 2010, 58, 436–444. [Google Scholar] [CrossRef]
- Melnikov, A.; Hidalgo, C.; Ido, T.A.; Shimizu, A.; Fujisawa, K.; Dyabilin, S.; Lysenko, S.E. Plasma Potential in Toroidal Devices: T-10, TJ-II, CHS and LHD. Plasma Fusion Res. 2012, 7, 2402114. [Google Scholar] [CrossRef] [Green Version]
- Bondarenko, I.S.; Chmuga, A.A.; Dreval, N.B.; Khrebtov, S.M.; Komarov, A.D.; Kozachok, A.S.; Krupnik, L.I.; Coelho, P.; Cunha, M.; Gonçalves, B.; et al. Installation of an advanced heavy ion beam diagnostic on the TJ-II stellarator. Rev. Sci. Instrum. 2001, 72, 583–585. [Google Scholar] [CrossRef]
- Melnikov, A.; Dyabilin, K.; Eliseev, L.; Lysenko, S.; Dnestrovskij, Y. Measurement and modelling of electric potential in the TJ-II stellarator. Probl. At. Sci. Technol. Ser. Thermonucl. Fusion 2011, 34, 54–73. (In Russian) [Google Scholar] [CrossRef]
- Lei, J.; Shah, U.; Demers, D.R.; Connor, K.A.; Schoch, P.M. Calibration and initial operation of the HIBP on the MST. Rev. Sci. Instrum. 2001, 72, 564–567. [Google Scholar] [CrossRef]
- Yoshikawa, M.; Sakamoto, M.; Miyata, Y.; Aoyama, M. Potential fluctuation study from the core plasma to end region in GAMMA 10. Nucl. Fusion 2013, 53, 073031. [Google Scholar] [CrossRef]
- Dreval, N.; Krupnik, L.; Chmyga, A.A.; Khrebtov, S.M.; Komarov, A.D.; Kozachek, A.S.; Hidalgo, C.; Melnikov, A.V.; Eliseev, L.G. Features of HIBP diagnostics application to stellarator-like devices. Probl. At. Sci. Technol. Ser. Plasma Phys. 2005, 2, 223–225. [Google Scholar]
- Dnestrovskii, Y.N.; Krupnik, L.I.; Mel’nikov, A.V.; Nedzel’skii, I.S. Density determination by probing with heavy-ion beams. Sov. J. Plasma Phys. 1986, 12, 130. [Google Scholar]
- Schwelberger, J.G.; Aceto, S.C.; Connor, K.A.; Zielinski, J.J.; Baylor, L.A.; England, A.C.; Isler, R.; Ma, C.H.; Murakami, M.; Uckan, T.; et al. Electron density profile measurement with a heavy ion beam probe. Rev. Sci. Instrum. 1992, 63, 4571–4573. [Google Scholar] [CrossRef]
- Khabanov, P.; Eliseev, L.; Melnikov, A.; Drabinskiy, M.; Hidalgo, C.; Kharchev, N.; Chmyga, A.; Kozachek, A.; Pastor, I.; De Pablos, J.; et al. Density profile reconstruction using HIBP in ECRH plasmas in the TJ-II stellarator. J. Instrum. 2019, 14, C09033. [Google Scholar] [CrossRef]
- Levinton, F.M. The motional Stark effect: Overview and future development (invited). Rev. Sci. Instrum. 1999, 70, 810–814. [Google Scholar] [CrossRef]
- Dnestrovskii, Y.N.; Mel’nikov, A.V. Determination of the current profile in a plasma by probing with heavy-ion beams. Sov. J. Plasma Phys. 1986, 12, 393. [Google Scholar]
- Weisen, H.; Melnikov, A.V.; Perfilov, S.; Lysenko, S. On the Possibility of Using a Heavy Ion Beam Probe for Local Poloidal Flux Measurements in a Tokamak. Fusion Sci. Technol. 2011, 59, 418–426. [Google Scholar] [CrossRef]
- Melnikov, A.V. Electric Potential in Toroidal Plasmas; Springer Nature Switzerland AG: Basel, Switzerland, 2019; p. 240. ISBN 978-3-030-03480-1. [Google Scholar]
- Khabanov, P.O. Computational analysis density fluctuations measurements with heavy ion beam probe. Comput. Nanotechnol. 2018, 1, 25–30. Available online: https://www.elibrary.ru/item.asp?id=32775186 (accessed on 1 January 2021). (In Russian).
- Melnikov, A.V.; Eliseev, L.G.; Jiménez-Gómez, R.; Ascasibar, E.; Hidalgo, C.; Chmyga, A.A.; Ido, T.; Khrebtov, S.M.; Könies, A.; Komarov, A.D.; et al. Study of Alfvén eigenmodes in the TJ-II stellarator. Plasma Fusion Res. 2010, 5, S2019. [Google Scholar] [CrossRef] [Green Version]
- Simcic, V.J.; Crowley, T.P.; Schoch, P.M. Internal magnetic and electrostatic fluctuation measurements of MHD modes in the TEXT tokamak. Phys. Fluids B 1993, 5, 1576. [Google Scholar] [CrossRef]
- McKee, G.R.; Fonck, R.J.; Jakubowski, M.; Burrell, K.H.; Hallatschek, K.; A Moyer, R.; Nevins, W.; Rudakov, D.L.; Xu, X. Observation and characterization of radially sheared zonal flows in DIII-D. Plasma Phys. Control. Fusion 2003, 45, A477–A485. [Google Scholar] [CrossRef] [Green Version]
- Zenin, V.N. Geodesic acoustic modes in the tokamaks. Comput. Nanotechnol. 2018, 1, 108–113. Available online: https://www.elibrary.ru/item.asp?id=32775193 (accessed on 1 January 2021). (In Russian).
- Zenin, V.N.; Eliseev, L.G.; Kozachek, A.S.; Krupnik, L.I.; Lysenko, S.E.; Melnikov, A.V.; Perfilov, S.V. Study of poloidal structure of geodesic acoustic modes in the T-10 tokamak with heavy ion beam probing. Probl. At. Sci. Technol. Ser. Plasma Phys. 2014, 6, 269–271. Available online: http://vant.kipt.kharkov.ua/TABFRAME.html (accessed on 1 January 2021).
- Eliseev, L.G.; Ivanov, N.V.; Kakurin, A.M.; Lysenko, S.E.; Maltsev, S.G.; Melnikov, A.V.; Perfilov, S.V.; Zenin, V.N. Study of the large-scale MHD mode and its effect on GAM in the T-10 tokamak. In Proceedings of the 42nd EPS Conference on Plasma Physics, Lisbon, Portugal, 22—26 June 2015; ECA. Volume 39E, p. P5.159. Available online: http://ocs.ciemat.es/EPS2015PAP/Pdf/P5.159.pdf (accessed on 1 January 2021).
- Melnikov, A.V.; Eliseev, L.G.; Lysenko, S.E.; Perfilov, S.V.; Shelukhin, D.A.; Vershkov, V.A.; Zenin, V.N.; Krupnik, L.I.; Kharchev, N.K. Correlation properties of Geodesic Acoustic Modes in the T-10 tokamak. J. Phys. Conf. Ser. 2015, 591, 012003. [Google Scholar] [CrossRef] [Green Version]
- Melnikov, A.V.; Eliseev, L.G.; Gudozhnik, A.V.; Lysenko, S.E.; Mavrin, V.A.; Perfilov, S.V.; Zimeleva, L.G.; Ufimtsev, M.V.; Krupnik, L.I.; Schoch, P.M. GAM evolution with ECRH Investigation of the plasma potential oscillations in the range of geodesic acoustic mode frequencies by heavy ion beam probing in tokamaks. Czech. J. Phys. 2005, 55, 349–360. [Google Scholar] [CrossRef] [Green Version]
- Breizman, B.N.; Pekker, M.S.; Sharapov, S.E. Plasma pressure effect on Alfvén cascade eigenmodes. Phys. Plasmas 2005, 12, 112506. [Google Scholar] [CrossRef] [Green Version]
- Eliseev, L.G.; Melnikov, A.V.; Ascasibar, E.; Cappa, A.; Drabinskiy, M.; Hidalgo, C.; Khabanov, P.O.; Kharchev, N.K.; Kozachek, A.S.; Liniers, M. Experimental observation of the geodesic acoustic frequency limit for the NBI-driven Alfvén eigenmodes in TJ-II. Phys. Plasmas 2021, 28. [Google Scholar] [CrossRef]
- Melnikov, A.V.; Eliseev, L.G.; Jiménez-Gómez, R.; Ascasibar, E.; Hidalgo, C.; Chmyga, A.A.; Komarov, A.D.; Kozachok, A.S.; Krasilnikov, I.A.; Khrebtov, S.M.; et al. Internal measurements of Alfvén eigenmodes with heavy ion beam probing in toroidal plasmas. Nucl. Fusion 2010, 50, 084023. [Google Scholar] [CrossRef]
- Melnikov, A.; Eliseev, L.; Lysenko, S.E.; Ufimtsev, M.; Zenin, V. Study of interactions between GAMs and broadband turbulence in the T-10 tokamak. Nucl. Fusion 2017, 57, 115001. [Google Scholar] [CrossRef] [Green Version]
- Gryaznevich, M.; Stockel, J.; Van Oost, G.; Del Bosco, E.; Svoboda, V.; Melnikov, A.; Kamendje, R.; Malaquias, A.; Mank, G.; Miklaszewski, R.; et al. Contribution of joint experiments on small tokamaks in the framework of IAEA coordinated research projects to mainstream fusion research. Plasma Sci. Technol. 2020, 22, 055102. [Google Scholar] [CrossRef]
- Riggs, G.A.; Nogami, S.; Koepke, M.; Melnikov, A.; Eliseev, L.; Lysenko, S.; Khabanov, P.; Drabinskij, M.; Kharchev, N.; Kozachek, A.; et al. Bispectral analysis of broadband turbulence and geodesic acoustic modes in the T-10 tokamak. J. Plasma Phys. 2021, 87. [Google Scholar] [CrossRef]
- Powers, E. Spectral techniques for experimental investigation of plasma diffusion due to polychromatic fluctuations. Nucl. Fusion 1974, 14, 749–752. [Google Scholar] [CrossRef]
- Melnikov, A.V.; Eliseev, L.G.; Alonso, A.; Ascasiba, E.; Cappa, A.; Chmyga, A.A.; Estrada, T.; Hidalgo, C.; Jiménez-Gómez, R.; Krasilnikov, I.; et al. Plasma potential profiles and oscillations in ECRH and NBI plasmas in the TJ-II stellarator. In Proceedings of the 37th EPS Conference on Plasma Physics, Dublin, Ireland, 21–25 June 2010; ECA. Volume 34A, p. Rep. P1.066. Available online: http://ocs.ciemat.es/EPS2010PAP/html/ (accessed on 1 January 2021).
- Melnikov, A.V.; Eliseev, L.G.; Ascasibar, E.; Chmyga, A.A.; Hidalgo, C.; Ido, T.; Jiménez-Gomez, R.; Komarov, A.D.; Kozachek, A.S.; Krupnik, L.I.; et al. Alfvén eigenmode properties and dynamics in the TJ-II stellarator. Nucl. Fusion 2012, 52, 123004. [Google Scholar] [CrossRef]
- Melnikov, A.; Eliseev, L.; Estrada, T.; Ascasibar, E.; Alonso, A.; Chmyga, A.; Hidalgo, C.; Komarov, A.; Kozachek, A.; Krupnik, L.; et al. The changes in plasma potential and turbulent particle flux in the core plasma measured by heavy ion beam probe during L-H transitions in the TJ-II stellarator. Nucl. Fusion 2013, 53, 092002. [Google Scholar] [CrossRef]
- Eliseev, L.G.; Lysenko, S.E.; Melnikov, A.V.; Krupnik, L.I.; Kozachek, A.S.; Zenin, V.N. Study of GAMs and related turbulent particle flux with HIBP in the T-10 tokamak. Probl. At. Sci. Technol. Ser. Plasma Phys. 2017, 107, 241–243. [Google Scholar]
- Eliseev, L.G.; Zenin, V.N.; Lysenko, S.E.; Melnikov, A.V. Measurement of geodesic acoustic modes and the turbulent particle flux in the T-10 tokamak plasmas. J. Phys. Conf. Ser. 2017, 907, 12002. [Google Scholar] [CrossRef]
- Eliseev, L.G.; Melnikov, A.V.; Lysenko, S.E.; Khabanov, P.O.; Zenin, V.N.; Drabinskij, M.A.; Kharchev, N.K.; Kozachek, A.S.; Krupnik, L.I.; Team, H. Evaluation of Turbulent Particle Flux by Heavy Ion Beam Probe in the T-10 Tokamak. Plasma Fusion Res. 2018, 13, 3402106. [Google Scholar] [CrossRef] [Green Version]
- Eliseev, L.; Melnikov, A.; Perfilov, S.; Hidalgo, C. Two point correlation technique for the measurements of poloidal plasma rotation by heavy ion beam probe. Plasma Fusion Res. 2012, 7, 2402064. [Google Scholar] [CrossRef] [Green Version]
- Drabinskiy, M.A.; Eliseev, L.G.; Khabanov, P.O.; Melnikov, A.V.; Khartchev, N.K.; Sergeev, N.S.; Grashin, S.A. Radial structure of quasi-coherent mode in ohmic plasma of the T-10 tokamak. J. Phys. Conf. Ser. 2019, 1383, 012004. Available online: https://iopscience.iop.org/article/10.1088/1742-6596/1383/1/012004 (accessed on 1 January 2021). [CrossRef]
- Melnikov, A.; Eliseev, L.; Perfilov, S.; Lysenko, S.; Shurygin, R.; Zenin, V.; Grashin, S.; Krupnik, L.; Kozachek, A.; Solomatin, R.; et al. The features of the global GAM in OH and ECRH plasmas in the T-10 tokamak. Nucl. Fusion 2015, 55, 063001. [Google Scholar] [CrossRef]
- Bondarenko, I.S.; Krupnik, L.I.; Nedzel’skii, I.S.; Mel’nikov, A.V. Plasma probing with a heavy ion beam in the TM-4 tokamak. Sov. J. Tech. Phys. 1986, 31, 1390. [Google Scholar]
- Melnikov, A.V.; Bondarenko, I.S.; Efremov, S.L.; Kharchev, N.K.; Khrebotv, S.M.; Krupnik, L.I.; Nedzelskij, I.S.; Zimeleva, L.G.; Trofimenko, Y.V. HIBP diagnostics on T-10. Rev. Sci. Instrum. 1995, 66, 317. [Google Scholar] [CrossRef]
- Melnikov, A.V.; Kharchev, N.K.; Eliseev, L.G.; Bondarenko, I.S.; Krupnik, L.I.; Khrebtov, S.M.; Nedzelskij, I.S.; Trofimenko, Y.V. Calibration of the heavy ion beam probe parallel plate analyzer using the gas target and reference beam. Rev. Sci. Instrum. 1997, 68, 308–311. [Google Scholar] [CrossRef]
- Krupnik, L.; Melnikov, A.; Nedselskij, I. Development of beam probe diagnostics and recent measurements on the TJ-1 and T-10 tokamaks. Fusion Eng. Des. 1997, 34–35, 639–644. [Google Scholar] [CrossRef]
- Melnikov, A.V.; Krupnik, L.I.; Nedzelskij, I.S.; Kharchev, N.K. Plasma potential measurements in the T-10 tokamak. In Proceedings of the 18th EPS Conference on Control. Fusion and Plasma Physics, Berlin, Germany, 3–7 June 1991; Volume 15C, p. 221. [Google Scholar]
- Melnikov, A.V.; Zimeleva, L.G.; Eliseev, L.G.; Bondarenko, I.S.; Krupnik, L.I.; Khrebtov, S.M.; Nedzelskij, I.S.; Kharchev, N.K. HIBP measurements of the plasma electric potential on T-10. In Proceedings of the 23rd EPS Conference on Controlled Fusion and Plasma Physics, Kiev, Ukraine, 24–28 June 1996; Volume I, p. 434. [Google Scholar]
- Melnikov, A.V.; Tarasyan, K.N.; Vershkov, V.A.; Dreval, V.A.; Sushkov, A.V.; Lysenko, S.E.; Sannikov, V.V.; Gorshkov, A.V.; Krupnik, L.I.; Nedzelskij, I.S. Space and time evolution of plasma potential in T-10 under variation of main gas influx. IEEE Trans. Plasma Sci. 1994, 22, 363–368. [Google Scholar] [CrossRef]
- Melnikov, A.; Drabinskiy, M.; Eliseev, L.; Khabanov, P.; Kharchev, N.; Krupnik, L.; De Pablos, J.; Kozachek, A.; Lysenko, S.; Molinero, A.; et al. Heavy ion beam probe design and operation on the T-10 tokamak. Fusion Eng. Des. 2019, 146, 850–853. [Google Scholar] [CrossRef]
- Kharchev, N.K. Correction of toroidal displacement of diagnostic heavy ion beam. Comput. Nanotechnol. 2018, 1, 58–61. Available online: https://www.elibrary.ru/item.asp?id=32775188 (accessed on 1 January 2021). (In Russian).
- Drabinskiy, M.A. The study of the electric potential of magnetically confined fusion plasmas. Comput. Nanotechnol. 2018, 1, 62–70. Available online: https://www.elibrary.ru/item.asp?id=32775189 (accessed on 1 January 2021). (In Russian).
- Bondarenko, I.S.; Khrebtov, S.M.; Krupnik, L.I.; Nedzelskij, I.S.; Gordeev, O.A.; Kharchev, N.K.; Melnikov, A.V.; Tarasyan, K.N.; Zimeleva, L.G.; Hidalgo, C.; et al. Heavy ion beam probe diagnostics on TJ-1 tokamak and the measurements of the plasma potential and density profiles. Rev. Sci. Instruments 1997, 68, 312–315. [Google Scholar] [CrossRef]
- Melnikov, A.V.; Zimeleva, L.G.; Krupnik, L.I.; Nedzelskij, I.S.; Trofimenko, Y.V.; Minaev, V. Heavy ion beam probe systems for tight aspect ratio tokamaks. Rev. Sci. Instrum. 1997, 68, 316–319. [Google Scholar] [CrossRef]
- Krupnik, L.I.; Deshko, G.N.; Zhezhera, A.I.; Chmyga, A.A.; Komarov, A.D.; Kozachek, A.S.; Melnikov, A.V.; Perfilov, S.V.; Otte, M.; Shubert, M. The heavy ion beam probing development for WEGA stellarator. Fusion Sci. Technol. 2006, 50, 276–280. [Google Scholar] [CrossRef] [Green Version]
- Podoba, Y.; Otte, M.; Wagner, F.; Bondarenko, I.; Chmyga, A.; Deshko, G.; Komarov, A.; Kozachek, A.; Krupnik, L.; Khrebtov, S.; et al. First HIBP results on the WEGA stellarator. AIP Conf. Proc. 2008, 993, 235–238. [Google Scholar] [CrossRef] [Green Version]
- Bondarenko, I.S.; Chmyga, A.A.; Deshko, G.N.; Komarov, A.D.; Kozachok, A.S.; Krupnik, L.I.; Khrebtov, S.M.; Zhezhera, A.I.; Podoba, Y.Y.; Otte, M.; et al. HIBP results on the WEGA stellarator. Probl. At. Sci. Technol. Ser. Plasma Phys. 2009, 15, 28–30. [Google Scholar]
- Krupnik, L.I.; Mel’nikov, A.V.; Nedzel’skii, I.S.; Samokhvalov, N.V.; Schwelberger, J.; Connor, K.A. Plasma diagnostics using a heavy-ion beam in the U-2M stellarator. Plasma Phys. Rep. 1994, 20, 173–175. [Google Scholar]
- Krupnik, L. 50 years of hot plasma diagnostic with heavy ion beam probing (HIBP) at the Kharkov institute of physics and technology. Probl. At. Sci. Technol. Ser. Plasma Phys. 2021, 154–162. [Google Scholar] [CrossRef]
- Bondarenko, I.S.; Chmyga, A.A.; Dreval, N.B.; Khrebtov, S.M.; Komarov, A.D.; Kozachok, A.S.; Krupnik, L.I.; Melnikov, A.V.; Yudina, O.A.; Coelho, P.; et al. Installation of the advanced heavy ion beam probing diagnostic on the TJ-II stellarator. Czechoslov. J. Phys. 2000, 50, 1397–1412. [Google Scholar] [CrossRef]
- Krupnik, L.; Bondarenko, I.; Chmyga, A.; Dreval, M.; Khrebtov, S.; Komarov, A.; Kozachok, A.; Hidalgo, C.; García-Cortés, I.; Rodriguez-Rodrigo, L.; et al. The first operation of the advanced heavy ion beam probing diagnostic on the TJ-II flexible heliac. Fusion Eng. Des. 2001, 56–57, 935–939. [Google Scholar] [CrossRef]
- Melnikov, A.V.; Hidalgo, C.; Chmyga, A.A.; Dreval, N.B.; Eliseev, L.; Khrebtov, S.M.; Komarov, A.D.; Kozachok, A.S.; Krupnik, L.I.; Pastor, I.; et al. Plasma potential measurements by the heavy ion beam probe diagnostic in fusion plasmas: Biasing experiments in the TJ-II stellarator and T-10 tokamak. Fusion Sci. Technol. 2004, 46, 299–311. [Google Scholar] [CrossRef]
- Hidalgo, C.; Pedrosa, M.A.; Dreval, N.; McCarthy, K.J.; Eliseev, L.; Ochando, M.A.; Estrada, T.; Pastor, I.; Ascasíbar, E.; Calderón, E.; et al. Improved confinement regimes induced by limiter biasing in the TJ-II stellarator. Plasma Phys. Control. Fusion 2003, 46, 287–297. [Google Scholar] [CrossRef]
- Estrada, T.; Krupnik, L.; Dreval, N.; Melnikov, A.; Khrebtov, S.M.; Hidalgo, C.; van Milligen, B.; Castejón, F.; Ascasíbar, E.; Eliseev, L.; et al. Electron internal transport barrier formation and dynamics in the plasma core of the TJ-II stellarator. Plasma Phys. Control. Fusion 2003, 46, 277–286. [Google Scholar] [CrossRef] [Green Version]
- Estrada, T.; Alonso, A.; Chmyga, A.A.; Dreval, N.; Eliseev, L.; Hidalgo, C.; Komarov, A.D.; Kozachok, A.S.; Krupnik, L.; Melnikov, A.V.; et al. Electron internal transport barriers, rationals and quasi-coherent oscillations in the stellarator TJ-II. Plasma Phys. Control. Fusion 2005, 47, L57–L63. [Google Scholar] [CrossRef] [Green Version]
- Estrada, T.; Happel, T.; Eliseev, L.; López-Bruna, D.; Ascasíbar, E.; Blanco, E.; Cupido, L.; Fontdecaba, J.M.; Hidalgo, C.; Jiménez-Gómez, R.; et al. Sheared flows and transition to improved confinement regime in the TJ-II stellarator. Plasma Phys. Control. Fusion 2009, 51. [Google Scholar] [CrossRef]
- Van Milligen, B.P.; Pedrosa, M.A.; Hidalgo, C.; Carreras, B.A.; Estrada, T.; Alonso, J.A.; de Pablos, J.L.; Melnikov, A.; Krupnik, L.; Eliseev, L.G.; et al. The dynamics of the formation of the edge particle transport barrier at TJ-II. Nucl. Fusion 2011, 51, 113002. [Google Scholar] [CrossRef]
- Melnikov, A.V.; Alonso, A.; Ascasíbar, E.; Balbin, R.; Chmyga, A.A.; Dnestrovskij, Y.N.; Eliseev, L.; Estrada, T.; Fontdecaba, J.M.; Fuentes, C.; et al. Plasma potential evolution study by HIBP diagnostic during NBI experiments in the TJ-II stellarator. Fusion Sci. Technol. 2007, 51, 31–37. [Google Scholar] [CrossRef]
- Melnikov, A.; Hidalgo, C.; Eliseev, L.; Ascasibar, E.; Chmyga, A.; Dyabilin, K.; Krasilnikov, I.; Krupin, V.; Krupnik, L.; Khrebtov, S.; et al. Plasma potential and turbulence dynamics in toroidal devices (survey of T-10 and TJ-II experiments). Nucl. Fusion 2011, 51. [Google Scholar] [CrossRef]
- Krupnik, L.I.; Melnikov, A.V.; Hidalgo, C.; Eliseev, L.G.; Chmyga, A.A.; Komarov, A.D.; Kozachok, A.S.; Perfilov, S.V.; Lysenko, L.G.; Zhezhera, A.I. Recent measurements of the electric potential profile and fluctuations in ECRH and NBI in TJ-II stellarator. Probl. At. Sci. Technol. Ser. Plasma Phys. 2009, 1, 31–33. [Google Scholar]
- Krupnik, L.; Alonso, A.; Ascasibar, E.; Estrada, T.; Hidalgo, C.; Van Milligen, B.; Ochando, M.; Pedrosa, M.; De Pablos, J.L.; Tribaldos, V.; et al. Radial electric fields and confinement in the TJ-II stellarator. Czechoslov. J. Phys. 2005, 55, 317–339. [Google Scholar] [CrossRef]
- Melnikov, A.V.; Eliseev, L.G.; Grashin, S.A.; Gudozhnik, A.V.; Lysenko, S.E.; Mavrin, V.A.; Perfilov, S.V.; Vershkov, V.A.; Krupnik, L.I.; Chmyga, A.A.; et al. Study of the plasma potential evolution during ECRH in the T-10 tokamak and TJ-II stellarator. Czechoslov. J. Phys. 2005, 55, 1569–1578. [Google Scholar] [CrossRef]
- Sharma, R.; Khabanov, P.O.; Melnikov, A.V.; Kharchev, N.K.; Sánchez, E.; Chmyga, A.A.; Deshko, G.N.; Eliseev, L.G.; Hidalgo, C.; Khrebtov, S.M.; et al. Poloidal 2D scans to investigate potential and density profiles in the TJ-II stellarator using heavy ion beam probe. In Proceedings of the 45th EPS Conference on Plasma Physics, Prague, Czech Republic, 2–6 July 2018; ECA. Volume 42A, p. P5.1061. Available online: http://ocs.ciemat.es/EPS2018PAP/pdf/P5.1061.pdf (accessed on 1 January 2021).
- Sharma, R.; Khabanov, P.O.; Melnikov, A.V.; Hidalgo, C.; Cappa, A.; Chmyga, A.; Eliseev, L.G.; Estrada, T.; Kharchev, N.K.; Kozachek, A.S.; et al. Measurements of 2D poloidal plasma profiles and fluctuations in ECRH plasmas using the heavy ion beam probe system in the TJ-II stellarator. Phys. Plasmas 2020, 27, 062502. [Google Scholar] [CrossRef]
- Eliseev, L.G.; Melnikov, A.V.; Drabinskiy, M.A.; Khabanov, P.O.; Kharchev, N.K.; Lysenko, S.E.; Hidalgo, C.; Barcala, J.M.; Cappa, A.; Liniers, M.; et al. 2D distributions of potential and density mean-values and oscillations in the ECRH and NBI plasmas at the TJ-II stellarator. In Proceedings of the 28th IAEA Fusion Energy Conference (FEC 2020), 10–15 May 2021; EX/P6-17. Available online: http://iaea.org/events/fec-2020 (accessed on 1 January 2021).
- Garbet, X.; Idomura, Y.; Villard, L.; Watanabe, T.H. Gyrokinetic simulations of turbulent transport. Nucl. Fusion 2010, 50, 043002. [Google Scholar] [CrossRef]
- Melnikov, A.; Krupnik, L.; Barcala, J.M.; Bravo, A.; Chmyga, A.; Deshko, G.; Drabinskij, M.; Eliseev, L.; Hidalgo, C.; Khabanov, P.O.; et al. Heavy ion beam probing—a tool to study geodesic acoustic modes and Alfven eigenmodes in the T-10 tokamak and TJ-II stellarator. Probl. Atom. Sci. Technol. Ser. Plasma Physics 2017, 107, 237–240. [Google Scholar]
- Chmyga, O.O.; Ascasibar, E.; Barcala, J.; Drabinskiy, M.A.; Eliseev, L.G.; Hidalgo, C.; Khabanov, P.O.; Khrebtov, S.M.; Komarov, O.D.; Kozachok, O.S.; et al. A dual heavy ion beam probe diagnostic on the TJ-II stellarator. Probl. Atom. Sci. Technol. Ser. Plasma Phys. 2019, 1, 248–251. [Google Scholar]
- Fujisawa, A.; Itoh, K.; Iguchi, H.; Matsuoka, K.; Okamura, S.; Shimizu, A.; Minami, T.; Yoshimura, Y.; Nagaoka, K.; Takahashi, C.; et al. Identification of zonal flows in a toroidal plasma. Phys. Rev. Lett. 2004, 93, 165002. [Google Scholar] [CrossRef]
- Fujisawa, A.; Ido, T.; Shimizu, A.; Okamura, S.; Matsuoka, K.; Iguchi, H.; Hamada, Y.; Nakano, H.; Ohshima, S.; Itoh, K.; et al. Experimental progress on zonal flow physics in toroidal plasmas. Nucl. Fusion 2007, 47, S718–S726. [Google Scholar] [CrossRef]
- Melnikov, A.V.; Krupnik, L.I.; Ascasíbar, E.; Cappa, A.; Chmyga, A.A.; Deshko, G.N.; Drabinskij, M.A.; Eliseev, L.G.; Hidalgo, C.; Khabanov, P.O.; et al. ECRH effect on the electric potential and turbulence in the TJ-II stellarator and T-10 tokamak plasmas. Plasma Phys. Control. Fusion 2018, 60, 084008. [Google Scholar] [CrossRef]
- Zhezhera, A.I.; Chmyga, A.; Deshko, G.N.; Eliseev, L.G.; Hidalgo, C.; Khrebtov, S.M.; Komarov, A.D.; Kozachek, A.S.; Krupnik, L.I.; Melnikov, A.V.; et al. New capabilities of plasma potential and density measurements using a dual heavy ion beam probing (HIBP) diagnostic in the TJ-II stellarator. Probl. Atom. Sci. Techn. Ser. Plasma Phys. 2017, 107, 261–264. [Google Scholar]
- Fujusawa, A. A review of zonal flow experiments. Nucl. Fusion 2009, 49, 013001. [Google Scholar] [CrossRef]
- Hidalgo, C.; Chmyga, A.; Chercoles, J.; Deshko, G.N.; Eliseev, L.G.; Khabanov, P.O.; Khrebtov, S.M.; Komarov, A.G.; Kozachek, A.S.; Krupnik, L.I.; et al. On the influence of ECRH on neoclassical and anomalous mechanisms using a dual heavy ion beam probe diagnostic in the TJ-II stellarator. In Proceedings of the 26th IAEA Fusion Energy Conference, Kyoto, Japan, 17–22 October 2016; Rep. EXC/P7-44. Available online: https://nucleus.iaea.org/sites/fusionportal/Shared%20Documents/FEC%202016/fec2016-preprints/preprint0209.pdf (accessed on 1 January 2021).
- Nagaoka, K.; Ido, T.; Ascasíbar, E.; Estrada, T.; Yamamoto, S.; Melnikov, A.V.; Cappa, A.; Hidalgo, C.; Pedrosa, M.A.; van Milligen, B.P.; et al. Mitigation of NBI driven Alfven eigenmodes by electron cyclotron heating in the TJ-II stellarator. Nucl. Fusion 2013, 53, 072004. [Google Scholar] [CrossRef]
- Jiménez-Gómez, R.; Könies, A.; Ascasíbar, E.; Castejón, F.; Estrada, T.; Eliseev, L.G.; Melnikov, A.V.; Jiménez, J.A.; Petty, D.G.; Jiménez-Rey, D.; et al. Alfvén eigenmodes measured in the TJ-II stellarator. Nucl. Fusion 2011, 51, 033001. [Google Scholar] [CrossRef]
- Melnikov, A.; Eliseev, L.; Castejón, F.; Hidalgo, C.; Khabanov, P.; Kozachek, A.; Krupnik, L.; Liniers, M.; Lysenko, S.; De Pablos, J.L.; et al. Study of NBI-driven chirping mode properties and radial location by the heavy ion beam probe in the TJ-II stellarator. Nucl. Fusion 2016, 56, 112019. [Google Scholar] [CrossRef]
- Garcia-Munoz, M.; Sharapov, S.E.; Van Zeeland, M.A.; Ascasibar, E.; Cappa, A.; Chen, L.; Ferreira, J.; Galdon-Quiroga, J.; Geiger, B.; Gonzalez-Martin, J.; et al. Active control of Alfvén eigenmodes in magnetically confined toroidal plasmas. Plasma Phys. Control. Fusion 2019, 61, 054007. [Google Scholar] [CrossRef]
- Yamamoto, S.; Nagasaki, K.; Nagaoka, K.; Varela, J.; Cappa, A.; Ascasibar, E.; Castejón, F.; Fontdecaba, J.M.; Regaña, J.M.G.; González-Jerez, Á.; et al. Effect of ECH/ECCD on energetic-particle-driven MHD modes in helical plasmas. Nucl. Fusion 2020, 60, 066018. [Google Scholar] [CrossRef]
- Alonso, J.A.; Sánchez, E.; Calvo, I.; Velasco, J.L.; McCarthy, K.J.; Chmyga, A.; Eliseev, L.G.; Estrada, T.; Kleiber, R.; Krupnik, L.I.; et al. Observation of oscillatory radial electric field relaxation in a helical plasma. Phys. Rev. Lett. 2017, 118, 185002. [Google Scholar] [CrossRef] [Green Version]
- McCarthy, K.J.; Panadero, N.; Combs, S.K.; Tamura, N.; Ascasíbar, E.; Calvo, M.; Chmyga, A.; Estrada, T.; Fontdecaba, J.M.; García, R.; et al. The impact of fast electrons on pellet injection in the stellarator TJ-II. Plasma Phys. Control. Fusion 2018, 61, 014013. [Google Scholar] [CrossRef]
- Chmyga, A.A.; Deshko, G.N.; Dreval, N.B.; Melnikov, A.V.; Perfilov, S.V.; Galvao, R.M.; Kuznetsov, Y.K. Heavy ion beam probe design study for TCABR. Probl. At. Sci. Technol. Ser. Plasma Phys. 2003, 1, 160–162. [Google Scholar]
- Kuznetsov, Y.; Nascimento, I.; Silva, C.G.; Figueiredo, H.; Guimarães-Filho, Z.; Caldas, I.; Galvão, R.; Severo, J.; Toufen, D.; Ruchko, L.; et al. Long-distance correlations in TCABR biasing experiments. Nucl. Fusion 2012, 52. [Google Scholar] [CrossRef]
- Melnikov, A.V.; Perfilov, S.V. Heavy Ion Beam Probe (HIBP) diagnostics design study for GLOBUS-M tokamak. In Proceedings of the 26th EPS Conference on Plasma Physics and Controlled Fusion, Maastricht, The Netherlands, 14–18 June 1999; ECA, 23J. p. P4.116. [Google Scholar]
- Melnikov, A.V.; Markovic, T.; Eliseev, L.; Adamek, J.; Aftanas, M.; Bilkova, P.; Boehm, P.; Gryaznevich, M.; Imrisek, M.; Lysenko, S.E.; et al. Quasicoherent modes on the COMPASS tokamak. Plasma Phys. Control. Fusion 2015, 57. [Google Scholar] [CrossRef]
- Seidl, J.; Krbec, J.; Hron, M.; Adamek, J.; Hidalgo, C.; Markovic, T.; Melnikov, A.; Stockel, J.; Weinzettl, V.; Aftanas, M.; et al. Electromagnetic characteristics of geodesic acoustic mode in the COMPASS tokamak. Nucl. Fusion 2017, 57, 126048. [Google Scholar] [CrossRef] [Green Version]
- Siegrist, M.; Tonetti, G.; Weisen, H.; Melnikov, A.; Perfilov, S.V.; Krupnik, L.; Karpushov, I. The Heavy Ion Beam Diagnostic Project for the TCV Tokamak. In Proceedings of the 21st IEEE/NPS Symposium on Fusion Engineering SOFE 05, Knoxville, TN, USA, 26–29 September 2005; pp. 1–4. [Google Scholar] [CrossRef]
- Melnikov, A.V.; Perfilov, S.V.; Sharapov, S.E. Heavy ion beam probe for studying potential and turbulence on MAST. In Proceedings of the 37th EPS Conference on Plasma Physics, Dublin, Ireland, 21–25 June 2010; ECA. Volume 34A, p. P5.120. Available online: http://ocs.ciemat.es/EPS2010PAP/html/ (accessed on 1 January 2021).
- Melnikov, A.V.; Perfilov, S.V. Effect of the sample volume splitting in heavy ion-beam probing (HIBP) for spherical tokamaks (by the example of HIBP for mega ampere spherical tokamak). Rev. Sci. Instrum. 1999, 70, 1402–1406. [Google Scholar] [CrossRef]
- Melnikov, A.V.; Sushkov, A.V.; Belov, A.M.; Dnestrovskij, Y.N.; Eliseev, L.G.; Ivanov, D.P.; Kirneva, N.A.; Korobov, K.V.; Krupin, V.A.; Lysenko, S.E.; et al. Physical program and conceptual design of the diagnostics of the T-15 upgrade tokamak. Fusion Eng. Design 2015, 96, 306–310. [Google Scholar] [CrossRef]
- Ilin, A.M.; Khabanov, P.O.; Melnikov, A.V. Probing ion trajectory simulations for the HIBP diagnostics at the T-15MD tokamak. J. Phys. Conf. Ser. 2019, 1383, 012006. [Google Scholar] [CrossRef]
- Drabinskiy, M.; Melnikov, A.; Khabanov, P.; Eliseev, L.; Kharchev, N.; Ilin, A.; Sarancha, G.; Vadimov, N. Conceptual design of the heavy ion beam probe diagnostic for the T-15MD tokamak. J. Instrum. 2019, 14, C11027. [Google Scholar] [CrossRef]
- Melnikov, A.; Eliseev, L.; Lysenko, S.; Perfilov, S.; Shelukhin, D.; Vershkov, V.; Zenin, V.; Krupnik, L.; Kozachek, A.; Kharchev, N.; et al. Long-distance correlations of geodesic acoustic modes in T-10. Probl. At. Sci. Technol. Ser. Thermonucl. Fusion 2015, 38. [Google Scholar] [CrossRef]
- Melnikov, A.V.; Vershkov, V.A.; Eliseev, L.; Grashin, S.A.; Gudozhnik, A.V.; Krupnik, L.I.; Lysenko, S.E.; Mavrin, V.A.; Perfilov, S.V.; Shelukhin, D.A.; et al. Investigation of geodesic acoustic mode oscillations in the T-10 tokamak. Plasma Phys. Control. Fusion 2006, 48, S87–S110. [Google Scholar] [CrossRef]
- Melnikov, A.V.; Eliseev, L.G.; Ascasíbar, E.; Cappa, A.; Castejón, F.; Hidalgo, C.; Ido, T.; Jiménez, J.A.; Kozachek, A.S.; Krupnik, L.I.; et al. Effect of magnetic configuration on nonlinear evolution of NBI-driven Alfvén modes in TJ-II. Nucl. Fusion 2016, 56, 076001. [Google Scholar] [CrossRef]
- Cappa, Á.; Varela, J.; Lopez-Bruna, D.L.; Ascasíbar, E.; Liniers, M.; Eliseev, L.; Fontdecaba, J.; García-Regaña, J.; González-Jerez, A.; Kharchev, N.; et al. Stability analysis of TJ-II stellarator NBI driven Alfvén eigenmodes in ECRH and ECCD experiments. Nucl. Fusion 2021, 61, 066019. [Google Scholar] [CrossRef]
- Ongena, J.; Messiaen, A.; Melnikov, A.; Ragona, R.; Kazakov, Y.O.; Van Eester, D.; Dnestrovskii, Y.N.; Khvostenko, P.; Roy, I.; Romannikov, A. Conceptual study of an ICRH system for T-15MD using traveling wave antenna (TWA) sections. Fusion Eng. Des. 2019, 146, 787–791. [Google Scholar] [CrossRef]
- Melnikov, A.V.; Ongena, J.; Messiaen, A.M.; Ragona, R.; Sushkov, A.V.; Kazakov, Y.O.; Van Eester, D.; Dnestrovskii, Y.N.; Khvostenko, P.P.; Roy, I.N. Conceptual study of an ICRH traveling wave antenna (TWA) for T-15MD at 60 MHz. AIP Conf. Proc. 2020, 2254, 070007. [Google Scholar] [CrossRef]
- Perfilov, S.; Melnikov, A.; Krupnik, L.; Hartfuss, H.J. Applicability of Heavy Ion Beam Probing for Stellarator W7-X. AIP Conf. Proc. 2006, 812, 199–202. [Google Scholar] [CrossRef] [Green Version]
- Perfilov, S.; Melnikov, A.; Krupnik, L.; Hartfuss, H.J. Applicability of Heavy Ion Beam Probing for Stellarator W7-X. Fusion Sci. Technol. 2007, 51, 38–45. [Google Scholar] [CrossRef] [Green Version]
- Melnikov, A.V.; Eliseev, L.G. Optimized heavy ion beam probing for International Thermonuclear Experimental Reactor. Rev. Sci. Instrum. 1999, 70, 951–954. [Google Scholar] [CrossRef]
- Melnikov, A.V.; Eliseev, L.G.; Razumova, K.A.; Krupnik, L.I.; Chistyakov, V.V.; Myalton, T.B.; Dnestrovskij, Y.N.; HIBP Team. On the sensitivity of the plasma electric potential to the edge transport barrier formation. Jpn. J. Plasma Fusion Res. Series 2000, 4, 203–208. [Google Scholar]
- Alikaev, V.V.; Borshchegovskij, A.A.; Vershkov, V.A.; Volkov, V.V.; Gorshkov, A.V.; Gott, Y.V.; Grashin, S.A.; Dremin, M.M.; Eliseev, L.G.; Esipchuk, Y.V.; et al. Investigation of the H-mode during ECRH in the T-10 tokamak. Plasma Phys. Rep. 2000, 26, 917. [Google Scholar] [CrossRef]
- Melnikov, A.V.; Eliseev, L.G.; Grashin, S.A.; Drabinskiy, M.A.; Khabanov, P.O.; Kharchev, N.K.; Krupin, V.A.; Lysenko, S.E.; Ryzhakov, D.A.; Soloviev, N.A.; et al. Evolution of the electric potential and turbulence in OH and ECRH low-density plasmas at the T-10 tokamak. In Proceedings of the 28th IAEA Fusion Energy Conference (FEC 2020), 10–15 May 2021; Conference was held online. EX/5-6 (Nucl. Fusion under review). Available online: https://conferences.iaea.org/event/214/contributions/17104/ (accessed on 1 January 2021).













































Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melnikov, A. Evolution of Heavy Ion Beam Probing from the Origins to Study of Symmetric Structures in Fusion Plasmas. Symmetry 2021, 13, 1367. https://doi.org/10.3390/sym13081367
Melnikov A. Evolution of Heavy Ion Beam Probing from the Origins to Study of Symmetric Structures in Fusion Plasmas. Symmetry. 2021; 13(8):1367. https://doi.org/10.3390/sym13081367
Chicago/Turabian StyleMelnikov, Alexander. 2021. "Evolution of Heavy Ion Beam Probing from the Origins to Study of Symmetric Structures in Fusion Plasmas" Symmetry 13, no. 8: 1367. https://doi.org/10.3390/sym13081367
APA StyleMelnikov, A. (2021). Evolution of Heavy Ion Beam Probing from the Origins to Study of Symmetric Structures in Fusion Plasmas. Symmetry, 13(8), 1367. https://doi.org/10.3390/sym13081367





