Three-Phase Symmetric Distribution Network Fast Dynamic Reconfiguration Based on Timing-Constrained Hierarchical Clustering Algorithm
Abstract
:1. Introduction
- (1)
- A novel time-division method based on hierarchical clustering with timing constraints, which can ensure the rationality of the time-division method, is firstly proposed to solve the statics of the dynamic reconfiguration problem.
- (2)
- An improved fireworks algorithm considering heuristic rules (H-IFWA), for the first time, is presented, which can both improve the solving speed of DNR and avoid falling into a local optimum or producing many infeasible solutions.
2. Hierarchical Clustering with Timing Constraints
3. Three-Phase Symmetric Dynamic DNR Model
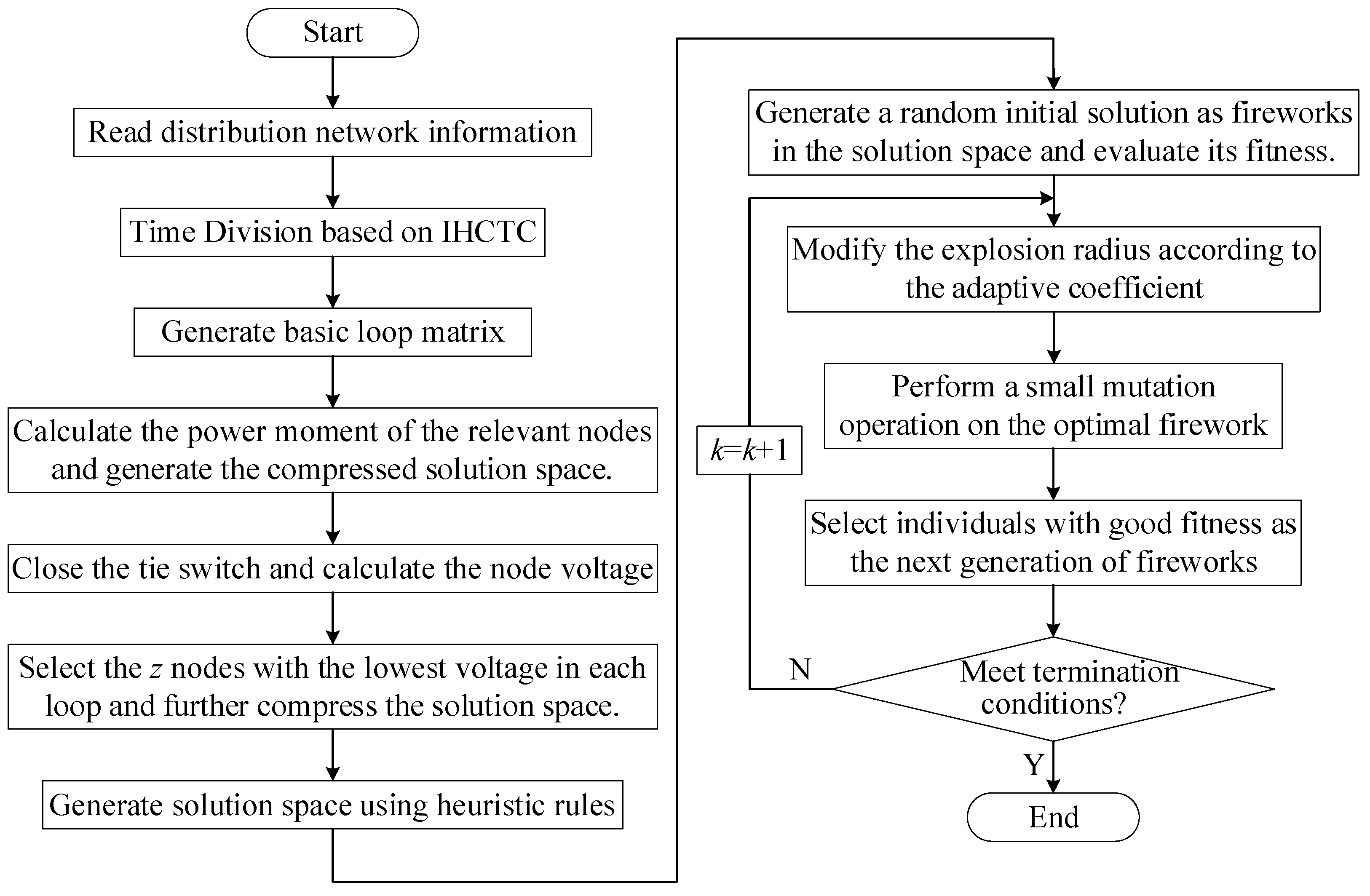
4. Solution Algorithm
4.1. Solution Space
4.2. Improved Fireworks Algorithm
4.3. Dynamic DNR Steps Based on IHCTC and H-IFWA
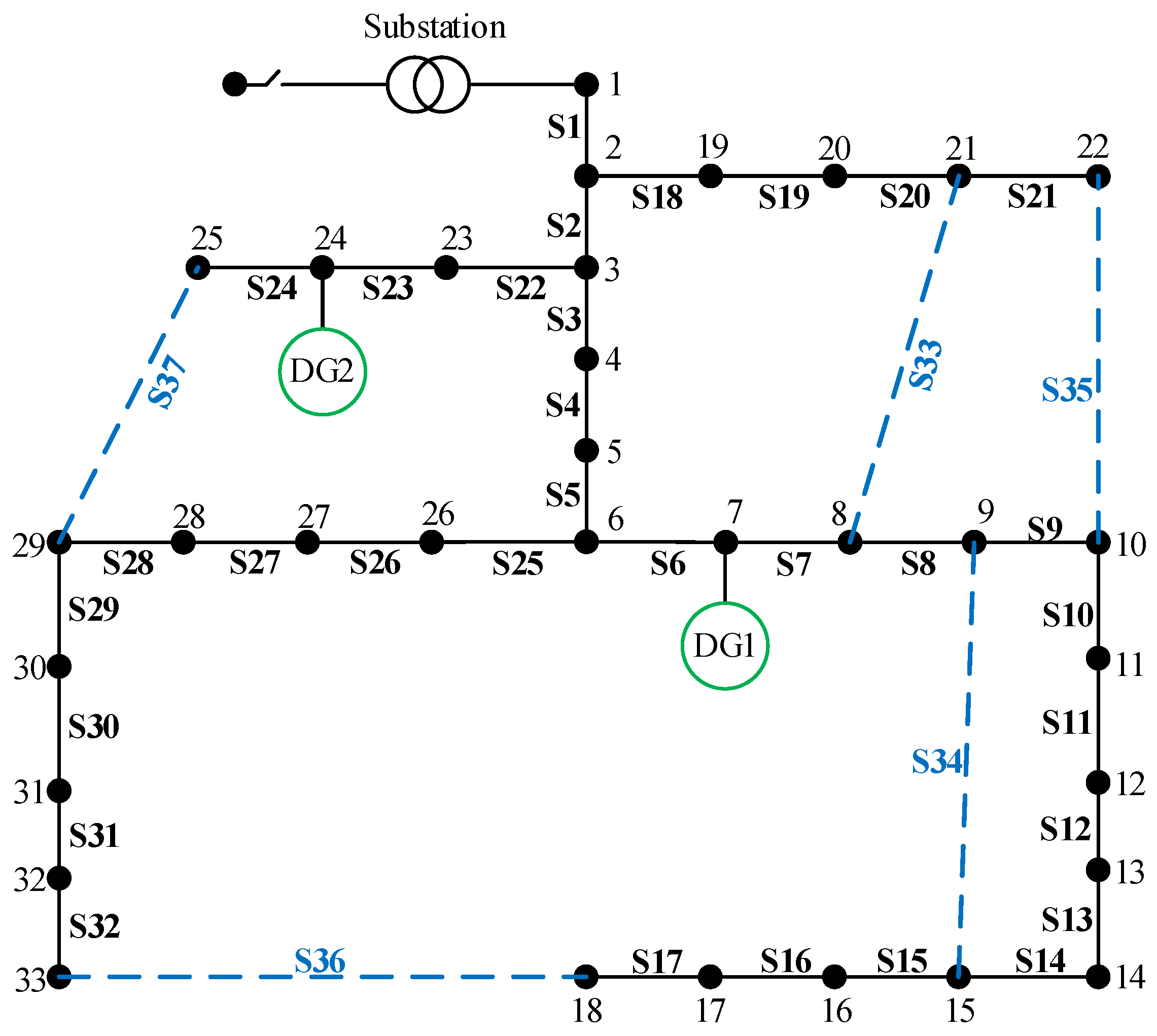
5. Case Studies
5.1. IEEE-33 Test System
5.1.1. Solution Spaces
5.1.2. H-IFWA Performance
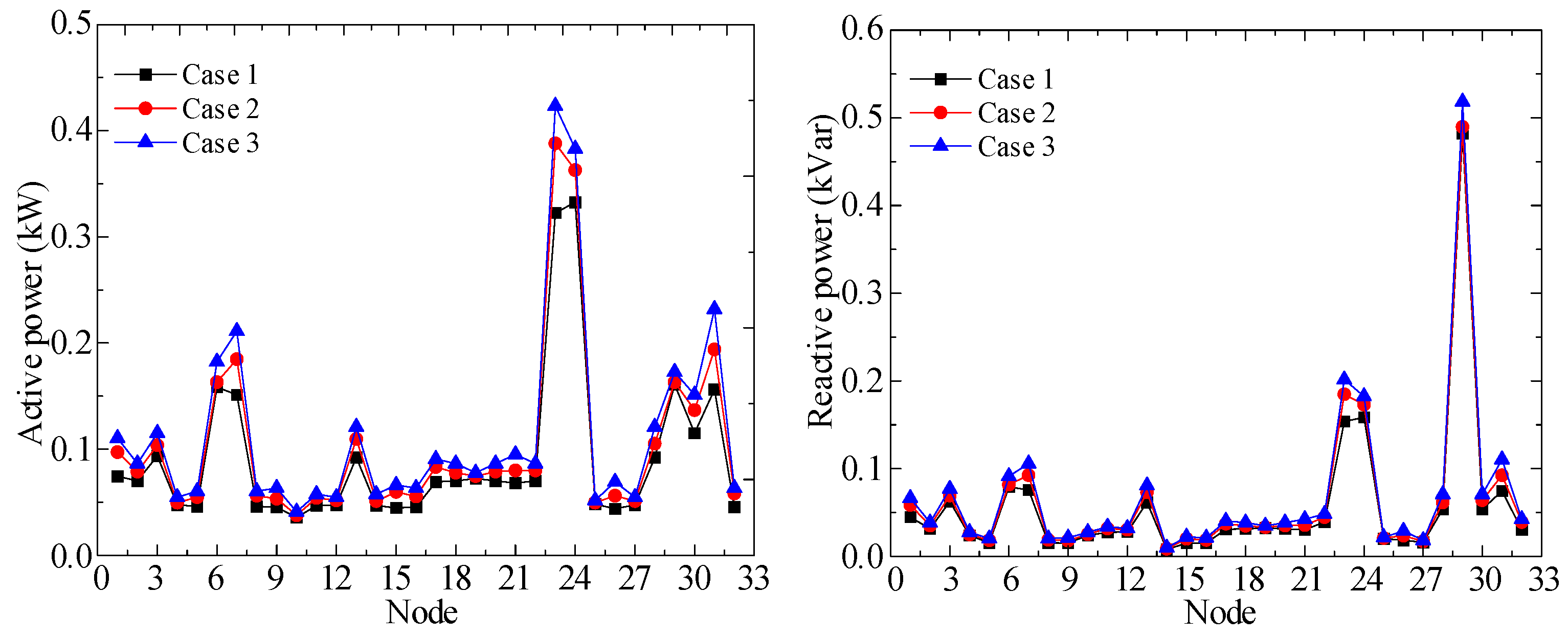
5.1.3. Sensitivity Analysis
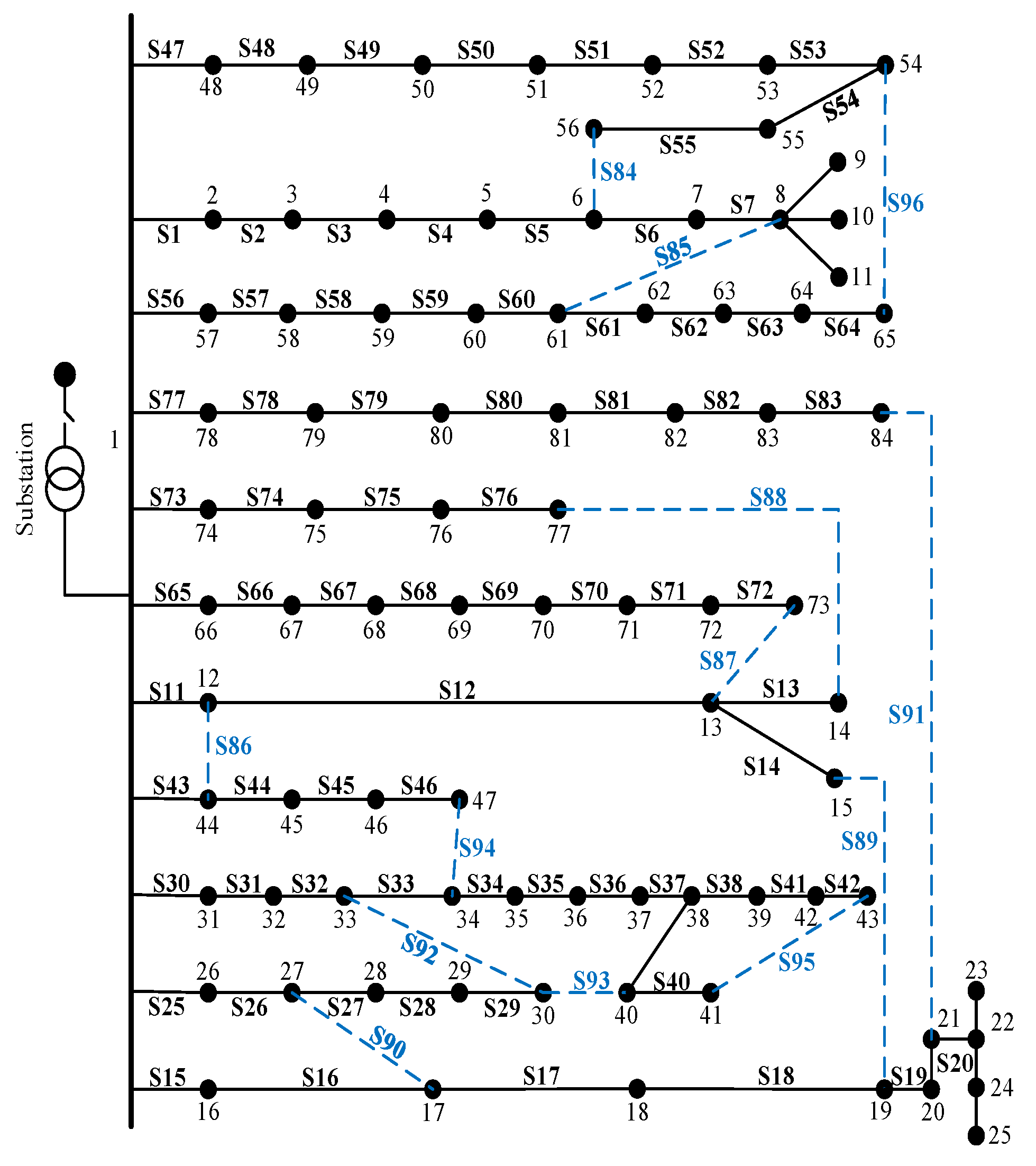
5.2. TPC 84-Bus and IEEE 119-Bus System
5.2.1. Solution Spaces
5.2.2. H-IFWA Performance
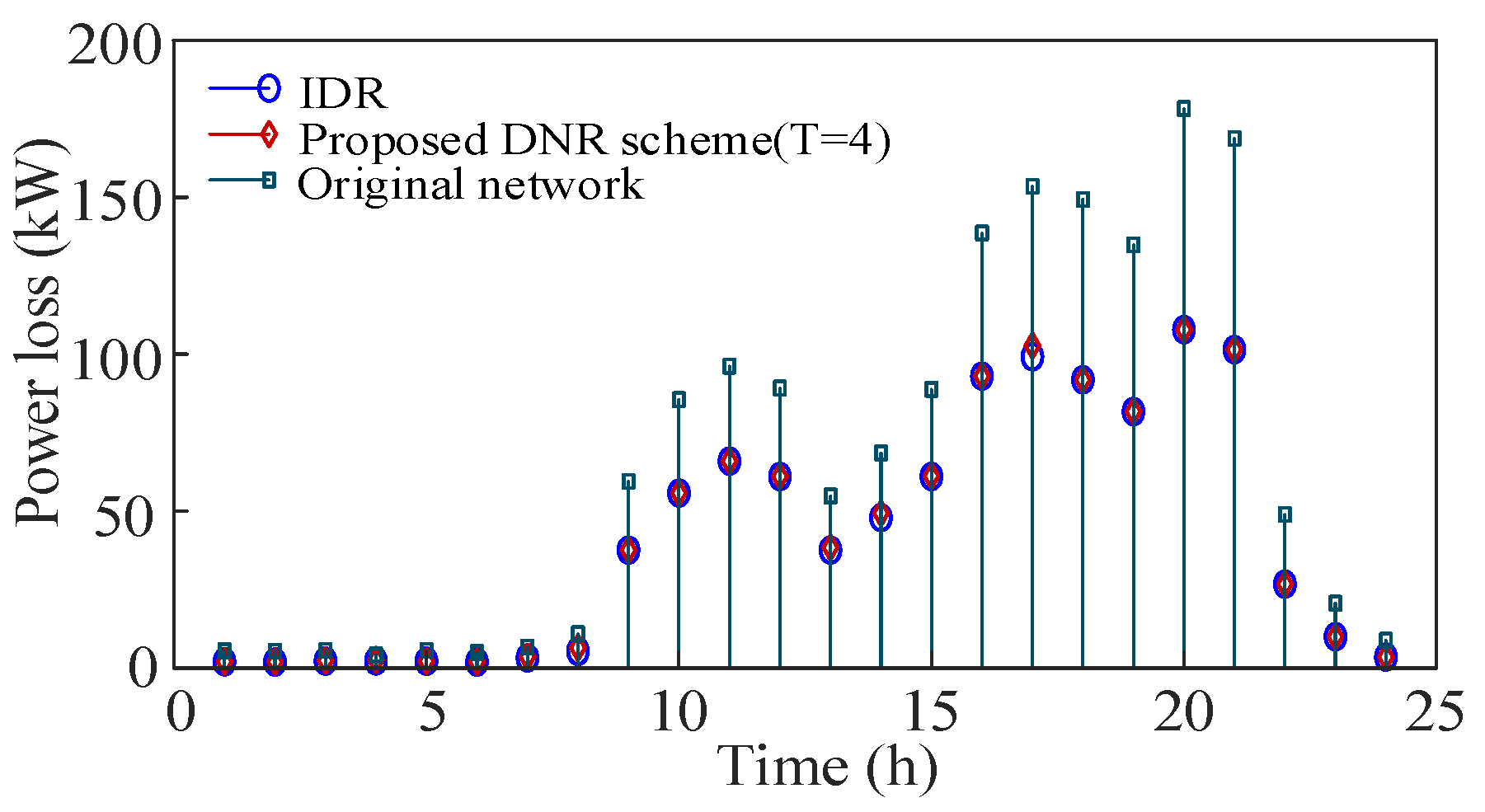
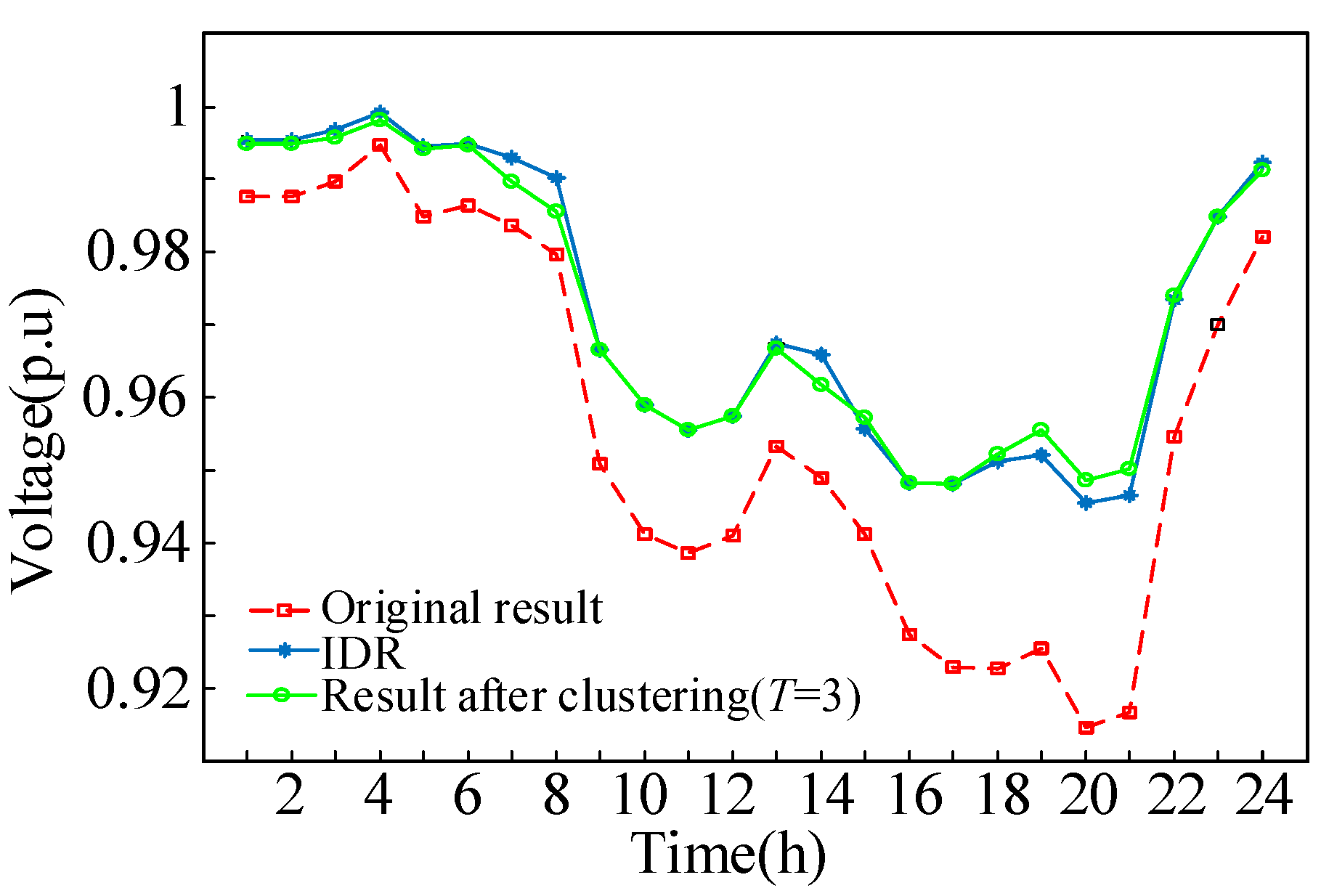
5.3. Comparison with IDR and MPTI Method
5.3.1. Comparison with IDR
5.3.2. Comparison with MPTI Method
6. Conclusions
- (1)
- IHCTC is developed to divide periods in terms of the load status and the output condition of DGs, and then the improved fireworks algorithm based on heuristic rules is proposed to recast the intractable dynamic reconfiguration problem as multiple single-stage static reconfiguration problems, which reduces the complexity of dynamic reconfiguration.
- (2)
- Compared with the advanced algorithms used in the existing literature, the proposed H-IFWA method not only has higher solution efficiency and avoids a large number of invalid solutions, but also can minimize the network loss as much as possible, so it is more suitable for the actual distribution network operation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhan, J.; Liu, W.; Chung, C.Y.; Yang, J. Switch opening and exchange method for stochastic distribution network reconfiguration. IEEE Trans. Smart Grid 2020, 11, 2995–3007. [Google Scholar] [CrossRef]
- Badran, O.; Mekhilef, S.; Mokhlis, H.; Dahalan, W. Optimal reconfiguration of distribution system connected with distributed generations: A review of different methodologies. Renew. Sustain. Energy Rev. 2017, 73, 854–867. [Google Scholar] [CrossRef]
- Mishra, S.; Das, D.; Paul, S. A comprehensive review on power distribution network reconfiguration. Energy Syst. 2017, 8, 227–284. [Google Scholar] [CrossRef]
- Shi, Q.; Li, F.; Olama, M.; Dong, J.; Xue, Y.; Starke, M.; Winstead, C.; Kuruganti, T. Network reconfiguration and distributed energy resource scheduling for improved distribution system resilience. Int. J. Electr. Power Energy Syst. 2021, 124, 1–10. [Google Scholar] [CrossRef]
- Jain, T.; Ghosh, D.; Mohanta, D.K. Augmentation of situational awareness by fault passage indicators in distribution network incorporating network reconfiguration. Prot. Control. Mod. Power Syst. 2019, 4, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Chandrakant, C.V.; Mikkili, S. A typical review on static reconfiguration strategies in photovoltaic array under non-uniform shading conditions. CSEE J. Power Energy Syst. 2020, 1–33. [Google Scholar] [CrossRef]
- Ajmal, A.M.; Ramachandaramurthy, V.K.; Naderipour, A.; Ekanayake, J.B. Comparative analysis of two-step GA-based PV array reconfiguration technique and other reconfiguration techniques. Energy Convers. Manag. 2021, 230, 113806. [Google Scholar] [CrossRef]
- Ji, X.; Yin, Z.; Zhang, Y.; Xu, B.; Liu, Q. Real-time autonomous dynamic reconfiguration based on deep learning algorithm for distribution network. Electr. Power Syst. Res. 2021, 195, 107132. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, W.; Shi, J.; Yu, N. Batch-constrained reinforcement learning for dynamic distribution network reconfiguration. IEEE Trans. Smart Grid 2020, 11, 5357–5369. [Google Scholar] [CrossRef]
- Azizivahed, A.; Arefi, A.; Ghavidel, S.; Shafie-Khah, M.; Li, L.; Zhang, J.; Catalao, J.P.S. Energy management strategy in dynamic distribution network reconfiguration considering renewable energy resources and storage. IEEE Trans. Sustain. Energy 2020, 11, 662–673. [Google Scholar] [CrossRef]
- Mukhopadhyay, B.; Das, D. Multi-objective dynamic and static reconfiguration with optimized allocation of PV-DG and battery energy storage system. Renew. Sustain. Energy Rev. 2020, 124, 109777. [Google Scholar] [CrossRef]
- Ajmal, A.M.; Babu, T.S.; Ramachandaramurthy, V.K.; Yousri, D.; Ekanayake, J.B. Static and dynamic reconfiguration approaches for mitigation of partial shading influence in photovoltaic arrays. Sustain. Energy Technol. Assess. 2020, 40, 100738. [Google Scholar] [CrossRef]
- Azad-Farsani, E.; Sardou, I.G.; Abedini, S. Distribution network reconfiguration based on LMP at DG connected busses using game theory and self-adaptive FWA. Energy 2021, 215, 119146. [Google Scholar] [CrossRef]
- Del Granado, P.C.; Wallace, S.W.; Pang, Z. The value of electricity storage in domestic homes: A smart grid perspective. Energy Syst. 2014, 5, 211–232. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, Z.; Shahidehpour, M.; Lai, L.L.; Wang, Z.; Zhu, Q. Reconfigurable distribution network for managing transactive energy in a multi-microgrid system. IEEE Trans. Smart Grid 2020, 11, 1286–1295. [Google Scholar] [CrossRef]
- Iris, Ç.; Lam, J.S.L. A review of energy efficiency in ports: Operational strategies, technologies and energy management systems. Renew. Sustain. Energy Rev. 2019, 112, 170–182. [Google Scholar] [CrossRef]
- Uniyal, A.; Sarangi, S. Optimal network reconfiguration and DG allocation using adaptive modified whale optimization algorithm considering probabilistic load flow. Electr. Power Syst. Res. 2021, 192, 106909. [Google Scholar] [CrossRef]
- Kahouli, O.; Alsaif, H.; Bouteraa, Y.; Ben Ali, N.; Chaabene, M. Power system reconfiguration in distribution network for improving reliability using genetic algorithm and particle swarm optimization. Appl. Sci. 2021, 11, 3092. [Google Scholar] [CrossRef]
- Aziz, T.; Lin, Z.; Waseem, M.; Liu, S. Review on optimization methodologies in transmission network reconfiguration of power systems for grid resilience. Int. Trans. Electr. Energy Syst. 2021, 31, 12704. [Google Scholar] [CrossRef]
- Yin, Z.; Ji, X.; Zhang, Y.; Liu, Q.; Bai, X. Data-driven approach for real-time distribution network reconfiguration. IET Gener. Transm. Distrib. 2020, 14, 2450–2463. [Google Scholar] [CrossRef]
- Samman, M.A.; Mokhlis, H.; Mansor, N.N.; Mohamad, H.; Suyono, H.; Sapari, N.M. Fast optimal network reconfiguration with guided initialization based on a simplified network approach. IEEE Access 2020, 8, 11948–11963. [Google Scholar] [CrossRef]
- Pfitscher, L.L.; Bernardon, D.P.; Canha, L.N.; Montagner, V.F.; Garcia, V.J.; Abaide, A.R. Intelligent system for automatic reconfiguration of distribution network in real time. Electr. Power Syst. Res. 2013, 97, 84–92. [Google Scholar] [CrossRef]
- Sun, X.; Qiu, J. Two-stage volt/var control in active distribution networks with multi-agent deep reinforcement learning method. IEEE Trans. Smart Grid 2021, 12, 2903–2912. [Google Scholar] [CrossRef]
- Yang, H.P.; Peng, Y.Y.; Xiong, N. Gradual approaching method for distribution network dynamic reconfiguration. In Proceedings of the 2008 Workshop on Power Electronics and Intelligent Transportation System (PEITS), Guangzhou, China, 2–3 August 2008; pp. 257–260. [Google Scholar]
- Milani, A.E.; Haghifam, M.R. An evolutionary approach for optimal time interval determination in distribution network re-configuration under variable load. Math. Comput. Model. 2013, 57, 68–77. [Google Scholar] [CrossRef]
- Bernardon, D.P.; Mello, A.; Pfitscher, L.L.; Canha, L.N.; Abaide, A.R.; Ferreira, A. Real-time reconfiguration of distribution network with distributed generation. Electr. Power Syst. Res. 2014, 107, 59–67. [Google Scholar] [CrossRef]
- Shariatkhah, M.-H.; Haghifam, M.-R.; Salehi, J.; Moser, A. Duration based reconfiguration of electric distribution networks using dynamic programming and harmony search algorithm. Int. J. Electr. Power Energy Syst. 2012, 41, 1–10. [Google Scholar] [CrossRef]
- Fathabadi, H. Power distribution network reconfiguration for power loss minimization using novel dynamic fuzzy c-means (dFCM) clustering based ANN approach. Int. J. Electr. Power Energy Syst. 2016, 78, 96–107. [Google Scholar] [CrossRef]
- Zhang, Y.; Ji, X.; Xu, J.; Yin, Z.; Han, X.; Zhang, C. Dynamic reconfiguration of distribution network based on temporal con-strained hierarchical clustering and fireworks algorithm. In Proceedings of the 2020 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Weihai, China, 13–15 July 2020; pp. 1702–1708. [Google Scholar]
- Su, C.-T.; Chang, C.-F.; Chiou, J.-P. Distribution network reconfiguration for loss reduction by ant colony search algorithm. Electr. Power Syst. Res. 2005, 75, 190–199. [Google Scholar] [CrossRef]
- Ji, X.; Liu, Q.; Yu, Y.; Fan, S.; Wu, N. Distribution network reconfiguration based on vector shift operation. IET Gener. Transm. Distrib. 2018, 12, 3339–3345. [Google Scholar] [CrossRef]
- Ding, F.; Loparo, K.A. Hierarchical decentralized network reconfiguration for smart distribution systems—Part I: Problem formulation and algorithm development. IEEE Trans. Power Syst. 2015, 30, 734–743. [Google Scholar] [CrossRef]
- Tan, Y.; Yu, C.; Zheng, S.; Ding, K. Introduction to fireworks algorithm. Int. J. Swarm Intell. Res. 2013, 4, 39–70. [Google Scholar] [CrossRef] [Green Version]
- Tan, Y. Fireworks Algorithm; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 2015; ISBN 978-3-662-46352-9. [Google Scholar]
- Zhang, K.; Lin, L.; Sun, Y. Dynamic reconfiguration of distribution network based on membership partition of time intervals. Power Syst. Prot. Cont. 2016, 44, 51–57. [Google Scholar]
- Baran, M.E.; Wu, F.F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Power Eng. Rev. 1989, 9, 101–102. [Google Scholar] [CrossRef]
- Imran, A.M.; Kowsalya, M. A new power system reconfiguration scheme for power loss minimization and voltage profile enhancement using Fireworks Algorithm. Int. J. Electr. Power Energy Syst. 2014, 62, 312–322. [Google Scholar] [CrossRef]
- Rajalakshmi, K.; Kumar, K.S.; Venkatesh, S.; Edward, J.B. Reconfiguration of distribution system for loss reduction using improved harmony search algorithm. In Proceedings of the 2017 International Conference on High Voltage Engineering and Power Systems (ICHVEPS), Denpasar, Indonesia, 2–5 October 2017; pp. 377–378. [Google Scholar]
- Koziel, S.; Rojas, A.L.; Moskwa, S. Power loss reduction through distribution network reconfiguration using feasibility-preserving simulated annealing. In Proceedings of the 2018 19th International Scientific Conference on Electric Power Engineering (EPE), Brno, Czech Republic, 16–18 May 2018. [Google Scholar]
- Ahmadi, H.; Martí, J.R. Linear current flow equations with application to distribution systems reconfiguration. IEEE Trans. Power Syst. 2015, 30, 2073–2080. [Google Scholar] [CrossRef]
- Zhang, D.; Fu, Z.; Zhang, L. An improved TS algorithm for loss-minimum reconfiguration in large-scale distribution systems. Electr. Power Syst. Res. 2007, 77, 685–694. [Google Scholar] [CrossRef]
- Rao, R.S.; Narasimham, S.V.L.; Raju, M.R.; Rao, A.S. Optimal network reconfiguration of large-scale distribution system using harmony search algorithm. IEEE Trans. Power Syst. 2011, 26, 1080–1088. [Google Scholar]
- Yang, H.; Peng, Y.; Xiong, N. A static method for distribution network dynamic reconfiguration. Power Syst. Prot. Cont. 2009, 37, 53–57. [Google Scholar]
- Reynolds, A.P.; Richards, G.; de la Iglesia, B.; Rayward-Smith, V.J. Clustering rules: A comparison of partitioning and hierarchical clustering algorithms. J. Math. Model. Algorithms 2006, 5, 475–504. [Google Scholar] [CrossRef]
- Iris, Ç.; Pacino, D.; Ropke, S.; Larsen, A. Integrated berth allocation and quay crane assignment problem: Set partitioning models and computational results. Transp. Res. Part E Logist. Transp. Rev. 2015, 81, 75–97. [Google Scholar] [CrossRef] [Green Version]


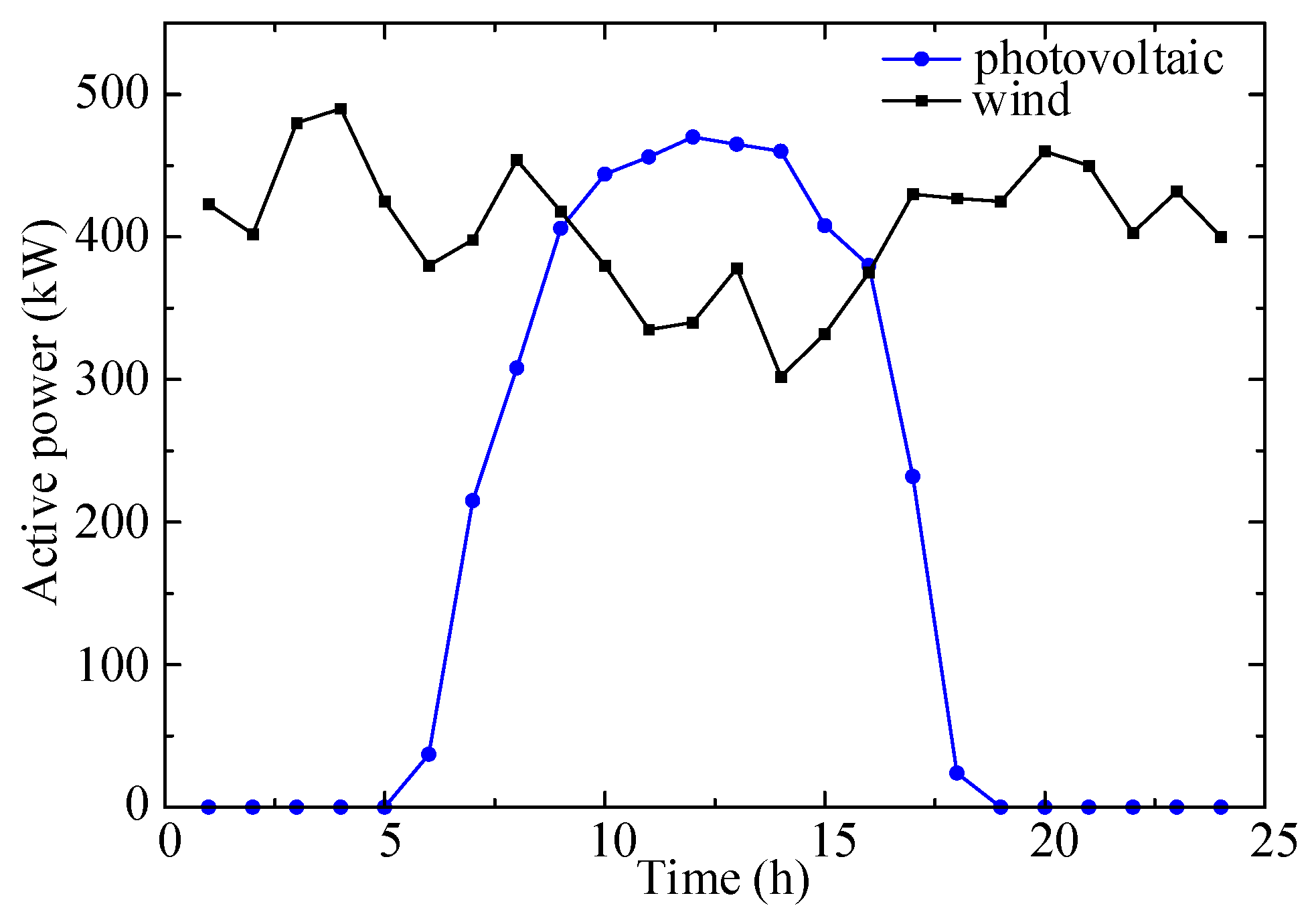
| Td | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| Time interval | 1–6; 7–24 | 1–6; 7–17; 18–24 | 7–17; 18–21; 22–24 | 1–5; 6–8; 9–17; 18–21; 22–24 |
| Inner-distance F | 8.19 | 5.43 | 4.80 | 4.45 |
| Loop Number | Tie Switch | Lowest Voltage Node | Adjacent Branches | Second Lowest Voltage Node | Adjacent Branches |
|---|---|---|---|---|---|
| 1 | B14 | 9 | B6, B8, B9 | 11 | B8, B14 |
| 2 | B15 | 8 | B5, B6, B7 | 10 | B7, B15 |
| 3 | B16 | 7 | B4, B16 | 6 | B3, B4 |
| Node | Rated Active Power (kW) | Rated Reactive Power (kVar) |
|---|---|---|
| 7 | 300 | 240 |
| 24 | 400 | 360 |
| Loop | Sp0 | Sp |
|---|---|---|
| 1 | {2, 3, 4, 5, 6, 7, 18, 19, 20, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0} | {5, 6, 7, 33} |
| 2 | {9, 10, 11, 12, 13, 14, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0} | {12, 13, 14, 34} |
| 3 | {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 18, 19, 20, 21, 0, 0, 0, 0, 0, 0} | {9, 10, 11, 35} |
| 4 | {6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 25, 26, 27, 28, 29, 30, 31, 32} | {17, 31, 32, 36} |
| 5 | {3, 4, 5, 22, 23, 24, 25, 26, 27, 28, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0} | {24, 27, 28, 37} |
| Items | Original Network | Reconfigured Network | |||||
|---|---|---|---|---|---|---|---|
| IHSA | FWA | MILP | H-IFWA | ||||
| Open switches | B33, B34, B35, B36, B37 | B9, B14, B28, B32, B33 | B9, B14, B28, B32, B33 | B9, B14, B28, B32, B33 | B9, B14, B28, B32, B33 | ||
| Power Loss (kWh) | Best | 146.02 | 94.67 | 94.67 | 94.67 | 94.67 | |
| Worst | 99.85 | 112.25 | 94.67 | 94.67 | |||
| Average | 97.58 | 102.69 | 94.67 | 94.67 | |||
| Lowest voltage (p.u) | 0.9193 | 0.9490 | 0.9490 | 0.9490 | 0.9490 | ||
| Average convergence time (s) | Best | -- | 5.9 | 6.1 | 1.8 | 1.7 | |
| Worst | 6.7 | 6.9 | 2.3 | 2.6 | |||
| Average | 6.1 | 6.4 | 1.9 | 2.1 | |||
| Case | Items | Original Network | H-IFWA |
|---|---|---|---|
| Case 1 | Power loss (kWh) | 110.29 | 81.58 |
| Lowest voltage (p.u) | 0.9725 | 0.9820 | |
| Case 2 | Power loss (kWh) | 143.86 | 105.52 |
| Lowest voltage (p.u) | 0.9671 | 0.9785 | |
| Case 3 | Power loss (kWh) | 176.95 | 128.55 |
| Lowest voltage (p.u) | 0.9629 | 0.9760 |
| Loop Number | Sp0 | Sp |
|---|---|---|
| 1 | {5, 4, 3, 2, 1, 55, 54, 53, 52, 51, 50, 49, 48, 47, 84, 0, 0} | {5, 54, 55, 84} |
| 2 | {7, 6, 5, 4, 3, 2, 1, 60, 59, 58, 57, 56, 85, 0, 0, 0, 0} | {6, 7, 85, 0} |
| 3 | {11, 43, 86, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0} | {11, 43, 86, 0} |
| 4 | {12, 11, 72, 71, 70, 69, 68, 67, 66, 65, 87, 0, 0, 0, 0, 0, 0} | {70, 71, 72, 87} |
| 5 | {13, 12, 11, 76, 75, 74, 73, 88, 0, 0, 0, 0, 0, 0, 0, 0, 0} | {13, 75, 76, 88} |
| 6 | {14, 12, 11, 18, 17, 16, 15, 89, 0, 0, 0, 0, 0, 0, 0, 0, 0} | {12, 14 18, 89} |
| 7 | {16, 15, 26, 25, 90, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0} | {15, 16, 26, 90} |
| 8 | {20, 19, 18, 17, 16, 15, 83, 82, 81, 80, 79, 78, 77, 91, 0, 0, 0} | {80, 81, 82, 83} |
| 9 | {28, 27, 26, 25, 32, 31, 30, 92, 0, 0, 0, 0, 0, 0, 0, 0, 0} | {27, 28, 31, 92} |
| 10 | {29, 28, 27, 26, 25, 39, 38, 37, 36, 35, 34, 33, 32, 31, 30, 93,0} | {37, 38, 39, 93} |
| 11 | {34, 33, 32, 31, 30, 46, 45, 44, 43, 94, 0, 0, 0, 0, 0, 0} | {32, 33, 34, 94} |
| 12 | {40, 39, 42, 41, 95, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0} | {40, 41, 43, 95} |
| 13 | {53, 52, 51, 50, 49, 48, 47, 64, 63, 62, 61, 60, 59, 58, 57, 56, 96} | {62, 63, 64, 96} |
| Items | Original Network | Reconfigured Network | ||||
|---|---|---|---|---|---|---|
| SA | GA | MILP | H-IFWA | |||
| Power Loss (kWh) | Best | 531.99 | 469.88 | 469.88 | 469.88 | 469.88 |
| Worst | 498.22 | 489.25 | 469.88 | 470.11 | ||
| Average | 489.82 | 479.73 | 469.88 | 469.89 | ||
| Lowest voltage (p.u) | 0.9193 | 0.9285 | 0.9285 | 0.9285 | 0.9285 | |
| Average convergence time (s) | -- | 257.43 | 303.43 | 9.77 | 4.86 | |
| Items | Original Network | Reconfigured Network | ||||
|---|---|---|---|---|---|---|
| HSA | ITS | MILP | H-IFWA | |||
| Power loss (kWh) | Best | 1301.9 | 865.86 | 854.21 | 869.7 | 869.7 |
| Worst | 1288.1 | 1282.1 | 869.7 | 870.1 | ||
| Average | 952.6 | 953.01 | 869.7 | 869.8 | ||
| Lowest voltage (p.u) | 0.8783 | 0.9323 | 0.9323 | 0.9383 | 0.9383 | |
| Average convergence time (s) | -- | 9.04 | 8.61 | 11.4 | 7.36 | |
| Reconfiguration Scheme | Original Network | IDR | H-IFWA | |
|---|---|---|---|---|
| T = 3 | T = 4 | |||
| Total energy loss (kWh) | 1593.99 | 1003.59 | 1012.37 | 1011.76 |
| Saved energy loss (kWh) | 0 | 590.40 | 581.62 | 582.23 |
| Energy reduction rate | 0 | 37.04% | 36.49% | 36.53% |
| Total number of switch actions | 0 | 33 | 8 | 10 |
| Reconfiguration Scheme | Time Interval | Open Switches | Energy Loss (kWh) | Saved Energy Loss (kWh) | Loss Reduction Rate | |
|---|---|---|---|---|---|---|
| Original network | -- | 33-34-35-36-37 | 2217.50 | 0 | 0 | |
| Literature [35] | 1–8 | 7-9-14-32-37 | 1540.91 | 676.59 | 30.51% | |
| 9–21 | 7-9-14-32-37 | |||||
| 22–24 | 7-9-14-32-37 | |||||
| Proposed method | T = 1 | 1–24 | 7-9-14-32-28 | 1530.10 | 687.40 | 31.00% |
| T = 2 | 1–16 | 7-9-14-32-28 | 1526.65 | 690.85 | 31.15% | |
| 17–24 | 7-9-14-32-37 | |||||
| T = 3 | 1–16 | 7-9-14-32-28 | 1525.78 | 691.72 | 31.19% | |
| 17–21 | 7-9-14-32-37 | |||||
| 22–24 | 7-9-14-32-28 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, X.; Zhang, X.; Zhang, Y.; Yin, Z.; Yang, M.; Han, X. Three-Phase Symmetric Distribution Network Fast Dynamic Reconfiguration Based on Timing-Constrained Hierarchical Clustering Algorithm. Symmetry 2021, 13, 1479. https://doi.org/10.3390/sym13081479
Ji X, Zhang X, Zhang Y, Yin Z, Yang M, Han X. Three-Phase Symmetric Distribution Network Fast Dynamic Reconfiguration Based on Timing-Constrained Hierarchical Clustering Algorithm. Symmetry. 2021; 13(8):1479. https://doi.org/10.3390/sym13081479
Chicago/Turabian StyleJi, Xingquan, Xuan Zhang, Yumin Zhang, Ziyang Yin, Ming Yang, and Xueshan Han. 2021. "Three-Phase Symmetric Distribution Network Fast Dynamic Reconfiguration Based on Timing-Constrained Hierarchical Clustering Algorithm" Symmetry 13, no. 8: 1479. https://doi.org/10.3390/sym13081479
APA StyleJi, X., Zhang, X., Zhang, Y., Yin, Z., Yang, M., & Han, X. (2021). Three-Phase Symmetric Distribution Network Fast Dynamic Reconfiguration Based on Timing-Constrained Hierarchical Clustering Algorithm. Symmetry, 13(8), 1479. https://doi.org/10.3390/sym13081479






