Dynamic Priority Real-Time Scheduling on Power Asymmetric Multicore Processors
Abstract
:1. Introduction
2. Related Work
2.1. Uniprocessor Scheduling
2.2. Semi-Partitioned Multi-Processor Scheduling
2.3. Power Asymmetric Multiprocessor Scheduling
3. System and Task Models
4. Dynamic Priority Semi-Partitioned Scheduling of Real-Time Tasks on Power-Asymmetric Multicore Processors
4.1. Task-Allocation in EDFwC=D-TS Scheduling
| Algorithm 1 Task-Allocation under the EDFwC=D-TS Algorithm |
| Input: (i) Set of real-time implicit-deadline periodic tasks where tasks are sorted in descending order of their utilization i.e., . (ii) Single-ISA heterogeneous multicore processor having processing cores where processing cores are sorted in descending order of their processing speed i.e.,. Output: Assigns tasks to cores; and returns success if is feasible on 1: 2: 3: 4: 5: 6: 7: 8: 9: 10: 11: 12: 13: 14: 15: 16: 17: 18: 19: 20: 21: 22: 23: 24: 25: 26: 27: 28: 29: 30: 31: = 32: 33: 34: 35: 36: 37: 38: |
4.2. Splitting Tasks in EDFwC=D-TS Scheduling
- A task such that it has the minimum deadline among the tasks in and is not previously tested is selected
- is split into two subtasks and using C=D heuristic such that
- In , is replaced by and its feasibility is determined using QPA algorithm
- If is feasible then it is allocated to the core m otherwise the next task is tested in the similar way
- If no task in is found feasible then for each task the worst-case execution time of is reduced and tested again
- This process continuous until a feasible task is found or the worst-case execution time of for each task becomes equal to zero
| Algorithm 2 Split-task process under EDFwC=D-TS Scheduling |
| Input: (i) Processing core having processing power , which is currently being considered for task allocation. (ii) Set of tasks where and contains the tasks which are assigned to core by Algorithm 1. (iii) System utilization of i.e., Output: Selects a task and splits it into two subtasks. 1: 2: 3: // sort tasks in ; in increasing order of deadline 4: 5: 6: 7: 8: 9: 10: 11: 12: 13: 14: 15: 16: 17: 18: 19: 20: 21: 22: 23: 24: 25: 26: 27: 28: 29: 30: 31: 32: I 33: 34: 35: 36: 37: 38: 39: I 40: 41: 42: 43: 44: 45: 46: 47: I 48: return “Task set is not feasible” 45: 46: 47: |
Analysis of Task-Splitting in EDFwC=D-TS Scheduling
4.3. The EDFwC=D-TS Scheduling Algorithm
| Algorithm 3: EDFwC=D-TS Scheduling Algorithm |
| Input: (i) Set of tasks with (ii) a Single-ISA heterogeneous multicore processor with Output: Schedule Γ on 1: // partition task-set using Algorithm 3.1 2: 3: 4: // Assign to core j 5: 6: 7: Assign priorities to each according to EDF Algorithm 8: 9: // At beginning 10: 11: 12: 13: 14: 15: 16: 17: 18: 19: Print “Fail to Schedule” 20: |
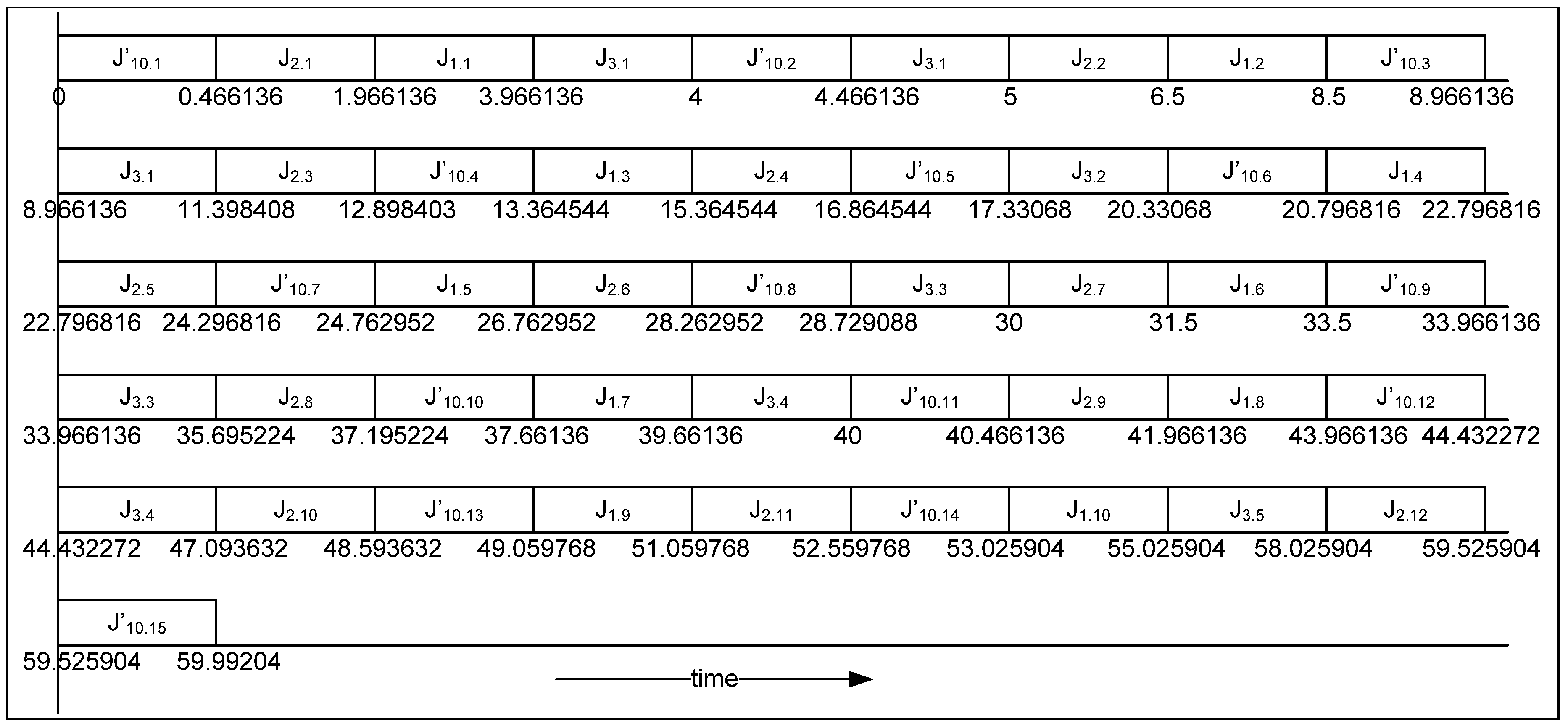
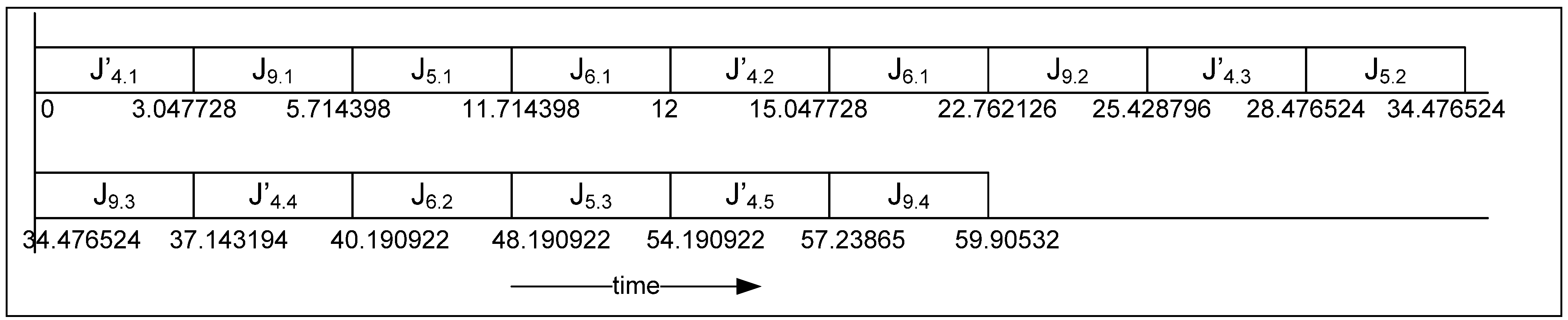
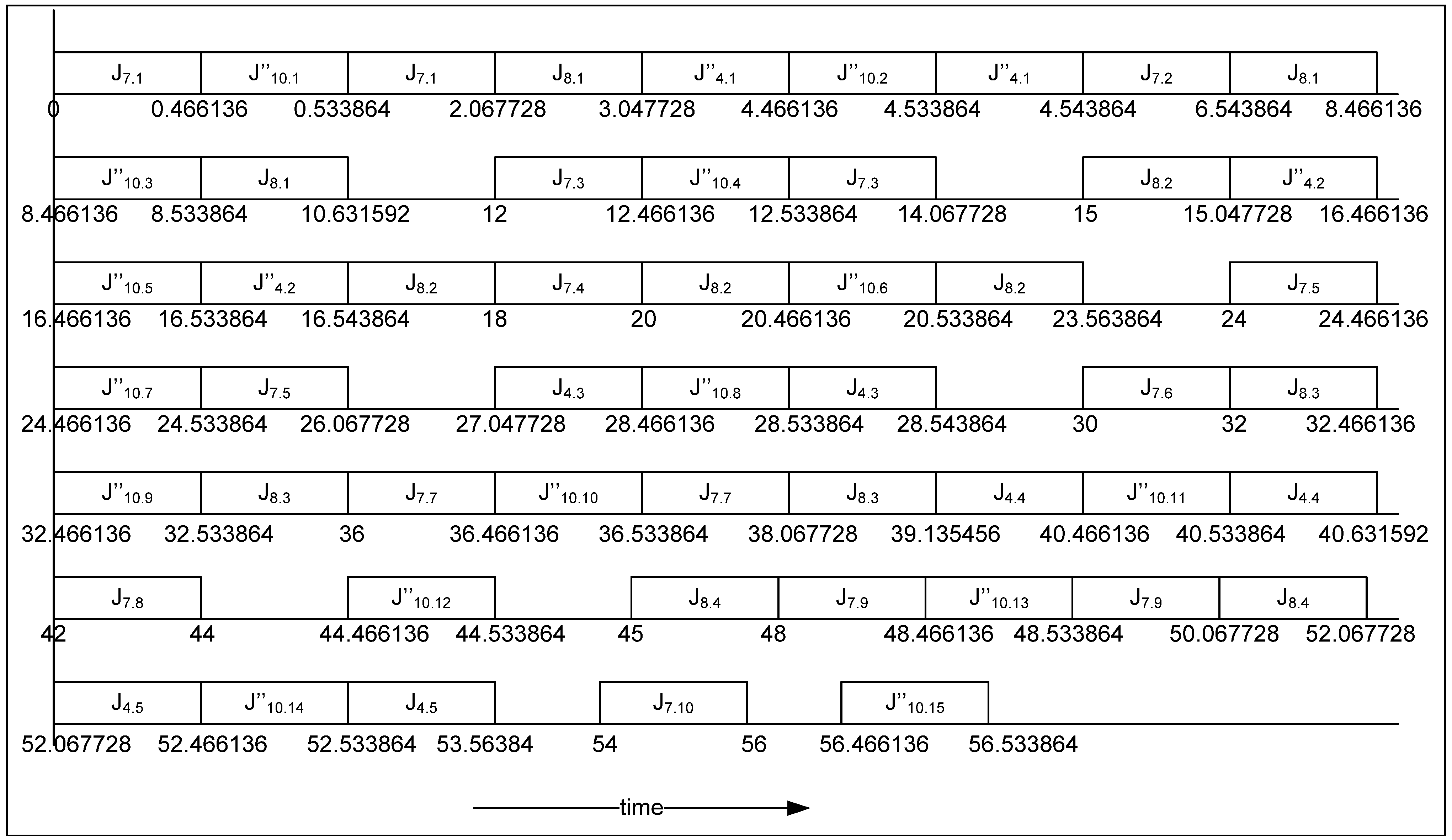
4.4. Working Example
- The value of L is calculated using Equation (3); L = 59.99204
- Value of is set to 0.466136
- The initial value of is assigned using ;
5. Experimental Evaluation
5.1. Experimental Setup
5.1.1. Task and System Parameters
5.1.2. Comparing Algorithms
- EDF-Partitioned: assigns tasks to a core to its full capacity on First-Fit basis using the EDF utilization bound, i.e.,
- EDF-DU-IS-FF: referred to the algorithm presented in [31] that assigns tasks to cores on First-Fit basis using EDF utilization bound assuming that cores are sorted in-order of increasing speed while the tasks are arranged in order of decreasing utilization.
5.1.3. Metrics Used for Comparison
- Processor Utilization: refers to the ability of an algorithm to utilize the capacity of available processor cores
- No. of cores used: is the number of cores used to feasibly schedule the provided workload
- Schedulability: is the ability of an algorithm to feasibly schedule the workload using the available processing cores
5.2. Simulation Results
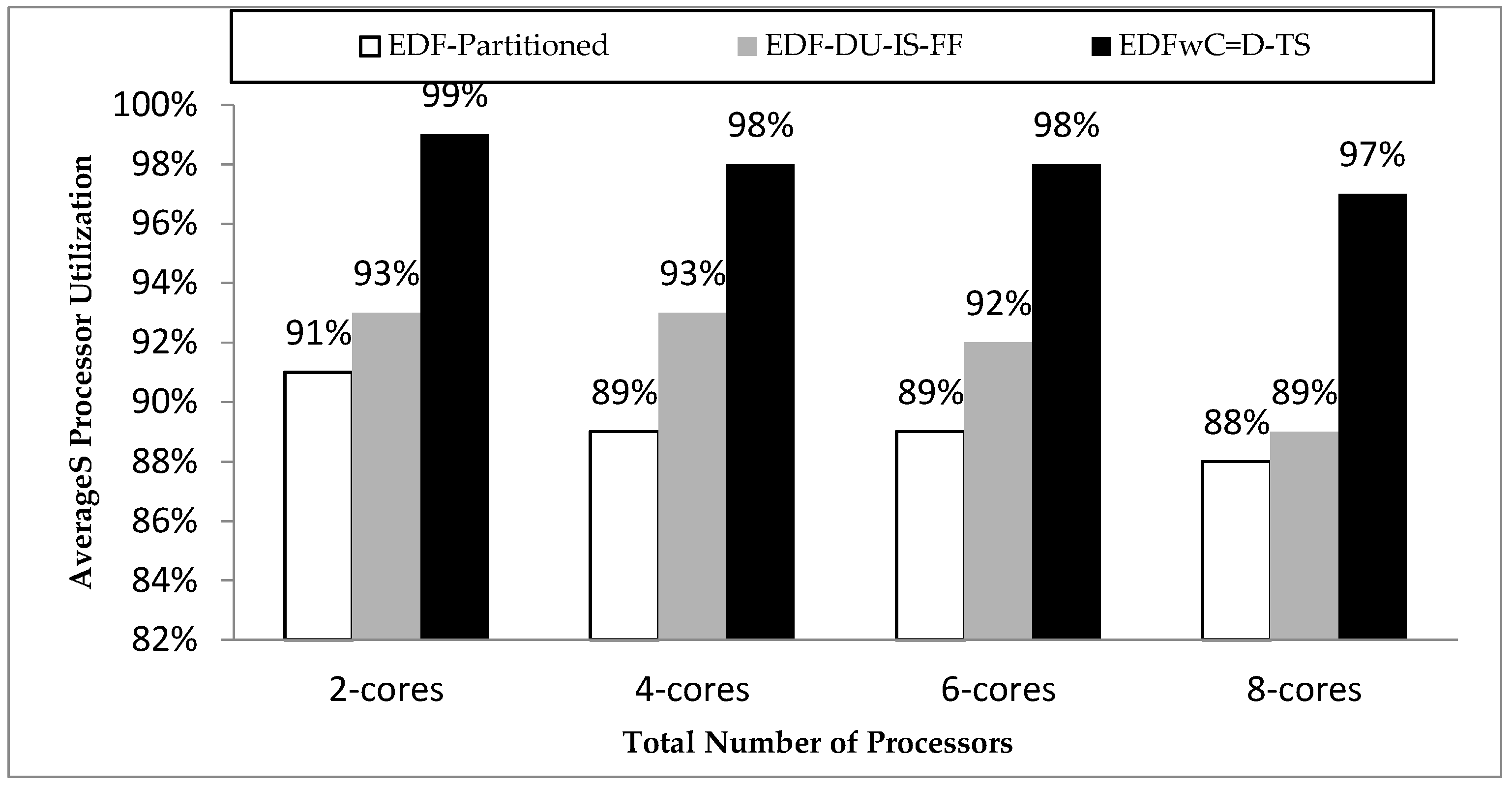
5.2.1. Processor Utilization
5.2.2. Number of Cores Used
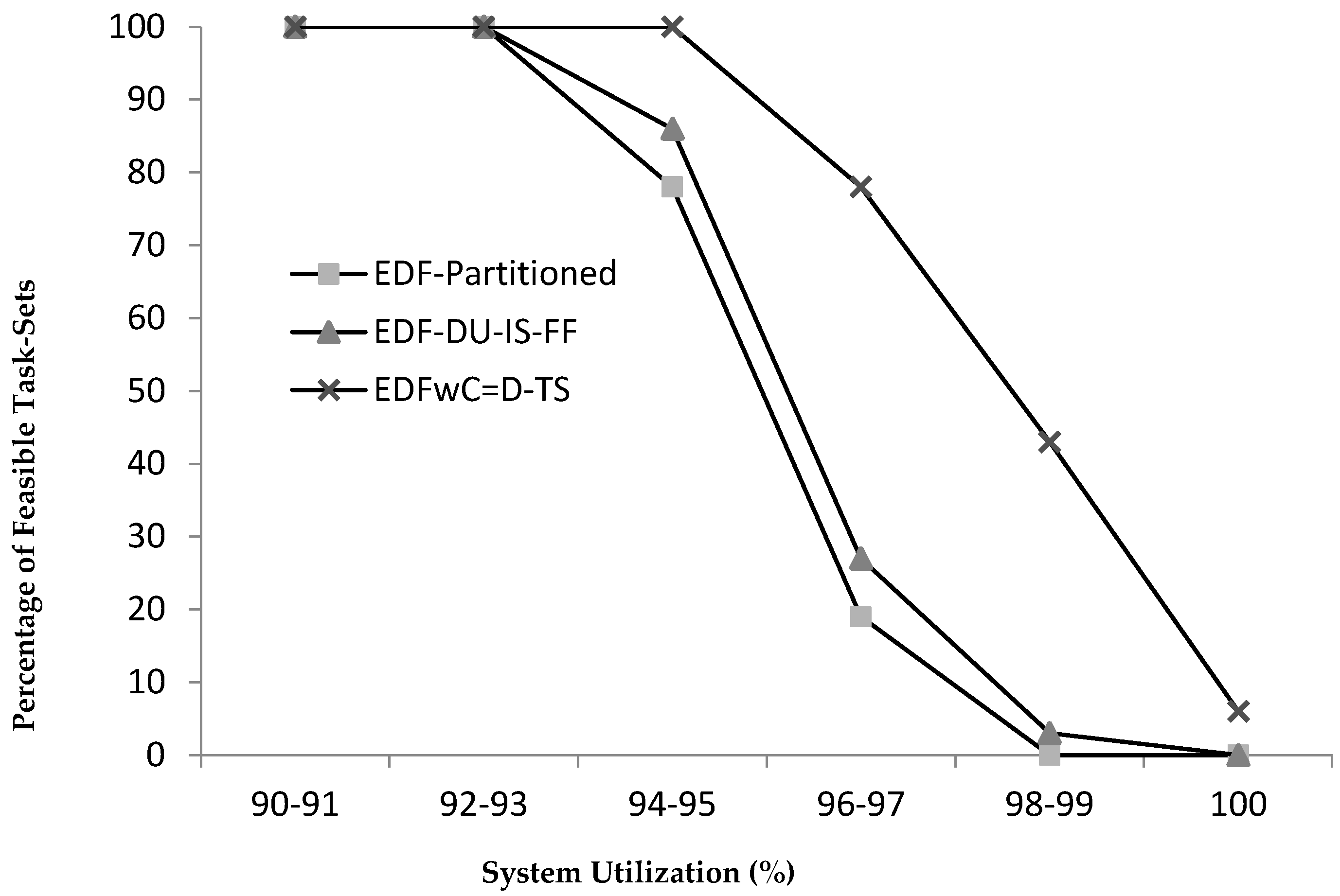
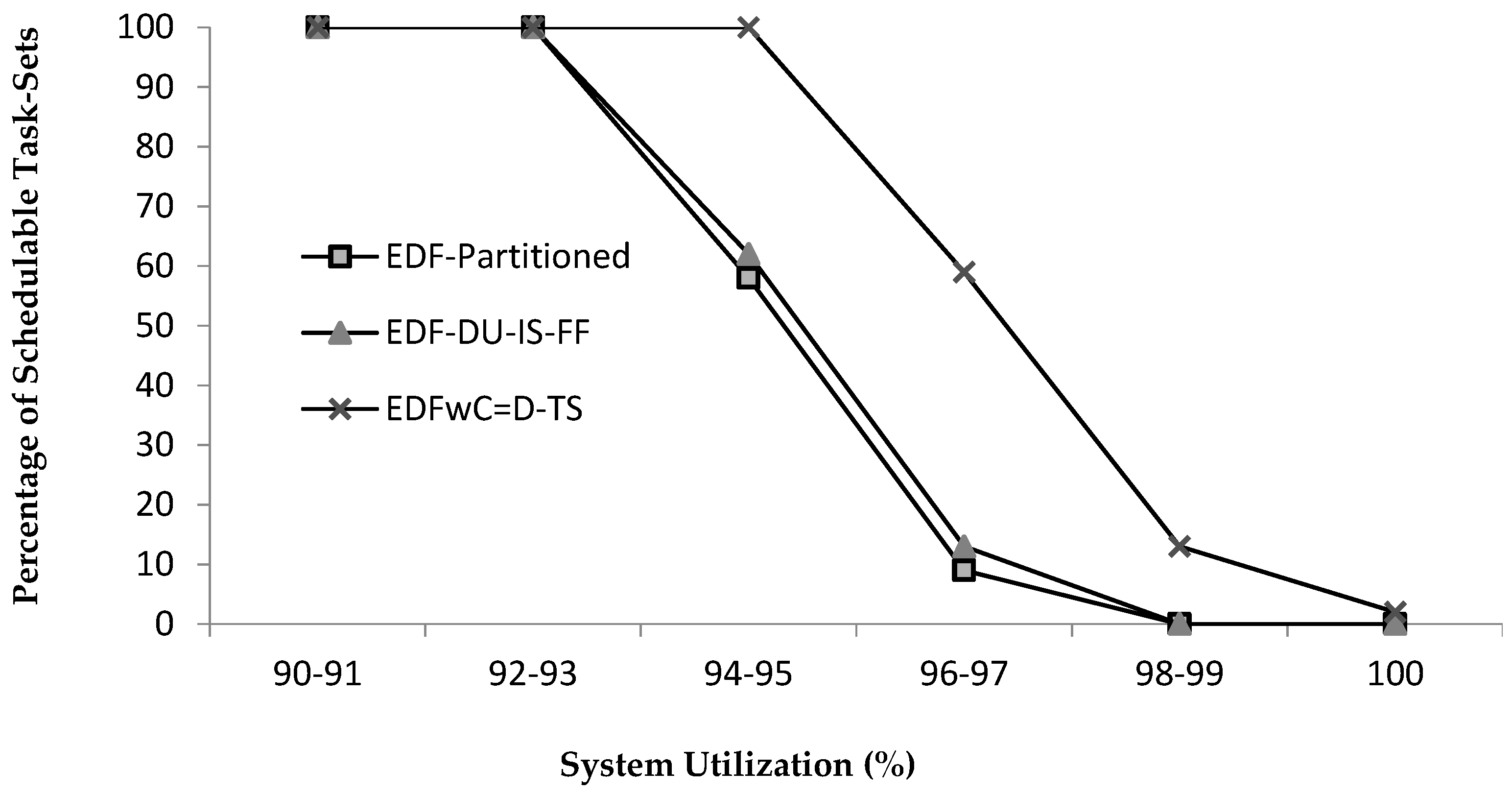
5.2.3. Schedulability
6. Discussion of Experimental Results
7. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Selim, Z.; El-Attar, N.E.; Ghoneim, M.E.; Awad, W.A. Performance Analysis of Real-Time Scheduling Algorithms. In Proceedings of the ICICSE ’20: 2020 International Conference on Internet Computing for Science and Engineering, Male, Maldives, 14–16 January 2020; pp. 70–75. [Google Scholar]
- Zhao, S.; Chang, W.; Wei, R.; Liu, W.; Guan, N.; Burns, A.; Wellings, A. Priority Assignment on Partitioned Multiprocessor Systems with Shared Resources. IEEE Trans. Comput. 2020, 70, 1006–1018. [Google Scholar] [CrossRef]
- Derafshi, D.; Norollah, A.; Khosroanjam, M.; Beitollahi, H. HRHS: A High-Performance Real-Time Hardware Scheduler. IEEE Trans. Parallel Distrib. Syst. 2020, 31, 897–908. [Google Scholar] [CrossRef]
- Seo, E.; Park, J.J.; Lee, J. Power Efficient Scheduling of Real-Time Tasks on Multicore Processors. IEEE Trans. Parallel Distrib. Syst. 2008, 19, 1541–1552. [Google Scholar]
- Weisberg, P.; Wiseman, Y. Efficient memory control for avionics and embedded systems. Int. J. Embed. Syst. 2013, 5, 225–238. [Google Scholar] [CrossRef] [Green Version]
- Maiza, C.; Rihani, H.; Rivas, J.M.; Goossens, J.; Altmeyer, S.; Davis, R.I. A Survey of Timing Verification Techniques for Multi-Core Real-Time Systems. ACM Comput. Surv. 2019, 52, 1–38. [Google Scholar] [CrossRef] [Green Version]
- Bertout, A.; Goossens, J.; Grolleau, E.; Poczekajlo, X. Template schedule construction for global real-time scheduling on unrelated multiprocessor platforms. In Proceedings of the 2020 Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 15 June 2020; pp. 2016–2221. [Google Scholar]
- Yu, T.; Petoumenos, P.; Janjic, V.; Leather, H.; Thomson, J. COLAB: A Collaborative Multi-Factor Scheduler for Asymmetric Multicore Processors. In Proceedings of the 18th ACM/IEEE International Symposium on Code Generation and Optimization, Seattle, WA, USA, 23–26 September 2019; pp. 268–279. [Google Scholar]
- Choudhury, A.M.; Nur, K. Qualitative Study of Contention-aware Scheduling Algorithm for Asymmetric Multicore Processors. In Proceedings of the International Conference on Computing Advancements, Dhaka, Bangladesh, 10–12 January 2020; pp. 1–6. [Google Scholar]
- Amina, M.; Kacem, Y.H.; Kerboeuf, M.; Mahfoudhi, A.; Abid, M. A design pattern-based approach for automatic choice of semi-partitioned and global scheduling algorithms. Inf. Softw. Technol. 2018, 97, 83–98. [Google Scholar]
- Davis, R.I.; Burns, A. A survey of hard real-time scheduling for multiprocessor. ACM Comput. Surv. 2011, 43, 1–44. [Google Scholar] [CrossRef] [Green Version]
- Guo, Z.; Yang, K.; Yao, F.; Awad, A. Inter-Task Cache Interference Aware Partitioned Real-Time Scheduling. In Proceedings of the SAC ’20: 35th Annual ACM Symposium on Applied Computing, Brno, Czech Republic, 30 March 2020; pp. 218–226. [Google Scholar]
- Hassan, H.A.; Salem, S.A.; Mostafa, A.M.; Saad, E.M. Harmonic segment-based semi-partitioning scheduling for multi-core real-time systems. ACM Trans. Embed. Comput. Syst. 2016, 15, 29. [Google Scholar]
- Liu, C.L.; Layland, J.W. Scheduling algorithms for multiprogramming in a hard real-time environment. J. ACM 1973, 20, 40–61. [Google Scholar] [CrossRef]
- Baruah, S.K.; Rosier, L.E.; Howell, R.R. Algorithms and Complexity Concerning the Preemptive Scheduling of Periodic Real-Time Tasks on One Processor. J. Real-Time Syst. 1990, 4, 301–324. [Google Scholar] [CrossRef]
- Ripoll, I.; Crespo, A.; Mok, A.K. Improvement in feasibility testing for real-time tasks. J. Real-Time Syst. 1996, 11, 19–39. [Google Scholar] [CrossRef]
- Spuri, M. Analysis of Deadline Schedule Real-Time Systems; Technical Report 2772; INRIA: Paris, France, 1996. [Google Scholar]
- Zhang, F.; Burns, A. Schedulability analysis for real-time systems with EDF scheduling. IEEE Trans. Comput. 2008, 58, 1250–1258. [Google Scholar] [CrossRef]
- Zhang, F.; Burns, A.; Baruah, S.K. Sensitivity analysis of arbitrary deadline real-time systems with EDF scheduling. J. Real-Time Syst. 2011, 47, 224–252. [Google Scholar] [CrossRef]
- Anderson, J.H.; Bud, V.; Devi, C. An EDF-based Scheduling Algorithm for Multiprocessor Soft Real-Time Systems. In Proceedings of the 17th Euromicro Conference on Real-Time Systems, Balearic Islands, Spain, 6–8 July 2005; pp. 199–208. [Google Scholar]
- Andersson, B.; Tovar, E. Multiprocessor scheduling with few preemptions. In Proceedings of the IEEE International Conference on Embedded and Real-Time Computing Systems and Applications, Sydney, NSW, Australia, 11 September 2006; pp. 322–334. [Google Scholar]
- Kato, S.; Yamasaki, N. Real-time scheduling with task splitting on multiprocessors. In Proceedings of the RTCSA ’07: 13th IEEE International Conference on Embedded and Real-Time Computing Systems and Applications, Daegu, Korea, 4 September 2007; pp. 441–450. [Google Scholar]
- Kato, S.; Yamasaki, N. Portioned EDF-based scheduling on multiprocessors. In Proceedings of the 8th ACM/IEEE International Conference on Embedded Software, Atlanta, GA, USA, 19–24 October 2008; pp. 139–148. [Google Scholar]
- Kato, S.; Yamasaki, N. Semi-partitioning technique for multiprocessor real-time scheduling. In Proceedings of the WIP Session of the 29th Real-Time Systems Symposium (RTSS), Yokohama, Japan, 30 November 2008; p. 4. [Google Scholar]
- Kato, S.; Yamasaki, N.; Ishikawa, Y. Semi-partitioned scheduling of sporadic task systems on multiprocessors. In Proceedings of the ECRTS ’09: 2009 21st Euromicro Conference on Real-Time Systems, Dublin, Ireland, 1–3 July 2009; pp. 249–258. [Google Scholar]
- Burns, A.; Davis, R.I.; Wang, P.; Zhang, F. Partitioned EDF scheduling for multiprocessors using a C = D task splitting scheme. Real-Time Syst. 2012, 48, 3–33. [Google Scholar] [CrossRef]
- Anderson, J.; Erickson, J.; Devi, U.C.; Casses, B. Optimal semi-partitioned scheduling in soft real-time systems. J. Signal Process. Syst. 2016, 84, 3–23. [Google Scholar] [CrossRef] [Green Version]
- Baruah, S.K. Scheduling Periodic Tasks on uniform multiprocessors. Inf. Process. Lett. 2001, 80, 97–104. [Google Scholar] [CrossRef]
- Funk, S.; Goossens, J.; Baruah, S.K. On-line Scheduling on Power asymmetric Multiprocessors. In Proceedings of the Real-Time Systems Symposium (RTSS), London, UK, 2–6 December 2001; pp. 183–192. [Google Scholar]
- Baruah, S.K.; Goossens, J. Rate-Monotonic Scheduling on Power asymmetric Multiprocessors. IEEE Trans. Comput. 2003, 52, 966–970. [Google Scholar] [CrossRef]
- Andersson, B.; Tovar, E. Competitive Analysis of Partitioned Scheduling on Uniform Multiprocessors. In Proceedings of the 2007 IEEE International Parallel and Distributed Processing Symposium, Daegu, Korea, 21–24 August 2007; pp. 1–8. [Google Scholar] [CrossRef] [Green Version]
- Andersson, B.; Tovar, E. Competitive Analysis of Static-Priority Partitioned Scheduling on Power asymmetric Multiprocessors. In Proceedings of the 13th IEEE International Conference on Embedded and Real-Time Computing Systems and Applications (RTCSA 2007), Daegu, Korea, 21–24 August 2007; pp. 111–119. [Google Scholar]
- Cucu, L.; Goossens, J. Feasibility Intervals for Fixed-Priority Real-Time Scheduling on Power asymmetric Multiprocessors. In Proceedings of the IEEE Conference on Emerging Technologies and Factory Automation, Prague, Czech Republic, 20–22 September 2006; pp. 397–404. [Google Scholar]
- Baruah, S.K.; Goossens, J. The EDF Scheduling of Sporadic Task Systems on Power asymmetric Multiprocessors. In Proceedings of the Real-Time Systems Symposium, Barcelona, Spain, 30 November–3 December 2008; pp. 367–374. [Google Scholar]
- Calandrino, J.M.; Baumberger, D.; Li, T.; Hahn, S.; Anderson, J.H. Soft Real-Time Scheduling on Performance Asymmetric Multicore Platforms. In Proceedings of the 13th IEEE Real Time and Embedded Technology and Applications Symposium (RTAS’07), Bellevue, WA, USA, 3–6 April 2007; pp. 101–112. [Google Scholar]
- Chen, S.Y.; Hsueh, C.W. Optimal Dynamic-Priority Real-Time Scheduling Algorithms for Power asymmetric Multiprocessors. In Proceedings of the Real-Time Systems Symposium, Barcelona, Spain, 30 November–3 December 2008; pp. 147–156. [Google Scholar]
- Xiaojian, L.; Xiang, L. A-S Algorithm: An Optimal on-line Real-Time Scheduling Algorithm for Power asymmetric Multiprocessors. In Proceedings of the 3rd IEEE International Conference on “Computational Intelligence and Communication Technology” (IEEE-CICT 2017), Ghaziabad, India, 9–10 February 2017. [Google Scholar]
- Pathan, R.M.; Jonsson, J. Parameterized Schedulability Analysis on Power asymmetric Multiprocessors. In Proceedings of the 39th International Conference on Parallel Processing, San Diego, CA, USA, 13–16 September 2010; pp. 323–332. [Google Scholar]
- Jung, M.J.; Seong, Y.P.; Lee, C.H. Optimal RM Scheduling for Simply Periodic Tasks on Power asymmetric Multiprocessors. In Proceedings of the 2009 International Conference on Hybrid Information Technology (ICHIT ’09), Daejeon, Korea, 27–29 August 2009; pp. 383–389. [Google Scholar]
- Bini, E.; Buttazzo, G. Measuring the Performance of Schedulability Tests. Real-Time Syst. 2005, 30, 129–154. [Google Scholar] [CrossRef]


| Notation | Meanings |
|---|---|
| Γ | Task-set representing the workload |
| Task | |
| CPU cycles required by task i in worst-case | |
| Relative deadline of the task i | |
| Period of the task i | |
| S | Set defining the power asymmetric multicore processor |
| Processing power of the core i | |
| Time required by task i to complete its execution on core j | |
| System utilization factor of the task i on core j | |
| Value of the L.L bound for n tasks | |
| Additional-offset of task i |
| Task (τi) | CPU Cycles Required in Worst-Case (Ci) | Task Period (Pi) | Task Deadline (Di) | System Utilization Factor |
|---|---|---|---|---|
| τ1 | 4 | 6 s * | 6 s | 0.6667 |
| τ2 | 3 | 5 s | 5 s | 0.6 |
| τ3 | 6 | 12 s | 12 s | 0.5 |
| τ4 | 6 | 12 s | 12 s | 0.5 |
| τ5 | 9 | 20 s | 20 s | 0.45 |
| τ6 | 12 | 30 s | 30 s | 0.40 |
| τ7 | 2 | 6 s | 6 s | 0.3333 |
| τ8 | 5 | 15 s | 15 s | 0.3333 |
| τ9 | 4 | 15 s | 15 s | 0.2667 |
| τ10 | 1 | 4 s | 4 s | 0.25 |
| 56.46136 | 53.49204 | 28.729088 | 25.229088 |
| 53.49204 | 49.525904 | 25.229088 | 24.762952 |
| 49.525904 | 47.559768 | 24.762952 | 23.262952 |
| 47.559768 | 42.093632 | 23.262952 | 17.796816 |
| 42.093632 | 40.127496 | 17.796816 | 13.83068 |
| 40.127496 | 37.66136 | 13.83068 | 11.86544 |
| 37.66136 | 36.16136 | 11.86544 | 6.398408 |
| 36.16136 | 35.695224 | 6.398408 | 4.432272 |
| 35.695224 | 30.695224 | 4.432272 | 0.466136 |
| 30.695224 | 28.729088 |
| Core | Allocated Tasks | Processor Utilization |
|---|---|---|
| 1 | , , , | 1 |
| 2 | , , , | 1 |
| 3 | , , , | 0.8454 |
| Task Parameters | |||
|---|---|---|---|
| Total Task-Sets | Task-Set Cardinality (n) | Task Parameters (Ci, Pi, Di) | System Utilization Factor (U) |
| 105 | {8, …, 64} | {10, …, 100}, {10, …, 100} | {0.90, …, 1.0} |
| Processor Specification | |||
| 2 | {1.01 GHz, 3.1 GHz} | ||
| 4 | {1.01 GHz,1.5 3 GHz, 2.1 GHz, 3.1 GHz} | ||
| 6 | {1.01 GHz, 1.53 GHz, 1.81 GHz, 2.1 GHz, 2.7 GHz, 3.1 GHz} | ||
| 8 | {1.01 GHz, 1.53 GHz, 1.26 GHz, 1.81 GHz, 2.1 GHz, 2.42 GHz,2.7 GHz, 3.1 GHz} | ||
| EDF-Partitioned | EDF-DU-IS-FF | EDFwC=D-TS | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2-cores | 4-cores | 6-cores | 8-cores | 2-cores | 4-cores | 6-cores | 8-cores | 2-cores | 4-cores | 6-cores | 8-cores | |
| Average No. of Cores Used | 2.42 | 5.12 | 7.04 | 9.22 | 2.34 | 4.94 | 6.95 | 8.98 | 2.10 | 4.68 | 6.52 | 8.28 |
| Average Processor Utilization | 91% | 89% | 89% | 88% | 93% | 93% | 92% | 89% | 99% | 98% | 98% | 97% |
| System Utilization (%) | EDF-Partitioned | EDF-DU-IS-FF | EDFwC=D-TS | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 4-cores | 6-cores | 8-cores | 4-cores | 6-cores | 8-cores | 4-cores | 6-cores | 8-cores | |
| 90–91 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| 92–93 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| 94–95 | 78 | 67 | 58 | 86 | 71 | 62 | 100 | 100 | 100 |
| 96–97 | 19 | 11 | 9 | 27 | 17 | 13 | 78 | 68 | 59 |
| 98–99 | 0 | 0 | 0 | 3 | 0 | 0 | 43 | 29 | 13 |
| 100 | 0 | 0 | 0 | 0 | 0 | 0 | 6 | 5 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmood, B.; Ahmad, N.; Khan, M.I.; Akhunzada, A. Dynamic Priority Real-Time Scheduling on Power Asymmetric Multicore Processors. Symmetry 2021, 13, 1488. https://doi.org/10.3390/sym13081488
Mahmood B, Ahmad N, Khan MI, Akhunzada A. Dynamic Priority Real-Time Scheduling on Power Asymmetric Multicore Processors. Symmetry. 2021; 13(8):1488. https://doi.org/10.3390/sym13081488
Chicago/Turabian StyleMahmood, Basharat, Naveed Ahmad, Majid Iqbal Khan, and Adnan Akhunzada. 2021. "Dynamic Priority Real-Time Scheduling on Power Asymmetric Multicore Processors" Symmetry 13, no. 8: 1488. https://doi.org/10.3390/sym13081488






