Endotracheal Tubes Design: The Role of Tube Bending
Abstract
:1. Introduction
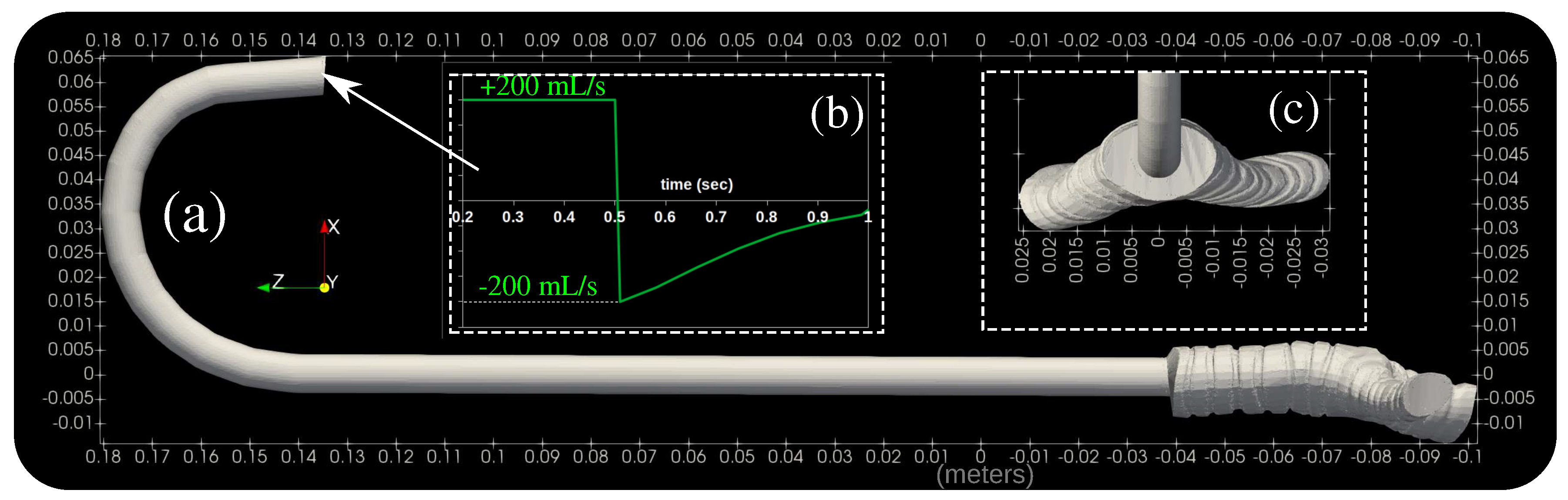
2. Computational Methodology
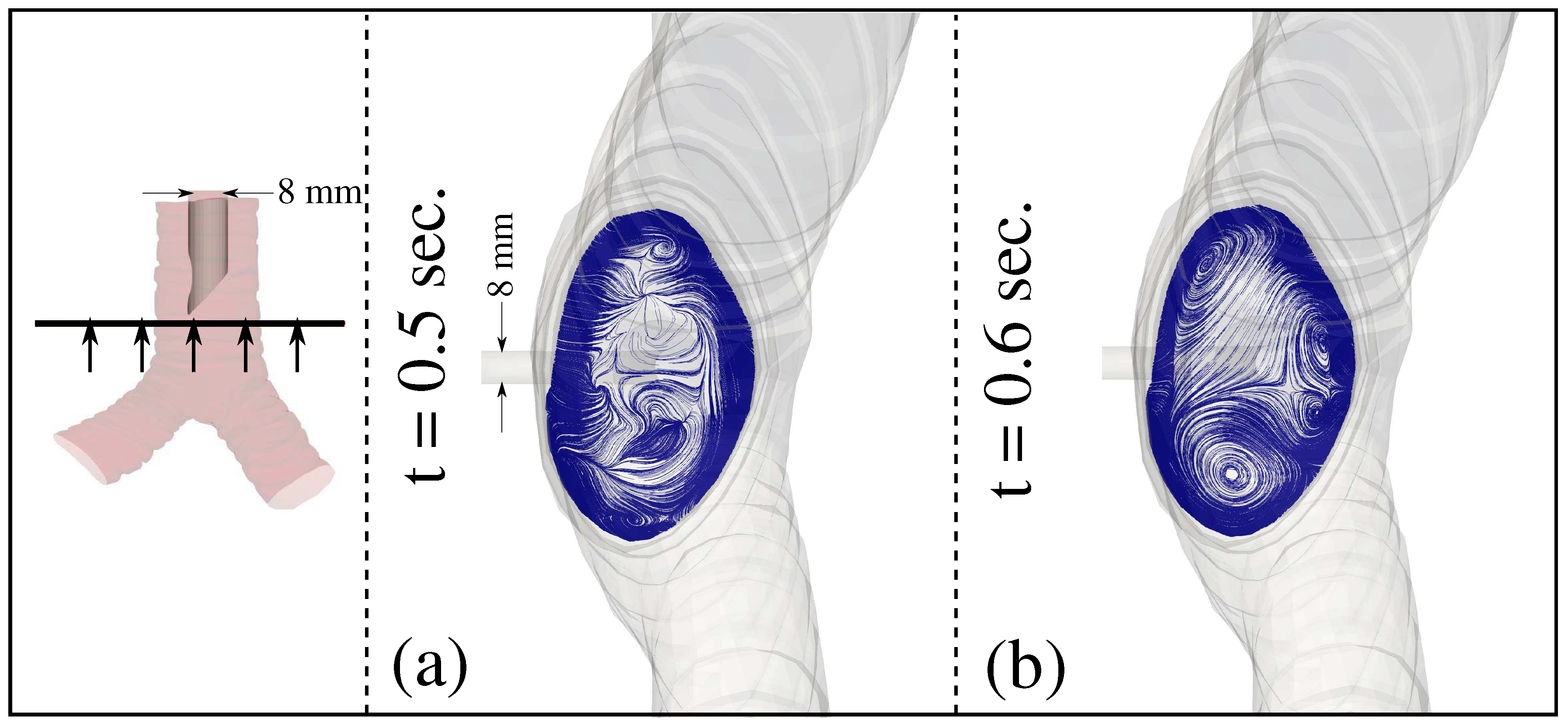
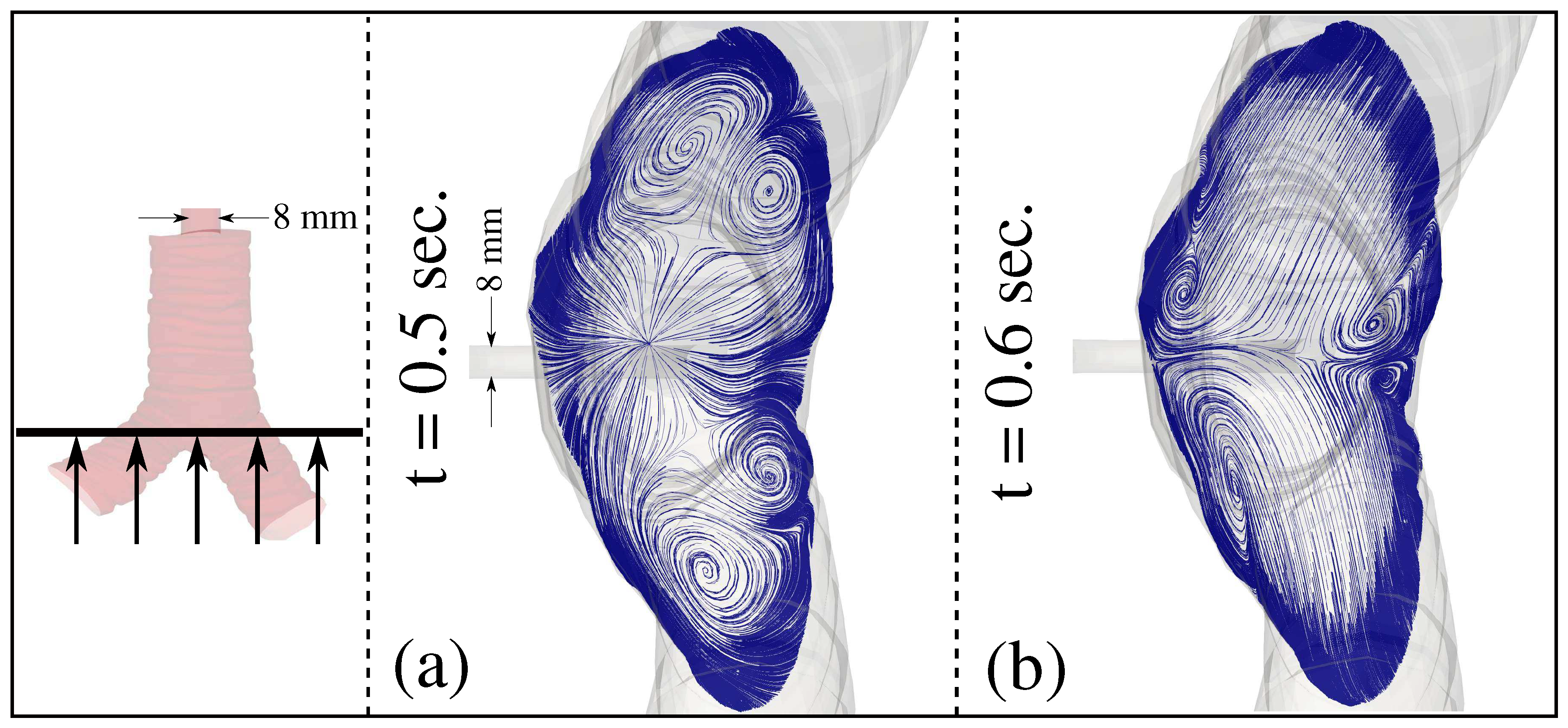
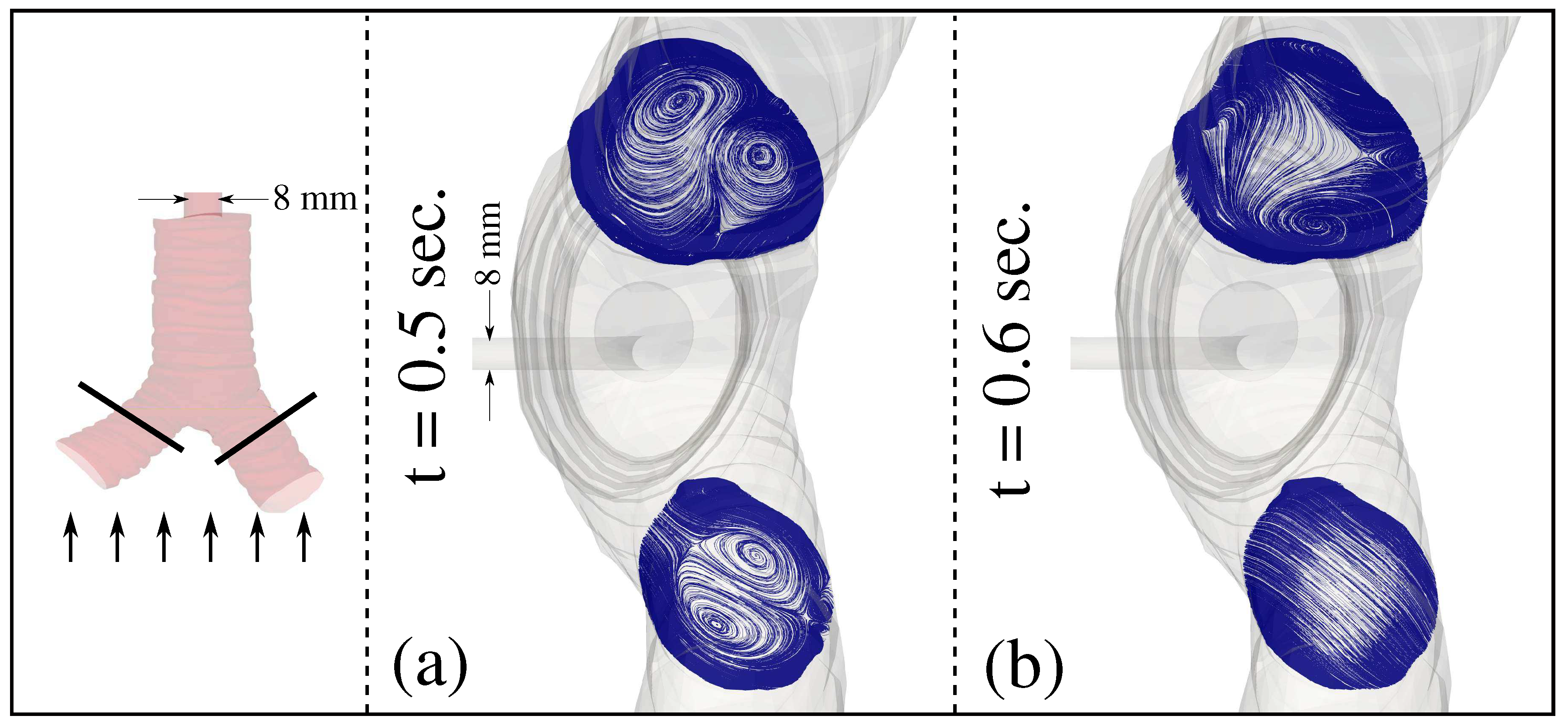
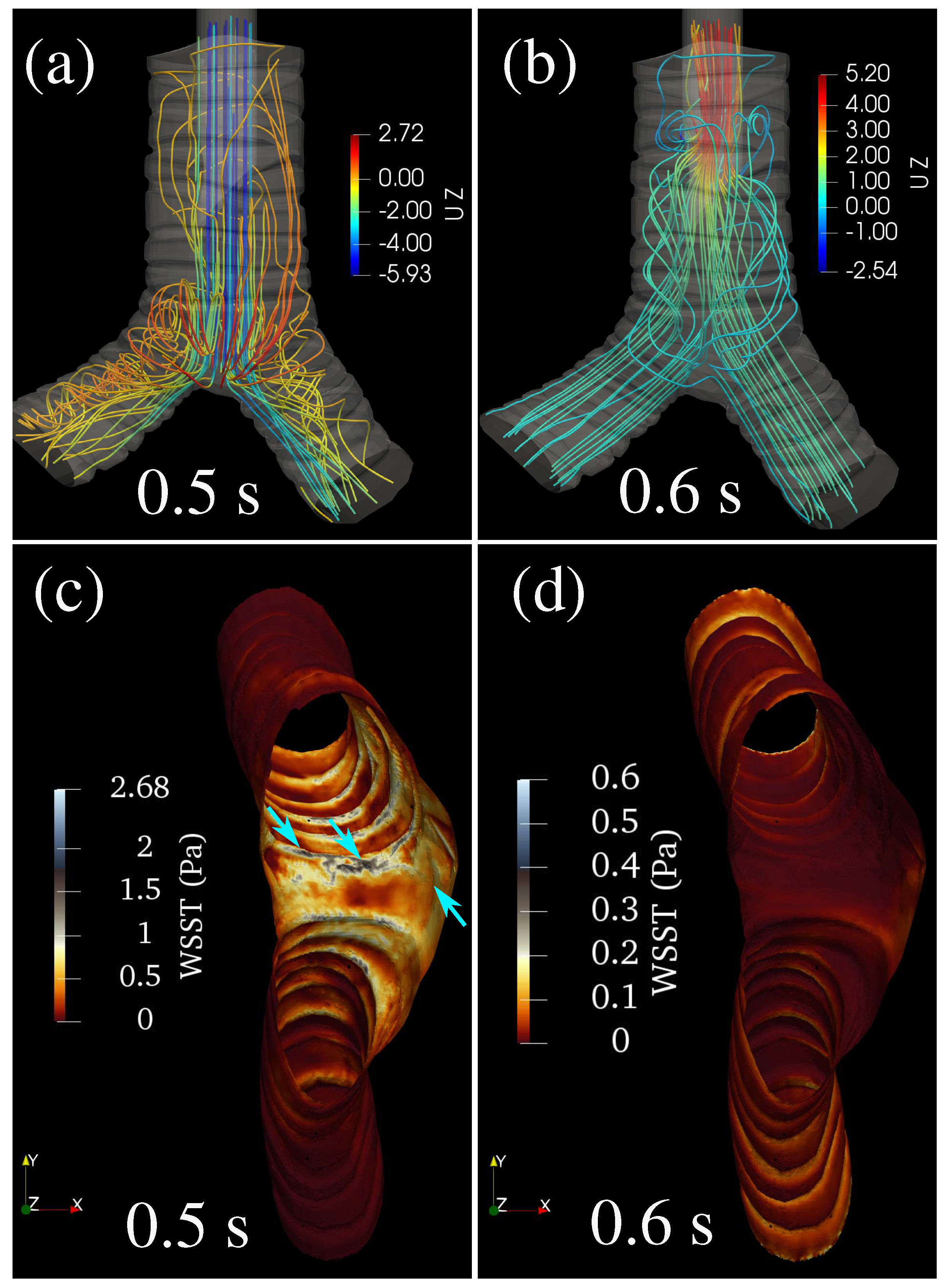
3. Results and Discussion
4. Conclusions and Perspectives
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| CT | Computerized Tomography |
| ET | Endotracheal Intubation |
| ETT | Endotracheal Tube |
| FVM | Finite Volume Method |
| GCI | Grid Convergence Index |
| MV | Mechanical Ventilation |
| VC | Volume Controlled |
| WSS | Wall Shear Stress |
References
- Benumof, J.L. Airway Management: Principles and Practice; Mosby: St. Louis, MO, USA, 1996. [Google Scholar]
- Farrow, S.; Farrow, C.; Soni, N. Size matters: Choosing the right tracheal tube. Anaesthesia 2012, 67, 815–819. [Google Scholar] [CrossRef]
- Calderon, L.G.; Moreira, M.M.; Barreto, G.; Tincani, A.J. Model of single-sized endotracheal tube for adults. Einstein 2019, 18, eAO4805. [Google Scholar] [CrossRef] [Green Version]
- Gandhi, A.; Sokhi, J.; Lockie, C.; Ward, P.A. Emergency Tracheal Intubation in Patients with COVID-19: Experience from a UK Centre. Anesthesiol. Res. Pract. 2020, 2020, 8816729. [Google Scholar] [CrossRef]
- Duggan, L.V.; Mastoras, G.; Bryson, G.L. Tracheal intubation in patients with COVID-19. CMAJ 2020, 192, E607. [Google Scholar] [CrossRef] [PubMed]
- Onayemi, A.; Pai, B.H.P. Endo tracheal tube exchange in a COVID positive patient. J. Clin. Anesth. 2020, 66, 109941. [Google Scholar] [CrossRef]
- Orser, B.A. Recommendations for Endotracheal Intubation of COVID-19 Patients. Anesth. Analg. 2020, 130, 1109–1110. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Technical Specifications of Medical Devices for the Case Management of COVID-19 in Healthcare Settings; Technical Report; World Health Organization: Washington, DC, USA, 2020. [Google Scholar]
- Piazza, C.; Filauro, M.; Dikkers, F.; Nouraei, S.; Sandu, K.; Sittel, C.; Amin, M.; Campos, G.; Eckel, H.; Peretti, G. Long-term intubation and high rate of tracheostomy in COVID-19 patients might determine an unprecedented increase of airway stenoses: A call to action from the European Laryngological Society. Eur. Arch. Otorhinolaryngol. 2021, 278, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Kou, G.; Li, X.; Wang, Y.; Lin, M.; Zeng, Y.; Yang, X.; Yang, Y.; Gan, Z. CFD Simulation of Airflow Dynamics During Cough Based on CT-Scanned Respiratory Airway Geometries. Symmetry 2018, 10, 595. [Google Scholar] [CrossRef] [Green Version]
- Krenkel, L.; Wagner, C.; Wolf, U.; Scholz, A.; Terekhov, M.; Rivoire, J.; Schreiber, W. Protective Artificial Lung Ventilation: Impact of an Endotracheal Tube on the Flow in a Generic Trachea. In New Results in Numerical and Experimental Fluid Mechanics VII; Springer: Berlin/Heidelberg, Germany, 2010; pp. 505–512. [Google Scholar] [CrossRef]
- Qi, S.; Li, Z.; Yue, Y.; Van Triest, H.; Kang, Y. Computational fluid dynamics simulation of airflow in the trachea and main bronchi for the subjects with left pulmonary artery sling. BioMed. Eng. OnLine 2014, 13, 85. [Google Scholar] [CrossRef] [Green Version]
- Wright, P.; Marini, J.; Bernard, G. In vitro versus comparison of endotracheal tube airflow resistance. Am. Rev. Respir. Dis. 1989, 140, 10–16. [Google Scholar] [CrossRef]
- Malvè, M.; Chandra, S.; López-Villalobos, J.L.; Finol, E.A.; Ginel, A.; Doblaré, M. CFD analysis of the human airways under impedance-based boundary conditions: Application to healthy, diseased and stented trachea. Comput. Methods Biomech. Biomed. Eng. 2013, 16, 198–216. [Google Scholar] [CrossRef] [PubMed]
- Van Rhein, T.; Alzahrany, M.; Banerjee, A.; Salzman, G. Fluid flow and particle transport in mechanically ventilated airways. Part I. Fluid flow structures. Med. Biol. Eng. Comput. 2016, 54, 1085–1096. [Google Scholar] [CrossRef] [PubMed]
- Lumb, A.B.; Burns, A.D.; Figueroa Rosette, J.A.; Gradzik, K.B.; Ingham, D.B.; Pourkashanian, M. Computational fluid dynamic modelling of the effect of ventilation mode and tracheal tube position on air flow in the large airways. Anaesthesia 2015, 70, 577–584. [Google Scholar] [CrossRef] [Green Version]
- Lzahrany, M.; Van Rhein, T.; Banerjee, A.; Salzman, G. Fluid flow and particle transport in mechanically ventilated airways. Part II: Particle transport. Med. Biol. Eng. Comput. 2016, 54, 1097–1109. [Google Scholar] [CrossRef]
- Zhu, L.; Shen, J.; Gong, X.; Liu, L.; Liu, J.; Xu, Z. Effects of Different Modes of Mechanical Ventilation on Aerodynamics of the Patient-Specific Airway: A Numerical Study. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 4961–4964. [Google Scholar] [CrossRef]
- Katz, I.; Milet, A.; Chalopin, M.; Farjot, G. Numerical analysis of mechanical ventilation using high concentration medical gas mixtures in newborns. Med. Gas Res. 2019, 9, 213–220. [Google Scholar] [CrossRef] [PubMed]
- Yousefi, M.; Safikhani, H.; Jabbari, E.; Yousefi, M.; Tahmsbi, V. Numerical modeling and Optimization of Respirational Emergency Drug Delivery Device using Computational Fluid Dynamics and Response Surface Method. Int. J. Eng. 2021, 34, 547–555. [Google Scholar] [CrossRef]
- Kingma, K.; Hofmeyr, R.; Zeng, I.; Coomarasamy, C.; Brainard, A. Comparison of four methods of endotracheal tube passage in simulated airways: There is room for improved techniques. Emerg. Med. Australas. 2017, 29, 650–657. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Forestner, J.E. Frank J. Murphy, M.D., C.M., 1900–1972: His life, career, and the Murphy eye. Anesthesiology 2010, 113, 1019–1025. [Google Scholar] [CrossRef] [Green Version]
- Tamakawa, S. Every endotracheal tube needs a Murphy eye! Can. J. Anaesth. 1999, 46, 998–999. [Google Scholar] [CrossRef] [Green Version]
- Krzanowski, T.J.; Mazur, W. A complication associated with the Murphy eye of an endotracheal tube. Anesth. Analg. 2005, 100, 1854–1855. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Moukalled, F.; Mangani, L.; Darwish, M. The Finite Volume Method in Computational Fluid Dynamics: An Advanced Introduction with OpenFOAM and Matlab, 1st ed.; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Jasak, H. OpenFOAM: Open source CFD in research and industry. Int. J. Nav. Archit. Ocean Eng. 2009, 1, 89–94. [Google Scholar] [CrossRef] [Green Version]
- Menter, F. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries, Inc.: La Canada, CA, USA, 2007. [Google Scholar]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J. Procedure for Estimation and Reporting of Uncertainty due to Discretization in CFD Applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dbouk, T.; Drikakis, D. Endotracheal Tubes Design: The Role of Tube Bending. Symmetry 2021, 13, 1503. https://doi.org/10.3390/sym13081503
Dbouk T, Drikakis D. Endotracheal Tubes Design: The Role of Tube Bending. Symmetry. 2021; 13(8):1503. https://doi.org/10.3390/sym13081503
Chicago/Turabian StyleDbouk, Talib, and Dimitris Drikakis. 2021. "Endotracheal Tubes Design: The Role of Tube Bending" Symmetry 13, no. 8: 1503. https://doi.org/10.3390/sym13081503
APA StyleDbouk, T., & Drikakis, D. (2021). Endotracheal Tubes Design: The Role of Tube Bending. Symmetry, 13(8), 1503. https://doi.org/10.3390/sym13081503






