Solutions of the Bullough–Dodd Model of Scalar Field through Jacobi-Type Equations

Abstract

A technique based on multiple auxiliary equations is used to investigate the traveling wave solutions of the Bullough–Dodd (BD) model of the scalar field. We place the model in a flat and homogeneous space, considering a symmetry reduction to a 2D-nonlinear equation. It is solved through this refined version of the auxiliary equation technique, and multiparametric solutions are found. The key idea is that the general elliptic equation, considered here as an auxiliary equation, degenerates under some special conditions into subequations involving fewer parameters. Using these subequations, we successfully construct, in a unitary way, a series of solutions for the BD equation, part of them not yet reported. The technique of multiple auxiliary equations could be employed to handle several other types of nonlinear equations, from QFT and from various other scientific areas.

1. Introduction

A model of a scalar field, $u\left(x^{\mu }\right)$, in Quantum Field Theory (QFT) can be described through a Lagrangian density of the form:

$$\mathcal{L}=\frac{1}{2}{\left({\partial }_{\mu }u\right)}^2-V\left(u\right).$$

(1)

Depending on the choice of the potential $V\left(u\right)$, the model can represent many types of physical situations. For example, the inflation phenomena in the early Universe is obtained when we choose a potential expressed through a tachyonic field. A tachyonic nonstandard Lagrangian of the DBI-type was proposed in [1]. It has the potential to be a multiplicative factor and a square root of derivatives as a “kinetic” term:

$$\mathcal{L}(u,{\partial }^{\mu }u)=-V\left(u\right)\sqrt{1+g_{\mu \nu }{\partial }^{\mu }u{\partial }^{\nu }u}.$$

(2)

This is a particularly attractive model of K-inflation, defined by the local action for a scalar field minimally coupled to Einstein gravity, useful, as we said, in describing the very early stage of the Universe.

In this paper, we investigate the model generated by the potential:

$$V\left(u\right)=p{e}^u-\frac{q}{2}{e}^{-2u}.$$

(3)

It is known as the Bullough–Dodd model [2], and its spectrum consists of a single massive particle. In the context of QFT, in the perturbative approach, the model has to be linearized in order to generate a quantum model. At the classical level, in the $2D$ space, it can be seen as a nonlinear integrable model, belonging to the class of affine Toda field theories and admitting a zero curvature representation with flat connections, defined in twisted affine Kac–Moody algebras [3]. This is an important feature that, at this classical level, ensures the existence of soliton-like solutions. Finding such solutions represents an important issue, as long as, under real circumstances, most of the physical phenomena are nonlinear ones. From this perspective, the Bullough–Dodd (BD) model became a toy model for testing various solving methods used in soliton theory. It can describe wave propagation through optical fibers [4], heat or fluid diffusion [5], or other phenomena from condensed matter. It is interesting to mention that our approach is in line with the similar ones that unify the theory of classical fields with that of dynamical systems. Along the same line, the Yang–Mills field can be transformed into a mechanical model [6], or the BRST approach can unify the gauge fields with the constrained dynamical systems [7].

Important progress has been achieved and many powerful and effective methods have been proposed for deriving explicit solutions of nonlinear equations: the inverse scattering [8], the Hirota bilinear transformation [9,10,11], the Jacobi elliptic function method [12,13], the generalized Kudryashov method [14,15], the dynamical system approach and the bifurcation method of the phase plane [16], the $(G^{\prime }/G)$-expansion method [17,18] and its extension to the functional expansion method [19,20], the Lie symmetry method [21,22,23,24,25] and the generalized conditional symmetry approach [26], various extended tanh methods [27,28,29], as well as other tools of investigation for the nonlinear dynamical models [30,31,32,33,34].

Many among the above-mentioned methods allow constructing traveling wave solutions of the model. The focus of this paper is on how such traveling waves can be obtained using a very general approach, based on the auxiliary equation technique. It consists of looking for solutions of a complicated nonlinear partial differential equation (NPDE) in terms of the known solutions of an “auxiliary equation”. The NPDE solutions will be combinations or series expansions of the auxiliary equation solutions, and they will strongly depend on the choice of this equation. Papers published so far, such as [17,18,19,20] or [35] and the references therein, tend to use a predefined and fixed auxiliary equation and do not investigate how NPDE solutions would depend on the choice of the auxiliary equation. This is actually exactly the main purpose of this study. To this end, we use the technique of multiple auxiliary equations [36], a refined version of the auxiliary equation technique in which any of the subequations belonging to a given class can be seen as an auxiliary equation. To be very specific, we consider as an auxiliary equations reductions arising from the generalized Jacobi elliptic equation, and we investigate the BD equation generated by (1) with the potential (3). It has the form:

$$u_{xt}+p{e}^u+q{e}^{-2u}=0.$$

(4)

Equation (4) contains in fact many nonlinear models. For example, for $q=0$, we obtain the Liouville equation, an important NPDE, which appears in many physical problems from QFT, but also from nonlinear optics and hydrodynamics. On the other hand, Equation (4) can be included, in its turn, in a more general equation, the generalized Tzitzeica–Dodd–Bullough–Mikhailov (gTDBM) equation [37,38].

Due to the nonpolynomial form of (4), special techniques have to be applied in order to obtain its solutions. Such solutions, both for BD and Liouville equations, were outlined in [39] using the tanh method combined with the Painlevé transformation. Soliton and compacton-like solutions were generated in [40], with the exponential function method, or in [41], by the generalized Kudryashov method and by an improved F-expansion method. Other traveling wave solutions were derived in [42] through the $\left(\frac{G^{\prime }}{G}\right)$-expansion method, while in [43], an approach close to the first integral method was presented.

Despite the numerous studies on the BD equation and the various techniques used to solve it, it seems that the model contains a much richer phenomenology, and as we will see, our investigation allows generating new classes of solutions, depending on a larger number of parameters. The key issue of our approach, based on this multiple auxiliary equation technique, is to take a full advantage of the algebraic relations that can be established among the parameters involved in the procedure. In our case, when the BD equation is studied using reductions of the generalized Jacobi equation as an auxiliary equations, these relations contain: four parameters appearing in (4) transformed in the ODE by passing to the wave variables, five parameters appearing in the general elliptic equation, and the parameters introduced by the auxiliary equation method. Various solutions of the algebraic system generated among all these parameters give us not only new, more complex, BD solutions, but also their dependence on the specific forms of auxiliary equations. As we mentioned, these equations represent in fact reductions of the general elliptic equation with five parameters. This approach seems to be indeed the most suitable, not only for solving the BD equation, but for investigating the majority of NPDEs of interest. In the BD case, as we will check, the technique provides all solutions reported already and, moreover, some new families of wave solutions, depending on a larger number of parameters. For various chosen values of the parameters, we generate various kinds of traveling wave solutions, starting from singular solutions under blow-up or broken forms, periodic solutions, kinks, or unbounded wave solutions.

The present paper is organized as follows: In Section 2, we explain some reductions of the general elliptic equation into several subequations that could occur under special conditions among their respective parameters. In Section 3, we outline the main steps specific to the use of the auxiliary equation technique. In Section 4, we apply this method to the nonlinear dynamical model (4), and therefore, several classes of new and more general wave solutions are highlighted. Section 5 is devoted to the discussion of our main results. Finally, some essential facts are pointed out as concluding remarks.

2. Reductions of the General Elliptic Equation

Let us take into consideration the general elliptic equation with five parameters $h_i,$$i=\overline{0,4}$:

$${\left({\varphi }^{\prime }\right)}^2={\left(\frac{d\varphi \left(\xi \right)}{d\xi }\right)}^2=h_0+h_1\varphi \left(\xi \right)+h_2{\varphi }^2\left(\xi \right)+h_3{\varphi }^3\left(\xi \right)+h_4{\varphi }^4\left(\xi \right).$$

(5)

In special conditions, Equation (5) can be rewritten in terms of fewer parameters. We point out here a few of the possible such reductions. They were presented in more detail in [44].

If $h_i\ne 0,$$i=\overline{0,4}$, there may exist $H_j,j=0,1,2$ such that (5) can be reduced from a five- to a three-parameter equation:

$$\begin{array}{cc}\hfill {\left({\varphi }^{\prime }\right)}^2& =h_0+h_1\varphi \left(\xi \right)+h_2{\varphi }^2\left(\xi \right)+h_3{\varphi }^3\left(\xi \right)+h_4{\varphi }^4\left(\xi \right)\hfill \\ \hfill & ={(H_0+H_1\varphi \left(\xi \right)+H_2{\varphi }^2\left(\xi \right))}^2.\hfill \end{array}$$

(6)

Equation (6) requires for its validity the following relationships:

$$h_0={\left(H_0\right)}^2,h_1=2H_0{H}_1,h_2=2H_0{H}_2+{\left(H_1\right)}^2,h_3=2H_1{H}_2,h_4={\left(H_2\right)}^2.$$

(7)

Practically, in this case, the general elliptic equation is reduced to the generalized Riccati equation [45].

When $h_0=h_1=0$ and $h_j\ne 0,$$j=2,$$3,$ 4, the general elliptic equation is transformed into an equation with three parameters:

$${\left({\varphi }^{\prime }\right)}^2=h_2{\varphi }^2\left(\xi \right)+h_3{\varphi }^3\left(\xi \right)+h_4{\varphi }^4\left(\xi \right).$$

(8)

This equation can be solved in special cases, and it is sometimes used as an auxiliary equation [46]. We do this in Section 4 below, considering the case when the parameters $h_2,h_3,$ and $h_4$ are expressed in terms of other parameters, $r,s,$and $\rho ,$ as:

$$h_2=4,h_3=-\frac{4(2s\pm \rho )}{r},h_4=\frac{{(2s\pm \rho )}^2}{r^2}.$$

(9)

In this case, (8) has the interesting solution [47]:

$$\varphi \left(\xi \right)=\frac{r{(sech\xi )}^2}{s{(sech\xi )}^2+\rho (tanh\xi \pm 1)}.$$

(10)

When $h_1=h_3=0$ and $h_n\ne 0,$$n=0,$$2,$ 4, the general elliptic equation is reduced to the Jacobi elliptic equation, again with three parameters:

$${\left({\varphi }^{\prime }\right)}^2=h_0+h_2{\varphi }^2\left(\xi \right)+h_4{\varphi }^4\left(\xi \right).$$

(11)

For $h_0=R^2,$$h_2=2R,$$h_4=1$, Equation (11) becomes the Riccati equation:

$${\left({\varphi }^{\prime }\right)}^2={(R+{\varphi }^2\left(\xi \right))}^2.$$

(12)

Therefore, the solutions of Equation (12) could be reduced from the ones of Equation (11) in the specific case where the modulus m of the Jacobi elliptic functions would be chosen as one and zero.

When $h_2=h_4=0$ and $h_{\alpha }\ne 0,$$\alpha =0,$$1,$$3,$ the general elliptic equation becomes:

$${\left({\varphi }^{\prime }\right)}^2=h_0+h_1\varphi \left(\xi \right)+h_3{\varphi }^3\left(\xi \right).$$

(13)

This is another example of the reduction of (5) to a solvable equation that can be considered as an auxiliary equation, as we explain below.

3. Basics of the Auxiliary Equation Method

In this section, we describe the auxiliary equation method for solving NPDEs. It consists of discovering if the studied NPDE accepts various types of solutions accepted by the considered auxiliary equation. In our case, it is the general elliptic Equation (5). The method allows finding, in a unified way, a series of new and more general solitons, triangular solutions, and doubly periodic solutions of NPDEs. The main steps of this method are as follows:

Step 1: For a given NPDE:

$$E(u,u_t,u_x,u_{tt},u_{xx},u_{tx},...)=0,$$

(14)

the wave transformation is applied:

$$\xi =kx+\omega t,u(t,x)=U\left(\xi \right),$$

(15)

where $k,$w are arbitrary constants. The traveling wave variable (15) allows us to reduce Equation (14) to an ODE for $U\left(\xi \right)$ and its derivatives $U^{\prime },U^{\prime \prime },...$:

$$F(U,U^{\prime },U^{\prime \prime },...)=0;$$

(16)

Step 2: Let us suppose that the solution of Equation (16) could be expressed in the form:

$$U\left(\xi \right)={\displaystyle \sum _{j=0}^N}{a}_j{\varphi }^j\left(\xi \right),$$

(17)

where $a_j$ are constants to be determined later and $\varphi \left(\xi \right)$ is the solution of the chosen auxiliary equation. The integer N is fixed by balancing in Equation (16) its term of the highest order in derivatives with its most nonlinear term. This means choosing N so that the two mentioned terms have the same polynomial degrees;

Step 3: Let us substitute the generic solution (17) along with the auxiliary Equation (5) into (16), and let us equate the coefficients of all the powers of $\varphi \left(\xi \right)$ to zero. This leads us towards a set of algebraic equations for the unknowns $k,$$\omega ,$$a_j,$ $j=\overline{1,N},$$h_i$, $i=\overline{0,4}.$ By solving the appropriate algebraic system by making use of the Maple program, the links that exist between the previous parameters and the ones that are related to the dynamical model (14) can be derived;

Step 4: By taking into consideration the results that we obtained through the above steps, a series of traveling wave solutions of Equation (16) that depend on the solutions of the generalized auxiliary Equation (5) can be derived. The latter possesses various types of traveling wave solutions that depend on the special conditions that can be imposed for the parameters $h_i$, $i=\overline{0,4}.$ They were explicitly enumerated in [44].

4. New and More General Solutions of the BD Equation

In this section, we illustrate the efficiency of the algorithmic method mentioned in Section 3 as concerns the BD class of equations. We derive a series of explicit traveling wave solutions of (4) that have not yet been spoken about in the specialized literature. Due to the transformation $u=lnv,$ the governing Equation (4) takes the form:

$$v_{xt}v-v_x{v}_t+p{v}^3+q=0.$$

(18)

By taking into consideration the wave transformation $v(x,t)$$=V\left(\xi \right)$, $\xi$ $=kx+\omega t$, Equation (18) can be written as:

$$k\omega [V^{\prime \prime }V-{\left(V^{\prime }\right)}^2]+p{V}^3+q=0.$$

(19)

We would like to find solutions of (19) using the technique of the auxiliary equation presented in the previous section. In fact, we use the technique of the multiple auxiliary equations, considering that the solutions of (19) can be expressed as expansions of the form (17), in terms of any solution of the general elliptic Equation (5), or of all its reductions considered in Section 2.

By asking, as mentioned in Step 2 before, that the term from (19) with the higher derivative, $V^{\prime \prime }V$, should have the same polynomial degrees as the most nonlinear term, $V^3$, we obtain that, in our case, the sum from (17) should stop at $N=2.$ Therefore, we have to look for a solution of (19) in the form:

$$V\left(\xi \right)=a+b\varphi \left(\xi \right)+c{\varphi }^2\left(\xi \right).$$

(20)

Substituting (20) along with Equation (5) into (19) yields a polynomial equation in ${\varphi }^{\alpha }$$\alpha =\overline{0,6}$. The fulfillment of this equation imposes that all coefficients vanish for the various powers of $\varphi \left(\xi \right)$. This requirement leads to the following set of algebraic equations in the unknown arbitrary constants $a,$$b,$$c,$$h_i$, $i=\overline{0,4},$$p,$$q,$k, and $\omega$:

$$\begin{array}{c}{c}^2(2k\omega h_4+p)=0,\\ 3pb{c}^2+k\omega c(4b{h}_4+c{h}_3)=0,\\ 3cp(ca+b^2)+k\omega \left[\frac{5bc}{2}{h}_3+(6ca+b^2)h_4\right]=0,\\ pb(6ac+b^2)+k\omega \left[-c^2{h}_1+bc{h}_2+\left(5ac+\frac{b^2}{2}\right)h_3+2ab{h}_4\right]=0,\\ 3pa(ac+b^2)+k\omega \left[-2c^2{h}_0-\frac{cb}{2}{h}_1+4ac{h}_2+\frac{3ab}{2}{h}_3+2ab{h}_4\right]=0,\\ pb{a}^2+k\omega \left[-2cb{h}_0+\left(3ac-\frac{b^2}{2}\right)h_1+ab{h}_2\right]=0,\\ q+p{a}^3+k\omega \left[(2ac-b^2)h_0+\frac{ab}{2}{h}_1\right]=0.\end{array}$$

(21)

The Maple program was used in order to solve the previously mentioned system, providing the following two solutions:

$$\begin{array}{c}{h}_0=\frac{h_2(8a{c}^3-b^2{c}^2)+h_4(b^4-6ac{b}^2-12a^2{c}^2)}{4c^4},\\ h_1=\frac{b(c^2{h}_2-b^2{h}_4)}{c^3},h_3=\frac{2b{h}_4}{c},p=-\frac{2k\omega h_4}{c},\\ q=\frac{k\omega [h_2(8a{b}^2{c}^3-c^2{b}^4-16a^2{c}^4)+h_4(b^6+32a^3{c}^3-6ac{b}^4)]}{4c^4},\\ \forall h_2,\forall h_4,\forall a,\forall b,\forall c,\forall k,\forall \omega .\end{array}$$

(22)

and:

$$\begin{array}{c}c=h_4=0,h_1=\frac{2a(3ap+k\omega h_2)}{k\omega b},h_3=-\frac{2pb}{k\omega },\\ q=k\omega (b^2{h}_0-a^2{h}_2)-4p{a}^3,\forall h_0,\forall h_2,\forall a,\forall b,\forall k,\forall \omega ,\forall p.\end{array}$$

(23)

4.1. Classes of Solutions Related to (22)

In this part of our work, several new solutions of the master Equation (18) are pointed out through the choice of several cases that are related to some special conditions for parameters $h_i$, $i=\overline{0,4}$ which appear in the elliptic auxiliary Equation (5).

$Case$I: Let us take into consideration the case when the main Equation (5) reduces to (8). We ask for the condition $h_2=4$ from (9). This means that we have to impose:

$$h_0=h_1=0;h_2=4.$$

(24)

Equating the parameters $h_{i,}$$i=\overline{0,1}$ from Equations (22) and (24), we come to the relations:

$$b^2=6ac,h_3=\frac{4b}{3a},h_4=\frac{2c}{3a}.$$

(25)

From (25), we observe that:

$$h_3=4\sqrt{h_4}.$$

(26)

If we also consider the choices from (9) for $h_i$, $i=3,$ 4, we can write down, in an explicit form, the solution (20) of the Equation (19). Coming back to the initial set of variables, {$x,t$}, we obtain:

$$v(x,t)=-b\left\{\frac{r}{3(2s\pm \rho )}-\varphi (x,t)+\frac{2s\pm \rho }{2r}\varphi {(x,t)}^2\right\}.$$

(27)

Here, $(2s\pm \rho )r<0$ and $\varphi \left(\xi \right)$ has the form (10), that is:

$$\varphi (x,t)=\frac{r{\left[sech(kx+\omega t)\right]}^2}{s{\left[sech(kx+\omega t)\right]}^2+\rho \left[tanh(kx+\omega t)\pm 1\right]}.$$

(28)

Practically, we generated a new six-parameter family of hyperbolic solutions for the master Equation (18). It is also worth pointing out that the hyperbolic solutions (27) and (28) correspond to the following relationship between p and q from (18), imposed by (22):

$$p={\left[\frac{3(2s\pm \rho )}{br}\right]}^{3}q.$$

(29)

The graphical representations of the solution (27) and (28) are shown in Figure 1 for the parametric relationships $b=-2s=6k=12,$ $\omega -20\rho =-34r=-10.$

$Case$$II$: Another type of hyperbolic solutions, also related to (29), could be generated by maintaining the condition (24), but considering for $h_3$ and $h_4$ the choices:

$$h_3=\frac{4(\pm \rho -2s)}{r},h_4=\frac{{(\pm \rho -2s)}^2}{r^2},$$

(30)

where $(\pm \rho -2s)r$> 0. For these choices, it was mentioned in [47] that (8) accepts another interesting solution of the form:

$$\varphi (x,t)=\frac{r{\left[csch(kx+\omega t)\right]}^2}{s{\left[csch(kx+\omega t)\right]}^2+\rho \left[coth(kx+\omega t)\pm 1\right]}.$$

(31)

The class of solutions for (18) associated with these conditions is a six-parameter one, with the form:

$$v(x,t)=b\left\{\frac{r}{3(\pm \rho -2s)}-\varphi (x,t)+\frac{\pm \rho -2s}{2r}\varphi {\left(\xi \right)}^2\right\}.$$

(32)

$Case$$III$: Starting from the same special constraint (29), we can also derive two types of periodic solutions for the governing Equation (18). We consider now the following conditions to be satisfied by $h_{i,}$$i=\overline{0,4:}$

$$h_0=h_1=0,h_2=-4,h_3=\frac{4(2s+\sigma )}{r},h_4=\frac{{\rho }^2-4s^2-4s\sigma }{r^2}.$$

(33)

Practically, we replaced the five parameters $h_{i,}$$i=\overline{0,4}$ through a set of four parameters: $r,s,\rho$, and $\sigma .$ In the case when $(2s\pm \rho )r$> 0, for similar reasons as in $CaseII$, we can write down the associated solutions as follows:

$$v(x,t)=b\left\{-\frac{r}{3(2s\pm \rho )}+\varphi (x,t)-\frac{2s\pm \rho }{2r}\varphi {\left(\xi \right)}^2\right\},\sigma =\pm \rho ,$$

(34)

We are again in the case when (5) reduces to (8), and it accepts as solutions:

$$\varphi (x,t)=\frac{r{\left[sec(kx+\omega t)\right]}^2}{s{\left[sec(kx+\omega t)\right]}^2+\rho \left[tan(kx+\omega t)\pm 1\right]}$$

(35)

or:

$$\varphi (x,t)=\frac{r{\left[csc(kx+\omega t)\right]}^2}{s{\left[csc(kx+\omega t)\right]}^2+\rho \left[cot(kx+\omega t)\pm 1\right]}.$$

(36)

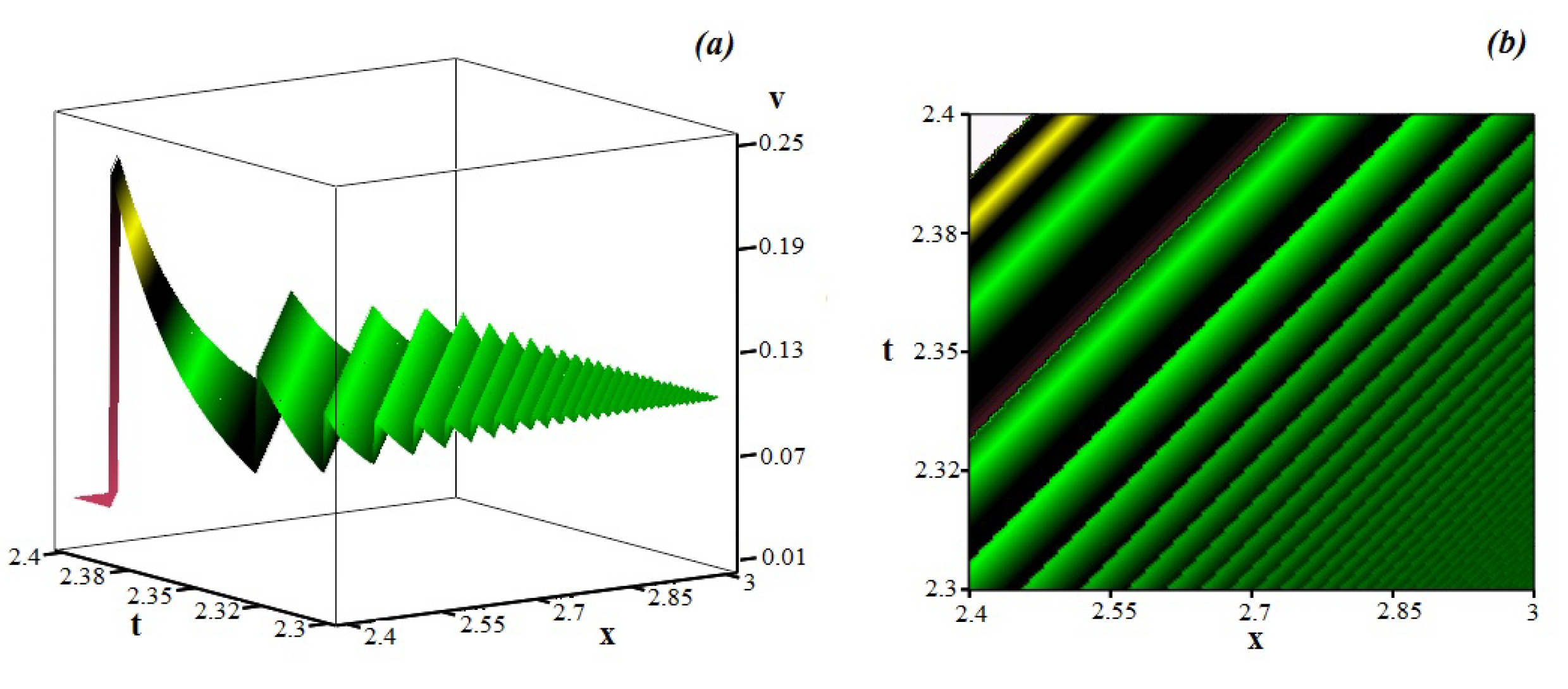
The solution (34) depicts a new class of six-parameter solutions of (18). For the particular choice of parameters $\omega =-2k=-8b=-16r=-16\rho =-8s/3=-4$, Figure 2 presents the surface configuration and the contour plot of the doubly periodic wave solution (34) and (35).

$Case$$IV$: Let us assume now that the parameters $h_i$, $i=\overline{0,4}$ are:

$$h_1=h_3=0,h_0=1,h_2=2-m^2,h_4=1-m^2,$$

(37)

where $0\le m\le 1$ is the modulus of the Jacobi elliptic function solution $\varphi$ of the NODE (5).

By imposing the compatibility between Equations (22) and (37), we obtain the following relationships among their parameters:

$$\begin{array}{c}c=2-m^2\pm \sqrt{1-m^2+m^4}a,p=-\frac{2k\omega (1-m^2)}{(2-m^2\pm \sqrt{1-m^2+m^4})a}.\\ q=\frac{4k\omega a^2[2+(m^2-2)(m^2-\sqrt{1-m^2+m^4})]}{m^2-2-\sqrt{1-m^2+m^4}},\forall k,\forall \omega ,\forall a,0\le m<1.\end{array}$$

(38)

Under the conditions (37), the master Equation (18) admits a Jacobian elliptic solution of the form:

$$v(x,t)=a\left\{1+(2-m^2\pm \sqrt{1-m^2+m^4}){\left[\frac{sn(kx+\omega t)}{cn(kx+\omega t)}\right]}^2\right\},\forall a,\forall m,0\le m<1.$$

(39)

In the limiting case of $m\to 0$, the solutions (39) become periodic ones:

$$v_1(x,t)=a\left\{1+3{\left[tan(kx+\omega t)\right]}^2\right\},v_2(x,t)=a\left\{1+{\left[tan(kx+\omega t)\right]}^2\right\}.$$

(40)

Remark 1.

The special values for $\{h_0,$$h_2,$$h_4\}$ from (37) represent one among the fifteen other possible expressions considered in [48]. The Jacobi elliptic functions associated with these values degenerate either into some hyperbolic functions or into some trigonometric functions, while $m\to 1$ and, respectively, $m\to 0$[44].

$Case$V: Let us consider now the case (6), when the general elliptic equation with five parameters is reduced to an equation with three parameters. The initial parameters $h_i,$$i=\overline{0,4}$ take the values mentioned in (7), but with the supplementary requirement $h_2=0,$ $h_i\ne 0,$$i=0,$$1,$$3,$$4.$ This means that we have:

$$h_0={\left(H_0\right)}^2,h_1=2H_0{H}_1,h_2=2H_0{H}_2+{\left(H_1\right)}^2=0,h_3=2H_1{H}_2,h_4={\left(H_2\right)}^2.$$

(41)

The compatibility between Equations (22) and (41) could be ensured if the following system is verified:

$$\begin{array}{c}2H_0{H}_1{c}^3+b^3{\left(H_2\right)}^2=0,\\ 4c^4{\left(H_0\right)}^2-{\left(H_2\right)}^2(b^4-12a^2{c}^2-6ac{b}^2)=0,\\ b{H}_2-c{H}_1=0,\\ {\left(H_1\right)}^2+2H_0{H}_2=0.\end{array}$$

(42)

By solving the previous system, we obtain the relations:

$$a=-\frac{c{\left(H_1\right)}^2}{2{\left(H_2\right)}^2},b=\frac{c{H}_1}{H_2},\forall c,\forall H_1,\forall H_2.$$

(43)

By substituting (43) into the general expressions for p and q from (22), we find the special parameter values:

$$p=-\frac{2k\omega {\left(H_2\right)}^2}{c},q=0.$$

(44)

Remark 2.

Should we look for $p=-1$ in (44) or, equivalently, should we choose $\omega =\frac{c}{2k{\left(H_2\right)}^2},$ we would turn towards a particular form of the master Equation (18), which is the so-called Liouville equation. Because under the conditions from (41), the general elliptic Equation (5) admits twelve solutions [44], we are able to provide the expression of a four-parameter family of solutions for the Liouville equation. It admits the generic form:

$$v(x,t)=c\left\{\frac{{\left(H_1\right)}^2}{2{\left(H_2\right)}^2}+\frac{H_1}{H_2}\varphi \left(kx+\frac{c}{2k{\left(H_2\right)}^2}t\right)+{\left[\varphi \left(kx+\frac{c}{2k{\left(H_2\right)}^2}t\right)\right]}^2\right\},\forall c,\forall H_1,\forall H_2,$$

(45)

where $\varphi \left(\xi \right)$ and $\xi =kx+\frac{c}{2k{\left(H_2\right)}^2}t$ is one of the twelve soliton solutions ${\varphi }_l(l=1,$$2,$$...12)$ of the general elliptic Equation (5).

Let us mention only a few among the possible expressions of $\varphi \left(\xi \right):$

$$\begin{array}{c}\varphi \left(\xi \right)=\frac{1}{2H_2}\left[\mp \sqrt{-2H_0{H}_2}+\frac{\sqrt{-6H_0{H}_2}(\sqrt{A^2+B^2}-Acosh\left(\sqrt{-6H_0{H}_2}\xi )\right)}{Asinh\left(\sqrt{-6H_0{H}_2}\xi \right)+B}\right],\\ \varphi \left(\xi \right)=\frac{2H_{0}cosh\left(\frac{\sqrt{-6H_0{H}_2}}{2}\xi \right)}{\sqrt{-6H_0{H}_2}sinh\left(\frac{\sqrt{-6H_0{H}_2}}{2}\xi \right)\mp \sqrt{-2H_0{H}_2}cosh\left(\frac{\sqrt{-6H_0{H}_2}}{2}\xi \right)},\\ \varphi \left(\xi \right)=-\frac{1}{4H_2}\left\{\pm 2\sqrt{-2H_0{H}_2}+\sqrt{-6H_0{H}_2}\left[tanh\left(\frac{\sqrt{-6H_0{H}_2}}{4}\xi \right)+coth\left(\frac{\sqrt{-6H_0{H}_2}}{4}\xi \right)\right]\right\},\end{array}$$

(46)

where $H_0{H}_2<0$ and $A,$B are real arbitrary constants with $B^2-A^2>0.$

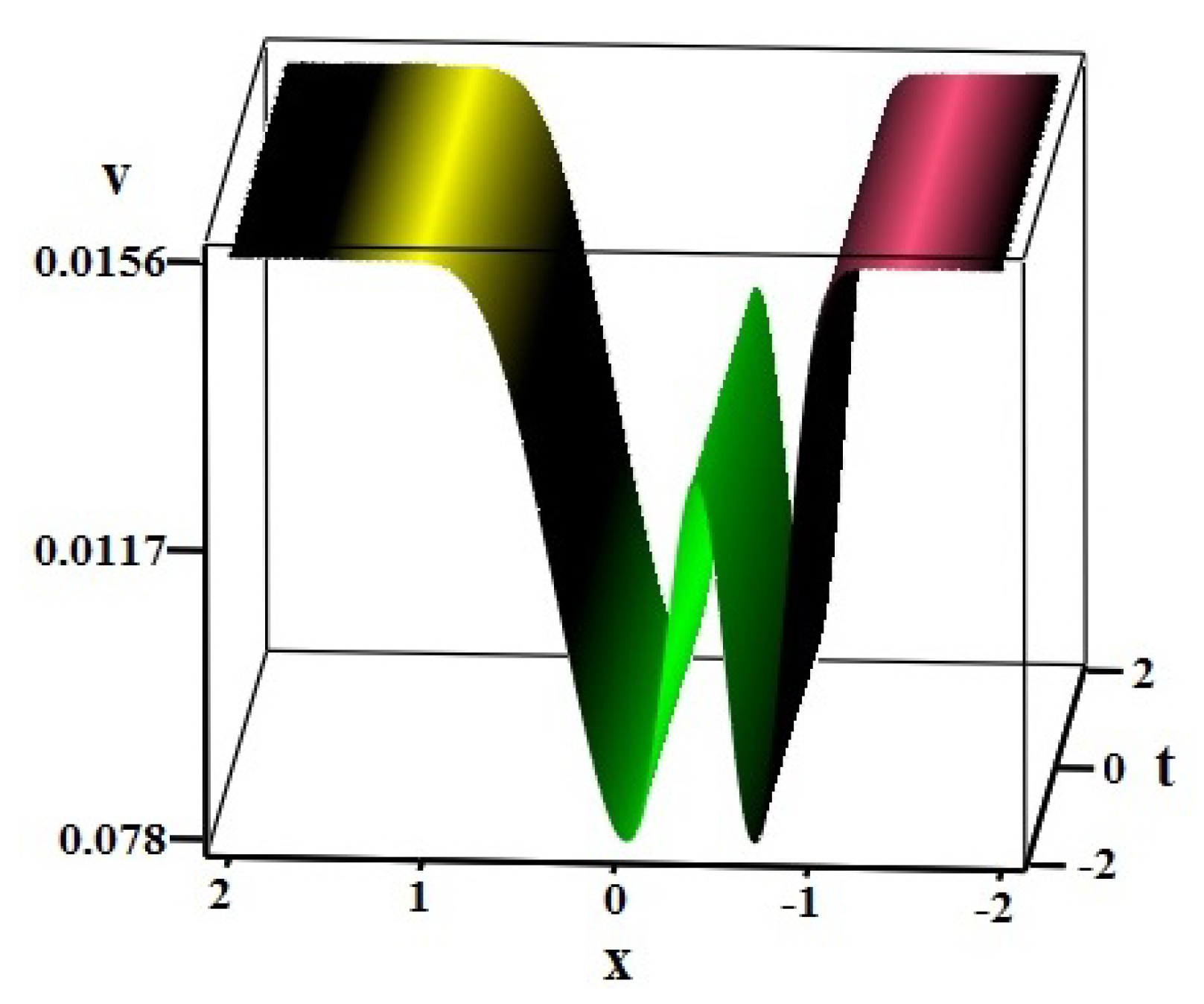
The numerical evolution of the localized W-shaped solitary wave solution (45) associated with the second expression of $\varphi$ from (46) is depicted in Figure 3.

4.2. Classes of Solutions Related to (23)

By choosing some other appropriate values for the parameters $h_i,$ $i=\overline{0,4}$ appearing in the general elliptic Equation (5), we can derive some new classes of traveling wave solutions for the studied model (18).

$Case$$VI$: Let us assume that the parameters $\alpha$ and $\beta$ exist so that the parameters $h_i,$$i=\overline{0,4}$ from (23) appear in the form:

$$h_0=h_1=0,h_2=1,h_3=-\frac{2\beta }{\alpha },h_4=0.$$

(47)

The compatibility requirement between Equations (23) and (47) imposes the fulfillment of the following constraint conditions:

$$b=-\frac{3\beta a}{\alpha },\omega =-\frac{3ap}{k},q=-p{a}^3,\forall p,\forall a,\forall k,\forall \alpha ,\forall \beta .$$

(48)

Taking into consideration the known solution of the auxiliary ODE (5) under the conditions (47), we can generate for the master Equation (18) with $q=-p{a}^3$ a four-parameter family of soliton solutions:

$$v(x,t)=a\left[\frac{1-2sech\left(kx-\frac{3ap}{k}t\right)}{1+sech(kx-\frac{3ap}{k}t)}\right].$$

(49)

$Case$$VII$: Let us use, instead of (47), some quite similar values of the parameters, namely:

$$h_0=h_1=0,h_2=-1,h_3=\frac{2\beta }{\alpha },h_4=0.$$

(50)

We could point out other four-parameter families of solutions, periodic this time:

$$v(x,t)=a\left[\frac{1-2sec\left(kx+\frac{3ap}{k}t\right)}{1+sec(kx+\frac{3ap}{k}t)}\right],v(x,t)=a\left[\frac{1-2csc\left(kx+\frac{3ap}{k}t\right)}{1+csc(kx+\frac{3ap}{k}t)}\right].$$

(51)

$Case$$VIII$: Let us look further for some parameters $\alpha ,$$\beta ,$$\gamma ,$$\rho$ so that the following specific conditions could be fulfilled:

$$h_0=h_1=0,h_2=4,h_3=-\frac{4(2\beta +\rho )}{\alpha },h_4=\frac{{\gamma }^2+4{\beta }^2+4\beta \rho }{{\alpha }^2}.$$

(52)

Invoking the compatibility condition between (23) and Equation (52), we can state that the nonlinear model (18) with $p=-\frac{4k\omega }{3\alpha }$ and $q=\frac{4k\omega a^2}{3}$ (or equivalently with $q=-p{\alpha }^3$) also admits another type of hyperbolic solutions, depending now on six parameters:

$$\begin{array}{c}v(x,t)=a\left[1-\frac{3({\gamma }^2-4{\beta }^2)}{8\beta }\frac{{\left[sech\left(kx+\omega t\right)\right]}^2}{\beta {\left[sech\left(kx+\omega t\right)\right]}^2+\gamma tanh(kx+\omega t)-\frac{{\gamma }^2+4{\beta }^2}{4\beta }}\right],\\ \forall a,\forall k,\forall \omega ,\forall \alpha ,\forall \beta ,\forall \gamma .\end{array}$$

(53)

$Case$$IX$: With a slight change into (52), we consider that:

$$h_0=h_1=0,h_2=4,h_3=-\frac{4(\rho -2\beta )}{\alpha },h_4=\frac{{\gamma }^2+4{\beta }^2-4\beta \rho }{{\alpha }^2}.$$

(54)

This choice could allow the transformation of the six-parameter family of solutions (53) into the following five-parameter one:

$$\begin{array}{c}v(x,t)=a\left[1-\frac{3({\gamma }^2-4{\beta }^2)}{8\beta }\frac{{\left[csch\left(kx+\omega t\right)\right]}^2}{\beta {\left[csch\left(kx+\omega t\right)\right]}^2+\gamma tanh(kx+\omega t)+\frac{{\gamma }^2+4{\beta }^2}{4\beta }}\right]\\ \forall a,\forall k,\forall \omega ,\forall \beta ,\forall \gamma .\end{array}$$

(55)

$Case$X: Should we operate a small modification to (54), as follows:

$$h_0=h_1=0,h_2=-4,h_3=-\frac{4(2\beta +\rho )}{\alpha },h_4=\frac{{\gamma }^2-4{\beta }^2-4\beta \rho }{{\alpha }^2},$$

(56)

we could attach to the previously mentioned solutions two other types of five-parameter periodic ones as:

$$v(x,t)=a\left[1-\frac{3({\gamma }^2+4{\beta }^2)}{8\beta }\frac{{\left[sec\left(kx+\omega t\right)\right]}^2}{\beta {\left[sec\left(kx+\omega t\right)\right]}^2+\gamma tan(kx+\omega t)+\frac{{\gamma }^2-4{\beta }^2}{4\beta }}\right]$$

(57)

and:

$$v(x,t)=a\left[1-\frac{3({\gamma }^2+4{\beta }^2)}{8\beta }\frac{{\left[csc\left(kx+\omega t\right)\right]}^2}{\beta {\left[csc\left(kx+\omega t\right)\right]}^2+\gamma cot(kx+\omega t)+\frac{{\gamma }^2-4{\beta }^2}{4\beta }}\right].$$

(58)

5. Results and Discussions of the Traveling Wave Solutions

In this paper, we used the general Jacobi elliptic Equation (5), associated with special choices of the parameters $h_i$, $i=\overline{0,4}$, as a multiple auxiliary equation. With the help of its solutions, we determined traveling wave solutions of the scalar BD field. The aim was not only to find more general solutions, but also to investigate how they depend on and how they are correlated with various types of auxiliary equations, in our case the reductions of (5). This is an important aim, as long as in the usual auxiliary equation technique, a pre-established and unique auxiliary equation is considered. This is the case with the results previously reported on the BD solutions, as well. They are restricted to combinations or extensions of solutions of the concerned auxiliary equation. Therefore, the great advantage brought by the technique used here is related exactly to the freedom of finding BD solutions in correlation with various types of auxiliary equations; this is true, as all of them are reductions of the general Jacobi elliptic equation. The main idea was to find relations among the 12 involved parameters: 4 in the BD Equation (19), 3 in the form of its desired solutions (20), and the 5 parameters {$h_i,i=0,1,2,3,4$} from the Jacobi Equation (5). The compatibility condition among the three mentioned equations generated an algebraic system among parameters that can be solved in various situations. Doing that, some already known classes of traveling wave solutions, but also some new and more general ones were pointed out for the BD model, in a unified way. More exactly, the solutions (39), the soliton-type solutions (49), as well as the periodic ones (51) were already analyzed, for example in [48,49]. Supplementary to this, at least 11 families of new solutions—to our best knowledge, not yet reported in the specialized literature—have been generated:

-

Five six-parameter classes—(27), (32) and (34) with (35), (36) and (53);

-

Three five-parameter classes—(55), (57) and (58);

-

At least three four-parameter classes—(45) with (46), (49) and (51).

It is important to note that each family of solutions corresponds to one or to another form of reduced Jacobi equation, considered as an auxiliary equation. We also need to mention the crucial role that the parameters play in controlling the physical properties of the solutions: by changing them, the dynamics can dramatically change. The features of some novel wave solutions are revealed in Figure 1, Figure 2, and Figure 3, respectively.

All our results stand as completions of some less parametric BD solutions that had been previously reported, in the references mentioned in the Introduction for example. Many of the solutions outlined here are completely new, which could help researchers investigate more complex physical phenomena associated with the dynamics of the BD fields.

6. Concluding Remarks

The present paper used the multiple auxiliary equations technique to construct traveling wave solutions of the scalar BD field. We applied the technique on the BD model because, in addition to a scalar field in QFT, it describes phenomena in many scientific applications, such as fluid dynamics, nonlinear optics, and solid-state physics.

Compared with the investigations of the BD equation mentioned in the Introduction, the multiple auxiliary equations technique led to more general solutions, depending on many parameters. We highlighted soliton-like solutions, triangular solutions, and doubly periodic ones. All these solutions are related to specific forms of the auxiliary equations, all of them representing here reductions of the general Jacobi elliptic equation. We displayed some of the novel solutions for suitable values of the parameters in order to show their evolutions in space and time, but also to illustrate their dependence on the specific form of the auxiliary equation.

We are therefore able to conclude that this technique, with multiple auxiliary equations, does indeed provide a powerful and more effective mathematical tool. Applied here to the BD equation, it might also become applicable to a large variety of other choices of potentials in (1), obtaining information on phenomena from plasma physics [50,51], solid-state physics, chemical kinetics, fluid mechanics [52], population models, and so on.