Riemann–Hilbert Approach for Constructing Analytical Solutions and Conservation Laws of a Local Time-Fractional Nonlinear Schrödinger Type Equation
Abstract
:1. Introduction
2. Lax Pair and the Related RH Problem
3. Solutions of the Related RH Problem and Time-Dependence of Scattering Data
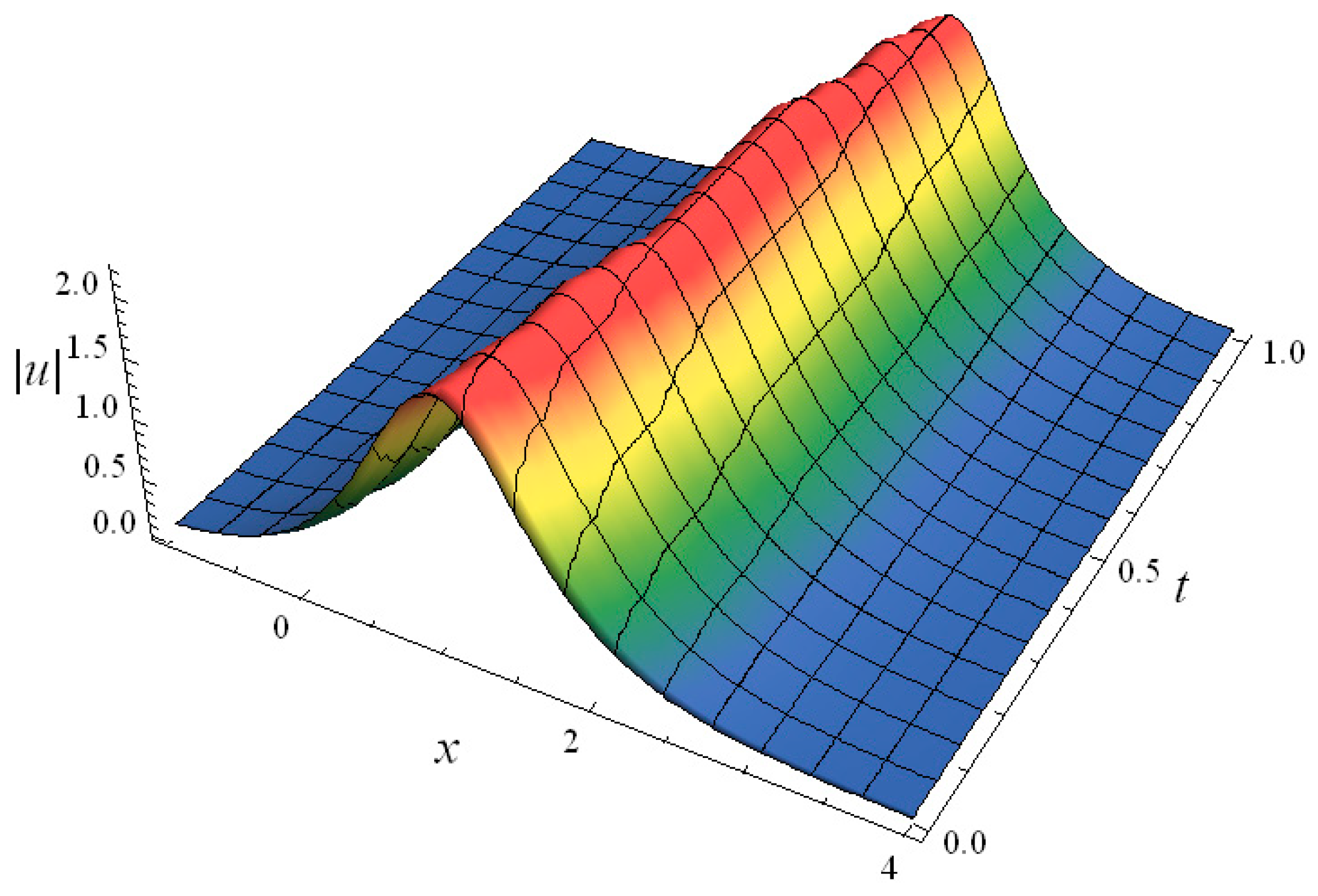
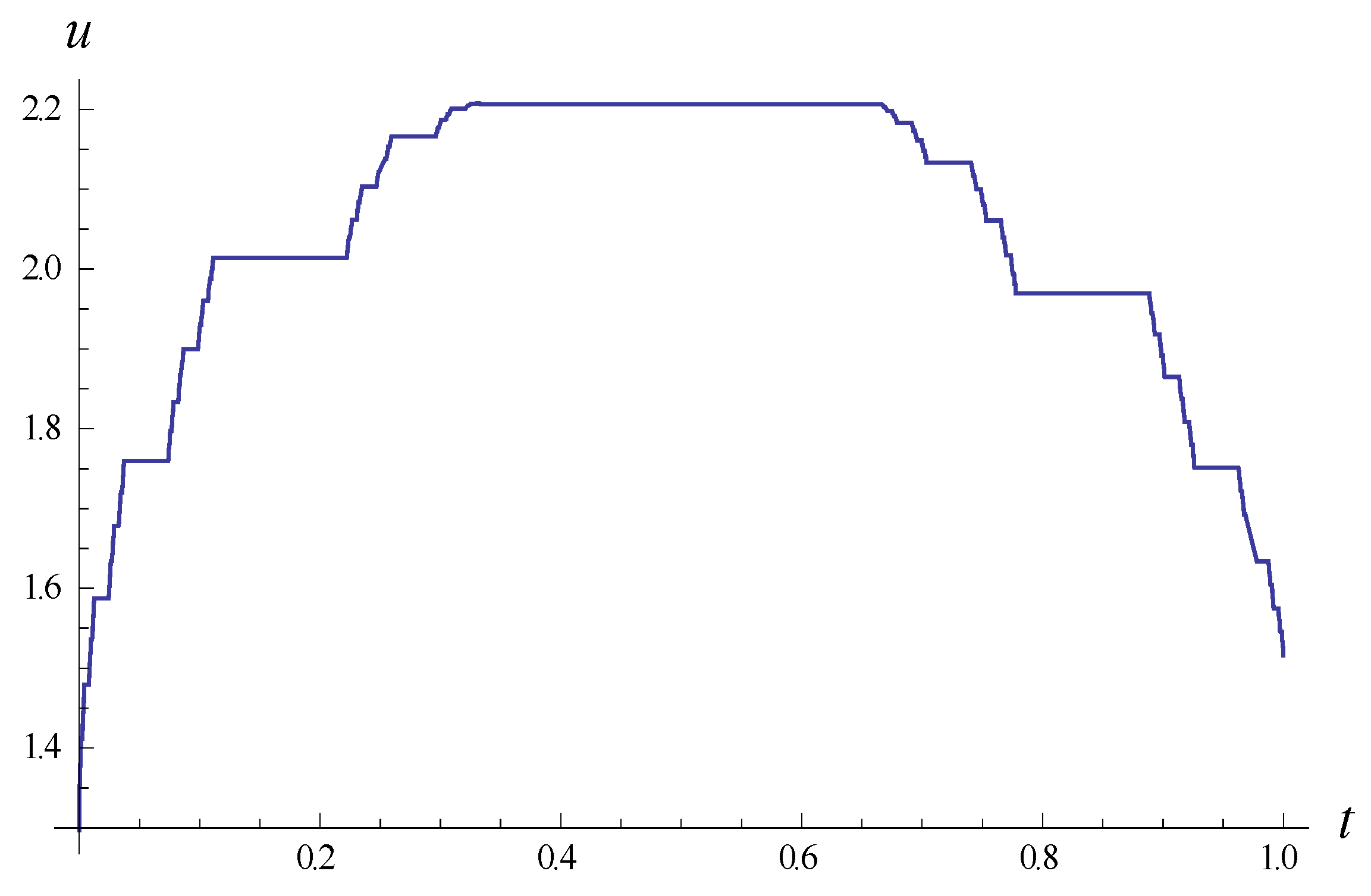
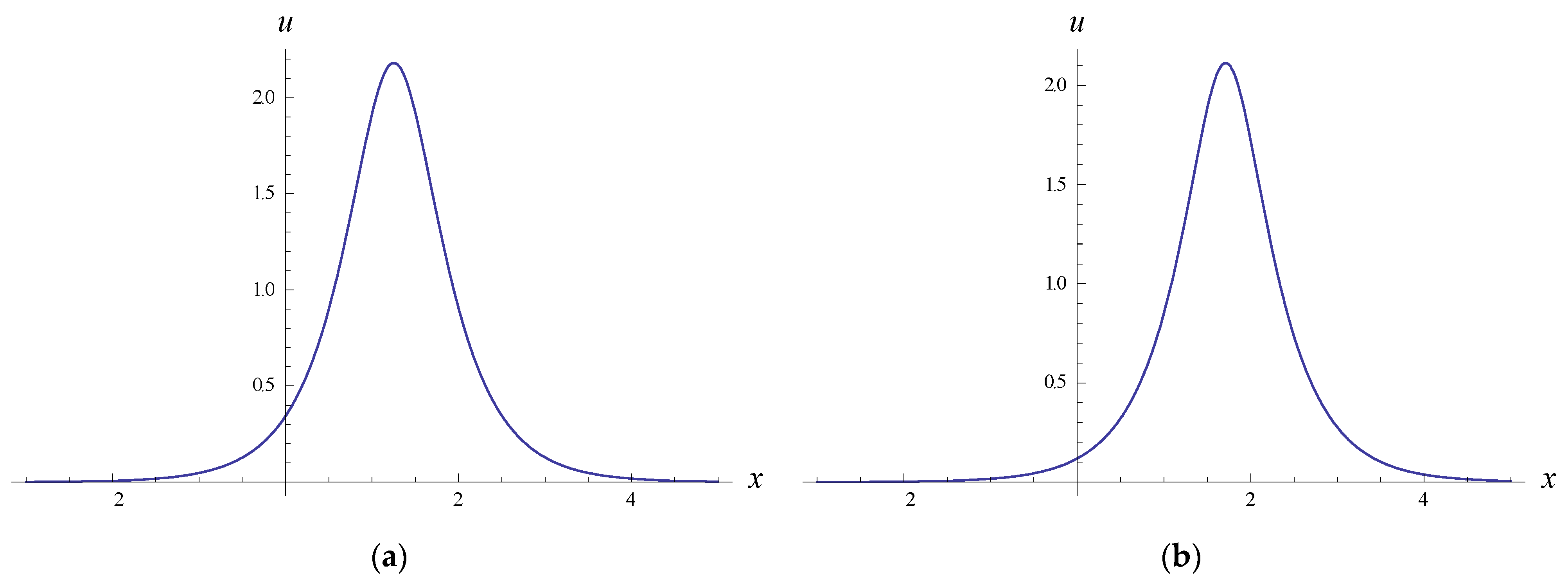
4. Long-Time Asymptotic Solution and N-Fractal-Soliton Solution
5. Infinitely Many Conservation Laws
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- He, J.H. Fractal calculus and its geometrical explanation. Results Phys. 2018, 10, 272–276. [Google Scholar] [CrossRef]
- He, J.H. A new fractal derivation. Therm. Sci. 2011, 15, S145–S147. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- He, J.H. A tutorial review on fractal spacetime and fractional calculus. Int. J. Theor. Phys. 2014, 53, 3698–3718. [Google Scholar] [CrossRef]
- Yang, X.J.; Baleanu, D.; Srivastava, H.M. Local Fractional Integral Transforms and Their Applications; Academic Press: London, UK, 2015. [Google Scholar]
- Fan, J.; Shang, X.M. Fractal heat transfer in wool fiber hierarchy. Heat Transf. Res. 2013, 44, 399–407. [Google Scholar] [CrossRef]
- Agarwal, R.; Hristova, S.; O’Regan, D. Lyapunov functions and Lipschitz stability for Riemann-Liouville non-instantaneous impulsive fractional differential equations. Symmetry 2021, 13, 730. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, H.Q. Fractional sub-equation method and its applications to nonlinear fractional PDEs. Phys. Lett. A 2011, 375, 1069–1073. [Google Scholar] [CrossRef]
- Zhang, S.; Cai, B.; Xu, B. Variable separation method for nonlinear time fractional biological population model. Int. J. Numer. Method. H. 2015, 25, 1531–1541. [Google Scholar] [CrossRef]
- Fujioka, J.; Espinosa, A.; Rodríguez, R.F. Fractional optical solitons. Phys. Lett. A 2010, 374, 1126–1134. [Google Scholar] [CrossRef]
- Vosika, Z.B.; Lazovic, G.M.L.; Misevic, G.N.; Simic-Krstic, J.B.; Rubinsky, B. Fractional calculus model of electrical impedance applied to human skin. PLoS ONE 2013, 8, e59483. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, J.H.; El-Dib, Y.O.; Mady, A.A. Homotopy perturbation method for the fractal Toda oscillator. Fractal Fract. 2021, 5, 93. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, Y.F.; Zhang, S. Line soliton interactions for shallow ocean-waves and novel solutions with peakon, ring, conical, columnar and lump structures based on fractional KP equation. Adv. Math. Phys. 2021, 2021, 6664039. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, Y.F.; Zhang, S. Fractional rogue waves with translational coordination, steep crest and modified asymmetry. Complexity 2021, 2021, 6669087. [Google Scholar]
- Xu, B.; Zhang, Y.F.; Zhang, S. Fractional isospectral and non-isospectral AKNS hierarchies and their analytic methods for N-fractal solutions with Mittag-Leffler functions. Adv. Differ. Equ. 2021, 2021, 223. [Google Scholar] [CrossRef]
- Ain, Q.T.; He, J.H. On two-scale dimension and its applications. Therm. Sci. 2019, 23, 1707–1712. [Google Scholar] [CrossRef] [Green Version]
- He, J.H.; Ji, F.Y.; Mohammad-Sedighi, H. Difference equation vs differential equation on different scales. Int. J. Numer. Method. H. 2020. [Google Scholar] [CrossRef]
- He, J.H. Seeing with a single scale is always unbelieving from magic to two-scale fractal. Therm. Sci. 2021, 25, 1217–1219. [Google Scholar] [CrossRef]
- He, J.H.; Ji, F.Y. Two-scale mathematics and fractional calculus for thermodynamics. Therm. Sci. 2019, 23, 2131–2133. [Google Scholar] [CrossRef]
- Kolwankar, K.M.; Gangal, A.D. Fractional differentiability of nowhere differentiable functions and dimensions. Chaos 1996, 6, 505–513. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.J. Advanced Local Fractional Calculus and Its Applications; World Science Publisher: New York, NY, USA, 2012. [Google Scholar]
- Khalil, R.; Horani, M.A.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, Y.F.; Zhang, S. Analytical methods for non-linear fractional Kolmogorov-Petrovskii-Piskunov equation: Soliton solution and operator solution. Therm. Sci. 2021, 25, 2159–2166. [Google Scholar] [CrossRef]
- Dai, C.Q.; Wu, G.Z.; Li, H.J.; Wang, Y.Y. Wick-type stochastic fractional solitons supported by quadratic-cubic nonlinearity. Fractals 2021. [Google Scholar] [CrossRef]
- Wu, G.Z.; Dai, C.Q. Nonautonomous soliton solutions of variable-coefficient fractional nonlinear Schrödinger equation. Appl. Math. Lett. 2020, 106, 106365. [Google Scholar] [CrossRef]
- Fang, J.J.; Dai, C.Q. Optical solitons of a time-fractional higher-order nonlinear Schrödinger equation. Optik 2020, 209, 164574. [Google Scholar] [CrossRef]
- Yang, X.J.; Machado, J.T.; Baleanu, D.; Cattani, C. On exact traveling-wave solutions for local fractional Korteweg-de Vries equation. Chaos 2016, 26, 110–118. [Google Scholar] [CrossRef]
- Yang, X.J.; Gao, F.; Srivastava, H.M. Non-differentiable exact solutions for the nonlinear ODEs defined on fractal sets. Fractal 2017, 25, 1740002. [Google Scholar] [CrossRef]
- Ghanbari, B. On novel nondifferentiable exact solutions to local fractional Gardner’s equation using an effective technique. Math. Method. Appl. Sci. 2021, 44, 4673–4675. [Google Scholar] [CrossRef]
- Jafari, H.; Kamil, H.; Baleanu, D.; Chu, Y.M. On the approximate solutions for a system of coupled Korteweg-de Vries equations with local fractional derivative. Fractals 2021, 29, 2140012. [Google Scholar] [CrossRef]
- Gardner, C.S.; Greene, J.M.; Kruskal, M.D.; Miura, R.M. Method for solving the Korteweg-deVries equation. Phys. Rev. Lett. 1967, 19, 1095–1097. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Clarkson, P.A. Solitons, Nonlinear Evolution Equations and Inverse Scattering; Cambridge University Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Yang, J.K. Nonlinear Waves in Integrable and Nonintegrable Systems; SIAM: Philadelphia, PA, USA, 2010. [Google Scholar]
- Deift, P.; Zhou, X. A steepest descent method for oscillatory Riemann-Hilbert problems. Ann. Math. 1993, 137, 295–368. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Fan, E.G.; Chen, Y. Long-time asymptotic for the derivative nonlinear Schrödinger equation with step-like initial value. Math. Phys. Anal. Geo. 2013, 16, 253–288. [Google Scholar] [CrossRef] [Green Version]
- Tian, S.F. Initial-boundary value problems for the general coupled nonlinear Schrödinger equation on the interval via the Fokas method. J. Diff. Equ. 2016, 262, 506–588. [Google Scholar] [CrossRef]
- Ma, W.X. Riemann-Hilbert problems and N-soliton solutions for a coupled mKdV system. J. Geo. Phys. 2018, 132, 45–54. [Google Scholar] [CrossRef]
- Hu, B.B.; Xia, T.C.; Ma, W.X. Riemann-Hilbert approach for an initial-boundary value problem of the two-component modified Korteweg-de Vries equation on the half-line. Appl. Math. Comput. 2018, 332, 148–159. [Google Scholar] [CrossRef]
- Wang, D.S.; Guo, B.; Wang, X.L. Long-time asymptotics of the focusing Kundu-Eckhaus equation with nonzero boundary conditions. J. Differ. Equ. 2019, 266, 5209–5253. [Google Scholar] [CrossRef]
- Hu, B.B.; Zhang, L.; Xia, T.C.; Zhang, N. On the Riemann-Hilbert problem of the Kundu equation. Appl. Math. Comput. 2020, 381, 125262. [Google Scholar] [CrossRef]
- Chen, S.Y.; Yan, Z.Y.; Guo, B.L. Long-time asymptotics for the focusing Hirota equation with non-zero boundary conditions at infinity via the Deift-Zhou approach. Math. Phys. Anal. Geom. 2021, 24, 17. [Google Scholar] [CrossRef]
- Guo, H.D.; Xia, T.C. Multi-soliton solutions for a higher-order coupled nonlinear Schrödinger system in an optical fiber via Riemann–Hilbert approach. Nonlinear Dyn. 2021, 103, 1805–1816. [Google Scholar] [CrossRef]
- Li, Z.Q.; Tian, S.F.; Zhang, T.T.; Yang, J.J. Riemann-Hilbert approach and multi-soliton solutions of a variable-coefficient fifth-order nonlinear Schrödinger equation with N distinct arbitrary-order poles. Mod. Phys. Lett. B 2021, 35, 2150194. [Google Scholar] [CrossRef]
- Zhang, B.; Fan, E.G. Riemann-Hilbert approach for a Schrödinger-type equation with nonzero boundary conditions. Mod. Phys. Lett. B 2021, 35, 2150208. [Google Scholar] [CrossRef]
- Wei, H.Y.; Fan, E.G.; Guo, H.D. Riemann-Hilbert approach and nonlinear dynamics of the coupled higher-order nonlinear Schrödinger equation in the birefringent or two-mode fiber. Nonlinear Dyn. 2021, 104, 649–660. [Google Scholar] [CrossRef]
- Liu, W.M.; Kengne, E. Schrödinger Equation in Nonlinear Systems; Springer Nature Singapore Pte Ltd.: Singapore, 2019. [Google Scholar]
- Ain, Q.T.; He, J.H.; Anjum, N.; Ali, M. The fractional complex transform: A novel approach to the time-fractional Schrödinger equation. Fractals 2020, 28, 2050141. [Google Scholar] [CrossRef]
- Zhang, S.; Wei, Y.Y.; Xu, B. Fractional soliton dynamics and spectral transform of time-fractional nonlinear systems: An concrete example. Complexity 2019, 2019, 7952871. [Google Scholar] [CrossRef] [Green Version]
- Plemelj, J. Riemannsche Funktionenscharen mit gegebener Monodromiegruppe. Monatsch. Math. Phys. 1908, 19, 211–246. [Google Scholar] [CrossRef] [Green Version]
- Zakharov, V.E.; Shabat, A.B. Integration of nonlinear equations of mathematical physics by the method of inverse scattering. II. Func. Anal. Appl. 1979, 13, 166–174. [Google Scholar] [CrossRef]
- He, C.H.; Tian, D.; Moatimid, G.M.; Salman, H.F.; Zekry, M.H. Hybrid Rayleigh-Van der Pol-Duffing oscillator (HRVD): Stability analysis and controller. J. Low Freq. Noise V. A. 2021. [Google Scholar] [CrossRef]
- He, J.H.; Moatimid, G.M.; Mostapha, D.R. Nonlinear instability of two streaming-superposed magnetic Reiner-Rivlin fluids by He-Laplace method. J. Electroanal. Chem. 2021, 895, 115388. [Google Scholar] [CrossRef]

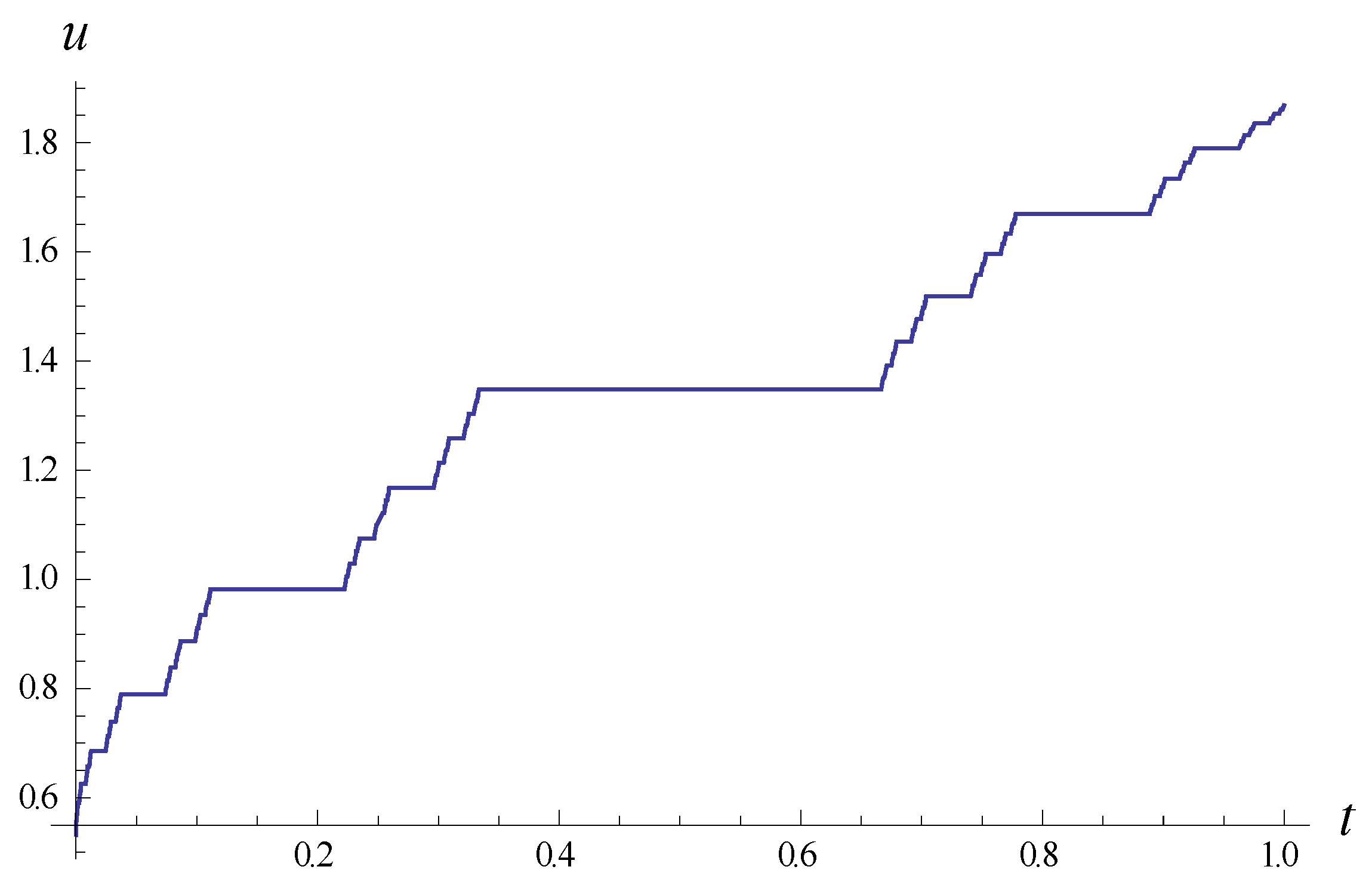
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, B.; Zhang, S. Riemann–Hilbert Approach for Constructing Analytical Solutions and Conservation Laws of a Local Time-Fractional Nonlinear Schrödinger Type Equation. Symmetry 2021, 13, 1593. https://doi.org/10.3390/sym13091593
Xu B, Zhang S. Riemann–Hilbert Approach for Constructing Analytical Solutions and Conservation Laws of a Local Time-Fractional Nonlinear Schrödinger Type Equation. Symmetry. 2021; 13(9):1593. https://doi.org/10.3390/sym13091593
Chicago/Turabian StyleXu, Bo, and Sheng Zhang. 2021. "Riemann–Hilbert Approach for Constructing Analytical Solutions and Conservation Laws of a Local Time-Fractional Nonlinear Schrödinger Type Equation" Symmetry 13, no. 9: 1593. https://doi.org/10.3390/sym13091593
APA StyleXu, B., & Zhang, S. (2021). Riemann–Hilbert Approach for Constructing Analytical Solutions and Conservation Laws of a Local Time-Fractional Nonlinear Schrödinger Type Equation. Symmetry, 13(9), 1593. https://doi.org/10.3390/sym13091593





