On Symmetrical Methods for Charged Particle Dynamics

Abstract

In this paper, we use the scalar auxiliary variable (SAV) approach to rewrite the charged particle dynamics as a new family of ODE systems. The systems own a conserved energy. It is shown that a family of symmetrical methods is energy-conserving for a new ODE system but may not be for the original systems. Moreover, the methods have high-order accuracy. Numerical results are given to confirm the theoretical findings.

1. Introduction

In this paper, we are interested in investigating high-order numerical methods for solving the following charged particle dynamics [1,2,3,4]:

$$\dot{q}=p,\dot{p}=p\times L\left(q\right)-\nabla U\left(q\right),q\left(0\right)=q_0,p\left(0\right)=p_0,(q_0,p_0)\in \Omega \subseteq {\mathbb{R}}^3\times {\mathbb{R}}^3,$$

(1)

where $L\left(q\right)$ and $-\nabla U\left(q\right)$ are, respectively, the magnetic and electric fields. In recent years, many energy-conserving numerical methods have been investigated within the framework of line integral methods [1,5] or Runge–Kutta methods [6,7,8,9]. The main results indicate that the method preserves polynomial Hamiltonians. For non-polynomial Hamiltonians, the energy errors appear in the long time simulation. As a result, the numerical methods may not exactly be energy-conserving.

In this short paper, we propose a novel approach to developing some energy-conserving numerical methods for the charged particle dynamics. The main idea can be viewed as an extension of the recent scalar auxiliary variable approach [10,11,12,13,14] or the invariant energy quadratization approach [15]. Firstly, we introduce an auxiliary variable and obtain an auxiliary ordinary differential equation. Together with the original equations (1), we obtain a new family for the ODE system. The new system has the same solution as the original problem (1), and the energy of the new system can be rewritten as the quadratic invariants. Then, we studied the energy-conserving methods in the framework of Runge–Kutta methods. It can be seen that certain Runge–Kutta methods are energy-conserving for the ODE system, while the same Runge–Kutta methods cannot generally preserve the energy of the original system (1). Within the framework of Runge–Kutta methods, it is easy to find some other energy-conserving methods, e.g., Gauss methods and Hamiltonian boundary value methods [6,7,8,9].

The rest of the paper is arranged as follows. In Section 2, we propose the main approach and energy-conserving methods. In Section 3, we present several numerical results to confirm the effectiveness of the numerical methods. In Section 4, we summarize our results.

2. Energy-Conserving Methods

In this section, we present the approach and the energy-conserving methods.

Let $r=\sqrt{U\left(q\right)+C_0}$, where $C_0$ is a constant so that $U\left(q\right)+C_0\ge 0$. The derivation of r yields:

$$\dot{r}=\frac{\nabla U{\left(q\right)}^{\top }p}{2r}.$$

Together with (1), we have a new ODE system:

$$\left\{\begin{array}{c}\dot{q}=p,\hfill \\ \dot{p}=p\times L\left(q\right)-\nabla U\left(q\right),\hfill \\ \dot{r}=\frac{\nabla U{\left(q\right)}^{\top }p}{2r},\hfill \end{array}\right.$$

(2)

where the initial condition of r is given by $r\left(0\right)=\sqrt{U\left(q_0\right)+C_0}$. The system has the same solutions for p and q, and the same conserved and continuous energy as (1), meaning that:

$$H(p,q,r)=\frac{1}{2}{p}^{T}p+U\left(q\right)=\frac{1}{2}{p}^{\top }p+r^2-C_0.$$

This is true because, by the chain rule, it holds that:

$$\frac{d}{dt}H(p,q,r)=p^{\top }\dot{p}+2r\dot{r}=p^{\top }(p\times L\left(q\right))-\nabla U{\left(q\right)}^{\top }p+\nabla U{\left(q\right)}^{\top }p=p^{\top }(p\times L\left(q\right))=0.$$

(3)

Let:

$$y={[p^T,q^T,r]}^T.$$

Then, system (2) can be viewed as the standard ordinary differential equations, having the form:

$$\dot{y}=f\left(y\right).$$

(4)

Let:

$$S=\left[\begin{array}{ccccccc}\frac{1}{2}& 0& 0& 0& 0& 0& 0\\ 0& \frac{1}{2}& 0& 0& 0& 0& 0\\ 0& 0& \frac{1}{2}& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1\end{array}\right],$$

$X,Y\in {\mathbb{R}}^n$ and define:

$${\langle X,Y\rangle }_s=Y^{T}SX.$$

(5)

One can directly check that:

$${\langle y,y\rangle }_s=\frac{1}{2}{p}^{\top }p+r^2=H(p,q,r)+C_0,$$

(6)

and:

$${\langle y,f\left(y\right)\rangle }_s={\langle y,\dot{y}\rangle }_s=\frac{1}{2}{p}^{\top }\dot{p}+r\dot{r}=0,$$

(7)

where we have noted (3).

We now consider an s-stage Runge–Kutta method to solve problem (4). Let $(A,b,c)$ be a given Runge–Kutta method with vectors $b={(b_1,b_2,\cdots ,b_s)}^T$, $c={(c_1,c_2,\cdots ,c_s)}^T$ and matrix $A={\left(a_{ij}\right)}_{s\times s}$. Let h be the stepsize and define grid points $t_n$ by $t_n=nh$, $n=0,1,2,\cdots$. Applying the s-stage Runge–Kutta method to solve problem (4) yields:

$$\begin{array}{c}\hfill Y_i^n=y_n+h\sum _{j=1}^s{a}_{ij}{f}_j,\end{array}$$

(8)

$$\begin{array}{c}\hfill y^{n+1}=y^n+h\sum _{j=1}^s{b}_j{f}_j,\end{array}$$

(9)

where $f_j=f\left(Y_j^n\right)$, $y^n$ and $Y_i^n$ are the numerical approximations to $y\left(t_n\right)$ and $y(t_n+c_{i}h)$, respectively.

Theorem 1.

Assume that the s-stage Runge–Kutta method is symplectic, i.e., it satisfies:

$$\begin{array}{c}\hfill b_i{a}_{ij}+b_j{a}_{ji}-b_i{b}_j=0.\end{array}$$

(10)

Then, the numerical solution defined in (8) and (9) preserves the energy:

$$H(p^{n+1},q^{n+1},r^{n+1})=H(p^n,q^n,r^n).$$

(11)

Proof. 

By (9) and definition (5), it holds that:

$$\begin{array}{ccc}\hfill {\langle y^{n+1},y^{n+1}\rangle }_s& =& {\langle y^n+h\sum _{j=1}^s{b}_j{f}_j,y^n+h\sum _{j=1}^s{b}_j{f}_j\rangle }_s\hfill \\ & =& {\langle y^n,y^n\rangle }_s+2h\sum _{i=1}^s{b}_i{\langle y^n,f_i\rangle }_s+h^2\sum _{i,j=1}^s{b}_i{b}_j{\langle f_i,f_j\rangle }_s\hfill \\ & =& {\langle y^n,y^n\rangle }_s+2h\sum _{i=1}^s{b}_i{\langle Y_i^n-h\sum _{j=1}^s{a}_{ij}{f}_j,f_i\rangle }_s+h^2\sum _{i,j=1}^s{b}_i{b}_j{\langle f_i,f_j\rangle }_s\hfill \\ & =& {\langle y^n,y^n\rangle }_s+2h\sum _{i=1}^s{b}_i{\langle Y_i^n,f_i\rangle }_s-h^2\sum _{i,j=1}^s(b_i{a}_{ij}+b_j{a}_{ji}-b_i{b}_j){\langle f_i,f_j\rangle }_s,\hfill \end{array}$$

(12)

where in the second equality, we have noted relation (8).

Together with relation (7), assumption (10) and (12), we have:

$${\langle y^{n+1},y^{n+1}\rangle }_s={\langle y^n,y^n\rangle }_s,$$

which further implies that (11) holds. This completes the proof. □

Remark 1.

The key in the proposed approach is to add an auxiliary ordinary differential equation. Then, the energy can be rewritten as a quadratic invariant. If the coefficients of a Runge–Kutta method satisfy (10), the method conserves quadratic invariants. For the quadratic-invariants conserving Runge–Kutta methods, we also refer readers to [6,7] or [8] for more details.

Remark 2.

The new system has the same solution as the original problem (1). However, we show that the proposed Runge–Kutta methods are energy-conserving for the ODE system, while the same Runge–Kutta methods cannot generally preserve the energy of the original system (1).

Remark 3.

The theoretical results can be similarly extended to the general Hamilton system of the form:

$$\dot{q}=-H_p(p,q),\dot{p}=H_q(p,q),$$

(13)

where the Hamiltonian $H(p,q)$ represents the total energy of the system. It is easy to confirm that $H(p,q)=Const,$ along the solution curves of (13). By the proposed approach, a scalar variable r can always be introduced to modify the energy to a quadratic form. In this way, we have a new modified system by letting $y={[p^T,q^T,r]}^T$ as follows:

$$\dot{y}=f\left(y\right),$$

(14)

with the energy $H\left(y\right)={\langle y,y\rangle }_{\tilde{S}},$ where $\tilde{S}$ is a symmetric matrix. Then, some symmetrical methods preserve the energy of (14).

3. Numerical Experiments

In this section, we present some numerical results to confirm the theoretical findings.

Example 1.

We consider problem (1) with:

$$\begin{array}{ccc}& & U\left(q\right)=2sin\left(q_1^2\right)+2cos\left(q_2^2\right)+q_3^6+20,L\left(q\right)={(0,0,\sqrt{q_1^2+q_2^2})}^T,\hfill \\ & & q\left(0\right)={(0,1,0.1)}^T,p\left(0\right)={(0.09,0.55,0.3)}^T.\hfill \end{array}$$

We let:

$$r=\sqrt{U\left(q\right)}\mathrm{and}error=H(p^n,q^n,r^n)-H(p^0,q^0,r^0).$$

We solve problems (1) and (2) by using the s-stage Gauss method with the stepsize $h=0.1$. The discrepancies of the discrete energy are shown in Figure 1, where s-Gauss stands for the s-stage Gauss method here and below. Clearly, by solving (2), the discrepancies of the discrete energy are of the order of machine precision. However, by solving (1) with the same stepsize, the discrepancies of the discrete energy depend on the stepsizes and the orders of the methods. Then, we take the stepsize $h=1/8000$ and consider the obtained numerical solutions as the reference solutions. We test the convergence of the numerical methods and list the maximum errors at $t=1$ in

Table 1. The maximum errors at $t=1$ and convergence orders for Example 1.

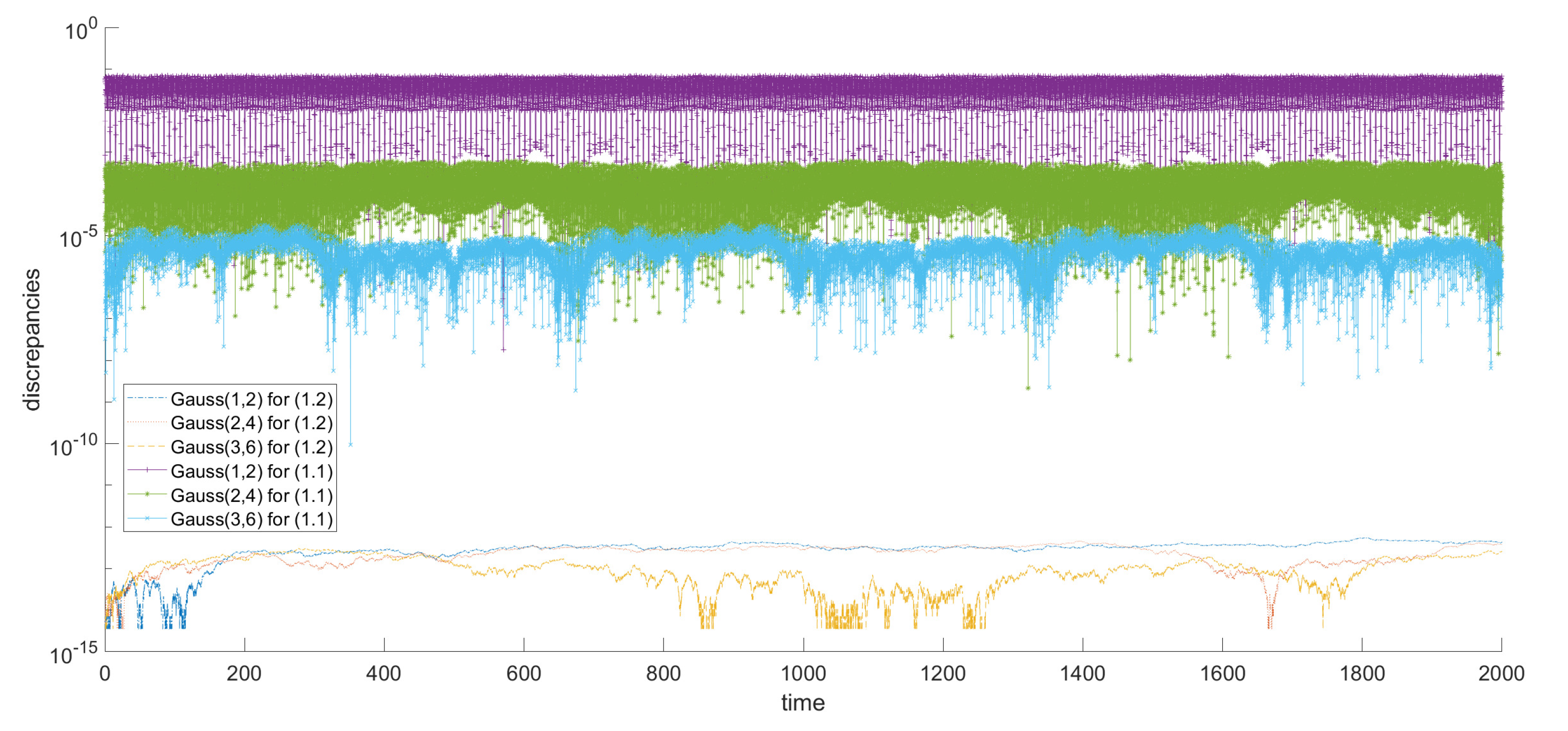
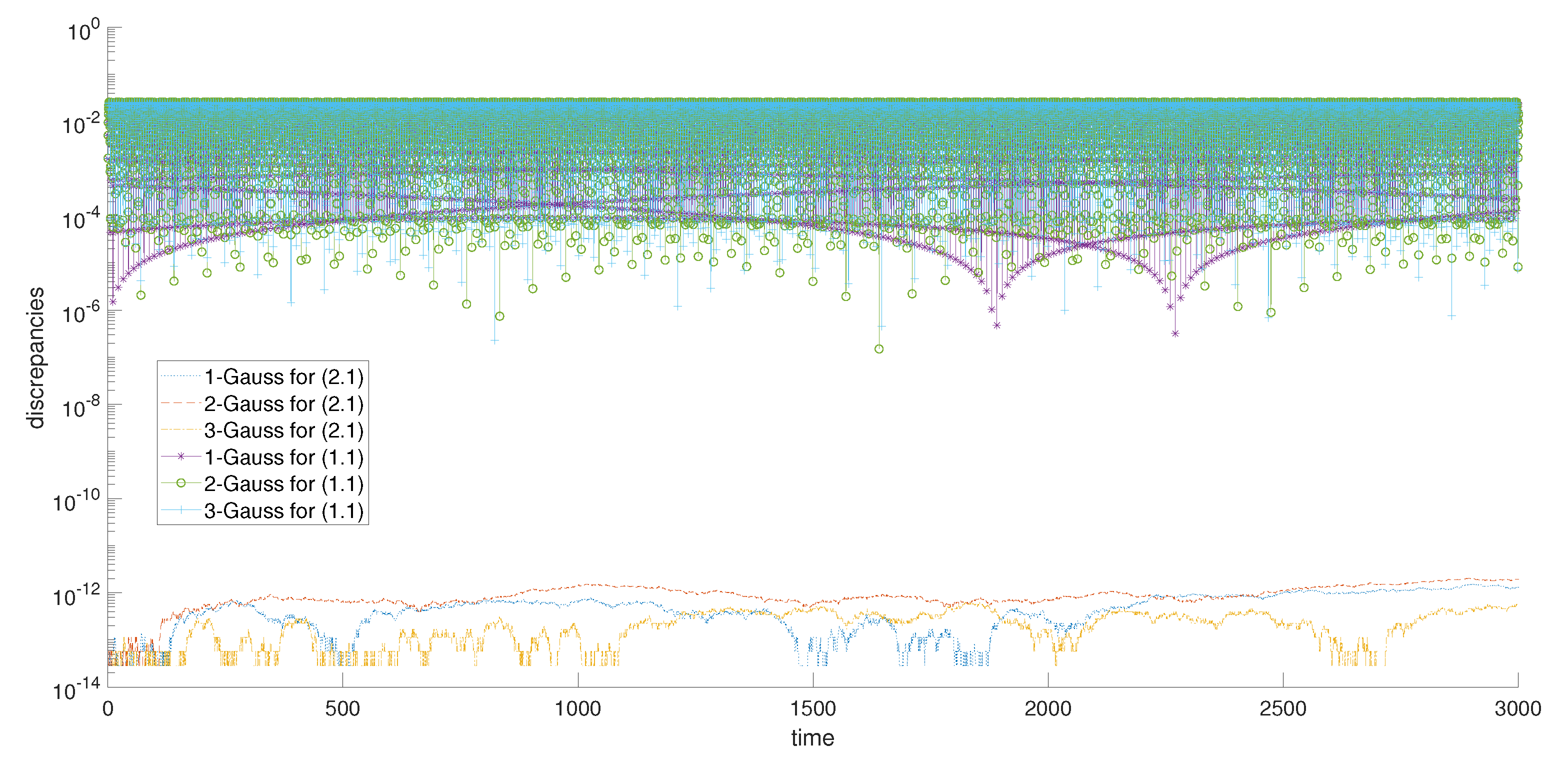
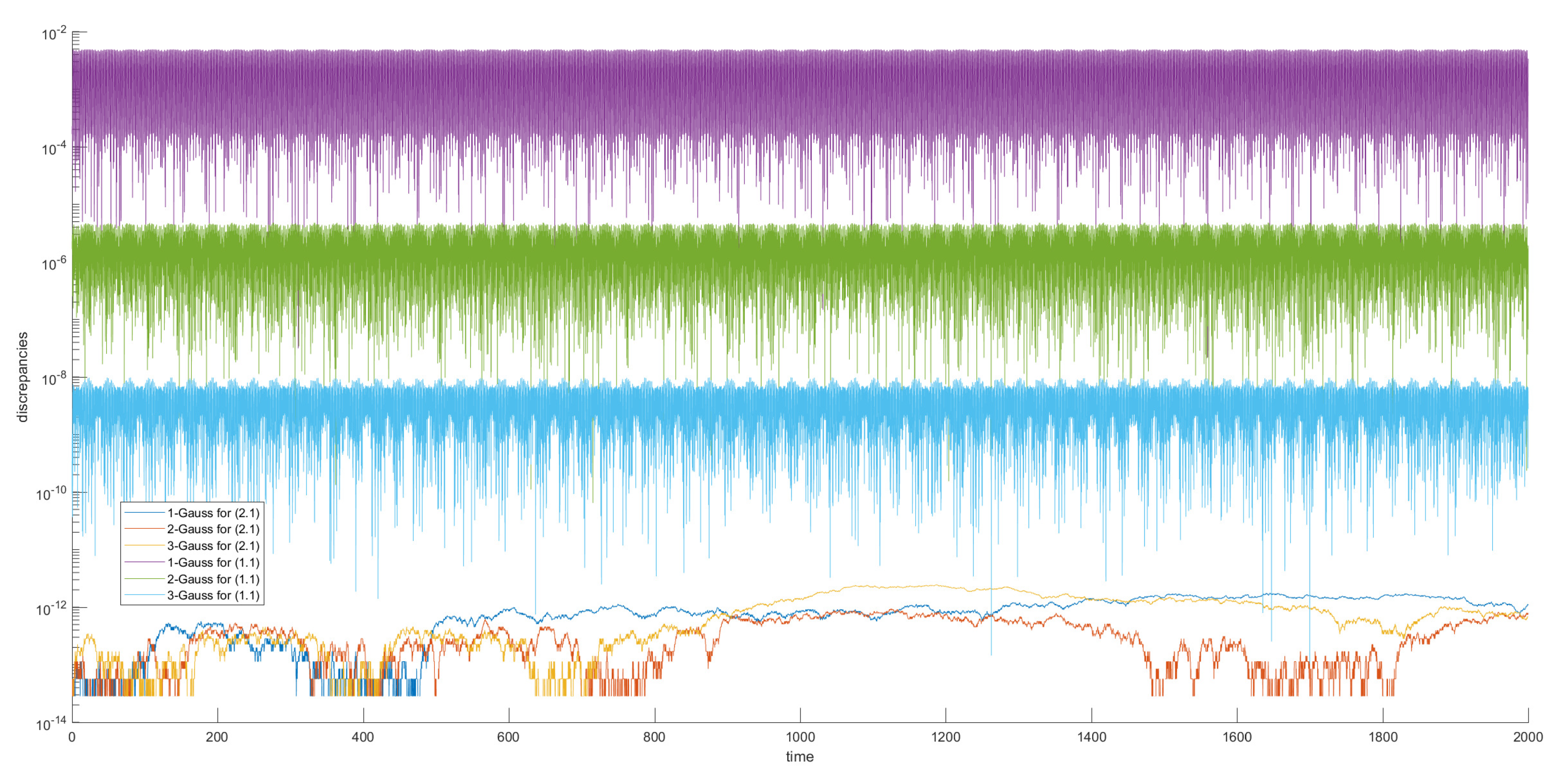
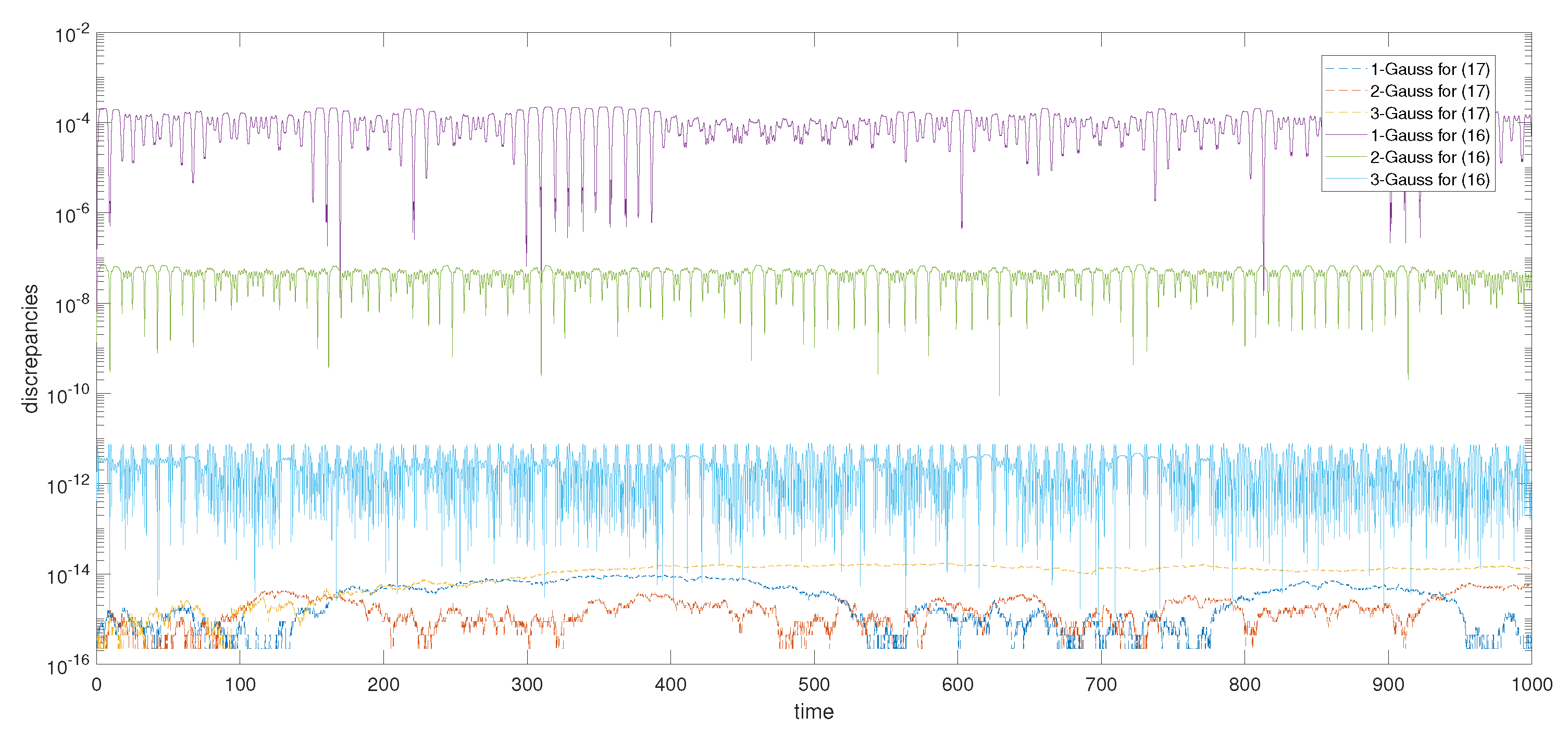
Method	h	p		q		r
		e	Order	e	Order	e	Order
	1/10	7.06E−2	-	2.45E−2	-	7.49E−3	-
1-Gauss	1/20	1.18E−2	1.98	6.27E−3	1.97	1.89E−3	1.99
	1/40	4.50E−3	1.98	1.58E−3	1.98	4.74E−4	1.99
	1/80	1.13E−3	1.99	3.95E−3	1.99	1.19E−4	1.99
	1/10	4.75E−4	-	1.26E−4	-	4.82E−5	-
2-Gauss	1/20	3.00E−5	3.99	8.09E−6	3.97	3.69E−6	3.71
	1/40	1.88E−6	3.99	5.08E−7	3.98	2.30E−7	3.85
	1/80	1.18E−7	3.99	3.18E−8	3.99	1.45E−8	3.90
	1/10	3.10E−6	-	6.79E−7	-	4.41E−7	-
3-Gauss	1/20	5.22E−8	5.90	1.09E−8	5.96	9.96E−9	5.47
	1/40	8.19E−10	5.94	1.73E−10	5.97	1.51E−10	5.76
	1/80	1.28E−11	5.96	2.71E−12	5.98	2.34E−12	5.84

. The results imply that the s-stage Gauss method is of the order of 2 s. These numerical results confirm the theoretical results and effectiveness of the methods.

Example 2.

In the second example, we consider (1) with:

$$\begin{array}{ccc}& & U\left(q\right)={\left[10\left(q_1^2+q_2^2\right)\right]}^{-1},L\left(q\right)={(0,0,\sqrt{q_1^2+q_2^2})}^T,\hfill \\ & & q\left(0\right)={(0,1,0)}^{\top },p\left(0\right)={(0.1,0.01,0)}^T.\hfill \end{array}$$

The model has an important application in the investigation of the single particle motion in a non-uniform and static electromagnetic field [1,2]. We numerically solve problem (2) by using the s-stage Gauss methods. We show the maximum errors at$t=1$and convergence orders in

Table 2. The maximum errors at $t=1$ and convergence orders for Example 2.

Method	h	p		q		r
		e	Order	e	Order	e	Order
	1/10	1.14E−4	-	1.27E−4	-	3.39E−5	-
1-Gauss	1/20	2.86E−5	2.00	3.18E−5	2.00	8.49E−6	2.00
	1/40	7.14E−6	2.00	7.95E−6	2.00	2.12E−6	2.00
	1/80	1.79E−6	2.00	1.99E−6	2.00	5.31E−7	2.00
	1/10	3.45E−8	-	3.69E−8	-	1.03E−8	-
2-Gauss	1/20	2.16E−9	4.00	2.31E−9	4.00	6.46E−10	4.00
	1/40	1.35E−10	4.00	1.44E−10	4.00	4.04E−11	4.00
	1/80	8.43E−12	4.00	9.02E−12	4.00	2.52E−12	4.00
	1/4	1.03E−9	-	1.12E−9	-	3.23E−10	-
3-Gauss	1/8	1.61E−11	6.00	1.75E−11	6.00	5.05E−12	6.00
	1/16	2.54E−13	5.99	2.67E−13	6.02	7.90E−14	6.00
	1/32	5.55E−15	5.83	4.22E−15	6.01	1.94E−15	5.78

, where the reference solutions are obtained by using the stepsize$h=1/8000$. Then, we set the stepsize$h=\pi /10$and solve problem (2) in the time interval$[0,{10}^3\pi ]$. Figure 2shows that the motion occurs in the$(q_1,q_2)$-plane. Moreover, Figure 3 shows that the discrepancies of discrete energy are of the order of machine precision. We also solved the original problem (1) by using the same s-stage Gauss method. From Figure 3, one can see that the discrepancies of discrete energy depend on the stepsizes and the orders of the methods. The numerical results further confirm the theoretical results of the present paper.

Example 3.

In the third example, we consider (1) with:

$$\begin{array}{ccc}& & U\left(q\right)=2sin(q_1^2+q_2^2+q_3^2),L\left(q\right)=\frac{1}{2}{(q_2-q_3,q_1+q_3,q_2-q_1)}^T,\hfill \\ & & q\left(0\right)={(0,1,0.1)}^T,p\left(0\right)={(0.09,0.55,0.3)}^T.\hfill \end{array}$$

We numerically solve problem (2) by using the s-stage Gauss methods. We show the maximum errors at $t=1$ and convergence orders in

Table 3. The maximum errors at $t=1$ and convergence orders for Example 3.

Method	h	p		q		r
		e	Order	e	Order	e	Order
	1/10	1.41E−2	-	6.74E−3	-	9.77E−3	-
1-Gauss	1/20	3.55E−3	2.00	1.68E−3	2.00	2.43E−3	2.01
	1/40	8.89E−4	2.00	4.21E−4	2.00	6.07E−4	2.00
	1/80	2.22E−4	2.00	1.05E−4	2.00	1.52E−4	2.00
	1/10	4.38E−6	-	2.03E−6	-	1.60E−6	-
2-Gauss	1/20	2.80E−7	3.97	1.27E−7	4.00	1.02E−7	3.98
	1/40	1.76E−8	3.98	7.95E−9	4.00	6.43E−9	3.98
	1/80	1.10E−9	3.99	4.97E−10	4.00	4.02E−10	3.99
	1/4	2.03E−6	-	1.39E−6	-	8.64E−7	-
3-Gauss	1/8	2.73E−8	6.21	1.62E−8	6.42	1.20E−8	6.17
	1/16	4.16E−10	6.13	2.48E−10	6.23	1.76E−10	6.13
	1/32	6.48E−12	6.09	3.83E−12	6.16	2.73E−12	6.09

, where the reference solutions are derived by using the stepsize $h=1/8000$. Then, we set stepsize $h=0.1$ and solve problem (2). Figure 4 further shows that the discrepancies of the discrete energy are again of the order of machine precision. However, by solving the original problem (1) with the same method and stepsize, one can see from the figure that the discrepancies of the discrete energy depend on the stepsizes and the orders of the methods. The numerical results again confirm the theoretical results.

Example 4.

The Hénon–Heiles Model is a well-known and frequently used model in certain fields of physics. For example, Hénon–Heiles equations arise in the description of a moving star in the axisymmetric potential of the galaxy. Consider the model mentioned in [7]:

$$\left\{\begin{array}{cc}\hfill & \dot{q_1}=p_1,\hfill \\ \hfill & \dot{q_2}=p_2,\hfill \\ \hfill & \dot{p_1}=-q_1-2q_1{q}_2,\hfill \\ \hfill & \dot{p_2}=-q_2-q_1^2+q_2^2,\hfill \end{array}\right.$$

(15)

with the initial values:

$$q\left(0\right)={(0.1,-0.5)}^T,p\left(0\right)={(0,0)}^T,$$

(16)

where $p_i,q_i,i=1,2,$ are the i-th coordinates of $p,q,$ respectively. This model has the conserved Hamiltonian:

$$H(p,q)=\frac{1}{2}(p_1^2+p_2^2+q_1^2+q_2^2)+q_1^2{q}_2-\frac{1}{3}{q}_2^3.$$

Using the approach, we let:

$$r=\sqrt{q_1^2{q}_2-\frac{1}{3}{q}_2^3+1}.$$

We have the new system:

$$\left\{\begin{array}{cc}\hfill & {\dot{q}}_1=p_1,\hfill \\ \hfill & {\dot{q}}_2=p_2,\hfill \\ \hfill & {\dot{p}}_1=-q_1-2q_1{q}_2,\hfill \\ \hfill & {\dot{p}}_2=-q_2-q_1^2+q_2^2,\hfill \\ \hfill & \dot{r}=\frac{2q_1{q}_2{p}_1+q_1^2{p}_2-q_2^2{p}_2}{2r},\hfill \end{array}\right.$$

(17)

with the energy:

$$H(p,q,r)=\frac{1}{2}(p_1^2+p_2^2+q_1^2+q_2^2)+r^2-1.$$

(18)

Firstly, we numerically solve model (17) by using s-stage Gauss methods. The maximum errors at $t=1$ and convergence orders are shown in

Table 4. The maximum errors at $t=1$ and convergence orders for Example 4.

Method	h	p		q		r
		e	Order	e	Order	e	Order
	1/4	2.43E−3	-	5.03E−3	-	2.07E−4	-
1-Gauss	1/8	6.14E−4	1.99	1.28E−3	1.98	5.31E−5	1.96
	1/16	1.54E−4	2.00	3.20E−4	2.00	1.34E−5	1.99
	1/32	3.85E−5	2.00	8.01E−5	2.00	3.35E−6	2.00
	1/4	6.64E−6	-	7.73E−6	-	1.11E−6	-
2-Gauss	1/8	4.15E−7	4.00	4.87E−7	3.99	6.90E−8	4.00
	1/16	2.59E−8	4.00	3.05E−8	4.00	4.31E−9	4.00
	1/32	1.62E−9	4.00	1.91E−9	4.00	2.69E−10	4.00
	1/4	2.71E−9	-	1.25E−8	-	3.80E−10	-
3-Gauss	1/8	4.40E−11	5.95	1.96E−10	6.00	5.56E−12	6.09
	1/12	3.88E−12	5.99	1.73E−11	6.00	4.86E−13	6.01
	1/16	6.90E−13	6.01	3.07E−12	6.00	8.93E−14	5.89

, where we obtain the reference solutions by Gauss methods with $h=1/8000.$

Secondly, we set stepsize$h=0.1$and solve the model (15) and (17) in the time interval $[0,1000]$. Figure 5 shows the discrepancies of the discrete energy. We can see that the discrepancies are of machine precision by applying Gauss methods to system (17), while the same methods cannot preserve the energy of the original system (15). One can also see that the discrepancies depend on the orders of methods for the original system.

Example 5.

Consider the two-body system:

$$\dot{q}=p,\dot{p}=-\frac{q}{{\left|q\right|}^3},$$

(19)

where $|·|$ represents the norm in Euclidean space, and the initial values are:

$$q\left(0\right)={(0.9,0)}^T,p\left(0\right)={(0,\sqrt{\frac{11}{9}})}^T.$$

This system owns the Hamiltonian:

$$H(p,q)=\frac{1}{2}(p_1^2+p_2^2)-\frac{1}{\left|q\right|}.$$

Letting:

$$r=\sqrt{\frac{1}{\left|q\right|}}$$

which leads to the new system:

$$\left\{\begin{array}{cc}\hfill & \dot{q}=p,\hfill \\ \hfill & \dot{p}=-\frac{q}{{\left|q\right|}^3},\hfill \\ \hfill & \dot{r}=-\frac{p_1{q}_1+p_2{q}_2}{{2r\left|q\right|}^3},\hfill \end{array}\right.$$

(20)

with the energy:

$$H(p,q,r)=\frac{1}{2}(p_1^2+p_2^2)-r^2.$$

We use different Gauss methods to solve system (20) to test the accuracy of our schemes. We present the maximum errors at$t=1$and the convergence orders with the reference solutions calculated by stepsize$h=1/8000$. The corresponding results are shown in

Table 5. The maximum errors at $t=1$ and convergence orders for Example 5.

Method	h	p		q		r
		e	Order	e	Order	e	Order
	1/4	3.28E−2	-	1.36E−2	-	8.82E−3	-
1-Gauss	1/8	7.86E−3	2.06	3.27E−3	2.05	2.04E−3	2.11
	1/16	1.95E−3	2.01	8.11E−4	2.01	5.01E−4	2.03
	1/32	4.85E−4	2.00	2.02E−4	2.00	1.25E−4	2.01
	1/4	8.43E−5	-	4.76E−5	-	2.24E−5	-
2-Gauss	1/8	5.30E−6	3.99	2.99E−6	3.99	1.41E−6	3.99
	1/16	3.32E−7	4.00	1.87E−7	4.00	8.84E−8	4.00
	1/32	2.08E−8	4.00	1.17E−8	4.00	5.53E−9	4.00
	1/4	1.14E−7	-	8.42E−8	-	4.12E−8	-
3-Gauss	1/8	1.80E−9	5.99	1.32E−9	6.00	6.48E−10	5.99
	1/16	2.81E−11	6.00	2.07E−11	6.00	1.01E−11	6.00
	1/32	4.42E−13	5.99	3.26E−13	5.98	1.54E−13	6.04

, from which we can see that the accuracy property is held.

Then, we set $h=0.1$ and solve (19) and (20) by different Gauss methods. We show the discrepancies of the discrete energy in Figure 6, in which we can see that our schemes are energy-conserving while the same methods are not for the original system.

4. Summary

In this paper, some energy-conserving numerical schemes were developed by introducing an auxiliary variable and an auxiliary ordinary differential equation. This approach, as an extension of the scalar auxiliary variable approach, was developed and applied for the charged particle dynamics. The new system has the same solution as the original system. It was shown that some symmetrical methods are energy-conserving for the new system, while the same methods cannot generally preserve the energy of the original system. Our numerical experiments confirmed the theoretical findings. Furthermore, the approach can be extended to other ODE systems or time-dependent partial differential equations.