Voronoi Entropy vs. Continuous Measure of Symmetry of the Penrose Tiling: Part I. Analysis of the Voronoi Diagrams
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Voronoi Entropy and the Continuous Symmetry Measure of the Set of Points
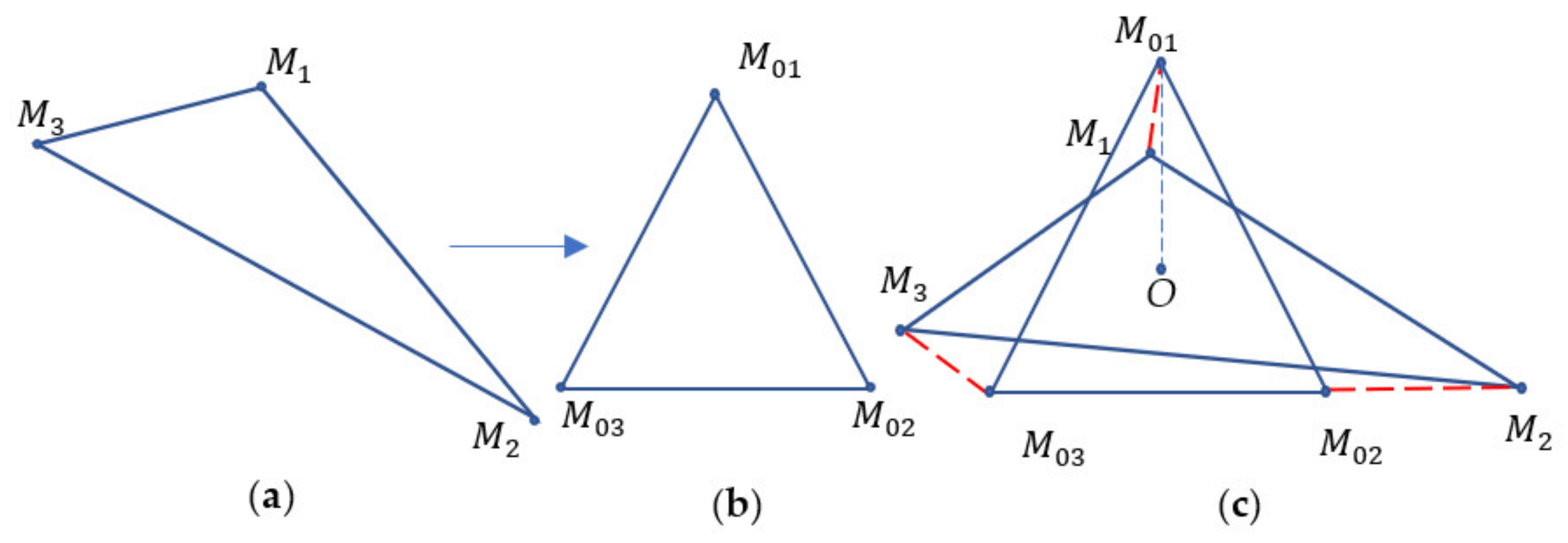
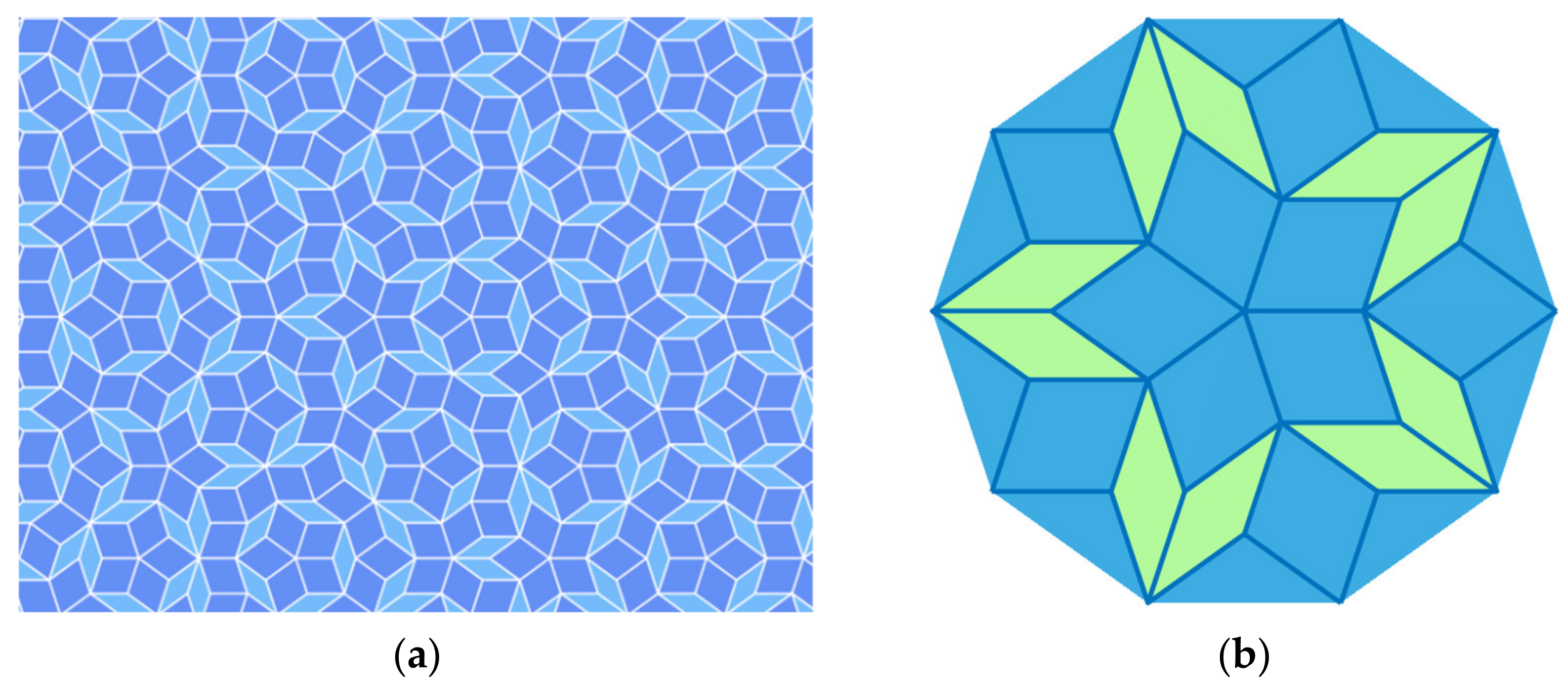
3.2. Voronoi Entropy and the Continuous Symmetry Measure of the Penrose Tiling
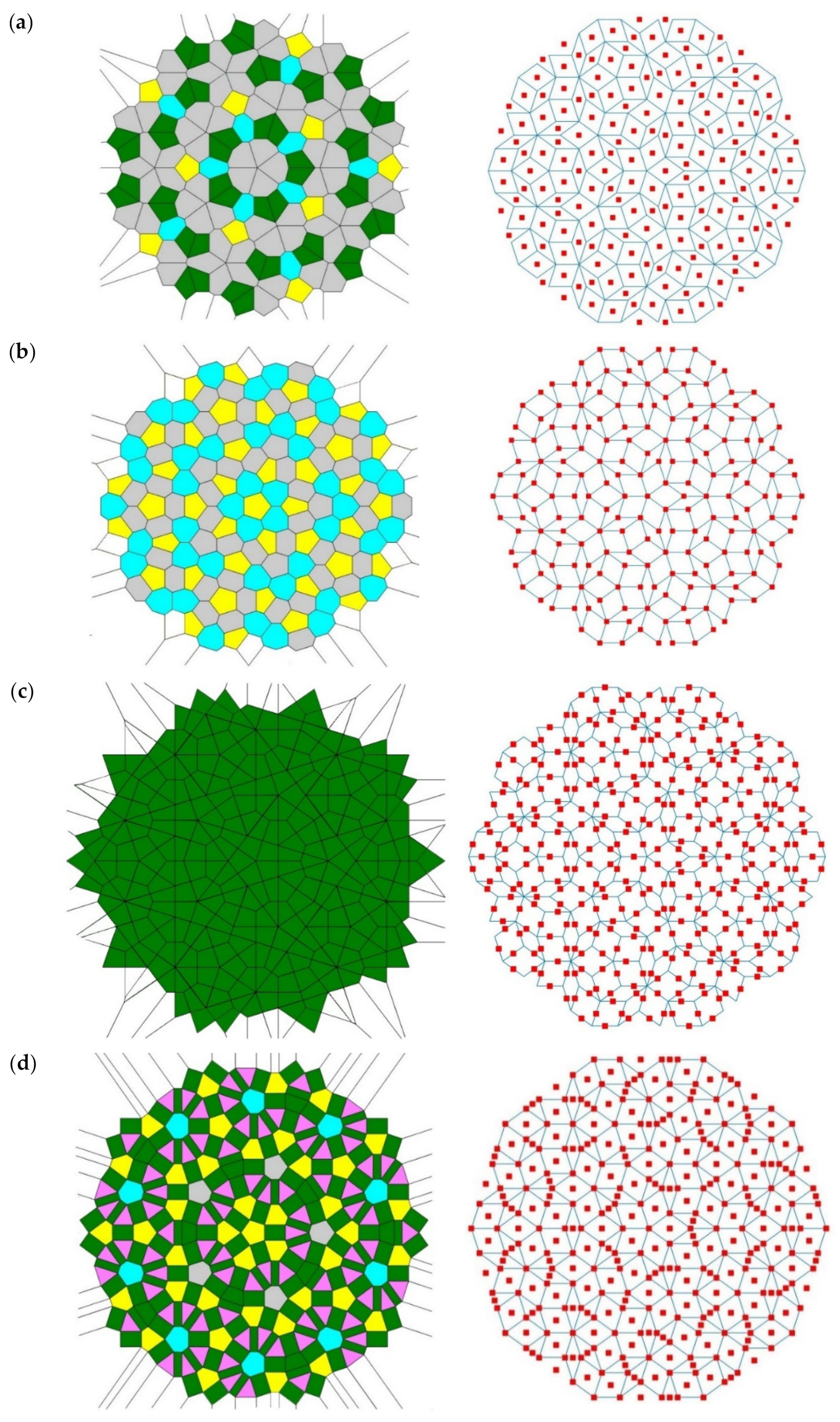

- (i)
- Voronoi diagrams generate new types of the Penrose tiling, which are different from the classical ones as shown in Figure 1.
- (ii)
- The Voronoi entropy is not necessarily an exact measure of symmetry of the given tiling on all spatial scales. It is possible that the Voronoi entropy of the entire pattern equals zero; however, it contains non-symmetrical elements.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lang, S. Algebra, 3rd ed.; Addison-Wesley: Reading, MA, USA, 1993. [Google Scholar]
- Radomsky, A.S.; Rachman, S. Symmetry, ordering and arranging compulsive behavior. Behav. Res. Ther. 2004, 42, 893–913. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Crutchfield, J.P. Between order and chaos. Nature Phys. 2012, 8, 17–24. [Google Scholar] [CrossRef]
- Voronoi, G. Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Deuxième mémoire. Recherches sur les paralléloèdres primitifs. Reine Angew. Math. 1908, 134, 198–287. [Google Scholar] [CrossRef]
- Descartes, R. Principia Philosophiae; Ludovicus Elzevirius: Amsterdam, The Netherlands, 1644; ISBN 978-90-277-1754-2. [Google Scholar]
- Barthélemy, M. Spatial networks. Phys. Rep. 2011, 499, 1–101. [Google Scholar] [CrossRef] [Green Version]
- Weaire, D.; Rivier, N. Soap, cells and statistics—random patterns in two dimensions. Contemp. Phys. 1984, 25, 59–99. [Google Scholar] [CrossRef]
- Xu, K. Geometric formulas of Lewis’s law and Aboav-Weaire’s law in two dimensions based on ellipse packing. Philos Mag. Lett. 2019, 99, 317–325. [Google Scholar] [CrossRef]
- Wang, S.; Tian, Z.; Dong, K.; Xie, Q. Inconsistency of neighborhood based on Voronoi tessellation and Euclidean distance. J. Alloys Compd. 2021, 854, 156983. [Google Scholar] [CrossRef]
- Fedorets, A.; Frenkel, M.; Shulzinger, E.; Dombrovsky, L.; Bormashenko, E.; Nosonovsky, M. Self-assembled levitating clusters of water droplets: Pattern-formation and stability. Sci. Rep. 2017, 7, 1888. [Google Scholar] [CrossRef]
- Fedorets, A.A.; Frenkel, M.; Bormashenko, E.; Nosonovsky, M. Small Levitating Ordered Droplet Clusters: Stability, Symmetry, and Voronoi Entropy. J. Phys. Chem. Lett. 2017, 8, 5599–5602. [Google Scholar] [CrossRef]
- Frenkel, M.; Arya, P.; Bormachenko, E.; Santer, S. Quantification of ordering in active light driven colloids. J. Colloid Interface Sci. 2021, 586, 866–875. [Google Scholar] [CrossRef]
- Bormashenko, E.; Frenkel, M.; Vilk, A.; Legchenkova, I.; Fedorets, A.A.; Aktaev, N.E.; Dombrovsky, L.A.; Nosonovsky, M. Characterization of self-assembled 2D patterns with Voronoi Entropy. Entropy 2018, 20, 956. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Parker, J.; Sherman, E.; van de Raa, M.; van der Meer, D.; Samelson, L.E.; Losert, W. Automatic sorting of point pattern sets using Minkowski functionals. Phys. Rev. E 2013, 88, 022720. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mantz, H.; Jacobs, K.; Mecke, K. Utilizing Minkowski functionals for image analysis: A marching square algorithm. J. Stat. Mech. Theor. Exp. 2008, 2008, P12015. [Google Scholar] [CrossRef]
- Bormashenko, E.; Malkin, A.; Musin, A. Mesoscopic patterning in evaporated polymer solutions: Poly (ethylene glycol) and room-temperature-vulcanized Polyorganosilanes/-siloxanes Promote formation of honeycomb structures. Macromol. Chem. Phys. 2008, 209, 567–576. [Google Scholar] [CrossRef]
- Bormashenko, E. Entropy, Information, and Symmetry: Ordered is Symmetrical. Entropy 2020, 22, 11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bormashenko, E. Entropy, Information, and Symmetry; Ordered Is Symmetrical, II: System of Spins in the Magnetic Field. Entropy 2020, 22, 235. [Google Scholar] [CrossRef] [Green Version]
- Zabrodsky, H.; Peleg, S.; Avnir, D. Continuous symmetry measures. J. Am. Chem. Soc. 1992, 114, 7843–7851. [Google Scholar] [CrossRef]
- Zabrodsky, H.; Peleg, S.; Avnir, D. Continuous symmetry measures. 2. Symmetry groups and the tetrahedron. J. Am. Chem. Soc. 1993, 115, 8278–8289. [Google Scholar] [CrossRef]
- Zabrodsky, H.; Avnir, D. Continuous Symmetry Measures. 4. Chirality. J. Am. Chem. Soc. 1995, 117, 462–473. [Google Scholar] [CrossRef]
- Pinsky, M.; Avnir, D. Continuous Symmetry Measures. 5. The Classical Polyhedra. Inorg. Chem. 1998, 37, 5575–5582. [Google Scholar] [CrossRef]
- Zabrodsky, H.; Peleg, S.; Avnir, D. Symmetry as a continuous feature. IEEE Trans. Pattern Anal. Mach. Intel. 1995, 17, 1154–1166. [Google Scholar] [CrossRef] [Green Version]
- Pinsky, M.; Dryzun, C.; Casanova, D.; Alemany, P.; Avnir, D. Analytical methods for calculating Continuous Symmetry Measures and the Chirality Measure. Comp. Chemistry 2008, 29, 2712–2721. [Google Scholar] [CrossRef]
- Sinai, H.E.; Avnir, D. Adsorption-induced Symmetry Distortions in W@Au12 Nanoclusters, Leading to Enhanced Hyperpolarizabilities. Israel J. Chem. 2016, 56, 1076–1081. [Google Scholar] [CrossRef]
- Ok, K.M.; Halasyamani, P.S.; Casanova, D.; Llunell, M.; Alemany, P.; Alvarez, S. Distortions in Octahedrally Coordinated d0 Transition Metal Oxides: A Continuous Symmetry Measures Approach. Chem. Mater. 2006, 18, 3176–3183. [Google Scholar] [CrossRef]
- Bonjack, M.; Avnir, D. The near-symmetry of protein oligomers: NMR-derived structures. Sci. Rep. 2020, 10, 8367. [Google Scholar] [CrossRef]
- Grimme, S. Continuous symmetry measures for electronic wavefunctions. Chem. Phys. Lett. 1998, 297, 15–22. [Google Scholar] [CrossRef]
- Frenkel, M.; Fedorets, A.A.; Dombrovsky, L.A.; Nosonovsky, M.; Legchenkova, I.; Bormashenko, E. Continuous Symmetry Measure vs Voronoi Entropy of Droplet Clusters. J. Phys. Chem. C 2021, 125, 2431–2436. [Google Scholar] [CrossRef]
- Graham, J.H.; Raz, S.; Hel-Or, H.; Nevo, E. Fluctuating Asymmetry: Methods, Theory, and Applications. Symmetry 2010, 2, 466–540. [Google Scholar] [CrossRef] [Green Version]
- De Bruijn, N.G. Algebraic theory of Penrose’s non-periodic tilings of the plane. Indag. Math. 1981, 84, 39–52. [Google Scholar] [CrossRef] [Green Version]
- Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J.W. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 1984, 53, 1951–1953. [Google Scholar] [CrossRef] [Green Version]
- Collins, L.C.; Witte, T.G.; Silverman, R.; Green, D.B.; Gomes, K.K. Imaging quasiperiodic electronic states in a synthetic Penrose tiling. Nat. Commun. 2017, 8, 15961. [Google Scholar] [CrossRef] [PubMed]
- Bursill, L.; Ju Lin, P. Penrose tiling observed in a quasi-crystal. Nature 1985, 316, 50–51. [Google Scholar] [CrossRef]
- Lanczos, C. The Variational Principles of Mechanics; Dover Publications Inc.: New York, NY, USA, 1986. [Google Scholar]
- Casanova, D.; Llunell, M.; Alemany, P.; Alvarez, S. The rich stereochemistry of eight-vertex polyhedra: A continuous shape measures study. Chem. Eur. J. 2005, 11, 1479–1494. [Google Scholar] [CrossRef] [PubMed]
- Zahrt, A.F.; Denmark, S.E. Evaluating continuous chirality measure as a 3D descriptor in chemoinformatics applied to asymmetric catalysis. Tetrahedron 2019, 75, 1841–1851. [Google Scholar] [CrossRef]
- Tuvi-Arad, I.; Alon, G. Improved algorithms for quantifying the near symmetry of proteins: Complete side chains analysis. J. Cheminform. 2019, 11, 39. [Google Scholar] [CrossRef] [Green Version]
- Aurenhammer, F.; Edelsbrunner, H. An optimal algorithm for constructing the weighted Voronoi diagram in the plane. Pattern Recognit. 1984, 17, 251–257. [Google Scholar] [CrossRef]
- Mu, L. Polygon characterization with the multiplicatively weighted Voronoi diagram. Prof. Geogr. 2004, 56, 223–239. [Google Scholar]
- Bormashenko, E.; Legchenkova, I.; Frenkel, M. Symmetry and Shannon Measure of Ordering. Entropy 2019, 21, 452. [Google Scholar] [CrossRef] [Green Version]
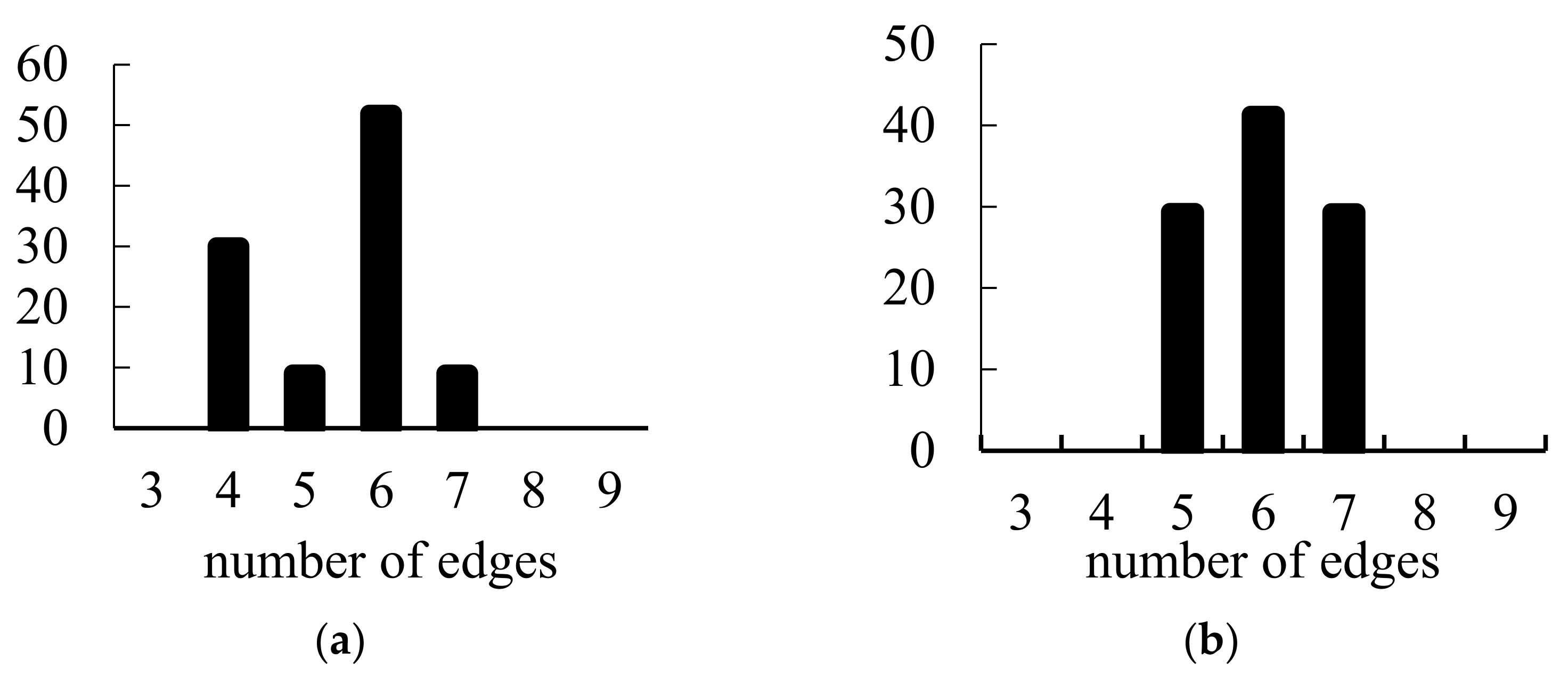
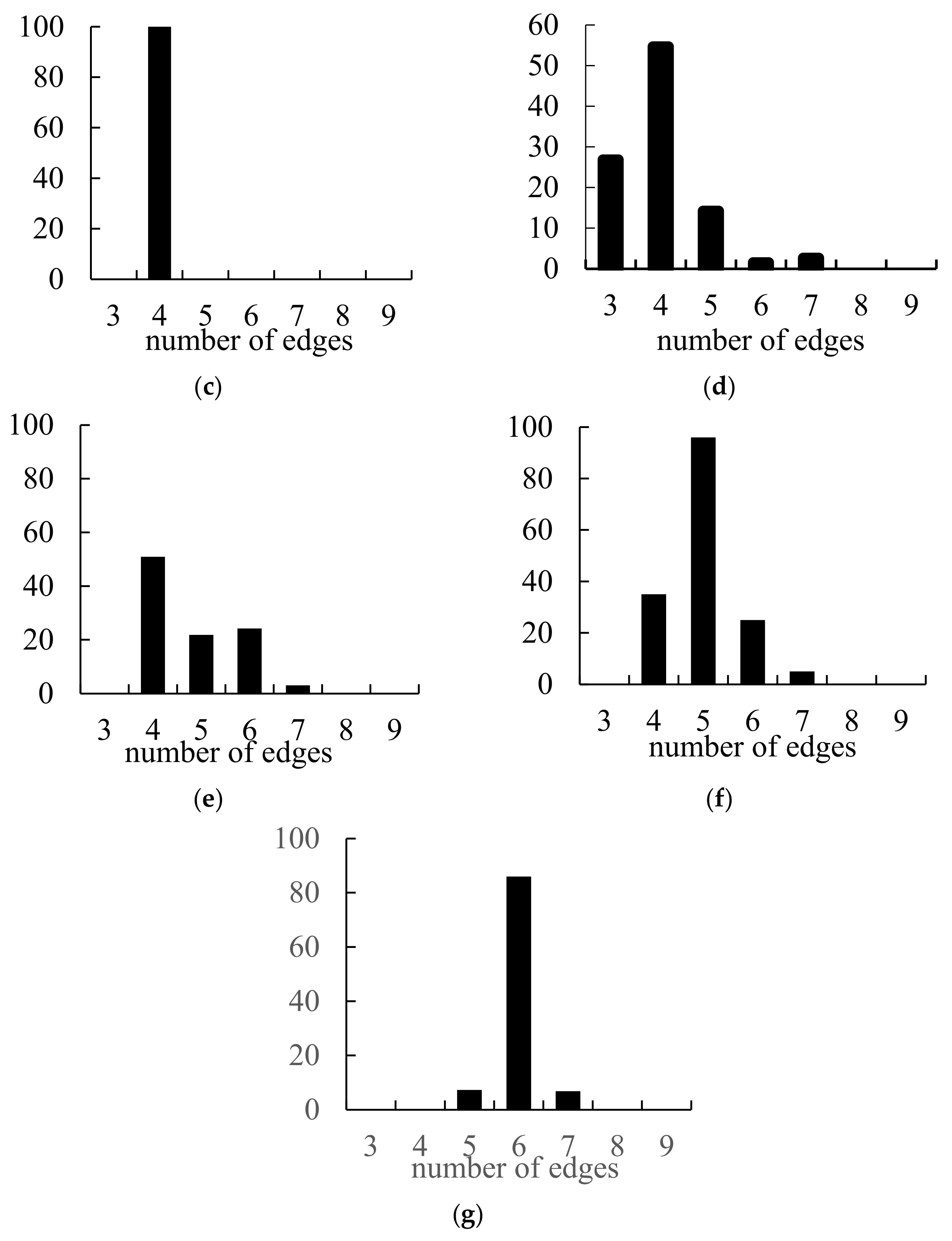
| Diagram Type | Polygons Number, | Polygon Types Number | Voronoi Entropy, | ||
|---|---|---|---|---|---|
| a | 140 | 4 | 1.1364 | 0.1138 | 33.74 |
| b | 141 | 3 | 1.0847 | 0.0367 | 19.15 |
| c | 290 | 1 | 0 | 0.1099 | 33.15 |
| ab | 375 | 5 | 1.122 | 0.0619 | 24.87 |
| ac | 205 | 4 | 1.1026 | 0.0931 | 30.52 |
| bc | 161 | 4 | 1.0371 | 0.0912 | 30.2 |
| abc | 221 | 3 | 0.5026 | 0.0515 | 22.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bormashenko, E.; Legchenkova, I.; Frenkel, M.; Shvalb, N.; Shoval, S. Voronoi Entropy vs. Continuous Measure of Symmetry of the Penrose Tiling: Part I. Analysis of the Voronoi Diagrams. Symmetry 2021, 13, 1659. https://doi.org/10.3390/sym13091659
Bormashenko E, Legchenkova I, Frenkel M, Shvalb N, Shoval S. Voronoi Entropy vs. Continuous Measure of Symmetry of the Penrose Tiling: Part I. Analysis of the Voronoi Diagrams. Symmetry. 2021; 13(9):1659. https://doi.org/10.3390/sym13091659
Chicago/Turabian StyleBormashenko, Edward, Irina Legchenkova, Mark Frenkel, Nir Shvalb, and Shraga Shoval. 2021. "Voronoi Entropy vs. Continuous Measure of Symmetry of the Penrose Tiling: Part I. Analysis of the Voronoi Diagrams" Symmetry 13, no. 9: 1659. https://doi.org/10.3390/sym13091659
APA StyleBormashenko, E., Legchenkova, I., Frenkel, M., Shvalb, N., & Shoval, S. (2021). Voronoi Entropy vs. Continuous Measure of Symmetry of the Penrose Tiling: Part I. Analysis of the Voronoi Diagrams. Symmetry, 13(9), 1659. https://doi.org/10.3390/sym13091659









