A Topological Selection of Folding Pathways from Native States of Knotted Proteins
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Knotoid Distribution Describes a Protein’s Entanglement
2.2. KnotoEMD: A Topological Distance to Distinguish Geometric Features of Knotted Proteins
2.3. Folding Hypotheses for Knotted Proteins
2.4. Methods
3. Results
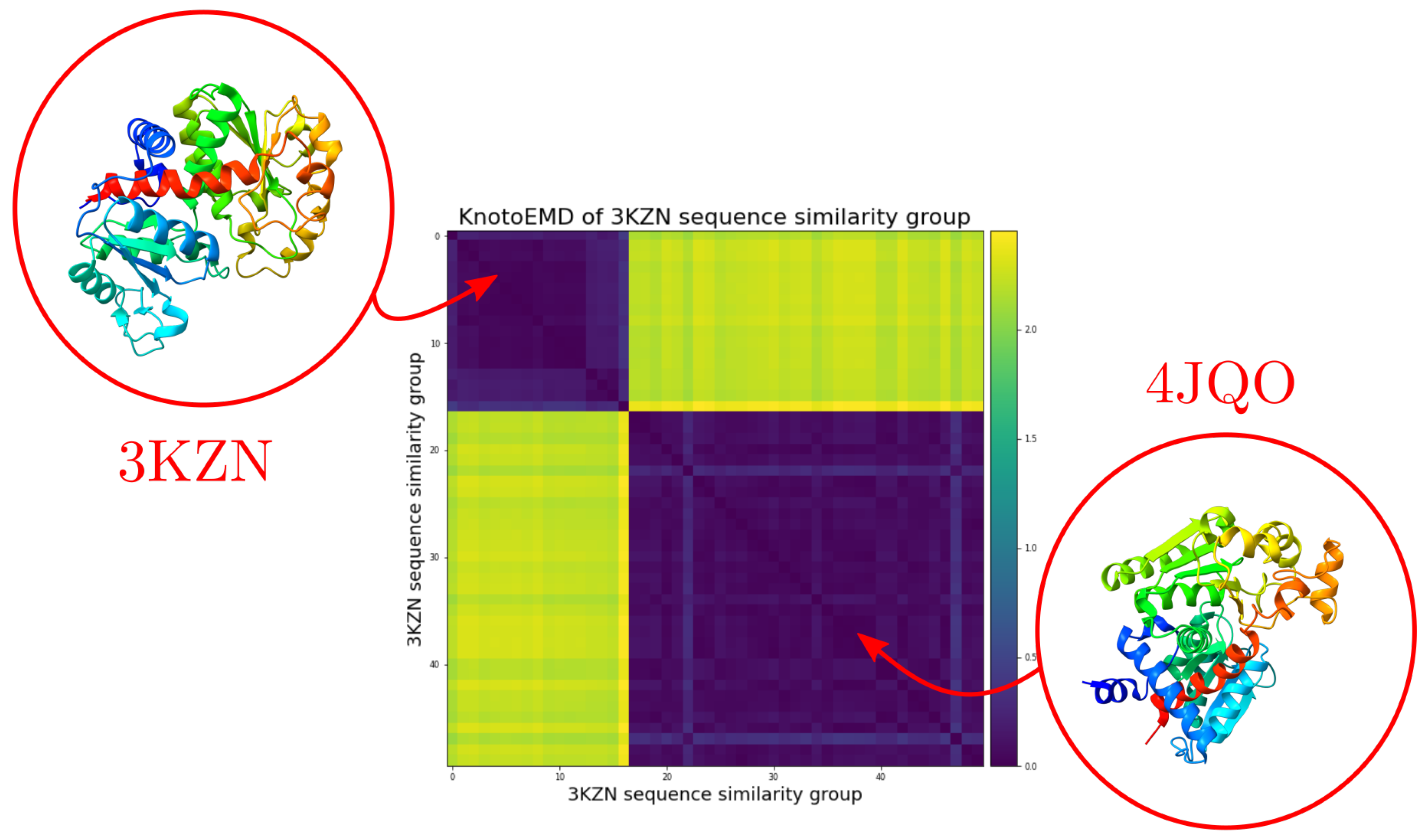
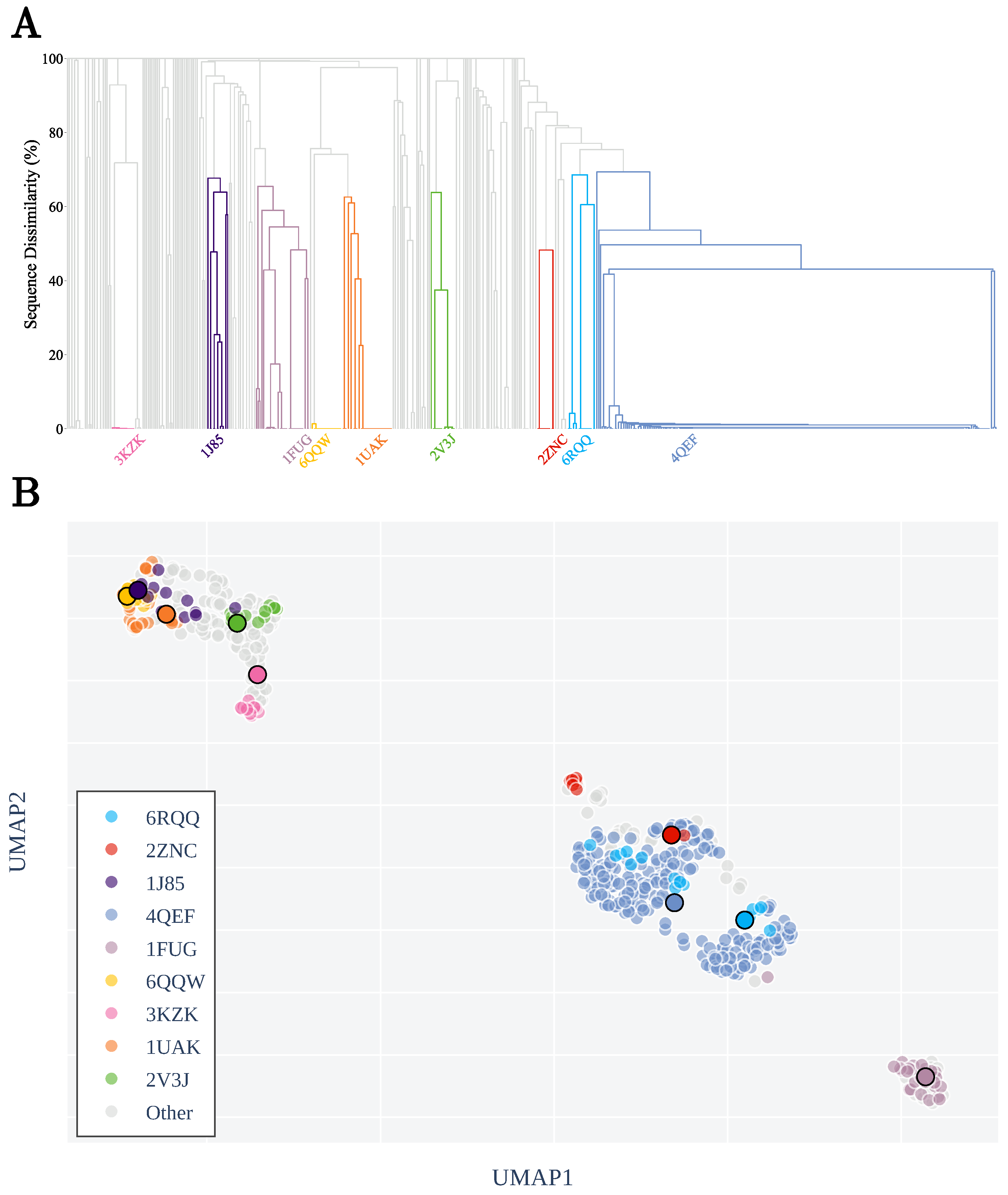
3.1. Sequence Similarity from the Geometry of Proteins’ Native States
3.2. KnotoEMD Captures Subtle Geometric Differences between Double-Loop and Single-Loop Open Trefoils
3.3. Local Geometric Features Suggest Different Folding Pathways for Trefoil Proteins
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PDB | Protein Data Bank |
| 2D | 2-dimensional |
| 3D | 3-dimensional |
| 1-L | Single-loop open trefoil configuration |
| 2-L | Double-loop open trefoil configuration |
| AOTCases | N-acetylornithine transcarbamylase |
| OTCases | Ornithine Carbamoyltransferase |
| alpha-carbon | |
| UMAP | Uniform Manifold Approximation and Projection for Dimension Reduction |
| SMOG | Structure-based Models for Biomolecules |
| DNA | Deoxyribonucleic acid |
| RNA | Ribonucleic acid |
| tRNA | Transfer RNA |
| PL | Piecewise-linear |
Appendix A. Trefoil Proteins
Appendix A.1. Restriction to Knot Core
Appendix A.2. Clustering by Sequence-Similarity
Appendix A.3. List of Non-Redundant Proteins
Appendix B. Double-Loop and Single-Loop Open Trefoil Configurations
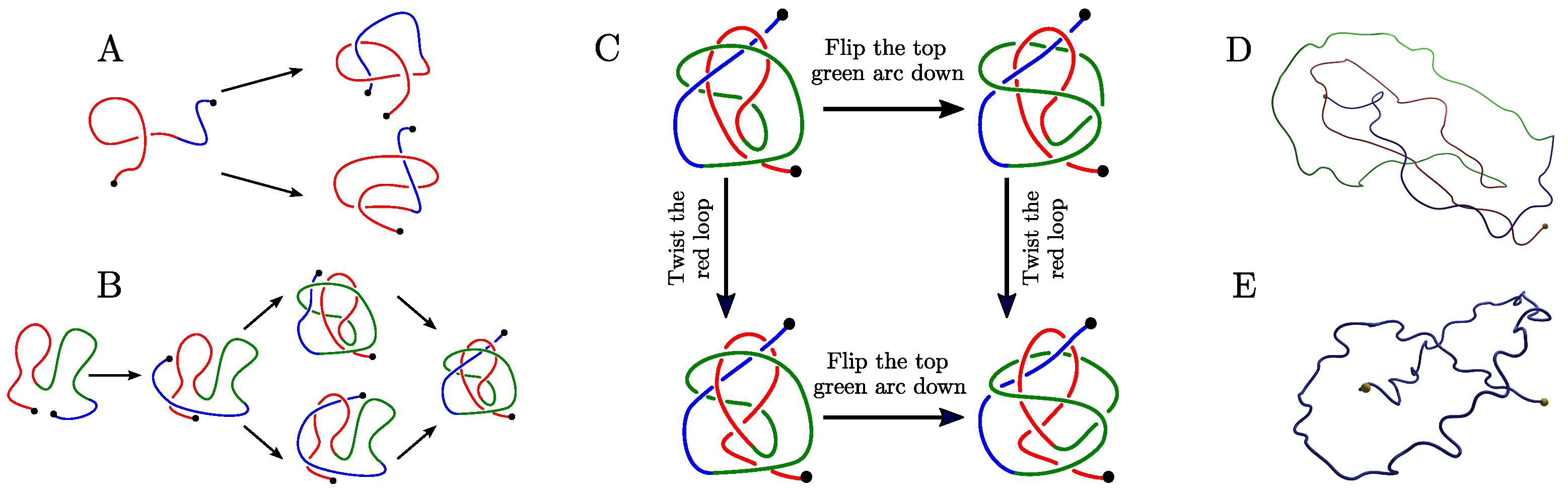
Appendix B.1. The Twelve 2-L Configurations and Local Moves between Them
- The mutual positions of the blue end and the two loops (indicated by a string of length two in R and L).
- The sign (+ or −) of the bottom crossing in each diagram.
- The (signed) number of (positive or negative) twists in the two loops (indicated by two integers a and b);

Appendix B.2. Generating Our Dataset of Trajectories
- Step 1: create the representative trajectories. For each of the 12 2-L configurations we created two different representative piecewise-linear (PL) curves using the software KnotPlot [51]. In the same way, we created four different 1-L PL curves representing minimal (thus, admitting a projection with only 3 crossings) geometrical embeddings of open trefoils. All the curves were drawn to be quite shallow (i.e., with most of the curve involved in the knot).
- Step 2: take different lengths of each curve. We then subdivide each trajectory in three different ways, to obtain curves of length approximately (here the length is measured as the number of segments in the PL curve) 80, 160 and 240 (this is to match the different lengths of trefoil proteins’ knotted cores). In this way, we obtain a total of six different PL curves for each 2-L configuration, and 12 curves representing a 1-L configuration, for a total of 84 curves.
- Step 3: perturb each curve. We then generate 10 different trajectories for each of the 84 curves by performing numerical perturbations. The minimal distance between vertices of each trajectory is determined. Each vertex is perturbed uniformly within a sphere of radius centred at the vertex. This step adds some randomness to a curve without breaking the geometry of the loops. The perturbation script is available in our GitHub repository [46].
Appendix C. Computation of Knotoid Distributions and KnotoEMD
Appendix C.1. Knotoid Distributions
Appendix C.2. KnotoEMD
Appendix C.3. Distance Matrices

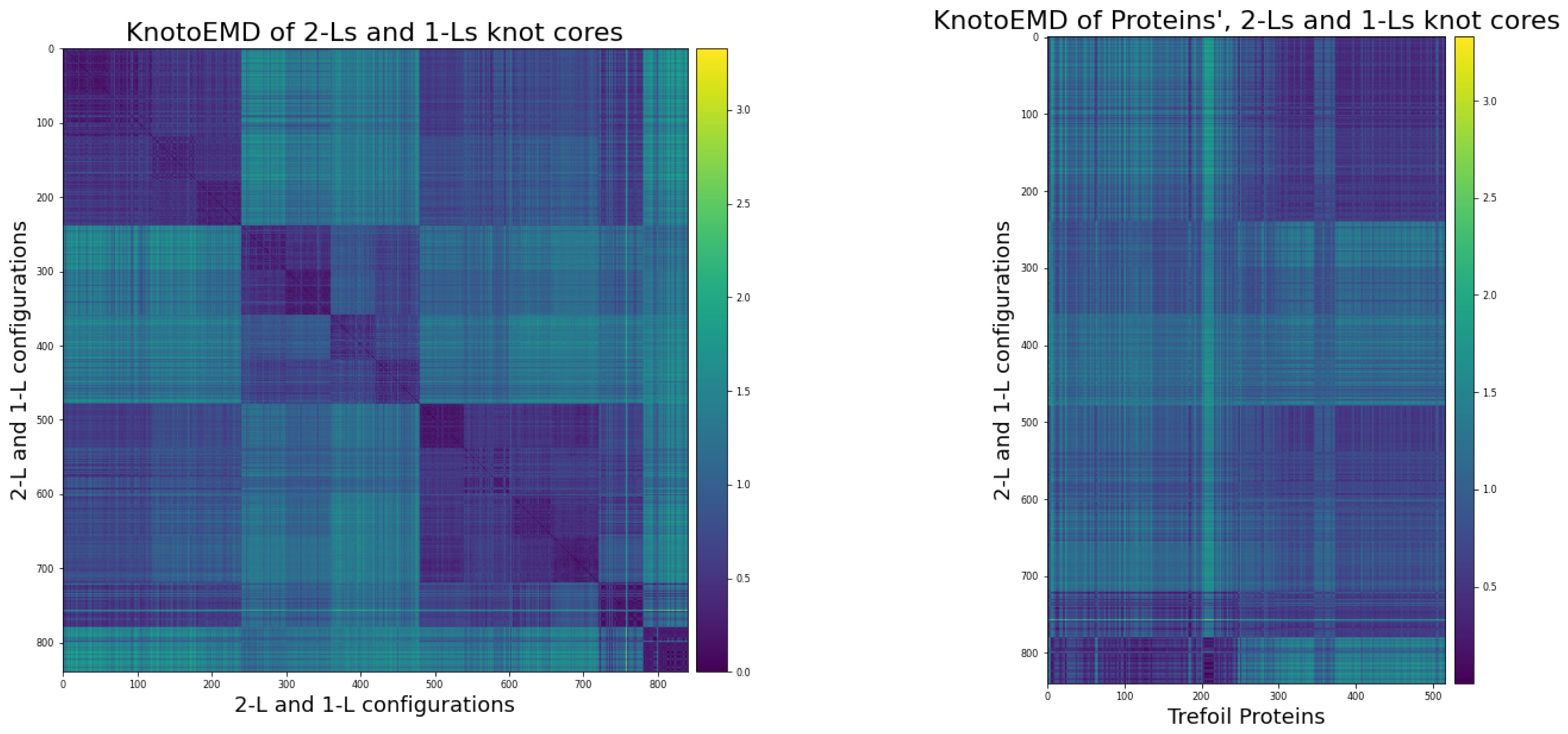
- The simple 2-L trajectories, in the following order:
- the 60 trajectories for RR(+,0,0);
- the 60 trajectories for RL(+,0,-1);
- the 60 trajectories for LR(+,-1,0);
- the 60 trajectories for LL(+,-1,-1).
- The first group of complex 2-L trajectories, in the following order:
- the 60 trajectories for LR(-,1,2);
- the 60 trajectories for LL(-,1,1);
- the 60 trajectories for RR(-,2,2);
- the 60 trajectories for RL(-,2,1).
- The second group of complex 2-L trajectories, in the following order:
- the 60 trajectories for LR(-,0,-2);
- the 60 trajectories for RR(-,1,-2);
- the 60 trajectories for RR(-,-2,1);
- the 60 trajectories for RL(-,-2,0).
- The 120 1-L trajectories.
Appendix C.4. UMAP Projections
- n_neighbors: a constraint on the size of local neighbourhood considered in the dimension reduction.
- min_dist: the minimum distance separating points in the reduced dimension space.
- metric: the metric used to compare the points of the input space (in our case rows of a large distance matrix).
- n_components: the target dimension of the low dimensional space to which we project.
Appendix C.5. The Knotted/Unknotted Homologous Pair
References
- Berman, H.; Henrick, K.; Nakamura, H.; Markley, J.L. The worldwide Protein Data Bank (wwPDB): Ensuring a single, uniform archive of PDB data. Nucleic Acids Res. 2007, 35, D301–D303. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dabrowski-Tumanski, P.; Rubach, P.; Goundaroulis, D.; Dorier, J.; Sułkowski, P.; Millett, K.C.; Rawdon, E.J.; Stasiak, A.; Sułkowska, J.I. KnotProt 2.0: A database of proteins with knots and other entangled structures. Nucleic Acids Res. 2019, 47, D367–D375. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sułkowska, J.I.; Sułkowski, P.; Onuchic, J. Dodging the crisis of folding proteins with knots. Proc. Natl. Acad. Sci. USA 2009, 106, 3119–3124. [Google Scholar] [CrossRef] [Green Version]
- Dabrowski-Tumanski, P.; Stasiak, A.; Sulkowska, J.I. In search of functional advantages of knots in proteins. PLoS ONE 2016, 11, e0165986. [Google Scholar] [CrossRef] [PubMed]
- Jackson, S.E. Why are there knots in proteins? Topol. Geom. Biopolym. 2020, 746, 129. [Google Scholar]
- Jackson, S.E.; Suma, A.; Micheletti, C. How to fold intricately: Using theory and experiments to unravel the properties of knotted proteins. Curr. Opin. Struct. Biol. 2017, 42, 6–14. [Google Scholar] [CrossRef] [Green Version]
- Mallam, A.L. How does a knotted protein fold? FEBS J. 2009, 276, 365–375. [Google Scholar] [CrossRef]
- Sułkowska, J.I.; Noel, J.K.; Onuchic, J.N. Energy landscape of knotted protein folding. Proc. Natl. Acad. Sci. USA 2012, 109, 17783–17788. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Terakawa, T.; Wang, W.; Takada, S. Energy landscape and multiroute folding of topologically complex proteins adenylate kinase and 2ouf-knot. Proc. Natl. Acad. Sci. USA 2012, 109, 17789–17794. [Google Scholar] [CrossRef] [Green Version]
- Chwastyk, M.; Cieplak, M. Cotranslational folding of deeply knotted proteins. J. Phys. Condens. Matter 2015, 27, 354105. [Google Scholar] [CrossRef] [Green Version]
- Covino, R.; Škrbić, T.; Beccara, S.A.; Faccioli, P.; Micheletti, C. The role of non-native interactions in the folding of knotted proteins: Insights from molecular dynamics simulations. Biomolecules 2014, 4, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Lim, N.C.; Jackson, S.E. Mechanistic insights into the folding of knotted proteins in vitro and in vivo. J. Mol. Biol. 2015, 427, 248–258. [Google Scholar] [CrossRef] [Green Version]
- Taylor, W.R. Protein knots and fold complexity: Some new twists. Comput. Biol. Chem. 2007, 31, 151–162. [Google Scholar] [CrossRef]
- Najafi, S.; Potestio, R. Folding of small knotted proteins: Insights from a mean field coarse-grained model. J. Chem. Phys. 2015, 143, 12B606_1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Noel, J.K.; Sułkowska, J.I.; Onuchic, J.N. Slipknotting upon native-like loop formation in a trefoil knot protein. Proc. Natl. Acad. Sci. USA 2010, 107, 15403–15408. [Google Scholar] [CrossRef] [Green Version]
- Wang, I.; Chen, S.Y.; Hsu, S.T.D. Folding analysis of the most complex Stevedore’s protein knot. Sci. Rep. 2016, 6, 1–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, C.; Li, S.; Gao, X.; Xiao, A.; Hu, C.; Hu, X.; Hu, X.; Li, H. Direct observation of the fast and robust folding of a slipknotted protein by optical tweezers. Nanoscale 2019, 11, 3945–3951. [Google Scholar] [CrossRef] [PubMed]
- Mallam, A.L.; Jackson, S.E. Knot formation in newly translated proteins is spontaneous and accelerated by chaperonins. Nat. Chem. Biol. 2012, 8, 147–153. [Google Scholar] [CrossRef]
- Dabrowski-Tumanski, P.; Piejko, M.; Niewieczerzal, S.; Stasiak, A.; Sulkowska, J.I. Protein knotting by active threading of nascent polypeptide chain exiting from the ribosome exit channel. J. Phys. Chem. B 2018, 122, 11616–11625. [Google Scholar] [CrossRef]
- Sulkowska, J.I. On folding of entangled proteins: Knots, lassos, links and θ-curves. Curr. Opin. Struct. Biol. 2020, 60, 131–141. [Google Scholar] [CrossRef]
- Flapan, E.; He, A.; Wong, H. Topological descriptions of protein folding. Proc. Natl. Acad. Sci. USA 2019, 116, 9360–9369. [Google Scholar] [CrossRef] [Green Version]
- Bölinger, D.; Sułkowska, J.I.; Hsu, H.P.; Mirny, L.A.; Kardar, M.; Onuchic, J.N.; Virnau, P. A Stevedore’s protein knot. PLoS Comput. Biol. 2010, 6, e1000731. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Turaev, V. Knotoids. Osaka J. Math. 2012, 49, 195–223. [Google Scholar]
- Goundaroulis, D.; Dorier, J.; Stasiak, A. Knotoids and protein structure. Topol. Geom. Biopolym. 2020, 746, 185. [Google Scholar]
- Pele, O.; Werman, M. Fast and robust earth mover’s distances. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 27 September–4 October 2009; pp. 460–467. [Google Scholar]
- Piejko, M.; Niewieczerzal, S.; Sulkowska, J.I. The Folding of Knotted Proteins: Distinguishing the Distinct behavior of Shallow and Deep Knots. Isr. J. Chem. 2020, 60, 713–724. [Google Scholar] [CrossRef]
- Chwastyk, M.; Cieplak, M. Multiple folding pathways of proteins with shallow knots and co-translational folding. J. Chem. Phys. 2015, 143, 07B611_1. [Google Scholar] [CrossRef]
- Rolfsen, D. Knots and Links; American Mathematical Society: Providence, RI, USA, 2003; Volume 346. [Google Scholar]
- Taylor, W.R. A deeply knotted protein structure and how it might fold. Nature 2000, 406, 916–919. [Google Scholar] [CrossRef] [PubMed]
- Dorier, J.; Goundaroulis, D.; Rawdon, E.J.; Stasiak, A. Open Knots. In Encyclopedia of Knot Theory; Chapman and Hall/CRC: Boca Raton, FL, USA, 2020; Chapter 84. [Google Scholar]
- Millett, K.C.; Rawdon, E.J.; Stasiak, A.; Sułkowska, J.I. Identifying knots in proteins. Biochem. Soc. Trans. 2013, 41, 533–537. [Google Scholar] [CrossRef]
- Sułkowska, J.I.; Rawdon, E.J.; Millett, K.C.; Onuchic, J.N.; Stasiak, A. Conservation of complex knotting and slipknotting patterns in proteins. Proc. Natl. Acad. Sci. USA 2012, 109, E1715–E1723. [Google Scholar] [CrossRef] [Green Version]
- King, N.P.; Yeates, E.O.; Yeates, T.O. Identification of rare slipknots in proteins and their implications for stability and folding. J. Mol. Biol. 2007, 373, 153–166. [Google Scholar] [CrossRef]
- Goundaroulis, D.; Gügümcü, N.; Lambropoulou, S.; Dorier, J.; Stasiak, A.; Kauffman, L. Topological models for open-knotted protein chains using the concepts of knotoids and bonded knotoids. Polymers 2017, 9, 444. [Google Scholar] [CrossRef] [Green Version]
- Dorier, J.; Goundaroulis, D.; Benedetti, F.; Stasiak, A. Knoto-ID: A tool to study the entanglement of open protein chains using the concept of knotoids. Bioinformatics 2018, 34, 3402–3404. [Google Scholar] [CrossRef] [Green Version]
- Gügümcü, N.; Kauffman, L.H. New invariants of knotoids. Eur. J. Comb. 2017, 65, 186–229. [Google Scholar] [CrossRef]
- Barbensi, A.; Goundaroulis, D. f-distance of knotoids and protein structure. Proc. R. Soc. A 2021, 477, 20200898. [Google Scholar] [CrossRef]
- Tubiana, L.; Orlandini, E.; Micheletti, C. Probing the entanglement and locating knots in ring polymers: A comparative study of different arc closure schemes. Prog. Theor. Phys. Suppl. 2011, 191, 192–204. [Google Scholar] [CrossRef]
- Community, B.O. Blender—A 3D Modelling and Rendering Package; Blender Foundation, Stichting Blender Foundation: Amsterdam, The Netherlands, 2018. [Google Scholar]
- McInnes, L.; Healy, J.; Saul, N.; Großberger, L. UMAP: Uniform Manifold Approximation and Projection. J. Open Source Softw. 2018, 3, 861. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1, 19–25. [Google Scholar] [CrossRef] [Green Version]
- Clementi, C.; Nymeyer, H.; Onuchic, J.N. Topological and energetic factors: What determines the structural details of the transition state ensemble and “en-route” intermediates for protein folding? An investigation for small globular proteins. J. Mol. Biol. 2000, 298, 937–953. [Google Scholar] [CrossRef] [PubMed]
- Noel, J.K.; Levi, M.; Raghunathan, M.; Lammert, H.; Hayes, R.L.; Onuchic, J.N.; Whitford, P.C. SMOG 2: A versatile software package for generating structure-based models. PLoS Comput. Biol. 2016, 12, e1004794. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Noel, J.K.; Whitford, P.C.; Onuchic, J.N. The shadow map: A general contact definition for capturing the dynamics of biomolecular folding and function. J. Phys. Chem. B 2012, 116, 8692–8702. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kufareva, I.; Abagyan, R. Methods of protein structure comparison. In Homology Modeling; Springer: Berlin/Heidelberg, Germany, 2011; pp. 231–257. [Google Scholar]
- Yerolemou, N.; Vipond, O.; Goundaroulis, D. KnotoEMD for Proteins. 2021. Available online: https://github.com/nyerolemou/proteins-knotoEMD (accessed on 1 June 2021).
- Rabbani, G.; Ahmad, E.; Khan, M.V.; Ashraf, M.T.; Bhat, R.; Khan, R.H. Impact of structural stability of cold adapted Candida antarctica lipase B (CaLB): In relation to pH, chemical and thermal denaturation. RSC Adv. 2015, 5, 20115–20131. [Google Scholar] [CrossRef]
- Zhao, Y.; Dabrowski-Tumanski, P.; Niewieczerzal, S.; Sulkowska, J.I. The exclusive effects of chaperonin on the behavior of proteins with 52 knot. PLoS Comput. Biol. 2018, 14, e1005970. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rose, Y.; Duarte, J.M.; Lowe, R.; Segura, J.; Bi, C.; Bhikadiya, C.; Chen, L.; Rose, A.S.; Bittrich, S.; Burley, S.K.; et al. RCSB Protein Data Bank: Architectural Advances Towards Integrated Searching and Efficient Access to Macromolecular Structure Data from the PDB Archive. J. Mol. Biol. 2020, 166704. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scharein, R.G.; Booth, K.S. Interactive knot theory with KnotPlot. In Multimedia Tools for Communicating Mathematics; Springer: Berlin/Heidelberg, Germany, 2002; pp. 277–290. [Google Scholar]
- Pele, O.; Werman, M. A linear time histogram metric for improved sift matching. In Computer Vision—ECCV 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 495–508. [Google Scholar]
- Goundaroulis, D.; Dorier, J.; Stasiak, A. A systematic classification of knotoids on the plane and on the sphere. arXiv 2019, arXiv:1902.07277. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barbensi, A.; Yerolemou, N.; Vipond, O.; Mahler, B.I.; Dabrowski-Tumanski, P.; Goundaroulis, D. A Topological Selection of Folding Pathways from Native States of Knotted Proteins. Symmetry 2021, 13, 1670. https://doi.org/10.3390/sym13091670
Barbensi A, Yerolemou N, Vipond O, Mahler BI, Dabrowski-Tumanski P, Goundaroulis D. A Topological Selection of Folding Pathways from Native States of Knotted Proteins. Symmetry. 2021; 13(9):1670. https://doi.org/10.3390/sym13091670
Chicago/Turabian StyleBarbensi, Agnese, Naya Yerolemou, Oliver Vipond, Barbara I. Mahler, Pawel Dabrowski-Tumanski, and Dimos Goundaroulis. 2021. "A Topological Selection of Folding Pathways from Native States of Knotted Proteins" Symmetry 13, no. 9: 1670. https://doi.org/10.3390/sym13091670
APA StyleBarbensi, A., Yerolemou, N., Vipond, O., Mahler, B. I., Dabrowski-Tumanski, P., & Goundaroulis, D. (2021). A Topological Selection of Folding Pathways from Native States of Knotted Proteins. Symmetry, 13(9), 1670. https://doi.org/10.3390/sym13091670






