A Novel Underdetermined Blind Source Separation Method Based on OPTICS and Subspace Projection
Abstract
:1. Introduction
2. Mathematical Model of UBSS
3. The Proposed Method
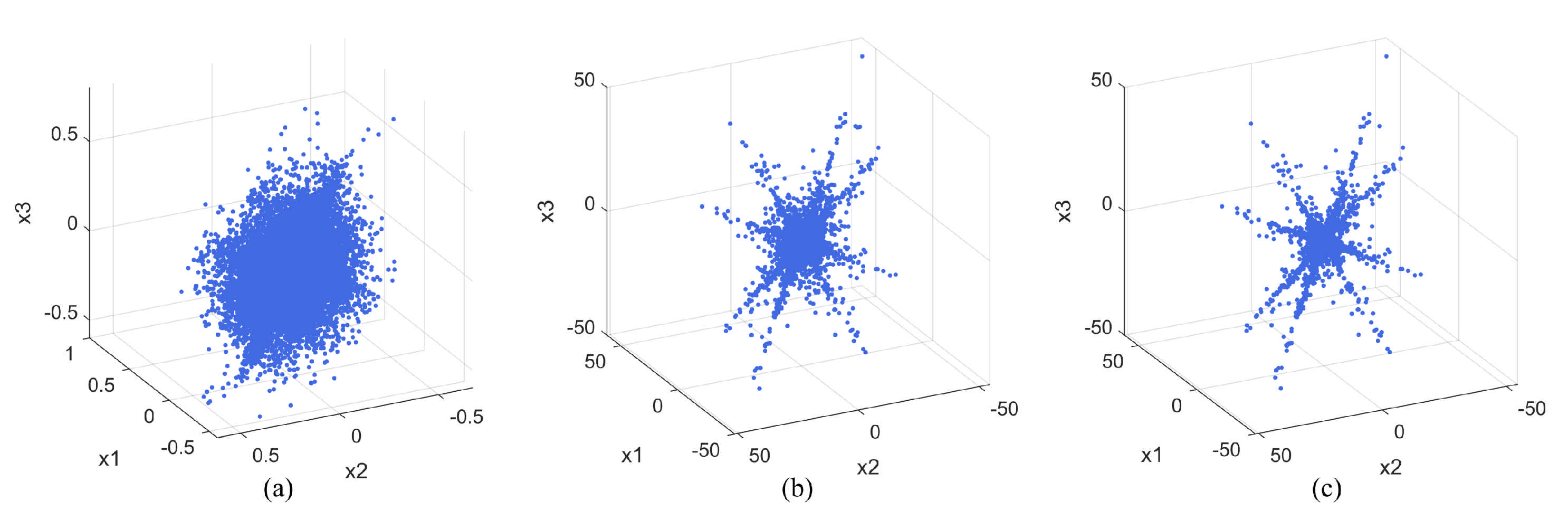
3.1. SSP Screening Method Based on PCA
3.2. Mixing Matrix Estimation
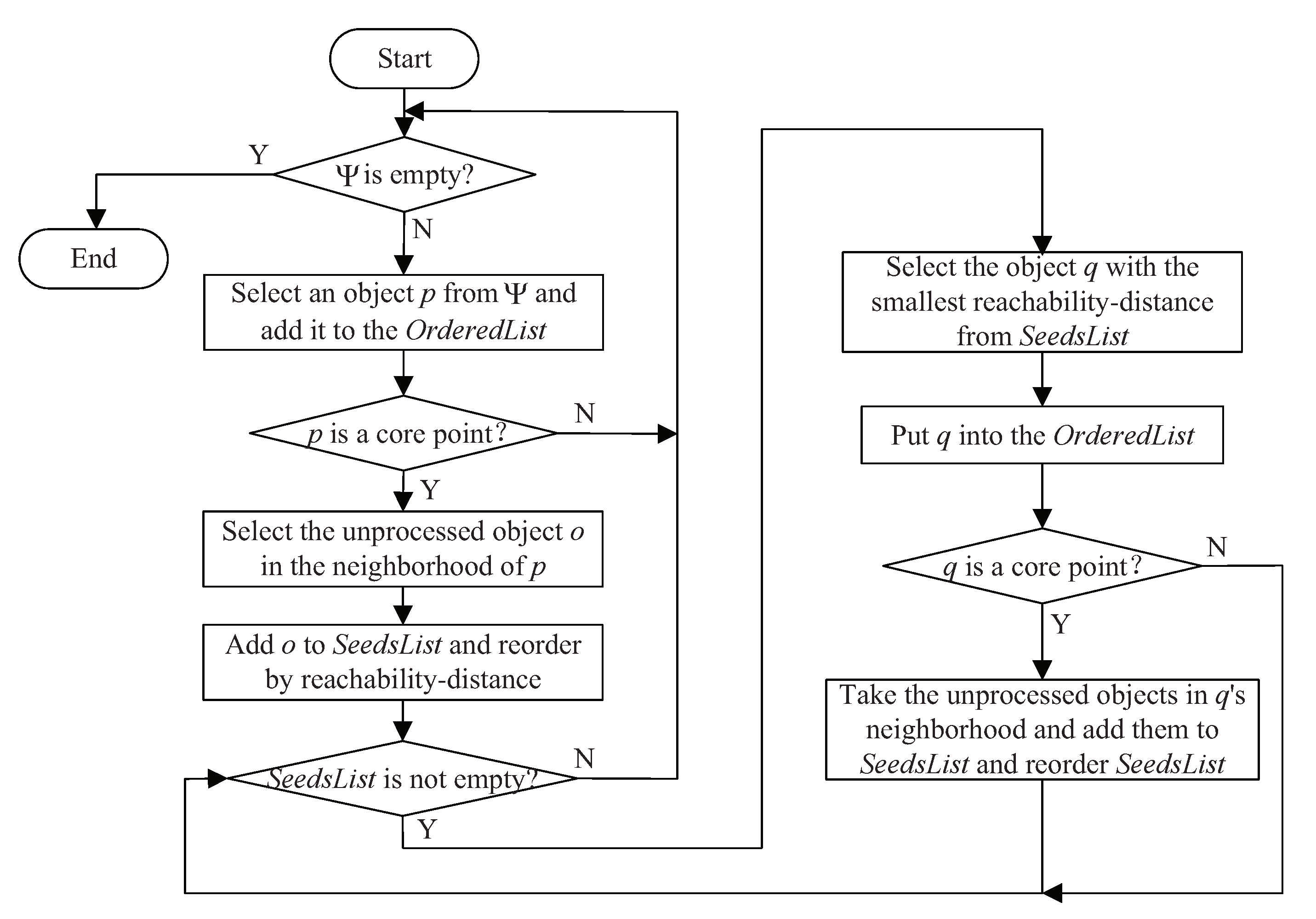
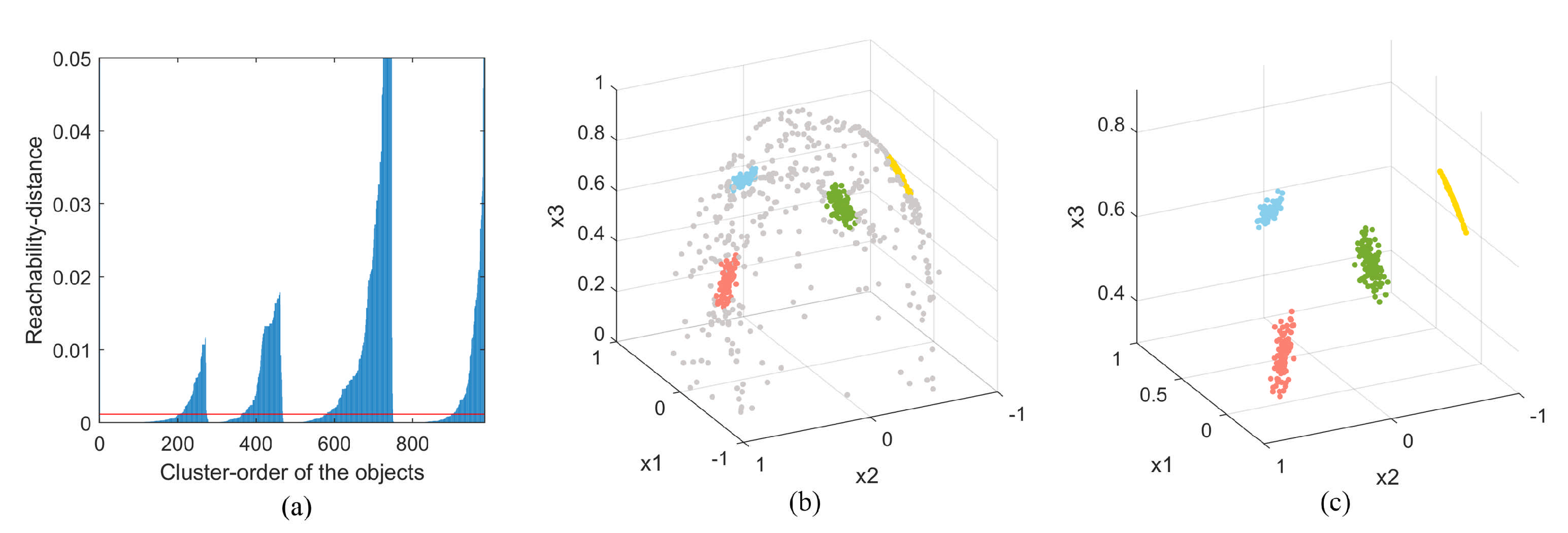
3.2.1. Source Signal Number Estimation Based on OPTICS
- Create a result queue OrderedList, which is used to store processed points in the order of processing; create an ordered queue SeedsList, which is used to store the points that will be processed, and arranged in ascending order of reachable distance;
- If is not empty, select the core object p from the point set and add it to the OrderedList. Find the unprocessed objects in its neighborhood and put them in the SeedsList, and reorder SeedsList according to the reachability-distance. If is empty, the algorithm ends;
- If the SeedsList is not empty, select the first object (the object with the smallest reachability-distance) into the OrderedList; if the SeedsList is empty, go back to step 2;
- If object q is the core object, select the unprocessed objects in its neighborhood and put them in SeedsList. Then update the reachability-distance and sorting of the objects in SeedsList; If q is not a core object, return step 3;
3.2.2. Mixing Matrix Estimation Based on Improved Potential Function
3.3. Source Signal Recovery Based on the Improved Subspace Projection Method
| Algorithm 1 The proposed method for UBSS. |
|
4. Results and Analysis
4.1. Algorithm Performance Evaluation Criteria
4.2. Experimental Results and Analysis
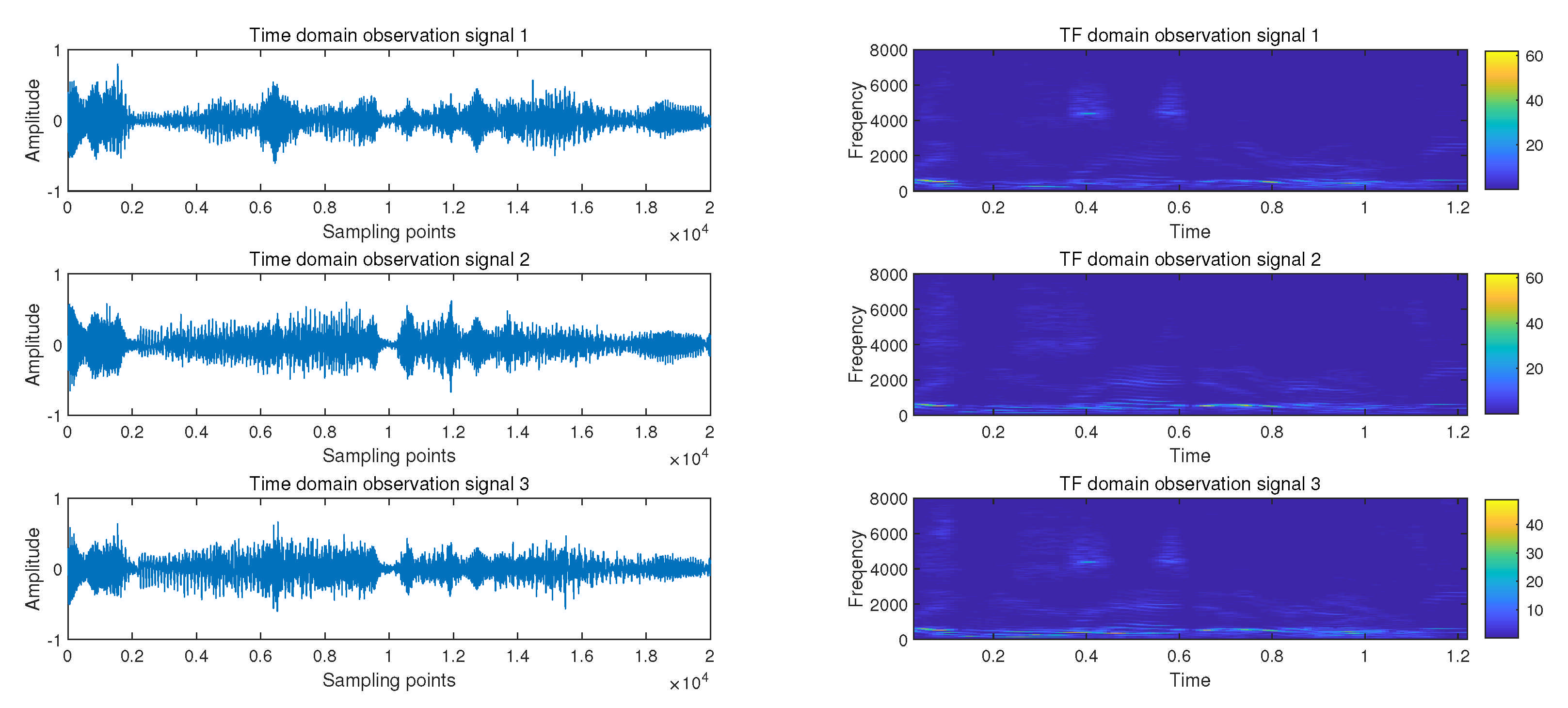
4.2.1. Experiment 1 A Complete Blind Source Separation Experiment
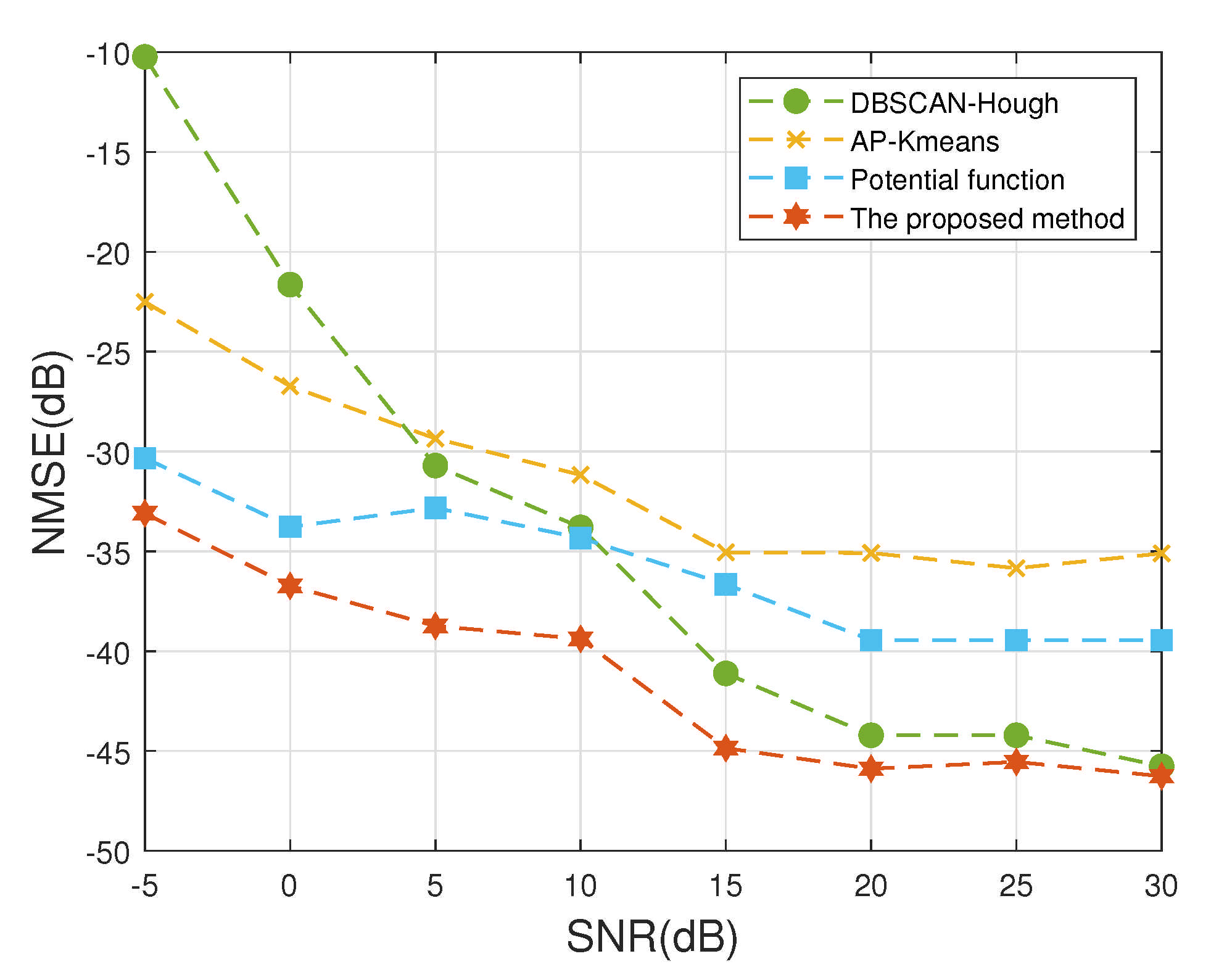
4.2.2. Experiment 2 Mixing Matrix Estimation Error
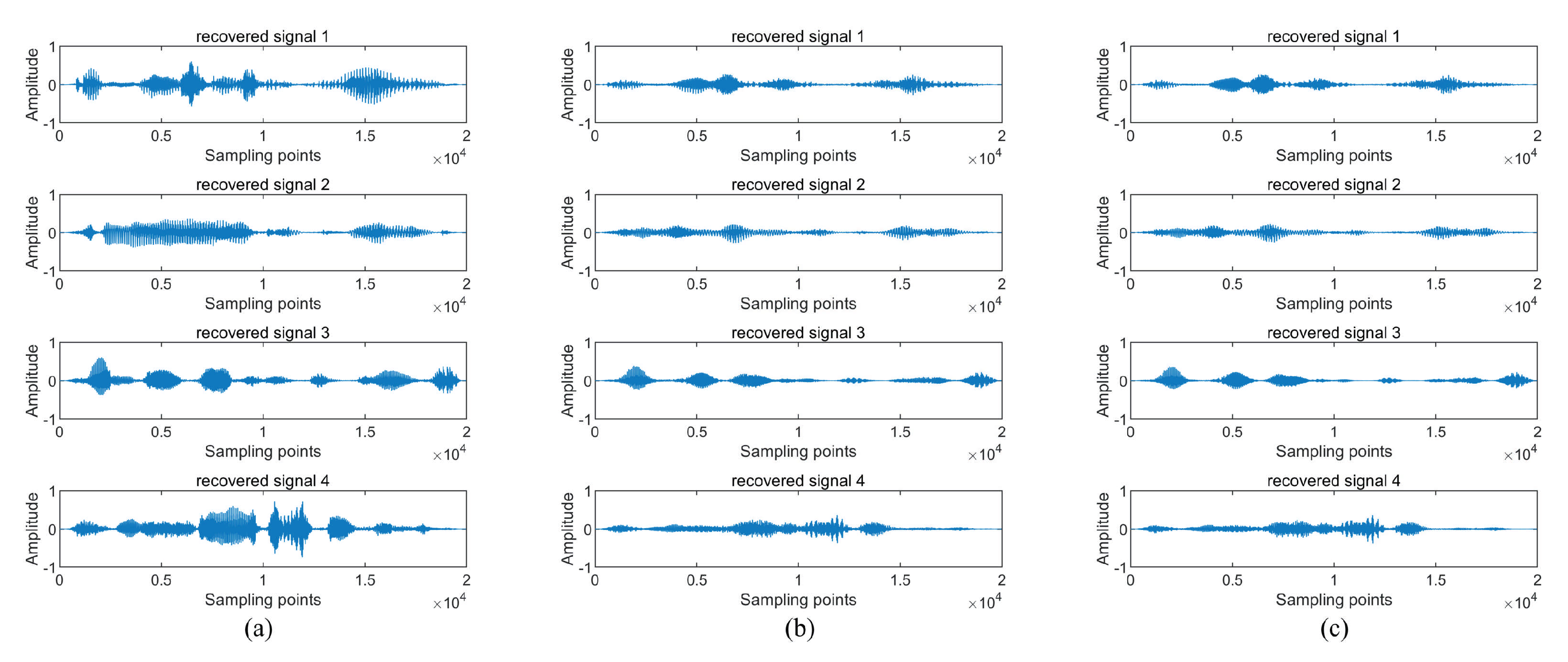
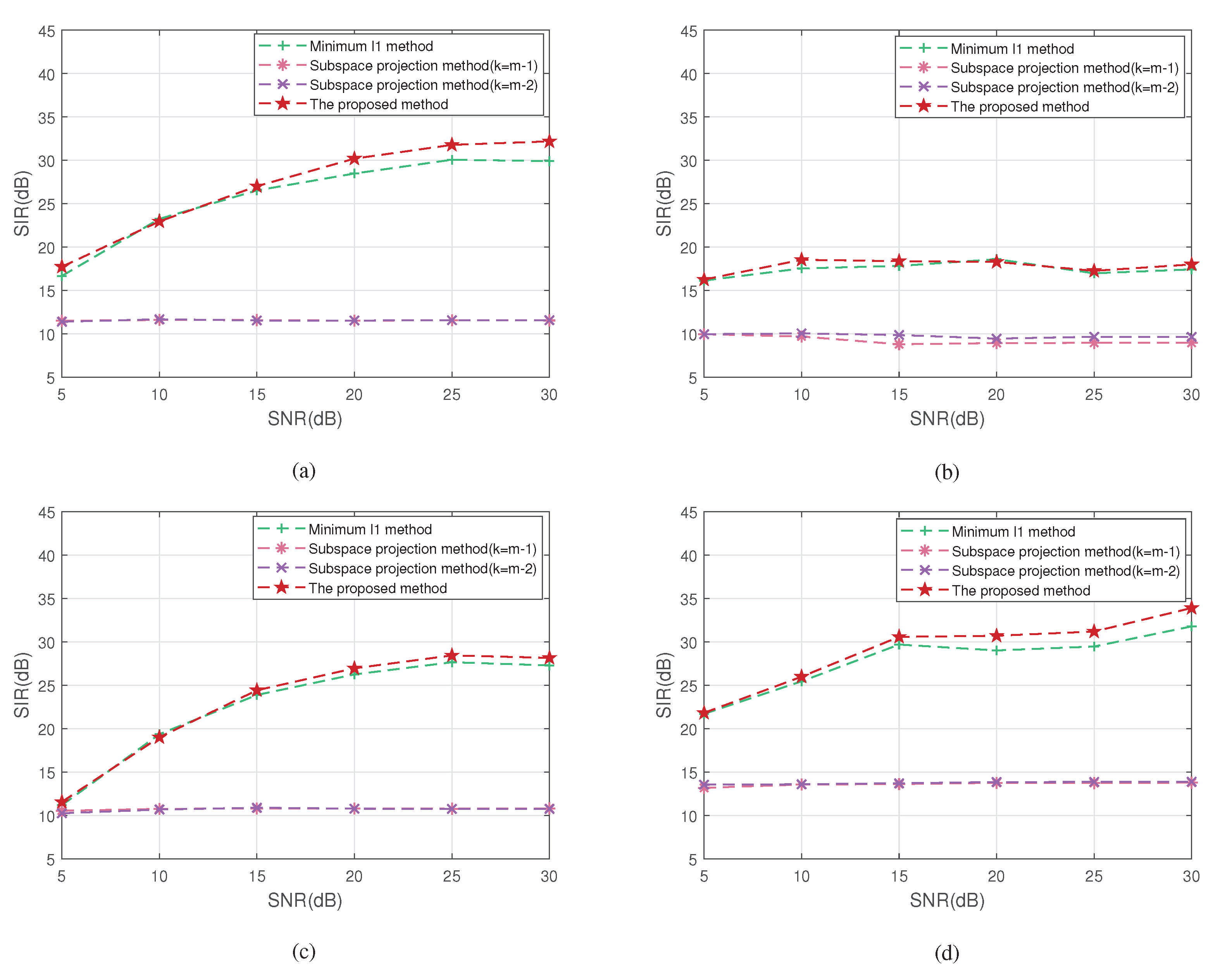
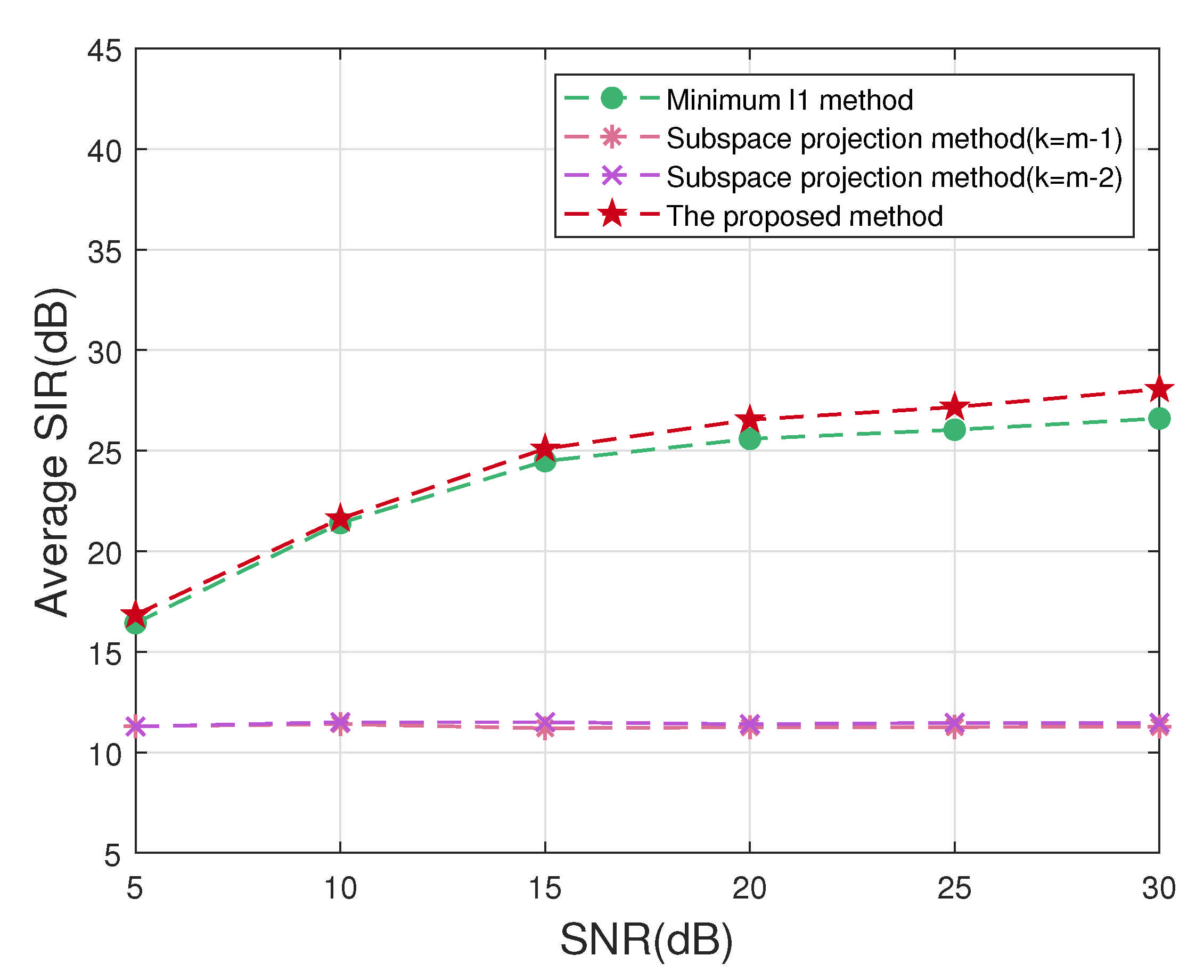
4.2.3. Experiment 3 Compares the Accuracy of Source Signal Recovery
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Mogami, S.; Takamune, N.; Kitamura, D.; Saruwatari, H.; Takahashi, Y.; Kondo, K.; Ono, N. Independent Low-Rank Matrix Analysis Based on Time-Variant Sub-Gaussian Source Model for Determined Blind Source Separation. IEEE Trans. Audio Speech Lang. Process. 2020, 28, 503–518. [Google Scholar] [CrossRef]
- Smith, S.; Pischella, M.; Terré, M. A Moment-Based Estimation Strategy for Underdetermined Single-Sensor Blind Source Separation. IEEE Signal Process. Lett. 2019, 26, 788–792. [Google Scholar] [CrossRef]
- Batalheiro, P.B.; Petraglia, M.R.; Haddad, D.B. New efficient subband structures for blind source separation. Signal Process. 2021, 182, 107957. [Google Scholar] [CrossRef]
- Xie, Y.; Xie, K.; Yang, J.; Xie, S. Underdetermined Blind Source Separation Combining Tensor Decomposition and Nonnegative Matrix Factorization. Symmetry 2018, 10, 521. [Google Scholar] [CrossRef] [Green Version]
- Feng, F.; Kowalski, M. Underdetermined Reverberant Blind Source Separation: Sparse Approaches for Multiplicative and Convolutive Narrowband Approximation. IEEE Trans. Audio Speech Lang. Process. 2019, 27, 442–456. [Google Scholar] [CrossRef]
- Zou, L.; Chen, X.; Dang, G.; Guo, Y.; Wang, Z.J. Removing Muscle Artifacts From EEG Data via Underdetermined Joint Blind Source Separation: A Simulation Study. IEEE Trans. Circuits Syst. II Exp. Briefs 2020, 67, 187–191. [Google Scholar] [CrossRef]
- Niknazar, H.; Nasrabadi, A.M.; Shamsollahi, M.B. A new blind source separation approach based on dynamical similarity and its application on epileptic seizure prediction. Signal Process. 2021, 183, 108045. [Google Scholar] [CrossRef]
- Guo, Q.; Li, C.; Ruan, G. Mixing Matrix Estimation of Underdetermined Blind Source Separation Based on Data Field and Improved FCM Clustering. Symmetry 2018, 10, 21. [Google Scholar] [CrossRef] [Green Version]
- Gu, Z.; Fan, T.; Lv, Q.; Chen, J.; Ye, D.; Huangfu, J.; Sun, Y.; Zhu, W.; Li, C.; Ran, L. Remote Blind Motion Separation Using a Single-Tone SIMO Doppler Radar Sensor. IEEE Trans. Geosci. Remote Sens. 2019, 57, 462–472. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, L.; Feng, Y.; Qian, Z.; Xu, X.; Chen, X. A recognition method for time-frequency overlapped waveform-agile radar signals based on matrix transformation and multi-scale center point detection. Appl. Acoust. 2021, 175, 107855. [Google Scholar] [CrossRef]
- Li, G.; Tang, G.; Wang, H.; Wang, Y. Blind source separation of composite bearing vibration signals with low-rank and sparse decomposition. Measurement 2019, 145, 323–334. [Google Scholar] [CrossRef]
- Lu, J.; Cheng, W.; He, D.; Zi, Y. A novel underdetermined blind source separation method with noise and unknown source number. J. Sound Vib. 2019, 457, 67–91. [Google Scholar] [CrossRef]
- Sen He, X.; He, F. Underdetermined mixing matrix estimation based on artificial bee colony optimization and single-source-point detection. Multimed. Tools Appl. 2020, 79, 13061–13087. [Google Scholar]
- Underdetermined Blind Source Separation for linear instantaneous mixing system in the non-cooperative wireless communication. Phys. Commun. 2021, 45, 101255. [CrossRef]
- Emura, S.; Sawada, H.; Araki, S.; Harada, N. Multi-Delay Sparse Approach to Residual Crosstalk Reduction for Blind Source Separation. IEEE Signal Process. Lett. 2020, 27, 1630–1634. [Google Scholar] [CrossRef]
- Xiao, Y.; Lu, W.; Yan, Q.; Zhang, H. Blind separation of coherent multipath signals with impulsive interference and Gaussian noise in time-frequency domain. Signal Process. 2021, 178, 107750. [Google Scholar] [CrossRef]
- Zou, L.; Chen, X.; Wang, Z.J. Underdetermined Joint Blind Source Separation for Two Datasets Based on Tensor Decomposition. IEEE Signal Process. Lett. 2016, 23, 673–677. [Google Scholar] [CrossRef]
- Jourjine, A.; Rickard, S.; Yilmaz, O. Blind separation of disjoint orthogonal signals: Demixing N sources from 2 mixtures. In Proceedings of the 2000 IEEE International Conference on Acoustics, Speech, and Signal, Istanbul, Turkey, 5–9 June 2000; Volume 5, pp. 2985–2988. [Google Scholar]
- Frédéric Abrard, Y.D. A time–frequency blind signal separation method applicable to underdetermined mixtures of dependent sources. Signal Process. 2005, 85, 1389–1403. [Google Scholar] [CrossRef]
- Reju, V.; Koh, S.N.; Soon, I.Y. An algorithm for mixing matrix estimation in instantaneous blind source separation. Signal Process. 2009, 89, 1762–1773. [Google Scholar] [CrossRef]
- Zhen, L.; Peng, D.; Yi, Z.; Xiang, Y.; Chen, P. Underdetermined Blind Source Separation Using Sparse Coding. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 3102–3108. [Google Scholar] [CrossRef] [PubMed]
- Zhen, L.; Peng, D.; Zhang, H.; Sang, Y.; Zhang, L. Underdetermined mixing matrix estimation by exploiting sparsity of sources. Measurement 2020, 152, 107268. [Google Scholar] [CrossRef]
- Bofill, P.; Zibulevsky, M. Underdetermined blind source separation using sparse representations. Signal Process. 2001, 81, 2353–2362. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Li, Y.; Wen, J.; Yan, S. Novel mixing matrix estimation approach in underdetermined blind source separation. Neurocomputing 2016, 173, 623–632. [Google Scholar] [CrossRef]
- Sen He, X.; He, F.; Hua Cai, W. Underdetermined BSS Based on K-means and AP Clustering. Circuits Syst. Signal Process. 2016, 35, 2881–2913. [Google Scholar]
- Sen He, X.; He, F.; Xu, L. Underdetermined mixing matrix estimation based on joint density-based clustering algorithms. Multimed. Tools Appl. 2021, 80, 8281–8308. [Google Scholar]
- Yang, J.; Guo, Y.; Yang, Z.; Xie, S. Under-Determined Convolutive Blind Source Separation Combining Density-Based Clustering and Sparse Reconstruction in Time-Frequency Domain. IEEE Trans. Circuits Syst. I Reg. Pap. 2019, 66, 3015–3027. [Google Scholar] [CrossRef]
- Mohimani, H.; Babaie-Zadeh, M.; Jutten, C. A Fast Approach for Overcomplete Sparse Decomposition Based on Smoothed ℓ0 Norm. IEEE Trans. Signal Process. 2009, 57, 289–301. [Google Scholar] [CrossRef] [Green Version]
- Guoqing, R.; Qiang, G.; Gao, J. Novel underdetermined blind source separation algorithm based on compressed sensing and K-SVD. Trans. Emerg. Telecommun. Tech. 2017, 29, e3427. [Google Scholar]
- Zhang, C.; Hao, D.; Hou, C.; Yin, X. A New Approach for Sparse Signal Recovery in Compressed Sensing Based on Minimizing Composite Trigonometric Function. IEEE Access 2018, 6, 44894–44904. [Google Scholar] [CrossRef]
- Mirzaei, S.; Van Hamme, H.; Norouzi, Y. Blind audio source counting and separation of anechoic mixtures using the multichannel complex NMF framework. Signal Process. 2015, 115, 27–37. [Google Scholar] [CrossRef] [Green Version]
- Nathwani, K.; Hegde, R.M. Joint source separation and dereverberation using constrained spectral divergence optimization. Signal Process. 2015, 106, 266–281. [Google Scholar] [CrossRef]
- Aissa-El-Bey, A.; Linh-Trung, N.; Abed-Meraim, K.; Belouchrani, A.; Grenier, Y. Underdetermined Blind Separation of Nondisjoint Sources in the Time-Frequency Domain. IEEE Trans. Signal Process. 2007, 55, 897–907. [Google Scholar] [CrossRef] [Green Version]
- Ankerst, M.; Breunig, M.M.; Kriegel, H.P.; Sander, J. OPTICS: Ordering Points to Identify the Clustering Structure. In Proceedings of the ACM SIGMOD International Conference on Management of Data, Philadelphia, PA, USA, 1–3 June 1999; pp. 2985–2988. [Google Scholar]


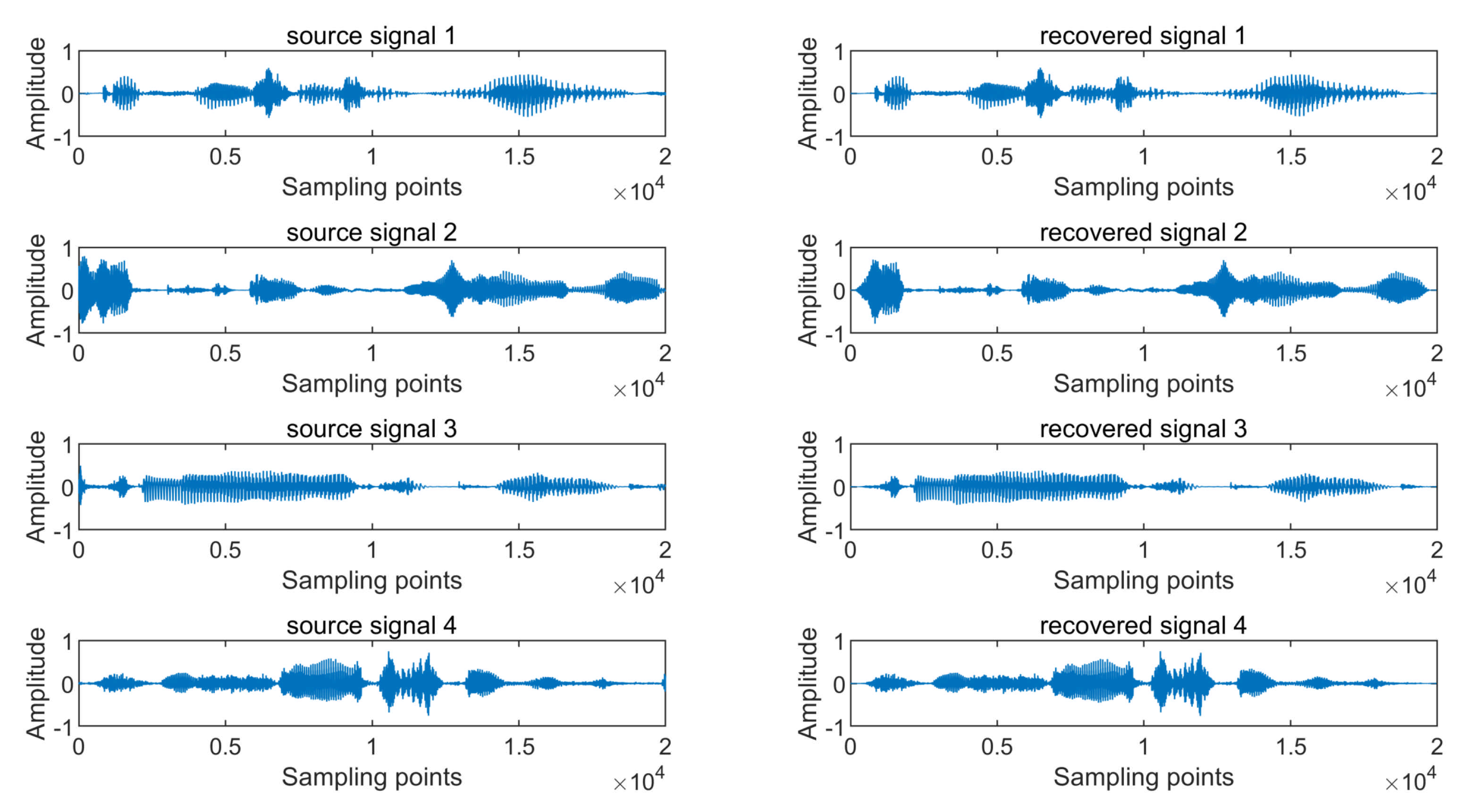
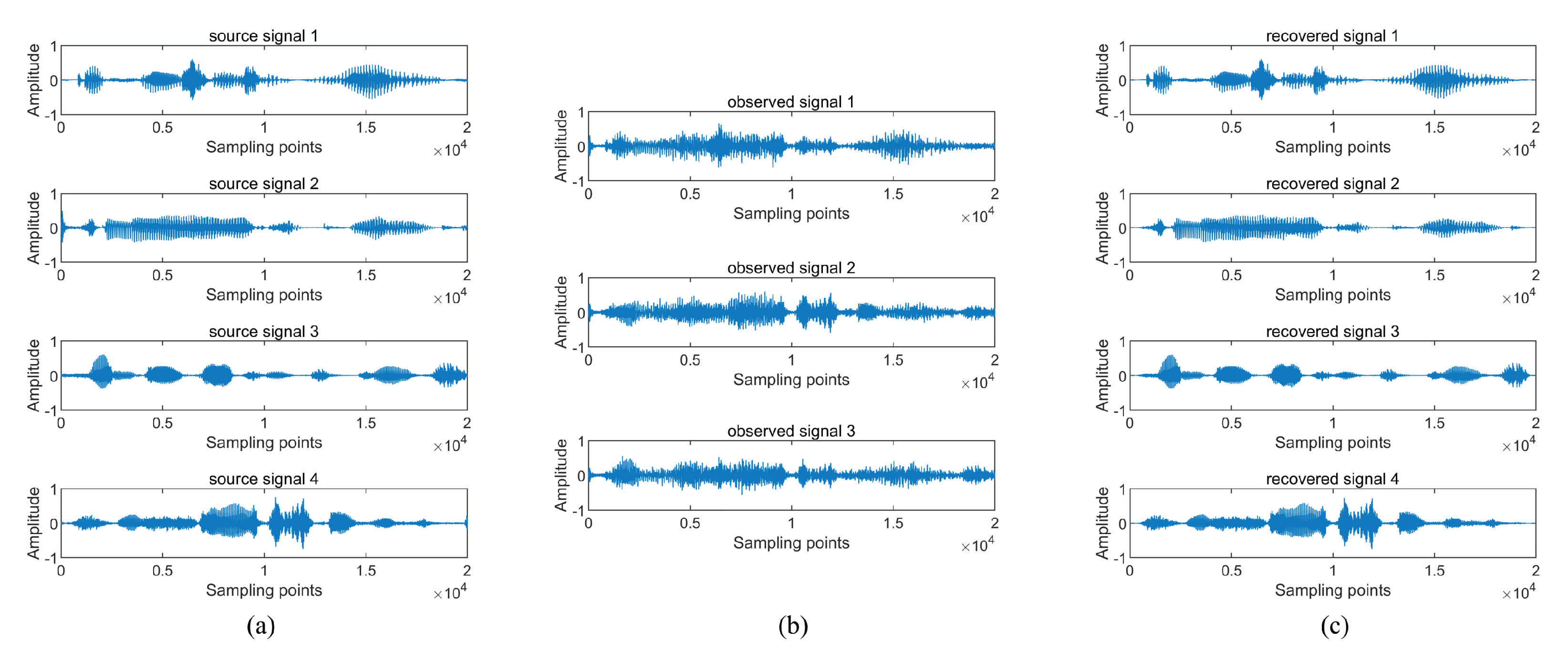
| Parameter | ||||||
|---|---|---|---|---|---|---|
| Value | 3 | 3 | 0.99 | 0.2 | 0.1 | 0.99 |
| Algorithm | The SIR of the Recovered Signal | ||||
|---|---|---|---|---|---|
| Average | |||||
| Minimum -norm method | 30.6500 | 17.4698 | 28.5059 | 30.6469 | 26.8182 |
| Original subspace projection method () | 11.6024 | 8.9246 | 10.8156 | 13.7702 | 11.2782 |
| Original subspace projection method () | 11.5598 | 9.6417 | 10.7634 | 13.8636 | 11.4571 |
| The proposed method | 32.6860 | 17.7190 | 28.9573 | 33.3265 | 28.1722 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Zhang, Y.; Yin, S.; Wang, Y.; Wu, G. A Novel Underdetermined Blind Source Separation Method Based on OPTICS and Subspace Projection. Symmetry 2021, 13, 1677. https://doi.org/10.3390/sym13091677
Wang Q, Zhang Y, Yin S, Wang Y, Wu G. A Novel Underdetermined Blind Source Separation Method Based on OPTICS and Subspace Projection. Symmetry. 2021; 13(9):1677. https://doi.org/10.3390/sym13091677
Chicago/Turabian StyleWang, Qingyi, Yiqiong Zhang, Shuai Yin, Yuduo Wang, and Genping Wu. 2021. "A Novel Underdetermined Blind Source Separation Method Based on OPTICS and Subspace Projection" Symmetry 13, no. 9: 1677. https://doi.org/10.3390/sym13091677
APA StyleWang, Q., Zhang, Y., Yin, S., Wang, Y., & Wu, G. (2021). A Novel Underdetermined Blind Source Separation Method Based on OPTICS and Subspace Projection. Symmetry, 13(9), 1677. https://doi.org/10.3390/sym13091677






