Rotating-Frame Overhauser Transfer via Long-Lived Coherences ^†

Abstract

Solution-state distance restraints for protein structure determination with Ångström-level resolution rely on through-space transfer of magnetization between nuclear spins. Such magnetization transfers, named Overhauser effects, occur via dipolar magnetic couplings. We demonstrate improvements in magnetization transfer using long-lived coherences (LLCs)—singlet-triplet superpositions that are antisymmetric with respect to spin-permutation within pairs of coupled magnetic nuclei—as the magnetization source. Magnetization transfers in the presence of radio-frequency irradiation, known as ‘rotating-frame’ Overhauser effects (ROEs), are predicted by theory to improve by the use of LLCs; calculations are matched by preliminary experiments herein. The LLC-ROE transfers were compared to the transmission of magnetization via classical transverse routes. Long-lived coherences accumulate magnetization on an external third proton, K, with transfer rates that depended on the tumbling regime. $\left\{I,S\right\} \to K$ transfers in the LLC configuration for (I,S) are anticipated to match, and then overcome, the same transfer rates in the classical configuration as the molecular rotational correlation times increase. Experimentally, we measured the LLC-ROE transfer in dipeptide AlaGly between aliphatic protons in different residues K = Ala − H^α and (I,S) = Gly − H^α1,2 over a distance $d\left[K,\left(I,S\right)\right]$ = 2.3 Å. Based on spin dynamics calculations, we anticipate that, for such distances, a superior transfer of magnetization occurs using LLC-ROE compared to classical ROE at correlation times above ${\tau }_C=10 ns$. The LLC-ROE effect shows potential for improving structural studies of large proteins and offering constraints of increased precision for high-affinity protein-ligand complexes in slow tumbling in the liquid state.

1. Introduction

Structure determination for proteins using liquid-state NMR was first demonstrated in the 1980s [1]. Sets of experiments were developed to tackle proteins of various sizes. The experimental approach consists of following connections between magnetic nuclei based on the existence of common electron clouds or on the proximity in space. For proteins below 10 kDa in size, considered ‘small’ by solution-state high-resolution analysis standards, the set consists of experiments rendered famous under the acronyms: COSY [2], TOCSY [3], NOESY [1] or ROESY [4]. The cornerstone of structure determination are the distance restraints derived from NOESY and ROESY experiments, in their two- or three-dimensional avatars. The transfer of magnetization between spins (A,X) in these NMR experiments is mediated by magnetic interactions. In this paper, we look at (A,X) neighbouring spins that transfer magnetization, and (I, S) pairs of J-coupled spins that can be locked in singlet-triplet configurations. Magnetic interactions suitable for magnetization transfer occur as scalar couplings, via J_AX-coupling constants, or dipolar–dipolar interactions, governed by dipolar coupling constants $b_{AX}=\frac{{\mu }_0{\gamma }_A{\gamma }_{X}h}{8{\pi }^2}⬝\frac{1}{r_{AX}^3}$, where $r_{AX}$ is the inter-nuclear distance between the two A and X spins. Besides inter-nuclear distances, the solution tumbling time constant, which correlates with the protein size, is important for the accumulation of a signal.

Though nuclear magnetic resonance is fairly free of perturbations compared to other spectroscopies, immediate magnetic neighbours of a detected site of resonance can dampen time-domain free-induction decays and, thus, broaden frequency-domain signals. The main issue in through-space transfer experiments is that dipolar cross-talk can only be detected with relatively short ranges of 5–6 Å, due in part to the small magnitude of nuclear magnetic dipoles, but mainly to the short relaxation time constants of coherences that yield detectable signals. That is, magnetization transfer time in NOESY/ROESY experiments depends critically on the relaxation time constants of the involved nuclei [5,6,7,8]. The signal transfer varies with the inverse sixth power of the distance between communicating spins A and X, $\frac{1}{r_{AX}^6}$, and is proportional with the product of squared gyromagnetic constants ${\gamma }_A^2{\gamma }_X^2$, thus limiting the maximum observable interaction distances to spheres of effective radii of 5-6 Å around the involved partners [9]. Two physical approaches are available to increase the radius of the sphere within which structural constraints can be established: (i) involve magnetic dipoles with increased gyromagnetic ratios, or (ii) increase the available transfer time between neighbouring coherently aligned magnetic dipoles. The first approach was used involving electron spins as one of the cross-talk partners, thus extending the boundaries for distance information to ca. 20 Å when using paramagnetic relaxation enhancement effects (PRE’s) [10].

The recent discovery of nuclear-spin singlet states [11,12,13] involving pairs of J-coupled spins I and S has led to enhanced spin memory and spectral resolution in high magnetic fields. This provides an option for extending the time for dipolar contact beyond the prior limits imposed by the decay of coherent alignment in each site and, therefore, enabling option (ii) above. There are several ways in which one can excite a two-spin long-lived state (LLS), which corresponds to a density operator of the form ${\widehat{\rho }}_{LLS}=-\frac{4}{3}\left({\widehat{I}}_x{\widehat{S}}_x+{\widehat{I}}_y{\widehat{S}}_y+{\widehat{I}}_z{\widehat{S}}_z\right)$ in the Cartesian product operator basis [14]. The optimal spin dynamics designed for transferring equilibrium magnetization to nuclear spin singlet-triplet population differences are widely different depending on the coupling regime. When the scalar coupling constant is much smaller than the difference in chemical shifts ($J_{IS}<∆{\omega }_{IS})$, the regime is known as the weakly-coupled regime, and a particular pulse sequence is desired [15]. In the strong-coupled regime, when $J_{IS}>∆{\omega }_{IS}$, there are other pulse sequences more appropriate for these systems [16,17]. In essence, all transfer pulse sequences necessitate switching a pair of magnetically inequivalent nuclear spins (where magnetization lifetimes are governed by the R₁ and R₂ relaxation rate constants) to a regime where they are rendered magnetically equivalent, and the ${\widehat{\rho }}_{LLS}$ operator is immune to the dipolar coupling, which is the main source of relaxation in the case of protons [18]. This is most effectively achieved by applying a continuous-wave irradiation, such that the chemical shift difference between the two spins becomes negligible. The resulting singlet-triplet population imbalance is immune to the dipolar coupling between the spins and, thus, exponentially decays with a small relaxation rate constant due to other interactions: chemical shift anisotropy, spin-rotation or inter-molecular dipolar interactions. Their counterparts, the singlet-triplet superpositions, also known as long-lived coherences (LLCs):

$${\widehat{\rho }}_{LLC}=({\widehat{I}}_x-{\widehat{S}}_x)+i\left(2{\widehat{I}}_y{\widehat{S}}_z-2{\widehat{I}}_z{\widehat{S}}_y\right).$$

(1)

display lifetimes up to nine times longer than that of transverse magnetization, for the case of two J-coupled spins [19,20], and a damped oscillatory evolution, given by $J_{IS}$ scalar coupling constant between the spins I and S. In order to excite such coherences, a symmetry-breaking mechanism (usually chemical shift difference) between the two spins is required to change the relative sign of the ${\widehat{I}}_x$ and ${\widehat{S}}_x$ magnetization components. The spins are then rendered equivalent by the application of a strong radio-frequency irradiation, as in ROESY experiments, where using a “spin-lock” establishes dipolar contacts between neighbouring nuclear spins.

We propose, in this paper, the use of long relaxation times of LLCs in the transfer of magnetization via the Overhauser effect, to a third spin via dipolar couplings. The LLC-ROESY experiments are proposed to facilitate the assignment and structure determination of proteins, potentially extending the protein-size limit for which through-space magnetization transfer can be attempted.

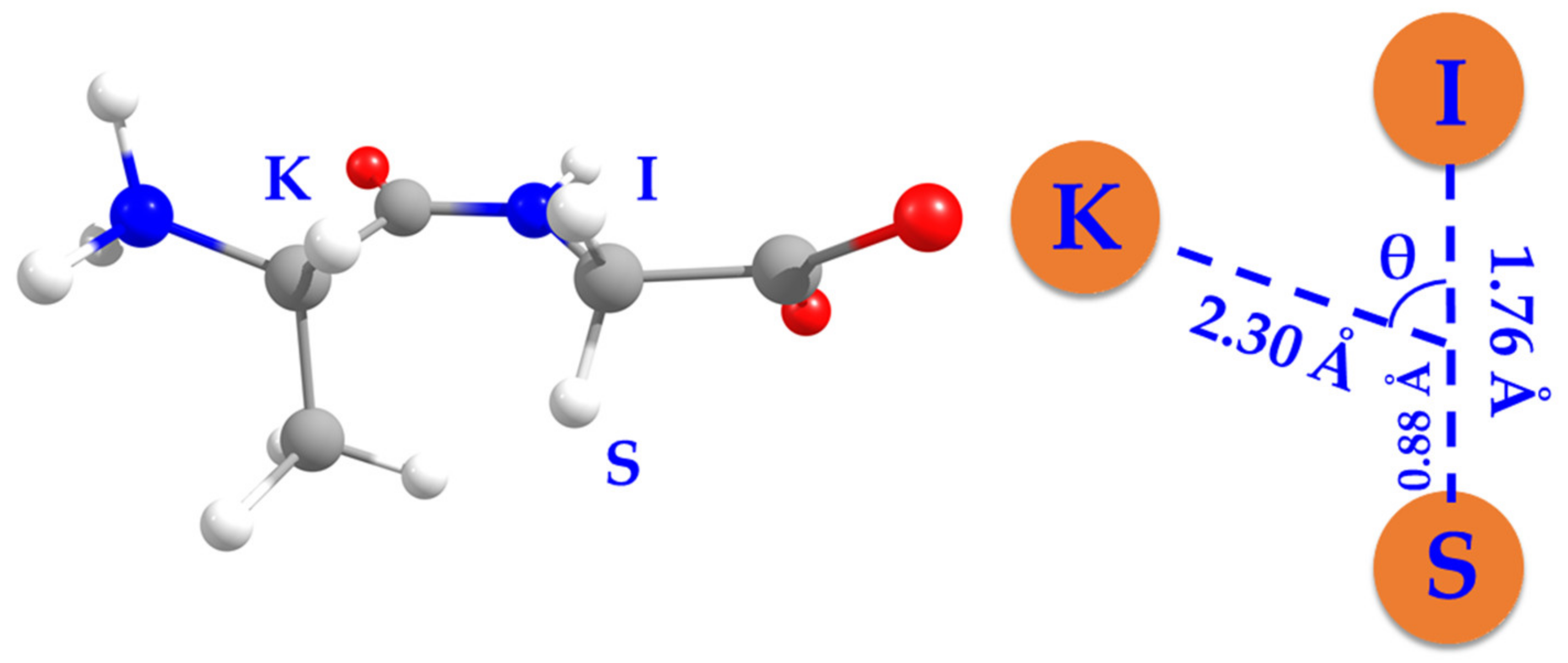
2. Materials and Methods

The transfer of magnetization by dipolar couplings was studied in an LLC-setting similar to the AlaGly dipeptide (Figure 1). The geometrical parameters, such as interatomic distances and angles, were computed with a Gaussian09 [21], using the density functional theory (DFT) with the Perdew–Burke–Ernzerhof (PBE0) hybrid functional along with the triple-ζ basis set with polarisation (‘def2tzvp’).

The spin set-up used in calculations consisted of two J-coupled spins (denoted I and S) that acted as a magnetization source. Spin dynamics started from either transverse magnetization, excited from the equilibrium state, (${\widehat{\rho }}_x\left(0\right)={\widehat{I}}_x+{\widehat{S}}_x$), or LLCs, (${\widehat{\rho }}_{LLC}\left(0\right)={\widehat{I}}_x-{\widehat{S}}_x$), and calculated the rotating-frame Overhauser transfer towards the third uncoupled spin, denoted by K ($J_{IS}\ne 0;J_{IK}=J_{SK}=0)$. We performed several simulations in which the scalar coupling constant $J_{IS}$ was varied, as well as the rotational correlation time ${\tau }_C$ and the inter-nuclear distances $d_{IK}$ and $d_{SK}$. The numerical simulations were performed with the Spinach [22] and SpinDynamica [23] software package, and the code is provided in the Supplementary Materials.

3. Results

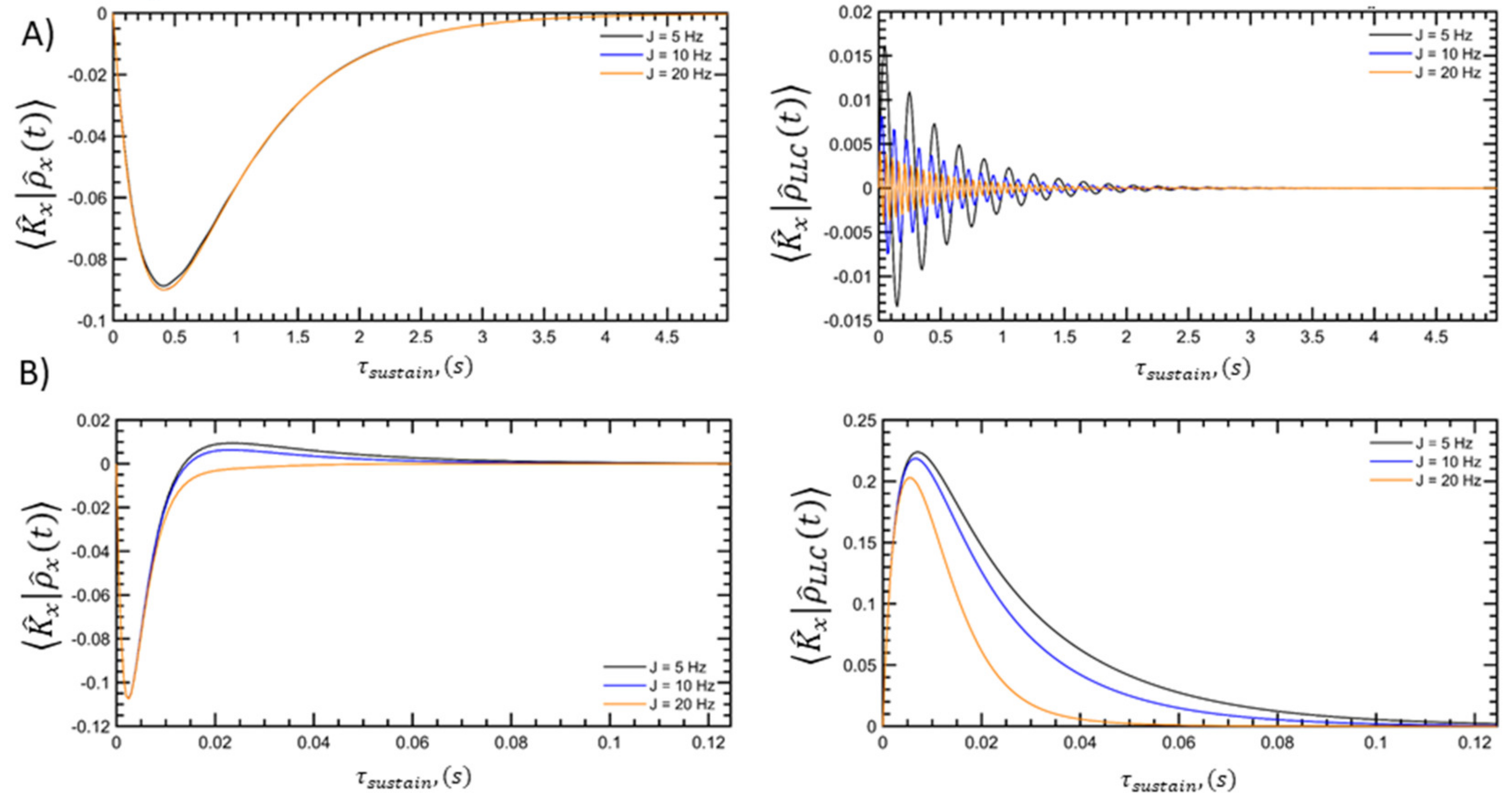
3.1. Rotating-Frame Overhauser Transfer in Different Rotational Tumbling Regimes

Starting from the configuration described in Figure 1, we followed the evolution of the density operators ${\widehat{\rho }}_x\left(t\right)$ $({\widehat{\rho }}_x\left(0\right)={\widehat{I}}_x+{\widehat{S}}_x)$ and ${\widehat{\rho }}_{LLC}\left(t\right)$ (${\widehat{\rho }}_{LLC}\left(0\right)={\widehat{I}}_x-{\widehat{S}}_x)$ by projecting them onto the initial density operators $\langle {\widehat{I}}_x+{\widehat{S}}_x|{\widehat{\rho }}_x\left(t\right)\rangle$ and $\langle {\widehat{I}}_x-{\widehat{S}}_x|{\widehat{\rho }}_{LLC}\left(t\right)\rangle$, respectively, and onto the transverse component of spins at site K, ${\widehat{K}}_x$, as $\langle {\widehat{K}}_x|{\widehat{\rho }}_x\left(t\right)\rangle$ and $\langle {\widehat{K}}_x|{\widehat{\rho }}_{LLC}\left(t\right)\rangle$, respectively. By doing so, we could follow the evolution of the initial magnetization, which was magnetically active and could be recorded in a NMR experiment, and at the same time follow the amount of transverse magnetization accumulated on the K spins. The Hamiltonian corresponding to the continuous-wave sustained evolution of both ${\widehat{\rho }}_x\left(t\right)$ and ${\widehat{\rho }}_{LLC}\left(t\right)$ is:

$${\widehat{H}}_{CW}=2\pi {\nu }_1\left({\widehat{I}}_x+{\widehat{S}}_x+{\widehat{K}}_x\right)+2\pi {\nu }_I⬝{\widehat{I}}_z+2\pi {\nu }_S⬝{\widehat{S}}_z+2\pi {\nu }_K⬝{\widehat{K}}_z+2\pi J_{IS}⬝\widehat{\overrightarrow{\mathit{I}}}⬝\widehat{\overrightarrow{\mathit{S}}}.$$

(2)

The first term in the Hamiltonian of Equation (2) describes the effect of the radio-frequency field of amplitude ${\nu }_1$ and phase x, which becomes the dominant effect when applied close to the resonance frequencies of the spins involved. The following three terms are the classical Zeeman contributions of spins I, S, and K (in the rotating frame), and the last term describes the J-coupling between spins I and S.

Spin parameters were extracted from the AlaGly ¹H spectrum: ${\nu }_I=-25\mathrm{Hz}$ is the frequency offset of the I spin; ${\nu }_S=25 \mathrm{Hz}$ is the frequency offset of the S spin; ${\nu }_K=100\mathrm{Hz}$ is the frequency offset of the K spin (these frequencies correspond to rotating-frame frequencies of AlaGly protons Gly-H^α1, H^α2 and Ala-H^α, respectively, at $B_0=9.4 \mathrm{T}$, i.e., with the radio-frequency carrier applied at the average Larmor frequencies of the I and S spins); ${\nu }_1=1000 \mathrm{Hz}$ is the amplitude of the continuous-wave (CW) sustaining rotating field; and $J_{IS}=17 \mathrm{Hz}$ is the scalar coupling constant between spins I and S. Taking into account the magnitude and commutation properties of the various terms, further transformations of Equation (2) were carried out to reflect the implications of the symmetry of the spin system. The operator corresponding to the total transverse magnetization ${\widehat{I}}_x+{\widehat{S}}_{x }+{\widehat{K}}_{x }$, commutes with the dominant part of ${\widehat{H}}_{CW}$, which can be re-written as:

$${\widehat{H}}_{CW}=2\pi {\nu }_1\left({\widehat{I}}_x+{\widehat{S}}_x+{\widehat{K}}_x\right)+\pi ({\nu }_I+{\nu }_S)⬝\left({\widehat{I}}_z+{\widehat{S}}_z\right)+\pi ({\nu }_I-{\nu }_S)⬝\left({\widehat{I}}_z-{\widehat{S}}_z\right)+2\pi {\nu }_K⬝{\widehat{K}}_z+2\pi J_{IS}⬝\widehat{\mathit{I}}⬝\widehat{\mathit{S}}.$$

(3)

The only term in the Hamiltonian that does not commute with ${\widehat{\rho }}_x\left(0\right)$, $\pi ({\nu }_I-{\nu }_S)\left({\widehat{I}}_z-{\widehat{S}}_z\right)$, transforms ${\widehat{I}}_x+{\widehat{S}}_x$ into components ${\widehat{I}}_y,{\widehat{ S}}_y$ that were rapidly dispersed by inhomogeneities in the radio-frequency field amplitude across the sample. Therefore, the initial density operator would not evolve in observable terms by coherent mechanisms: ${\widehat{\rho }}_x\left(t\right)\stackrel{{\widehat{H}}_{CW}}{\to }{\widehat{I}}_x+{\widehat{S}}_x$. On the other hand, LLCs feature coherent evolution [19,20], as detailed in the Supporting Information, is given by:

$${\widehat{\rho }}_{LLC}\left(t\right)\stackrel{{\widehat{H}}_{CW}}{\to }\left({\widehat{I}}_x-{\widehat{S}}_x\right)\cos \left(2\pi J_{IS}t\right)+\left(2{\widehat{I}}_y{\widehat{S}}_z-2{\widehat{I}}_z{\widehat{S}}_y\right)\sin \left(2\pi J_{IS}t\right).$$

(4)

The decay rate constant of this term is given by the Bloch–Redfield–Wangsness relaxation rate calculation approach [24]. Herein, we considered only dipole–dipole interactions between the three spins. We considered the rotational correlation times ${\tau }_C=100\mathrm{ps}$ and ${\tau }_C\prime =50 ns$, characteristic for the fast and slow-tumbling regimes, respectively.

The time evolutions of the transverse magnetization and LLCs occurred with the former decaying mono-exponentially, while the latter featured an oscillatory evolution with a frequency equal to $J_{IS}$ and an extended lifetime (Figure 2A). In a fast-tumbling regime, the ROE transferred to ${\widehat{K}}_x$ from the two sources, ${\widehat{\rho }}_x$ and ${\widehat{\rho }}_{LLC}$, differed significantly: starting from ${\widehat{\rho }}_x\left(0\right)={\widehat{I}}_x+{\widehat{S}}_x$, the $K_x$ component accumulated up to a maximum and then decayed [5], while, starting from ${\widehat{\rho }}_{LLC}\left(0\right)={\widehat{I}}_x-{\widehat{S}}_x$, the ${\widehat{K}}_x$ component oscillated with a frequency close to the $J_{IS}$ constant (see below).

In the slow-tumbling regime, ${\tau }_C=50 ns,$ (Figure 2B), oscillations were wiped out by relaxation, as the lifetimes of all forms of magnetization decreased. The most interesting feature of the LLC transfer in this regime is that it acted as a better magnetization source for ROE transfer than classical transverse magnetization. The improvement at this specific molecular rotational correlation time, ${\tau }_C=50 ns,$ measured as the ratio of predicted cross-peak intensities $I_{ROE-LLC}/I_{ROEClassic}$, was by a factor of 2.

3.2. Analytical Derivation of the Evolution of Magnetization Components

In order to understand the peculiar rotating-frame transfer from coupled magnetic nuclei in LLC configurations to a third neighbouring spin, one needs to solve the system of differential equations describing the evolution of both LLCs and the ${\widehat{K}}_x$ components (Equations (5) and (6)) sustained by the radio-frequency field. We compared the obtained results to the analytical form of the evolution of transverse magnetization (${\widehat{I}}_x+{\widehat{S}}_x)$ and LLC (${\widehat{I}}_x-{\widehat{S}}_x)$:

$$\frac{d}{dt}\left(\begin{array}{c}\langle {\widehat{I}}_x+{\widehat{S}}_x|{\widehat{\rho }}_x\left(t\right)\rangle \\ \langle {\widehat{K}}_x|{\widehat{\rho }}_x\left(t\right)\rangle \end{array}\right)=\left(\begin{array}{cc}{\rho }_{+}& {\sigma }_{+}\\ {\sigma }_{+}& {\rho }_K\end{array}\right)\left(\begin{array}{c}\langle {\widehat{I}}_x+{\widehat{S}}_x|{\widehat{\rho }}_x\left(t\right)\rangle \\ \langle {\widehat{K}}_x|{\widehat{\rho }}_x\left(t\right)\rangle \end{array}\right).$$

(5)

$$\frac{d}{dt}\left(\begin{array}{c}\langle {\widehat{I}}_x-{\widehat{S}}_x|{\widehat{\rho }}_{LLC}\left(t\right)\rangle \\ \langle {\widehat{K}}_x|{\widehat{\rho }}_{LLC}\left(t\right)\rangle \end{array}\right)=\left(\begin{array}{cc}{\rho }_{-}+i⬝2\pi J_{IS}& {\sigma }_{-}\\ {\sigma }_{-}& {\rho }_K\end{array}\right)\left(\begin{array}{c}\langle {\widehat{I}}_x-{\widehat{S}}_x|{\widehat{\rho }}_{LLC}\left(t\right)\rangle \\ \langle {\widehat{K}}_x|{\widehat{\rho }}_{LLC}\left(t\right)\rangle \end{array}\right).$$

(6)

where $\langle \widehat{A}|\widehat{B}\rangle$ is the scalar product between operators $\widehat{A}$ and $\widehat{B}$ in the Liouville space; ${\rho }_{\pm }$ are the auto-relaxation rate constants of ${\widehat{I}}_x\pm {\widehat{S}}_x$; ${\rho }_K$ is the auto-relaxation rate constant of ${\widehat{K}}_x$, and ${\sigma }_{\pm }$ are cross-relaxation rate constants describing a magnetization transfer between ${\widehat{I}}_x\pm {\widehat{S}}_x$ on one side, and ${\widehat{K}}_x$ on the other side. The analytical expressions for ${\rho }_{\pm }$, ${\sigma }_{\pm }$ were derived using the SpinDynamica [23] software package for a relaxation superoperator, constructed using exclusively dipolar couplings between the three spins (see Supplementary Materials). Equation (7) indicates that the two cross-relaxation constants differ significantly when transverse magnetization or LLCs are used as magnetization sources. Notably, the cross-relaxation rate constant from LLCs to the third spin K is always smaller than that from ${\widehat{I}}_x+{\widehat{S}}_x$.

$${\sigma }_{\pm }=\frac{\langle {\widehat{I}}_x\pm {\widehat{S}}_x\left|\widehat{\widehat{\Gamma }}\right|{\widehat{K}}_x\rangle }{\langle {\widehat{I}}_x\pm {\widehat{S}}_x|{\widehat{I}}_x\pm {\widehat{S}}_x\rangle }=\frac{b_{IK}^2\pm b_{SK}^2}{20}\left(2J\left(0\right)+3J\left(\omega \right)\right).$$

(7)

where $\widehat{\widehat{\Gamma }}$ is the relaxation superoperator, $b_{IK}$ and $b_{SK}$ are the dipolar coupling constants between spins $\left\{I,K\right\}$ and $\left\{S,K\right\}$, and $J\left(m⬝\omega \right)=\frac{2}{5}\frac{{\tau }_C}{1+{\tau }_c^2⬝{\omega }^2⬝m^2}$ is the spectral density function. The transfer is null when K is placed on the perpendicular bisector of the line that connects the I and S spins. The dependence of the LLC-based transfer on the geometry of the three-spin system is discussed in the Supporting Information, and the results are shown in Figures S2 and S3.

The solutions for the Equations (5) and (6) result in a different behaviour for the accumulation of ${\widehat{K}}_x$ magnetization is described by:

$$\langle {\widehat{K}}_x|{\widehat{\rho }}_x\left(t\right)\rangle =\frac{e^{\frac{1}{2}t\left({\rho }_K+{\rho }_{+}\right)}{\sigma }_{+}\sin h\left(\frac{1}{2}t\sqrt{{\left({\rho }_K-{\rho }_{+}\right)}^2+4{\sigma }_{+}^2}\right)}{\sqrt{{\left({\rho }_K-{\rho }_{+}\right)}^2+4{\sigma }_{+}^2}}.$$

(8)

$$\langle {\widehat{K}}_x|{\widehat{\rho }}_{LLC}\left(t\right)\rangle =Re\{\frac{e^{\frac{1}{2}t\left(2\pi iJ+{\rho }_K+{\rho }_{-}\right)}{\sigma }_{-}\sin h\left(\frac{1}{2}t\sqrt{-\left[2\pi J+i{\left({\rho }_K-{\rho }_{-}\right)}^2\right]+4{\sigma }_{-}^2}\right)}{\sqrt{-\left[2\pi J+i{\left({\rho }_K-{\rho }_{-}\right)}^2\right]+4{\sigma }_{-}^2}}\}.$$

(9)

Starting from the sum of transverse magnetization (${\widehat{I}}_x+{\widehat{S}}_x)$, the ROE transfer towards the K spin is described by a bi-exponential function (Equation (8)). For the case of ROE transfer from LLCs, there was an apparent oscillation close to J-coupling constant between the I and S spins. The $i\left({\rho }_K-{\rho }_{-}\right)$ factor in Equation (9) would perturb the J-oscillation in a similar manner to “relaxation-induced oscillations” [25,26], leading to a different oscillation frequency. The derivation of Equations (8) and (9) is provided in the Supporting Materials as a Mathematica notebook.

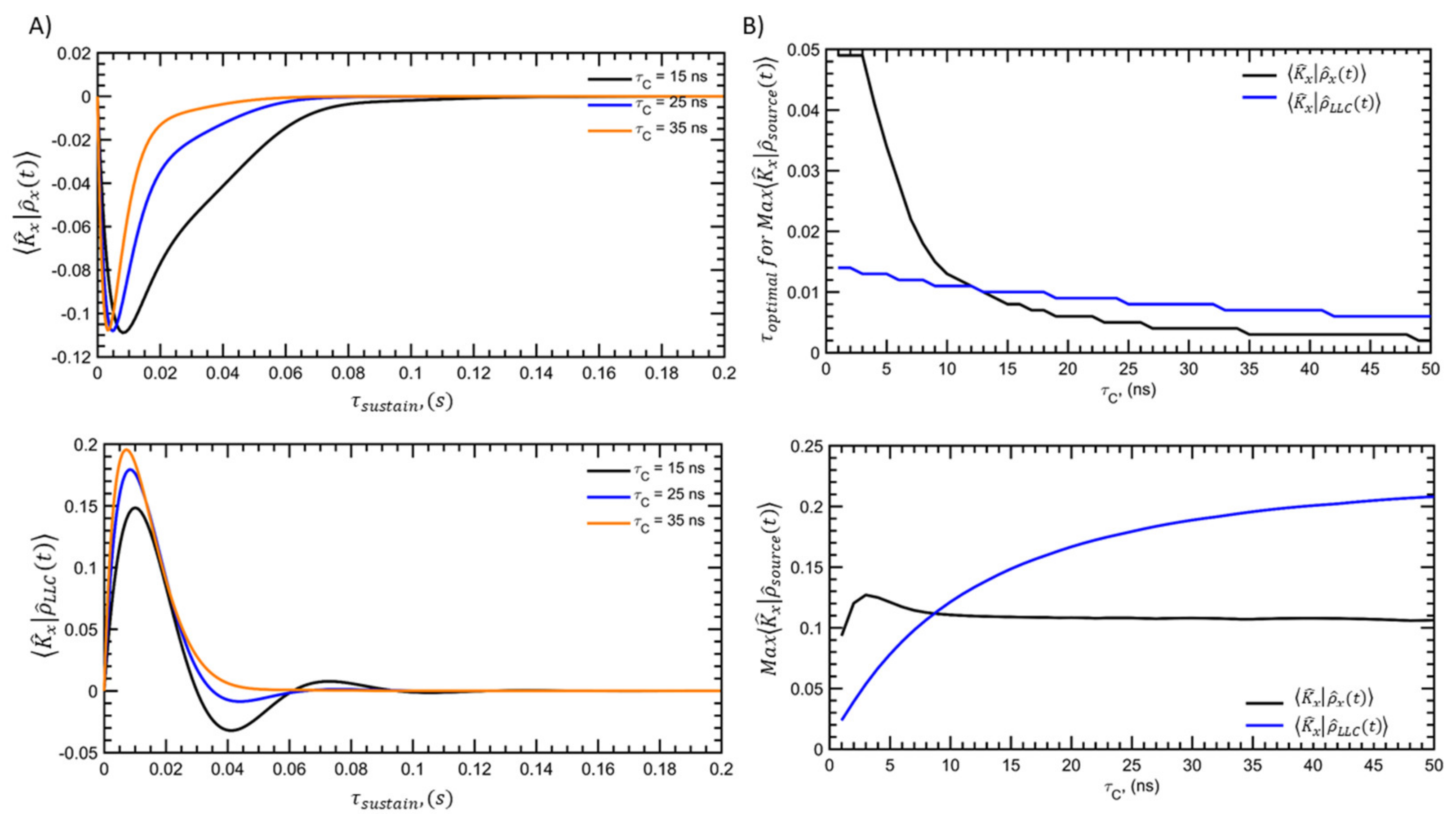
3.3. Modulation Induced by the J-Coupling Constant

To better understand the influence of the J-coupling on the ROE transfer, we performed the same simulations using different values of the $J_{IS}=\left\{5\mathrm{Hz},10\mathrm{Hz},20\mathrm{Hz}\right\}$. There was no significant difference in the case of the ROE transfer from the transverse magnetization, but a significant decrease of the transfer was observed when increasing the value of the $J_{IS}$ constant using LLCs as a magnetization source (Figure 3A). Both behaviours were predicted by Equations (8) and (9). We analysed transverse magnetization transfer at the rotational correlation time ${\tau }_C=50ns$, which in water solvent at ambient temperature corresponded to molecular species of tens of nm in diameter (Figure 3B). In this slow-tumbling condition, we also performed $\left\{I,S\right\}\to K$ transfer simulations with different values of the coupling constant $J_{IS}=\left\{5\mathrm{Hz},10\mathrm{Hz},20\mathrm{Hz}\right\}$. For this scenario, the classical ROE depended little on the scalar coupling constant, while the transfer from LLC decreased with increasing value of J, but was always enhanced compared to that from transverse magnetization.

3.4. LLC-ROE in the Slow-Tumbling Regime

Due to their extended lifetime, the LLCs were expected to transfer magnetization towards neighbouring spins for long periods and, thus, enhance their signal considerably, notwithstanding the relatively low transfer rates. This effect was however inhibited in fast-tumbling regimes by the J frequency oscillations of the LLCs. Accumulated transverse magnetization on the third spin changed sign twice in each period. Equation (9) shows that only in the slow-tumbling regime, i.e., for large molecules or in high-viscosity solvents, were LLCs a better source for ROE experiments than transverse magnetization.

Based on the spin dynamics simulations (Figure 3), we derived that there exists a molecular rotational correlation time where the maximum transfers from transverse magnetization and LLC towards the third spin are equal. The LLC-ROE transfer overcame the classical ROE at correlation times above the range ${\tau }_C>10ns$ (Figure 4). Moreover, the optimal irradiation delay, for which the maximum magnetization transfer took place, shifted for both cases as a function of the rotational correlation time. For big correlation times, the maximum ROE transfer was delayed, compared to the transfer from transverse magnetization (Figure 4B). For even slower-tumbling motion, the LLC-based transfer outperformed classical magnetization transfer in the rotating frame as a magnetization source for an Overhauser transfer (Figure 4B).

In the slow-tumbling regime at ${\tau }_C=50ns$, magnetization transfer in the rotating-frame from an (I,S) spin pair to a neighbouring spin K in the geometry shown in Figure 1 was twice as effective when using LLCs as a source (Figure 3B) than by starting from the transverse magnetization of the I and S spins. Consistently, the time point at which the maximum accumulation of transverse magnetization ${\widehat{K}}_x$ took place was delayed when using slowly-relaxing LLCs compared to standard magnetization.

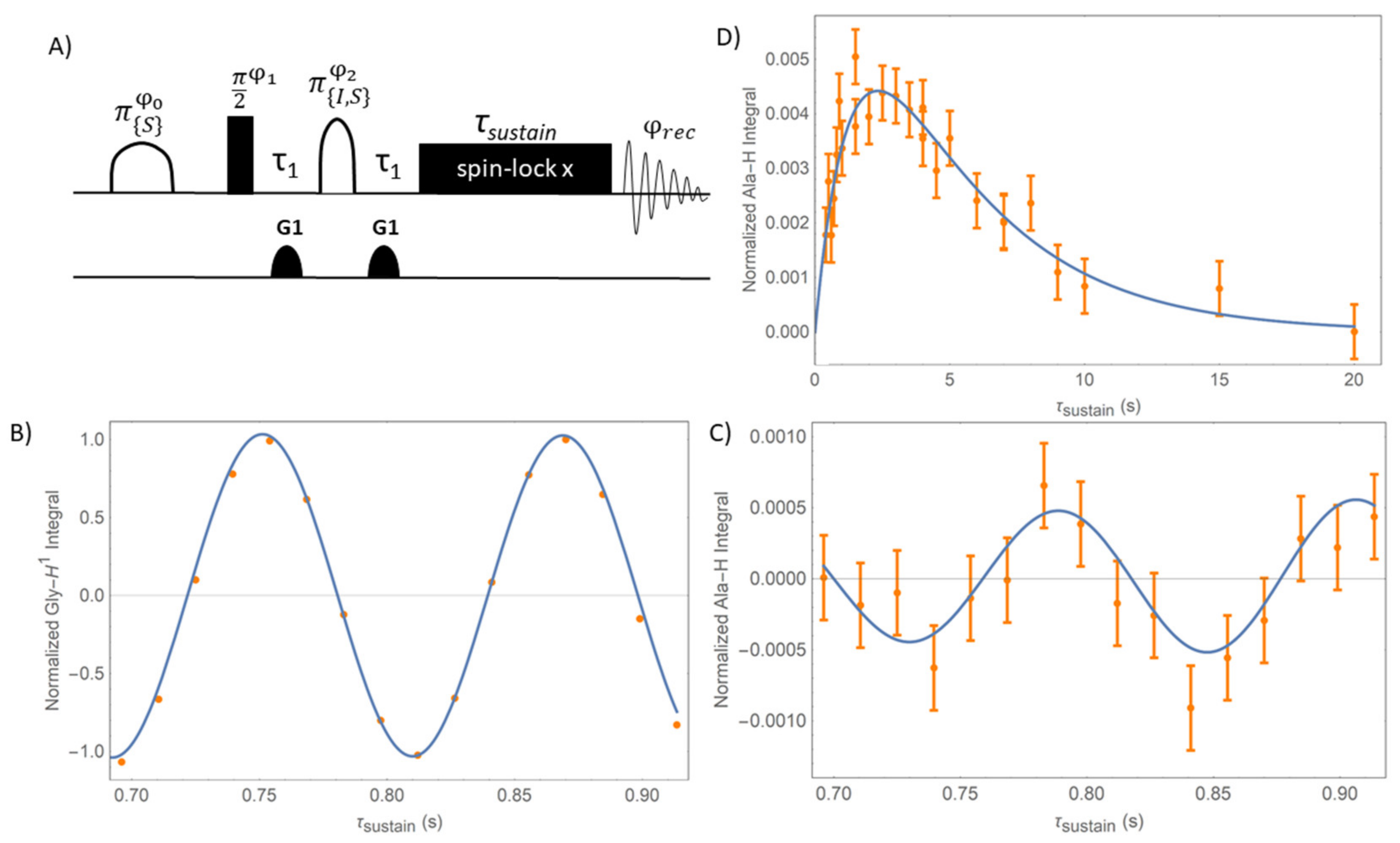
3.5. Experimental Evidence for the Oscillating ROE Transfer Starting from LLC

The theoretical predictions were tested by following the auto- and cross-relaxation of the long-lived coherence, excited on the Gly-H^1,2 protons (I and S) of AlaGly. A 10 mM solution of AlaGly dissolved in D₂O was placed in a 9.4 T NMR spectrometer, and the LLC was generated using the pulse sequence from Figure 5A. Prior to the spin-lock period, the long-lived coherence was isolated by selectively refocusing only the magnetization corresponding to I and S during gradient dephasing, which obliterated the magnetizations from other spins. Thus, the build-up of the K_x magnetization (the Ala-H protons) could be followed during the dipolar contacts between the LLC and the K spins. The auto- and cross-relaxation of the LLC are shown in Figure 5B,C for a total duration of the spin-lock/sustain period equal to ${\tau }_{sustain}=4/J$. Similar to the simulations, the build-up of K_x magnetization was oscillating at the same frequency $1/J$ as the auto-relaxation of the LLC, but in an antiphase manner. By eliminating the first ${\pi }_{\left\{S\right\}}^{{\phi }_2}$ pulse, the density operator was ${\widehat{I}}_x+{\widehat{S}}_x$ prior to the spin-lock, so that the classical ROE transfer could be monitored at the K spin (Figure 5D). The maximum amplitude of the transfer was four orders of magnitude smaller than the LLC magnetization, and one order of magnitude smaller than the ROE transfer from transverse magnetization. This small magnetization build-up was due to the small rotational correlation time of the AlaGly molecule in water solution estimated at around ${\tau }_C~100ps$, according to the longitudinal relaxation rate constant of the spins I and S $R_1^{IS}=\frac{3}{2}{b}_{IS}^2{\tau }_C$, which was measured as $R_1^{IS}=0.65s^{-1}$.

4. Conclusions

We reveal through calculations and preliminary experiments that the slow relaxation rates of LLCs facilitate magnetization transfer to outer spins. In the context of ROESY experiments for protein structure determination, the use of LLC is predicted to improve signal transfer compared to using classical transverse magnetization in macromolecules with rotational correlation times beyond ${\tau }_C=10 ns$. The reported experiments confirm theoretical predictions in the fast limit for molecular rotational motions (${\tau }_C~0.1 ns\ll \frac{1}{{\omega }_0})$. In this ‘extreme narrowing’ limit, the theoretical intensities of LLC-ROEs, predicted by Equation (9) and confirmed by experiments in Figure 5, are ca 1/10 of intensities in classical ROEs. This observation can lead to an increased protein-size limit for which magnetization can be transferred, and to extended radii of observation for distance constraints derived in proteins. LLC-ROE experiments can improve structural studies of proteins and high-affinity protein-ligand complexes in slow tumbling in the liquid state.