Rolling Bearing Fault Diagnosis Based on Deep Learning and Autoencoder Information Fusion
Abstract
:1. Introduction
2. Background Theory
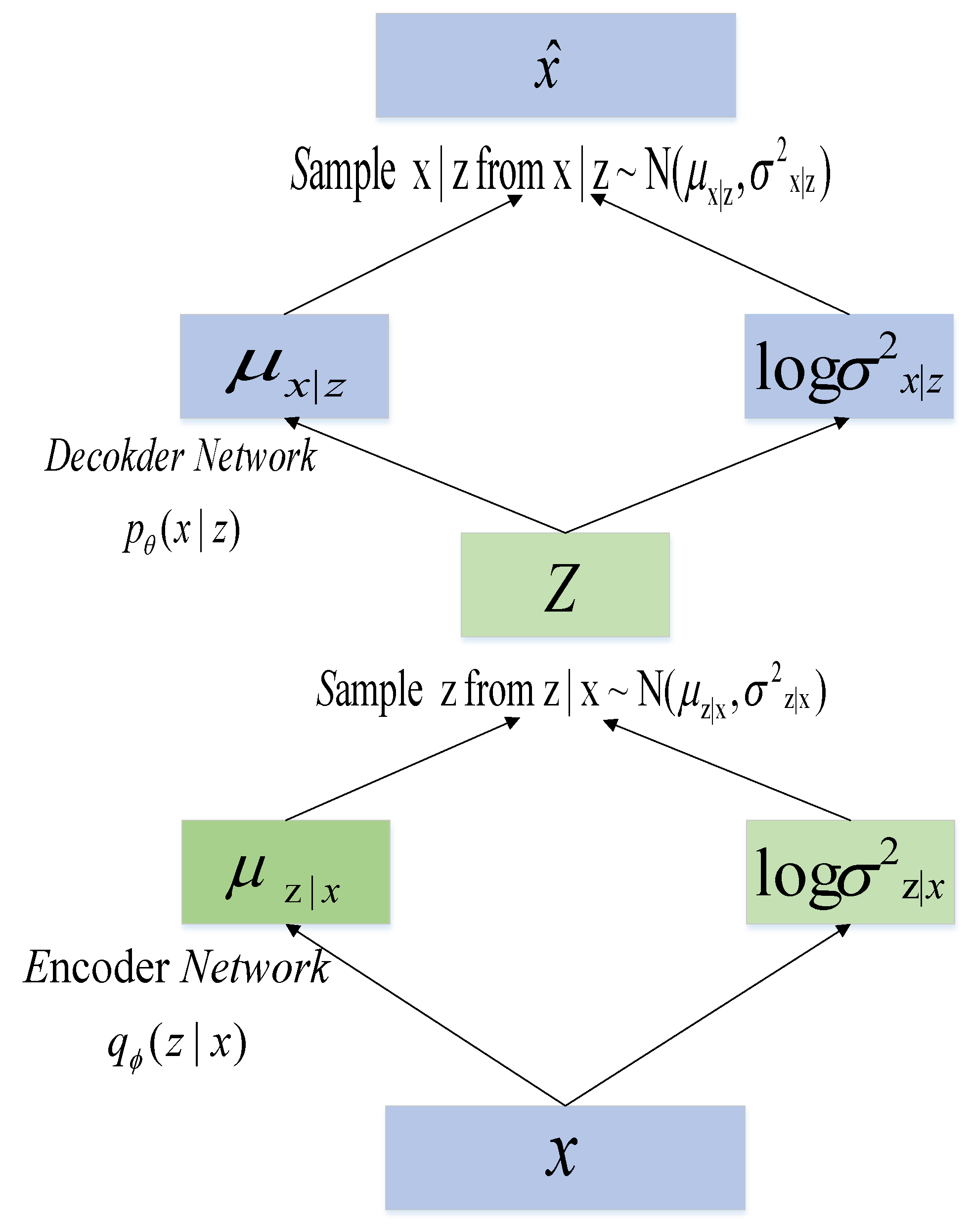
2.1. Variational Autoencoders
| Algorithm 1 VAE algorithm |
| Input: data Output: Probability Encoder E, Probability Decoder D |
| 1. and are initialization parameters; |
| 2. Repeat: |
| 3. For to do |
| 4. Take L samples from |
| 5. |
| 6. End for |
| 7. |
|
8. and are updated parameters by random gradient descent 9. Until parameters and converge |
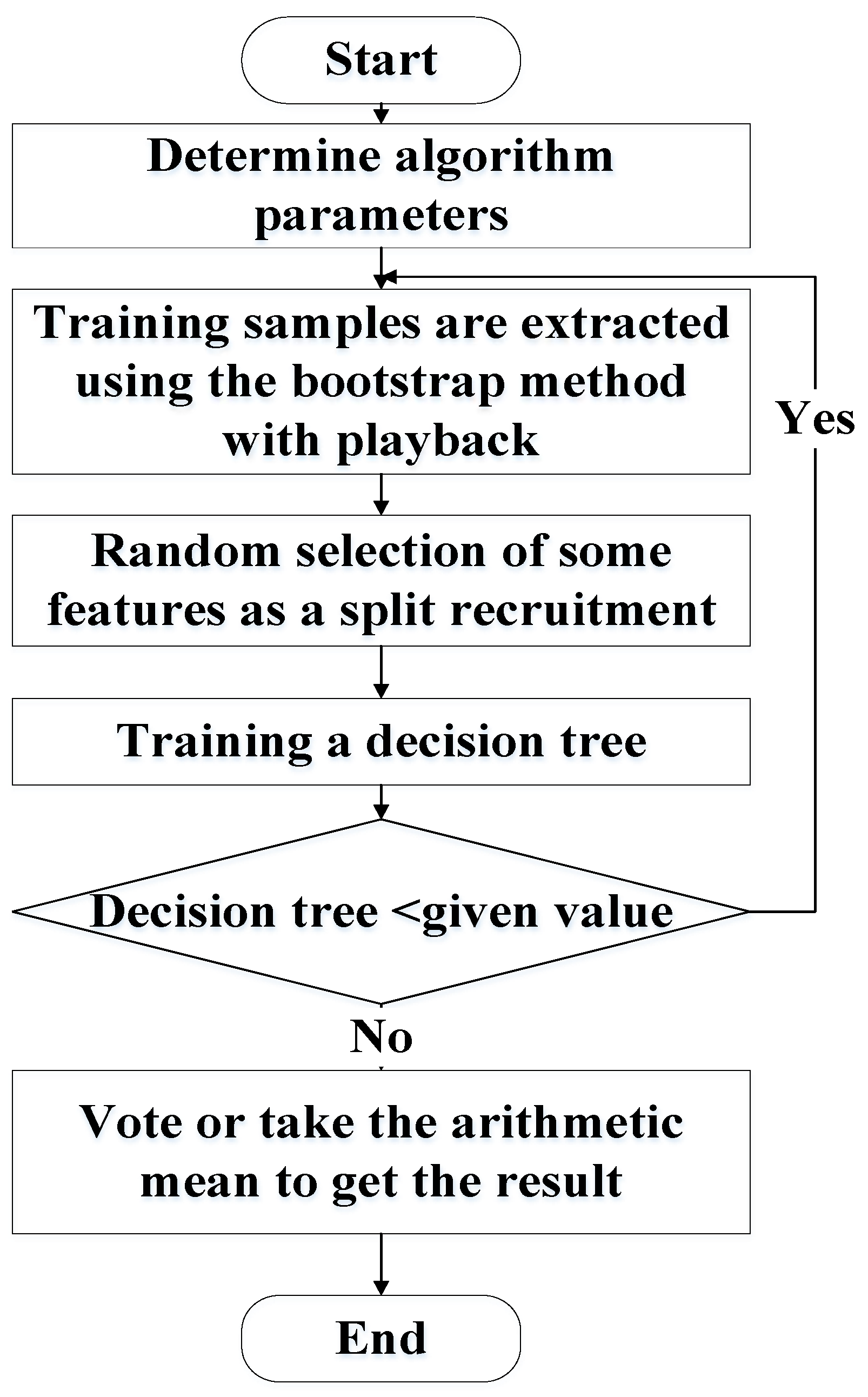
2.2. Random Forest
- (1)
- The original training dataset is . Extract dataset with observation values using the bootstrap method to build a decision tree.
- (2)
- There are variables. Randomly select variables from each node of each tree. Then, select the variable with the best classification ability among the variables to derive the best segmentation point.
- (3)
- Each tree grows to the fullest extent without any modification.
- (4)
- The result tree constructs a random forest to predict new data; the result is determined by the voting of trees in the random forest. Figure 2 shows the random forest algorithm flowchart.
2.3. Dynamic Simulation Model
3. Proposed Method
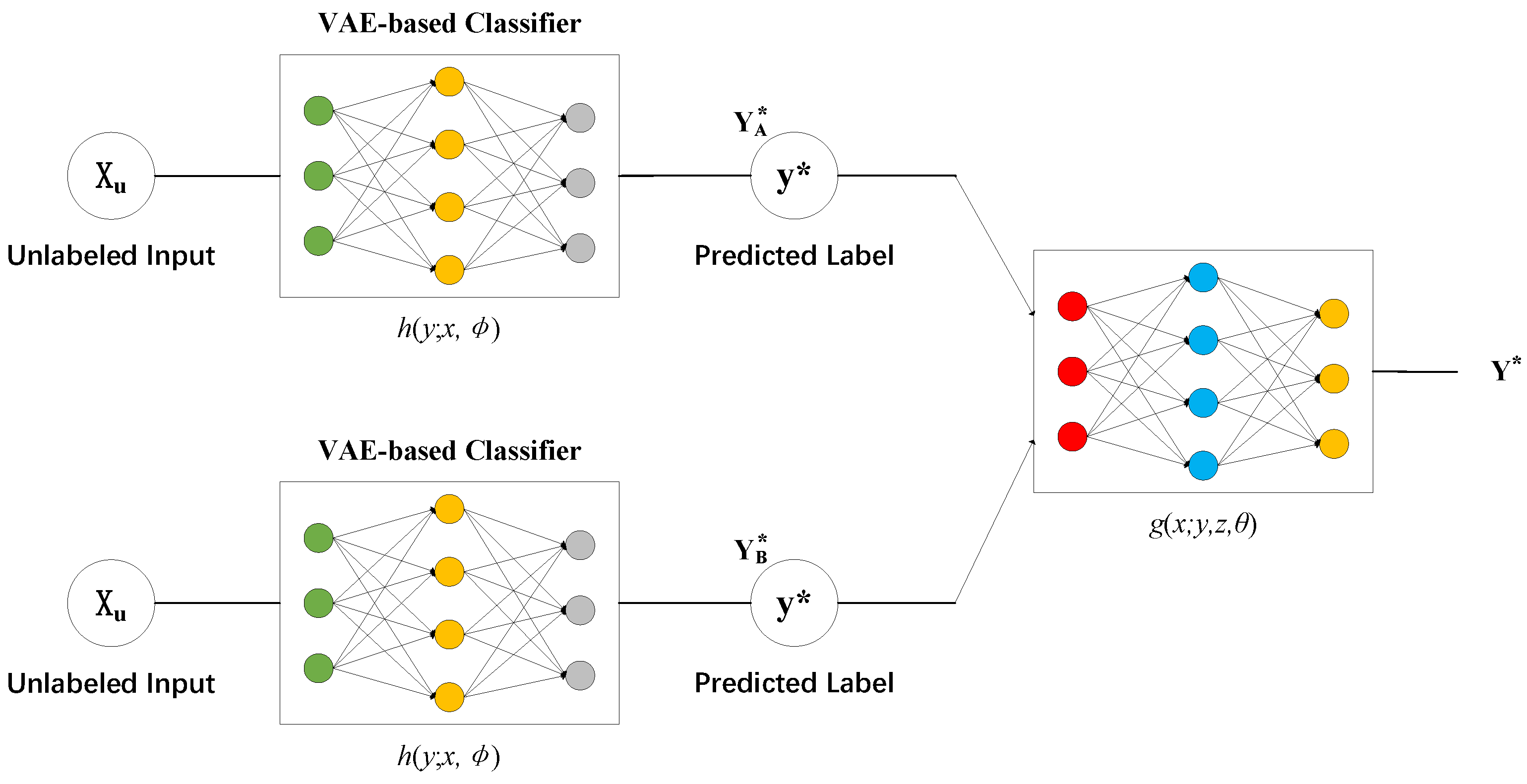
3.1. Latent Feature Decision (M1 Model)
3.2. Semi-Supervised Generation M2 Model
3.3. Proposed Method
4. Experimental Verification
- (1)
- PCA-SVM: The PCA-SVM benchmark was trained using low-dimensional features extracted from labeled data segments (each data segment consists of 1024 data samples). The feature space dimension was 128, which is consistent with the dimensions of the potential space of M1 and M2 models. It supports the SVM in using the radial basis function kernel; its regularization parameter was set as . Moreover, the kernel coefficient was set to “sample” (), where is the input data variance. This method first performed PCA cluster analysis on the original data, and then performed SVM classification.
- (2)
- AE: The AE structure is similar to that of VAE; hence, the AE baseline inherits the same network structure (encoder–decoder) as those of the M1 and SVM-based external classifiers.
- (3)
- CNN: the CNN benchmark treats each data segment of the time-series vibration (consisting of 1024 data samples) as a 2-D 32 × 32 image, in which it is a common practice to apply the vanilla CNN on bearing fault diagnosis. Specifically, the CNN baseline has two ReLU activation of convolution layers, each one has 2 × 2 convolutions and 32 filters, and a 2 × 2 max-pooling layer and a 0.25 dropout layer, respectively. In addition, we also set up a fully connected hidden layer with dimension 512, and its output is used as the input of softmax layer. At the same time, we use the cross entropy loss method and use the empirical value to set the batch to 10.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Rai, A.; Upadhyay, S.H. A review on signal processing techniques utilized in the fault diagnosis of rolling element bearings. Tribol. Int. 2016, 96, 289–306. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Y.; Wang, X.; Liu, B.; Liang, X. Early fault diagnosis of rolling bearings based on hierarchical symbol dynamic entropy and binary tree support vector machine. J. Sound Vib. 2018, 428, 72–86. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, B.; Qin, Y.; Huang, T. Rolling bearing fault detection of civil aircraft engine based on adaptive estimation of instantaneous angular speed. IEEE Trans. Ind. Inform. 2020, 16, 4938–4948. [Google Scholar] [CrossRef]
- Li, H.; Liu, T.; Wu, X.; Chen, Q. Research on bearing fault feature extraction based on singular value decomposition and optimized frequency band entropy. Mech. Syst. Signal Process. 2019, 118, 477–502. [Google Scholar] [CrossRef]
- Ma, J.; Zhan, L.; Li, C.; Li, Z. An improved intrinsic time-scale decomposition method based on adaptive noise and its application in bearing fault feature extraction. Meas. Sci. Technol. 2021, 32, 025103. [Google Scholar] [CrossRef]
- Hou, D.; Qi, H.; Luo, H.; Wang, C.; Yang, J. Comparative study on the use of acoustic emission and vibration analyses for the bearing fault diagnosis of high-speed trains. Struct. Health Monit. 2021, 2021, 14759217211036025. [Google Scholar] [CrossRef]
- Morales-Espejel, G. Thermal damage and fatigue estimation in heavily loaded lubricated rolling/sliding contacts with Micro-Geometry. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 235, 1680–1691. [Google Scholar] [CrossRef]
- Xie, Z.; Zhu, W. An investigationn on the lubrication characteristics of floating ring bearing with consideration of multi-coupling factors. Mech. Syst. Signal Process. 2022, 162, 108086. [Google Scholar] [CrossRef]
- Przysowa, R.; Rokicki, E.; Majewski, P. Optimized magnetic sensors to measure speed and position in adverse environments. In Proceedings of the IET & ISA 60th International Instrumentation Symposium, London, UK, 24–26 June 2014. [Google Scholar]
- Han, Q.K.; Li, X.L.; Chu, F.L. Skidding behavior of cylindrical roller bearings under time-variable load conditions. Int. J. Mech. Sci. 2018, 135, 203–214. [Google Scholar] [CrossRef]
- Selvaraj, A.; Marappan, R. Experimental analysis of factors influencing the cage slip in cylindrical roller bearing. Int. J. Adv. Manuf. Technol. 2011, 53, 635–644. [Google Scholar] [CrossRef]
- Hou, Y.; Wang, X. Development of an experimental system to measure the cage slip of cylindrical roller bearing. Struct. Health Monit. 2020, 19, 510–519. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, C.; Li, M.; Wang, Q.; Liu, H. Study on the rotational speed of bearing cage based on ultrasonic measurement. Porc. Imeche Part K J. Multi-Body Dyn. 2017, 231, 684–689. [Google Scholar]
- Tu, W.; Yu, W.; Shao, Y.; Yu, Y. A nonlinear dynamic vibration model of cylindrical roller bearing considering skidding. Nonlinear Dyn. 2021, 103, 2299–2313. [Google Scholar]
- Ma, J.; Zhuo, S.; Li, C.; Zhan, L.; Zhang, G. Study on Noncontact Aviation Bearing Faults and Speed Monitoring; IEEE: Piscataway, NJ, USA, 2021; pp. 1–21. [Google Scholar] [CrossRef]
- Gao, S.; Li, T.; Zhang, Y. Rolling bearing fault diagnosis of PSO–LSSVM based on CEEMD entropy fusion. Trans. Can. Soc. Mech. Eng. 2020, 44, 405–418. [Google Scholar] [CrossRef]
- Hoang, D.T.; Tran, X.T.; Van, M.; Kang, H.J. A Deep Neural Network-Based Feature Fusion for Bearing Fault Diagnosis. Sensors 2021, 21, 244. [Google Scholar] [CrossRef]
- Jiao, J.; Yue, J.; Pei, D. Multi-sensor information fusion method for vibration fault diagnosis of rolling bearing. In Proceedings of the 5th Asia Conference on Mechanical and Materials Engineering (ACMME 2017), Tokyo, Japan, 9–11 June 2017; Volume 241, p. 012034. [Google Scholar]
- Song, Q.; Zhao, S.; Wang, M. On the accuracy of fault diagnosis for rolling element bearings using improved DFA and multi-sensor data fusion method. Sensors 2020, 20, 6465. [Google Scholar] [CrossRef]
- Tang, X.; Gu, X.; Wang, J.; He, Q.; Zhang, F.; Lu, J. A bearing fault diagnosis method based on feature selection feedback network and improved DS evidence fusion. IEEE Access 2020, 8, 20523–20536. [Google Scholar] [CrossRef]
- Soualhi, A.; Taleb, S. Data fusion for fault severity estimation of ball bearings. In Proceedings of the 2018 IEEE International Conference on Industrial Technology, Lyon, France, 20–22 February 2018; pp. 2105–2110. [Google Scholar]
- Liu, Y.; Yan, X.; Zhang, C.; Liu, W. An ensemble convolutional neural networks for bearing fault diagnosis using multi-sensor data. Sensors 2019, 19, 5300. [Google Scholar] [CrossRef] [Green Version]
- Kamat, P.V.; Sugandhi, R.; Kumar, S. Deep learning-based anomaly-onset aware remaining useful life estimation of bearings. PeerJ Comput. Sci. 2021, 7, e795. [Google Scholar] [CrossRef]
- Sayyad, S.; Kumar, S.; Bongale, A.; Kamat, P.; Patil, S.; Kotecha, K. Data-Driven Remaining Useful Life Estimation for Milling Process: Sensors, Algorithms, Datasets, and Future Directions. IEEE Access 2021, 9, 110255–110286. [Google Scholar] [CrossRef]
- Safizadeh, M.S.; Latifi, S.K. Using multi-sensor data fusion for vibration fault diagnosis of rolling element bearings by accelerometer and load cell. Inf. Fusion 2014, 18, 1–8. [Google Scholar] [CrossRef]
- Safizadeh, M.S.; Golmohammadi, A. Ball bearing fault detection via multi-sensor data fusion with accelerometer and microphone. Insight Non-Destr. Test. Cond. Monit. 2021, 63, 168–175. [Google Scholar] [CrossRef]
- Li, Z.; Yan, X. Study on data fusion of multi-dimensional sensors for health monitoring of rolling bearings. Insight Non-Destr. Test. Cond. Monit. 2013, 55, 147–151. [Google Scholar] [CrossRef]
- Gunerkar, R.S.; Jalan, A.K. Classification of ball bearing faults using vibro-acoustic sensor data fusion. Exp. Tech. 2019, 43, 635–643. [Google Scholar] [CrossRef]
- Wang, X.; Mao, D.; Li, X. Bearing fault diagnosis based on vibro-acoustic data fusion and 1D-CNN network. Measurement 2021, 173, 108518. [Google Scholar] [CrossRef]
- Mostafa, S.A.; Mustapha, A.; Hazeem, A.A.; Khaleefah, S.H.; Mohammed, M.A. An Agent-Based Inference Engine for Efficient and Reliable Automated Car Failure Diagnosis Assistance. IEEE Access 2018, 6, 8322–8331. [Google Scholar] [CrossRef]
- Mohammed, M.A.; Abd Ghani, M.K.; Arunkumar, N.A.; Obaid, O.I.; Mostafa, S.A.; Jaber, M.M.; Burhanuddin, M.A.; Matar, B.M.; Ibrahim, D.A. Genetic case-based reasoning for improved mobile phone faults diagnosis. Comput. Electr. Eng. 2018, 71, 212–222. [Google Scholar] [CrossRef]
- Zhang, S.; Ye, F.; Wang, B.; Habetler, T.G. Semi-supervised bearing fault diagnosis and classification using variational autoencoder-based deep generative models. IEEE Sens. J. 2021, 21, 6476–6486. [Google Scholar] [CrossRef]
- Chen, Y.; Zaki, M.J. Kate: K-competitive autoencoder for text. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 85–94. [Google Scholar]
- Kingma, P.; Welling, M. Max welling. Auto-encoding variational bayes. In Proceedings of the 26th ACM Sigspatial International Conference on Advances in Geographic Information Systems, Seattle, WA, USA, 6–9 November 2018; pp. 973–978. [Google Scholar]
- Hershey, J.R.; Olesen, P.A. Approximating the Kullback Leibler divergence between Gaussian mixture models. In Proceedings of the IEEE International Conference on Acoustics Speech and Signal Processing, Honolulu, HI, USA, 15–21 April 2007; p. 317. [Google Scholar]
- Jiang, M.; Beutel, A.; Cui, P.; Hooi, B.; Yang, S.; Faloutsos, C. A general suspiciousness metric for dense blocks in multimodal data. In Proceedings of the IEEE International Conference on Data Mining, Atlantic City, NJ, USA, 14–17 November 2015; pp. 781–786. [Google Scholar]
- Van Engelen, J.E.; Hoos, H.H. A survey on semi-supervised learning. Mach. Learn. 2020, 109, 373–440. [Google Scholar] [CrossRef] [Green Version]
- Lahouar, A.; Slama, J.B.H. Hour-ahead wind power forecast based on random forests. Renew. Energy 2017, 109, 529–541. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, Z.N.; Bai, X.T.; Shi, H.T.; Wang, Q. Effect of preload on the dynamic characteristics of ceramic bearings based on a dynamic thermal coupling model. Adv. Mech. Eng. 2020, 12, 1687814020903851. [Google Scholar] [CrossRef] [Green Version]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [Green Version]
- Shao, L.; Wu, D.; Li, X. Learning deep and wide: A spectral method for learning deep networks. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 2303–2308. [Google Scholar] [CrossRef]
- Bordoloi, D.J.; Tiwari, R. Optimum multi-fault classification of gears with integration of evolutionary and SVM algorithms. Mech. Mach. Theory 2014, 73, 49–60. [Google Scholar] [CrossRef]
- Lee, J.; Qiu, H.; Yu, G.; Lin, J. Rexnord Technical Services, IMS, University of Cincinnati. Bearing Data Set, NASA Ames Prognostics Data Repository; NASA Ames Research Center: Moffett Field, CA, USA, 2017.
- Burgess, C.P.; Higgins, I.; Pal, A.; Matthey, L.; Watters, N.; Desjardins, G.; Lerchner, A. Understanding disentangling in β-VAE. arXiv 2018, arXiv:1804.03599. [Google Scholar]
- Fu, H.; Li, C.; Liu, X.; Gao, J.; Celikyilmaz, A.; Carin, L. Cyclical annealing schedule: A simple approach to mitigating KL vanishing. arXiv 2019, arXiv:1903.10145.2019. [Google Scholar]
- Case Western Reserve University Bearing Data Center Website [EB/OL]. 2011. Available online: http://csegroups.case.edu/bearingdatacenter/pages/download-data-file (accessed on 16 December 2020).
- Chapelle, O.; Zien, A. Semi-Supervised Classification by Low Density Separation. In Proceedings of the International Workshop on Artificial Intelligence and Statistics (AISTATS), Bridgetown, Barbados, 6–8 January 2005; pp. 57–64. [Google Scholar]
- Li, Y.-F.; Zhou, Z.-H. Towards making unlabeled data never hurt. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 175–188. [Google Scholar]
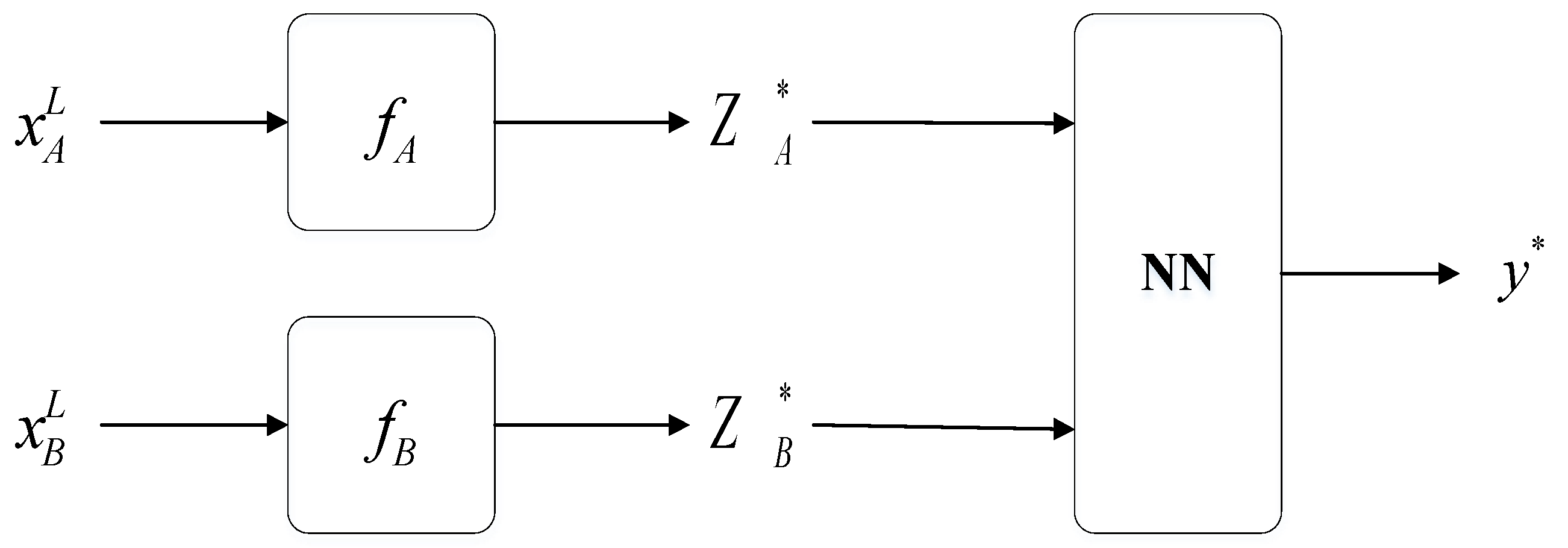



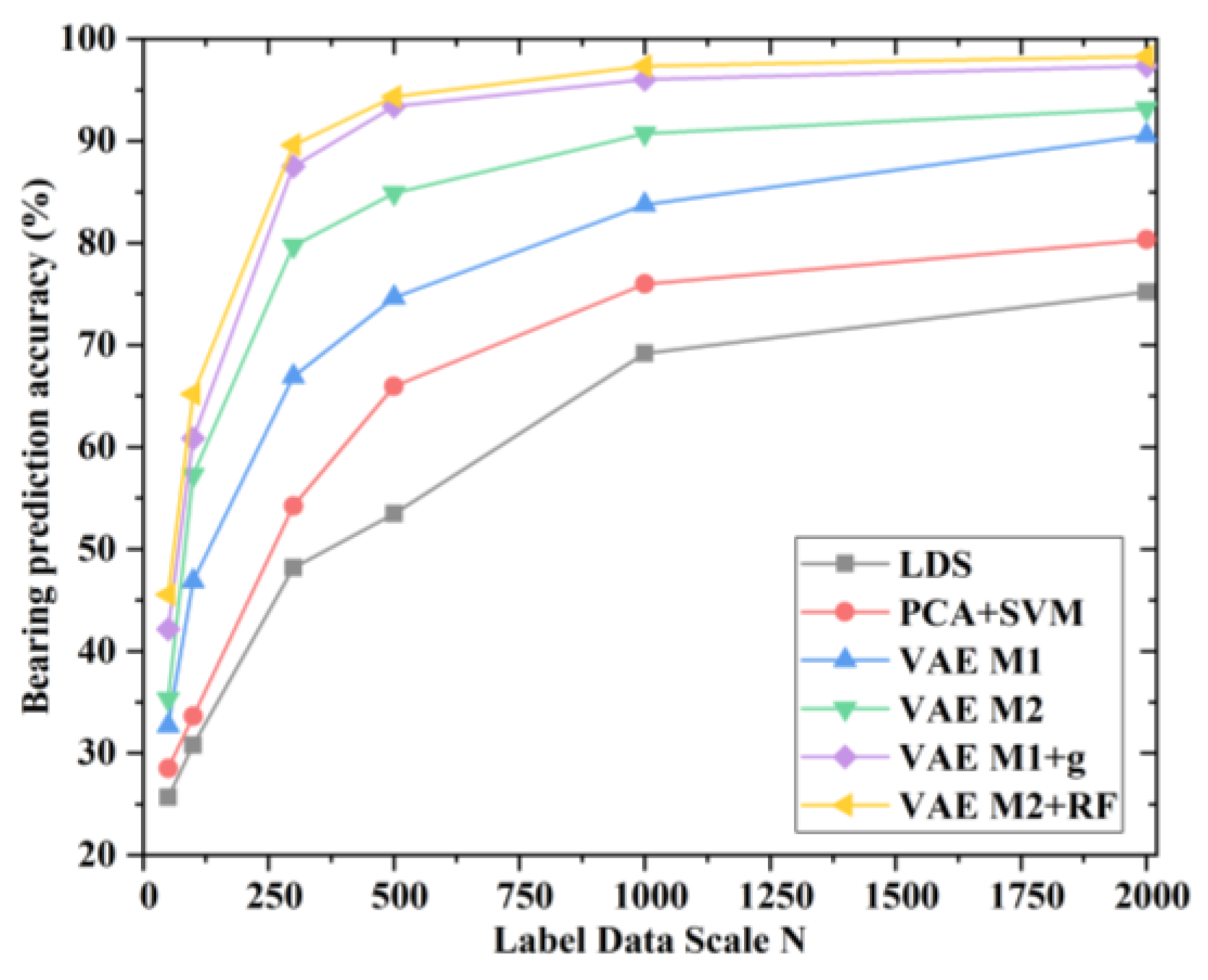

| N | 50 | 100 | 300 | 500 | 1000 | 2000 |
|---|---|---|---|---|---|---|
| Proportion of labeled data training | 0.49% | 0.98% | 2.95% | 4.92% | 9.83% | 19.67% |
| CNN | 25.74 ± 2.88% | 30.50 ± 2.16% | 48.28 ± 3.42% | 53.41 ± 2.74% | 69.07 ± 1.46% | 75.19 ± 0.99% |
| PCA + SVM | 28.57 ± 0.38% | 33.77 ± 2.81% | 54.43 ± 1.59% | 66.27 ± 2.21% | 75.83 ± 1.27% | 80.40 ± 1.47% |
| VAE M1 | 32.93 ± 2.01% | 46.91 ± 1.37% | 67.03 ± 1.22% | 75.06 ± 1.76% | 83.97 ± 1.40% | 90.59 ± 1.43% |
| VAE M2 | 35.57 ± 2.91% | 57.04 ± 3.57% | 79.63 ± 2.80% | 85.16 ± 1.66% | 90.86 ± 0.51% | 93.06 ± 0.88% |
| VAE M1 + NN | 41.85 ± 2.34% | 62.34 ± 2.37% | 88.12 ± 1.63% | 93.33 ± 2.55% | 96.25 ± 0.90% | 97.32 ± 1.12% |
| VAE M2 + RF | 45.66 ± 2.45% | 65.12 ± 2.36% | 89.53 ± 1.89% | 94.33 ± 1.35% | 97.49 ± 0.38% | 98.22 ± 0.26% |
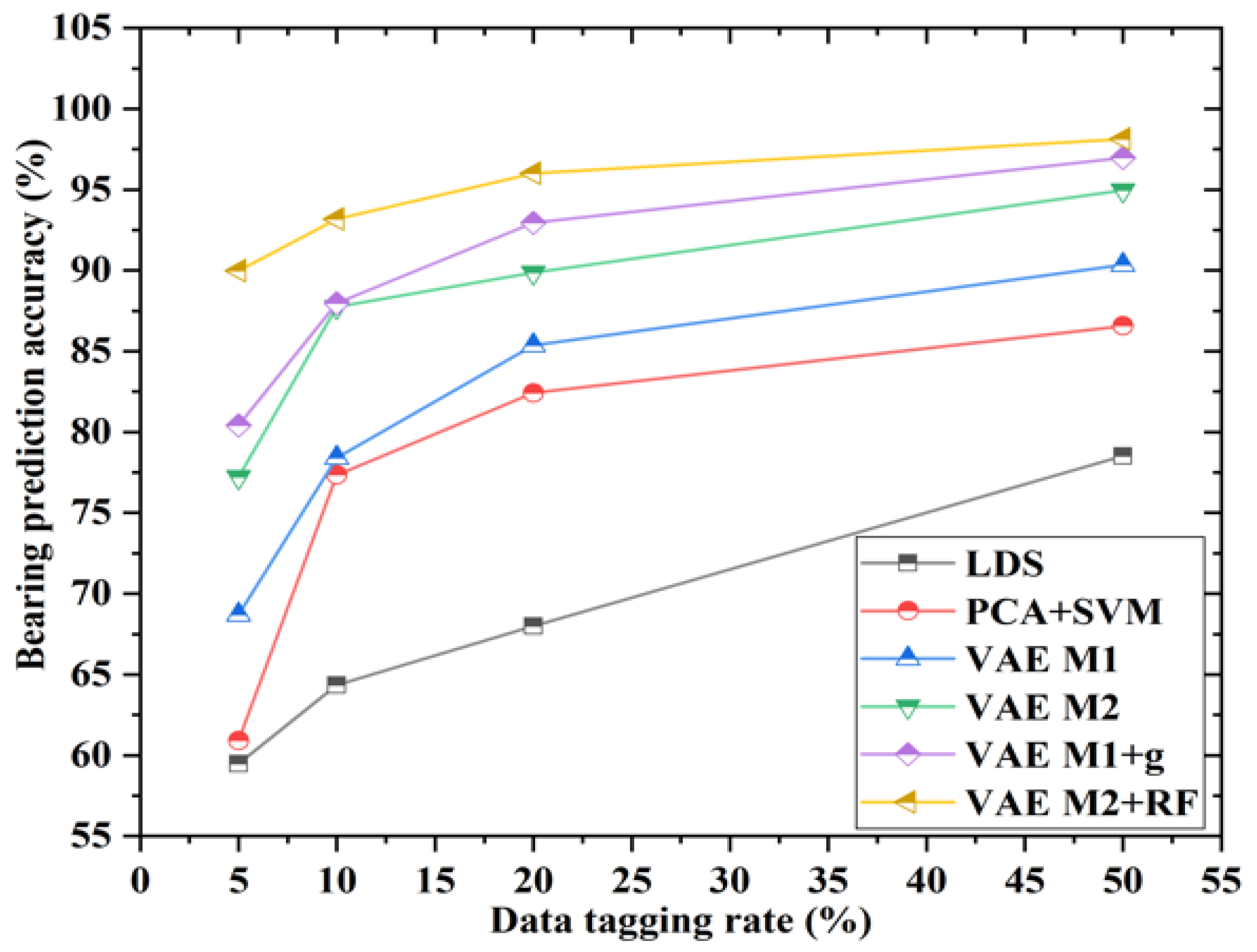
| Algorithm | a = 5% | a = 10% | a = 20% | a = 50% | Ranking |
|---|---|---|---|---|---|
| CNN | 59.60 ± 15.43% | 64.49 ± 13.72% | 67.90 ± 12.98% | 78.53 ± 15.34% | 6 |
| PCA + SVM | 60.85 ± 12.54% | 77.52 ± 12.48% | 82.44 ± 8.18% | 86.55 ± 13.34% | 5 |
| VAE M1 | 68.75 ± 7.75% | 78.53 ± 8.37% | 85.40 ± 7.08% | 90.36 ± 8.37% | 4 |
| VAE M2 | 77.17 ± 7.18% | 87.82 ± 4.63% | 89.80 ± 0.47% | 94.95 ± 0.26% | 3 |
| VAE M1 + NN | 80.51 ± 5.47% | 88.02 ± 5.57% | 92.91 ± 5.18% | 96.97 ± 4.91% | 2 |
| VAE M2 + RF | 90.12 ± 6.64% | 93.17 ± 5.59% | 95.95 ± 0.44% | 98.19 ± 0.11% | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Li, C.; Zhang, G. Rolling Bearing Fault Diagnosis Based on Deep Learning and Autoencoder Information Fusion. Symmetry 2022, 14, 13. https://doi.org/10.3390/sym14010013
Ma J, Li C, Zhang G. Rolling Bearing Fault Diagnosis Based on Deep Learning and Autoencoder Information Fusion. Symmetry. 2022; 14(1):13. https://doi.org/10.3390/sym14010013
Chicago/Turabian StyleMa, Jianpeng, Chengwei Li, and Guangzhu Zhang. 2022. "Rolling Bearing Fault Diagnosis Based on Deep Learning and Autoencoder Information Fusion" Symmetry 14, no. 1: 13. https://doi.org/10.3390/sym14010013
APA StyleMa, J., Li, C., & Zhang, G. (2022). Rolling Bearing Fault Diagnosis Based on Deep Learning and Autoencoder Information Fusion. Symmetry, 14(1), 13. https://doi.org/10.3390/sym14010013





