Improved Path Planning for Indoor Patrol Robot Based on Deep Reinforcement Learning

Abstract

To solve the problems of poor exploration ability and convergence speed of traditional deep reinforcement learning in the navigation task of the patrol robot under indoor specified routes, an improved deep reinforcement learning algorithm based on Pan/Tilt/Zoom(PTZ) image information was proposed in this paper. The obtained symmetric image information and target position information are taken as the input of the network, the speed of the robot is taken as the output of the next action, and the circular route with boundary is taken as the test. The improved reward and punishment function is designed to improve the convergence speed of the algorithm and optimize the path so that the robot can plan a safer path while avoiding obstacles first. Compared with Deep Q Network(DQN) algorithm, the convergence speed after improvement is shortened by about 40%, and the loss function is more stable.

1. Introduction

Path planning is an essential direction of robot research [1]. It is the key to realizing autonomous navigation tasks, which means a robot can independently explore a smooth and collision-free path trajectory from the starting position to the target position [2]. Traditional path planning algorithms include the A-star algorithm [3], Artificial Potential Field Method [4], and Rapidly Exploring Random Tree [5], and so on, which are used to solve the path planning in a known environment and are easy to implement. Still, robots have poor exploration ability in path planning. Given, because of the problems in traditional algorithms, a deep reinforcement learning algorithm has been introduced to enable robots to make more accurate movement directions in environmental states, which is a combination of deep learning and reinforcement learning [6,7,8]. Deep learning obtains the observation information of the target state by perceiving the environment. In contrast, reinforcement learning, which uses the reward and punishment functions to guide whether the action is good or not, is a process in which the patrol robot and the environment interact trial and error constantly.

The first deep reinforcement learning model, namely DQN, was proposed by Mnih et al. [9], which combined neural network with Q-learning and used a neural network to replace the Q value table to solve the problem of dimension disaster in Q-learning. Still, the convergence speed was slow in network training. DQN was applied to path planning for model-free obstacle avoidance by Tai et al. [10], which was the over-estimation of state-action value, inevitably resulting in sparse rewards and not the optimal path for robots. The artificial potential field, which accelerated the convergence speed of the network, increased the action step length and adjusted the direction of the robot to improve the precision of the robot’s route planning, was introduced in the initialization process of Q value [11], leading to having good effect in the local path planning of the robot but poor implementation in the global path planning.

Because of the fixed and symmetrical patrol route, it is difficult for the patrol robot to avoid obstacles. The A-star algorithm is characterized by large performance consumption when encountering target points with obstacles. Artificial Potential Field Method cannot find a path between similar obstacles. The path planned by the Artificial Potential Field Method may oscillate and swing in narrow channels when new environmental obstacles are detected. Rapidly Exploring Random Tree is challenging to find the path in an environment with limited channels. Therefore, to effectively solve the patrol robot exploration algorithm problems of slow convergence speed and poor ability, an improved path planning for indoor patrol robot based on deep reinforcement learning is put forward in this paper, which use PTZ to perceive the surrounding environment information, combining the patrol robot’s position information with the target of a state-space as network input [12,13,14,15]. The position and speed of the patrol robot are taken as the output, and a reasonable reward and punishment function is designed to significantly improve the convergence speed of the algorithm and optimize the reward sparsity of the environmental state space in the paper [16,17,18,19].

2. Background

Reinforcement learning is a process in which different rewards are obtained by way of “trial and error” when the patrol robot and the environment interact, which means that the patrol robot will not be affected by the initial stage of the environment, which does not guide the patrol robot to move but only rate its interaction [20,21,22]. High score behavior and low score behavior need to be remembered by the patrol robot, which just needs to use the same behavior to get a high score and avoid a low score when it interacts next time [23,24,25,26]. The interaction process of reinforcement learning is shown in Figure 1. DQN, which uses a neural network for fusion, is based on Q-learning for overcoming the defect of “dimension disaster” caused by large memory consumption of Q-learning to store data [27,28,29].

Deep reinforcement learning mainly realizes the learning interaction between the patrol robot and the environment, which is composed of deep learning and reinforcement learning. Deep learning uses the patrol robot’s built-in sensors to receive and perceive the information of the surrounding environment and obtain the information of the current state of the patrol robot. While reinforcement learning is responsible for the patrol robot to explore and analyze the acquired environmental information, which helps the patrol robot to make correct decisions and makes the patrol robot can achieve navigation tasks come true [30,31,32].

The DQN algorithm combines a neural network, which needs to model Q table and uses RGB image as input to generate all Q values and Q-learning which uses Markov decision for modeling and uses the current state, action, reward, strategy, and next action in Markov decision for representation. The experience playback mechanism is introduced to improve the sample correlation of the robot and solve the efficiency utilization problem of the robot in DQN, which uses the uniqueness of the target Q value to enhance the smoothness of the action update. DQN includes three steps: establishing target function, target network, and introducing experience replay.

Target function. The target function of DQN is constructed by Q-learning, and the formula is as follows:

$${\mathrm{Q}}^{\prime }\left(\mathrm{s},\mathrm{a}\right)\leftarrow \mathrm{Q}\left(\mathrm{s},\mathrm{a}\right)+\mathsf{\alpha }\left[\mathrm{r}+{\mathsf{\gamma }\max }_{{\mathrm{a}}^{\prime }}\mathrm{Q}\left({\mathrm{s}}^{\prime },{\mathrm{a}}^{\prime }\right)-\mathrm{Q}\left(\mathrm{s},\mathrm{a}\right)\right]$$

(1)

where (s,a) indicates the current status and action. (s′,a′) indicates the next state and action. Q(s,a) represents the current state-action value. Q′(s,a) represents the updated state-action value. $\mathsf{\alpha }$ represents the learning rate which means how many errors in the current state will be updated and learned. The value ranges from 0 to 1. $\mathsf{\gamma }$ represents the attenuation value of future rewards, ranging from 0 to 1. Because the Q value in the DQN algorithm is mostly randomly generated. For the convenience of calculation, we need to use the maximum value max.${\max }_{{\mathrm{a}}^{\prime }}\mathrm{Q}\left({\mathrm{s}}^{\prime },{\mathrm{a}}^{\prime }\right)$ means the maximum value of Q at the next state-action value. Breaking down the expression for Q values yields the following expression:

$$\left(\mathrm{s}1\right)=\mathrm{r}2+\mathsf{\gamma }\mathrm{Q}\left(\mathrm{s}2\right)=\mathrm{r}2+\mathsf{\gamma }\left[\mathrm{r}3+\mathsf{\gamma }\mathrm{Q}\left(\mathrm{s}3\right)\right]=\mathrm{r}2+\mathsf{\gamma }\left\{\mathrm{r}3+\mathsf{\gamma }\left[\mathrm{r}4+\mathsf{\gamma }\mathrm{Q}\left(\mathrm{s}4\right)\right]\right\}=\cdots$$

(2)

$$\mathrm{Namely} \mathrm{Q}\left(\mathrm{s}1\right)=\mathrm{r}2+\mathsf{\gamma }·\mathrm{r}3+{\mathsf{\gamma }}^2·\mathrm{r}4+{\mathsf{\gamma }}^3·\mathrm{r}5+{\mathsf{\gamma }}^4·\mathrm{r}6+\cdots$$

(3)

It is not difficult to conclude that the value of Q is correlated with the rewards at each subsequent step, but these associated rewards decay over time, and the further away from state s1, the more state decay.

The target state-action value function can be expressed by the Bellman equation as follows:

$${\mathrm{y}}^{\prime }=\mathrm{r}+\mathsf{\gamma }\mathrm{maxQ}\left({\mathrm{s}}^{\prime },{\mathrm{a}}^{\prime },\mathsf{\theta }\right)$$

(4)

where ${\mathrm{y}}^{\prime }$ is the target Q value. $\mathsf{\theta }$ is the weight parameter trained in the neural network structure model. $\mathrm{maxQ}\left({\mathrm{s}}^{\prime },{\mathrm{a}}^{\prime },\mathsf{\theta }\right)$ means the maximum value of Q ant the next state-action value and $\mathsf{\theta }$.

The loss function is the mean square error loss function, and the formula is as follows:

$$\mathrm{L}\left(\mathsf{\theta }\right)=\mathrm{E}\left[{\left({\mathrm{y}}^{\prime }-\mathrm{Q}\left(\mathrm{s},\mathrm{a},\mathsf{\theta }\right)\right)}^2\right]$$

(5)

Target network. The current state-action value function is evaluated by DQN through the target network and prediction network. The target network is based on a neural network to get the target Q value, using the target Q value to estimate the Q value of the next action. The prediction network uses the stochastic gradient descent method to update the weight of the network $∆\mathsf{\theta }$, and the formula of the gradient descent algorithm is shown as follows:

$$∆\mathsf{\theta }=\mathrm{E}\left[{\mathrm{y}}^{\prime }-\mathrm{Q}\left(\mathrm{s},\mathrm{a},{\mathsf{\theta }}_1\right){\nabla }_{\mathsf{\theta }}\mathrm{Q}\left(\mathrm{s},\mathrm{a},{\mathsf{\theta }}_1\right)\right]$$

(6)

where $\nabla$ is Hamiltonian.

Experience replay. The experiential replay mechanism improves the sample relevance of the patrol robot and solves the problem of efficient utilization of the patrol robot. The patrol robot can obtain the sample database during the information interaction between the patrol robot and the environment. It stores the sample database into the established experience pool and randomly selects a small part of data for training samples, and then sends the training samples into the neural network for training. The experience replay mechanism utilizes the repeatability of the sample itself to improve learning efficiency.

The structure of the DQN algorithm is shown in Figure 2. s (state) represents the current cycle step, r (reward) represents the reward value generated by the current cycle step, a(action) represents the behavior caused according to the current cycle step state, and s_(next State) represents the next cycle step. Target_net and Eval_net refer to Q_target and Q_eval, respectively. Parameters of Eval_net are deferred to parameters in Target_net. Q_target and Q_eval represent the two neural networks of the DQN algorithm, which follows Q-learning, the predecessor of the DQN algorithm. They are not much different, just different parameters. Q_eval contains behavioral parameters, and theoretical behavior is bound to deviate from actual conduct (loss). Thus, in the traditional DQN algorithm, parameters s, loss, and symmetric Q_target and Q_eval will affect the Train value.

3. Improved Algorithm

The main goal of the patrol robot is to be able to reach the target point and return to the starting point autonomously in the indoor route environment. So a kind of improved deep reinforcement learning algorithm is put forward in this paper, which takes the acquired image information and target position information as the input of the network, the position and speed of the patrol robot as the output of the next action, and the specified circular route with a boundary as the test. Thus, the patrol robot can realize the process of its running towards the target point in the specified route with limited conditions and finally returning to the starting point to complete the automatic walking task. Since the robot needs to walk on the indoor prescribed route to realize the patrol function, the conventional DQN algorithm is easy to find the optimal path for the open route. Still, for the circular prescribed route, it is easy to fall into the local optimal and cannot complete the path. Therefore, the DQN algorithm needs to be improved.

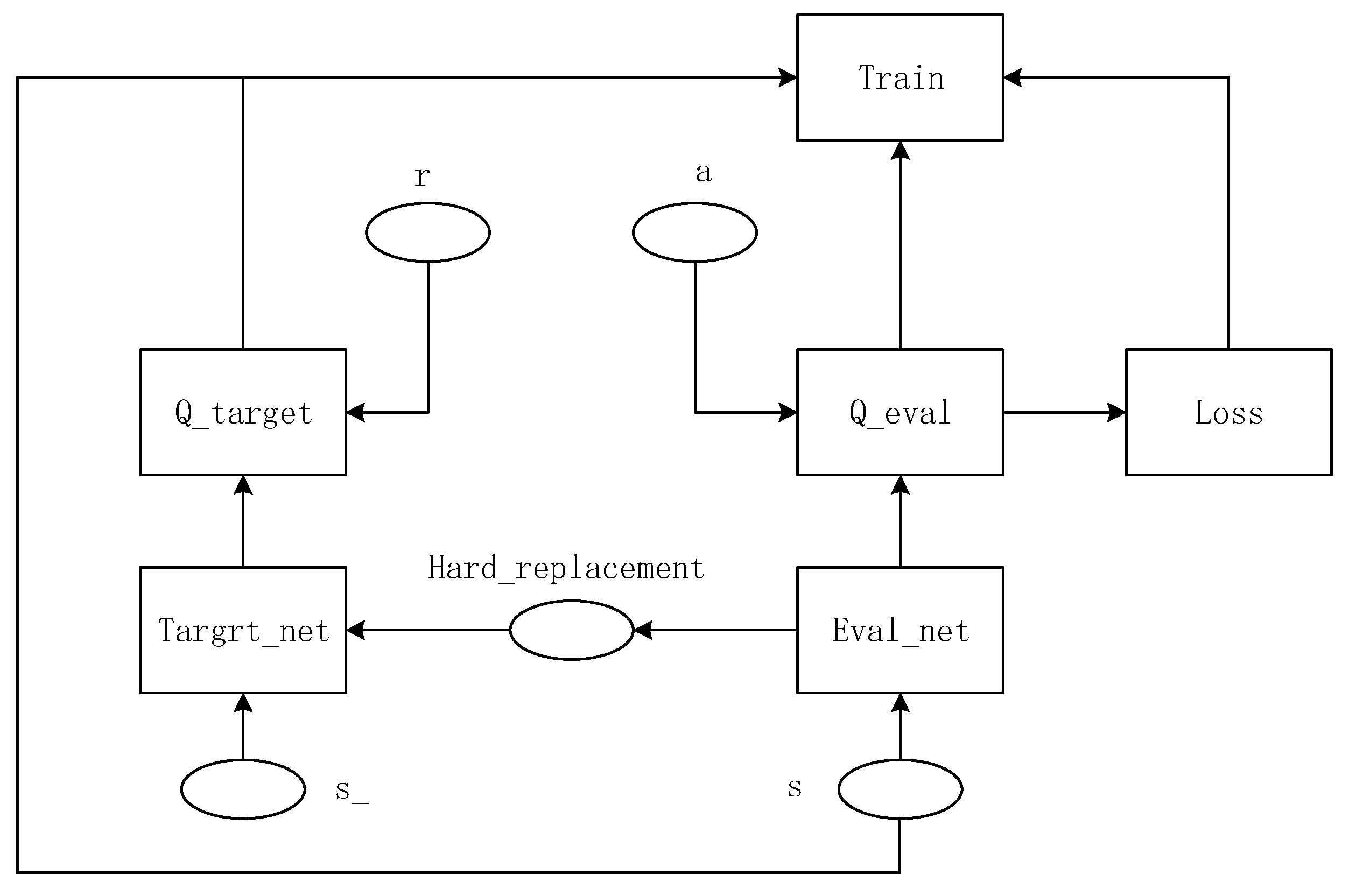
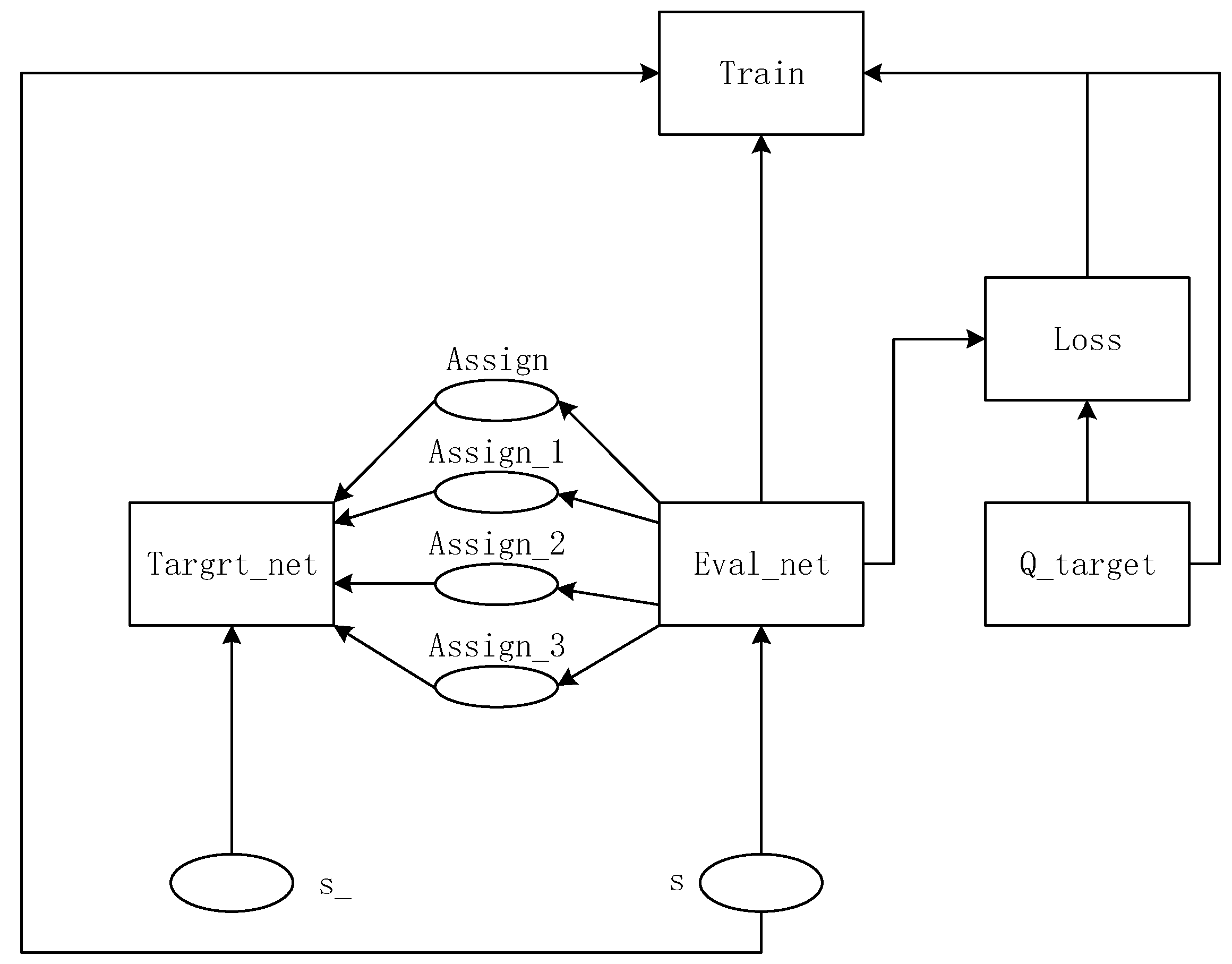
3.1. Overview of Improved DQN Algorithm

The structure of the improved DQN algorithm is shown in Figure 3, which is transmitted to the evaluation function through the current iteration step s. The evaluation function generates four different data types and sends the data to the target function through four symmetric routes. In addition to the four transmission lines of the objective function, the next iteration step s_ also affects them. The evaluation function and Q function often have a loss value during operation, which, together with the evaluation function, Q function, and the current iterative step s, guides the patrol robot training.

In the simulation environment, the patrol robot takes the directly collected image information as the training sample, then combines its environmental state characteristics and the target point to be reached as the input of the network, and takes the Q value of the current position as the output of the network model, and uses the ε-greedy strategy to select the action to reach the next state. When the next state is reached, a complete data tuple (s,a,r,s′) can be obtained by calculating the corresponding reward value r. Then, data of this series are stored in the experience replay pool D, and small-batch samples are extracted from the experience replay pool D and put into the neural network for training.

In the course of network training, if the patrol robot uses PTZ to identify the obstacle, the improved algorithm can make the robot avoid the block effectively. Otherwise, the patrol robot will continue to navigate until the target point is reached. The improved algorithm design is shown in Algorithm 1.

Algorithm 1. Improved Deep Q-learning Network Based on Patrol Robot.

Initialize replay memory D to capacity N

Initialize action-value function Q with random weights

for episode = 1, M do

Initialize sequence $s_t$ from replay memory D and preprocess sequenced θ, $\mathit{\theta }={\mathit{\theta }}_1$

for t = 1, T do

With probability ε select a random action $a_t$

Otherwise select optimal action $a_t={\max }_a{Q}^{\prime }\left(\left(s_t\right),a;\theta \right)$

Execute action $a_t$ in emulator, observe new reward function $r_t$ and next image $s_{t+1}$

Set transition $(s_t,a_t,r_t,s_{t+1})$ and store it in D

Preprocess ${\theta }_{t+1}={\theta }_{\left(s_{t+1}\right)}$

Sample random mini-batch of transitions $\left(s_j,a_j,r_j,s_{j+1}\right)$ from D

Set $y_j\left(a|s\right)=\{\begin{array}{cc}{r}_j& for termina{l}_{j+1}\\ r_j+\gamma ma{x}_{a^{\prime }}Q\left(s_{j+1},a^{\prime };\theta \right)& for non-termina{l}_{j+1}\end{array}$

Perform a gradient descent step on $L\left(\theta \right)$ $$L\left(\theta \right)=E{\left(y_j-Q\left(s,a,\theta \right)\right)}^2$$

Update policy gradient

end for

end for

3.2. Improved Target Point Function

The target point is the coordinate of the position that the patrol robot needs to achieve in the motion state and represents the final position of the patrol robot. It needs to drive on a fixed route for the patrol robot when performing tasks and return to the initial position after completing the patrol. If the target point is placed in the starting position, the DQN algorithm will skip to the end without iteration, thus skipping the patrol step. Even if the design function makes the algorithm stop iteration when it reaches the initial position for the second time, due to the characteristics of the DQN algorithm, it will also stop iteration quickly, and the final walking path may only be a small lattice.

In the circular path, the patrol robot has a long distance to walk as the start point of the path is just the endpoint. When encountering obstacles, the conventional DQN algorithm will begin from the starting point again, resulting in a long calculation cycle of the whole circle.

Therefore, the paper improves the target point function, which the circular route used in this paper is abstracted. In a grid of 30*30, the track boundary is set in black to represent obstacle points. The red point represents the starting point which is the initial position of the patrol robot. The yellow point represents the target point. The paper segments the whole ring line, the yellow spot under an initial state for the first target of the patrol robot. While the patrol robot achieves the first target point, the second target point will be set in the forward line of the patrol robot, at the same time, the first target point will be the new starting point, and turn the white grid point closest to the first target point on the previous route into an obstacle point to make it become the barriers for which the patrol robot can accelerate the efficiency of iteration in the subsequent iterations of the patrol robot, and it also prevents the patrol robot from going “backward” in each iteration. The target point of the last stage is set as the starting point of the initial step to ensure that the patrol robot can complete the whole loop route.

3.3. Improved Reward and Punishment Function

The calculation is performed only according to the improved target point function modified in Section 3.2. As the robot has a relatively large space for walking and the degree of freedom is greatly improved, the algorithm calculation time is too long, which violates the original intention of using the DQN algorithm. Therefore, this paper starts from the reward and punishment function r, and the reward and punishment function r of the design change is shown as follows.

$$r_{\left(i,j\right)}=\{\begin{array}{c}-1, \left(i,j\right) is an obstacle\\ 1, \left(i,j\right) is a target point\\ \mu , r_{\left(m,n\right)}\ne -1,m\in \left[i-1,i+1\right],n\in \left[j-1,j+1\right]\\ 0, others\end{array}$$

(7)

In the original algorithm, the reward value of all points except the obstacle point and target point is 0. However, the reward and punishment function used in this paper adds a new reward and punishment value $\mathsf{\mu }$, which ranges from 0 to 1. The point to which this value is assigned must have the following characteristics: the nine points centered on this point, including the eight surrounding points, are not obstacle points. This point is better than other blank points, and the patrol robot should choose it first.

As shown in Figure 4, the blue point is the new punishment and reward point, but the green point is not because the point to the lower left of the green point is the obstacle point.

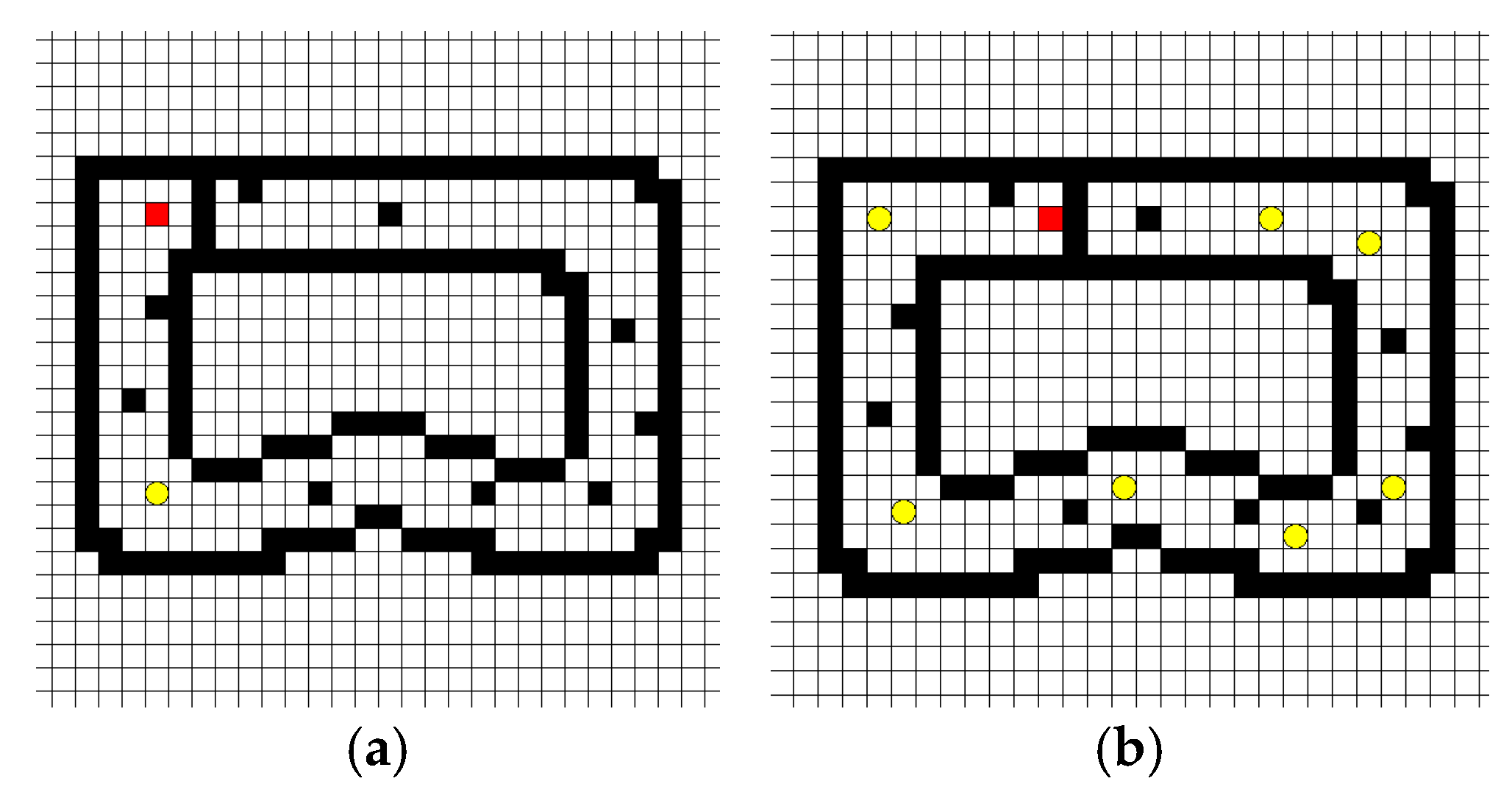
4. Experimental Analysis and Results

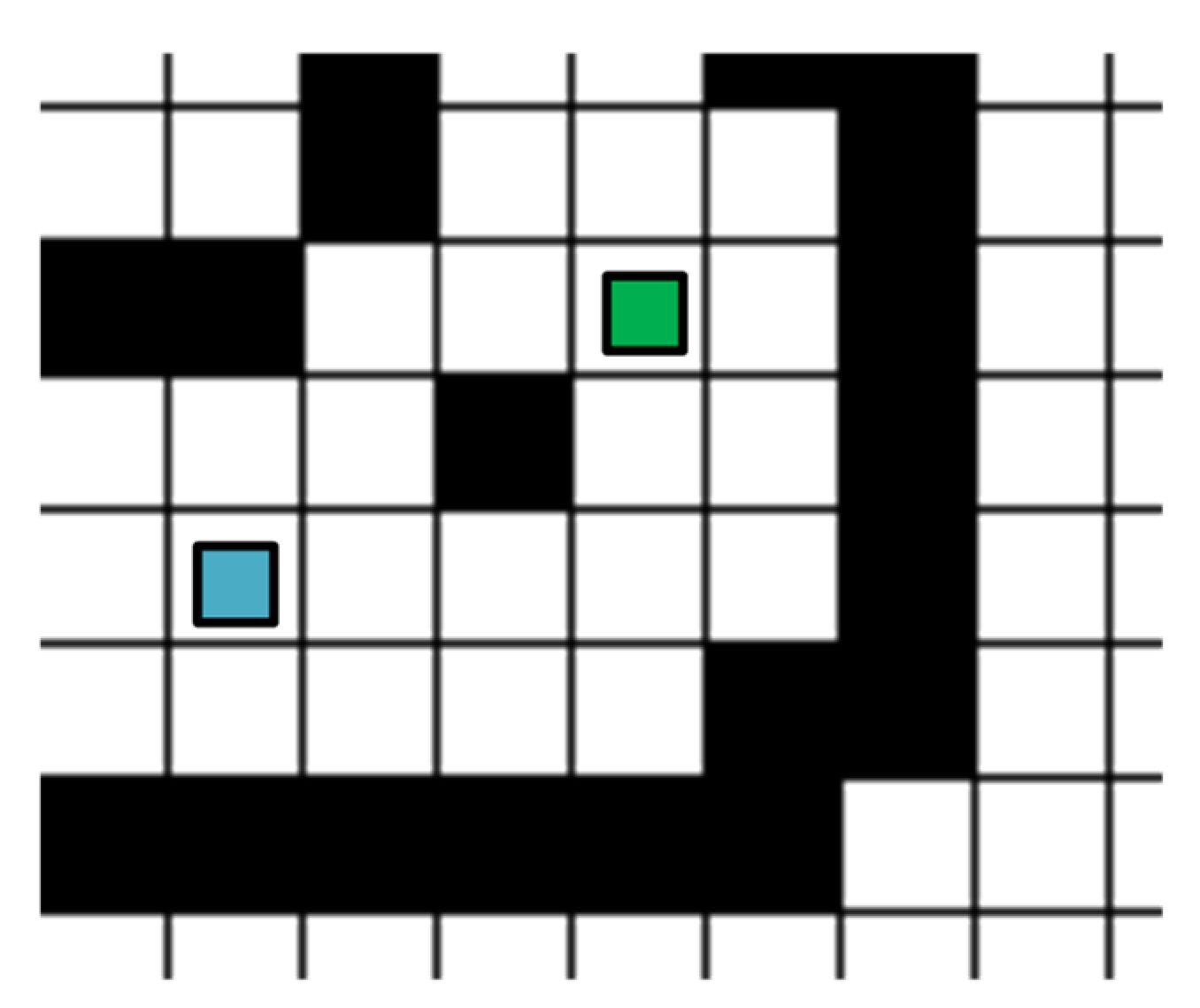
4.1. Experimental Environment and Parameter Configuration

To realize the running experiment of patrol robots and verify the validity of the algorithm in this paper under the specified route, the following experiments comparing with DQN are carried out in this paper. The experimental environment is composed of NVIDIA GeForce GTX 1660 SUPER GPU server, ROS operating system of the robot and Pycharm. The patrol robot training process is trained in the simulation environment built by Pycharm and then transplanted into the patrol robot named Raspblock with PTZ.

The patrol robot takes the state Q value as the input and the action Q value as the output, thus forming a state-action pair. If the patrol robot bumps into obstacles while running, it will get a negative reward. If the patrol robot reaches the target point, it will get a positive reward; the patrol robot also receives fewer positive rewards if it walks on a road point with no obstacles around it. The patrol robot can avoid obstacles in the learning process and keep approaching the target to complete the path planning process through the method of reward and punishment mechanism. Parameter Settings of the improved deep reinforcement learning algorithm are shown in

Table 1. Parameter Settings.

Parameter	Value
Batch	32
Episode	10,000
Learning rate α	0.01
Reward decay γ	0.9
$\mathsf{\epsilon }-\mathrm{greedy}$	0.9

.

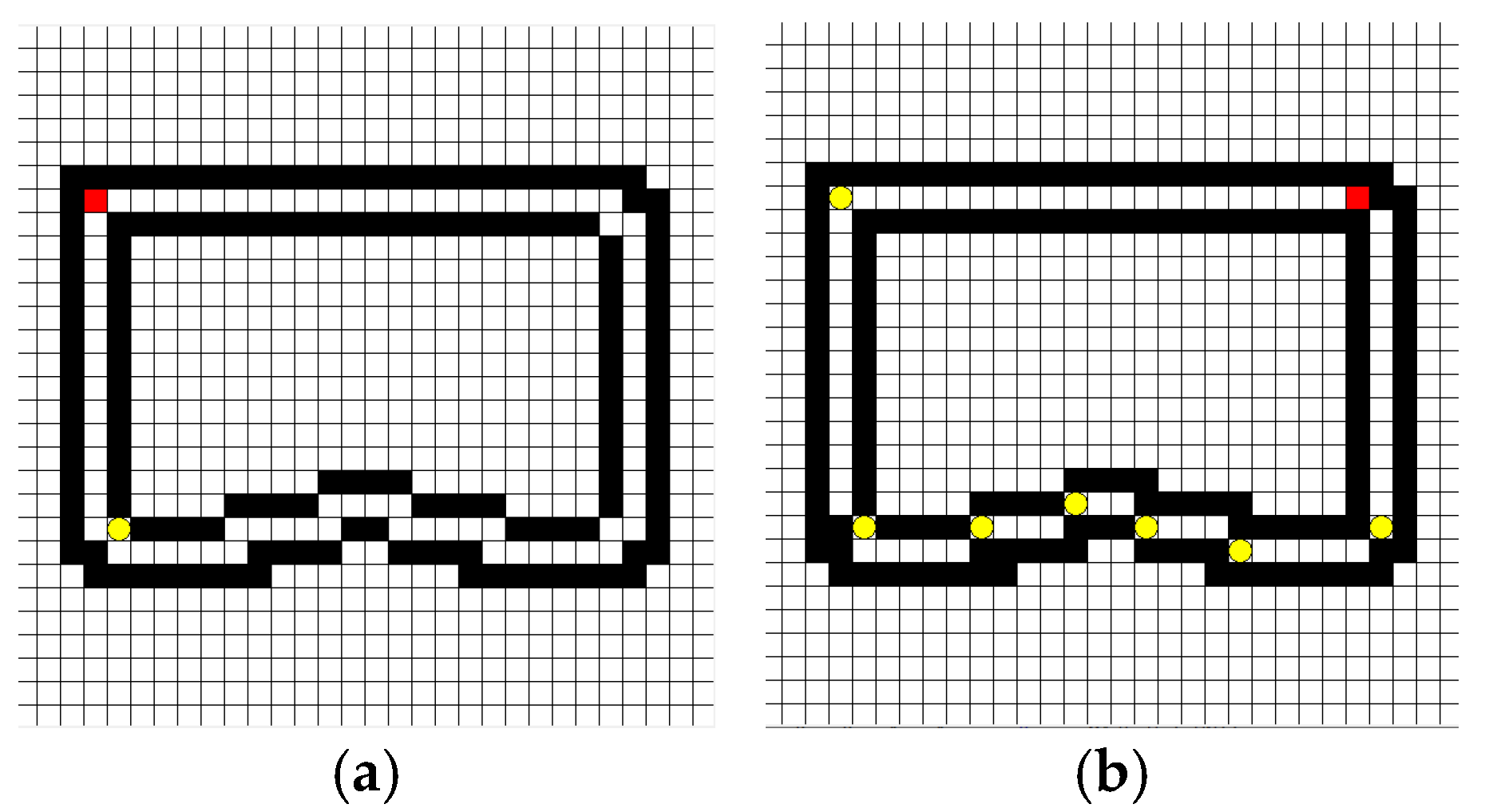
4.2. Experimental Modeling Procedure

The paper is modeling as described in Section 3.2 and the characteristics of map symmetry are shown in Figure 5a. The red point represents the starting point of the robot, which can change as needed. The yellow point represents the target point, and the next target point will generate after the robot reaches it until it runs a full lap. The black points represent obstacles or track boundaries. The state of the final phase is shown in Figure 5b. The last target point is in the same position as the start of the first stage.

The annular region described above conforms to the general condition. However, when obstacles suddenly appear in the specified path, the patrol robot must prioritize obstacle avoidance and then patrol according to the loop. In this paper, the corridor shape is retained, and the white area in the middle of the two black circles is enlarged to deal with obstacles in the line. The new model that preserves the map symmetry is shown in Figure 6. As the black block points in the corridor are randomly set in Figure 6a, the randomness of barriers and the rationality of the algorithm are ensured. The black spots representing obstacles in the model include the original track boundary and the newly added obstacle spots. The new reward and punishment value $\mathsf{\mu }$ at the part of Section 3.3 is introduced. The state of the last stage under the new model is shown in Figure 6b.

4.3. Analysis of Experimental Results

In this paper, the DQN algorithm and the improved algorithm using training times and loss function values are analyzed, and the experimental results are compared. With the same parameters, the convergence speed of the improved DQN algorithm is about 30% faster than that of the DQN algorithm, and the average loss function value of the improved DQN algorithm is about 25% smaller than that of The DQN algorithm under the same training times. As shown in Figure 7, Figure 7a represents the change curve of training times-loss function obtained by the operation of the DQN algorithm, and Figure 7b represents the same by the operation of improved DQN algorithm with a value of 0.5 for the particular reward and punishment value $\mathsf{\mu }$. The number of training times is less than 500, which belongs to the initial training stage. The patrol robot is in the stage of exploration and learning and fails to make correct judgments on obstacles, resulting in a significant loss. When the number of training reaches 500 times, the patrol robot is still exploring the learning obstacle avoidance stage, indicating that it has begun to identify obstacles and correctly avoid some obstacles. However, due to the lack of training, it is still learning and interacting with the environment to adjust further actions to avoid more obstacles to reduce losses. The improved DQN algorithm in the current state is more stable. When the training times are between 500 and 1500, the patrol robot is unstable under the DQN algorithm and the improved DQN algorithm. When the training times reach about 1800, the loss function of the improved DQN algorithm tends to be balanced. When the training times reach about 2600, the loss function of the DQN algorithm is regionally balanced. In the testing stage, the training result model is used to test the network in the same environment to verify its effectiveness further. The objective function and reward value function of test and training are consistent. Therefore, the improved algorithm can shorten the network training time and make the patrol robot plan a shorter path.

Although the improved objective function and reward value function reduces the convergence speed of the algorithm, the corresponding loss function slightly increases. The analysis results show that because the particular reward and punishment value of 0.5 set in the above experiment is too large, the accumulation speed of the reward and punishment value of the patrol robot is too fast, which makes the patrol robot have serious interference in the judgment of the later stage. Therefore, the following modifications are made in this paper, which is the special reward and punishment value 0.5 is changed to ${10}^{-6}$, and it only affects the initial learning, adjusted to 0 after training. The training-loss function generated by the modified algorithm is shown in Figure 8. Figure 8a represents the change curve of the training-loss function obtained when the value of $\mathsf{\mu }$ is ${10}^{-6}$ forever. Figure 8b illustrates the corresponding change curve obtained when the value of $\mathsf{\mu }$ is ${10}^{-6}$ at the initial stage of the experiment and 0 at the later stage of the investigation. Compared with the improved algorithm before, the training times of the two algorithms are increased, which is caused by the sharp decrease of the particular reward and punishment value $\mathsf{\mu }$. However, by comparison, the convergence speed of the optimized algorithm with changing $\mathsf{\mu }$ value is about 40% less than that of the algorithm with unchanged $\mathsf{\mu }$ value. The number of training times is less than 500, which belongs to the initial training stage. The patrol robot is in the stage of exploration and learning and fails to make a correct judgment on obstacles. The loss value is still large, but both algorithms have a downward trend, which the loss function of the algorithm with $\mathsf{\mu }$ value changing declines earlier. When the number of training reaches 500 times, both algorithms tend to balance, and the algorithm with changed $\mathsf{\mu }$ value has fewer training times, which means that the improved DQN algorithm with changed $\mathsf{\mu }$ value can complete the training faster, and the patrol robot can avoid obstacles and reach the target point more quickly. The feasibility of the improved algorithm is further verified.

After several rounds of learning according to the improved algorithm, the patrol robot patrols according to the route shown in Figure 9. If the improved algorithm is not used, the patrol robot is prone to an infinite loop at the yellow target point in the lower-left corner of Figure 9, thus unable to complete the walking task. Because this algorithm is cyclic, no matter which small segment of the target point to take a screenshot will contain part of the obstacle point. Figure 9 is the final part of the target point of the algorithm in the whole circle. The corresponding obstacle point of the last part will be displayed, and other screenshots will also contain the related obstacle point. To distinguish, the transformation of the obstacle points is especially changed to blue.

The calculation time of the four algorithms are analyzed, including the convergence steps of their curves to be smooth, the total number of training steps, and the loss function tabulation of convergence. The data is shown in

Table 2. Some data for four algorithms.

	$\mathsf{\mu }=0$	$\mathsf{\mu }=0.5$	$\mathsf{\mu }={10}^{-6}$	$\mathbf{Changeable} \mathsf{\mu }$
Operation time	300 s	80 s	63 s	35 s
Convergence steps	2000	1500	750	600
Total training steps	2600	1800	5500	3100
Loss function	0.030	0.040	0.010	0.015

. Particular reward values are used to distinguish the four algorithms, $\mathsf{\mu }=0$ for Figure 7a, $\mathsf{\mu }=0.5$ for Figure 7b, $\mathsf{\mu }={10}^{-6}$ for Figure 8a, and changeable $\mathsf{\mu }$ for Figure 8b.

5. Conclusions

To solve the problem that the patrol robot can complete the loop route, an improved DQN algorithm based on deep image information is proposed. The depth image information of the obstacle is obtained by using PTZ, and then the information is directly input into the network, which improves the convergence speed of network training. By enhancing the reward and punishment functions and adding new reward value points, the reward value of the robot is improved, the problem of sparse reward in the environment state space is solved by optimizing the state-action space, and the robot’s action selection is more accurate to complete the patrol task. Simulation and experimental results show that the training times and loss function values of the DQN algorithm and the improved DQN algorithm are analyzed through comparative experiments, and the effective implementation of the improved algorithm is further verified in the testing stage. The improved algorithm not only enhances the robot’s exploration ability and obstacle avoidance ability but also makes the planned path length safer, which verifies the improved DQN algorithm’s feasibility in path planning.

In addition to the black ring boundary, the target point, the starting point, and the intermediate obstacle point in this paper are randomly set, so the improved algorithm has strong universality. According to the previous experiments, the DQN algorithm cannot achieve the best stability and the fastest calculation speed. The optimal result of this paper is to select the optimal operating speed based on ensuring stability. In the future, more restrictive conditions can be added to verify the correctness and reliability of the improved DQN algorithm.