Group Theoretical Description of the Periodic System
Abstract
:1. Introduction
2. Single Quantum System and Rumer–Fet Group
- A.I (Energy and fundamental symmetry) A single quantum system at the fundamental level is characterized by a -algebra with a unit consisting of the energy operator H and the generators of the fundamental symmetry group attached to H, forming a common system of eigenfunctions with H.
- A.II (States and GNS construction) The physical state of a -algebra is determined by the cyclic vector of the representation π of a -algebra in a separable Hilbert space :The set of all pure states of a -algebra coincides with the set of all states associated with all irreducible cyclic representations π of an algebra , (Gelfand–Naimark–Segal construction).
- A.III (Physical Hilbert space) The set of all pure states under the condition forms a physical Hilbert space (in general, the space is nonseparable). For each state vector there is a unit ray , where α runs through all real numbers and . The ray space is a quotient-space , that is, the projective space of one-dimensional subspaces of . All states of a single quantum system are described by the unit rays.
- A.IV (Axiom of spectrality) In there is a complete system of states with non-negative energy.
- A.V (Superposition principle) The basic correspondence between physical states and elements of space involves the superposition principle of quantum theory; that is, there is a set of basic states such that arbitrary states can be constructed from them using linear superpositions.
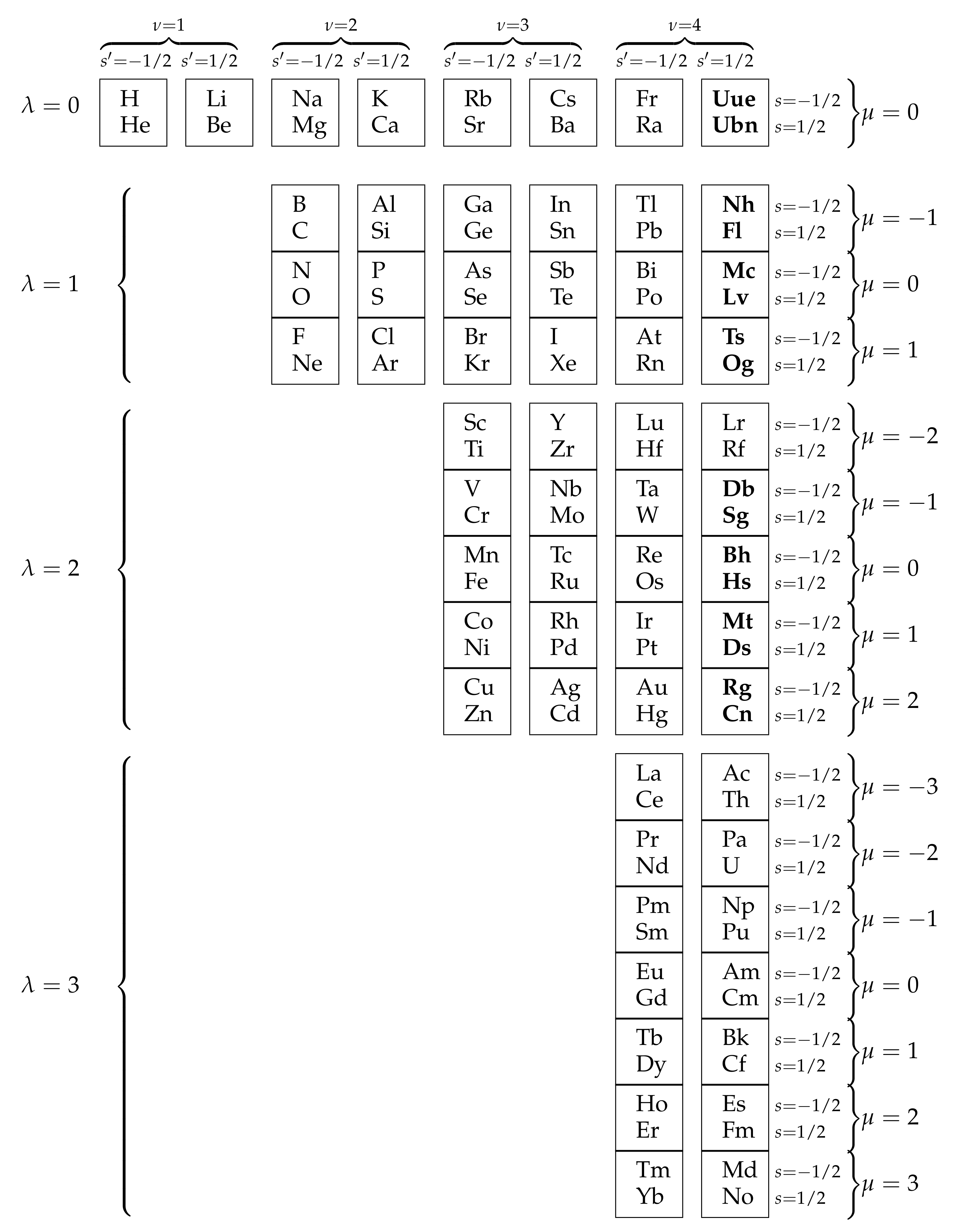
2.1. Rumer–Fet Group
- (1)
- elements are arranged in increasing order of atomic number Z;
- (2)
- collections are arranged in increasing order of ; at the given in increasing order of n; at the given , n in increasing order of m; at the given , n, m in increasing order of s;
- (3)
- the Z-th element corresponds to Z-th collection.
- (1)
- the elements are arranged in increasing order of atomic number Z;
- (2)
- collections are arranged in increasing order of ; at the given in increasing order of ; at the given , in decreasing order of ; at the given , , in increasing order of ; at the given , , , in increasing order of s;
- (3)
- the Z-th element corresponds to Z-th collection.
2.2. Mendeleev Table
3. Implementation of the Operator Algebra
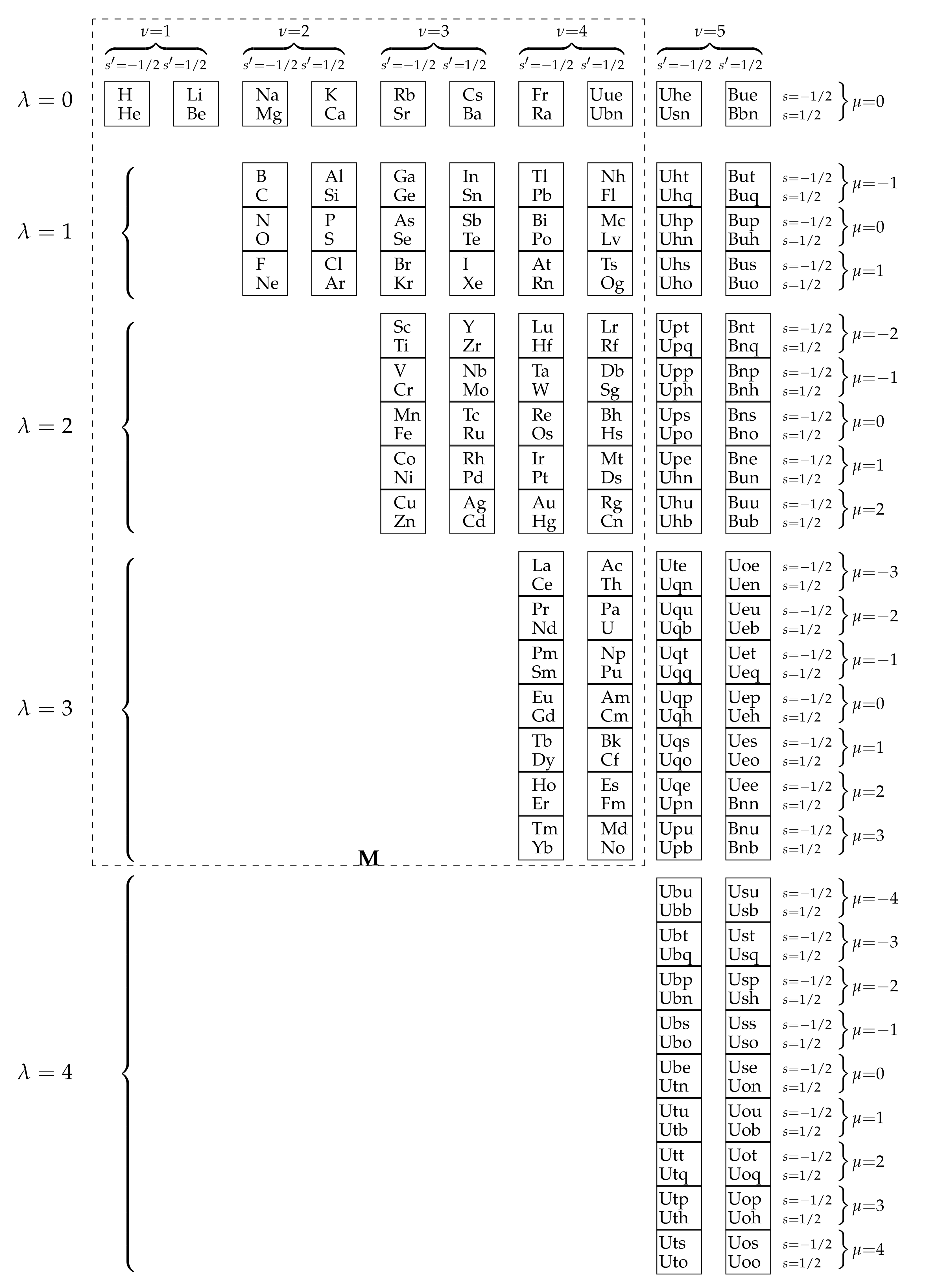
4. Seaborg Table
Masses of Elements
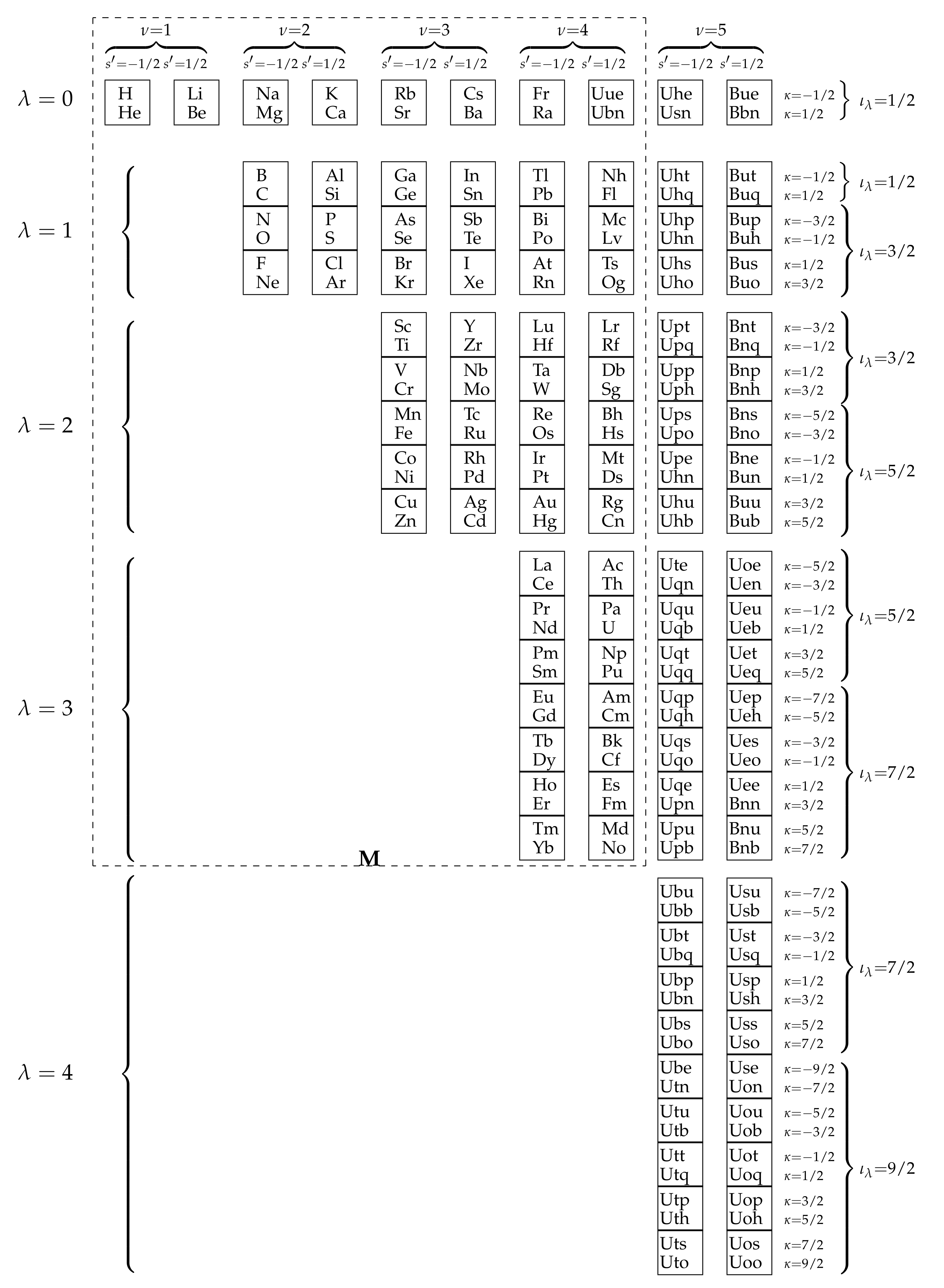
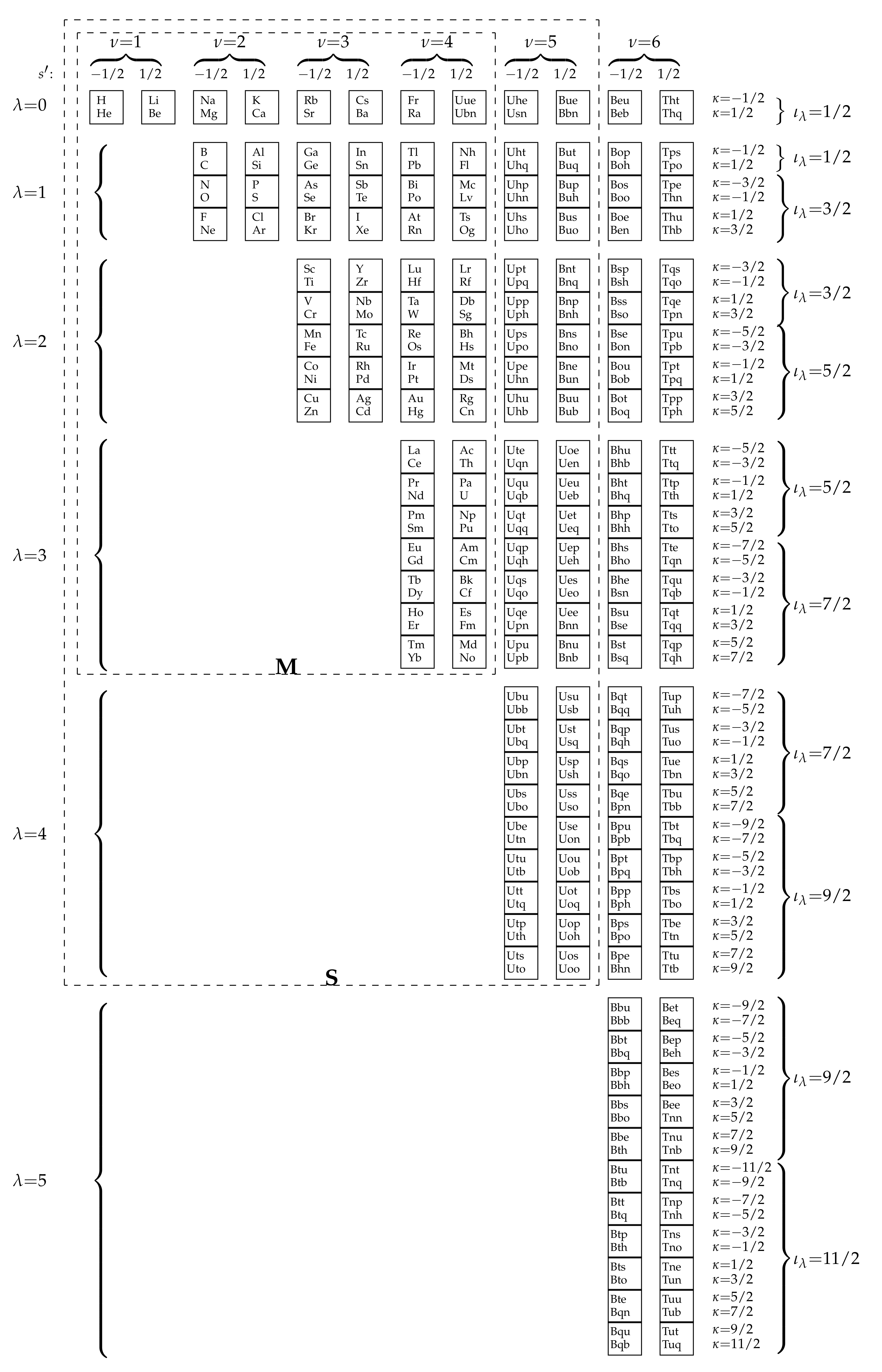
5. 10-Periodic Extension
Masses of Elements of 10th and 11th Periods
6. Homological Series
7. Hypertwistors
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Lorentz Group and van der Waerden Representation
Appendix B. Group and Fock Representation
Appendix C. Twistor Structure and Group
References
- Korableva, T.P.; Korolkov, D.V. Theory of the Periodic System; Saint-Petersburg University Press: Saint-Petersburg, Russia, 2005. (In Russian) [Google Scholar]
- Fock, V.A. Do the chemical properties of atoms fit into the framework of purely spatial representations. In The Periodic Law and the Structure of the Atom; Atomizdat: Moscow, Russia, 1971; pp. 107–117. (In Russian) [Google Scholar]
- Rumer, Y.B.; Fet, A.I. Spin(4) group and the Mendeleev system. Teor. Mat. Fiz. 1971, 9, 203–209. [Google Scholar] [CrossRef]
- Barut, A. Group Structure of the Periodic System. In The Structure of Matter: Ruterford Centennial Symposium; Wyborne, B.G., Ed.; Univercity of Canterburry Press: Christchurch, New Zeland, 1972. [Google Scholar]
- Barut, A. Dynamical Groups and Generilized Symmetries in Quantum Theory; Brooks, A.H., Ed.; Univercity of Canterburry Press: Christchurch, New Zeland, 1972. [Google Scholar]
- Navaro, O.; Wolf, K.B. A Model Hamiltonian for the Periodic Table. Rev. Mex. Fis. 1971, 20, 71. [Google Scholar]
- Navaro, O.; Berrondo, M. Approximate Symmetry of the Periodic Table. J. Phys. B At. Mol. Phys. 1972, 5, 6. [Google Scholar] [CrossRef]
- Demkov, Y.N.; Ostrovsky, V.N. n+l Filling Rule in the Periodic System and Focusing Potentials. Sov. Phys. JETP 1972, 35, 1. [Google Scholar]
- Ostrovsky, V.N. The Periodic Table and Quantum Physics. In The Periodic Table: Into the 21st Century; Rouvray, D.H., King, R.B., Eds.; Research Studies Press: Baldock, UK, 2004. [Google Scholar]
- Ostrovsky, V.N. Group Theory Applied to the Periodic Table of the Elements. In The Mathematics of the Periodic Table; Rouvray, D.H., King, R.B., Eds.; Nova Science Publishers: New York, NY, USA, 2006. [Google Scholar]
- Thyssen, P.; Ceulemans, A. Particular Symmetries: Group Theory of the Periodic System. Substantia 2020, 4, 7–22. [Google Scholar]
- Gelfand, I.; Neumark, M. On the Imbedding of Normed Rings into the Ring of Operators in Hilbert Space. Rec. Math. [Mat. Sb.] N.S. 1943, 12, 197–217. [Google Scholar]
- Segal, I. Postulates for general quantum mechanics. Ann. Math. 1947, 48, 930–948. [Google Scholar] [CrossRef]
- Varlamov, V.V. Lorentz Group and Mass Spectrum of Elementary Particles. arXiv 2017, arXiv:1705.02227. [Google Scholar]
- Varlamov, V.V. Fundamental Automorphisms of Clifford Algebras and an Extension of Da̧browski Pin Groups. Hadron. J. 1999, 22, 497–535. [Google Scholar]
- Varlamov, V.V. Discrete Symmetries and Clifford Algebras. Int. J. Theor. Phys. 2001, 40, 769–805. [Google Scholar] [CrossRef]
- Varlamov, V.V. Discrete symmetries on the spaces of quotient representations of the Lorentz group. Math. Struct. Model. 2001, 7, 115–128. [Google Scholar]
- Varlamov, V.V. CPT groups for spinor field in de Sitter space. Phys. Lett. B 2005, 631, 187–191. [Google Scholar] [CrossRef] [Green Version]
- Varlamov, V.V. CPT Groups of Higher Spin Fields. Int. J. Theor. Phys. 2012, 51, 1453–1481. [Google Scholar] [CrossRef] [Green Version]
- Varlamov, V.V. Spinor Structure and Internal Symmetries. Int. J. Theor. Phys. 2015, 54, 3533–3576. [Google Scholar] [CrossRef] [Green Version]
- Heisenberg, W. Introduction to the Unified Field Theory of Elementary Particles; Interscience Publishers: London, UK; New York, NY, USA; Sydney, Australia, 1966. [Google Scholar]
- Segal, I. A class of operator algebras which are determined by groups. Duke Math. J. 1951, 18, 221–265. [Google Scholar] [CrossRef]
- Fock, V.A. Hydrogen atom and non-Euclidean geometry. Izv. AN SSSR. Ser. VII 1935, 2, 169–179. [Google Scholar]
- Konopelchenko, B.G. Group SO(2,4)+R and Mendeleev System; SO RAN; Instite of Nuclear Physics: Novosibirsk, Russia, 1972. [Google Scholar]
- Kibler, M.R. From the Mendeleev periodic table to particle physics and back to periodic table. Found. Chem. 2006, 9, 221–234. [Google Scholar] [CrossRef] [Green Version]
- Fet, A.I. Symmetry Group of Chemical Elements; Nauka: Novosibirsk, Russia, 2010. (In Russian) [Google Scholar]
- Yao, T. Unitary Irreducible Representations of SU(2,2). J. Math. Phys. 1967, 8, 1931–1954. [Google Scholar] [CrossRef]
- Madelung, E. Die Mathematischen Hilfsmittel des Physikers; Springer: Berlin, Germany, 1957. [Google Scholar]
- Kleczkowski, V.M. Atomic Electron Distribution and the Rule of Sequential Filling of (n+l)-Groups; Atomizdat: Moscow, Russia, 1968. (In Russian) [Google Scholar]
- Gell-Mann, M. Symmetries of Baryons and Mesons. Phys. Rev. 1962, 125, 1067–1084. [Google Scholar] [CrossRef] [Green Version]
- Okubo, S.; Ryan, C. Quadratic mass formula in SU(3). Nuovo C. 1964, 34, 776–779. [Google Scholar] [CrossRef]
- Bég, M.; Singh, V. Splitting of the 70-Plet of SU(6). Phys. Rev. Lett. 1964, 13, 509–511. [Google Scholar] [CrossRef]
- Emch, G.G. Algebraic Methods in Statistical Mechanics and Quantum Field Theory; Wiley-Interscience: New York, NY, USA, 1972. [Google Scholar]
- Bogoljubov, N.N.; Logunov, A.A.; Oksak, A.I.; Todorov, I.T. General Principles of Quantum Field Theory; Springer: Dordrecht, Germany, 1990. [Google Scholar]
- Horuzhy, S.S. Introduction to Algebraic Quantum Field Theory; Nauka: Moscow, Russia, 1986. (In Russian) [Google Scholar]
- Lounesto, P. Clifford Algebras and Spinors; Cambridge Univ. Press: Cambridge, UK, 2001. [Google Scholar]
- Varlamov, V.V. Generalized Weierstrass representation for surfaces in terms of Dirac-Hestenes spinor field. J. Geom. Phys. 2000, 32, 241–251. [Google Scholar] [CrossRef] [Green Version]
- Varlamov, V.V. Spinor Structure and Periodicity of Clifford Algebras. Math. Struct. Model. 2015, 35, 4–20. [Google Scholar]
- Heisenberg, W. Across the Frontiers; Harper & Row: New York, NY, USA, 1974. [Google Scholar]
- Fet, A.I. Conformal symmetry of chemical elements. Theor. Math. Phys. 1975, 22, 323–334. [Google Scholar] [CrossRef]
- Heisenberg, W. Physics and Beyond: Encounters and Conversations; Harper & Row: New York, NY, USA, 1974. [Google Scholar]
- Varlamov, V.V. Spinor Structure and SU(3)-Symmetry. Math. Struct. Model. 2016, 39, 5–23. [Google Scholar]
- Varlamov, V.V. Heisenberg Matter Spectrum in Abstract Algebraic Approach. Math. Struct. Model. 2015, 33, 18–33. [Google Scholar]
- Wigner, E.P. On unitary representations of the inhomogeneous Lorentz group. Ann. Math. 1939, 40, 149–204. [Google Scholar] [CrossRef]
- Varlamov, V.V. CPT groups of spinor fields in de Sitter and anti-de Sitter spaces. Adv. Appl. Clifford Algebr. 2015, 25, 487–516. [Google Scholar] [CrossRef] [Green Version]
- Seaborg, G. Expansion of the limits of the periodic system. In One Hundred Years of the Periodic Law of the Chemical Elements; Nauka: Moscow, Russia, 1971; pp. 21–39. (In Russian) [Google Scholar]
- Greiner, W.; Reinhardt, J. Quantum Electrodynamics; Springer: Berlin, Germany, 2009. [Google Scholar]
- Wick, G.G.; Wigner, E.P.; Wightman, A.S. Intrinsic Parity of Elementary Particles. Phys. Rev. 1952, 88, 101. [Google Scholar] [CrossRef] [Green Version]
- Varlamov, V.V. Relativistic wavefunctions on the Poincaré group. J. Phys. A Math. Gen. 2004, 37, 5467–5476. [Google Scholar] [CrossRef] [Green Version]
- Varlamov, V.V. Relativistic spherical functions on the Lorentz group. J. Phys. A Math. Gen. 2006, 39, 805–822. [Google Scholar] [CrossRef] [Green Version]
- Varlamov, V.V. Spherical functions on the de Sitter group. J. Phys. A Math. Theor. 2007, 40, 163–201. [Google Scholar] [CrossRef]
- Varlamov, V.V. Universal Coverings of Orthogonal Groups. Adv. Appl. Clifford Algebr. 2004, 14, 81–168. [Google Scholar] [CrossRef] [Green Version]
- Rashevskii, P.K. The Theory of Spinors. Uspekhi Mat. Nauk. 1955, 10, 3–110. [Google Scholar]
- Baez, J.C. Division Algebras and Quantum Mechanics. Found. Phys. 2012, 42, 819–855. [Google Scholar] [CrossRef]
- Pauli, W. Zur Quantenmechanik des magnetischen Elektronen. Z. Phys. 1927, 43, 601. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The Quantum Theory of the Electron. Proc. R. Soc. Lond. A 1928, 117, 610–624. [Google Scholar]
- Knapp, A.W. Representation Theory of Semisimple Groups; Princeton University Press: Princeton, NJ, USA, 1986. [Google Scholar]
- Gelfand, I.M.; Minlos, R.A.; Shapiro, Z.Y. Representations of the Rotation and Lorentz Groups and Their Applications; Pergamon Press: Oxford, UK, 1963. [Google Scholar]
- Naimark, M.A. Linear Representations of the Lorentz Group; Pergamon: London, UK, 1964. [Google Scholar]
- Akhiezer, A.I.; Berestetskii, V.B. Quantum Electrodynamics; John Wiley & Sons: New York, NY, USA, 1965. [Google Scholar]
- Schweber, S.S. An Introduction to Relativistic Quantum Field Theory; Harper & Row: New York, NY, USA, 1961. [Google Scholar]
- Rumer, Y.B.; Fet, A.I. Group Theory and Quantized Fields; Nauka: Moscow, Russia, 1977. (In Russian) [Google Scholar]
- Van der Waerden, B.L. Group Theory and Quantum Mechanics; Springer: Berlin, Germany, 1974. [Google Scholar]
- Penrose, R. The twistor programme. Rep. Math. Phys. 1977, 12, 65–76. [Google Scholar] [CrossRef]
- Penrose, R.; MacCallum, M.A.H. Twistor theory: An approach to the quantization of fields and space-time. Phys. Rep. 1972, 6, 241–316. [Google Scholar] [CrossRef]
| Multiplet | Mass (exp.) | Mass (theor.) | Approx. % | |
|---|---|---|---|---|
| 1. | 53 | |||
| 2. | 75 | |||
| 3. | 86 | |||
| 4. | 104 | |||
| 5. | 126 | |||
| 6. | 137 | |||
| 7. | 156 | |||
| 8. | 189 | |||
| 9. | 211 | |||
| 10. | 222 | |||
| 11. | 241 | |||
| 12. | 274 | |||
| 13. | 296 | |||
| 14. | 318 * | 307 | * |
| Multiplet | Mass (theor.) | |
|---|---|---|
| 1. | 316 | |
| 2. | 360 | |
| 3. | 393 | |
| 4. | 415 | |
| 5. | 426 | |
| 6. | 435 | |
| 7. | 479 | |
| 8. | 512 | |
| 9. | 534 | |
| 10. | 545 |
| Multiplet | Mass (exp.) | Mass (theor.) | Approx. % | |
|---|---|---|---|---|
| 1. | ||||
| 2. | 8.00 | +0.31 | ||
| 3. | 14.10 | −8.05 | ||
| 4. | 24.10 | +1.90 | ||
| 5. | 30.20 | −6.35 | ||
| 6. | 40.20 | +1.54 |
| Z | Element | Vector | Mass (exp.) | Mass (theor.) | Approx. % |
|---|---|---|---|---|---|
| 1 | H | 1.01 | |||
| 2 | He | 4.00 | |||
| 3 | Li | 6.94 | |||
| 4 | Be | 9.01 | |||
| 5 | B | 10.81 | |||
| 6 | C | 12.01 | |||
| 7 | N | 14.01 | |||
| 8 | O | 16.00 | |||
| 9 | F | 19.00 | |||
| 10 | Ne | 20.18 | |||
| 11 | Na | 22.99 | |||
| 12 | Mg | 24.31 | |||
| 13 | Al | 26.98 | |||
| 14 | Si | 28.09 | 32.30 | +14.38 | |
| 15 | P | 30.97 | 31.77 | +2.58 | |
| 16 | S | 32.06 | 35.04 | +9.29 | |
| 17 | Cl | 35.45 | 39.25 | +10.72 | |
| 18 | Ar | 39.95 | 42.52 | +6.43 | |
| 19 | K | 39.10 | 38.09 | −2.58 | |
| 20 | Ca | 40.08 | 42.30 | +5.54 | |
| 21 | Sc | 44.96 | 50.25 | +11.76 | |
| 22 | Ti | 47.90 | 51.92 | +8.39 | |
| 23 | V | 50.94 | 54.08 | +6.16 | |
| 24 | Cr | 52.00 | 55.75 | +7.21 | |
| 25 | Mn | 54.94 | 58.28 | +6.08 | |
| 26 | Fe | 55.85 | 59.00 | +5.64 | |
| 27 | Co | 58.93 | 60.67 | +2.95 | |
| 28 | Ni | 58.70 | 62.83 | +7.03 | |
| 29 | Cu | 63.55 | 64.49 | +1.48 | |
| 30 | Zn | 65.38 | 65.21 | −0.26 | |
| 31 | Ga | 69.72 | 73.92 | +6.02 | |
| 32 | Ge | 72.59 | 76.08 | +4.81 | |
| 33 | As | 74.92 | 77.10 | +2.91 | |
| 34 | Se | 78.96 | 78.77 | −0.24 | |
| 35 | Br | 79.90 | 80.93 | +1.29 | |
| 36 | Kr | 83.80 | 82.60 | −1.43 | |
| 37 | Rb | 85.47 | 84.92 | −0.64 | |
| 38 | Sr | 87.62 | 87.07 | −0.63 | |
| 39 | Y | 88.91 | 101.25 | +13.88 | |
| 40 | Zr | 91.22 | 102.92 | +12.83 | |
| 41 | Nb | 92.91 | 105.07 | +13.09 | |
| 42 | Mo | 95.94 | 106.75 | +11.27 | |
| 43 | Tc | 98.91 | 109.28 | +10.48 | |
| 44 | Ru | 101.07 | 110.00 | +8.83 | |
| 45 | Rh | 102.91 | 111.67 | +8.51 | |
| 46 | Pd | 106.42 | 113.83 | +6.96 | |
| 47 | Ag | 107.87 | 115.49 | +7.06 | |
| 48 | Cd | 112.41 | 116.21 | +3.38 | |
| 49 | In | 114.82 | 124.92 | +8.79 | |
| 50 | Sn | 118.69 | 127.07 | +7.06 | |
| 51 | Sb | 121.75 | 128.10 | +5.21 | |
| 52 | Te | 127.60 | 129.77 | +1.77 | |
| 53 | I | 126.90 | 131.02 | +3.96 | |
| 54 | Xe | 131.30 | 133.59 | +1.74 | |
| 55 | Cs | 132.91 | 135.92 | +2.26 | |
| 56 | Ba | 137.33 | 138.08 | +0.55 | |
| 57 | La | 138.91 | 152.53 | +9.80 | |
| 58 | Ce | 140.12 | 153.25 | +9.37 | |
| 59 | Pr | 140.91 | 154.92 | +9.94 | |
| 60 | Nd | 144.24 | 157.07 | +8.89 | |
| 61 | Pm | [145] | 158.75 | +9.48 | |
| 62 | Sm | 150.40 | 159.46 | +6.02 | |
| 63 | Eu | 151.96 | 164.72 | +8.39 | |
| 64 | Gd | 157.25 | 165.18 | +5.04 | |
| 65 | Tb | 158.93 | 165.90 | +4.38 | |
| 66 | Dy | 162.50 | 167.52 | +3.09 | |
| 67 | Ho | 164.93 | 169.72 | +2.90 | |
| 68 | Er | 167.26 | 171.39 | +2.47 | |
| 69 | Tm | 168.93 | 172.11 | +1.88 | |
| 70 | Eu | 173.04 | 172.58 | −0.26 | |
| 71 | Lu | 174.97 | 186.25 | +6.45 | |
| 72 | Hf | 178.49 | 187.92 | +5.28 | |
| 73 | Ta | 180.95 | 190.07 | +5.04 | |
| 74 | W | 183.85 | 191.75 | +4.29 | |
| 75 | Re | 186.21 | 194.28 | +4.33 | |
| 76 | Os | 190.20 | 195.00 | +2.52 | |
| 77 | Ir | 192.22 | 196.67 | +2.31 | |
| 78 | Pt | 195.09 | 198.82 | +1.91 | |
| 79 | Au | 196.97 | 200.49 | +1.79 | |
| 80 | Hg | 200.59 | 201.21 | +0.30 | |
| 81 | Tl | 204.37 | 209.92 | +2.71 | |
| 82 | Pb | 207.20 | 212.07 | +2.35 | |
| 83 | Bi | 208.98 | 213.10 | +1.97 | |
| 84 | Po | 208.98 | 214.77 | +2.77 | |
| 85 | At | [210] | 216.93 | +3.30 | |
| 86 | Rn | 222.08 | 218.60 | −1.57 | |
| 87 | Fr | 223.08 | 220.92 | −0.97 | |
| 88 | Ra | 226.03 | 223.07 | −1.31 | |
| 89 | Ac | 227.03 | 237.53 | +4.62 | |
| 90 | Th | 232.04 | 238.25 | +2.67 | |
| 91 | Pa | 231.04 | 239.92 | +3.84 | |
| 92 | U | 238.03 | 242.07 | +1.69 | |
| 93 | Np | 237.05 | 243.75 | +2.82 | |
| 94 | Pu | 244.06 | 244.46 | +0.16 | |
| 95 | Am | [243] | 249.72 | +2.76 | |
| 96 | Cm | 247.07 | 250.19 | +1.26 | |
| 97 | Bk | 247.07 | 250.90 | +1.55 | |
| 98 | Cf | 251.08 | 252.57 | +0.59 | |
| 99 | Es | 252.08 | 254.72 | +1.08 | |
| 100 | Fm | 257.09 | 256.40 | −0.27 | |
| 101 | Md | 258.10 | 257.11 | −0.38 | |
| 102 | No | 259.10 | 257.58 | −0.59 | |
| 103 | Lr | [266] | 271.25 | +1.93 | |
| 104 | Rf | 267 | 272.92 | +2.22 | |
| 105 | Db | 268 | 275.07 | +2.64 | |
| 106 | Sg | [269] | 276.75 | +2.88 | |
| 107 | Bh | [267] | 279.28 | +4.60 | |
| 108 | Hs | [269] | 280.00 | +4.09 | |
| 109 | Mt | [278] | 281.67 | +1.32 | |
| 110 | Ds | [281] | 283.83 | +1.01 | |
| 111 | Rg | [282] | 285.50 | +1.24 | |
| 112 | Cn | [285] | 286.21 | +0.42 | |
| 113 | Nh | [286] | 294.92 | +3.12 | |
| 114 | Fl | [289] | 297.08 | +2.79 | |
| 115 | Mc | [290] | 298.10 | +2.79 | |
| 116 | Lv | [293] | 299.77 | +2.31 | |
| 117 | Ts | [294] | 301.92 | +2.69 | |
| 118 | Og | [294] | 303.59 | +3.26 | |
| 119 | Uue | 305.92 | |||
| 120 | Ubn | 308.08 |
| Z | Element | Vector | Mass (theor.) |
|---|---|---|---|
| 121 | Ubu | 312.07 | |
| 122 | Ubb | 312.59 | |
| 123 | Ubt | 313.25 | |
| 124 | Ubq | 314.92 | |
| 125 | Ubp | 317.07 | |
| 126 | Ubn | 318.75 | |
| 127 | Ubs | 319.46 | |
| 128 | Ubo | 319.93 | |
| 129 | Ube | 326.61 | |
| 130 | Utn | 328.62 | |
| 131 | Utu | 329.08 | |
| 132 | Utb | 329.80 | |
| 133 | Utt | 331.47 | |
| 134 | Utq | 333.63 | |
| 135 | Utp | 335.29 | |
| 136 | Uth | 336.01 | |
| 137 | Uts | 336.48 | |
| 138 | Uto | 338.49 | |
| 139 | Ute | 356.54 | |
| 140 | Uqn | 357.25 | |
| 141 | Uqu | 358.92 | |
| 142 | Uqb | 361.07 | |
| 143 | Uqt | 362.75 | |
| 144 | Uqq | 363.46 | |
| 145 | Uqp | 368.72 | |
| 146 | Uqh | 369.19 | |
| 147 | Uqs | 369.90 | |
| 148 | Uqo | 371.57 | |
| 149 | Uqe | 373.72 | |
| 150 | Upn | 375.39 | |
| 151 | Upu | 376.11 | |
| 152 | Uqb | 376.58 | |
| 153 | Upt | 390.25 | |
| 154 | Upq | 391.92 | |
| 155 | Upp | 394.08 | |
| 156 | Uph | 395.75 | |
| 157 | Ups | 398.28 | |
| 158 | Upo | 399.00 | |
| 159 | Upe | 400.67 | |
| 160 | Uhn | 402.83 | |
| 161 | Uhu | 404.50 | |
| 162 | Uhb | 405.21 | |
| 163 | Uht | 413.92 | |
| 164 | Uhq | 416.07 | |
| 165 | Uhp | 417.10 | |
| 166 | Uhn | 418.77 | |
| 167 | Uhs | 420.93 | |
| 168 | Uho | 422.59 | |
| 169 | Uhe | 424.92 | |
| 170 | Usn | 427.08 | |
| 171 | Usu | 431.07 | |
| 172 | Usb | 431.54 | |
| 173 | Ust | 432.55 | |
| 174 | Usq | 433.92 | |
| 175 | Usp | 436.08 | |
| 176 | Ush | 437.75 | |
| 177 | Uss | 438.46 | |
| 178 | Uso | 438.93 | |
| 179 | Use | 445.61 | |
| 180 | Uon | 447.62 | |
| 181 | Uou | 448.09 | |
| 182 | Uob | 448.80 | |
| 183 | Uot | 450.47 | |
| 184 | Uoq | 452.63 | |
| 185 | Uop | 454.30 | |
| 186 | Uoh | 455.01 | |
| 187 | Uos | 455.48 | |
| 188 | Uoo | 457.49 | |
| 189 | Uoe | 475.54 | |
| 190 | Uen | 476.25 | |
| 191 | Ueu | 477.92 | |
| 192 | Ueb | 480.07 | |
| 193 | Uet | 481.75 | |
| 194 | Ueq | 482.46 | |
| 195 | Uep | 487.72 | |
| 196 | Ueh | 488.19 | |
| 197 | Ues | 488.90 | |
| 198 | Ueo | 490.57 | |
| 199 | Uee | 492.73 | |
| 200 | Bnn | 494.40 | |
| 201 | Bnu | 495.11 | |
| 202 | Bnb | 495.58 | |
| 203 | Bnt | 509.25 | |
| 204 | Bnq | 510.92 | |
| 205 | Bnp | 513.08 | |
| 206 | Bnh | 514.75 | |
| 207 | Bns | 517.29 | |
| 208 | Bno | 518.00 | |
| 209 | Bne | 519.67 | |
| 210 | Bun | 521.83 | |
| 211 | Buu | 523.50 | |
| 212 | Bub | 524.21 | |
| 213 | But | 532.92 | |
| 214 | Buq | 535.08 | |
| 215 | Bup | 536.10 | |
| 216 | Buh | 537.77 | |
| 217 | Bus | 539.93 | |
| 218 | Buo | 541.60 | |
| 219 | Bue | 543.92 | |
| 220 | Bbn | 546.08 |
| Z | Element | Vector | Mass (theor.) |
|---|---|---|---|
| 221 | Bbu | 527.06 | |
| 222 | Bbb | 529.07 | |
| 223 | Bbt | 529.54 | |
| 224 | Bbq | 530.25 | |
| 225 | Bbp | 531.92 | |
| 226 | Bbh | 534.08 | |
| 227 | Bbs | 535.75 | |
| 228 | Bbo | 536.46 | |
| 229 | Bbe | 536.93 | |
| 230 | Btn | 536.93 | |
| 231 | Btu | 542.64 | |
| 232 | Btb | 547.51 | |
| 233 | Btt | 549.52 | |
| 234 | Btq | 549.99 | |
| 235 | Btp | 550.70 | |
| 236 | Bth | 552.37 | |
| 237 | Bts | 554.53 | |
| 238 | Bto | 556.20 | |
| 239 | Bte | 556.91 | |
| 240 | Bqn | 557.38 | |
| 241 | Bqu | 559.39 | |
| 242 | Bqb | 564.26 | |
| 243 | Bqt | 584.07 | |
| 244 | Bqq | 584.54 | |
| 245 | Bqp | 585.25 | |
| 246 | Bqh | 586.92 | |
| 247 | Bqs | 589.08 | |
| 248 | Bqo | 590.75 | |
| 249 | Bqe | 591.46 | |
| 250 | Bpn | 591.93 | |
| 251 | Bpu | 598.61 | |
| 252 | Bpb | 600.62 | |
| 253 | Bpt | 601.09 | |
| 254 | Bpq | 601.80 | |
| 255 | Bpp | 603.47 | |
| 256 | Bph | 605.63 | |
| 257 | Bps | 607.30 | |
| 258 | Bpo | 608.01 | |
| 259 | Bpe | 608.48 | |
| 260 | Bhn | 610.49 | |
| 261 | Bhu | 628.54 | |
| 262 | Bhb | 629.25 | |
| 263 | Bht | 630.92 | |
| 264 | Bhq | 633.08 | |
| 265 | Bhp | 634.75 | |
| 266 | Bhh | 635.46 | |
| 267 | Bhs | 640.72 | |
| 268 | Bho | 641.19 | |
| 269 | Bhe | 641.90 | |
| 270 | Bsn | 643.57 | |
| 271 | Bsu | 645.73 | |
| 272 | Bsb | 647.40 | |
| 273 | Bst | 648.11 | |
| 274 | Bsq | 648.58 | |
| 275 | Bsp | 662.25 | |
| 276 | Bsh | 663.92 | |
| 277 | Bss | 666.08 | |
| 278 | Bso | 667.75 | |
| 279 | Bse | 670.29 | |
| 280 | Bon | 671.00 | |
| 281 | Bou | 672.67 | |
| 282 | Bob | 674.83 | |
| 283 | Bot | 676.50 | |
| 284 | Boq | 677.21 | |
| 285 | Bop | 685.92 | |
| 286 | Boh | 688.08 | |
| 287 | Bos | 689.10 | |
| 288 | Boo | 690.77 | |
| 289 | Boe | 692.93 | |
| 290 | Ben | 694.60 | |
| 291 | Beu | 696.92 | |
| 292 | Beb | 699.08 | |
| 293 | Bet | 680.06 | |
| 294 | Beq | 682.07 | |
| 295 | Bep | 682.54 | |
| 296 | Beh | 683.25 | |
| 297 | Bes | 684.92 | |
| 298 | Beo | 687.08 | |
| 299 | Bee | 688.75 | |
| 300 | Tnn | 689.46 | |
| 301 | Tnu | 689.93 | |
| 302 | Tnb | 691.94 | |
| 303 | Tnt | 695.64 | |
| 304 | Tnq | 700.51 | |
| 305 | Tnp | 702.52 | |
| 306 | Tnh | 702.59 | |
| 307 | Tns | 703.70 | |
| 308 | Tno | 705.37 | |
| 309 | Tne | 707.53 | |
| 310 | Tun | 709.20 | |
| 311 | Tuu | 709.91 | |
| 312 | Tub | 710.38 | |
| 313 | Tut | 712.39 | |
| 314 | Tuq | 717.26 | |
| 315 | Tup | 737.07 | |
| 316 | Tuh | 737.54 | |
| 317 | Tus | 738.25 | |
| 318 | Tuo | 739.92 | |
| 319 | Tue | 742.08 | |
| 320 | Tbn | 743.75 | |
| 321 | Tbu | 744.46 | |
| 322 | Tbb | 744.93 | |
| 323 | Tbt | 751.61 | |
| 324 | Tbq | 753.62 | |
| 325 | Tbp | 754.09 | |
| 326 | Tbh | 754.80 | |
| 327 | Tbs | 756.47 | |
| 328 | Tbo | 758.63 | |
| 329 | Tbe | 760.30 | |
| 330 | Ttn | 761.01 | |
| 331 | Ttu | 761.48 | |
| 332 | Ttb | 763.49 | |
| 333 | Ttt | 781.54 | |
| 334 | Ttq | 782.25 | |
| 335 | Ttp | 783.92 | |
| 336 | Tth | 786.08 | |
| 337 | Tts | 787.75 | |
| 338 | Tto | 788.46 | |
| 339 | Tte | 793.72 | |
| 340 | Tqn | 794.19 | |
| 341 | Tqu | 794.90 | |
| 342 | Tqb | 796.57 | |
| 343 | Tqt | 798.73 | |
| 344 | Tqq | 800.34 | |
| 345 | Tqp | 801.11 | |
| 346 | Tqh | 801.58 | |
| 347 | Tqs | 815.25 | |
| 348 | Tqo | 816.92 | |
| 349 | Tqe | 819.08 | |
| 350 | Tpn | 820.75 | |
| 351 | Tpu | 823.29 | |
| 352 | Tpb | 824.00 | |
| 353 | Tpt | 825.67 | |
| 354 | Tpq | 827.83 | |
| 355 | Tpp | 829.50 | |
| 356 | Tph | 830.21 | |
| 357 | Tps | 838.92 | |
| 358 | Tpo | 841.08 | |
| 359 | Tpe | 842.10 | |
| 360 | Thn | 843.77 | |
| 361 | Thu | 845.93 | |
| 362 | Thb | 847.60 | |
| 363 | Tht | 849.92 | |
| 364 | Thq | 852.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varlamov, V.V.; Pavlova, L.D.; Babushkina, O.S. Group Theoretical Description of the Periodic System. Symmetry 2022, 14, 137. https://doi.org/10.3390/sym14010137
Varlamov VV, Pavlova LD, Babushkina OS. Group Theoretical Description of the Periodic System. Symmetry. 2022; 14(1):137. https://doi.org/10.3390/sym14010137
Chicago/Turabian StyleVarlamov, Vadim V., Larisa D. Pavlova, and Olga S. Babushkina. 2022. "Group Theoretical Description of the Periodic System" Symmetry 14, no. 1: 137. https://doi.org/10.3390/sym14010137






