Symmetry and Combinatorial Concepts for Cyclopolyarenes, Nanotubes and 2D-Sheets: Enumerations, Isomers, Structures Spectra & Properties

Abstract

This review article highlights recent developments in symmetry, combinatorics, topology, entropy, chirality, spectroscopy and thermochemistry pertinent to 2D and 1D nanomaterials such as circumscribed-cyclopolyarenes and their heterocyclic analogs, carbon and heteronanotubes and heteronano wires, as well as tessellations of cyclopolyarenes, for example, kekulenes, septulenes and octulenes. We establish that the generalization of Sheehan’s modification of Pólya’s theorem to all irreducible representations of point groups yields robust generating functions for the enumeration of chiral, achiral, position isomers, NMR, multiple quantum NMR and ESR hyperfine patterns. We also show distance, degree and graph entropy based topological measures combined with techniques for distance degree vector sequences, edge and vertex partitions of nanomaterials yield robust and powerful techniques for thermochemistry, bond energies and spectroscopic computations of these species. We have demonstrated the existence of isentropic tessellations of kekulenes which were further studied using combinatorial, topological and spectral techniques. The combinatorial generating functions obtained not only enumerate the chiral and achiral isomers but also aid in the machine construction of various spectroscopic and ESR hyperfine patterns of the nanomaterials that were considered in this review. Combinatorial and topological tools can become an integral part of robust machine learning techniques for rapid computation of the combinatorial library of isomers and their properties of nanomaterials. Future applications to metal organic frameworks and fullerene polymers are pointed out.

1. Introduction

Two-dimensional nanomaterials, especially those arising from different forms of graphenes, for example, circumscribed-cyclopolyarenes, tessellations of kekulenes, septulenes and octulenes, nanobelts, and various forms of macrocycles that have pores have received significant attention over the years [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36]. These nanomaterials not only possess interesting electronic properties but their pores with desirable electronic and geometrical features have opened up a plethora of novel applications [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36]. Related one-dimensional nanomaterials such as carbon nanotubes and heteronanotubes and nanowires composed of B/N, Ga/N, C/N, Ga/As have been the topic of a number of studies because these materials exhibit very interesting electronic, geometrical, topological, chiral, polarizability, and optical properties [37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59]. Heteronuclear one-dimensional nanomaterials have novel opto-electronic properties and thus find many applications in the fabrication of nanodevices, for example, photonics, nanoelectronics, nanochirality and so forth [37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59]. Two-dimensional nanomaterials and mesoporous materials with cavities, for example, nanobelts comprising of several kekulene/octulene moieties and tubular forms of carbons and nitrogens are becoming increasingly important, as they exhibit optimal cavities for sequestration and transport of both anions such as chloride ions and cations such as toxic heavy metal ions including actinyl ions in high level nuclear wastes and other nuclear environmental geo/biochemical applications [60,61,62,63,64,65]. Specifically, these environmental actinide studies have considered high coordination complexes of actinyls with mesoporous silica [61], minerals such as carbonates [63], phosphates [64] and solvated complexes [62,65]. Our understanding of such actinide complexes and the related laser spectroscopic studies [64] requires a detailed knowledge of their symmetries, coordination spheres, electronic structure, and symmetries of various electronic states and their geometries. For example, as shown in [63] the plutonyl carbonates form high coordination and high symmetry complexes which in turn govern their spectroscopic selection rules and the symmetry aspects of their electronic states. The high coordination and symmetries exhibited by these actinide complexes are in turn influenced by the symmetries of the 5f and 6d orbitals of actinides [62,63,64,65] within the symmetry of molecular or nanosphere environment. The symmetry, combinatorial, graph-theoretical and topological properties of polycyclic aromatics with cavities have been studied over the years [66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113]. Such polycyclic aromatics, for example, those made by circumscribing cyclopolyarenes are especially intriguing from the standpoint of enumerations of isomers, their electronic and magnetic properties which have given rise to a number of interesting concepts such ring currents, topological delocalization energies, conjugated circuits, aromaticity and superaromaticity [66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113]. Cycloarenes are derived from a synthesis of angular and linear annulations of benzene rings that result macro-cyclic systems with cavities that are especially suitable for sequestration of both anions and cations. As they exhibit intriguing magnetic as well as electronic properties, several graph-theory-based and combinatorial methods have been developed and employed as robust alternatives over the years to study the spectroscopic properties, electronic structures, and energetics of polycyclic aromatics, nanotubes and fullerenes including giant fullerenes over the decades [114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134]. Among several computational methods, topologically-based methods such as the conjugated circuit method, ring currents, topological resonance theories, aromatic sextets, spectral and matching polynomials etc., and combinatorial enumeration methods have been of considerable use in rapid and robust enumerations of structures and spectra as well as estimation for their stabilities [66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134], The advent of kekulene made of 12 fused benzene rings with a central cavity with D_6h symmetry stimulated significant interest in superaromaticity or superbenzene as a consequence of its planar cyclic conjugation [1,2,3,4]. A novel electronic feature of kekulene is that its π-electrons are delocalized within benzene rings as opposed to the entire framework providing a platform to study aromaticity in a new dimension. Moreover their structures with cavities offer intriguing possibilities for the environmental management, organic chemistry, rational drug design and delivery, as they possess optimal electronic and geometrical features for both trapping of toxic ions to transportation of heavy metal ions, halide anions, drugs and so forth [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36].

Carbon nanotubes and their heteroanalogs such as GaN, GaAs nanowires and related decorations with metals such as gold have opened up a new vista and a new state of matter that has culminated into significant research activities over the years [37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59]. These nanotubes exhibit intriguing optical properties and chirality, and thus their relative stabilities and reactivities in different forms such as zigzag, armchair, chiral etc., have been the subject matters of intense scrutiny over the years [34,35,39,57]. Heteronanotubes are especially interesting because of their structures that contain intertwining helical patterns [37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59]. Moreover chirality of heteronanotubes is caused by intriguing chiral interface states that give rise to very interesting conductivity patterns [35,39]. In particular heteronanotubes made of Ga/N, Ga/As, C/N and B/N as well as transition metals are promising materials as building blocks of metal organic frameworks. These nanomaterials find a variety of applications due to their unusual hyperpolarizability and conductive properties- all of which arise because of interesting combinatorics. These materials exhibit interesting aesthetics and thus the entire collection of nanowires, fullerenes, graphenes, giant fullerenes, nanotubes, and their heteroanalogs have been studied over the years [37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134]. Both structures and dynamics arising from rearrangements of pentagons on nanocones through Stone-Wales rotations of faces, and thus face colorings of fullerenes have been of interest [130]. Combinatorial studies can provide enlightening topological information on the isomerization paths pertinent to the dynamics of pentagons on nanocones. The structures, enumeration of isomers arising from substituents of heteroatoms, chirality, spectroscopy, and topological indices of all these nanomaterials have been studied in recent times [120,121,122,123,124,125,126,127,128,129,130,131,132,133,134]. Furthermore other related fields of biological interest such as computational toxicology, drug discovery and design have been benefited by the techniques of combinatorial and topological origin such as quantitative molecular similarity analysis, quantitative structure activity relations, and targeted therapeutic approaches for computer aided drug discovery [135,136,137,138,139,140,141,142,143]. Quantitative descriptors are derived from their structures which in turn can yield quantitative measures from their molecular topologies, quantum chemically derived electronic parameters, shape, and other biological descriptors [135,136,137,138,139,140,141,142,143]. Combinatorial techniques not only facilitate the constructions of large data sets or libraries of a number of chemical compounds including nanomaterials but also aid in rapid computations of chemical properties of combinatorial libraries of molecules [106,107,108,109,110,111,112,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,143,144,145,146,147]. The related metal organic frameworks have opened up an entire field of reticular chemistry and MOFs and related COFs have enormous potentials in numerous applications including water harvesting [148,149]. Furthermore symmetry-based combinatorial enumeration of electronic states and geometries of heteronuclear clusters such as Ga_mAs_n [150,151] are critical to planning and interpretations of computations of heteronuclear clusters, heteronuclear nanomaterials and nanowires comprised of Ga/N, Ga/As, B/N, C/N, and so forth. Relativistic electronic structure computations of molecules and clusters [152] are benefited by the inherent double group symmetries when spin-orbit coupling is included. The symmetry interplay between Jahn-Teller and spin-orbit effects is critical to our understanding of laser spectroscopic studies of clusters containing heavy atoms such as gold [153] and so forth. Detailed understanding of clusters and heteronano materials and heteronanowires is enhanced by the enumeration of structures, spectroscopic patterns, nuclear spin statistics and the symmetry properties of the electronic potential energy surfaces of such heteronuclear clusters [150,151] and molecules.

Topological entropy of a nanomaterial is an important information-theoretic concept which appears to characterize the information content or order/disorder content of such nanomaterials. Consequently, graph entropy has been a subject matter of some recent works on tessellations of kekulenes and metal organic frameworks [144,154]. The relative stabilities of various phases of graphenes and nanotubes, for example, the chiral form, zigzag, armchair, and so forth, have been the topic of several studies [35,39], it is believed that graph entropies can provide additional insights into these materials. Phase transformation of armchair to zigzag graphene edge structures, since the synthesis of single-walled carbon nanotubes, has been of interest, especially as such studies could provide insights into the origin of chirality in nanotubes [39]. The relative stabilities of different phases depend on their Gibbs free energies which in turn depend on both energetics and entropies [39,40,41,144]. Stimulated by such vast studies on these nanomaterials, we have undertaken the present review of this interesting subject with focus on their combinatorial properties.

The objective of this review is to outline symmetry-based combinatorial techniques, and in particular, Sheehan’s modification of Pólya’s theorem that the present author has generalized to all irreducible representations as well as computational techniques based on such enumerations including walks and sequences [134,155,156,157,158,159]. Group-theoretically based combinatorial structures for all irreducible representations of the point groups of the nanomaterials such as tessellations of cyclopolyarenes, heteronanotubes, etc., are applied to the enumerations of chiral structures, achiral structures and position isomers of such materials. We have also reviewed the used of topologically based techniques such as distance degree sequence vectors for partitioning the vertices of nanomaterials for rapid and robust computations of their thermodynamic and spectroscopic properties. We have applied the techniques to demonstrate the rapid construction of the ESR hyperfine patterns of nanomaterials as well as ¹³C NMR and proton NMR spectroscopic patterns including multiple quantum NMR. This review brings together combinatorics, group theory and topological techniques with applications to heteronanotubes, circumscribed-cyclopolyarenes, tessellations of graphene fragments with cavities such as tessellations of kekulenes, and so forth.

2. Combinatorial Methods: Generalized Character Cycle Indices, Sheehan’s Method, Euler’s Totient Function and Character Based Enumerations

Pólya’s enumeration theorem [155,156,157] deals with the enumeration of equivalence classes of configurations when a group acts on a set of objects. Pólya’s work was inspired by the isomer enumeration and Burnside’s lemma which enumerates different necklaces for a set of colored beads with different colors. In 1937 Pólya [156] developed his enumeration technique which became subsequently known as Pólya‘s theorem. The current author [155] extended this method as well as the Harary-Palmer power group enumeration theorem to all IRs of the group under action. The present author [134] also extended Sheehan’s [157] modification of Pólya’s theorem to encompass all irreducible representations of the acting group. Such generalized combinatorial methods have been applied to nuclear spin statistics of rovibronic levels of molecules, multiple quantum NMR, ESR hyperfine patterns, vibrational modes of large molecules, and the enumeration of chiral and stereo isomers of polysubstituted molecules, nanotubes and giant fullerenes and. The present author’s generalization of Sheehan’s modification to all IRs was recently applied to the combinatorial enumerations that dealt with isomers and chirality of heteronanotubes [134]. Consequently, we briefly summarize this formalism which is applied to the nanotubes in a subsequent section

There are several large systems such as nanotubes, 2D-nanosheets, tessellations of cyclopolyarenes, and circumscribed cyclopolyarenes, etc., for which the combinatorial enumerations become efficient if the set D of vertices of such nanomaterials is partitioned into equivalence classes denoted by Y₁, Y₂, … Y_n/2 for even n, and Y₁, Y₂, … Y_{(n + 1)/2} for odd n. For instance, for a cylindrical nanotube with a cross section of m vertices, the total number of vertices in the tube (D) is mn, and hence the equivalence classes of vertices Y_i have following orders depending on the odd/even parity of n:

$$\left|{\mathrm{Y}}_{\mathrm{i}}\right|=2\mathrm{m}, \mathrm{for} \mathrm{a} \mathrm{nanotube} \mathrm{of} \mathrm{even} \mathrm{length} n, \mathrm{for} \mathrm{all} \mathrm{i}, 1\le i\le \mathrm{n}/2.$$

(1)

$$\left|{\mathrm{Y}}_1\right|=\mathrm{m}, \left|{\mathrm{Y}}_{\mathrm{i}}\right|=2\mathrm{m} |\mathrm{for} \mathrm{a} \mathrm{nanotube} \mathrm{of} \mathrm{odd} \mathrm{length} n, \mathrm{for} \mathrm{all} \mathrm{i} \ne 1, 2\le i\le (\mathrm{n}+1)/2.$$

(2)

Consequently, a vertex coloring of the set of vertices in D, a map from the sets D to R, with R as the set of colors and D further divided into Y-sets can be represented as:

$$D=i=1n/2Y_i{Y}_i\cap Y_j=\varnothing fori\ne j\wedge forevenn\vee D=i=1\frac{n+1}{2}{Y}_i{Y}_i\cap Y_j=\varnothing fori\ne j\wedge foroddn.$$

(3)

Sheehan’s modification [157] of Pόlya’s theorem [156] facilitates partitioning of colorings for the various equivalence classes, and thus it is more powerful than the ordinary Pόlya’s combinatorial enumeration. The current author has further generalized Sheehan’s theorem to all characters of irreducible representations of the group of action, and thus a direct technique has been developed to enumerate both chiral and achiral colorings. Suppose the generalized character cycle index (GCCI) for the character χ of the irreducible representation Γ is defined by

$$P_G^{\chi }=\frac{1}{\left|G\right|}{\displaystyle \sum }_{g\epsilon G\text{'}}\chi \left(g\right){{\displaystyle \prod }}_i{{\displaystyle \prod }}_j{s}_{\mathrm{ij}}^{c_{\mathrm{ij}}\left(g\right)}$$

(4)

where the sum is over all permutation representations of g ∈ G; c_ij(g) is the number of j-cycles of g ∈ G contained in the set Y_i upon its action on the members of the objects in the D set which may be for example carbon centers of a nanotube. The index i varies from 1 to n/2 or (n + 1)/2 for even and odd n, respectively. The second index j is the orbit length for the orbit of a permutation contained within the Y_i set for the action of g ∈ G.

A number of nanostructures contain cross sections with cyclic rotational symmetries, and hence the rotational subgroup for the cyclic part yields a cycle index provided by the Euler totient function. Therefore such an enumeration scheme can be applied to a variety of nanostructures such as cylindrical nanotubes, circumscribed-kekulenes, septulenes, octulenes, tessellations of kekulenes and nanosheets and nanobelts derived from graphenes.

We can obtain multinomial generators from the GCCIs shown above for each of the irreducible representations in the group G acting on the structure. For this purpose we introduce [n] as an ordered partition of n into p parts given that n₁ ≥ 0, n₂ ≥ 0, …, n_p ≥ 0, ${{\displaystyle \sum }}_{i=1}^p{n}_i=n$. Let us assign arbitrary weights λs and n₁ colors of the type λ₁, n₂, colors of the type λ₂… n_p colors of the type λ_p. Then a multinomial generator is constructed by a generalization of Pólya’s enumeration to all IRs using the multinomial expansion:

$${\left({\lambda }_1+{\lambda }_2+\dots +{\lambda }_p\right)}^n={{\displaystyle \sum }}_{\left[\mathit{n}\right]}^{\mathit{p}}\left(\begin{array}{ccccc}& & \mathit{n}& & \\ {\mathit{n}}_{\mathbf{1}}& {\mathit{n}}_{\mathbf{2}}& .& .& {\mathit{n}}_{\mathit{p}}\end{array}\right){\mathit{\lambda }}_{\mathbf{1}}{}^{n_{\mathbf{1}}}{\mathit{\lambda }}_{\mathbf{2}}{}^{{\mathit{n}}_{\mathbf{2}}}\dots \dots {\mathit{\lambda }}_{\mathit{p}-\mathbf{1}}{}^{{\mathit{n}}_{\mathit{p}-\mathbf{1}}}{\mathit{\lambda }}_{\mathit{p}}{}^{{\mathit{n}}_{\mathit{p}}}$$

(5)

$\left(\begin{array}{ccccc}& & \mathrm{n}& & \\ {\mathrm{n}}_1& {\mathrm{n}}_2& .& .& {\mathrm{n}}_{\mathrm{p}}\end{array}\right)$ are multinomials defined as

$$\left(\begin{array}{ccccc}& & \mathit{n}& & \\ {\mathit{n}}_{\mathbf{1}}& {\mathit{n}}_{\mathbf{2}}& .& .& {\mathit{n}}_{\mathit{p}}\end{array}\right)=\frac{\mathit{n}\mathbf{!}}{{\mathit{n}}_{\mathbf{1}}\mathbf{!}{\mathit{n}}_{\mathbf{2}}\mathbf{!}\dots \dots {\mathit{n}}_{\mathit{p}-\mathbf{1}}\mathbf{!}{\mathit{n}}_{\mathit{p}}\mathbf{!}}$$

(6)

Furthermore, the coloring palette, R can be divided into sets R₁, R₂… such that $R={{\displaystyle \cup }}_{i=1}^{m/2}{R}_i$, for an even m and $R={{\displaystyle \cup }}_{i=1}^{\left(m+1\right)/2}{R}_i$ for an odd m and |R_i| = p_i Hence in the most general case, the weight w_ij is assigned for each color r_j in the set R_i. In such a set up the multinomial generator for each IR for coloring the vertices of structures that can be divided is obtained as follows:

$$G{F}^{\chi }\left({\lambda }_1,{\lambda }_2\dots {\lambda }_p\right) = P_G^{\chi }\left\{s_{ik}\to \left(w_{i1}^k+w_{i2}^k+\dots +w_{i,p_i-1}^k+w_{i,p_i}^k\right)\right\},$$

(7)

The current author provided a geometrical interpretation for the above expansion. That is, the multinomial function thus obtained for each IR different colors yield the equivalence classes of vertex colorings that transform according to the IR with the character χ. It can thus be seen that the number of such multinomial generators equals the number of IRs of the acting group.

3. Applications to Polyarenes Enumeration & Spectroscopy

3.1. Enumeration of Hetero-Substituted Polyarenes and Polysubstituted Polyarenes

Circum-polyarenes are usually planar circumscribed structures comprising of macrocycles that are reminiscent of donut structures (See Figure 1) with D_mh point group symmetries and the combinatorics of these structures were considered by the author in [124]. In this section we consider these cicum-polyarenes of considerable recent interest. A special case of such structures are kekulenes for m = 6 for (Figure 1, Structure 1). Likewise other circum-polyarenes are obtained with holes, for example, when m = 7 for septulenes (Figure 1, Structure 2), m = 8 corresponds to octulenes (Figure 1, Structure 3) and so forth. Table 1 displays such a general series comprising of circum-polyarenes together with their general formula for various values of m and n. We define m as the cyclicity and n as the number of circumscribings around the primitive structure (n = 1). As most structures of circum-polyarenes are considered to be planar, the combinatorics of polysubstituted isomers of such circum-polyarenes can be constructed within the rotational subgroup or the D_m group. The GCCIs of such structures depend on the point groups as well as the set D (carbon nuclei or protons) and also if the cardinality of the set D is odd or even. Let D be the set of carbon nuclei of polyarenes (structures are displayed in Figure 1 and Figure 2). When carbon vertices are colored in effect, we would be enumerating the hetero-polyarenes for example, aza-polyarenes. For circumscribed m-cyclic polyarenes let n be the order of circumscribing (for example, for Structure 8 in Figure 2, n = 2). In the case of regular kekulene (Structure 1; Figure 1), it can be seen that n = 1 and m = 6 and for circumscribed kekulene (Structure 8; Figure 2), n = 2 and m = 6 while the corresponding values for circumscribed septulenes are n = 2 and m = 7 For the sake of self-completeness and illustrations, we have used the same notations and reproduced the equations from Ref. [124].

Figure 1. Structures of kekulene, septulene and circumkekulene in the series of circum-polyarenes. Reprinted with permission from [124] copyright (2018) American Chemical Society.

Table 1. m-Cyclopolyarenes Series with circumscribings of order n. Reprinted with permission from [124] copyright (2018) American Chemical Society.

n	M	Name	Formulae
1	6	Kekulene	C48H24
1	7	Septulene	C56H28
1	8	Octulene	C64H32
1	9	Nonulene	C72H36
2	6	2-Kekulene	C90H30
2	7	2-Septulene	C105H35
2	8	2-Octulene	C120H40
2	9	2-Nonulene	C135H45
…	…	…	…
n	N	ncir-m-cycloarene	Cm(n2+4n+3)Hm(n+3)

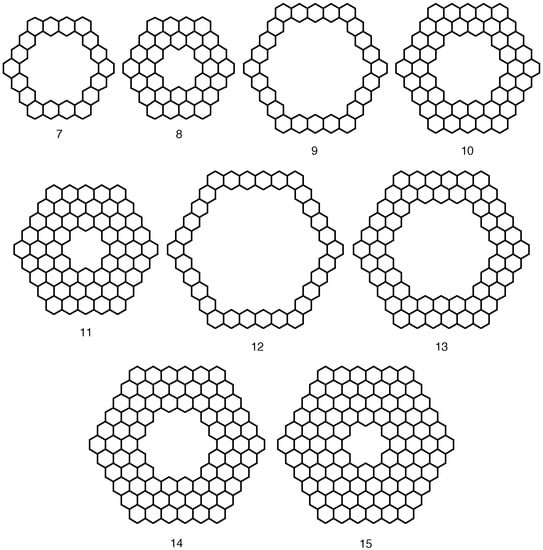
Figure 2. Structures of coronoids and circumscribed-coronoids with holes forming D_6h symmetries (Reprinted with permission from [75] copyright (1993) American Chemical Society).

For doubly-circumscribed septulene, etc. Hence different cases of polysubstituted circumscribed Cyclopolyarenes can be encumbered by the general formalism outlined in Section 2. For any n-circumscribed m-cyclopolyarene one obtains the GCCI for even m as:

$$P_{D_m}^{\chi }=\frac{1}{2m}{{\displaystyle \sum }}_{g\epsilon D_m}\chi \left(g\right)s_1^{b_1}{s}_2^{b_2}\dots \dots s_n^{\mathrm{bn}}=\frac{1}{2m}\{{{\displaystyle \sum }}_{d/m}\chi \left(g\right)\phi \left(d\right)s_d^{\frac{m\left(n^2+4n+3\right)}{d}}+\frac{m}{2}{s}_1^{\left(2n+2\right)}{s}_2^k+\frac{m}{2}{s}_2^{\frac{m\left(n^2+4n+3\right)}{2}}\} \mathrm{if} \mathrm{m} \mathrm{is} \mathrm{even},$$

(8)

where k = m(n² + 4n + 3)/2 − (n + 1) and n is even, sum is over all divisors d of m, and φ(d) is the Euler totient function defined in the previous section.

The GCCI for odd m is given by

$$P_{D_m}^{\chi }=\frac{1}{2m}{{\displaystyle \sum }}_{g\epsilon D_m}\chi \left(g\right)s_1^{b_1}{s}_2^{b_2}\dots \dots s_n^{\mathrm{bn}}=\frac{1}{2m}\{{{\displaystyle \sum }}_{d/m}\chi \left(g\right)\phi \left(d\right)s_d^{\frac{m\left(n^2+4n+3\right)}{d}}+m{s}_1^{\left(n+1\right)}{s}_2^k \mathrm{if} \mathrm{m} \mathrm{is} \mathrm{odd}$$

(9)

and

k = [m(n² + 4n + 3) − (n + 1)]/2

(10)

The above GCCIs can be applied to any circum-polyarenes, for example, kekulene (Figure 1, Structure 1) which corresponds to case m = 6 and n = 1. In this case, the GCCI for the totally symmetric representation is obtained by (11):

$$P_{D_6}=\frac{1}{12}\left[s_1^{48}+2s_6^8+2s_3^{16}+4s_2^{24}+3s_1^4{s}_2^{22}\right]$$

(11)

The GCCI when applied to 2-circumscribed-kekulene (structure 8 in Figure 2) or n = 2 and m = 6 we arrive at:

$$P_{D_6}=\frac{1}{12}\left[s_1^{90}+2s_6^{15}+2s_3^{30}+4s_2^{45}+3s_1^6{s}_2^{42}\right]$$

(12)

For septulene (structure 2 in Figure 1) which corresponds to m = 7 and n = 1 the GCCI becomes:

$$P_{D_7}=\frac{1}{14}\left[s_1^{56}+6s_7^8+7s_1^2{s}_2^{27}\right]$$

(13)

The 2-circumscribed septulene corresponds to circumscribing Structure 2 in Figure 1 or m = 7 and n = 2, that is, C₁₀₅H₃₅. By substituting m = 7 and n = 2 in the general equation we obtain:

$$P_{D_7}=\frac{1}{14}\left[s_1^{105}+6s_7^{15}+7s_1^3{s}_2^{51}\right]$$

(14)

For octulene we substitute m = 8 and n = 1in the general expression to obtain:

$$P_{D_8}=\frac{1}{16}\left[s_1^{64}+4s_8^8+2s_4^8+5s_2^{32}+4s_1^4{s}_2^{30}\right]$$

(15)

Likewise for a 2-circumscribed octulene, C₁₂₀H₄₀, we compute the GCCI by substituting m = 8 and n = 2 in Equation (8) resulting in Equation (16):

$$P_{D_8}=\frac{1}{16}\left[s_1^{120}+4s_8^{15}+2s_4^{30}+5s_2^{60}+4s_1^4{s}_2^{58}\right]$$

(16)

Next we take up polysubstitution of circum-polyarenes that is, replacing some or all of the protons of circum-polyarenes with other atoms such as F, Cl, Br, I, etc. For this scenario we construct the GCCIs, with the object set D defined as the set of protons of the circum-polyarenes. We obtain the following cases for circum-polyarenes depending on the parities of m and n, where m is the cyclicity and n is the circumscribing order. First case: m even and n are both odd we have:

• Case (1): m even, n odd, D: protons:

  $$P_{D_m}^{\chi }=\frac{1}{2m}{{\displaystyle \sum }}_{g\epsilon D_m}\chi \left(g\right)s_1^{b_1}{s}_2^{b_2}\dots \dots s_n^{\mathrm{bn}}=\frac{1}{2m}\{{{\displaystyle \sum }}_{d/m}\chi \left(g\right)\phi \left(d\right)s_d^{\frac{m\left(n+3\right)}{d}}+\frac{m}{2}{s}_1^4{s}_2^p+\frac{m}{2}{s}_2^{\frac{m\left(n+3\right)}{2}}\}, \mathrm{p}=\{\mathrm{m}(\mathrm{n}+3)/2-2\}$$

  (17)
• Case (2): m even, n even, D: protons:

  $$P_{D_m}^{\chi }=\frac{1}{2m}{{\displaystyle \sum }}_{g\epsilon D_m}\chi \left(g\right)s_1^{b_1}{s}_2^{b_2}\dots \dots s_n^{\mathrm{bn}}=\frac{1}{2m}\{{{\displaystyle \sum }}_{d/m}\chi \left(g\right)\phi \left(d\right)s_d^{\frac{m\left(n+3\right)}{d}}+\frac{m}{2}\left(s_1^2| |s_2^q\right)+\frac{m}{2}{s}_2^{\frac{m\left(n+3\right)}{2}}\}, \mathrm{q}=\{\mathrm{m}(\mathrm{n}+3)/2-1\}$$

  (18)
• Case (3): m odd, n odd, D: protons:

  $$P_{D_m}^{\chi }=\frac{1}{2m}{{\displaystyle \sum }}_{g\epsilon D_m}\chi \left(g\right)s_1^{b_1}{s}_2^{b_2}\dots \dots s_n^{\mathrm{bn}}=\frac{1}{2m}\{{{\displaystyle \sum }}_{d/m}\chi \left(g\right)\phi \left(d\right)s_d^{\frac{m\left(n+3\right)}{d}}+m{s}_1^2{s}_2^r\}, \mathrm{r}=\{\mathrm{m}(\mathrm{n}+3)/2-1\}$$

  (19)
• Case (4): m odd, n even, D: protons:

  $$P_{D_m}^{\chi }=\frac{1}{2m}{{\displaystyle \sum }}_{g\epsilon D_m}\chi \left(g\right)s_1^{b_1}{s}_2^{b_2}\dots \dots s_n^{\mathrm{bn}}=\frac{1}{2m}\{{{\displaystyle \sum }}_{d/m}\chi \left(g\right)\phi \left(d\right)s_d^{\frac{m\left(n+3\right)}{d}}+m{s}_1^{}{s}_2^t\}, \mathrm{t}=\{\mathrm{m}(\mathrm{n}+3)-1\}/2$$

  (20)

For kekulene with m = 6 and n = 1 we obtain

$$P_{D_6}=\frac{1}{12}\left[s_1^{24}+2s_6^4+2s_3^8+4s_2^{12}+3s_1^4{s}_2^{10}\right]$$

(21)

For a 2-circumscribed kekulene (Str 8, Figure 2), m = 6, n = 2 we obtain Equation (22):

$$P_{D_6}=\frac{1}{12}\left[s_1^{30}+2s_6^5+2s_3^{10}+4s_2^{15}+3s_1^2{s}_2^{14}\right]$$

(22)

The cycle index of septulene, m = 7, n = 1, we obtain,

$$P_{D_6}=\frac{1}{14}\left[s_1^{28}+2s_7^4+7s_1^2{s}_2^{13}\right]$$

(23)

For a 2-circumscribed septulene, m = 7, n = 2 the GCCI is given by

$$P_{D_6}=\frac{1}{14}\left[s_1^{35}+2s_7^5+7s_1^{}{s}_2^{17}\right]$$

(24)

For an octulene, m = 8, n = 1 we obtain

$$P_{D_8}=\frac{1}{16}\left[s_1^{32}+4s_8^4+2s_4^8+5s_2^{16}+4s_1^4{s}_2^{14}\right]$$

(25)

Thus for a 2-circumscribed octulene, m = 8, n = 2,

$$P_{D_8}=\frac{1}{16}\left[s_1^{40}+4s_8^5+2s_4^{10}+5s_2^{20}+4s_1^2{s}_2^{18}\right]$$

(26)

All structures in Figure 2 exhibit D_6h symmetry and they arise from circumcising the graphene structure with holes of various sizes. In particular, the kekulene series belong to the C_pH_q series with p = 6(n² + 4n + 3) and q = 6(n + 3). Likewise structures 7,10,14 (Figure 2) correspond to the series C_pH_q where p = 6(n² + 6n + 5) and q = 6(n + 5) and structures 9,13 correspond to C_pH_q where p = 6(n² + 8n + 7) and q = 6(n + 7), and the subsequent members of the series are given by C_pH_q, p = 6(n² + 10n + 9) and q = 6(n + 9). Therefore all coronoids with D_6h symmetry form the series C_pH_q with p = 6(n² + 2n(m + 1)+ 2m + 1) and q = 6(n + 2m + 1) for positive integers m and n. The GCCIs that are derived for the circumscribed kekulenes (D_6h groups) can also be employed for all other circumscribed coronoids that exhibit D_6h point groups. For instance, the GCCI for carbon nuclei of Str 11, Figure 2, with m = 6 and n = 3 is displayed in Equation (27):

$$P_{D_6}=\frac{1}{12}\left[s_1^{144}+2s_6^{24}+2s_3^{48}+4s_2^{72}+3s_1^8{s}_2^{68}\right]$$

(27)

The corresponding cycle index for the protons of Str 11 (m = 6 and n = 3: Figure 2) with 36 protons is:

$$P_{D_6}=\frac{1}{12}\left[s_1^{36}+2s_6^6+2s_3^{12}+4s_2^{18}+3s_1^4{s}_2^{16}\right]$$

(28)

Structure 13 (Figure 2) corresponds to C₁₆₂H₅₄ and thus the GCCI for the carbons is given by (29):

$$P_{D_6}=\frac{1}{12}\left[s_1^{162}+2s_6^{27}+2s_3^{54}+4s_2^{81}+3s_1^6{s}_2^{78}\right]$$

(29)

The number of polysubstituted isomers is enumerated from the GCCI by Pólya’s substitution, that is, substituting for every s_k by (w₁^k + w₂^k + w₃^k + w₄^k) in the GCCI. To illustrate we obtain the expression (30) for kekulenes by such a substitution:

$$\begin{gathered} G{F}_{D_6}=\frac{1}{12}\left[{\left(w_1+w_2+w_3+w_4\right)}^{48}+2{\left(w_1^6+w_2^6+w_3^6+w_4^6\right)}^8+2{\left(w_1^3+w_2^3+w_3^3+w_4^3\right)}^{16} \\ +4{\left(w_1^2+w_2^2+w_3^2+w_4^2\right)}^{24}+3{\left(w_1+w_2+w_3+w_4\right)}^4{\left(w_1^2+w_2^2+w_3^2+w_4^2\right)}^{22}\right] \end{gathered}$$

(30)

The coefficient of w₁^b1w₂^b2 w₃^b3 w₄^b4 in (30) generates the number of heterosubstituted kekulenes or colorings of carbon vertices by b₁ substituents of first kind, b₂ substituents of second kind, b₃ substituent of third kind, and b₄ substituents of fourth kind. Table 2 shows some of the terms thus obtained for 3 colors (w₁, w₂, w₃). As seen from Table 2 five monosubstituted compounds are enumerated. There are 109 isomers for disubstitution and so on. In accord with a binomial distribution, the maximum distribution of isomers is reached for substitution of carbons by 16 substituents of the first kind, 16 substituents of the second kind and 16 substituents of the third kind, etc., which can be inferred from Table 2 as 112,945,455,375,981,823,980. Table 2 displays the unique terms in the multinomial expansion as partition vectors. Total number of isomers when there are 3 substituents is obtained as

$$I=\frac{1}{12}\left[3^{48}+2x{3}^8+2x{3}^{16}+4x{3}^{24}+3x{3}^{4}x{3}^{22}\right]$$

(31)

Table 2. Enumeration of 3-colorings of Carbon Vertices of Kekulene. Reprinted with permission from [124] copyright (2018) American Chemical Society.

Coefficient	Vector	Coefficient	Vector	Coefficient
1	48 0 0	103561517895	37 9 2	88851068896152860	29 10 9
5	47 1 0	383177575979	36 10 2	234243726928693460	28 11 9
109	46 2 0	1254034278774	35 11 2	546568695999885020	27 12 9
1467	45 3 0	11184050659015080	29 14 5	1135181137598290860	26 13 9
16398	44 4 0	21622497914498712	28 15 5	2108193541021176180	25 14 9
142945	43 5 0	37839371323512066	27 16 5	3513655901417556180	24 15 9
1024059	42 6 0	60097825014257646	26 17 5	5270483851893361530	23 16 9
6137527	41 7 0	86807969439172982	25 18 5	7130654622923896350	22 17 9
31453488	40 8 0	114221012397502010	24 19 5	8715244538987104690	21 18 9
139767835	39 9 0	137065214861482908	23 20 5	9632638700903207990	20 19 9
545091767	38 10 0	150119044840161540	22 21 5	257668099806453820	28 10 10
1882967013	37 11 0	5364479296722	36 6 6	655882435174711976	27 11 10
5805816362	36 12 0	27588742194948	35 7 6	1475735479246515564	26 12 10
16077455055	35 13 0	120700745906895	34 8 6	2951470957321010124	25 13 10
40193661777	34 14 0	455980568919225	33 9 6	5270483852702315676	24 14 10
91105252497	33 15 0	1504735876402143	32 10 6	8432774162750027376	23 15 10
187904675706	32 16 0	4377413392313808	31 11 6	12122112859683551010	22 16 10
353702280690	31 17 0	11308317935237736	30 12 6	15687440169664356522	21 17 10
609154167250	30 18 0	26096118180492360	29 13 6	18302013532416736122	20 18 10
961821475230	29 19 0	54056244829095960	28 14 6	19265277401095105380	19 19 10
1394641595644	28 20 0	100904990136381816	27 15 6	1609893249573173544	26 11 11
1859521084850	27 21 0	170277170927824422	26 16 6	3488102040361648164	25 12 11
2282140209534	26 22 0	260423908201122666	25 17 6	6707888538605476404	24 13 11
2579809646726	25 23 0	361699872642264870	24 18 6	11499237494286660144	23 14 11
2687302591938	24 24 0	456884049357215480	23 19 6	17632164157359925680	22 15 11
191	46 1 1	525416656969664460	22 20 6	24244225715985790086	21 16 11
4349	45 2 1	550436497519708228	21 21 6	29948749413533412462	20 17 11
64927	44 3 1	137943703250100	34 7 7	33276388237117085060	19 18 11
713757	43 4 1	586260729113235	33 8 7	7266879251045544564	24 12 12
6136471	42 5 1	2149622651528715	32 9 7	13415777076559133640	23 13 12
42952525	41 6 1	6878792458628112	31 10 7	22040205198015185064	22 14 12
251570847	40 7 1	19385687790199632	30 11 7	32325634287639864600	21 15 12
1257841915	39 8 1	48464219421777720	29 12 7	42427395004047433380	20 16 12
5450620065	38 9 1	108112489398538680	28 13 7	49914582355035448050	19 17 12
20712315283	37 10 1	216224978713510800	27 14 7	52687614710209402350	18 18 12
69668620785	36 11 1	389204961579264336	26 15 7	23735605596070004280	22 13 13
209005757019	35 12 1	632458062469307646	25 16 7	37298808793141434264	21 14 13
562707643953	34 13 1	930085385883855630	24 17 7	52218332309646863976	20 15 13
1366575493563	33 14 1	1240113847767543320	23 18 7	65272915386631793610	19 16 13
3006465804441	32 15 1	1501190447237652600	22 19 7	72952081902429966390	18 17 13
6012931267794	31 16 1	1651309491932965436	21 20 7	55948213191205903656	20 14 14
10964756631510	30 17 1	2418325503348480	32 8 8	74597617584478171920	19 15 14
18274593959490	29 18 1	8598490570300620	31 9 8	88584670884029471910	18 16 14
27892800895190	28 19 1	26655320766887340	30 10 8	93795533874004088610	17 17 14
39049920855330	27 20 1	72696329114759460	29 11 8	94490315606290645536	18 15 15
50207040787046	26 21 1	175682795387902440	28 12 8	106301605056802235190	17 16 15
59335593422274	25 22 1	378393712685968980	27 13 8	112945455375981823980	16 16 16
64495210129142	24 23 1	729759303148399260	26 14 8
97657	44 2 2	1264916124783420252	25 15 8
1427470	43 3 2	1976431445242048080	24 16 8
15343647	42 4 2	2790256157185981770	23 17 8
128856651	41 5 2	3565327312427067330	22 18 8
880512171	40 6 2	4128273729405627230	21 19 8
5031358420	39 7 2	4334687416503640196	20 20 8
24527846695	38 8 2	29617022995256180	30 9 9

There exists no chirality as kekulene is a planar macrocycle.

Table 3 displays the isomers of C₄₈H_xF_yCl_z which correspond to tri-substituted kekulenes or. In order to enumerate these isomers, we invoke the proton cycle index for kekulene derived from the general equation, that is, Equation (19). In order to enumerate the isomers of C₄₈H_xF_yCl_z we substitute every s_k by (w₁^k + w₂^k + w₃^k) in Equation (19). The coefficients for various terms w₁^xw₂^yw₃^z are shown in Table 3 yield the isomers of C₄₈H_xF_yCl_z. As can be seen from Table 3, There are 3 isomers for (23,1,0) or 3 isomers for C₄₈H₂₃F (see, Table 3). Likewise, the number of isomers for C₄₈H₁₂F₁₂ is 226,150 and 788,825,460 isomers are enumerated for C₄₈H₈F₈Cl_8. The results displayed in Table 3 required such an elegant combinatorial technique and the computer codes that we have developed for up to 10 substituents.

Table 3. Enumeration of isomers of tri-substituted kekulenes or C₄₈H_xF_yCl_z (Reprinted with permission from [124] copyright (2018) American Chemical Society).

Coefficient	Vector (x, y, z)	Coefficient	Vector (x, y, z)
1	24 0 0	4292790	16 4 4
3	23 1 0	13731492	15 5 4
31	22 2 0	34329060	14 6 4
181	21 3 0	68650260	13 7 4
934	20 4 0	111559140	12 8 4
3597	19 5 0	148738030	11 9 4
11395	18 6 0	163616810	10 10 4
29007	17 7 0	41190876	14 5 5
61698	16 8 0	96108684	13 6 5
109298	15 9 0	178483956	12 7 5
164110	14 10 0	267723414	11 8 5
208474	13 11 0	327216106	10 9 5
226150	12 12 0	208237164	12 6 6
49	22 1 1	356962872	11 7 6
519	21 2 1	490830354	10 8 6
3573	20 3 1	545356070	9 9 6
17785	19 4 1	560936856	10 7 7
67443	18 5 1	701168970	9 8 7
202149	17 6 1	788825460	8 8 8

Both kekulene and septulene have the same number of monosubstituted isomers for the substitution carbon centers. There are 124 isomers for disubtituted hetero-septulenes that contain two N atoms. The maximum is reached at 536,056,343,620,384,863,061,500 for (19,19,18) for carbon colorings for septulenes. The combinatorics for the protons implies 3 isomers for monosubstituion of septulene with say Cl. Likewise we obtain 34 isomers for a dichloro-septulenes; the maximum is reached at 45,574,776,390 for (10,9,9). The results for octulenes can also be obtained in an analogous manner and they can be found in ref. [124].

Combinatorial identities for all n-circum-m-polyarenes that contain u substituents for carbon centers are obtained as:

• Case (1): m even

  $$\mathrm{I}\left(\mathrm{C}\right) =\frac{1}{2\mathrm{m}}\left\{{\displaystyle {{\displaystyle \sum }}_{\frac{\mathrm{d}}{\mathrm{m}}}}\chi \left(g\right) \mathsf{\phi }\left(\mathrm{d}\right){\mathrm{u}}_{}^{\frac{\mathrm{m}\left(\mathrm{k}\right)}{\mathrm{d}}}+\frac{\mathrm{m}}{2}({\mathrm{u}}_{}^{\frac{\mathrm{mk}}{2}}\left(1+{\mathrm{u}}_{}^{\mathrm{n} +1}\right)\right\}, \mathrm{k}=\{n^2+4n+3\}$$

  (32)
• Case (2): m odd

  $$\mathrm{I}\left(\mathrm{C}\right) = \frac{1}{2\mathrm{m}}\left\{{\displaystyle {{\displaystyle \sum }}_{\frac{\mathrm{d}}{\mathrm{m}}}}\chi \left(g\right) \mathsf{\phi }\left(\mathrm{d}\right){\mathrm{u}}_{}^{\frac{\mathrm{m}\left(\mathrm{k}\right)}{\mathrm{d}}}+{ \mathrm{mu}}_{}^{\frac{\mathrm{mk}+\mathrm{n} +1}{2}}\right\}\}, \mathrm{k}=\{n^2+4n+3\}$$

  (33)

The combinatorial identities for proton substituents are given:

• Case (1): m even, n odd, protons:

  $$\mathrm{I}\left(\mathrm{H}\right) = \frac{1}{2\mathrm{m}}\{{{\displaystyle \sum }}_{\mathrm{d}/\mathrm{m}}\chi \left(g\right) \mathsf{\phi }\left(\mathrm{d}\right){\mathrm{u}}_{}^{\frac{\mathrm{m}\left(\mathrm{n} +3\right)}{\mathrm{d}}} +\frac{m}{2}{u}_{}^{\frac{m\left(n+3\right)}{2}}\left(u^2+1\right)\},$$

  (34)
• Case (2): m even, n even, protons:

  $$\mathrm{I}\left(\mathrm{H}\right) = \frac{1}{2\mathrm{m}}\{{{\displaystyle \sum }}_{\mathrm{d}/\mathrm{m}}\chi \left(g\right) \mathsf{\phi }\left(\mathrm{d}\right){\mathrm{u}}_{}^{\frac{\mathrm{m}\left(\mathrm{n} +3\right)}{\mathrm{d}}} +\frac{m}{2}{u}_{}^{\frac{m\left(n+3\right)}{2}}\left(u^{}+1\right)\}$$

  (35)
• Case (3): m odd, n odd, protons:

  $$\mathrm{I}\left(\mathrm{H}\right) = \frac{1}{2\mathrm{m}}\{{{\displaystyle \sum }}_{\mathrm{d}/\mathrm{m}}\chi \left(g\right) \mathsf{\phi }\left(\mathrm{d}\right){\mathrm{u}}_{}^{\frac{\mathrm{m}\left(\mathrm{n} +3\right)}{\mathrm{d}}} +m{u}_{}^{\frac{m\left(n+3\right)}{2}+1}\}$$

  (36)
• Case (4): m odd, n even, protons:

  $$\mathrm{I}\left(\mathrm{H}\right) = \frac{1}{2\mathrm{m}}\{{{\displaystyle \sum }}_{\mathrm{d}/\mathrm{m}}\chi \left(g\right) \mathsf{\phi }\left(\mathrm{d}\right){\mathrm{u}}_{}^{\frac{\mathrm{m}\left(\mathrm{n} +3\right)}{\mathrm{d}}} +m{u}_{}^{\frac{m\left(n+3\right)+1}{2}}\}$$

  (37)

3.2. Applications to ¹³C, Proton NMR and Multiple Quantum NMR of Polyarenes

Combinatorial techniques discussed in the previous sections can be applied to ¹³C NMR, proton NMR and multiple-quantum NMR patterns. The number of ¹³C NMR signals or the number of equivalence classes of carbons for the cycloarenes is the number of isomers for the monosubstitution; the coefficient of (n − 1, 1) where n is the number of carbons enumerates the NMR signals. There are 5 monosubstituted isomers for carbon replacements of kekulene (see Table 2) suggesting that there are 5 ¹³C NMR signals for kekulenes. Analogously there are five ¹³C NMR signals for septulene and the same for octulene. By using the general combinatorial identities derived for isomer counts, we prove below that for all cycloarenes with D_mh groups, there are 5 ¹³C NMR signals:

$${\mathrm{P}}_{{\mathrm{D}}_{\mathrm{m}}}=\frac{1}{2\mathrm{m}}\{{{\displaystyle \sum }}_{\mathrm{d}/\mathrm{m}}\chi \left(g\right) \mathsf{\phi }\left(\mathrm{d}\right){\mathrm{s}}_{\mathrm{d}}^{\frac{8\mathrm{m}}{\mathrm{d}}}+\frac{\mathrm{m}}{2}{\mathrm{s}}_1^4{\mathrm{s}}_2^{\mathrm{k}}+\frac{m}{2}{s}_2^{4m}\} \mathrm{if} \mathrm{m} \mathrm{is} \mathrm{even}.$$

(38)

Consequently, the coefficient of w₁^8m−1w₂ in (41) can be seen to be

$$\frac{1}{2m}\left[\left(\begin{array}{c}8m\\ 1\end{array}\right)+\frac{m}{2}\left(4\right)\right]=\frac{1}{2m}\left[8m+2m\right]=5$$

(39)

A similar simplification can be carried out to gather the coefficient for m even and n = 1, and it can be shown to be 5. It can be shown that for any n-circumscribed cyclopolyarene, the number enumerated for monosubstitution is given by Equation (40):

$$\begin{array}{cc}\hfill P_{D_m}^{\chi }& =\frac{1}{2\mathrm{m}}\left\{ \left(\mathrm{m}\left(\begin{array}{c}{\mathrm{n}}^2+4\mathrm{n} +3\\ 1\end{array}\right)\right)+\frac{\mathrm{m}}{2}\left(2\mathrm{n} +2\right)\right\}=\frac{1}{2\mathrm{m}}\left\{\mathrm{m} \left({\mathrm{n}}^2+4\mathrm{n} +3\right)+\frac{\mathrm{m}}{2}\left(2\mathrm{n} +2\right)\right\}\hfill \\ & =\frac{1}{2}\left({\mathrm{n}}^2+5\mathrm{n} +4\right)\hfill \end{array}$$

(40)

As can be seen from the above expression, the number of ¹³C NMR signal enumeration for all circumscribed polyarenes is only dependent on n, the order of circumscribing and not on the cyclicity or m.

The combinatorial methods can be applied to enumerate the proton NMR signals for any order n of circumscribing and the result is shown below:

(n + 5)/2 if n is odd,
(n + 4)/2 if n is even.

(41)

For example, as seen from the above expression for n = 3, that is, for the triply circumscribed polyarenes, the number of proton NMR signals is 4.

Two-quantum or n-2 quantum NMR spectra bear direct relation to structurally dependent dipolar couplings compared to ordinary 1-quantum NMR spectra. Likewise enumeration of triangular interactions contain information on 3-quantum and so on. That is, from a graph-theoretical standpoint 2-quantum spectra depend on various equivalence classes of edges in the graph while n-1 quantum NMR depends only the vertex automorphisms. The GCCI polynomials can be applied for both bosons and fermions. For multiple quantum NMR of protons or ¹³C (fermions) the two possible spin orientations can be represented by α or β. Thus the combinatorial generators for multiple quantum NMR of circumscribed-cyclopolyarenes for ¹³C nuclei are given as follows for even and odd m:

$$G{F}_{D_m}^{\chi }=\frac{1}{2m}\{{{\displaystyle \sum }}_{d/m}\chi \left(g\right)\phi \left(d\right){\left({\alpha }^d+{\beta }^d\right)}_{}^{\frac{m\left(n^2+4n+3\right)}{d}}+\frac{m}{2}{\left(\alpha +\beta \right)}_{}^{\left(2n+2\right)}{\left({\alpha }^2+{\beta }^2\right)}_{}^k+\frac{m}{2}{\left({\alpha }^2+{\beta }^2\right)}_{}^{\frac{m\left(n^2+4n+3\right)}{2}}\} \mathrm{if} \mathrm{m} \mathrm{is} \mathrm{even},$$

(42)

where k = m(n² + 4n + 3)/2 − (n + 1), sum is over all divisors d of m, and φ(d) is the Euler totient function.

$$G{F}_{D_m}^{\chi }=\frac{1}{2m}\{{{\displaystyle \sum }}_{\frac{d}{m}}\chi \left(g\right)\phi \left(d\right){\left({\alpha }^d+{\beta }^d\right)}_{}^{\frac{m\left(n^2+4n+3\right)}{d}}+m{\left(\alpha +\beta \right)}_{}^{\left(n+1\right)}{\left({\alpha }^2+{\beta }^2\right)}_{}^k\} \mathrm{if} \mathrm{m} \mathrm{is} \mathrm{odd}$$

and

k = [m(n² + 4n + 3) − (n + 1)]/2

(43)

As a special case, for ¹³C multiple quantum NMR of kekulene and circumscribed kekulene the generating function for the totally symmetric representation is given by Equation (44).

GF(kekulene-multiple-quantum ¹³C NMR) =
α⁴⁸ + 5α⁴⁷β + 109α⁴⁶β² + 1467α⁴⁵β³ + 16398α⁴⁴β⁴ +142945α⁴³β⁵ +1024059α⁴²β⁶ +6137527α⁴¹β⁷ + 31453488α⁴⁰β⁸ + 139767835α³⁹β⁹ + 545091767α³⁸β¹⁰ + 1882967013α³⁷β¹¹ + 5805816362α³⁶β¹² +16077455055α³⁵β¹³ + 40193661777α³⁴β¹⁴ + 91105252497α³³β¹⁵ + 187904675706α³²β¹⁶ + 353702280690α³¹β¹⁷ + 609154167250α³⁰β¹⁸ + 961821475230α²⁹β¹⁹ + 1394641595644α²⁸β²⁰ + 1859521084850α²⁷β²¹ + 2282140209534α²⁶β²² + 2579809646726α²⁵β²³ + 2687302591938α²⁴β²⁴ +…

(44)

The terms that are not shown can be generated by an interchange of α with β which is attributed to the symmetry of binomial distribution, and it also arises from color symmetry of spin-1/2 fermions. Although both kekulene and septulene have the same second coefficient of 5, the third term has a coefficient of 124 for septulene and 109 for kekulene suggesting that n-2-quantum NMR spectra of the two structures are different. The corresponding proton multiple-quantum NMR yield four different expressions depending on the odd/even parties of m and n. In particular, the generating function for multiple quantum proton NMR of kekulene is computed by Equation (45):

GF(kekulene-m-quantum proton NMR) =
α²⁴ + 3α²³β + 31α²²β² + 181α²¹β³ + 934α²⁰β⁴ + 3597α¹⁹β⁵ + 11395α¹⁸β⁶ + 29007α¹⁷β⁷+ 61698α¹⁶β⁸ + 109298α¹⁵β⁹ + 164110α¹⁴β¹⁰ + 208474α¹³β¹¹ + 226150α¹²β¹² +…

(45)

The coefficient of the third term for the expression for septulene is 34 which is different from kekulene; the first 2 terms are the same implying that n-2 quantum spectra yield structural contrasts of these species because these spectra include dipolar couplings.

4. Applications to Nanotubes: Enumerations & Chirality

In this section we consider the applications of the GCCI combinatorial methods for the enumeration of chiral and achiral isomers of nanotubes of any cross section and length. For example, a cylindrical nanotube with a square cross section is shown in Figure 3 and hence the symmetry group is D_4h (m = 4). In the general case of a cylindrical nanotube with a cross-section composed of m vertices, the GCCI for such a cylindrical nanotube length n are obtained with four expressions depending on the parities of m and n:

Figure 3. A TUC4[4,m]-Tubular nanotube of cross section C₄ of length m. Reprinted with permission from [129] copyright (2021) Taylor & Francis.

m odd; n odd; σ_h plane passes through the central layer; each of m C₂ axes passes through a vertex of the central layer; σ_v/σ_d planes pass through n vertices:

$$\begin{gathered} P_{D_{mh}}^{\chi }=\frac{1}{4\mathrm{m}}{{\displaystyle \sum }}_{g\epsilon D_{mh}}\chi \left(g\right)s_1^{b_1}{s}_2^{b_2}\dots \dots s_n^{\mathrm{bn}}=\frac{1}{4\mathrm{m}}\{{{\displaystyle \sum }}_{\mathrm{d}/\mathrm{m}}\chi \left(g\right) \mathsf{\phi }\left(\mathrm{d}\right){\mathrm{s}}_{\mathrm{d}}^{\frac{\mathrm{mn}}{\mathrm{d}}}+{ \mathrm{ms}}_1{\mathrm{s}}_2^{\left(\mathrm{mn}-1\right)/2} \\ +s_1^m{\mathrm{s}}_2^{\mathrm{m}\left(\mathrm{n}-1\right)/2}+{{\displaystyle \sum }}_{\mathrm{d}/\mathrm{m}}\chi \left(g\right) \mathsf{\phi }\left(\mathrm{d}\right){\mathrm{s}}_{\mathrm{d}}^{\frac{\mathrm{m}}{\mathrm{d}}}{\mathrm{s}}_{2\mathrm{d}}^{\frac{\mathrm{m}\left(\mathrm{n}-1\right)}{2\mathrm{d}}}+m{s}_1^m{\mathrm{s}}_2^{\mathrm{m}\left(\mathrm{n}-1\right)/2}\} \end{gathered}$$

(46)

m odd; n even; σ_h plane does not pass through any vertex of the tube; each of m C₂ axes passes through the centers of edges; σ_v/σ_d planes pass through n vertices:

$$\begin{gathered} P_{D_{mh}}^{\chi }=\frac{1}{4\mathrm{m}}{{\displaystyle \sum }}_{g\epsilon D_{mh}}\chi \left(g\right)s_1^{b_1}{s}_2^{b_2}\dots \dots s_n^{\mathrm{bn}}=\frac{1}{4\mathrm{m}}\{{{\displaystyle \sum }}_{\mathrm{d}/\mathrm{m}}\chi \left(g\right) \mathsf{\phi }\left(\mathrm{d}\right){\mathrm{s}}_{\mathrm{d}}^{\frac{\mathrm{mn}}{\mathrm{d}}}+{ \mathrm{ms}}_2^{\mathrm{mn}/2} \\ +{\mathrm{s}}_2^{\mathrm{mn}/2}+{{\displaystyle \sum }}_{\mathrm{d}/\mathrm{m}}\chi \left(g\right) \mathsf{\phi }\left(\mathrm{d}\right){\mathrm{s}}_{2\mathrm{d}}^{\frac{\mathrm{mn}}{2\mathrm{d}}}+m{s}_1^m{\mathrm{s}}_2^{\mathrm{m}\left(\mathrm{n}-1\right)/2}\} \end{gathered}$$

(47)

m even; n odd;; each of m/2 C₂ axes passes through the centers of edges; each of m/2 C₂ axes passes through two vertices; m2 σ_v planes pass through 2n vertices; m/2 σ_d planes pass through the centers of the edges:

$$\begin{gathered} P_{D_{mh}}^{\chi }=\frac{1}{4\mathrm{m}}{{\displaystyle \sum }}_{g\epsilon D_{mh}}\chi \left(g\right)s_1^{b_1}{s}_2^{b_2}\dots \dots s_n^{\mathrm{bn}}=\frac{1}{4\mathrm{m}}\{{{\displaystyle \sum }}_{\mathrm{d}/\mathrm{m}}\chi \left(g\right) \mathsf{\phi }\left(\mathrm{d}\right){\mathrm{s}}_{\mathrm{d}}^{\frac{\mathrm{mn}}{\mathrm{d}}}+\frac{m}{2}{s}_1^2{\mathrm{s}}_2^{\left(\mathrm{mn}-2\right)/2}+\frac{m}{2}{\mathrm{s}}_2^{\mathrm{mn}/2} \\ +{\mathrm{s}}_2^{\mathrm{mn}/2}+{{\displaystyle \sum }}_{\frac{\mathrm{d}}{\mathrm{m}};\mathrm{d} \mathrm{even}}\chi \left(g\right) \mathsf{\phi }\left(\mathrm{d}\right){\mathrm{s}}_{\mathrm{d}}^{\frac{\mathrm{mn}}{\mathrm{d}}}+{{\displaystyle \sum }}_{\frac{\mathrm{d}}{\mathrm{m}};\mathrm{d} \mathrm{odd}}\chi \left(g\right) \mathsf{\phi }\left(\mathrm{d}\right){\mathrm{s}}_{\mathrm{d}}^{\frac{\mathrm{m}}{\mathrm{d}}}{\mathrm{s}}_{2\mathrm{d}}^{\frac{\mathrm{m}\left(\mathrm{n}-1\right)}{2\mathrm{d}}}+\frac{m}{2}{s}_1^{2n}{\mathrm{s}}_2^{\mathrm{n}\left(\mathrm{m}-2\right)/2}+\frac{m}{2}{\mathrm{s}}_2^{\mathrm{mn}/2}\} \end{gathered}$$

(48)

m even; n even; each of m C₂ axes passes through the centers of the edges; m/2 σ_v planes pass through 2n vertices; m/2 σ_d planes pass through the centers of the edges:

$$\begin{gathered} P_{D_{mh}}^{\chi }=\frac{1}{4\mathrm{m}}{{\displaystyle \sum }}_{g\epsilon D_{mh}}\chi \left(g\right)s_1^{b_1}{s}_2^{b_2}\dots \dots s_n^{\mathrm{bn}}=\frac{1}{4\mathrm{m}}\{{{\displaystyle \sum }}_{\mathrm{d}/\mathrm{m}}\chi \left(g\right) \mathsf{\phi }\left(\mathrm{d}\right){\mathrm{s}}_{\mathrm{d}}^{\frac{\mathrm{mn}}{\mathrm{d}}}+{\mathrm{ms}}_2^{\mathrm{mn}/2} \\ +{\mathrm{s}}_2^{\mathrm{mn}/2}+{{\displaystyle \sum }}_{\frac{\mathrm{d}}{\mathrm{m}};\mathrm{d} \mathrm{even}}\chi \left(g\right) \mathsf{\phi }\left(\mathrm{d}\right){\mathrm{s}}_{\mathrm{d}}^{\frac{\mathrm{mn}}{\mathrm{d}}}+{{\displaystyle \sum }}_{\frac{\mathrm{d}}{\mathrm{m}};\mathrm{d} \mathrm{odd}}\chi \left(g\right) \mathsf{\phi }\left(\mathrm{d}\right){\mathrm{s}}_{2\mathrm{d}}^{\frac{\mathrm{mn}}{2\mathrm{d}}}+\frac{m}{2}{s}_1^{2n}{\mathrm{s}}_2^{\mathrm{n}\left(\mathrm{m}-2\right)/2}+\frac{m}{2}{\mathrm{s}}_2^{\mathrm{mn}/2}\} \end{gathered}$$

(49)

In the above expressions, the sum is over divisors d of m, φ(d) is the Euler totient function defined as follows:

$$\phi \left(d\right)=d{{\displaystyle \prod }}_{p/d}\left(1-\frac{1}{p}\right).$$

(50)

The above product is computed over all prime numbers p that divide d. The Euler totient function is expressible in terms of the Möbius as shown in Equation (51):

$$\phi \left(d\right)=d{{\displaystyle \sum }}_{p/d}\frac{\mu \left(p\right)}{p},$$

(51)

where the sum is computed over all prime divisors of d and μ(d) is the Möbius function.

The GCCIs can de exemplified by considering a cylindrical nanotube with a cross section of 10-beaded necklace. For such a tube, the character table of the D_10h point group with 16 conjugacy classes and 16 IRs needs to be considered. We note that character values g and g⁻¹ which are golden ratio and its inverse, respectively; an accidental degeneracy of the GCCIs arises, resulting in several GCCIs of two dimensional IRs to become identical. Moreover even though the golden ratio is irrational, the sum g + g⁻¹ and g − g⁻¹ is an integer resulting in integral GCCIs for all IRs of the group D_mh. Note that the GCCIs of the A_1g and A_1u IRs are of special interest, as these GCCIs enumerate the achiral, chiral as well as all stereo-position isomers for the colorings of the nanotubes for various vertex colorings. Furthermore, the GCCIs enumerate both heteronanotubes of different kinds and polysubstituted nanotubes including fluorochloro nanotubes and hydrogenated nanotubes, etc. Balasubramanian et al. [129] have applied these techniques to a variety of nanotube enumerations and we shall consider some of their salient findings.

Figure 4 and Figure 5 show nanotubes of cross section C₆ of even length m (20) and odd m (21), respectively with a D_6h symmetry while the a tube with C₄ cross section is considered in Figure 3. Application of the formulae derived earlier, for example, for the simplest case of a tube with 3 layers (n = 3) and C₆ (m = 6) and odd length (Figure 5) gives the cycle indices for the A_1g and A_1u IRs of the D_6h group as

$$P_{D6h}^{A1g}=\frac{1}{24}\left\{s_1^{18}+2s_6^3+2s_3^6+s_2^9+3s_1^2{s}_2^8+3s_2^9+s_2^9+2s_3^2{s}_6^2+2s_6^3+s_1^6{s}_2^6+3s_1^6{s}_2^6+3s_2^9\right\}$$

(52)

$$P_{D6h}^{A1u}=\frac{1}{24}\left\{s_1^{18}+2s_6^3+2s_3^6+s_2^9+3s_1^2{s}_2^8+3s_2^9-s_2^9-2s_3^2{s}_6^2-2s_6^3-s_1^6{s}_2^6-3s_1^6{s}_2^6-3s_2^9\right\}$$

(53)

Figure 4. Tubular nanotube of cross section C₆ of even length m (20): D_6h.

Figure 5. Tubular nanotube of cross section C₆ of odd length m (21): D_6h. Reprinted with permission from [129] copyright (2021) Taylor & Francis.

Likewise for a tube of C₄ cross section (Figure 3) of length 99, the cycle indices are given by:

$$P_{D4h}^{A1g}=\frac{1}{16}\left\{s_1^{396}+2s_4^{99}+s_2^{198}+2s_1^2{s}_2^{197}+2s_2^{198}+s_2^{198}+2s_4^{99}+s_1^4{s}_2^{196}+2s_1^{198}{s}_2^{99}+2s_2^{198}\right\}$$

(54)

$$P_{D4h}^{A1u}=\frac{1}{16}\left\{s_1^{396}+2s_4^{99}+s_2^{198}+2s_1^2{s}_2^{197}+2s_2^{198}-s_2^{198}-2s_4^{99}-s_1^4{s}_2^{196}-2s_1^{198}{s}_2^{99}-2s_2^{198}\right\}$$

(55)

The cycle indices thus obtained in the above illustration is for the entire set D of all mn vertices of the nanotube. To illustrate the Sheehan’s modification, the explicit partitions of equivalence classes of the vertices are considered. For the example under consideration, we use the case of a tube with C₆ cross section and length of 3. For this case, we obtain two equivalences classes Y₁ and Y₂ where the first class is for the central layer and hence contains 6 vertices. The set Y₂ for this case consists of the top and bottom equivalent layers and thus 12 vertices. The GCCIs thus obtained for the D_6h symmetry nanotubes are show below with explicit partitions of the vertices so that Sheehan’s modification can be applied:

$$P_{D6h}^{A1g}=\frac{1}{24}\left\{s_{11}^6{s}_{21}^{12}+2s_{16}{s}_{26}^2+2s_{13}^2{s}_{23}^4+s_{12}^3{s}_{22}^6+3s_{11}^2{s}_{22}^8+3s_{12}^3{s}_{22}^6+s_{12}^3{s}_{22}^6+2s_{13}^2{s}_{26}^2+2s_{16}{s}_{26}^2+s_{11}^6{s}_{22}^6+3s_{11}^6{s}_{22}^6+3s_{12}^3{s}_{22}^6\right\}$$

(56)

$$P_{D6h}^{A1u}=\frac{1}{24}\left\{s_{11}^6{s}_{21}^{12}+2s_{16}{s}_{26}^2+2s_{13}^2{s}_{23}^4+s_{12}^3{s}_{22}^6+3s_{11}^2{s}_{22}^8+3s_{12}^3{s}_{22}^6-s_{12}^3{s}_{22}^6-2s_{13}^2{s}_{26}^2-2s_{16}{s}_{26}^2-s_{11}^6{s}_{22}^6-3s_{11}^6{s}_{22}^6-3s_{12}^3{s}_{22}^6\right\}$$

(57)

As the vertices are partitioned, the Sheehan technique facilitates the assignment of different coloring palettes for the distinct equivalence classes. Consider a hexagonal cylinder with 3 layers wherein the color weights 1, a, b, c are assigned for the central layer, and color weights 1, d, e for the top and bottom layers. In this setup the Sheehan’s modification yields the following generating functions for the A_1g and A_1u IRs of the D_6h group:

$$\begin{array}{ll}G{F}_{D6h}^{A1g}& =\frac{1}{24}\{{\left(1+a+b+c\right)}^6{\left(1+d+e\right)}^{12}+2\left(1+a^6+b^6+c^6\right){\left(1+d^6+e^6\right)}^2\\ & +2{\left(1+a^3+b^3+c^3\right)}^2{\left(1+d^3+e^3\right)}^4+{\left(1+a^2+b^2+c^2\right)}^3{\left(1+d^2+e^2\right)}^6\\ & +3{\left(1+a+b+c\right)}^2{\left(1+d^2+e^2\right)}^6+3{\left(1+a^2+b^2+c^2\right)}^3{\left(1+d^2+e^2\right)}^6\\ & +{\left(1+a^2+b^2+c^2\right)}^3{\left(1+d^2+e^2\right)}^6+2{\left(1+a^3+b^3+c^3\right)}^2{\left(1+d^6+e^6\right)}^2\\ & +2\left(1+a^6+b^6+c^6\right){\left(1+d^6+e^6\right)}^2+{\left(1+a+b+c\right)}^6{\left(1+d^2+e^2\right)}^6\\ & +3{\left(1+a+b+c\right)}^6{\left(1+d^2+e^2\right)}^6+3{\left(1+a^2+b^2+c^2\right)}^3{\left(1+d^2+e^2\right)}^6\}\end{array}$$

(58)

$$\begin{array}{ll}G{F}_{D6h}^{A1u}& =\frac{1}{24}\{{\left(1+a+b+c\right)}^6{\left(1+d+e\right)}^{12}+2\left(1+a^6+b^6+c^6\right){\left(1+d^6+e^6\right)}^2\\ & +2{\left(1+a^3+b^3+c^3\right)}^2{\left(1+d^3+e^3\right)}^4+{\left(1+a^2+b^2+c^2\right)}^3{\left(1+d^2+e^2\right)}^6\\ & +3{\left(1+a+b+c\right)}^2{\left(1+d^2+e^2\right)}^6+3{\left(1+a^2+b^2+c^2\right)}^3{\left(1+d^2+e^2\right)}^6\\ & -{\left(1+a^2+b^2+c^2\right)}^3{\left(1+d^2+e^2\right)}^6-2{\left(1+a^3+b^3+c^3\right)}^2{\left(1+d^6+e^6\right)}^2\\ & -2\left(1+a^6+b^6+c^6\right){\left(1+d^6+e^6\right)}^2-{\left(1+a+b+c\right)}^6{\left(1+d^2+e^2\right)}^6\\ & -3{\left(1+a+b+c\right)}^6{\left(1+d^2+e^2\right)}^6-3{\left(1+a^2+b^2+c^2\right)}^3{\left(1+d^2+e^2\right)}^6\}\end{array}$$

(59)

We shall demonstrate the flexibility of the above GFs in that different scenarios with given restrictions can be considered in coloring palettes as a result of partitioning of vertices of the central layers and vertices of the top/bottom layers. Consequently, we obtain the results shown below:

(a)

all vertices of the top/bottom layers are colored with a single color (white) while the vertices of the central layers are colored with different colors;

(b)

all vertices of the central layers are colored with a single color (white) while the vertices of the top/bottom layers are colored with different colors;

(c)

all vertices of the central layers and vertices of the top/bottom layers are colored with different colors chosen from a single set of colors without making any distinction between vertices of the central layers and vertices of the top/bottom layers.

(d)

all vertices of the central layers are colored with colors chosen from one set while all vertices of the top/bottom layers are colored with colors chosen from a different set of colors thus making a distinction between vertices of the central layers and vertices of the top/bottom layers.

The GF(A_1g) for the case (a) is computed by setting d and e to 0 in Equation (58):

$$\begin{array}{ll}G{F}_{D6h}^{A1g}& =\frac{1}{24}\{{\left(1+a+b+c\right)}^6+2\left(1+a^6+b^6+c^6\right)+2{\left(1+a^3+b^3+c^3\right)}^2+{\left(1+a^2+b^2+c^2\right)}^3\\ & +3{\left(1+a+b+c\right)}^2+3{\left(1+a^2+b^2+c^2\right)}^3+{\left(1+a^2+b^2+c^2\right)}^3+2{\left(1+a^3+b^3+c^3\right)}^2\\ & +2\left(1+a^6+b^6+c^6\right)+{\left(1+a+b+c\right)}^6+3{\left(1+a+b+c\right)}^6+3{\left(1+a^2+b^2+c^2\right)}^3\}\end{array}$$

(60)

The GF thus obtained for A_1g can likewise be computed for other IRs and the coefficient obtained for each term enumerates the colorings of the vertices of the central layer with the corresponding color palette that transform according to the IR. That is, for instance, the partition [2 2 1 1] is enumerated by the term 1²a²bc or the number of ways to color the central vertices with 2 white, 2 blue, 1 green and 1 red, such that only the central vertices are colored keeping the top/bottom layers constant.

The GF for the A_1u IR for case (b) generated by setting a, b and c to 0 in Equation (59), yielding:

$$\begin{array}{ll}G{F}_{D6h}^{A1u}& =\frac{1}{24}\{{\left(1+d+e\right)}^{12}+2{\left(1+d^6+e^6\right)}^2+2{\left(1+d^3+e^3\right)}^4+{\left(1+d^2+e^2\right)}^6+3{\left(1+d^2+e^2\right)}^6\\ & +3{\left(1+d^2+e^2\right)}^6-{\left(1+d^2+e^2\right)}^6-2{\left(1+d^6+e^6\right)}^2-2{\left(1+d^6+e^6\right)}^2-{\left(1+d^2+e^2\right)}^6\\ & -3{\left(1+d^2+e^2\right)}^6-3{\left(1+d^2+e^2\right)}^6\}\end{array}$$

(61)

The GF(A_1u) shown above generates the number of chiral pairs for vertex-colorings for the top/bottom layers with 3 different colors (blue, red, purple) and retaining all central vertices of the tube in white colors.

The case (c) is the most common single-set-coloring scheme, as it involves coloring of all vertices of the nanotube with colors chosen from a single set of colors. Here no distinction is made between the central vertices and the vertices of the top/bottom layers, and thus all vertices are placed in one D set. Here the GF for each IR is obtained by replacing w_{ij =} w_j for all i and colors are selected from a single color set R. For four-coloring of the vertices, the GF (A_1g) is shown below for the tube with C₆ cross section and 3 layers:

$$\begin{array}{ll}G{F}_{D6h}^{A1g}& =\frac{1}{24}\{{\left(1+a+b+c\right)}^{18}+2{\left(1+a^6+b^6+c^6\right)}^3+2{\left(1+a^3+b^3+c^3\right)}^6+{\left(1+a^2+b^2+c^2\right)}^9\\ & +3{\left(1+a+b+c\right)}^2{\left(1+a^2+b^2+c^2\right)}^8+3{\left(1+a^2+b^2+c^2\right)}^9+{\left(1+a^2+b^2+c^2\right)}^9\\ & +2{\left(1+a^3+b^3+c^3\right)}^2{\left(1+a^6+b^6+c^6\right)}^2+2{\left(1+a^6+b^6+c^6\right)}^3\\ & +{\left(1+a+b+c\right)}^6{\left(1+a^2+b^2+c^2\right)}^6+3{\left(1+a+b+c\right)}^6{\left(1+a^2+b^2+c^2\right)}^6\\ & +3{\left(1+a^2+b^2+c^2\right)}^9\}\end{array}$$

(62)

Table 4 and Table 5 display the combinatorial results for the C₆-tubes shown in Figure 4 and Figure 5, respectively. Table 4 and Table 5 were generated from the corresponding GFs obtained from their GCCIs for the binomial colorings of these tubes which are shown below:

Table 4. Combinatorics of binomial colorings of C6 tube of even length (20). Reprinted with permission from [129] copyright (2021) Taylor & Francis.

[λ]	A1g	A1u
120 0	1	0
119 1	10	0
118 2	430	200
117 3	13140	10270
116 4	358580	327000
115 5	8076302	7805200
114 6	153228940	151186610
113 7	2485281890	2472015520
112 8	35049847010	34972263360
111 9	435895574270	435487149890
110 10	4837163423172	4835187982608
109 11	48366143812740	48357338386240
108 12	439304123944130	439267535249120
107 13	3649522483044260	3649380289048000
106 14	27892495987962020	27891975424030480
105 15	197106031753154350	197104231299671570
104 16	1293505382317706270	1293499470458272960
103 17	7913200546609255430	7913182073007147040
102 18	45281066731050988200	45281011600933676850
101 19	243087762638665331530	243087605202533277680
100 20	1227593019502352645116	1227592588139680180808
99 21	5845680586016149192080	5845679450165058565230
98 22	26305561521626686809770	26305558641388642521880
97 23	112084563868390564619870	112084556825344707148480
96 24	453008439719843093324185	453008423084819935550720
95 25	1739552395580465510782712	1739552357586305907062080
94 26	6356056802607579048149000	6356056718581715136103840
93 27	22128493997304209628417280	22128493817196173268087480
92 28	73498212093520559324283920	73498211718937259300046560
91 29	233166741598000966442884040	233166740841488289311513600
90 30	707272449109079345066275200	707272447624069094082039400
89 31	2053371625707638595138215800	2053371622872379689408576320
88 32	5710939832691184420347395710	5710939827422078705100951680
87 33	15229172884919521763241151730	15229172875382280514199523400
86 34	38968765907621805546447563950	38968765890797737924153754120
85 35	95751824795384727236237065030	95751824766445595988072443312
84 36	226080697423665918179837712780	226080697375100662367959790680
83 37	513264286027563834692713658510	513264285948013123131287760080
82 38	1121077256300109181440804823910	1121077256172862735028690940680
81 39	2357136795263310515884594697290	2357136795064474082599295897160
80 40	4773202010358707257612086114170	4773202010055058999556359513408
79 41	9313564898191311432444888679940	9313564897737983810337193741600
78 42	17518372070312058850710272631220	17518372069650191620702994780120
77 43	31777512127415150509871599803740	31777512126469853524471252843840
76 44	55610646222809929010711390106200	55610646221488836306052022553040
75 45	93920202509422472913833055244500	93920202507615427898786969026968
74 46	153130764960751689179624148240700	153130764958331858395428437922800
73 47	241099502278311827209649491672420	241099502275138843239010973758880
72 48	366672159714557209135122371215500	366672159710482373202785259933120
71 49	538783581620959439539367888026550	538783581615833385238761111253600
70 50	765072685901281807653064962794306	765072685894964033815883701208344
69 51	1050099764962022784801615163283710	1050099764954393034471851047572500
68 52	1393401611199060099344586013233020	1393401611190030163150578065198920
67 53	1787760557764276241571586760097890	1787760557753801778758977126918480
66 54	2218147358706984761747143844517710	2218147358695075055554709343916900
65 55	2661776830447873212340258083935022	2661776830434598506818581481178240
64 56	3089562392483687387382849613409250	3089562392469181632858390724145920
63 57	3468982335419907262008024739287820	3468982335404366657697752965321340
62 58	3768032536748931605487595238564080	3768032536732607374058506770897600
61 59	3959627411498706582271887678528880	3959627411481893631161976216665600
60 60	4025621201690294701317661934726204	4025621201673315584661128579342944

Table 5. Combinatorics of binomial colorings of C6 tube of odd length (21). Reprinted with permission from [129] copyright (2021) Taylor & Francis.

[λ]	A1g	A1u
126 0	1	0
125 1	11	0
124 2	473	220
123 3	15253	11910
122 4	436673	398560
121 5	10348033	10004800
120 6	206573169	203879874
119 7	3527122728	3508834432
118 8	52385696704	52274232236
117 9	686407979303	685795703012
116 10	8028934612915	8025849284552
115 11	84659644031796	84645309793480
114 12	811283921490655	811221894648266
113 13	7114189337715709	7113938271431488
112 14	57421136296522190	57420179480527816
111 15	428742633734011054	428739188570867700
110 16	2974395957907605578	2974384184884777864
109 17	19246072541004160475	19246034252371767360
108 18	116545605020781110873	116545486120454041778
107 19	662469593565669880140	662469240221433288120
106 20	3544211884087688220237	3544210876693600321224
105 21	17889830252498885495425	17889827492074590075716
104 22	85383277805294190143784	85383270521181826240644
103 23	386080901136593900270904	386080882599144920683392
102 24	1656930517051376784683269	1656930471481634923631114
101 25	6760276470775467874719927	6760276362433949041317696
100 26	26261073896914647611843439	26261073647477690543603952
99 27	97263236471662895274416233	97263235914956931417312702
98 28	343895014286357966923112919	343895013080626398572379156
97 29	1162127978543417947038420093	1162127976007021782564392832
96 30	3757547129116693561369533113	3757547123929752463745097544
95 31	11636274977618676741474605088	11636274967299175559427516672
94 32	34545191334481858494269819958	34545191314493091129392663952
93 33	98401454094672584680155613591	98401454056952557263117170000
92 34	269156918536182307562667604533	269156918466792562463927930652
91 35	707498185837591596996314883276	707498185713084020804419188984
90 36	1788398191930007116460908717629	1788398191711979048251416225608
89 37	4350157764075290579543044835397	4350157763702510856253493800128
88 38	10188527394682682072242746308316	10188527394060064806948032860284
87 39	22989497710884551633808458024272	22989497709868307190203644545008
86 40	50002157520879567765636859278504	50002157519257903388142469358316
85 41	104882574311653493200042912232931	104882574309122653904387904539904
84 42	212262352772955598204815146300663	212262352769091372968466328442032
83 43	414652037974188760093034977579044	414652037968414603187921841451176
82 44	782184526177360507348845920120703	782184526168914032231473122983532
81 45	1425314025477099466617348186776881	1425314025465000766616408261522640
80 46	2509792088337944983451863878699918	2509792088320970669250957680677753
79 47	4271986533338402240952986091515568	4271986533315071146968456514703232
78 48	7030977836115966289850178437041004	7030977836084542036709394169335632
77 49	11192168800343594818507662954115382	11192168800302112216589382096345792
76 50	17235939952524034981288300451784128	17235939952470353920645281657293988
75 51	25684930125323990978539590227007264	25684930125255882540509198550606740
74 52	37045572296133623677675596842206368	37045572296048886307617780234533304
73 53	51724006602141374421656431169602456	51724006602037978956693506504856184
72 54	69923194110294214696088434473985680	69923194110170466866523001472260968
71 55	91535817744376799116378300971826720	91535817744231511058933713108728176
70 56	116054340354469299983499331537508704	116054340354301950607134075303190832
69 57	142522874119515507211110040589336016	142522874119326379203129178324865584
68 58	169553074383553918092169927083932224	169553074383344188394338933483678944
67 59	195417102679343529229105477101092448	195417102679115305059831028491385312
66 60	218215764658594707645979394768009504	218215764658350990916595981027726176
65 61	236102302745360626194077729265514496	236102302745105211277102095497067808
64 62	247526607716907796799690373591361056	247526607716645097621485771818723552
63 63	251455601490191198999846211143625568	251455601489926026768523441574344800

C₆ tube of length 20:

$$\begin{array}{ll}G{F}_{D6h}^{A1g}& =\frac{1}{24}\{{\left(a+b\right)}^{120}+2{(a^6+b^6)}^{20}+2{(a^3+b^3)}^{40}+{\left(a^2+b^2\right)}^{60}+3{\left(a^2+b^2\right)}^{60}+3{\left(a^2+b^2\right)}^{60}\\ & +{\left(a^2+b^2\right)}^{60}+2{\left(a^6+b^6\right)}^{20}+2{\left(a^6+b^6\right)}^{20}+{\left(a^2+b^2\right)}^{60}+3{\left(a+b\right)}^{40}{\left(a^2+b^2\right)}^{40}\\ & +3{\left(a^2+b^2\right)}^{60}\}\end{array}$$

(63)

$$\begin{array}{ll}G{F}_{D6h}^{A1u}& =\frac{1}{24}\{{\left(a+b\right)}^{120}+2{(a^6+b^6)}^{20}+2{(a^3+b^3)}^{40}+{\left(a^2+b^2\right)}^{60}+3{\left(a^2+b^2\right)}^{60}+3{\left(a^2+b^2\right)}^{60}\\ & -{\left(a^2+b^2\right)}^{60}-2{\left(a^6+b^6\right)}^{20}-2{\left(a^6+b^6\right)}^{20}-{\left(a^2+b^2\right)}^{60}-3{\left(a+b\right)}^{40}{\left(a^2+b^2\right)}^{40}\\ & -3{\left(a^2+b^2\right)}^{60}\}\end{array}$$

(64)

C₆ tube of length 21:

$$\begin{array}{ll}G{F}_{D6h}^{A1g}=& \frac{1}{24}\{{\left(a+b\right)}^{126}+2{(a^6+b^6)}^{21}+2{(a^3+b^3)}^{42}+{\left(a^2+b^2\right)}^{63}+3{\left(a+b\right)}^2{\left(a^2+b^2\right)}^{62}\\ & +3{\left(a^2+b^2\right)}^{63}+{\left(a^2+b^2\right)}^{63}+2{\left(a^6+b^6\right)}^{21}+2{(a^3+b^3)}^2{\left(a^6+b^6\right)}^{20}+{\left(a^2+b^2\right)}^{63}\\ & +3{\left(a+b\right)}^{42}{\left(a^2+b^2\right)}^{42}+3{\left(a^2+b^2\right)}^{63}\}\end{array}$$

(65)

$$\begin{array}{ll}G{F}_{D6h}^{A1u}& =\frac{1}{24}\{{\left(a+b\right)}^{126}+2{(a^6+b^6)}^{21}+2{(a^3+b^3)}^{42}+{\left(a^2+b^2\right)}^{63}+3{\left(a+b\right)}^2{\left(a^2+b^2\right)}^{62}\\ & +3{\left(a^2+b^2\right)}^{63}-{\left(a^2+b^2\right)}^{63}-2{\left(a^6+b^6\right)}^{21}-2{(a^3+b^3)}^2{\left(a^6+b^6\right)}^{20}-{\left(a^2+b^2\right)}^{63}\\ & -3{\left(a+b\right)}^{42}{\left(a^2+b^2\right)}^{42}-3{\left(a^2+b^2\right)}^{63}\}\end{array}$$

(66)

In order to generate a chiral coloring, at least 2 black colors are needed, as seen from Table 4 and Table 5, and these numbers are 200 and 220, respectively for the number of chiral pairs. The chiral colorings explode combinatorially as a function of k culminating into every coloring becoming chiral. For example, there are 4,025,621,201,673,315,584,661,128,579,342,944 chiral pairs of colorings for 60 black and 60 white colors for the tube shown in Figure 4. Figure 6 and Figure 7 show one such achiral and chiral coloring for the partition [100 20] for a tube with length 20; helical patterns of colorings can be seen in these figures. Such chiral helical patterns have received considerable interest in recent years in nanomaterials, as such chiral patterns exhibit interesting optoelectronic properties. Figure 8 and Figure 9 show achiral and chiral isomers for the case of 21 blue colors (nitrogen) and remaining carbons for the case of C₆ tube with length 21. Figure 9 shows one of chiral isomers enumerated (Table 5) out of 17,889,827,492,074,590,075,716 chiral pairs for the partition [105 21] whereas the corresponding achiral isomer is depicted in Figure 8. Figure 10 and Figure 11 illustrate achiral colorings for equal number of grey and blue colors for the C₆ tubular nanotube of and even and odd lengths containing alternating arrangement of carbon and nitrogen atoms, respectively.

Figure 6. Tubular nanotube of cross section C₆ of even length: One of achiral isomers enumerated in Table 4 for the partition [100 20].

Figure 7. Tubular nanotube of cross section C₆ of even length: One of chiral isomers enumerated in Table 4 out of 1,227,592,588,139,680,180,808 chiral pairs for the partition [100 20]. Reprinted with permission from [129] copyright (2021) Taylor & Francis.

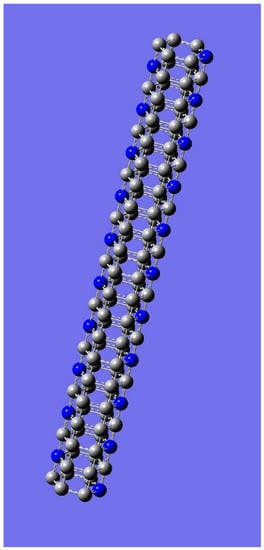
Figure 8. Tubular nanotube of cross section C₆ of odd length: One of achiral isomers enumerated in Table 5 for the partition [105 21].

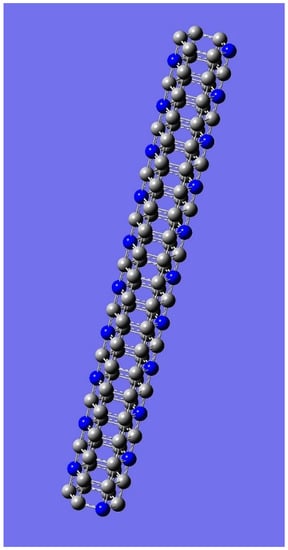
Figure 9. Tubular nanotube of cross section C₆ of odd length: One of chiral isomers enumerated in Table 4 out of 17,889,827,492,074,590,075,716 chiral pairs for the partition [105 21].

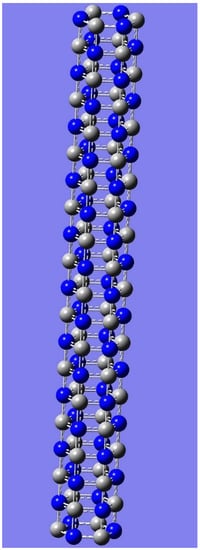
Figure 10. Tubular nanotube of cross section C₆ of even length with alternating arrangement of carbon and nitrogen atoms: One of achiral isomers enumerated in Table 4 for the partition [60 60].

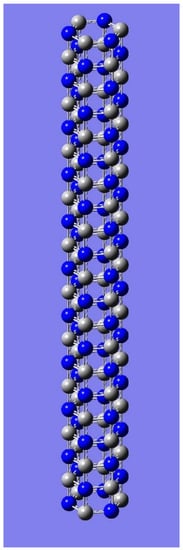
Figure 11. Tubular nanotube of cross section C₆ of odd length with alternating arrangement of carbon and nitrogen atoms: One of achiral isomers enumerated in Table 5 for the partition [63 63]. Reprinted with permission from [129] copyright (2021) Taylor & Francis.

5. Applications to Tessellations of Kekulenes, Nanobands, C₆₀ Polymers, Spectroscopy & Topology

Tessellations of polyarenes such as kekulenes and octulenes are of considerable interest because they are excellent candidates for sequestering both anions such as Cl⁻ (Figure 12 Left). Moreover heterosubstituted tessellations of these structures, for example, crown ether analogs and porphyrin analogs can be candidates for sequestration of toxic heavy metal ions such as Cd²⁺ (Figure 12 Right) as well as actinyl ions in high level nuclear wastes such as UO₂²⁺ and PuO₂²⁺. Another variation to the heavy metal ion trap made possible by polyphenolic kekulene us shown in Figure 12 (bottom) and thus one could make tessellations of these structures possessing multiple cavities for efficient trapping of heavy metal ions. Consequently, such derivatives of graphenes with cavities have been proposed as molecular belts for the sequestration and transport of both anions and cations [25,32,35]. Furthermore phase transformations among various topological configurations such as the square, armchair and zigzag structures have been considered in previous studies [39,40,41] for both carbon nanotubes and various structures arising from graphene sheets. Furthermore enthalpies of formation and Gibbs free energies of such large systems are extremely challenging to compute from the ab initio techniques for example, Gaussian-3 theories. Our understanding of the phase transformations among various tessellations needs the Gibbs free energies of these systems which depend not only the enthalpies but also the entropies of different phases. As there are a large number of vibrational modes for tessellations of kekulenes, computations of thermodynamic properties by ab initio theory would be a mammoth task. Hence robust topological techniques [144] based on graph theory have been developed for large tessellations of kekulenes for the characterization of the structures and spectra using machine learning/artificial intelligence methods. Machine learning that can integrate topology with ab initio techniques through by partitions into equivalence classes can be extremely valuable. Topological methods dissect such large tessellations into edge partitions of tessellations of cyclopolyarenes, which can then be harnessed for rapid and robust computations of enthalpies of formations through bond partitions. Analytical expressions for graph-theoretically based information theoretic entropies of such large tessellations have been derived [144]. In this process two different structures that exhibit the same graph entropies were discovered, and they are shown in Figure 13. The existence of isentropic tessellations for kekulenes is quite interesting as it appears to be previously unknown. Hence these structures were taken up for further studies [144] including computing measures of contrasts in their electronic and other spectra that we discus in the ensuing paragraphs.

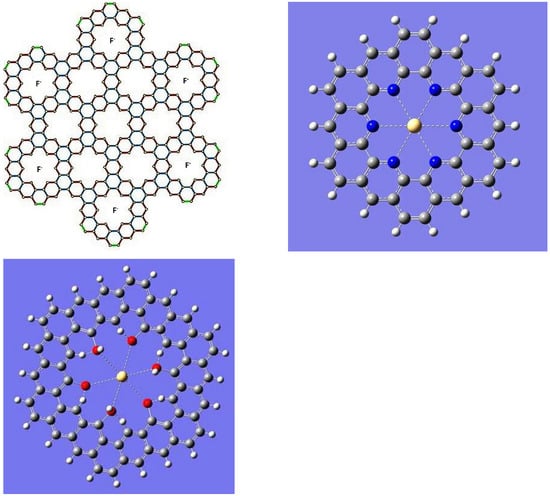
Figure 12. (Left) A Tessellation of kekulene providing cavities to trap F⁻ ions; Octulenes have been proposed to have suitable pore size to transport Cl⁻. Reprinted with permission from [144] copyright (2021) American Chemical Society. (Right) Porphyrin-analogs of Kekulene tessellations as complexation traps for metal ions such as Cd2+, Hg+2, and U(VI) ions. Figure shows a complex of Cd2+ with porphyrin-analog of kekulene; the distance between Cd and N is roughly 2.75 Ǻ° providing an optimal cavity trap Cd2+. Reprinted with permission from [160] copyright (2021) Springer Nature. (Bottom) A polyphenolic compound derived from septulene as a marcocycle crown for toxic heavy metal ions. Figure shows a proposed complex with Cd(II) and also intramolecular hydrogen bonds exhibited by the complex. Reprinted with permission from [160] copyright (2021) Springer Nature.

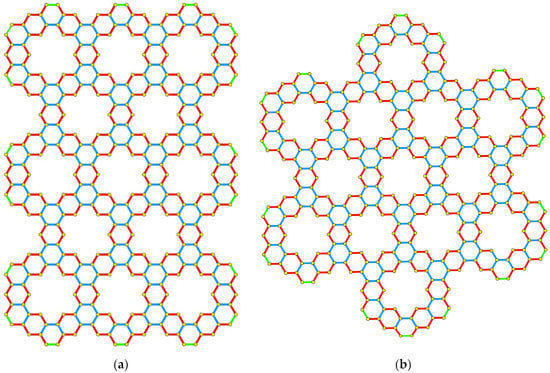
Figure 13. Two topological tessellations of kekulenes that exhibit the same graph entropies: (Left; (a)) AHK(2) (Right; (b)) RK(3,3). Reprinted with permission from [144] copyright (2021) American Chemical Society.

There exists greater variations in entropies among the various possible tessellations for relatively smaller tessellations whereas for larger tessellations, different configurations converge to the entropies of the 2D graphitic sheet with holes. Among the smaller tessellations, the zigzag tessellation exhibits the largest entropy whereas the armchair tessellation exhibits the lowest entropy. Liu et al. [39] have investigated the energy changes from the armchair to zigzag graphene structures when studying nanotube chirality selection and chemical control. Thess et al. [37] and Okada [41] have both independently shown that the armchair structure is more stable than the zigzag structure because of the possibility of a triple bond at the edges for the armchair structure. The binding energy/atom and the state density at the edge seems to compete resulting in an enhanced stability of about 15% for the armchair relative to the zigzag structure.

The stabilities of various phases are determined by the Gibbs free energies and thus bond enthalpies and entropies compete in the determination of their free energies. Consequently, the relative entropies of different phases can provide important insights into the relative stabilities of various tessellations or phases. Hence the topological entropies imply that the zigzag structure is more stable than the armchair but an opposite energetic trend is seen for the two structures. The two tessellations of kekulenes shown in Figure 13 contain the same number of vertices (360) and C−C edges (468), and identical topological edge partitions (Figure 13). Table 6 displays the various topological indices, graph spectra and energetics for the two isentropic kekulene structures. Note that the vertex degree based topological indices such as the Padmakar-Ivan, Zagreb-1, Zagreb-2, ABC, and Randić indices are identical for the two isentropic kekulene tessellations (Table 6). On the other hand, the distance-dependent topological distances such as the Wiener, hyper Wiener, Mostar, Szeged, Gutman, Harary and Balaban, indices differ for the two isentropic kekulene tessellations. The graph spectra and their spectral degeneracies were computed for the two tessellations (see Table 6). The two tessellations in Figure 13 yield different spectral patterns, as AHK(2) belongs to the nonabelian D_6h group and thus contains two-dimensional irreducible representations whereas the RK(3,3) structure with a D2h abelian symmetry contains only uni-dimensional irreducible representations. Thus the spectral difference index and the root mean square of the spectral difference for the two isentropic structures were computed to measure their contrasts. These spectral difference measures are defined as follows:

$$\delta =\frac{1}{n}\left\{{{\displaystyle \sum }}_{i=1}^n\right|{\lambda }_i^I-{\lambda }_i^{II}\},$$

(67)

$$\mathrm{RMS}=\sqrt{\frac{1}{n}{\left({\lambda }_i^I-{\lambda }_i^{II}\right)}^2}$$

(68)

Table 6. Comparison of various topological indices for the two isentropic structures: AHK(2) and RK(3,3). Reprinted with permission from [144] copyright (2021) American Chemical Society.

TI	AHK(2)	RK(3,3)
Zagreb-1	2520	2520
Zagreb-2	3366	3366
Randić	177.8786	177.8786
Atom-bond connectivity	322.9188	322.9188
Padmakar Ivan	168,480	168,480
Wiener	1,140,348	1,185,720
Hyper-Wiener	12,876,702	14,183,508
Schultz	589,684	6,134,528
Gutman	7,622,832	7,934,112
Harary	5635.002	5565.1216
Balaban	0.3237	0.3120
Mostar	80,256	79,920
Szeged	10,338,816	10,325,272
Harmonic Szeged	66,834.8034	67,043.7870
Edge Partitions	(22)18(23)252(33)198	(22)18(23)252(33)198
Vertex Partitions	641228	24488
Spectral Pattern	1 2 2 1 1 1 2 2 2 1 2 1 2 1 2 1 2 1 1 2	112421154.154211124
	2 2 1 1 1 2 2 1 1 1 2 2 1 2 1 2 1 2 2 1
	1 2 2 1 1 2 2 1 1 2 1 2 2 1 2 1 2 2 1 1
	2 2 1 1 2 2 1 1 2 2 1 2 1 2 1 1 1 1 2 2
	2 2 2 1 1 2 2 1 1 2 2 1 2 1 1 2 1 2 2 1
	2 2 1 2 1 1 1 2 2 1 2 2 1 2 1 1 2 1 2
	2 1 2 1 1 2 1 2 2 1 2 2 1 1 1 2 1 2 2 1
	2 2 1 2 1 1 2 1 2 2 1 1 2 2 1 1 2 2 2 2
	2 1 1 1 1 2 1 2 1 2 2 1 1 2 2 1 1 2 2 1
	1 2 2 1 2 1 2 2 1 2 1 1 2 2 1 1 2 2 1 1
	2 2 1 2 1 2 1 2 2 1 1 1 2 2 1 1 1 2 2 2
	1 1 2 1 2 1 2 1 2 1 2 2 2 1 1 1 2 2 1
Spectral Difference	0.009612
RMS Spectral Difference	0.013128
HOMO-LUMO	0.755β a	0.744β
Eπ	524.4053β	524.4139β
13C-NMR	32 signals	92 signals
Proton NMR	14 signals 1:1:1:1:2:2:2:2:2:2:2:2:2:2	38 signals 1:1:1:1:2:2:2:2:2:2:2:2:2:2: 2:2:2:2:2:2:2:2:2:2: 2:2:2:2:2:2:2:2:2:2:

^a The HOMO-LUMO gap obtained by Dias and coworkers [75], for kekulene is 0.8744β is reproduced by the spectra computed here; the HOMO-LUMO gap of kekulene at 631G* = 3.58 eV, 6-311g(d) = 3.55 eV and 6-311g(2d) = 3.54 eV. Table reprinted with permission from [144] copyright (2021) American Chemical Society.

The above-defined spectral indices of these two structures reveal that the isentropic structures are energetically quite close but they are certainly not degenerate (Table 6). Moreover the HOMO-LUMO energy gaps are different for the two structures, in that the armchair structure’s HOMO-LUMO gap is greater, although by only ~1.5% compared to the square structure; the armchair structure is kinetically more stable than the square tessellation. The total π-electronic energies imply that the rectangular tessellation is roughly a kcal/mol more stable than the armchair structure. The square tessellation exhibits a less symmetric D2h group compared to the armchair (D_6h) and thus the greater stability of the square tessellation is analogous to the energy stabilization induced by symmetry-breaking in E⊗e Jahn-Teller distortion [144]. This is a consequence of doubly-degenerate HOMO and LUMO of the armchair tessellation both of which transform as the two-dimensional E representations of the D_6h group. In contrast, the HOMO and LUMO of the rectangular structures are one dimensional. Consequently, the metamorphosis from the armchair to the rectangular tessellation leads to symmetry and hence stabilizing the rectangular structure.

Both ¹³C and proton NMR spectral patterns can be generated for the two isentropic tessellations by combinatorial generation of their vertex partitions. The same technique can be employed to generate the ESR hyperfine structures and multiple quantum NMR spectra of these structures. In order to accomplish this, we invoke the distance degree sequence vectors (DDSV) of graphs introduced by Bloom et al. [158]. In general for any vertex v in a graph G can be assigned an integer sequence that corresponds to the number of vertices at distances 0, 1, 2, …, ev, where ev is defined as the eccentricity of v in G. Hence we can assign a p-tuple vector (Di0, Di1, Di2, …, Dij, … Dip) for each vertex vi in the graph where Dij is defined as the number of vertices at distance j from vi. This can be carried out by the use of the graph distance matrix generator. The DDSV is can be computed by the computer code developed by the author [159]. As the two tessellations shown in Figure 13 contain 360 vertices there are 360 such DDSV tuples of variable lengths. It can be seen that two equivalent vertices under the graph automorphism would have the same DDSV although the converse is not true for all graphs. For tessellations of kekulene structures, the DDSV offers a viable alternative to the graph vertex partitioning problem, which is in general a O(n!) problem as there are n! ways to label a graph of n vertices in the most general case. The DDSV vectors of variable lengths are concatenated in order to generate an integral label. As these integral labels rapidly grow, the labels are represented as real numbers in quadruple precision. In this setup the algorithm to generate vertex partitions simplifies to O(n²) where n is the number of vertices.

The vertex partitions for both carbon and hydrogen atoms were computed using the DDSV algorithm for the two kekulene tessellations in Figure 13 with the objective of generating their ESR hyperfine and NMR patterns. Through the application of the DDSV computational technique, the vertices of RK(3,3) are partitioned into 2⁴4⁸⁸ partition of 360 vertices whereas the vertices of AHK(2) are partitioned into the 6⁴12²⁸ partition. Consequently, there are 92 equivalence classes of vertices for RK(3,3) whereas there are 32 equivalence classes for AHK(2). Hence these carbon vertex partitions yield the numbers of ¹³C NMR signal signals for the two tessellations shown in Figure 13. In an analogous manner, the number of proton NMR signals for the AHK(2) tessellation is obtained as 14. That is, 144 protons are divided 14 classes with the partition 6⁴12¹⁰ for AHK(2). On the other hand, for the RK(3,3) structure the DDSV technique partitions the protons into 38 classes with the partition 2⁴4³⁴ for the RK(3,3) (Figure 13), as shown in Table 6 for the two structures.

The machine generation of the ESR hyperfine patterns of the two tessellations can be made possible by combinatorial generating functions analogous to the ones obtained in the previous sections. For example, for the AHK(2) structure, the ESR GF can be constructed from the equivalence class partitions assuming that all ¹³C nuclei are coupled equally to the unpaired electron. Such radicals can be generated by a single deprotonation of the kekulene tessellation. Suppose we include only the ¹³C nuclear-electron coupling in order to devise techniques for the machine learning of the ESR hyperfine pattern. As there are 4 equivalence classes of ¹³C nuclei with each class containing 6 members, and 28 classes with 12 nuclei in each class, the net ESR generating function for the hyperfine structure arising from ¹³C-e coupling is given by Equation (69):

$$\mathrm{GF}(\mathrm{ESR}{:}^{13}\mathrm{C};\mathrm{AHK}(2))={{\displaystyle \prod }}_{i=1}^4{\left({\alpha }_i+{\beta }_i\right)}^6{{\displaystyle \prod }}_{j=1}^{28}{\left({\alpha }_j+{\beta }_j\right)}^{12}$$

(69)

In an analogous manner we obtain the combinatorial ESR for the RK(3,3) as:

$$\mathrm{GF}(\mathrm{ESR}{:}^{13}\mathrm{C};\mathrm{RK}(3,3))={{\displaystyle \prod }}_{i=1}^4{\left({\alpha }_i+{\beta }_i\right)}^2{{\displaystyle \prod }}_{j=1}^{88}{\left({\alpha }_j+{\beta }_j\right)}^4$$

(70)

When the above GFs are binomially expanded for the ¹³C nuclei-electron couplings we arrive at too many lines for graphical representation of the hyperfine pattern. Furthermore the ¹³C−e- hyperfine coupling constant depends on the Euclidian distance between the unpaired electron density and the geometrical position of the nuclei. Hence one can reduce the combinatorial complexity by considering only equivalence class of nuclei that are nearest to the unpaired electron of the radical. Thus if the radical is generated at the inner periphery of the kekulene ring via deprotonating one of the six protons, we obtain a more amenable ESR hyperfine structure. In this event we generate the equivalence class partition for the AHK(2) as 6²12³ whereas for RK(3,3) it is 2²4¹¹ yielding the ESR GFs shown below as Equations (71) and (72) for the two tessellations of kekulenes, respectively (Figure 13):

$$\mathrm{GF}(\mathrm{ESR}{:}^{13}\mathrm{C};\mathrm{AHK}(2))={{\displaystyle \prod }}_{i=1}^2{\left({\alpha }_i+{\beta }_i\right)}^6{{\displaystyle \prod }}_{j=1}^3{\left({\alpha }_j+{\beta }_j\right)}^{12}$$

(71)

$$\mathrm{GF}(\mathrm{ESR}{:}^{13}\mathrm{C};\mathrm{RK}(3,3))={{\displaystyle \prod }}_{i=1}^2{\left({\alpha }_i+{\beta }_i\right)}^2{{\displaystyle \prod }}_{j=1}^{11}{\left({\alpha }_j+{\beta }_j\right)}^4$$

(72)

These combinatorial GFs for the two tessellations generate 7²13³ lines for the AHK(2) structure and 3²5¹¹ lines for the RK(3,3) structure, respectively. The computed ESR hyperfine patterns for the two kekulene tessellations are displayed in Figure 14a,b, respectively. One can also obtain the proton ESR hyperfine structures for the two tessellations as well as the multiple quantum NMR patterns in a manner analogous to the techniques demonstrated in the previous sections.

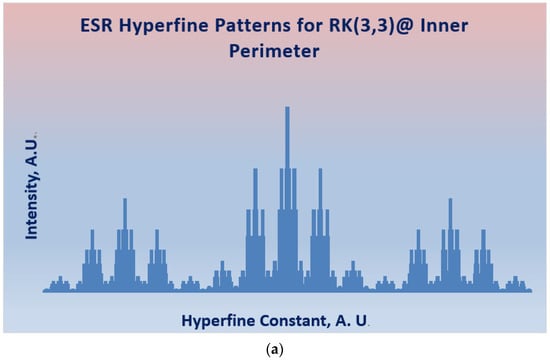
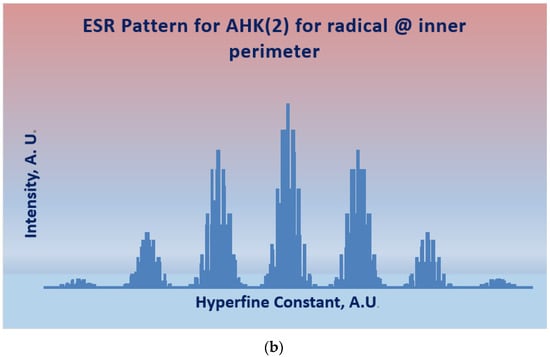
Figure 14. Computed ESR hyperfine patterns of (Top; (a)) AHK(2) (Bottom; (b)) RK(3,3). Reprinted with permission from [144] copyright (2021) American Chemical Society.

The other set of structures for which Euler totient based combinatorial techniques would apply are nanobands or a necklace-choker composed of hexagons as displayed in Figure 15. The structures can be tailored to various pore sizes so that they serve as sequestering agents for the complexation of metal anions or halide ions. These materials also offer optimal sites for functionalization or substitutions of carbon sites with heteroatoms such as nitrogen atoms in order to synthesize nanobands that could complex with metal ions analogous to porphyrins.

Figure 15. A 3D geometrical structure of a nanoband or a necklace-choker made of 16 hexagons.

In a recent study Sabirov et al. [161] have considered various arrangements arising from (C₆₀)_n polymers such as the zigzag and linear configurations of C₆₀ polymers. These authors have studied the topological indices such as the Wiener indices, roundness and graph entropies of these structures such as the ones in Figure 16. Combinatorial tools developed herein can be applied for the enumeration of heteronuclear fullerene polymers arising from different configurations shown in Figure 16. Analogous to the spectroscopic studies that were outlined for the tessellations of kekulenes, future research should be devoted for the machine generation of the spectra of fullerene polymers (Figure 16). By extending the linkers between the two fullerenes with small alkane chains, one can obtain longer polymers. The longer linkers would then provide sufficient flexibility to generate necklaces of fullerenes where each bead would be a C₆₀ cage. For such structures, the techniques outlined here on the basis of Euler’s totient functions can become extremely useful and applicable.

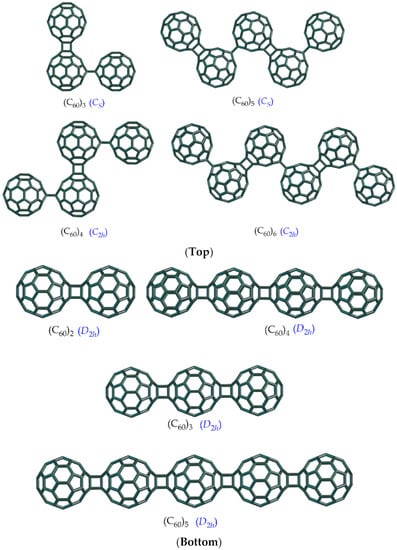
Figure 16. (Top) Zigzag versus (Bottom) Linear Arrangements of (C₆₀)_n, Reproduced under creative commons License from Ref. [161].

6. Conclusions, Helical Structures, Fullerene Polymers and Other Structural Derivatives & Future Perspectives

This review considered combinatorics and topology of circum-polycycloarenes, heteronanotubes and tessellations of cyclopolyarenes such as kekulenes in different configurations, for example, armchair, zigzag and square, etc. We showed the power of Sheehan’s modification of Pólya’s theorem when generalized to all the characters of the point symmetry groups of nanostructures. Topologically-derived edge partition techniques revealed the existence of isentropic kekulene tessellations, that is, the existence of two kekulene tessellations with the same graph entropies. These structures were also shown to be quite close in their energy separations. Consequently, their spectral differences, ESR hyperfine patterns and NMR signal patterns were combinatorially constructed using the DDSV techniques followed by the generating function methods. While these combinatorial techniques were shown to be very powerful in their applications to novel nanomaterials that were considered here, there are several emerging structures comprising of fullerenes.

The emerging field of reticular metal organic frameworks, mesoporous cages, zeolites, sodalite materials, other nanomaterials such nanobelts 2D-nanosheets and other nanomaterials [25,32,35,60,61,144,145,146,147,148,149,150] could all be benefited by such robust graph-theoretical and combinatorial tools for the rapid computations of their properties and creation of combinatorial libraries of these structures. Consequently, the advent of these novel materials has rekindled our research interest in such interesting applications of combinatorics, group theory, graph theory and topological indices. Such techniques would offer robust and rapid computational tools for the computations of their thermodynamic, optoelectric, spectroscopic, phase transformation and chiral properties. We envisage several nanowires and 2D-sheets of such molecules [25,32,35,47,48,49,59,60,61,144,145,146,147,148,149,150] to be synthesized in the future, which would also provide a platform for the combinatorics of big data pertinent to these structures. Finally we believe that combinatorial and graph-theoretical techniques would be of considerable value for the enumeration and computation of electronic properties of materials such as gallium arsenide, GaN nanowires, topological characterization of 2D materials, zeolites, their helical structures made from kekulenes, and the emerging novel expanded kekulenes, and so forth [9,17,23,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59]. There are a number of combinatorial techniques and applications of variants of Pólya’s theorem and related applications to graphs and chemical enumerations, and readers are referred to references [162,163,164,165,166,167,168,169,170,171].