1. Introduction
To cope with the increasingly fierce market competition, manufacturers need to deal with a series of issues such as product diversity, product customization, shorter product life cycles, and rapidly changing policies and environments [
1]. The idea of modularity in product architecture is widely recommended as a corporate strategic decision to deal with these issues all at once [
2]. As a scientific methodology supporting product development, modularity is to plan a series of modules (including basic modules and optional modules) for product families or product platform modularity based on the products’ structural characteristics [
3]. Compared with the conventional product architecture, the advantages of modular architecture are reflected in all stages of the product life cycle [
4,
5]. Reasonable product module planning is not only conducive to product development, manufacturing, and upgrading but also can effectively reduce the impact on the environment during product service and after scrapping [
6,
7]. Modularity is recognized as a product development strategy by academia and industry, and the openness of modular architecture makes it play an important role in sustainable product development [
8,
9]. Modular design concepts and methods have been used in many electromechanical product design processes, such as coffee makers [
10], industrial steam turbines [
11], wind turbines [
12], and large tonnage crawler cranes [
13,
14]. The modular design methods, as the crucial supporting technique for the design of mechanical and electronic products, are still regarded as a research hot spot in product design for life cycle and sustainability [
15].
To meet the different requirements of product module design, researchers around the world have put forward a lot of practical methods for product modularization. These methods can be grouped into two main types: the heuristic methods and the clustering methods [
16]. The heuristic methods mainly employ all kinds of swarm intelligence optimization algorithms to gain the optimal or approximate solution of the specific fitness function built upon some module driving forces. These algorithms include the simulated annealing [
17], genetic algorithm (GA) [
18], grouping genetic algorithm (GGA) [
19], and strength Pareto evolutionary algorithm 2 (SPEA2) [
20]. For example, to reduce the production cost and lead time of filament winding process equipment to cope with the change in customer demands, Xu et al. established the relationship matrix between the product components in consideration of the structure, function, and stability factors, and then used the GGA to solve the model with the objective function of maximizing the interaction and stability in the module [
21]. The clustering method is based on the membership degree between components and clustering centers or the closeness of the relationship between components to obtain the modular scheme of products, such as fuzzy c-means [
22], k-means [
23], and hierarchical clustering [
24]. For instance, Li et al. proposed an integrated product modularization scheme based on flow analysis, design structure matrix (DSM), and fuzzy clustering to compose a flexible platform [
25]. In addition, some methods in other fields, such as the atomic theory [
26] and community discovery algorithm [
27], are also used for product module partitioning by some scholars.
In the initial stage of module partitioning, the most important preparatory work is to establish a mathematical model of product structure to express the complicated relationship between product components [
28]. Graph-based and matrix-based representational tools provide a graphic method to represent the relationships between modules and the interrelations among components. The function, structure, maintenance, and material information are usually considered as the main factors for assessing the correlation strength between components. To generate a mathematical model of product structure, it is first necessary to understand the interactions between the components. To capture these interactions, the majority of published studies have used surveys, manual coding of documents, interviews, and meetings with engineers [
29]. The manual modeling process is inefficient and boring, and due to the negligence of the engineer, it is very easy to cause missing and wrong filling of the model [
30]. Therefore, the automatic identification of product component association and the automatic construction of the product structure model can not only effectively reduce the impact of human factors on the modular results, but also greatly improve the efficiency of the module partition method.
With computer-aided design (CAD) systems employed widely in the industrial field, enterprises have accumulated a lot of 3D models of products and components in the product design, manufacturing, and assembly stages, which contain a lot of product structure, material, and assembly information [
31]. Many works have been carried out to extract information directly from CAD assembly models in past decades. The emphasis has been put on identifying assembly liaisons, translating CAD model information, and determining assembly sequences. However, the application of 3D assembly information automatic extraction technology to product modular design is relatively less concerned. Li et al. realized the automatic extraction of the product assembly information of the product 3D model and established the DSM of the product structure based on the assembly information [
24]. Nevertheless, the purpose of the cited work is to realize the reuse of the module structure of a 3D assembly model, so only the structural information is considered when modeling. In addition, Li et al. also established a product structure model based on the extracted product information and used hierarchical clustering and an elbow assessment method to obtain the optimal product modular granularity [
32]. This method can only obtain the structural relationship between product components. Therefore, this method cannot meet actual needs well when companies need to consider sustainable design factors such as the environment or recycling.
The product structure model is the basis of modular design. Modeling efficiency and model accuracy have a far-reaching impact on the popularization and application of modular design methods. The existing product structure modeling methods have the following two shortcomings: first, the establishment process of product multi-attribute DSM is mostly manual, which is inefficient and error-prone. Second, the existing method of automatically establishing product DSM only considers the structural relationship, and the factors considered are too single and do not meet the actual needs of the enterprise. Therefore, an integrated method for modular design based on auto-generated multi-attribute DSM and improved GA is proposed in this paper. The main contributions and novelty of this work are as follows: (1) an automatic method for establishing product multi-attribute DSM is proposed. Based on the product’s 3D assembly model and the secondary development tools provided by commercial CAD software, a product information extraction algorithm was developed, and then the DSM model was established based on the automatically extracted product information. (2) An improved GA is proposed to realize product module division. The traditional GA mutation operation is improved to break through the limitation of the number of initial modules on the algorithm to obtain the global optimal solution.
The remainder of the paper is organized as follows.
Section 2 introduces the research framework and related operators, such as information extraction of a product’s 3D assembly model, digitization of product information, formation of the comprehensive correlation DSM, and an improved GA-based module division method. Two illustrative case studies are presented in
Section 3, and the module division of the gear oil pump and the bicycle is executed to prove the effectiveness of the method proposed in this paper. Discussions and conclusions are given in
Section 4 and
Section 5, respectively.
2. The Proposed Module Partition Methodology
This section introduces the proposed module partition methodology, as shown in
Figure 1, which contains the automatic extraction of 3D model information, the pre-processing of product information, the formation of a comprehensive component correlation DSM of the product, and the module partition method based on improved GA.
- (1)
Automatic extraction of 3D model information mainly refers to step 1 in
Figure 1. Firstly, the type of product information required is determined according to the modeling requirements, then the appropriate interface function is selected to extract the corresponding product information.
- (2)
Step 2 in
Figure 1 refers to the pre-processing of product information. The product information extracted from the product 3D assembly model is mostly text information and the information contains a large number of software design marks. Therefore, the text information is converted into digital information through the pre-processing of the information to improve the efficiency of the subsequent product DSM establishment.
- (3)
The main purpose of step 3 in
Figure 1 is to generate the comprehensive component correlation DSM of the product. According to the different types of extracted product information, their correlation strength evaluation standards are formulated, respectively. Then, the comprehensive product component correlation DSM is obtained by the weighted summation method.
- (4)
The main function of step 4 in
Figure 1 is to realize the module division of the product. The modular index
Q is selected as the fitness function to transform the module partition problem into an optimization problem, and then the optimal product module partition scheme is obtained based on the improved GA.
2.1. Information Extraction Algorithm of Product 3D Assembly Model
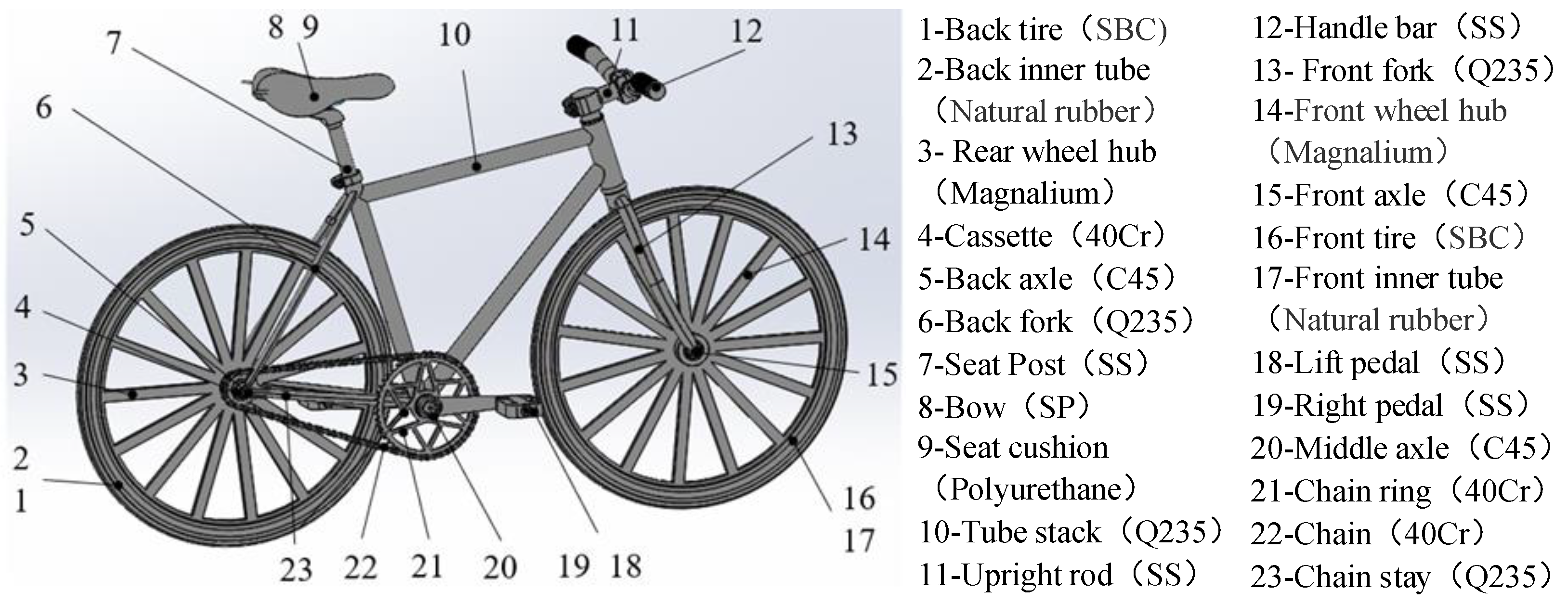
As for a product 3D assembly model, it contains a lot of product-related information, such as structure, name, material, and matching relationship [
33]. In the design of the extraction algorithm, we only need to extract the information required to establish the product DSM model. After analyzing the commonly used modular driving factors and the product information content contained in the 3D assembly model, the connection strength and material similarity between components are selected as the main factors of module division. Dividing the components with high connection strength into one module is conducive to the assembly and disassembly of the module. The materials of components are closely related to their recycling methods, so the components with the same or similar materials are grouped together to facilitate the disposal of product scrap.
This work divides the product information to be extracted into three categories: the basic information of product components, the assembly information of product components, and the material information of product components. The basic information of product components mainly refers to the number and name of product components, which are used to determine the size, row, and column elements of the correlation matrix of product components. The assembly information of product components mainly includes the constraint relationship between components and the degree of freedom of components. The type and quantity of the constraint relationship between components can be used to analyze whether two components are in contact, and the strength of the connection relationship can be determined by the degree of freedom of components. As the name suggests, the material information of a product component refers to the name of the material used to produce the component. The material information of the product component can be used to obtain the disposal method of the component when the product is at the end of the lifecycle.
Most of the current CAD software, such as SolidWorks, Pro/Engineer, and UG, offer their own standard automated programmable interfaces (APIs) for customizing software applications. Based on the standardized APIs, the file of the assembly model is instantiated by selecting the corresponding interface and the required product information can be obtained directly by accessing the members of the instantiated object. The assembly information extraction algorithm developed in this paper is oriented to the assembly model file of SolidWorks. SolidWorks software supports secondary development using a variety of programming languages, and this paper features VB language to develop an information extraction algorithm on the Microsoft Visual Studio platform. The function brief of some main interface members used in the extraction algorithm is shown in
Table 1. For example, to obtain the material information of the component, we can directly read it by calling the member “GetMaterialPropertyName2” under the “IPartDoc” interface.
A common assembly model of SolidWorks is a typical tree-like hierarchy, which includes a number of components in multiple levels as shown in
Figure 2 (take the hydraulic cylinder in
Figure 1 as an example). As shown in the bottom half of this figure, a list of features can offer a concise and clear description of how the assembly was constructed. The name information of the product component can be directly extracted from the feature tree and the sub-feature tree, and the assembly information of the component is extracted from the “Mates” feature at the bottom of the feature tree and the sub-feature tree. The acquisition of component materials and degrees of freedom data is to lock the pointer to the corresponding target and directly extract it. The pseudo code of the information extraction algorithm is shown in
Figure 3.
The extraction algorithm proposed in this paper can realize the automatic acquisition of product assembly information, but the algorithm has certain limitations in its application and promotion. From the perspective of the application, the object of this algorithm is a standard SolidWorks assembly document, and the constraint relationship between components must strictly follow reality. Otherwise, there will be errors in the product DSM data established based on the extracted information. As for the promotion of algorithms, the interfaces and functions in the secondary development tools provided by mature commercial CAD are different. When the object of extracting information is other types of 3D assembly models (Pro/E, UG, etc.), it is necessary to update the corresponding interface and function information under the framework of the information extraction algorithm.
2.2. Pre-Processing of Extracted Product Information
The original product information extracted from the 3D assembly is mostly in text format and contains a lot of system setting information of CAD software, which is not suitable for directly constructing the correlation matrix of product components. Therefore, pre-processing of extracted product information facilitates the improvement of the construction efficiency of the component correlation matrix.
The main operations of the pre-processing of the basic product information include deleting the system setting information of the CAD software and adding the sequence information of the product components. By deleting the system setting information of the CAD software, the extracted product information can be kept consistent with reality to enhance the legibility of the extracted information. The sequence information of the product components is added to facilitate the subsequent processing of the matching information and the material information of the product components.
The pre-processing of assembly information of product components mainly includes two steps: assembly information simplification and text information digitization. In this paper, the contact between two components is judged by whether there is an assembly relationship between components, and the assembly information extraction algorithm extracts all the assembly relationships between components, which leads to information redundancy and is not conducive to the subsequent DSM construction. Through information simplification, only the information of whether there is an assembly relationship between components is retained and the quantity and type of assembly information is removed. In the process of simplification of assembly information, the digitization of text information is realized by replacing text information with digital information. That is, the numbers 0 and 1 are used to indicate whether there is contact between two components, and a set of N-dimensional vectors are used to indicate the contact relationship between a certain component and the remaining components. As for the degree of freedom information of product components, the fixed and floating states of components are represented by values 1 and 0, respectively.
The pre-processing of material information of product components mainly includes two aspects: digitization of material information and increasing material compatibility information. Commercial CAD software has carried out a very detailed division of material types. For example, the types of ordinary carbon steel include Q225, Q235, and Q245. Therefore, when digitizing material information, it is only necessary to use a serial number instead of corresponding material text information. In the process of digitization, there is a lack of material compatibility information, that is, although the two materials are different, they belong to the same kind of materials, such as Q235 and Q245 of carbon steel. Therefore, the material compatibility information is added during digitization to facilitate the subsequent component material similarity evaluation.
The component information of the product after pre-processing is composed of the component’s name and an N + 6-dimensional vector, where N is the number of product components. The first two bits of the vector represent the sequence information of the component and the 3 to N + 2 bits of the vector represent the matching information of the component; the degree of freedom information of the component is in the N + 3 bit of the vector and the last three bits of the vector are composed of material information and recycling information.
2.3. Formation of the Comprehensive Correlation DSM
By analyzing the extracted product information, the comprehensive correlation DSM of products can be established. The process of establishing product comprehensive correlation DSM is mainly divided into three steps: structural correlation analysis between assembled components, material correlation analysis between assembled components, and comprehensive evaluation of correlation strength between assembled components.
2.3.1. Structure Correlation Analysis between Components
The structural correlation strength analysis between components mainly includes two steps: the construction of the adjacency matrix of components and the evaluation of the structural correlation strength between components.
The construction of the adjacency matrix of product components. During manual modeling, engineers or designers can judge whether two product components are in contact according to the product entity, design experience, and engineering data to establish an adjacency matrix of product components. This process is easy to understand for people, but difficult for computers. Therefore, this work uses the extracted product assembly information to determine the contact relationship between the components, that is, when there is an assembly constraint relationship between the two components, the two components are considered to be in contact, and vice versa.
The structural correlation strength between components is evaluated. To gain the structure correlation strengths between product components, a dependency rating criterion based on the degree of freedom (DoF) of components is proposed in this paper. A lot of dependency rating standards have been developed to assess correlation strengths in the literature. Helmer et al. investigated these schemes from the perspective of the consistency and applicability of the evaluation results and explained their limitations [
34]. These rating schemes usually judge the difficulty of disassembly based on the type of connection relationship between components, to obtain the strength of the association between them. However, the connection relationship type of the component can neither be directly extracted from the 3D model of the product nor indirectly obtained through the extracted component assembly information. Turner et al. proposed a reduction algorithm to calculate the DoFs between assembled components by analyzing constraints between them [
35]. The main idea of this method is that as the DoFs increase, the intensity of dependence also increases. Based on the methods mentioned in the literature [
24,
35], this paper proposes a dependency rating criterion based on the counts of DoFs in which four rating scales from 0 to 1 are introduced to indicate different dependency strengths.
Table 2 shows the structure correlation strength evaluation between product assembled components, where
S(
a,
b) refers to structure correlation strength between component
a and component
b.
2.3.2. Material Correlation Analysis between Components
The sustainability factor has been paid more and more attention by researchers in modular design. In the process of product modularization, full consideration of the relevance of component material and grouping components with the same or similar materials into the same module can greatly reduce the environmental impact of the product scrapping process.
Table 3 shows the material correlation strength evaluation between assembled components, where
M(
a,
b) represents material correlation strength between component
a and component
b.
2.3.3. Comprehensive Assessment of Correlation Strength between Components
Based on the above-mentioned structural and material correlation strength evaluation criteria, the structural correlation strength and material correlation strength between components can be easily obtained. As for the calculation of the comprehensive correlation strength between product components, the commonly used weighted summation method is used. The weight
wi (
i = 1, 2) corresponds to the structural correlation strength and the material correlation strength. The value range of
i is greater than zero and less than one, and the sum of the two weights is equal to one. According to the design specifications and usage scenarios of mechanical products, the weight values of structure correlation strength and material correlation strength are various and determined by the product engineer in the relevant engineering field. Accordingly, the comprehensive correlation strength
C(
a,
b) between component
i and
j can be expressed as follows:
where
C(
a,
b),
S(
a,
b), and
M(
a,
b) represent the comprehensive correlation strength, structure correlation strength, and material correlation strength between components
a and
b, respectively.
ω1 and
ω2, respectively, represent the weight of
S(
a,
b) and
M(
a,
b), which are assigned in light of expert evaluation. According to the calculation result of the comprehensive correlation strength, the correlation matrix
C between product components is a square matrix of order
k, where
k is the number of product components, which is given by
2.4. Improved GA-Based Module Division Method
The purpose of modular design is to improve the degree of cohesion of each module while reducing the degree of coupling between modules. Therefore, by constructing a reasonable objective function, the problem of module division can be transformed into an optimization problem. As a classic intelligent evolutionary algorithm, GA is often used to solve combinatorial programming problems. However, as the number of modules and the size of the modules need to be set in advance, the traditional GA is susceptible to the influence of the initial settings and it is difficult to obtain the optimal solution. In this paper, an improved GA is proposed to overcome the disadvantages of the classic GA in cluster solving of modularization. The framework of the improved GA-based module division method is shown in
Figure 4. Compared with the traditional GA, the improved GA mainly improves the mutation operation to break through the constraint of the initial number of modules on its global optimization. The improved mutation operation process is shown in the dotted box in
Figure 4. The mutation operation of the traditional GA is only a transfer mutation, that is, according to the random number, the components corresponding to the mutation point are divided from the corresponding module before mutation to the corresponding module after mutation. As the value of the random number is constrained by the number of initial modules, product components can only be transferred in existing modules. In order to break through the limitation of the initial modular number on the global optimization of the algorithm, the separation mutation is added on the basis of the transfer mutation, that is, the mutation operation is allowed to generate new modules. By generating new modules through mutation operation, the constraint of the number of initial modules is weakened, and the improved GA has better global optimization ability.
2.4.1. Encoding and Initial Population Generation
In the improved GA, the position indices of the chromosome genes indicate the corresponding product component, and the value in the gene represents the module to which the component belongs. Taking the hydraulic cylinder in
Figure 1 as an example, the coding method of the algorithm is further described. As shown in
Figure 5a, the total number of components of the hydraulic cylinder determines the length of the chromosome is 9. The position indices of chromosome genes 1 to 9, respectively, indicate the components of the corresponding hydraulic cylinder: lifting lug, piston rod, buffering ring, etc. The value 1–3 of the chromosome gene refers to the division of the hydraulic cylinder into 3 modules and which components each module contains.
The generation of the initial population mainly consists of three steps. The first step is to set the parameters, including the number of populations, the length of chromosomes, and the number of initial modules. The second step is to generate a fixed-length chromosome and randomly assign a random number within the range of the total number of modules to each gene of the chromosome. The last step is to repeat step 2 until the initial population is generated.
2.4.2. Crossover
The function of the crossover operation is to make the improved GA have a stronger spatial search ability and the offspring can inherit the high-quality genes of the parent. Crossover is conducted by the following three steps: (1) according to the length of the chromosome, a one-dimensional array of 0 and 1 is randomly generated. (2) When the value of the array position corresponding to the chromosome gene is 1, the values of the two parent chromosome genes are exchanged. When it is 0, no operation is performed. (3) From the first gene of the parent chromosome, perform step (2) until the last gene. An example of the crossover is described in
Figure 5b based on two randomly selected parent chromosomes.
2.4.3. Mutation
In this improved GA, the mutation is a very important operation to help the algorithm break through the limit of the initial number of modules to search for the global optimal solution. In this work, the mutation is performed by transfer mutation and separation mutation. Transfer mutation refers to the movement of a component from the original module to other modules, while separation mutation refers to the separation of a component from the original module to form a new module. The specific process of mutation operation is shown in
Figure 5c. Firstly, according to the probability of mutation operation, a chromosome to be mutated is randomly selected as the parent. Then, a one-dimensional array composed of 0 and 1 is randomly generated according to the chromosome length, and the genes corresponding to the array of 1 are mutated. When the variation value of the gene is less than or equal to the number of initial modules, it is a transfer mutation, otherwise, it is a separation mutation.
2.4.4. Modular Object Adaptive Function
The role of the modular object adaptive function is to calculate the fitness number of each chromosome when the genetic algorithm is iterating and to give more opportunities for excellent chromosomes to be selected. Therefore, the criterion for selecting the modular object adaptive function should be to analyze whether it can effectively evaluate the pros and cons of the module division scheme. In related research work, scholars have proposed many indexes to evaluate product module division schemes, such as the partition coefficient (PC(
c)) [
36], the modularity index (MI) [
37], the minimum description length [
38], the integrative complexity (IC) [
39], and the modularity assessment index (
Q) [
15]. Among them, the modularity
Q, as an index introduced from the complex network theory, has been popular in the field of modular design in recent years. Therefore, this paper features the modularity index
Q as the objective function to calculate the fitness of each chromosome. To facilitate the calculation of the value of
Q, a module matrix
e is constructed as:
where
yii represents the fraction of intra-module interfaces while
yij represents the fraction of inter-module interfaces. For the module matrix
e, the row sum is written as:
The modularity index
Q is defined as:
where
eii represents the fraction of edges with both end vertices in the same module
i, and
ai represents fraction of edges with at least one end vertex inside module
i.
k refers to the number of modules in the modular scheme. The modularity index
Q has a numerical range of (−1~1). The larger the value, the more reasonable the result of the module division, and vice versa.