Optimization of the Motion Algorithm and Reduction of the External Dynamic Load of the Machinery Actuator in Translational and Rotational Modes
Abstract
:1. Problem Formulation
2. The Analysis of Research Results and Publications
3. Statement of Basic Materials
- -
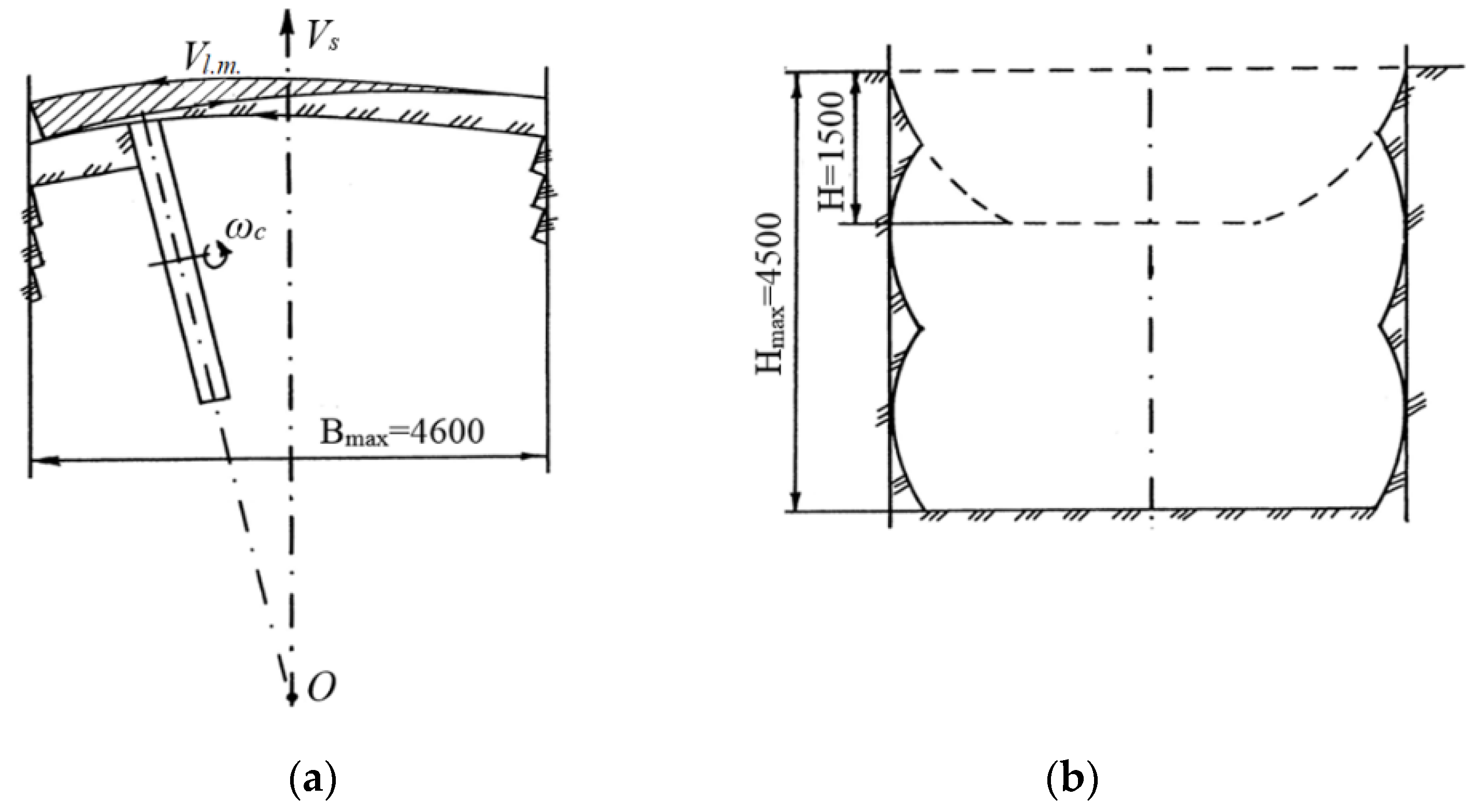
- the soil will be excavated with shavings of constant thickness provided that the motion trajectories of the soil-digging symmetrical actuator in the face for each half-cycle of oscillating motion are parallel to each other regardless of the speed values Vs and Vl.m.
- -
- the trajectory of the symmetrical-actuator motion in the face can be adjusted by additional rotation of the intermediate frame at the end of each half-cycle of reciprocating (oscillating) motion of the symmetrical actuator.
- -
- the duration and value of the symmetrical-actuator advance supply to the face at the end of each half-cycle are determined by the stability of the Vs/Vc ratio.
- -
- the patterns of the actuator motion in a wide face that satisfy the above-mentioned conditions can be determined.
- -
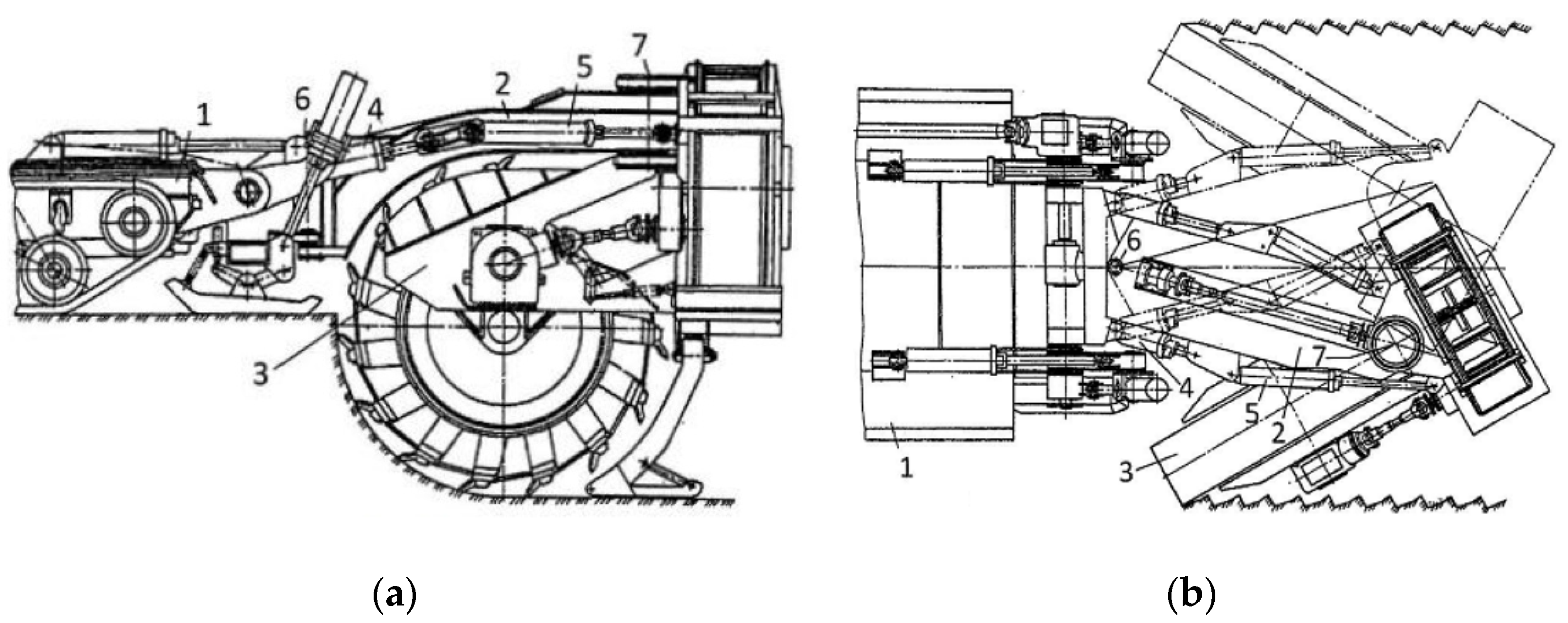
- direct motion of the squaring plate 4 of the base chassis stern.
- -
- rotational (oscillating) motion of the intermediate frame 3 relative to the plate 4, provided by the motion of the hydraulic cylinder rods 7 and 8.
- -
- rotational (oscillating) motion of the actuator frame 2 together with the rotor 1 relative to the frame 3, which is the result of the motion of the hydraulic cylinder rods 5 and 6.
4. Discussion
5. Conclusions
6. Patents
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| UCEM | Universal continuous earthmoving machine |
| PZM-1 | Earthmoving machines |
| PZM-2 | Earthmoving machines |
| B | Width of the excavation |
| Vs | Speed of supplying the actuator to the face |
| Vc | Soil cutting speed |
| Vl.m. | Speed of the lateral supply of the actuator to the face |
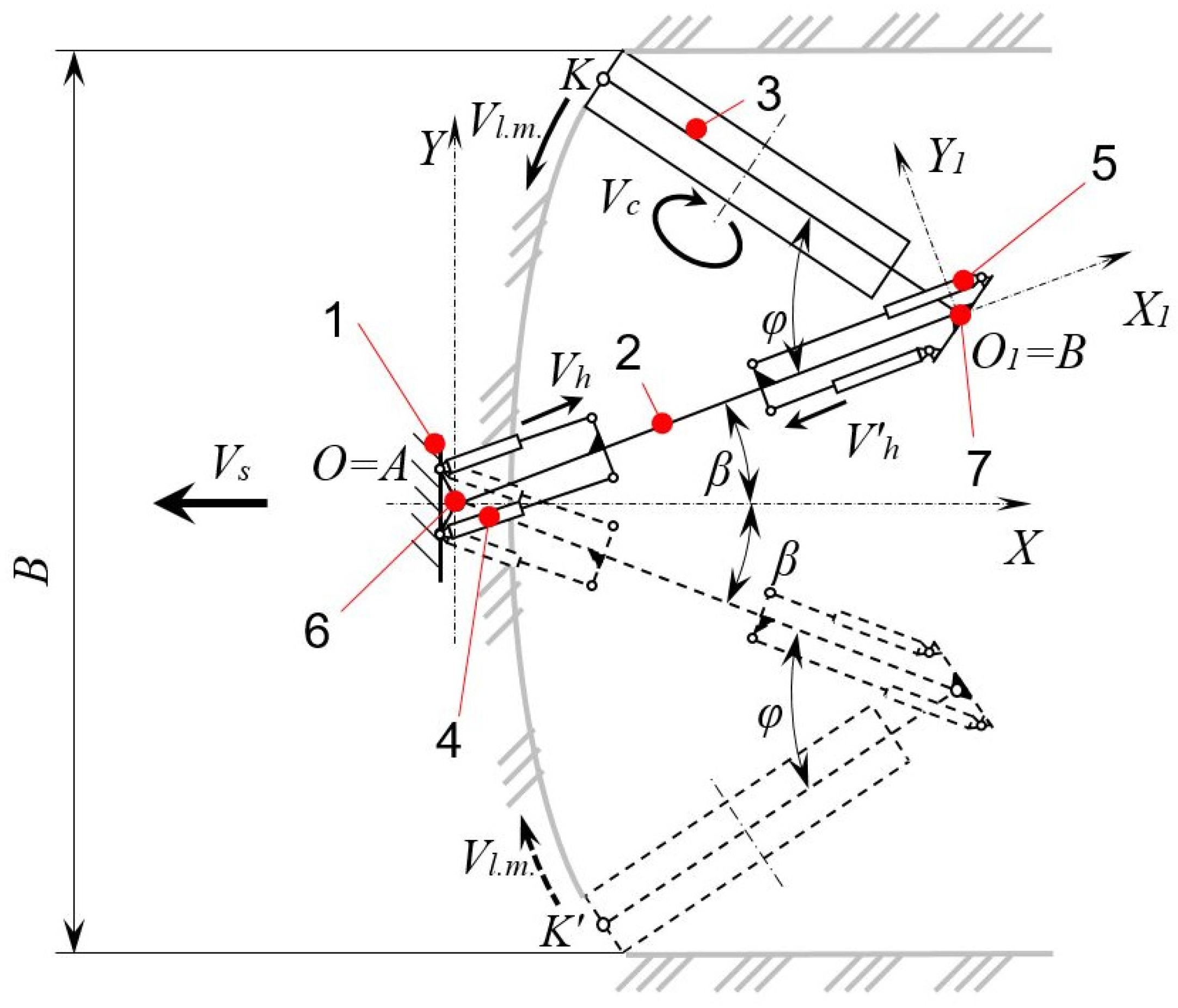
| Vh | Stem extension speed of the hydraulic cylinder (4) (Figure 3) of the intermediate-frame rotation |
| V’h | Stem extension speed of the hydraulic cylinders (5) (Figure 3) of the actuator-frame rotation |
| β | Angle of the intermediate-frame rotation |
| φ | Rotor-frame rotation angle |
| F(x1, x2 … xn; y1, y2 … yn) | Operator function |
| xi | Input parameters |
| yi | Output parameters |
| M1(a, b, R1, c, d, R2; x1, x2, y1, y2) | Operator function determines the coordinates of the intersection points of two circles |
| R1 | Radius from the center with coordinates (a, b) |
| R2 | Radius R2 from the center with coordinates (c, d) |
| M2(xM,yM,xU,yU,LMC;x1,x2, y1,y2) | Operator function determines the coordinates of the intersection points C1(x1, y1) and C2(x2, y2) of the straight line passing through the point M(xM, yM) perpendicular to the straight line passing through the points U(xU, yU) and M, and the circle centered in point M |
| LMC | Radius by Figure 5b |
| k1, k2, k3, k4, k5, k6,k7, k8, k9, k10, k11, k12,k13, k14, | Coefficients |
| M3(xA, yA, xB, yB, xQ, yQ, LTF; x1, x2, y1, y2) | Operator function determines the coordinates of the intersection points F1(x1, y1), F2(x2, y2) of the straight line passing through the point T(xT, yT), perpendicular to the straight line AB, and a circle drawn from the point T with radius LTF. |
| LTF | Radius drawn from point T |
| M4(xM, yM, xG, yG, LUM; x1, x2, y1, y2) | Operator function to determine the coordinates of the points U1(x1, y1) and U2(x2, y2) of the straight line intersection passing through the points M(xM, yM) and G(xG, yG), and the circle drawn by the radius LUM from the center M |
| LUM | Radius from the center M |
| L(x1, y1, x2, y2; L1,2) | Operator function is used to determine the distance between two points |
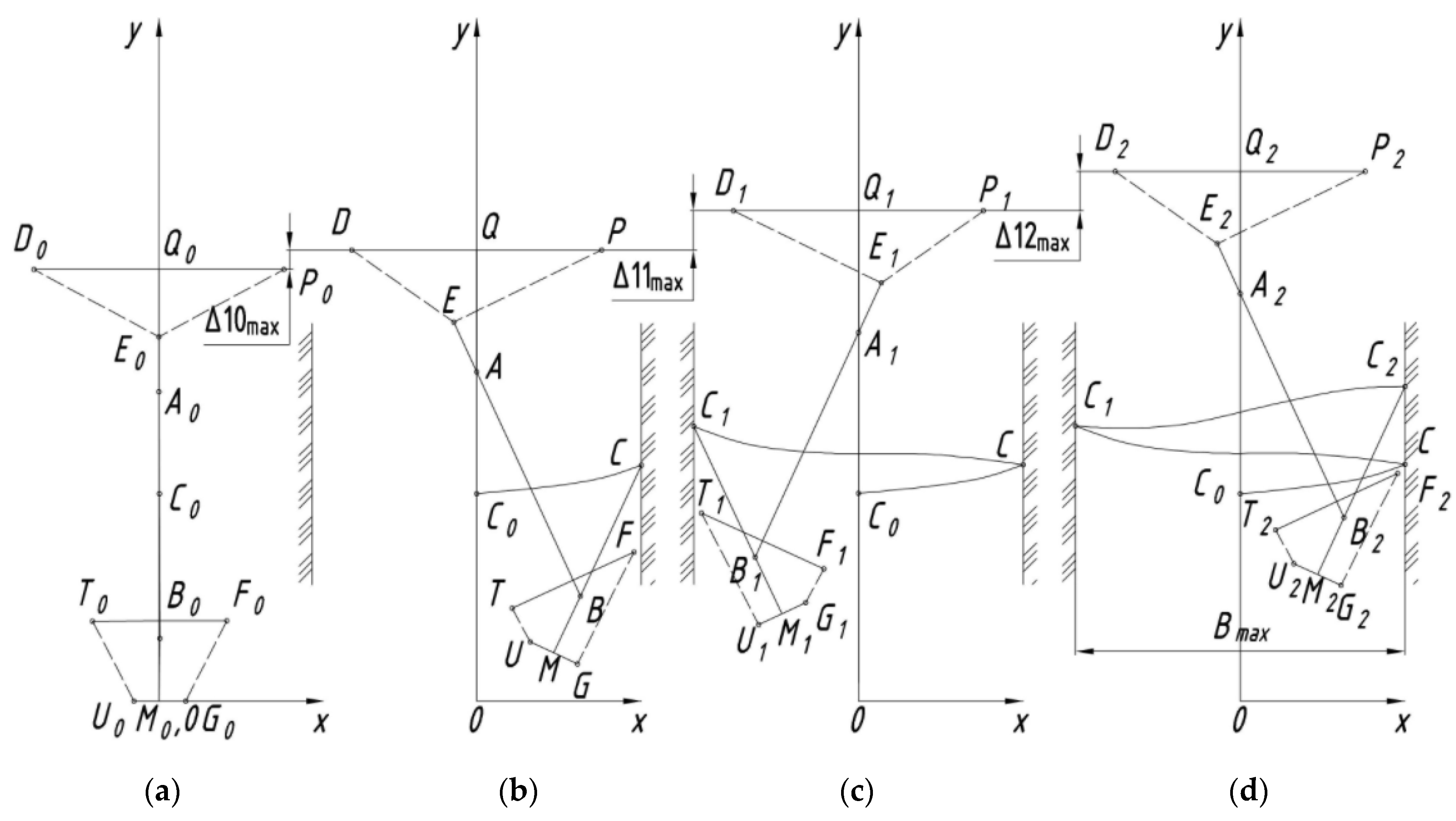
| LA0D0, LA0P0, LA0E0, LA0B0, LB0T0, LB0F0, LB0U0, LB0G0, LB0M0 | Lengths of rigid rods |
| LP0E0, and LF0G0 | Distances that characterize the positions of the hydraulic cylinders rods of the revolution mechanism |
| A0(xA0, yA0), B0(xB0, yB0) | Coordinates of the characteristic points of the rotor frame and the intermediate frame and elements of their structures |
| Δ20max | Maximum allowable rod motions of hydraulic cylinder 7 (Figure 4) |
| Δ30max | Maximum allowable rod motions of hydraulic cylinder 5 (Figure 4) |
| n | Number of positions |
| kΔ2, kΔ3 | Rods motion that corresponds to the transition of mechanism from one to another adjacent position |
| kΔ1 | Distance of the move of the chassis stern |
| Δ1i | Chassis stern motion 4 |
| Δ2i | Hydraulic cylinder rod motion 7 |
| Δ3i | Hydraulic cylinder rod motion 5 |
| LTUj | Distances that characterize the positions of the rods of the hydraulic cylinders 6 |
| LDEj | Distances that characterize the positions of the rods of the hydraulic cylinders 8 |
| bmax | Maximum width of the trench |
| Bmax | Distance between the extreme positions of the centers of the cutting edge of the actuator buckets |
| Vt | Base chassis speed |
| tmax | Half-cycle time at the maximum trench width |
| S78 | Stroke of the hydraulic cylinder rods of the intermediate frame |
| S56 | Stroke of the hydraulic cylinders of the actuator frame |
| Δ | Shaving thickness in the half-cycle |
References
- Gerlici, J.; Yefymenko, A.; Kravchenko, A.; Kravchenko, K. The stability analysis of two-wheeled vehicle model. MATEC Web Conf. 2018, 15714, 01007. [Google Scholar] [CrossRef]
- Gorbunov, M.; Gerlici, J.; Kara, S.; Nozhenko, O.; Chernyak, G.; Kravchenko, K.; Lack, T. New principle schemes of freight cars bogies. Manuf. Technol. 2018, 18, 233–238. [Google Scholar] [CrossRef]
- Gerlici, J.; Gorbunov, M.; Nozhenko, O.; Pistek, V.; Kara, S.; Lack, T.; Kravchenko, K. About creatiion of bogiie of the freiight car. Commun.-Sci. Lett. Univ. Zilina 2017, 19, 29–35. [Google Scholar]
- Musiiko, V.D.; Koval, A.B. Theory and Creation of Innovative Continuous Earthmoving Vehicle, 2nd ed.; Publishing house Lyudmyla: Kiev, Ukraine, 2018; 282p. [Google Scholar]
- Blatnický, M.; Dižo, J.; Timošcuk, M. Design of a three-finger robot manipulator. Manuf. Technol. 2016, 16, 485–489. [Google Scholar] [CrossRef]
- Sága, M.; Blatnický, M.; Vaško, M.; Dižo, J.; Kopas, P.; Gerlici, J. Experimental determination of the manson−coffin curves for an original unconventional vehicle frame. Materials 2020, 13, 4675. [Google Scholar] [CrossRef]
- Quan, Z.; Ge, L.; Wei, Z.; Li, Y.W.; Quan, L. A Survey of Powertrain Technologies for Energy-Efficient Heavy-Duty Machinery. Proc. IEEE 2021, 109, 279–308. [Google Scholar] [CrossRef]
- Brodny, J.; Alszer, S.; Krystek, J.; Tutak, M. Availability analysis of selected mining machinery. Arch. Control. Sci. 2017, 27, 197–209. [Google Scholar] [CrossRef] [Green Version]
- Bravo, R.; Ortiz, P.; Molina, J. Modelling initial motion of non-spherical sediment particles on inclined and seeped beds. Appl. Math. Model. 2021, 96, 678–696. [Google Scholar] [CrossRef]
- Kudra, S.E.; Bykov, A.V. Chain-and-girder working body of the universal earthmoving car. Constr. Road Cars 1979, 12, 6–7. [Google Scholar]
- Strel’nikov, A.N. Determination of Rational Operating Modes of Chain Trench Excavators with a Scraper Working Body. Ph.D. Thesis, The Siberian State Automobile and Highway University (SibADI), Omsk, Russia, 2003; 19p. [Google Scholar]
- Vetrov, Y.A.; Baladinskij, V.P. Special Excavation Machines; High School: Kiev, Ukraine, 1980; 192p. [Google Scholar]
- Sokolski, M. Mining Machines and Earth-Moving Equipment: Problems of Design, Research and Maintenance; Springer International Publishing: Cham, Switzerland, 2019; pp. 1–226. [Google Scholar]
- Bykov, A.B. The Study of the Structural and Kinematic Parameters of the Chain and Bar Actuator of a Universal Earth-Moving Vehicle. Ph.D. Thesis, Kharkov Automobile Road Institute, Kharkiv, Ukraine, 1986; 205p. [Google Scholar]
- Lu, J.; Bi, Q.; Li, Y.; Li, X. Estimation of fill factor for earth-moving machines based on 3D point clouds. Meas. J. Int. Meas. Confed. 2020, 165, 108114. [Google Scholar] [CrossRef]
- Yang, Y.; Long, P.; Song, X.; Pan, J.; Zhang, L. Optimization-Based Framework for Excavation Trajectory Generation. IEEE Robot. Autom. Lett. 2021, 6, 1479–1486. [Google Scholar] [CrossRef]
- Luengo, O.; Singh, S.; Cannon, H. Modeling and identification of soil-tool interaction in automated excavation. IEEE Int. Conf. Intell. Robot. Syst. 1998, 3, 1900–1906. [Google Scholar]
- Demyanyuk, V.A.; Musiiko, V.D.; Koval, A.B. Synthesis of the algorithm for operating the universal earthmoving vehicle with a linear trajectory of cutting the soil perpendicular to the axis of the tractor. Sci. Tech. Collect. 2016, 1, 153–164. [Google Scholar]
- Bandurov, V.; Syrovchenko, I. Features of work on a regimental earth-moving car. Tech. Armament 1974, 2, 31. [Google Scholar]
- Mednikov, A.; Bykov, A. Features of work on a regimental earth-moving car (EMC-2). Tech. Armament 1981, 4, 22–23. [Google Scholar]
- Dombrovsky, M.H. Multi-Bucket Excavators. Design, Theory and Calculation; Mechanical Engineering: Moscow, Russia, 1972; 432p. [Google Scholar]
- Fedorov, D.I. Actuators of Earthmoving Vehicle; Mechanical Engineering: Moscow, Russia, 1977; 288p. [Google Scholar]
- Harbuzov, Z.Y.; Ilgisonis, V.K.; Mutushev, H.A.; Naret, G.B.; Podborsky, L.E.; Uspensky, B.P.; Podborsky, L.E. Continuous Earthmoving Machinery; Mechanical Engineering: Moscow, Russia, 1965; 275p. [Google Scholar]
- Balovnev, V.I. Modeling the Processes of Environmental Interaction of Road Construction Vehicle Actuators; High School: Moscow, Russia, 1981; 335p. [Google Scholar]
- Kravets, S.; Suponyev, V.; Goponov, A.; Kovalevskyi, S.; Koval, A. Determination efficient operating modes and sizes of blades for multi-scrapertrench excavators. East.-Eur. J. Enterp. Technol. 2020, 4, 23–28. [Google Scholar]
- Kyrychenko, I.H. Modular Concept for Designing Technological Vehicle in the Construction Industry; KhNARU: Kharkov, Ukraine, 2002; 120p. [Google Scholar]
- Khmara, L.A. Trends in the improvement of specialized earthmoving equipment for tractors and excavators. Intensif. Oper. Processes Constr. Veh. Collect. Sci. Pap. 2002, 15, 4–27. [Google Scholar]
- Shatskiy, A.S. On the state of mechanization of pipeline construction. Pipeline Transp. 2007, 4, 10–14. [Google Scholar]
- Rudachenko, A.V.; Shmurygin, V.A.; Krets, V.H. Vehicle and Equipment for Gas and Oil Pipelines: Textbook; TPU Publishing House: Tomsk, Russia, 2013; 376p. [Google Scholar]
- Dombrovsky, N.H.; Tsipursky, I.L. Specific resistance to digging of foreign rotor trench excavators. Constr. Road Veh. 1969, 8, 7–9. [Google Scholar]
- Dombrovsky, N.H.; Tsipursky, I.L. Specific digging effort developed by chain trench excavators. Proc. Univ. 1970, 1, 15–17. [Google Scholar]
- Smetanka, L.; Gerlici, J.; Lack, T.; Pelagic, Z. Homogenization of fibers reinforced composite materials for simulation analysis. Manuf. Technol. 2015, 15, 914–920. [Google Scholar] [CrossRef]


| Methods | Operator Function or Mathematical Expression Used | Conditions for Selecting Actual Values |
|---|---|---|
| Δ1i | i·kΔ1 = i·Δ10max/n | |
| Δ2i | i·kΔ2 = i·Δ20max/n | |
| Δ3i | i·kΔ3 = i·Δ30max/n | |
| yAi | yA0 + Δ1i | |
| yPi | yP0 + Δ1i | |
| xEi, yEi | M1(xPi, yPi, LPEi, xAi, yAi, LA0E0; x1, y1, x2, y2) | yEi = max(y1,y2) |
| xBi, yBi | M4(xAi, yAi, xEi, yEi, LA0B0; x1, y1, x2, y2) | yBi = min(y1,y2) |
| xFi, yFi | M1(xAi, yAi, LA0F0, xBi, yBi, LB0F0; x1, y1, x2, y2) | xFi = max(x1,x2) |
| xGi, yGi | M1(xFi, yFi, LFGi, xBi, yBi, LB0G0; x1, y1, x2, y2) | yGi = min(y1,y2) |
| xMi, yMi | M1(xGi, yGi, LM0G0, xBi, yBi, LB0M0; x1, y1, x2, y2) | xMi = min(x1,x2) |
| xCi, yCi | M2(xMi, yMi, xGi, yGi, LM0C0; x1, y1, x2, y2) | yCi > yMi |
| Object to Be Determined | Operator Function or Mathematical Expression Used | Conditions for Selecting Actual Values |
|---|---|---|
| Δ11i | i·Δ11max/n | |
| Δ21i | i·Δ21max/n | |
| Δ31i | i·Δ31max/n | |
| yAi | yA0 + Δ1i + Δ11i | |
| LD1E1i | LDEj + Δ21i | |
| xE1i, yE1i | M1(xDi, yDi, LD1E1i, xA1i, yA1i, LA0E0; x1, y1, x2, y2) | yE1i = max(y1,y2) |
| xB1i, yB1i | M4(xA1i, yA1i, xE1i, yE1i, LA0B0; x1, y1, x2, y2) | yB1i = min(y1,y2) |
| xT1i, yT1i | M1(xA1i, yA1i, LA0F0, xB1i, yB1i, LB0F0; x1, y1, x2, y2) | xT1i < xB1i |
| LT1U1i | LTUj + Δ31i | |
| xU1i, yU1i | M1(xT1i, yT1i, LT1U1i, xB1i, yB1i, LB0U0; x1, y1, x2, y2) | yU1i < yB1i |
| xM1i, yM1i | M1(xU1i, yU1i, LM0U0, xB1i, yB1i, LB0M0; x1, y1, x2, y2) | xM1i > xU1i |
| xC1i, yC1i | M2(xM1i, yM1i, xU1i, yU1i, LM0C0; x1, y1, x2, y2) | yC1i > yM1i |
| xF1i, yF1i | M3(xA1i, yA1i, xB1i, yB1i, xT1i, yT1i, LF0T0; x1, y1, x2, y2) | xf1i > xT1i |
| xG1i, yG1i | M4(xM1i, yM1i, xU1i, yU1i, LG0M0; x1, y1, x2, y2) | xG1i > xM1i |
| Object to Be Determined | Operator function or Mathematical Expression Used | Conditions for Selecting Actual Values |
|---|---|---|
| Δ12i | i·Δ11max/n | |
| Δ22i | i·Δ21max/n | |
| Δ32i | i·Δ31max/n | |
| yAi | yD1k+ Δ12i | |
| yP2i | yD1k+ Δ12i | |
| yA2i | yA1k+ Δ12i | |
| LP2E2i | LP1E1j+ Δ22i | |
| xE2i, yE2i | M1(xP2i, yP2i, LP2E2i, xA2i, yA2i, LA0E0; x1, y1, x2, y2) | yE1i = max(y1,y2) |
| xB2i, yB2i | M4(xA2i, yA2i, xE2i, yE2i, LA0B0; x1, y1, x2, y2) | yB1i = min(y1,y2) |
| xF2i, yF2i | M1(xA2i, yA2i, LA0F0, xB2i, yB2i, LB0G0; x1, y1, x2, y2) | xF2i > xB2i |
| LF2G2i | LF1G1j+ Δ32i | |
| xG2i, yG2i | M1(xF2i, yF2i, LF2G2i, xB2i, yB2i, LB0G0; x1, y1, x2, y2) | yG2i < yB2i |
| xM2i, yM2i | M1(xG2i, yG2i, LM0G0, xB2i, yB2i, LB0G0; x1, y1, x2, y2) | xM2i < xG2i |
| xC2i, yC2i | M2(xM2i, yM2i, xG2i, yG2i, LM0C0; x1, y1, x2, y2) | yC2i < yM2i |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Musiiko, V.; Šťastniak, P.; Honchar, M.; Nikolaienko, V.; Lazaruk, J.; Korpach, A.; Suchánek, A. Optimization of the Motion Algorithm and Reduction of the External Dynamic Load of the Machinery Actuator in Translational and Rotational Modes. Symmetry 2022, 14, 51. https://doi.org/10.3390/sym14010051
Musiiko V, Šťastniak P, Honchar M, Nikolaienko V, Lazaruk J, Korpach A, Suchánek A. Optimization of the Motion Algorithm and Reduction of the External Dynamic Load of the Machinery Actuator in Translational and Rotational Modes. Symmetry. 2022; 14(1):51. https://doi.org/10.3390/sym14010051
Chicago/Turabian StyleMusiiko, Volodymyr, Pavol Šťastniak, Mykhailo Honchar, Volodymyr Nikolaienko, Jurii Lazaruk, Anatolii Korpach, and Andrej Suchánek. 2022. "Optimization of the Motion Algorithm and Reduction of the External Dynamic Load of the Machinery Actuator in Translational and Rotational Modes" Symmetry 14, no. 1: 51. https://doi.org/10.3390/sym14010051
APA StyleMusiiko, V., Šťastniak, P., Honchar, M., Nikolaienko, V., Lazaruk, J., Korpach, A., & Suchánek, A. (2022). Optimization of the Motion Algorithm and Reduction of the External Dynamic Load of the Machinery Actuator in Translational and Rotational Modes. Symmetry, 14(1), 51. https://doi.org/10.3390/sym14010051






