A Quadruple Integral Involving Product of the Struve Hv(βt) and Parabolic Cylinder Du(αx) Functions
Abstract
1. Significance Statement
2. Introduction
3. Definite Integral of the Contour Integral
4. The Hurwitz–Lerch Zeta Function and Infinite Sum of the Contour Integral
4.1. The Hurwitz–Lerch Zeta Function
4.2. Infinite Sum of the Contour Integral
5. Definite Integral in Terms of the Hurwitz–Lerch Zeta Function
6. The Invariance of Indices and Relative to the Hurwitz–Lerch Zeta Function
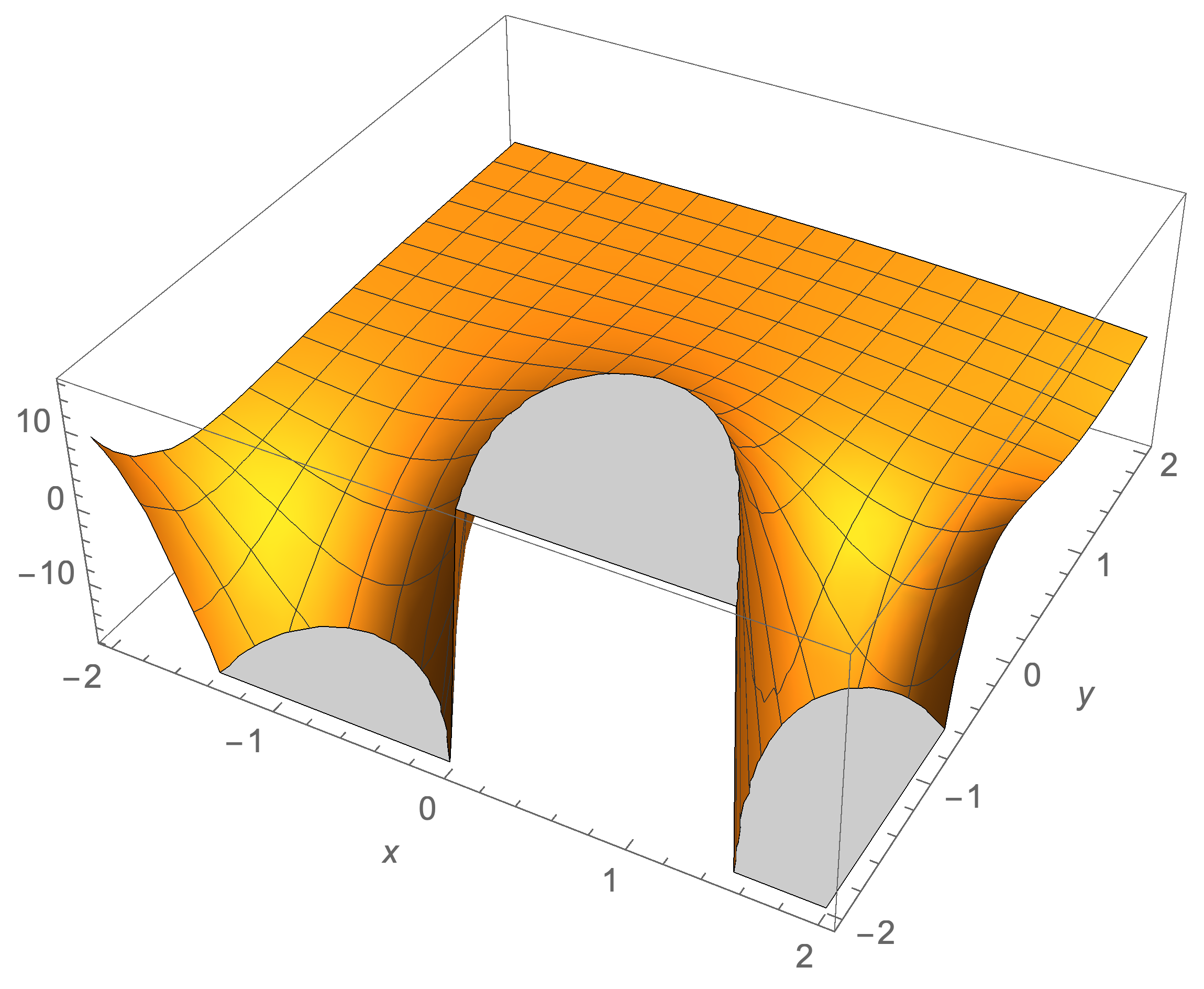
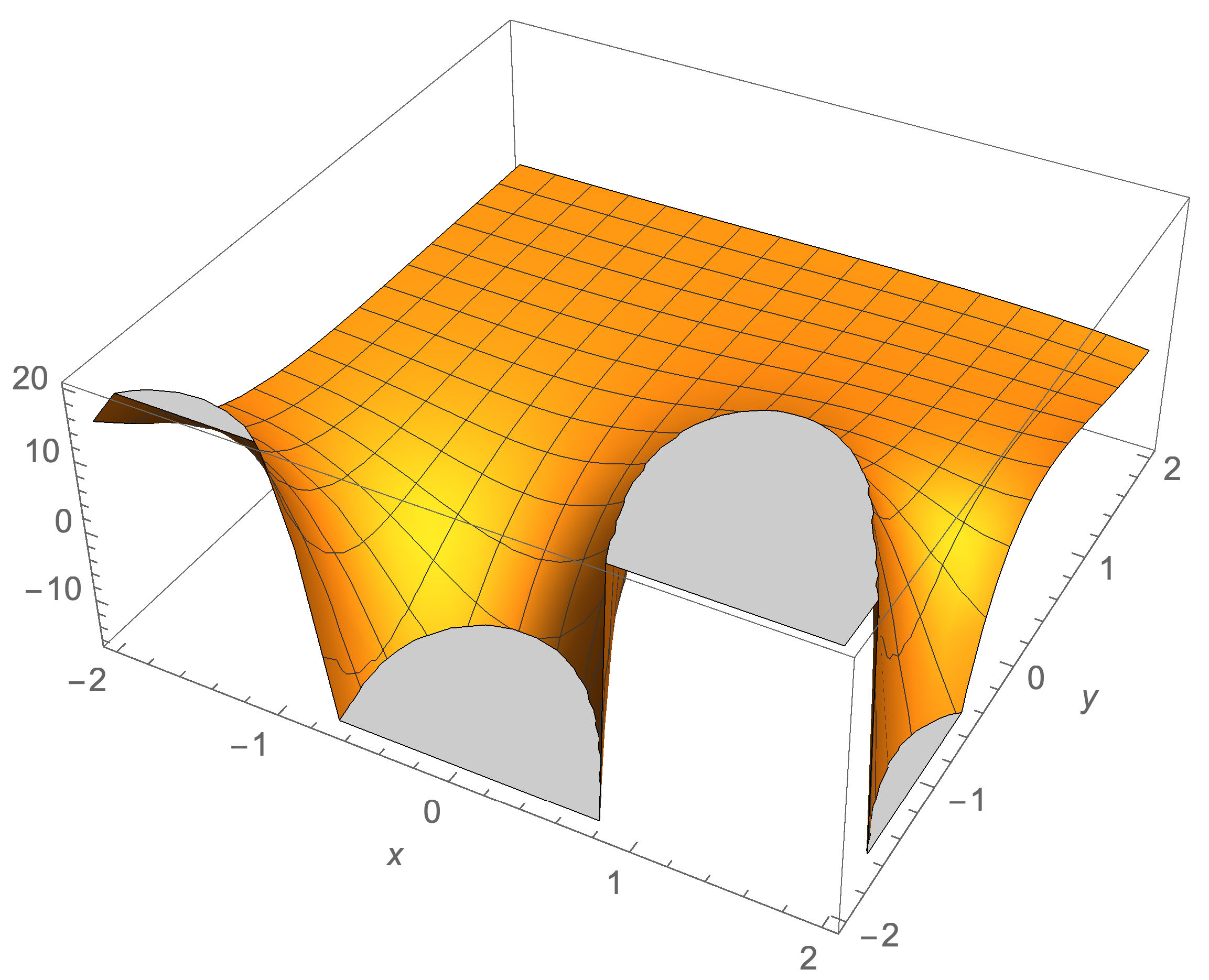
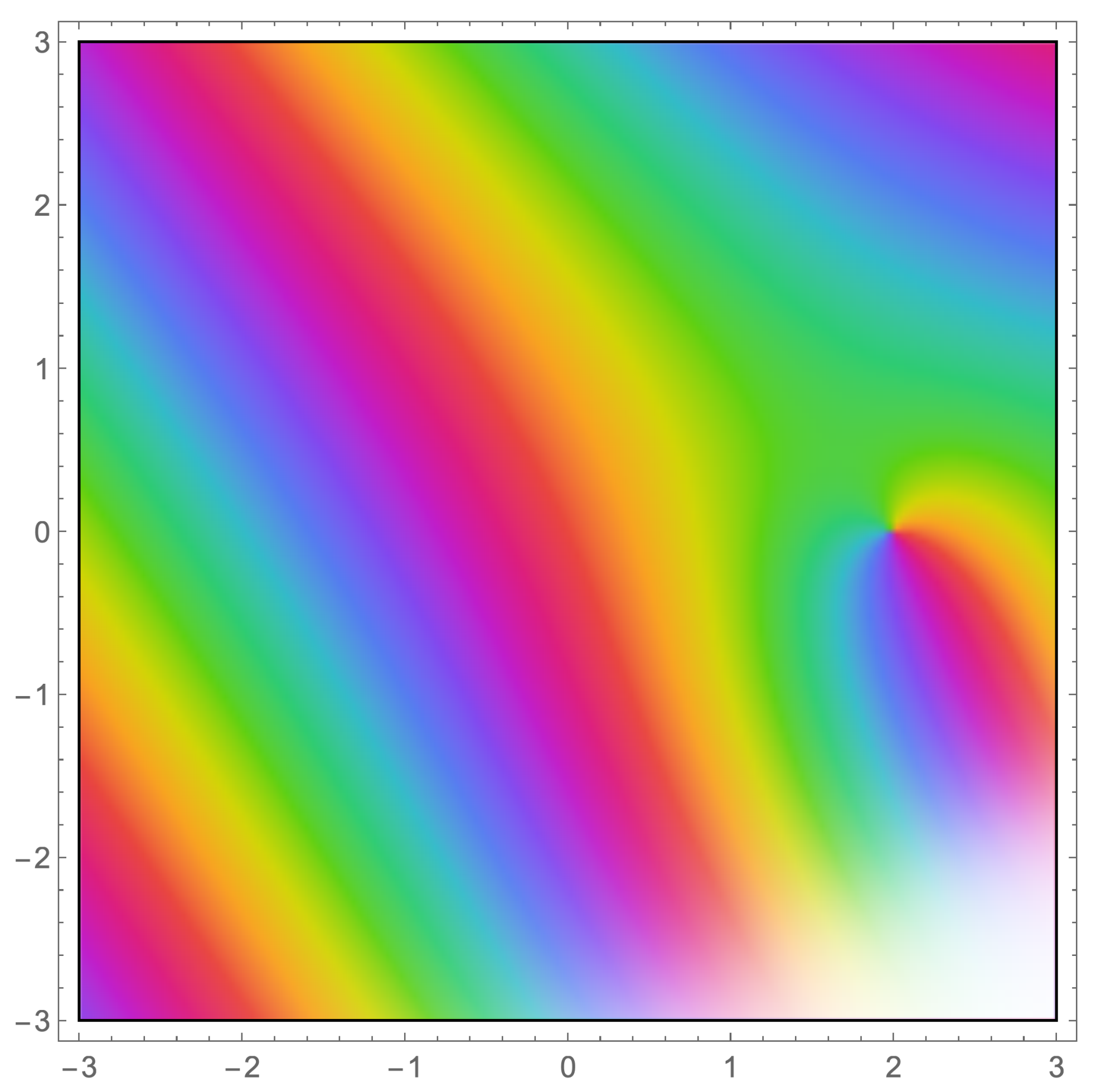
Plots of a Special Case Involving
7. Conclusions and Observation
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Watson, G.; Whittaker, N.; Taylor, E. A course of Modern Analysis, 3rd ed.; Cambridge Mathematical Library: Cambridge, UK, 1927; p. 353. [Google Scholar]
- Mitra, S. On certain infinite integrals involving Struve functions and Parabolic cylinder functions. Proc. Edinb. Math. Soc. 1946, 7, 171–173. [Google Scholar] [CrossRef][Green Version]
- Reynolds, R.; Stauffer, A. A Method for Evaluating Definite Integrals in Terms of Special Functions with Examples. Int. Math. Forum 2020, 15, 235–244. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Tables of Integrals, Series and Products, 6th ed.; Academic Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Brychkov, Y.A.; Marichev, O.I.; Savischenko, N.V. Handbook of Mellin Tranforms; CRC Press: Boca Raton, FL, USA, 2019; p. 149. [Google Scholar]
- Harrison, M.; Waldron, P. Mathematics for Economics and Finance; Taylor & Francis: Abingdon, UK, 2011. [Google Scholar]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. (Eds.) NIST Digital Library of Mathematical Functions; With 1 CD-ROM (Windows, Macintosh and UNIX). MR 2723248 (2012a:33001); U.S. Department of Commerce, National Institute of Standards and Technology: Washington, DC, USA; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Laurincikas, A.; Garunkstis, R. The Lerch Zeta-Function; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Oldham, K.B.; Myland, J.C.; Spanier, J. An Atlas of Functions: With Equator, the Atlas Function Calculator, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Lewin, L. Polylogarithms and Associated Functions; North-Holland Publishing Co.: New York, NY, USA, 1981. [Google Scholar]
- Adamchik, V.S. Polygamma Functions of Negative Order. J. Comput. Appl. Math. 1999, 100, 191–199. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reynolds, R.; Stauffer, A. A Quadruple Integral Involving Product of the Struve Hv(βt) and Parabolic Cylinder Du(αx) Functions. Symmetry 2022, 14, 9. https://doi.org/10.3390/sym14010009
Reynolds R, Stauffer A. A Quadruple Integral Involving Product of the Struve Hv(βt) and Parabolic Cylinder Du(αx) Functions. Symmetry. 2022; 14(1):9. https://doi.org/10.3390/sym14010009
Chicago/Turabian StyleReynolds, Robert, and Allan Stauffer. 2022. "A Quadruple Integral Involving Product of the Struve Hv(βt) and Parabolic Cylinder Du(αx) Functions" Symmetry 14, no. 1: 9. https://doi.org/10.3390/sym14010009
APA StyleReynolds, R., & Stauffer, A. (2022). A Quadruple Integral Involving Product of the Struve Hv(βt) and Parabolic Cylinder Du(αx) Functions. Symmetry, 14(1), 9. https://doi.org/10.3390/sym14010009






