Analysis and Design of Enhanced Distributed Fountain Codes in Multiple Access Networks with Cooperative Relay
Abstract
1. Introduction
- (1)
- A novel multiple-access network with a cooperative relay is proposed. By introducing an enhanced cooperative relay in a distributed network, the coverage of the relays can be extended, and the transmission efficiency and reliability of the network can be improved. Based on this network model, a novel enhanced distributed fountain coding scheme is proposed.
- (2)
- An improved analysis method is developed to analyze the asymptotic performance of the proposed codes. The expressions of degree distributions are derived and proven. It is shown that there are two kinds of overall degree distributions, corresponding to two source types, respectively. Furthermore, the decoding performance is analyzed theoretically using the And-Or tree method.
- (3)
- A design method of degree distributions using joint iterative optimization algorithms is proposed. Based on the results of the asymptotic performance analysis, the degree distributions of the sources and relays can be optimized in an iterative way.
- (4)
- The effectiveness of the proposed enhanced distributed fountain codes is verified by a series of simulations. The degree distributions are validated to be consistent with the analysis and derivation, and the effectiveness of the optimization method is verified. The proposed codes are validated to have a good performance on both lossless and lossy channels through simulations with different parameter settings.
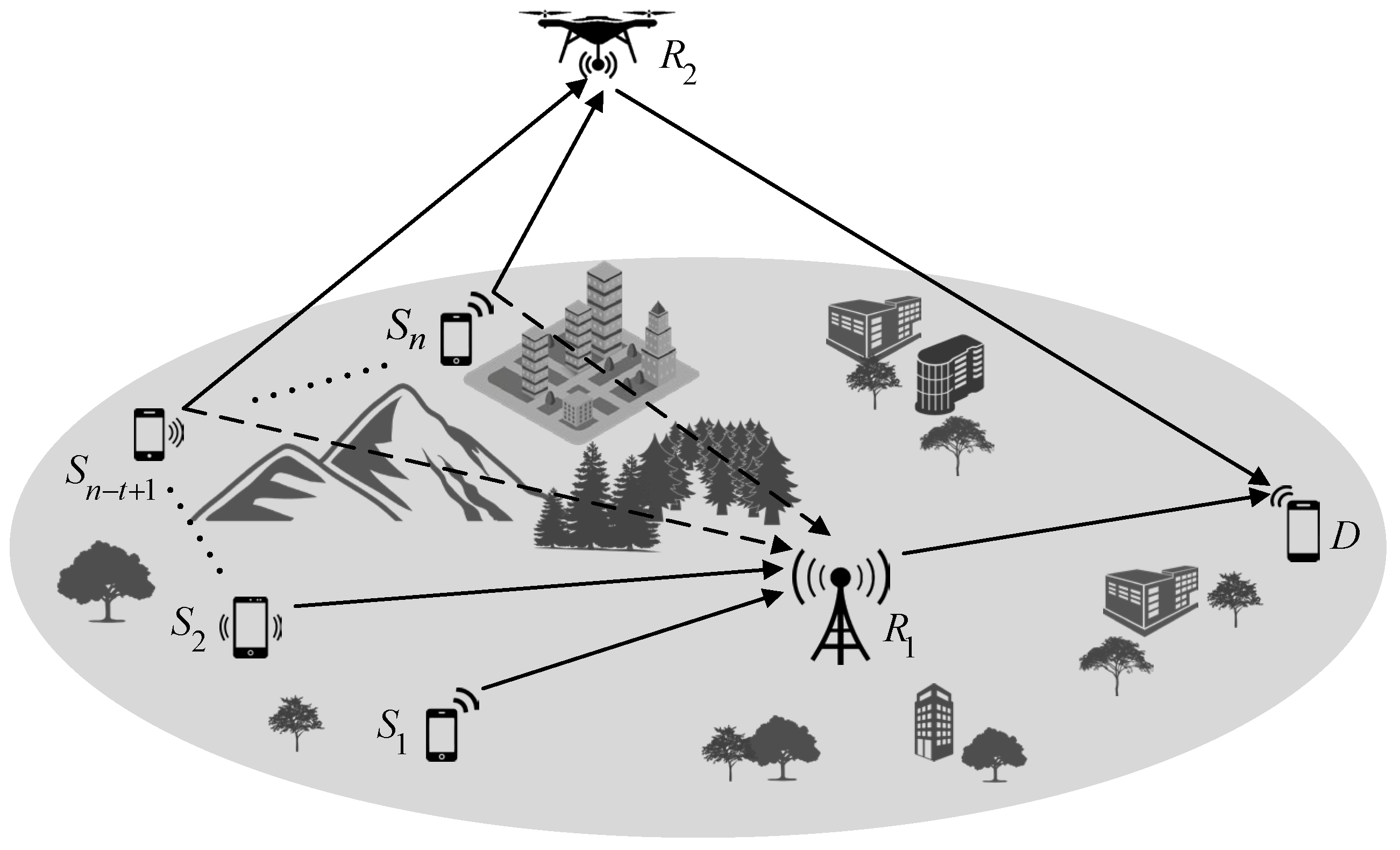
2. System Model of Multiple-Access Relay Networks with Cooperative Relay
3. Enhanced Distributed Fountain Coding for Multiple-Access Relay Networks with Cooperative Relay
4. Asymptotic Analysis of Proposed Enhanced Distributed Fountain Codes
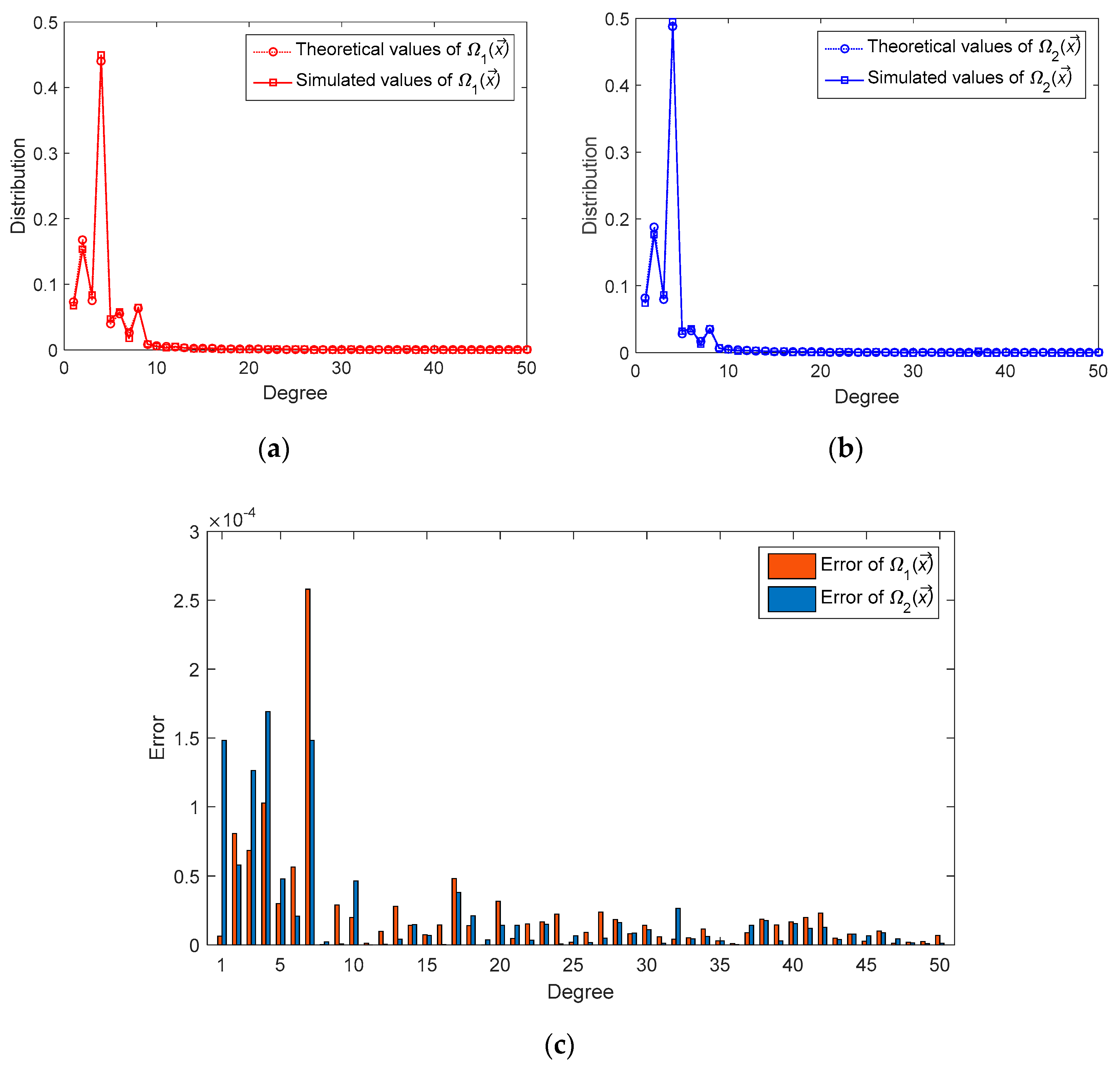
4.1. Description of Degree Distributions
- Case 1: Sources are connected to relay only. Obviously, the overall degree distribution of these sources is .
- Case 2: Sources are connected to relay and simultaneously. The encoded symbols from both relays are received alternately at the destination. We assume that half of these received symbols are from relay and the other half from relay . Then, the overall degree distribution of these sources can be expressed as . □
4.2. Asymptotic Analysis of Decoding Performance
- Case 1: The source is connected to relay only. The partial derivative of can be calculated asThe average output degree is the partial derivative of at as followsThe average input degree can be represented byThus, the edge-perspective degree distribution of can be expressed asBy substituting (7) into (6), we can obtain the expression of asymptotic performance in (4).
- Case 2: The source is connected to relay and simultaneously. From Lemma 1, the partial derivative of can be calculated as followsThe average output degree is the partial derivative of at asThe average input degree can be calculated asThe edge-perspective degree distribution can be expressed asFinally, by substituting (11) into (6), we can obtain the expression of asymptotic performance in (5). □
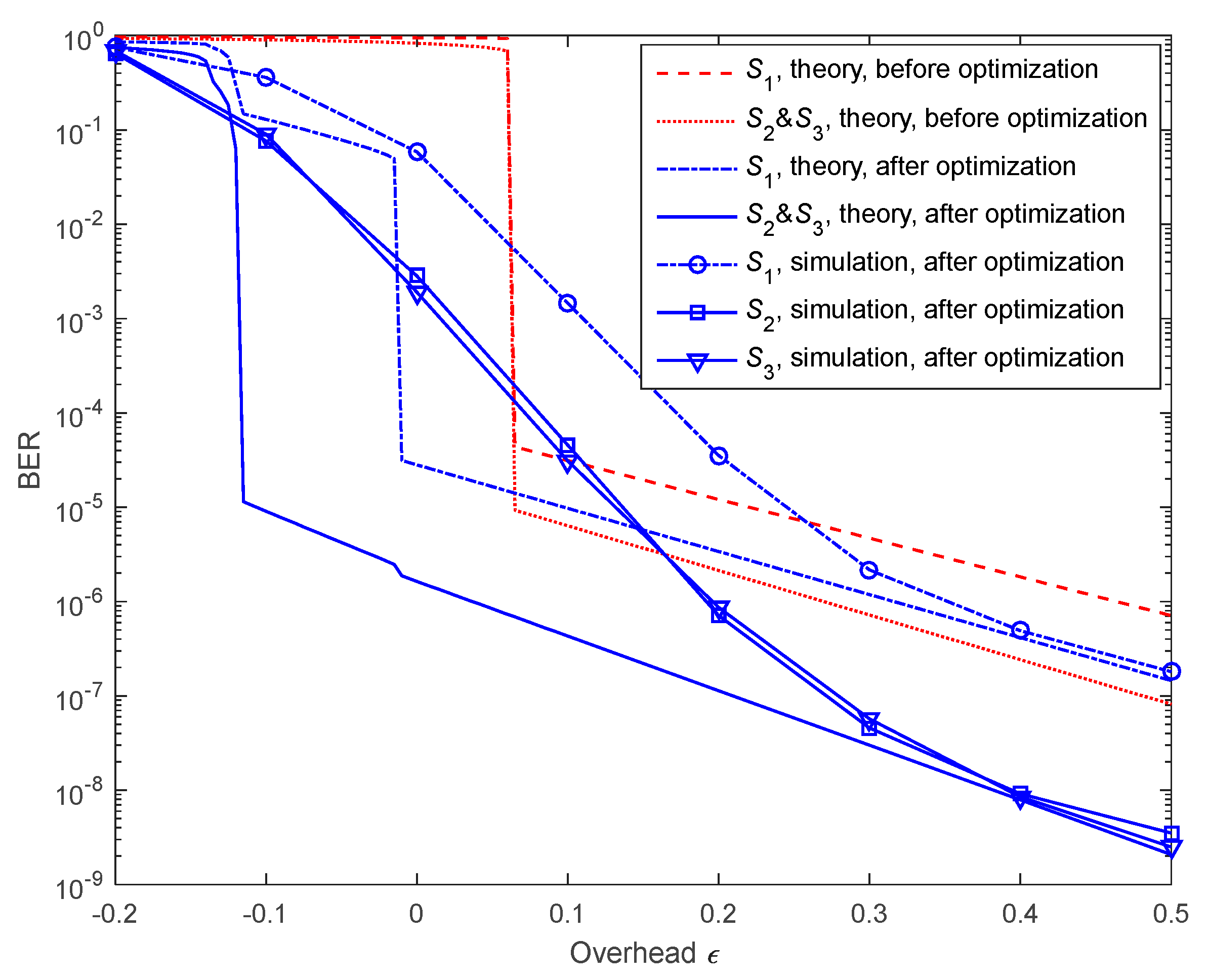
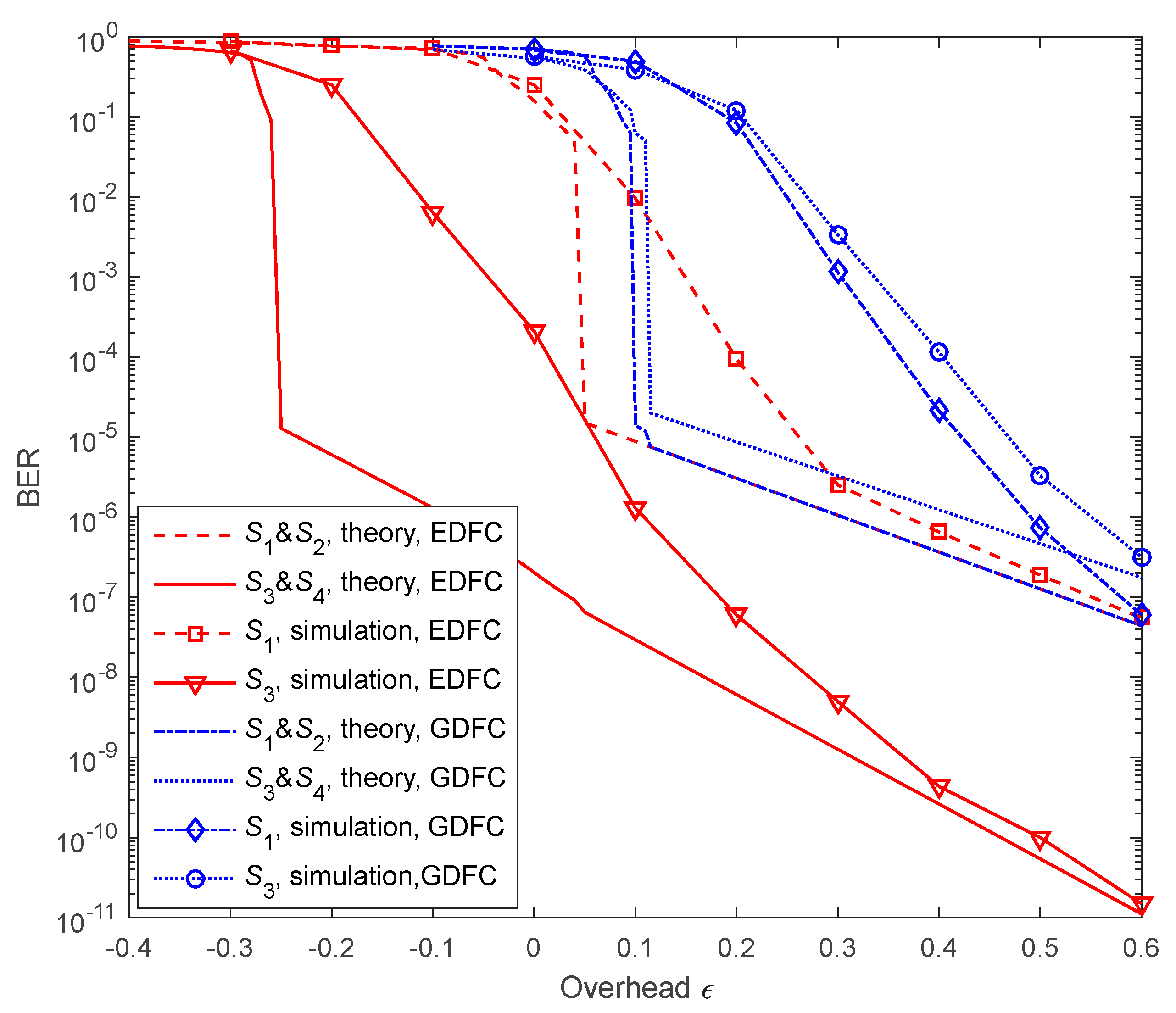
5. Optimization Design of Degree Distributions for Proposed Enhanced Distributed Fountain Codes
5.1. Optimization of the Relays
5.2. Optimization of the Sources
- Case 1: When , the source is connected to relay only. For source , the objective of the optimization is to achieve the desired decoding failure probability while minimizing the overall overhead . By substituting (9) into (1), we can obtain the code overhead as followswhich can be used as the objective function. By substituting (4) into , we can obtainThe inequality in (20) must be satisfied on all equidistant points , that isThe optimization equation of source () can be expressed as follows
- Case 2: When , the source is connected to relay and simultaneously. Similar to the analysis of Case 1, the optimization equation of source () can be expressed as follows
5.3. Joint Iterative Optimization of Degree Distributions
- Choose a robust soliton distribution as the initial value of degree distribution of source ;
- Fix the degree distribution of each source, and optimize degree distributions and of the relays with (18);
- Fix the degree distributions and obtained from step 2, then optimize degree distribution of source () with (22) and optimize degree distribution of source () with (23);
- Repeat steps 2 and 3 until the degree distributions meet the specified requirements.
6. Simulation Results
6.1. Degree Distributions
6.2. Performance on Lossless Source-Relay and Relay-Destination Links
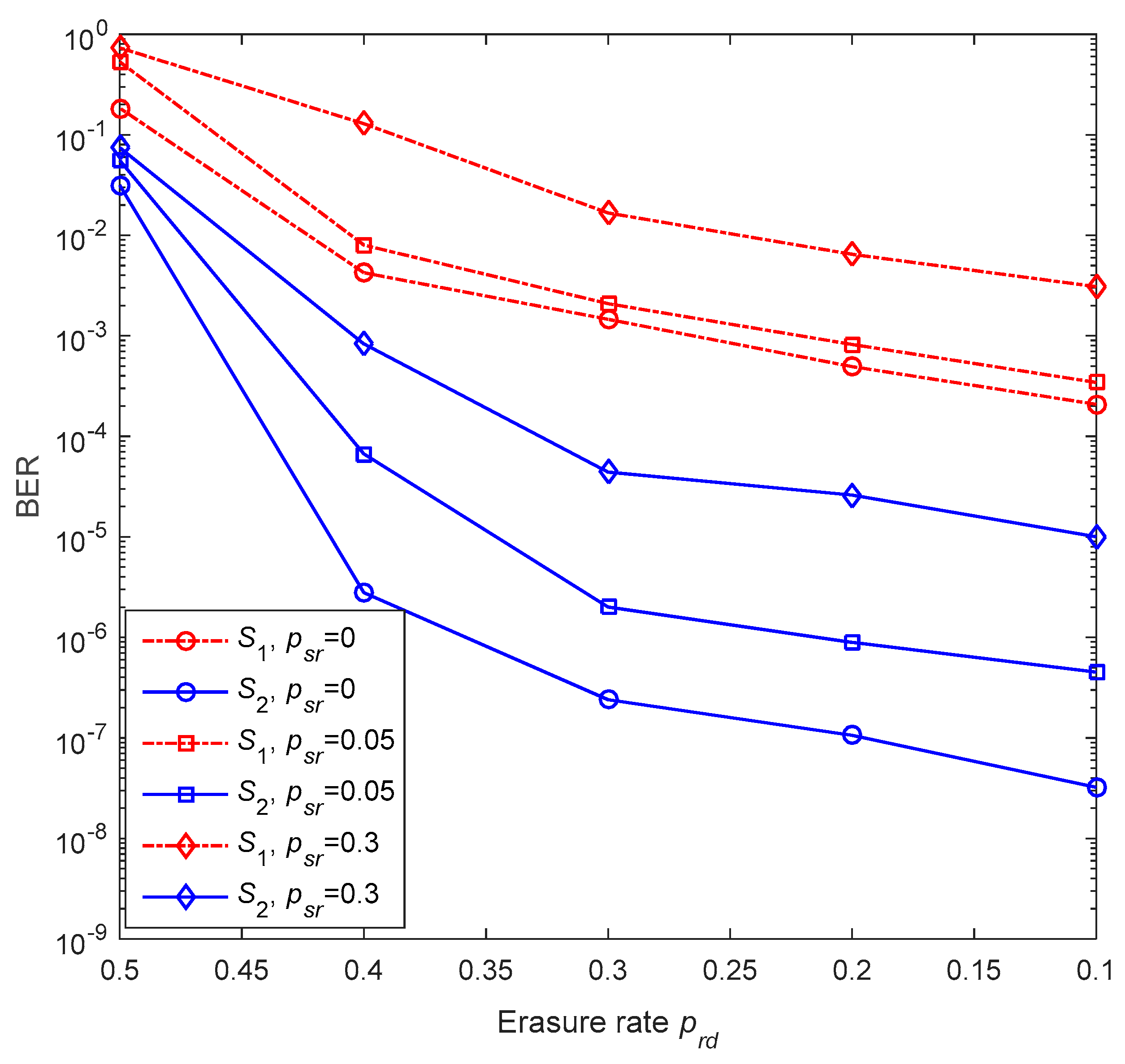
6.3. Performance on Lossy Source-Relay and Relay-Destination Links
7. Results and Discussions
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Puducheri, S.; Kliewer, J.; Fuja, T.E. The design and performance of distributed LT codes. IEEE Trans. Inform. Theory 2007, 53, 3740–3754. [Google Scholar] [CrossRef]
- Yang, H.; Jiang, M.; Shen, H.; Zhao, C. A distributed LT code design for multiple-access relay networks subject to erasures. IEEE Commun. Lett. 2015, 19, 509–512. [Google Scholar] [CrossRef]
- Liao, J.; Zhang, L.; Li, T.; Wang, J.; Qi, Q. A generalized design of distributed rateless codes with decreasing ripple size for multiple-access relay networks. Wirel. Netw. 2017, 23, 2177–2188. [Google Scholar] [CrossRef]
- Sejdinović, D.; Piechocki, R.J.; Doufexi, A. AND-OR tree analysis of distributed LT codes. In Proceedings of the 2009 IEEE Information Theory Workshop on Networking and Information Theory, Volos, Greece, 12–10 June 2009; pp. 261–265. [Google Scholar]
- Shao, H.; Xu, D.; Zhang, X. Asymptotic analysis and optimization for generalized distributed fountain codes. IEEE Commun. Lett. 2013, 17, 988–991. [Google Scholar] [CrossRef]
- Sejdinović, D.; Piechocki, R.; Doufexi, A.; Ismail, M. Decentralised distributed fountain coding: Asymptotic analysis and design. IEEE Commun. Lett. 2010, 14, 42–44. [Google Scholar] [CrossRef]
- Shao, H.; Zhu, H.; Bao, J. Analysis and Design of Wireless Distributed Fountain Codes with Multiplicative Network Coding. In Proceedings of the 5th Machine Learning and Intelligent Communications (MLICOM 2020), Shenzhen, China, 26–27 September 2020; pp. 250–264. [Google Scholar]
- Shang, L.; Perrins, E. Optimal Memory Order of Memory-Based LT Encoders for Finite Block-Length Codes over Binary Erasure Channels. IEEE Trans. Commun. 2019, 67, 875–889. [Google Scholar] [CrossRef]
- Okpotse, T.; Yousefi, S. Systematic Fountain Codes for Massive Storage Using the Truncated Poisson Distribution. IEEE T. Commun. 2019, 67, 943–954. [Google Scholar] [CrossRef]
- Song, X.; Cheng, N.; Liao, Y.; Ni, S.; Lei, T. Design and Analysis of LT Codes with a Reverse Coding Framework. IEEE Access 2021, 9, 116552–116563. [Google Scholar] [CrossRef]
- Deng, D.; Xu, D.; Xu, S. Optimisation design of systematic LT codes over AWGN multiple access channel. IET Commun. 2018, 12, 1351–1358. [Google Scholar] [CrossRef]
- Shao, H.; Xu, D.; Zhang, X. The design and analysis of unequal error protection fountain coding for multiple source networks over binary erasure channels. Sci. China Inf. Sci. 2014, 57, 1–9. [Google Scholar] [CrossRef]
- Chen, S.; Effros, M.; Kostina, V. Lossless Source Coding in the Point-to-Point, Multiple Access, and Random Access Scenarios. IEEE T. Inform. Theory 2020, 66, 6688–6722. [Google Scholar] [CrossRef]
- Zheng, Z.; Yuan, L.; Fang, F. Performance Analysis of Fountain Coded Non-Orthogonal Multiple Access with Finite Blocklength. IEEE Wirel. Commun. Lett. 2021, 10, 1752–1756. [Google Scholar] [CrossRef]
- Monir, A.; Mazen, O.H. A Secrecy Study of UAV Based Networks with Fountain Codes and FD Jamming. IEEE Commun. Lett. 2021, 25, 1796–1800. [Google Scholar]
- Talari, A.; Rahnavard, N. Distributed rateless codes with UEP property. In Proceedings of the 2010 IEEE International Symposium on Information Theory, Austin, TX, USA, 13–18 June 2010; pp. 2453–2457. [Google Scholar]
- He, J.; Hussain, I.; Li, Y.; Juntti, M.; Matsumoto, T. Distributed LT codes with improved error floor performance. IEEE Access 2019, 7, 8102–8110. [Google Scholar] [CrossRef]
- Hayajneh, K.F. Memory-based lt codes for efficient 5g networks and beyond. Electronics 2021, 10, 3169. [Google Scholar] [CrossRef]
- Han, W.; Xu, S.; Huang, D.; Xu, C. Analysis and design of rateless two-way relay networks based on a multiply-and-forward scheme. Appl. Sci. 2020, 10, 2389. [Google Scholar] [CrossRef]
- Peng, T.; Lambotharan, S.; Zheng, G.; Shikh-Bahaei, M. Opportunistic Fountain Coding with Coordinative Routing. IEEE Wirel. Commun. Lett. 2022, 11, 851–855. [Google Scholar] [CrossRef]
- Li, Y.; Du, Q. A Cooperative Multi-RSU Caching Scheme in Vehicular Networks with Fountain Codes. In Proceedings of the 2021 IEEE 32nd Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Helsinki, Finland, 13–16 September 2021; pp. 1445–1450. [Google Scholar]
- Wang, F.; Jiao, J.; Li, L.; Zhang, K.; Wu, S.; Zhang, Q. Finite Length Non-Binary Raptor Codes under Ordered Statistics Decoder. In Proceedings of the 2020 IEEE 92nd Vehicular Technology Conference (VTC2020-Fall); IEEE: Victoria, BC, Canada, 2020; pp. 1–5. [Google Scholar]
- Zhang, K.; Jiao, J.; Huang, Z.; Wu, S.; Zhang, Q. Finite Block-Length Analog Fountain Codes for Ultra-Reliable Low Latency Communications. IEEE T Commun. 2020, 68, 1391–1404. [Google Scholar] [CrossRef]
- Yildiz, H.U. Maximization of Underwater Sensor Networks Lifetime via Fountain Codes. IEEE Trans. Ind. Inf. 2019, 15, 4602–4613. [Google Scholar] [CrossRef]
- Hsiao, H.F.; Ciou, Y.J. Layer-Aligned Multipriority Rateless Codes for Layered Video Streaming. IEEE Trans. Circuits Syst. Video Technol. 2014, 24, 1395–1404. [Google Scholar] [CrossRef]
- Qin, S.; Feng, G.; Zhang, Y. Capacity bounds of cooperative communications with fountain codes. In Proceedings of the 2010 IEEE Wireless Communication and Networking Conference, Sydney, NSW, Australia, 18–21 April 2010; pp. 1–4. [Google Scholar]
- Duy, T.T.; Anpalagan, A.; Kong, H. Multi-hop cooperative transmission using fountain codes over Rayleigh fading channels. J. Commun. Netw.-S. Kor. 2012, 14, 267–272. [Google Scholar] [CrossRef]
- Di, X.; Xiong, K.; Fan, P.; Qiu, Z. Cooperative multi-relay transmission for high-speed railway mobile communication system with fountain codes. In Proceedings of the 2013 International Workshop on High Mobility Wireless Communications (HMWC), Shanghai, China, 1–3 November 2013; pp. 63–68. [Google Scholar]
- Molisch, A.F.; Mehta, N.B.; Yedidia, J.S.; Zhang, J. Cooperative relay networks using fountain codes. In Proceedings of the IEEE Globecom 2006, San Francisco, CA, USA, 27 November–1 December 2006; pp. 1–6. [Google Scholar]
- Xu, K.; Du, Z.; Jiang, B. Dynamic Coded Cooperation with Incremental Redundancy: Throughput and Diversity-Multiplexing Tradeoff Analysis. IEEE Commun. Lett. 2020, 24, 506–509. [Google Scholar] [CrossRef]
- Jain, S.; Bose, R. Rateless-Code-Based Secure Cooperative Transmission Scheme for Industrial IoT. IEEE Internet Things. J. 2020, 7, 6550–6565. [Google Scholar] [CrossRef]
- Nessa, A.; Kadoch, M.; Rong, B. Fountain Coded Cooperative Communications for LTE-A Connected Heterogeneous M2M Network. IEEE Access 2016, 4, 5280–5292. [Google Scholar] [CrossRef]
- Cao, R.; Yang, L. Decomposed LT codes for cooperative relay communications. IEEE J. Sel. Area. Comm. 2012, 30, 407–414. [Google Scholar] [CrossRef]
- Mozaffari, M.; Saad, W.; Bennis, M.; Nam, Y.H.; Debbah, M. A Tutorial on UAVs for Wireless Networks: Applications, Challenges, and Open Problems. IEEE Commun. Surv. Tut. 2019, 21, 2334–2360. [Google Scholar] [CrossRef]
- Kumar, P.; Singh, P.; Darshi, S.; Shailendra, S. Drone Assisted Network Coded Co-operation. In Proceedings of the TENCON 2019-2019 IEEE Region 10 Conference (TENCON), Kochi, India, 12 December 2019; pp. 1174–1179. [Google Scholar]
- Zeng, Y.; Zhang, R.; Lim, T.J. Throughput maximization for UAV-enabled mobile relaying systems. IEEE T. Commun. 2016, 64, 4983–4996. [Google Scholar] [CrossRef]
- Zhu, Q.; Bai, F.; Pang, M.; Li, J.; Zhong, W.; Chen, X.; Mao, K. Geometry-Based Stochastic Line-of-Sight Probability Model for A2G Channels Under Urban Scenarios. IEEE T. Antenn. Propag. 2022, 70, 5784–5794. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, H.; Fu, Y.; Wang, C.; Tan, Y.; Chen, X.; Wu, Q. A Novel 3D Non-Stationary Wireless MIMO Channel Simulator and Hardware Emulator. IEEE T. Commun. 2018, 66, 3865–3878. [Google Scholar] [CrossRef]
- Du, X.; Zhu, Q.; Ding, G.; Li, J.; Wu, Q.; Lan, T.; Lin, Z.; Zhong, W.; Han, L. UAV-assisted three-dimensional spectrum mapping driven by spectrum data and channel model. Symmetry 2021, 13, 2308. [Google Scholar] [CrossRef]
- Rahnavard, N.; Vellambi, B.N.; Fekri, F. Rateless codes with unequal error protection property. IEEE T. Inform. Theory 2007, 53, 1521–1532. [Google Scholar] [CrossRef]
- Luby, M. LT Codes. In Proceedings of the 43rd Annual IEEE Symposium on Foundations of Computer Science (FOCS); IEEE: Vancouver, BC, Canada, 2002; pp. 271–280. [Google Scholar]
- Shokrollahi, A. Raptor Codes. IEEE Trans. Inform. Theory 2006, 52, 2551–2567. [Google Scholar] [CrossRef]



| Degree | n = 2, t = 1 | n = 3, t = 2 | n = 4, t = 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| , | , | , | ||||||||||
| 1 | 0.16 | 0.16 | 0.6654 | 1 | 0.13 | 0.13 | 0.6899 | 0.79 | 0.22 | 0.22 | 0.8579 | 0.68 |
| 2 | 0.4386 | 0.1424 | 0.3346 | - | 0.4134 | 0.3273 | 0.23 | 0.21 | 0.0227 | 0.1698 | 0.12 | 0.32 |
| 3 | 0.2845 | 0.5418 | - | - | 0.3626 | 0.4249 | 0.0801 | - | 0.6235 | 0.4966 | 0.01 | - |
| 13 | 0.01 | <0.005 | - | - | <0.005 | <0.005 | - | - | <0.005 | <0.005 | 0.0121 | - |
| 14 | 0.1069 | 0.1305 | - | - | <0.005 | 0.0109 | - | - | 0.0354 | <0.005 | - | - |
| 15 | <0.005 | 0.0253 | - | - | <0.005 | 0.054 | - | - | 0.0409 | <0.005 | - | - |
| 16 | <0.005 | <0.005 | - | - | 0.0092 | <0.005 | - | - | <0.005 | 0.0613 | - | - |
| 17 | <0.005 | <0.005 | - | - | 0.0376 | <0.005 | - | - | <0.005 | <0.005 | - | - |
| 100 | <0.005 | <0.005 | - | - | 0.0472 | 0.0529 | - | - | 0.0575 | 0.0523 | - | - |
| Methods | Advantages | Disadvantages |
|---|---|---|
| Decode-and-forward (DF) |
|
|
| DLT |
|
|
| GDFC |
|
|
| EDFC |
|
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, H.; Zhu, H.; Bao, J. Analysis and Design of Enhanced Distributed Fountain Codes in Multiple Access Networks with Cooperative Relay. Symmetry 2022, 14, 2026. https://doi.org/10.3390/sym14102026
Shao H, Zhu H, Bao J. Analysis and Design of Enhanced Distributed Fountain Codes in Multiple Access Networks with Cooperative Relay. Symmetry. 2022; 14(10):2026. https://doi.org/10.3390/sym14102026
Chicago/Turabian StyleShao, Hanqin, Hongbo Zhu, and Junwei Bao. 2022. "Analysis and Design of Enhanced Distributed Fountain Codes in Multiple Access Networks with Cooperative Relay" Symmetry 14, no. 10: 2026. https://doi.org/10.3390/sym14102026
APA StyleShao, H., Zhu, H., & Bao, J. (2022). Analysis and Design of Enhanced Distributed Fountain Codes in Multiple Access Networks with Cooperative Relay. Symmetry, 14(10), 2026. https://doi.org/10.3390/sym14102026






