Flow of a Viscous Incompressible Fluid from a Moving Point Source
Abstract
:1. Introduction
2. Problem Statement
3. Exact Solution of Simplified Navier–Stokes Equations
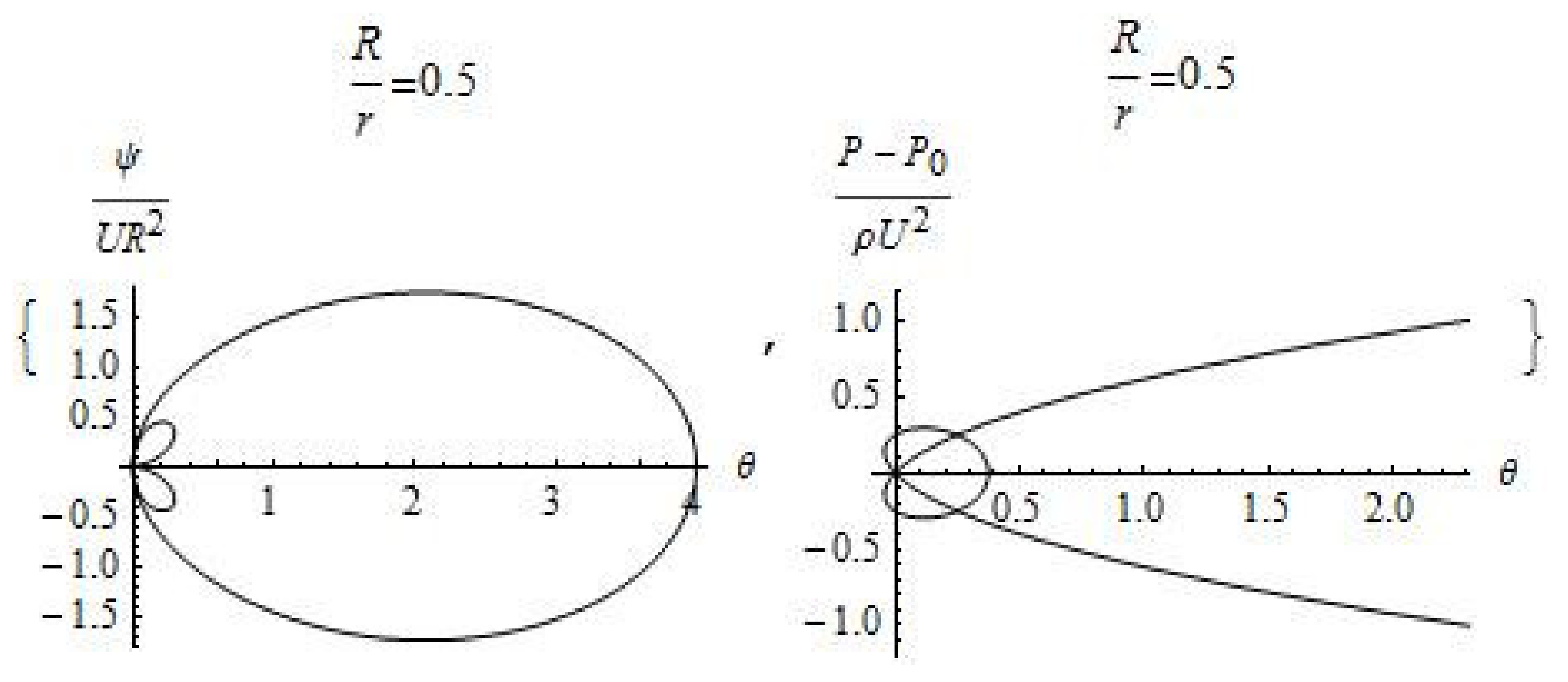
4. Investigation of Hydrodynamic Fields
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Stokes, G.G. Mathematical and Physical Papers; Cambridge University Press: Cambridge, UK, 1880; Volume 1. [Google Scholar]
- Moiseyev, N.N.; Rumyantsev, V.V. Dynamic Stability of Bodies Containing Fluid; Springer: New York, NY, USA, 1968. [Google Scholar]
- Ratner, B.D.; Hoffman, A.S.; Schoen, F.J.; Lemons, J.E. (Eds.) Nanomedicine, Biomaterials Science: An Introduction to Materials in Medicine; Academic Press: San Diego, CA, USA, 1996. [Google Scholar]
- Humphrey, J.D.; Delange, S.L. An Introduction to Biomechanics: Solids and Fluids, Analysis and Design; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Planas, G.; Sueur, F. On the “viscous incompressible fluid + rigid body” system with Navier conditions. Ann. Inst. H. Poincaré Anal. Non Linéaire 2014, 31, 55–80. [Google Scholar] [CrossRef]
- Ershkov, S.V.; Prosviryakov, E.Y.; Burmasheva, N.V.; Christianto, V. Towards understanding the algorithms for solving the Navier-Stokes equations. Fluid Dyn. Res. 2021, 53, 044501. [Google Scholar] [CrossRef]
- Aristov, S.N.; Knyazev, D.V.; Polyanin, A.D. Exact solutions of the Navier–Stokes equations with the linear dependence of velocity components on two space variables. Theor. Found. Chem. Eng. 2009, 43, 642–662. [Google Scholar] [CrossRef]
- Drazin, P.G.; Riley, N. The Navier–Stokes Equations: A Classification of Flows and Exact Solutions; Cambridge University Press: Cambridge, UK, 2006; 196p. [Google Scholar]
- Aristov, S.N. An Exact Solution to the Point Source Problem. Dokl. Phys. 1995, 40, 346–348. [Google Scholar]
- Aristov, S.N. Stationary Cylindrical Vortex in a Viscous Fluid. Dokl. Phys. 2001, 46, 251–253. [Google Scholar] [CrossRef]
- Leporini, M.; Terenzi, A.; Marchetti, B.; Giacchetta, G.; Corvaro, F. Experiences in numerical simulation of wax deposition in oil and multiphase pipelines: Theory versus reality. J. Pet. Sci. Eng. 2019, 174, 997–1008. [Google Scholar] [CrossRef]
- Sedov, L.I. Mechanics of Continuous Media; World Scientific: Singapore, 1997; Volume 1. [Google Scholar]
- Liu, Y.; Peng, Y. Study on the Collapse Process of Cavitation Bubbles Including Heat Transfer by Lattice Boltzmann Method. J. Mar. Sci. Eng. 2021, 9, 219. [Google Scholar] [CrossRef]
- Ershkov, S.V. Non-stationary helical flows for incompressible 3D Navier–Stokes equations. Appl. Math. Comput. 2016, 274, 611–614. [Google Scholar] [CrossRef]
- Ershkov, S.V. About existence of stationary points for the Arnold-Beltrami-Childress (ABC) flow. Appl. Math. Comput. 2016, 276, 379–383. [Google Scholar] [CrossRef] [Green Version]
- Ershkov, S.V.; Shamin, R.V. A Riccati-type solution of 3D Euler equations for incompressible flow. J. King Saud Univ. - Sci. 2020, 32, 125–130. [Google Scholar] [CrossRef]
- Ershkov, S.V.; Rachinskaya, A.; Prosviryakov, E.Y.; Shamin, R.V. On the semi-analytical solutions in hydrodynamics of ideal fluid flows governed by large-scale coherent structures of spiral-type. Symmetry 2021, 13, 2307. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ershkov, S.V.; Prosviryakov, E.Y.; Leshchenko, D.D. Flow of a Viscous Incompressible Fluid from a Moving Point Source. Symmetry 2022, 14, 2156. https://doi.org/10.3390/sym14102156
Ershkov SV, Prosviryakov EY, Leshchenko DD. Flow of a Viscous Incompressible Fluid from a Moving Point Source. Symmetry. 2022; 14(10):2156. https://doi.org/10.3390/sym14102156
Chicago/Turabian StyleErshkov, Sergey V., Evgeniy Yu. Prosviryakov, and Dmytro D. Leshchenko. 2022. "Flow of a Viscous Incompressible Fluid from a Moving Point Source" Symmetry 14, no. 10: 2156. https://doi.org/10.3390/sym14102156
APA StyleErshkov, S. V., Prosviryakov, E. Y., & Leshchenko, D. D. (2022). Flow of a Viscous Incompressible Fluid from a Moving Point Source. Symmetry, 14(10), 2156. https://doi.org/10.3390/sym14102156









