Topological Data Analysis of m-Polar Spherical Fuzzy Information with LAM and SIR Models

Abstract

The concept of m-polar spherical fuzzy sets (mPSFS) is a combination of m-polar fuzzy sets (mPFS) and spherical fuzzy sets (SFS). An mPSFS is an optimal strategy for addressing multipolarity and fuzziness in terms of ordered triples of positive membership grades (PMGs), negative membership grades (NMGs), and neutral grades (NGs). In this study, the innovative concept of m-polar spherical fuzzy topology (mPSF-topology) is proposed for data analysis and information aggregation. We look into the characteristics and results of mPSF-topology with the help of several examples. Topological structures on mPSFSs help with both the development of new artificial intelligence (AI) tools for different domain strategies and the study of different kinds of uncertainty in everyday life problems. These strategies make it possible to recognise and look into a situation early on, which helps professionals to reduce certain risks. In order to address various group decision-making issues in the m-polar spherical fuzzy domain, one suggestion has been to apply an extended linear assignment model (LAM) along with the SIR method known as superiority and inferiority ranking methodology in order to analyze road accident issues and dispute resolution. In addition, we examine the symmetry of optimal decision and perform a comparative study between the research carried out using the suggested methodology and several existing methods.

1. Introduction

The conditions of our everyday life provide us with obstacles that arise from imprecise information and an absence of appropriate modelling, both of which can lead to imprecise answers and questionable reasoning. While human intelligence (HI), machine learning intelligence (MLI), and online social networks have only been around for a short time, they have changed the economic and social paradigms of society. Because of the rapid expansion of HI, MLI, and big data over the past few years, incredible improvements in our day-to-day lives have been made [1,2,3,4,5,6,7]. The theory of topology pertains to the interaction between spatial components or modules. It can be utilised to design large datasets with the ability to explain certain spatial functions. The definition of topological spaces is listed in

Table 1. Topological structures on fuzzy sets and soft sets.

Year	Researchers	Field of contribution
1968	Chang [5]	Fuzzy topological spaces and concepts such as open set, closed set, neighbourhood, interior set, continuity, and compactness
1955	Kelley [6]	Definitions, theorems, and proofs of topological concepts
1974	Wong [8]	Fuzzy points and local countability, separability
1976	Lowen [9]	Definitions for fuzzy topological spaces
1975	Hutton [10]	Normality
1980	Ming and Ming [11]	Link between fuzzy sets and their systems
1991, 1992	Ying [12,13]	Technique of continuous valued logic
1993	Shen [14]	Introduced separation axioms and several of their equivalences as well as their relations with each other in fuzzifying topology
1995, 1997	Coker [15,16]	Invented the idea of intuitionistic fuzzy topological space
2011	Shabir and Naz [17]	Soft topological spaces
2011	Cagman et al. [18]	Soft topology
2019	Riaz et al. [19]	N-soft topology and decision analysis
2019	Olgun et al. [20]	Topological properties of Pythagorean fuzzy sets
2021	Alshammari et al. [21]	Pythagorean fuzzy soft topological spaces

.

We have extended the study of topology to a new hybrid approach of SFS and mPFS, i.e., m polar spherical fuzzy sets (mPSFS), by following the idea of Chang [5]. We define the concept of mPSF-topological space using an mPSF-null set, mPSF-absolute set, and certain basic operations of mPSFSs, such as union and intersection. Here, we investigate several basic properties and analyse them with the help of theorems and examples.

Fuzzy mathematics differs from traditional mathematics, primarily in the field of set theory. Fuzzy mathematics was first developed only a few years ago, and is rich in ideas. In automobiles and traffic control systems, where logic circuits control anti-lock brakes, electronic systems, and other functions, its application is widespread. This is an even more specific form of the phrase “crisp set.” It has the ability to decide either yes or no, which corresponds to the numbers 1 and 0. Several of the ideas that are discussed in this article were anticipated by an American philosopher by the name of Black [22], who lived thirty years ago. The author of [22] developed a theory that has as its primary building blocks “fuzzy sets,” which are simply sets with “imperfect” bounds. An important work produced by Zadeh [23] in 1965 makes a crucial argument concerning the evolution of contemporary ideas around ambiguity, and was an immediate extension of the crisp set concept. Atanassov [24,25,26] suggested the idea of intuitionistic fuzzy sets (IFS) and intuitionistic fuzzy numbers (IFN) in 1983. Yager proposed “Pythagorean fuzzy sets (PFS)” [27,28], and Yager further introduced “q-rung orthopair fuzzy sets (q-ROFS)” [29]. Soft sets (SS) and SS theory were originated by Molodtsov [30,31]. Smarandache [32] suggested a new model called neutrosophic sets by introducing another grade to FS. Picture fuzzy sets (PiFS) were proposed by Cuong [33]. Spherical fuzzy sets (SFSs), which were recently introduced by Kutlu Gündodu and Kahraman [34], are the most recent extension of fuzzy sets; in these, the squared sum of the hesitancy-neutral degree, membership degree, and non-membership degree does not exceed 1. Ashraf et al. [35] and Mahmood et al. [36] introduced spherical fuzzy sets with certain operational rules and aggregation operations based on Archimedean t-norm and t-conorms. SFS covers a wider area as compared to picture fuzzy set (PFS). Feng et al. [37] proposed new score functions of q-rung orthopair fuzzy sets for further utilization in decision analysis. Deveci et al. proposed the idea of personal mobility in metaverse with autonomous vehicles based on q-ROFs [38]. Riaz et al. [39] presented an application of bipolar fuzzy soft sets (BFSSs) to supply chain management.

Due to the sheer uncertainty and ambiguity of real-world circumstances, the approaches frequently employed in classical mathematics are not always suitable for solving real-world problems. Using a variety of multi-criteria decision-making (MCDM) techniques that analyse a collection of choices against a variety of methodologies, the reliability of human judgments can be determined [40]. Information aggregation and synthesis are fundamental to technological innovations such as deep learning, decision-making processes, remote sensing data, principal component analysis, and mathematical abilities. The process of combining individual preferences on a specific list of options into a single unified collective preference is an example of a type of MADM problem known as group decision-making. This type of MADM problem is typically thought of as the procedure by which group decision-making is carried out. The process of making decisions as a group involves the participation of multiple individuals, each of whom brings a unique set of skills, years of experience, and relevant information to bear on the analysis of the various facets of the issue. Multiple-Attribute Group Decision-Making (MAGDM) is the term used to describe this category of problems [41]. Several MADM algorithms have been changed to work with spherical fuzzy sets, and the applications of these changes have been examined in the literature. The conventional approach to decision analysis known as MCDM, utilises the linear assignment model (LAM) and the superiority and inferiority ranking (SIR) method in mPSFS to determine an order of liability for the causes of road accidents. In 1977, Bernardo and Blin [42] came up with the idea for what would become known as the linear assignment technique (LAM), which took its influence from an assignment problem in linear programming for MADM [43]. The fundamental concept behind the LAM is that the rankings of the criteria provide an overall preference ranking that, when combined with the other component rankings, results in the best possible compromise [44,45]. Many acandemics have extended LAM under a variety of fuzzy extensions and making use of a variety of modelling and solution methodologies to account for the unavoidable uncertainty that is inherent in real-life decision-making situations; several of these are mentioned in

Table 2. Applications based on LAM in different fuzzy domains.

Researchers	Applications
Bashiri et al. (2011) [46]	Optimum maintenance strategy
Chen (2013) [47]	Optimal preference
Chen (2014) [48]	Solution of interval-valued MCDM problems
Wei et al. (2017) [49]	Solution of MCDM problems under a hesitant fuzzy environment
Hajiagha et al. (2018) [50]	Solution of MCGDM using hesitant fuzzy linguistic term sets
Yang et al. (2018) [51]	MCGDM based on interval neutrosophic sets
Liang et al. (2019) [44]	Solution of MCDM problems under Pythagorean fuzzy environment
Donyatalab et al. (2020) [52]	Determination of ranking for allocation under spherical fuzzy environment
Gundogdu (2021) [53]	Selection of penthouse location using picture fuzzy set
Moslem et al. (2021) [54]	Evaluation of service quality ranking in picture fuzzy environment

.

In a similar way, the SIR method has been used by a number of researchers in different fields of FSs. First, in 2001, Xu [55] gave a presentation on the approach known as the superiority and inferiority ranking (SIR). In the SIR method, the placement of the options is determined by two different segmentation overviews, which are as follows. In this method, the various options are ordered according to the predominance positioning arrangement as well as the inadequacy positioning arrangement. Notably, the major degree of latitude afforded by the use of the SIR method merges the characteristics of various other MCDM procedures. Numerous researchers have added their expertise using this method in various fields and domains, which are discussed in

Table 3. Applications based on SIR in different fuzzy domains.

Researchers	Applications
Tam et al. (2004) [56]	Used the strategy to choose a solid siphon
Tam and Tong (2008) [57]	Utilized the method for venture enhancements to locate the an expansive harbour
Liu (2010) [58]	Solutions fo supply chain management issues under intuitionistic fuzzy environment
Ma et al. (2014) [59]	Proposed an expanded SIR approach to HFS
Peng and Yang (2015) [60]	Introduced the PF-SIR approach
Rouhani (2017) [61]	Applied the F-SIR method to the selection of software in the IT sector
Tavana et al. (2018) [62]	Solved the third-party reverse logistics problem using the IFG-SIR approach
Zhao et al. (2019) [63]	Solve the investment selection problem, the IVIF-SIR method was applied

.

The following are the main objectives of the suggested framework:

• Construction of the topological structure on mPSFFSs.
• Analyzing the fundamental topology concepts of mPSF-open set, mPSF-closed set, mPSF-interior, mPSF-closure, mPSF-base, and mPSF-subbase, as well as their instances.
• Introducing theorems and the proofs that support them in order to illustrate how mPSF-topology works;
• Description of a case study entitled “Day by Day Increasing Road Accidents”.
• As an expansion of MCDM, LAM is used to elaborate the application for finding the causes of road accidents.
• The SIR framework is a well-known and frequently used MCDM technique that is useful for finding the rankings of similar applications in order to obtain precise results.
• A comparison analysis is provided to conclude our work.

Recent developments in fuzzy techniques in decision-making include those proposed in [64,65,66,67,68]. Further details on group decision-making are discussed in [69,70].

The rest of the present paper is categorised in the following fashion across the remaining sections. Section 2 explores core mPSF principles. The most important findings of mPSF-Topology are outlined in Section 3. In Section 4, we demonstrate a SIR and LAM framework that is embedded inside the mPSFSs and has an application to vehicular mishaps. In Section 5, the most important results of the investigation are provided.

2. Preliminaries

In this section, we concisely review a few primary concepts related to different kinds of sets, including fuzzy sets, soft sets, spherical fuzzy sets and spherical fuzzy soft sets, that are employed during the rest of this paper.

Definition 1

([23]). Let $\breve{⨿}$ be a classical set and ${\tilde{\mu }}_A:\breve{⨿}\to [0,1]$ be the membership function. Then, a fuzzy set A can be written in the form

$$A=(\breve{⨿},{\tilde{\mu }}_A)=\{(\rho ,{\tilde{\mu }}_A(\rho )):\rho \in X\}$$

The value of the mapping ${\tilde{\mu }}_A$ at $\rho \in \breve{⨿}$ i.e., ${\tilde{\mu }}_A(\rho )$ denotes the degree of membership of ρ to fuzzy set A. The aggregate of all fuzzy sets in $\breve{⨿}$ is designated as $\mathcal{F}(\breve{⨿})$.

Definition 2

([34,35,36]). Let U be the universe of discourse; then, a spherical fuzzy set (SFS) $\overline{\mathcal{G}}$ U is an object with the form

$$\overline{\mathcal{G}}=\left\{(\breve{⨿},\tilde{\mu }(\breve{⨿}),\gamma (\breve{⨿}),\tilde{\eta }(\breve{⨿})):x\in U\right\}$$

$$\overline{\mathcal{G}}=\left\{\frac{\breve{⨿}}{\left(\tilde{\mu }(\breve{⨿}),\gamma (\breve{⨿}),\tilde{\eta }(x)\right)}:\breve{⨿}\in U\right\}$$

where $\tilde{\mu }(\breve{⨿})\in [0,1]$ is called the “degree of membership (MG) of $\breve{⨿}$ in U”, $\gamma (\breve{⨿})\in [0,1]$ is called the “degree of hesitancy (HG) of $\breve{⨿}$ in U”, and $\tilde{\eta }(\breve{⨿})\in [0,1]$ is called the “degree of non-membership (NMG) of $\breve{⨿}$ in U”; furthermore, $\tilde{\mu }(\breve{⨿}),\gamma (x)$ and $\tilde{\eta }(\breve{⨿})$ satisfy the following condition:

$${\tilde{\mu }}^2(\breve{⨿})+{\gamma }^2(x\breve{⨿}+{\tilde{\eta }}^2(\breve{⨿}))\le 1,\forall \breve{⨿}\in U$$

Then, for $\breve{⨿}\in U$,

$$\pi (\breve{⨿})=\sqrt{1-{\tilde{\mu }}^2(\breve{⨿})-{\gamma }^2(\breve{⨿})-{\tilde{\eta }}^2(\breve{⨿})}$$

is called "refusal degree" of $\breve{⨿}\in U$. A spherical fuzzy number $(SFN)$ can be simply represented as

$$e=({\tilde{\mu }}_e,{\gamma }_e,{\tilde{\eta }}_e)$$

where ${({\tilde{\mu }}_e)}^2+{({\gamma }_e)}^2+{({\tilde{\eta }}_e)}^2\le 1$

Definition 3.

Let U be a universal set of discourse. An m-polar fuzzy set on U is defined on interval ${[0,1]}^m$ and can be expressed as

$$\mathfrak{M}=\left\{\left(\breve{⨿},\left({\tilde{\mu }}_i{(\breve{⨿})}_{i=1}^m\right):\breve{⨿}\in U\right\}\right.$$

3. m-Polar Spherical Fuzzy Set

Now we define m-polar spherical fuzzy sets (mPSFSs) as a hybrid structure comprised of both spherical fuzzy sets (SFS) and m-polar fuzzy sets (mPSFS). For $m=1$, an mPSFS turns into an SFS.

Definition 4.

A fuzzy $\overline{{\mathbb{S}}^{\Gamma }}$ defined on a universal set U of the following form is called an m-polar spherical fuzzy set (mPSFS)

$$\begin{array}{ccc}\hfill \overline{{\mathbb{S}}^{\Gamma }}& =& \{<({\tilde{\mu }}^{(1)}(\breve{⨿}),{\gamma }^{(1)}(\breve{⨿}),{\tilde{\eta }}^{(1)}(\breve{⨿})),({\tilde{\mu }}^{(2)}(\breve{⨿}),{\gamma }^{(2)}(\breve{⨿}),{\tilde{\eta }}^{(2)}(\breve{⨿})),\hfill \\ & & \cdots ,({\tilde{\mu }}^{(m)}(\breve{⨿}),{\gamma }^{(m)}(\breve{⨿}),{\tilde{\eta }}^{(m)}(\breve{⨿}))>:\breve{⨿}\in U\}\hfill \\ & =& \left\{{〈\breve{⨿},\left({\tilde{\mu }}^{(j)}(\breve{⨿}),{\gamma }^{(j)}(\breve{⨿}),{\tilde{\eta }}^{(j)}(x)\right)〉}_{j=1}^m:\breve{⨿}\in U\right\}\hfill \end{array}$$

where ${\tilde{\mu }}^{(j)}:M\to [0,1],{\gamma }^{(j)}:M\to [0,1],{\tilde{\eta }}^{(j))}:M\to [0,1]$ represent the membership function (MF), hesitancy function (IF), and non-membership function (NMF), respectively, and the values ${\tilde{\mu }}^{(j)}(\breve{⨿}),{\gamma }^{(j)}(x\breve{⨿},{\tilde{\eta }}^{(j)}(\breve{⨿})\in [0,1]$ represent the membership grade (MG), hesitancy grade (HG), and non-membership grade (NMG), respectively, which satisfy the condition

$$0\le {\left({\tilde{\mu }}^{(j)}(\breve{⨿})\right)}^2+{\left({\gamma }^{(j)}(\breve{⨿})\right)}^2+{\left({\tilde{\eta }}^{(j)}(\breve{⨿})\right)}^2\le 1.$$

The refusal degree is $\mathfrak{R}=\sqrt{1-{\left({\tilde{\mu }}^{(j)}(\breve{⨿})\right)}^2-{\left({\gamma }^{(j)}(\breve{⨿})\right)}^2-{\left({\tilde{\eta }}^{(j)}(\breve{⨿})\right)}^2}$, j = 1, 2, 3, …, m.

An m-polar spherical fuzzy number (mPSFN) can be written as

$$\begin{array}{ccc}\hfill \mathcal{N}& =& 〈({\tilde{\mu }}^{(1)}(x),{\gamma }^{(1)}(x),{\tilde{\eta }}^{(1)}(x)),({\tilde{\mu }}^{(2)}(x),{\gamma }^{(2)}(x),{\tilde{\eta }}^{(2)}(x)),\cdots ,({\tilde{\mu }}^{(m)}(x),{\gamma }^{(m)}(x),{\tilde{\eta }}^{(m)}(x))〉\hfill \\ & =& {〈({\tilde{\mu }}^{(j)}(\breve{⨿}),{\gamma }^{(j)}(x),{\tilde{\eta }}^{(j)}(x)〉}_{j=1}^m\hfill \end{array}$$

with the constraint

$$0\le {\left({\tilde{\mu }}^{(j)}(\breve{⨿})\right)}^2+{\left({\gamma }^{(j)}(\breve{⨿})\right)}^2+{\left({\tilde{\eta }}^{(j)}(\breve{⨿})\right)}^2\le 1$$

For a fixed $\breve{⨿}$, $N=〈({\tilde{\mu }}^{(1)},{\gamma }^{(1)},{\tilde{\eta }}^{(1)}),({\tilde{\mu }}^{(2)},{\gamma }^{(2)},{\tilde{\eta }}^{(2)}),\cdots ,({\tilde{\mu }}^{(m)},{\gamma }^{(m)},{\tilde{\eta }}^{(m)})〉$ is called m-polar spherical fuzzy number (mPSFN).

Tabular representation of (mPSFS) with cardinality K is expressed in

Table 4. m-polar spherical fuzzy sets.

$\overline{{\mathbb{S}}^{\mathbf{\Gamma }}}$	$\mathit{mPSFSs}$
${\breve{⨿}}_1$	$\left({\tilde{\mu }}^{(1)}({\breve{⨿}}_1),{\gamma }^{(1)}({\breve{⨿}}_1),{\tilde{\eta }}^{(1)}({\breve{⨿}}_1)\right)\left({\tilde{\mu }}^{(2)}({\breve{⨿}}_1),{\gamma }^{(2)}({\breve{⨿}}_1),{\tilde{\eta }}^{(2)}({\breve{⨿}}_1)\right)\cdots \left({\tilde{\mu }}^{(m)}({\breve{⨿}}_1),{\gamma }^{(m)}({\breve{⨿}}_1),{\tilde{\eta }}^{(m)}({\breve{⨿}}_1)\right)$
${\breve{⨿}}_2$	$\left({\tilde{\mu }}^{(1)}({\breve{⨿}}_2),{\gamma }^{(1)}({\breve{⨿}}_2),{\tilde{\eta }}^{(1)}({\breve{⨿}}_2)\right)\left({\tilde{\mu }}^{(2)}({\breve{⨿}}_2),{\gamma }^{(2)}({\breve{⨿}}_2),{\tilde{\eta }}^{(2)}({\breve{⨿}}_2)\right),\cdots \left({\tilde{\mu }}^{(m)}({\breve{⨿}}_2),{\gamma }^{(m)}({\breve{⨿}}_2),{\tilde{\eta }}^{(m)}({\breve{⨿}}_2)\right)$
${\breve{⨿}}_3$	$\left({\tilde{\mu }}^{(1)}({\breve{⨿}}_3),{\gamma }^{(1)}({\breve{⨿}}_3),{\tilde{\eta }}^{(1)}({\breve{⨿}}_3)\right)\left({\tilde{\mu }}^{(2)}({\breve{⨿}}_3),{\gamma }^{(2)}({\breve{⨿}}_3),{\tilde{\eta }}^{(2)}({\breve{⨿}}_3)\right),\cdots \left({\tilde{\mu }}^{(m)}({\breve{⨿}}_3),{\gamma }^{(m)}({\breve{⨿}}_3),{\tilde{\eta }}^{(m)}({\breve{⨿}}_3)\right)$
⋮	⋮
${\breve{⨿}}_k$	$\left({\tilde{\mu }}^{(1)}({\breve{⨿}}_k),{\gamma }^{(1)}({\breve{⨿}}_k),{\tilde{\eta }}^{(1)}({\breve{⨿}}_k)\right),\left({\tilde{\mu }}^{(2)}({\breve{⨿}}_k),{\gamma }^{(2)}({\breve{⨿}}_k),{\tilde{\eta }}^{(2)}({\breve{⨿}}_k)\right),\cdots \left({\tilde{\mu }}^{(m)}({\breve{⨿}}_k),{\gamma }^{(m)}({\breve{⨿}}_k),{\tilde{\eta }}^{(m)}({\breve{⨿}}_k)\right)$

.

And matrix representation of m-polar spherical fuzzy set(mPSFS) is

$${\overline{{\mathbb{S}}^{\Gamma }}}_{k,m}=\left(\begin{array}{cccc}\left({\tilde{\mu }}^{(1)}({\breve{⨿}}_1),{\gamma }^{(1)}({\breve{⨿}}_1),{\tilde{\eta }}^{(1)}({\breve{⨿}}_1)\right),& \left({\tilde{\mu }}^{(2)}({\breve{⨿}}_1),{\gamma }^{(2)}({\breve{⨿}}_1),{\tilde{\eta }}^{(2)}({\breve{⨿}}_1)\right),& \cdots & \left({\tilde{\mu }}^{(m)}({\breve{⨿}}_1),{\gamma }^{(m)}({\breve{⨿}}_1),{\tilde{\eta }}^{(m)}({\breve{⨿}}_1)\right)\\ \left({\tilde{\mu }}^{(1)}({\breve{⨿}}_2),{\gamma }^{(1)}({\breve{⨿}}_2),{\tilde{\eta }}^{(1)}({\breve{⨿}}_2)\right),& \left({\tilde{\mu }}^{(2)}({\breve{⨿}}_2),{\gamma }^{(2)}({\breve{⨿}}_2),{\tilde{\eta }}^{(2)}({\breve{⨿}}_2)\right),& \cdots & \left({\tilde{\mu }}^{(m)}({\breve{⨿}}_2),{\gamma }^{(m)}({\breve{⨿}}_2),{\tilde{\eta }}^{(m)}({\breve{⨿}}_2)\right)\\ \left({\tilde{\mu }}^{(1)}({\breve{⨿}}_3),{\gamma }^{(1)}({\breve{⨿}}_3),{\tilde{\eta }}^{(1)}({\breve{⨿}}_3)\right),& \left({\tilde{\mu }}^{(2)}({\breve{⨿}}_3),{\gamma }^{(2)}({\breve{⨿}}_3),{\tilde{\eta }}^{(2)}({\breve{⨿}}_3)\right),& \cdots & \left({\tilde{\mu }}^{(m)}({\breve{⨿}}_3),{\gamma }^{(m)}({\breve{⨿}}_3),{\tilde{\eta }}^{(m)}({\breve{⨿}}_3)\right)\\ ⋮& ⋮& \ddots & ⋮\\ \left({\tilde{\mu }}^{(1)}({\breve{⨿}}_k),{\gamma }^{(1)}({\breve{⨿}}_k),{\tilde{\eta }}^{(1)}({\breve{⨿}}_k)\right),& \left({\tilde{\mu }}^{(2)}({\breve{⨿}}_k),{\gamma }^{(2)}({\breve{⨿}}_k),{\tilde{\eta }}^{(2)}({\breve{⨿}}_k)\right),& \cdots & \left({\tilde{\mu }}^{(m)}({\breve{⨿}}_k),{\gamma }^{(m)}({\breve{⨿}}_k),{\tilde{\eta }}^{(m)}({\breve{⨿}}_k)\right)\end{array}\right)$$

Example 1.

Let $M=\{{\breve{⨿}}_1,{\breve{⨿}}_2,{\breve{⨿}}_3\}$ be the set of vehicles. Then, 5PSFS in M is expressed in

Table 5. 5-polar spherical fuzzy set $\overline{{\mathbb{S}}^{\mathbf{\Gamma }}}$.

$\overline{{\mathbb{S}}^{\mathbf{\Gamma }}}$	$5\mathit{PSFSs}$
${\breve{⨿}}_1$	$\left(0.389,0.175,0.412\right),\left(0.655,0.423,0.392\right),\left(0.622,0.183,0.245\right),\left(0.417,0.118,0.279\right),\left(0.397,0.271,0.369\right)$
${\breve{⨿}}_2$	$\left(0.546,0.253,0.645\right),\left(0.391,0.125,0.629\right),\left(0.620,0.187,0.390\right),\left(0.445,0.198,0.322\right),\left(0.467,0.218,0.329\right)$
${\breve{⨿}}_3$	$\left(0.719,0.345,0.283\right),\left(0.320,0.217,0.691\right),\left(0.543,0.165,0.281\right),\left(0.623,0.346,0.479\right),\left(0.517,0.118,0.249\right)$

.

In 5PSFS, each vehicle namely, ${\breve{⨿}}_1$, ${\breve{⨿}}_2$, and ${\breve{⨿}}_3$ is examined under 5 attributes $(j=1,2,3,4,5)$, and evaluated in terms of mPSFNs. From the first row of the table, the first triplet $\left(0.389,0.175,0.412\right)$ shows that vehicle ${\breve{⨿}}_1$ has a 38.9% membership grade, 17.5% hesitancy grade, and 41.2% non-membership grade for the first attribute. Similarly, we may see the additional values that relate to each attribute.

Definition 5.

Let ${\overline{{\mathbb{S}}^{\Gamma }}}_A$ and ${\overline{{\mathbb{S}}^{\Gamma }}}_B$ be two mPSFSs. Then,

• ${\overline{{\mathbb{S}}^{\Gamma }}}_A\cup {\overline{{\mathbb{S}}^{\Gamma }}}_B=\left\{{〈x,\left(max\left({\tilde{\mu }}_A^{(j)}(\breve{⨿}),{\tilde{\mu }}_B^{(j)}(\breve{⨿})\right),min\left({\gamma }_A^{(j)}(\breve{⨿}),{\gamma }_B^{(j)}(\breve{⨿})\right),min\left({\tilde{\eta }}_A^{(j)}(\breve{⨿}),{\tilde{\eta }}_B^{(j)}(\breve{⨿})\right)\right)〉}_{j=1}^m:\breve{⨿}\in U\right\}$
• ${\overline{{\mathbb{S}}^{\Gamma }}}_A\cap {\overline{{\mathbb{S}}^{\Gamma }}}_B=\left\{{〈\breve{⨿},\left(min\left({\tilde{\mu }}_A^{(j)}(\breve{⨿}),{\tilde{\mu }}_B^{(j)}(\breve{⨿})\right),max\left({\gamma }_A^{(j)}(\breve{⨿}),{\gamma }_B^{(j)}(\breve{⨿})\right),max\left({\tilde{\eta }}_A^{(j)}(\breve{⨿}),{\tilde{\eta }}_B^{(j)}(\breve{⨿})\right)\right)〉}_{j=1}^m:\breve{⨿}\in U\right\}$
• ${\overline{{\mathbb{S}}^{\Gamma }}}_A\subseteq {\overline{{\mathbb{S}}^{\Gamma }}}_{B}iff{\tilde{\mu }}_A^{(j)}(\breve{⨿})⪯{\tilde{\mu }}_B^{(j)}(\breve{⨿}),{\gamma }_A^{(j)}(\breve{⨿})⪰{\gamma }_B^{(j)}(\breve{⨿}),{\tilde{\eta }}_A^{(j)}(\breve{⨿})⪰{\tilde{\eta }}_B^{(j)}(\breve{⨿}),\forall \breve{⨿}\in U,j=1,2,3,...,m$
• ${\overline{{\mathbb{S}}^{\Gamma }}}_A\doteq {\overline{{\mathbb{S}}^{\Gamma }}}_{B}iff{\overline{{\mathbb{S}}^{\Gamma }}}_A\subseteq {\overline{{\mathbb{S}}^{\Gamma }}}_{B}and{\overline{{\mathbb{S}}^{\Gamma }}}_A\supseteq {\overline{{\mathbb{S}}^{\Gamma }}}_B$
• ${\overline{{\mathbb{S}}^{\Gamma }}}_A^c=\left\{{〈\breve{⨿},\left({\tilde{\eta }}_A^{(j)}(\breve{⨿}),{\gamma }_A^{(j)}(\breve{⨿}),{\tilde{\mu }}_A^{(j)}(\breve{⨿})\right)〉}_{j=1}^m:x\in U\right\}$
• ${\overline{{\mathbb{S}}^{\Gamma }}}_A\oplus {\overline{{\mathbb{S}}^{\Gamma }}}_B=\left\{{〈\breve{⨿},\left({\left(({\tilde{\mu }}_A^{(j)}(\breve{⨿}){)}^2+({\tilde{\mu }}_B^{(j)}(\breve{⨿}){)}^2-({\tilde{\mu }}_A^{(j)}(\breve{⨿}){)}^2({\tilde{\mu }}_B^{(j)}(\breve{⨿}){)}^2)\right)}^{1/2},{\left({(1-({\tilde{\mu }}_B^{(j)}(\breve{⨿}))}^2)({\gamma }_A^{(j)}(\breve{⨿}){)}^2+{(1-({\tilde{\mu }}_A^{(j)}(\breve{⨿}))}^2)({\gamma }_B^{(j)}(\breve{⨿}){)}^2-({\gamma }_A^{(j)}(\breve{⨿}){{)}^2({\gamma }_B^{(j)}(\breve{⨿}))}^2\right)}^{1/2},{\tilde{\eta }}_A^{(j)}(x\breve{⨿}){\tilde{\eta }}_B^{(j)}(\breve{⨿})\right)〉}_{j=1}^m:x\in U\right\}$
• ${\overline{{\mathbb{S}}^{\Gamma }}}_A\otimes {\overline{{\mathbb{S}}^{\Gamma }}}_B=\left\{{〈x,\left({\tilde{\mu }}_A^{(j)}(x){\tilde{\mu }}_B^{(j)}(x),{\left({(1-({\tilde{\eta }}_B^{(j)}(\breve{⨿}))}^2)({\gamma }_A^{(j)}(\breve{⨿}){)}^2+{(1-({\tilde{\eta }}_A^{(j)}(\breve{⨿}))}^2)({\gamma }_B^{(j)}(\breve{⨿}){)}^2-({\gamma }_A^{(j)}(\breve{⨿}){{)}^2({\gamma }_B^{(j)}(\breve{⨿}))}^2\right)}^{1/2},{\left(({\tilde{\eta }}_A^{(j)}(\breve{⨿}){)}^2+({\tilde{\eta }}_B^{(j)}(\breve{⨿}){)}^2-({\tilde{\eta }}_A^{(j)}(\breve{⨿}){{)}^2({\tilde{\eta }}_B^{(j)}(\breve{⨿}))}^2\right)}^{1/2}\right)〉}_{j=1}^m:\breve{⨿}\in U\right\}$
• $\lambda {\overline{{\mathbb{S}}^{\Gamma }}}_A=\left\{{〈\breve{⨿},\left({\left(1-{\left(1-({\tilde{\mu }}_A^{(j)}(\breve{⨿}){)}^2\right)}^{\lambda }\right)}^{1/2},{\left({\left(1-{\tilde{\mu }}_A^{(j)}(\breve{⨿}{))}^2\right)}^{\lambda }-{\left(1-({\tilde{\mu }}_A^{(j)}(\breve{⨿}){{)}^2-({\gamma }_A^{(j)}(\breve{⨿}))}^2\right)}^{\lambda }\right)}^{1/2},({\tilde{\eta }}_A^{(j)}(\breve{⨿}){)}^{\lambda }\right)〉}_{j=1}^m:x\in U\right\},\lambda >0$
• ${\overline{{\mathbb{S}}^{\Gamma }}}_A^{\lambda }=\{{〈x,\left(({\tilde{\mu }}_A^{(j)}(\breve{⨿}){)}^{\lambda },{\left({(1-({\tilde{\eta }}_A^{(j)}(\breve{⨿}))}^2{)}^{\lambda }-{\left(1-({\tilde{\eta }}_A^{(j)}(\breve{⨿}){{)}^2-({\gamma }_A^{(j)}(\breve{⨿}))}^2\right)}^{\lambda }\right)}^{1/2},{\left(1-{\left(1-({\tilde{\eta }}_A^{(j)}(\breve{⨿}){)}^2\right)}^{\lambda }\right)}^{1/2}\right)〉}_{j=1}^m:\in U\},\lambda >0$

Example 2.

Let $M=\{{\breve{⨿}}_1,{\breve{⨿}}_2,{\breve{⨿}}_1^{·},{\breve{⨿}}_2^{·}\}$ and let ${\overline{{\mathbb{S}}^{\Gamma }}}_A$ and ${\overline{{\mathbb{S}}^{\Gamma }}}_B$ be two 5PSFSs defined as shown in the

Table 6. 5-polar spherical fuzzy set A.

${\overline{{\mathbb{S}}^{\mathbf{\Gamma }}}}_{\mathit{A}}$	$5\mathit{PSFSs}$
${\breve{⨿}}_1$	$\left(0.389,0.145,0.422\right),\left(0.665,0.126,0.351\right),\left(0.682,0.183,0.295\right),\left(0.678,0.112,0.299\right),\left(0.419,0.197,0.382\right)$
${\breve{⨿}}_2$	$\left(0.576,0.243,0.391\right),\left(0.217,0.450,0.632\right),\left(0.690,0.119,0.351\right),\left(0.442,0.198,0.454\right),\left(0.523,0.215,0.323\right)$

and

Table 7. 5-polar spherical fuzzy set B.

${\overline{{\mathbb{S}}^{\mathbf{\Gamma }}}}_{\mathit{B}}$	$5\mathit{PSFSs}$
${\breve{⨿}}_1^{\prime }$	$\left(0.362,0.189,0.614\right),\left(0.699,0.009,0.298\right),\left(0.389,0.267,0.510\right),\left(0.477,0.120,0.321\right),\left(0.411,0.179,0.399\right)$
${\breve{⨿}}_2^{\prime }$	$\left(0.541,0.275,0.332\right),\left(0.341,0.195,0.324\right),\left(0.594,0.167,0.336\right),\left(0.543,0.116,0.313\right),\left(0.492,0.289,0.314\right)$

, respectively.

Then, union ${\overline{{\mathbb{S}}^{\Gamma }}}_A\cup {\overline{{\mathbb{S}}^{\Gamma }}}_B$ of ${\overline{{\mathbb{S}}^{\Gamma }}}_A$ and ${\overline{{\mathbb{S}}^{\Gamma }}}_B$ can be defined as shown in the

Table 8. Union of two 5-polar spherical fuzzy sets ${\overline{{\mathbb{S}}^{\Gamma }}}_A\cup {\overline{{\mathbb{S}}^{\Gamma }}}_B$.

${\overline{{\mathbb{S}}^{\mathbf{\Gamma }}}}_{\mathit{A}}\cup {\overline{{\mathbb{S}}^{\mathbf{\Gamma }}}}_{\mathit{B}}$	$5\mathit{PSFSs}$
${\breve{⨿}}_1\cup {\breve{⨿}}_1^{\prime }$	$\left(0.389,0.145,0.422\right),\left(0.699,0.009,0.298\right),\left(0.389,0.183,0.295\right),\left(0.477,0.02,0.29\right),\left(0.419,0.179,0.382\right)$
${\breve{⨿}}_2\cup {\breve{⨿}}_2^{\prime }$	$\left(0.576,0.243,0.332\right),\left(0.341,0.195,0.324\right),\left(0.690,0.119,0.336\right),\left(0.543,0.116,0.313\right),\left(0.523,0.215,0.314\right)$

.

Then, intersection ${\overline{{\mathbb{S}}^{\Gamma }}}_A\cap {\overline{{\mathbb{S}}^{\Gamma }}}_B$ of ${\overline{{\mathbb{S}}^{\Gamma }}}_A$ and ${\overline{{\mathbb{S}}^{\Gamma }}}_B$ can be defined as shown in the

Table 9. Intersection of two 5-polar spherical fuzzy sets ${\overline{{\mathbb{S}}^{\Gamma }}}_A\cap {\overline{{\mathbb{S}}^{\Gamma }}}_B$.

${\overline{{\mathbb{S}}^{\mathbf{\Gamma }}}}_{\mathit{A}}\cap {\overline{{\mathbb{S}}^{\mathbf{\Gamma }}}}_{\mathit{B}}$	$5\mathit{PSFSs}$
${\breve{⨿}}_1\cap {\breve{⨿}}_1^{\prime }$	$\left(0.362,0.189,0.614\right),\left(0.665,0.126,0.351\right),\left(0.389,0.267,0.510\right),\left(0.477,0.120,0.321\right),\left(0.411,0.197,0.399\right)$
${\breve{⨿}}_2\cap {\breve{⨿}}_2^{\prime }$	$\left(0.541,0.275,0.391\right),\left(0.217,0.450,0.632\right),\left(0.594,0.167,0.351\right),\left(0.442,0.198,0.454\right),\left(0.492,0.289,0.323\right)$

.

And the complement of ${\overline{{\mathbb{S}}^{\Gamma }}}_A^c$ can be calculated as shown in the

Table 10. Complement operation on 5-polar spherical fuzzy set.

${\overline{{\mathbb{S}}^{\mathbf{\Gamma }}}}_{\mathit{A}}^{\mathit{c}}$	$5\mathit{PSFSs}$
${\breve{⨿}}_1^c$	$\left(0.422,0.145,0.389\right),\left(0.351,0.126,0.665\right),\left(0.295,0.183,0.682\right),\left(0.299,0.112,0.678\right),\left(0.382,0.197,0.419\right)$
${\breve{⨿}}_2^c$	$\left(0.391,0.243,0.576\right),\left(0.632,0.450,0.217\right),\left(0.351,0.119,0.690\right),\left(0.454,0.198,0.442\right),\left(0.323,0.215,0.523\right)$

.

Definition 6.

The score function for any $mPSFN$ $e=({\tilde{\mu }}_e^{(j)},{\gamma }_e^{(j)},{\tilde{\eta }}_e^{(j)})$, j = 1, 2, 3, …, m is defined as

$$s(e)=\frac{1}{m}\left({\displaystyle \sum _{j=1}^m}{\tilde{\mu }}_p^{(j)2}-{\gamma }_p^{{(j)}^2}-{\tilde{\eta }}_p^{{(j)}_2}\right)$$

where $-1\le s(e)\le 1$. If $e_i$ and $e_j$ are two spherical fuzzy numbers, then

• Given $s(e_i)<s(e_j)$, $e_i$ precedes $e_j$ i.e., $e_i\prec e_j$,
• Given $s(e_i)>s(e_j)$, $e_i$ succeeds $e_j$ i.e., $e_i\succ e_j$,
• Given $s(e_i)=s(e_j)$, $e_i$∼$e_j$.

Definition 7. 

The accuracy function for any $SFN$$e=({\tilde{\mu }}_e^{(j)},{\gamma }_e^{(j)},{\tilde{\eta }}_e^{(j)})$, j = 1, 2, 3, …, m is defined as

$$a(e)=\frac{1}{m}\left({\displaystyle \sum _{j=1}^m}{\tilde{\mu }}_p^{(j)2}+{\gamma }_p^{{(j)}^2}+{\tilde{\eta }}_p^{(j)2}\right)$$

where $0\le s(e)\le 1$. If $e_i$ and $e_j$ are two spherical fuzzy numbers, then

• If $s(e_i)$ and $s(e_j)$ coincide and $a(e_i)$ exceeds $a(e_j)$, then $e_i\succ e_j$,
• If both $s(e_i),s(e_j)$ and $a(e_i),a(e_j)$ coincide, then $e_i$∼$e_j$

Definition 8.

An m-PSFS is said to be an empty or null m-PSFS if ${\tilde{\mu }}^{(j)}(x)=0, {\gamma }^{(j)}(x)=k$ and ${\tilde{\eta }}^{(j)}(x)=1-k$ for all $\mathrm{j}=1,2,3,\dots \mathrm{m}$ and $0\le k\le 1$. It is denoted as $\overline{\overline{⌀}}$ and scripted as

$$\overline{\overline{⌀}}=\{\langle x,((0,k,1-k),(0,k,1-k),\dots ,(0,k,1-k))\rangle :0\le k\le 1\&x\in U\}$$

Its matrix representation is

$$\overline{\overline{⌀}}=\left[\begin{array}{cccc}(0,k,1-k)& (0,k,1-k)& \cdots & (0,k,1-k)\\ (0,k,1-k)& (0,k,1-k)& \cdots & (0,k,1-k)\\ ⋮& ⋮& \ddots & ⋮\\ (0,k,1-k)& (0,k,1-k)& \cdots & (0,k,1-k)\end{array}\right]$$

Definition 9.

An m-PSFS is said to be an absolute m-PSFS if ${\tilde{\mu }}^{(j)}(x)=1-k,{\pi }^{(j)}(x)=k$ and $v^{(j)}(x)=0$ for all $\mathrm{j}=1,2,3,\dots \mathrm{m}$ and $0\le k\le 1$. It is denoted as $\overline{\mathbb{X}}$ and scripted as

$$\overline{\mathbb{X}}=\{\langle x,((1-k,k,0),(1-k,k,0),\dots ,(1-k,k,0))\rangle :0\le k\le 1\&x\in U\}$$

Its matrix representation is

$$\overline{\mathbb{X}}=\left[\begin{array}{cccc}(1-k,k,0)& (1-k,k,0)& \cdots & (1-k,k,0)\\ (1-k,k,0)& (1-k,k,0)& \cdots & (1-k,k,0)\\ ⋮& ⋮& \ddots & ⋮\\ (1-k,k,0)& (1-k,k,0)& \cdots & (1-k,k,0)\end{array}\right]$$

4. m-Polar Spherical Fuzzy Topology

This section describes the idea of mPSF-topology in relation to a mPSF set. The concepts of mPSF-union and mPSF-intersection are used as building blocks while designing mPSF topology. Several elements of the mPSF-topology are defined, and the accompanying illustrations are presented in an optimized way.

Definition 10.

Assume ${\mathbb{X}}^{\Gamma }$ is a set which is non-empty and mPSFS(${\mathbb{X}}^{\Gamma }$) is the collection of all the mPSF-subsets. A sub-collection ${\mathfrak{T}}^{\Omega }$ of mPSFS(${\mathbb{X}}^{\Gamma }$) is called m-polar Spherical fuzzy topology (mPSFT) on ${\mathbb{X}}^{\Gamma }$ if the following properties hold true:

(i)

$\overline{\overline{⌀}}$, ${\mathbb{X}}^{\Gamma }\in {\mathfrak{T}}^{\Omega }$

(ii)

${\mathfrak{T}}^{\Omega }$ is closed under arbitrary union, i.e., if ${\overline{{\mathbb{S}}^{\Gamma }}}_q\in {\mathfrak{T}}^{\Omega },\forall q\in Q$, then ${\cup }_{q\in Q}{\overline{{\mathbb{S}}^{\Gamma }}}_q\in {\mathfrak{T}}^{\Omega }.$

(iii)

${\mathfrak{T}}^{\Omega }$ is closed under finite intersection, i.e., if ${\overline{{\mathbb{S}}^{\Gamma }}}_{\tilde{\mu }},{\overline{{\mathbb{S}}^{\Gamma }}}_{\tilde{\eta }}\in {\mathfrak{T}}^{\Omega }$, then ${\overline{{\mathbb{S}}^{\Gamma }}}_{\tilde{\mu }}\cap {\overline{{\mathbb{S}}^{\Gamma }}}_{\tilde{\eta }}\in {\mathfrak{T}}^{\Omega }.$

The couplet ($X,{\mathfrak{T}}^{\Omega }$), or simply ${\mathfrak{T}}^{\Omega }$, is known as m-polar spherical fuzzy topological space, shortened as mPSFTS.

Example 3.

Let $\overline{\mathbb{X}}=\{{\breve{⨿}}_1,{\breve{⨿}}_2,{\breve{⨿}}_3\}$ be a universal set and $S_1,S_2$, and $S_3$ be as shown in

Table 11. 4-polar spherical fuzzy set $S_1$.

$S_1$	$4\mathit{PSFSs}$
${\breve{⨿}}_1$	$\left(0.429,0.738,0.275\right),\left(0.372,0.669,0.232\right),\left(0.731,0.384,0.419\right),\left(0.556,0.423,0.361\right)$
${\breve{⨿}}_2$	$\left(0.542,0.821,0.121\right),\left(0.734,0.298,0.467\right),\left(0.657,0.156,0.279\right),\left(0.459,0.325,0.576\right)$
${\breve{⨿}}_3$	$\left(0.425,0.145,0.361\right),\left(0.421,0.264,0.532\right),\left(0.541,0.121,0.219\right),\left(0.785,0.312,0.421\right)$

,

Table 12. 4-polar spherical fuzzy set $S_2$.

$S_2$	$4\mathit{PSFSs}$
${\breve{⨿}}_1$	$\left(0.411,0.761,0.312\right),\left(0.352,0.731,0.248\right),\left(0.653,0.451,0.527\right),\left(0.418,0.598,0.426\right)$
${\breve{⨿}}_2$	$\left(0.398,0.865,0.178\right),\left(0.645,0.357,0.576\right),\left(0.611,0.257,0.343\right),\left(0.405,0.399,0.586\right)$
${\breve{⨿}}_3$	$\left(0.365,0.198,0.376\right),\left(0.405,0.357,0.545\right),\left(0.445,0.267,0.376\right),\left(0.634,0.398,0.499\right)$

and

Table 13. 4-polar spherical fuzzy set $S_3$.

$S_3$	$4\mathit{PSFSs}$
${\breve{⨿}}_1$	$\left(0.521,0.678,0.229\right),\left(0.439,0.547,0.165\right),\left(0.763,0.249,0.211\right),\left(0.618,0.403,0.267\right)$
${\breve{⨿}}_2$	$\left(0.632,0.765,0.18\right),\left(0.76,0.269,0.424\right),\left(0.721,0.136,0.234\right),\left(0.532,0.234,0.477\right)$
${\breve{⨿}}_3$	$\left(0.534,0.132,0.256\right),\left(0.468,0.213,0.461\right),\left(0.545,0.167,0.189\right),\left(0.798,0.254,0.345\right)$

below

Then ${\mathfrak{T}}_1^{\Omega }=\{\overline{\overline{⌀}},\overline{\mathbb{X}}\}$, ${\mathfrak{T}}_2^{\Omega }=\{\overline{\overline{⌀}},S_1,\overline{\mathbb{X}}\}$, ${\mathfrak{T}}_3^{\Omega }=\{\overline{\overline{⌀}},S_2,\overline{\mathbb{X}}\}$, ${\mathfrak{T}}_4^{\Omega }=\{\overline{\overline{⌀}},S_3,\overline{\mathbb{X}}\}$,${\mathfrak{T}}_5^{\Omega }=\{\overline{\overline{⌀}},S_1,S_2,\overline{\mathbb{X}}\}$, ${\mathfrak{T}}_6^{\Omega }=\{\overline{\overline{⌀}},S_1,S_3,\overline{\mathbb{X}}\}$,${\mathfrak{T}}_7^{\Omega }=\{\overline{\overline{⌀}},S_2,S_3,\overline{\mathbb{X}}\}$, and ${\mathfrak{T}}_8^{\Omega }=\{\overline{\overline{⌀}},S_1,S_2,S_3,\overline{\mathbb{X}}\}$ all are 4-PSFTS over $\overline{\mathbb{X}}$. The components $\overline{\overline{⌀}}$ and $\overline{\mathbb{X}}$ in all these topologies are both 4-polar spherical fuzzy open and closed sets.

Definition 11.

Let ${\mathfrak{T}}_1^{\Omega }$ and ${\mathfrak{T}}_2^{\Omega }$ be two mPSF-topologies over X. If every member of ${\mathfrak{T}}_1^{\Omega }$ is also a member of ${\mathfrak{T}}_2^{\Omega }$, i.e., ${\mathfrak{T}}_1^{\Omega }\subseteq {\mathfrak{T}}_2^{\Omega }$, then ${\mathfrak{T}}_1^{\Omega }$ and ${\mathfrak{T}}_2^{\Omega }$ are comparable. In such situations, ${\mathfrak{T}}_1^{\Omega }$ is purported to be coarser or weaker than ${\mathfrak{T}}_2^{\Omega }$ and ${\mathfrak{T}}_2^{\Omega }$ is purported to be finer or stronger than ${\mathfrak{T}}_1^{\Omega }$. In Example 3, ${\mathfrak{T}}_3^{\Omega }$ is coarser than ${\mathfrak{T}}_2^{\Omega }$, and hence these are comparable.

Remark 1.

The mPSFTS intersection is always an mPSFTS, however, its union does not have to be an mPSFTS.

Example 4.

Let X=$\{{\breve{⨿}}_1,{\breve{⨿}}_2\}$ be the universal set and ${\overline{{\mathbb{S}}^{\Gamma }}}_1$ and ${\overline{{\mathbb{S}}^{\Gamma }}}_2$ be 3PSFSs as provided below in

Table 14. 3-polar spherical fuzzy set ${\overline{{\mathbb{S}}^{\Gamma }}}_1$.

${\overline{{\mathbb{S}}^{\mathbf{\Gamma }}}}_1$	$3\mathit{PSFSs}$
${\breve{⨿}}_1$	$\left(0.276,0.413,0.720\right),\left(0.425,0.511,0.623\right),\left(0.324,0.256,0.163\right),\left(0.536,0.168,0.256\right)$
${\breve{⨿}}_2$	$\left(0.424,0.563,0.471\right),\left(0.265,0.891,0.314\right),\left(0.476,0.145,0.67\right),\left(0.406,0.211,0.321\right)$

and

Table 15. 4-polar spherical fuzzy set ${\overline{{\mathbb{S}}^{\Gamma }}}_2$.

${\overline{{\mathbb{S}}^{\mathbf{\Gamma }}}}_2$	$4\mathit{PSFSs}$
${\breve{⨿}}_1$	$\left(0.414,0.320,0.646\right),\left(0.387,0.569,0.648\right),\left(0.368,0.217,0.11\right),\left(0.571,0.116,0.215\right)$
${\breve{⨿}}_2$	$\left(0.587,0.465,0.381\right),\left(0.322,0.735,0.247\right),\left(0.413,0.243,0.717\right),\left(0.503,0.213,0.712\right)$

,

Then,

$${\mathfrak{T}}_1^{\Omega }=\{\overline{\overline{⌀}},{\overline{{\mathbb{S}}^{\Gamma }}}_1,\overline{\mathbb{X}}\},$$

$${\mathfrak{T}}_2^{\Omega }=\{\overline{\overline{⌀}},{\overline{{\mathbb{S}}^{\Gamma }}}_2,\overline{\mathbb{X}}\}$$

are 4PSF topologies over X. However,

$${\mathfrak{T}}_1^{\Omega }\cup {\mathfrak{T}}_2^{\Omega }=\{\overline{\overline{⌀}},{\overline{{\mathbb{S}}^{\Gamma }}}_1,{\overline{{\mathbb{S}}^{\Gamma }}}_2,\overline{\mathbb{X}}\}$$

fails to be a 4PSFT over X.

Theorem 1.

Let $(X,{\mathfrak{T}}^{\Omega })$ be m-polar spherical fuzzy topological spaces. Then, the following conditions are satisfied:

(i)

$\overline{\overline{⌀}}$, $\overline{\mathbb{X}}$ are closed.

(ii)

${\mathfrak{T}}^{\Omega }$ is closed under an arbitrary intersection of closed mPSFSs.

(iii)

${\mathfrak{T}}^{\Omega }$ is closed under a finite number of unions of closed mPSFSs.

Proof. 

(i)

${\overline{\overline{⌀}}}^c=\overline{\mathbb{X}}$ and ${\overline{\mathbb{X}}}^c=\overline{\overline{⌀}}$ both are open and closed mPSFSs.

(ii)

If $\{{\overline{{\mathbb{S}}^{\Gamma }}}_q:{\overline{{\mathbb{S}}^{\Gamma }}}_q^c\in {\mathfrak{T}}^{\Omega },q\in Q\}$ is the collection of all closed mPSFSs, then

$${\left({\cap }_{q\in Q}{\overline{{\mathbb{S}}^{\Gamma }}}_q\right)}^c={\cup }_{q\in Q}{\overline{{\mathbb{S}}^{\Gamma }}}_q^c$$

is open. This shows that ${\cap }_{q\in Q}{\overline{{\mathbb{S}}^{\Gamma }}}_q$ is a closed mPSFS.

(iii)

Because ${\overline{{\mathbb{S}}^{\Gamma }}}_q$ is closed for q = 1, 2, 3, …, n,

$${\left({\cup }_{q=1}^n{\overline{{\mathbb{S}}^{\Gamma }}}_q\right)}^c={\cap }_{q=1}^n{\overline{{\mathbb{S}}^{\Gamma }}}_q^c$$

is an open mPSFS. Thus, ${\cup }_{q=1}^n{\overline{{\mathbb{S}}^{\Gamma }}}_q$ is a closed mPSFS.

□

Definition 12.

Let (X,${\mathfrak{T}}^{\Omega }$) be an mPSFTS and $\mathcal{Y}\subseteq X$ and $\overline{\mathcal{Y}}$ be an absolute $mPSFS$ on $\mathcal{Y}$. Then ${{\mathfrak{T}}^{\Omega }}_{\mathcal{Y}}$ is an mPSF topology on $\mathcal{Y}$ with mPSF open sets as ${\overline{{\mathbb{S}}^{\Gamma }}}_{\mathcal{Y}}={\overline{{\mathbb{S}}^{\Gamma }}}_X\cap \overline{Y}$, where ${\overline{{\mathbb{S}}^{\Gamma }}}_X$ are mPSF open sets of ${\mathfrak{T}}_X^{\Omega }$ and ${\overline{{\mathbb{S}}^{\Gamma }}}_{\mathcal{Y}}$ are mPSF open sets of ${\mathfrak{T}}_Y^{\Omega }$. Then, $\overline{\mathcal{Y}}$ is termed the mPSF-subspace of $\overline{\mathbb{X}}$, i.e.,

$${\mathfrak{T}}_{\mathcal{Y}}^{\Omega }=\{{\overline{{\mathbb{S}}^{\Gamma }}}_{\mathcal{Y}}:{\overline{{\mathbb{S}}^{\Gamma }}}_{\mathcal{Y}}={\overline{{\mathbb{S}}^{\Gamma }}}_X\cap \overline{\mathcal{Y}},{\overline{{\mathbb{S}}^{\Gamma }}}_X\in {\mathfrak{T}}_X^{\Omega }\},$$

with ${\mathfrak{T}}_{\mathcal{Y}}^{\Omega }$ also known as the relative mPSF topology or induced mPSF topology on $\mathcal{Y}$.

Example 5.

Suppose that X=$\{{\breve{⨿}}_1,{\breve{⨿}}_2,{\breve{⨿}}_3\}$ is the universal set. If 4-polar spherical fuzzy set ${\overline{{\mathbb{S}}^{\Gamma }}}_1$ and ${\overline{{\mathbb{S}}^{\Gamma }}}_2$ are defined as in the

Table 16. 4-polar spherical fuzzy set ${\overline{{\mathbb{S}}^{\Gamma }}}_1$.

${\overline{{\mathbb{S}}^{\mathbf{\Gamma }}}}_1$	$4\mathit{PSFSs}$
${\breve{⨿}}_1$	$\left(0.319,0.428,0.486\right),\left(0.398,0.546,0.622\right),\left(0.495,0.809,0.134\right),\left(0.525,0.239,0.284\right)$
${\breve{⨿}}_2$	$\left(0.268,0.297,0.432\right),\left(0.660,0.447,0.081\right),\left(0.168,0.439,0.134\right),\left(0.295,0.099,0.534\right)$
${\breve{⨿}}_3$	$\left(0.635,0.489,0.217\right),\left(0.489,0.317,0.159\right),\left(0.719,0.563,0.443\right),\left(0.455,0.092,0.387\right)$

and

Table 17. 4-polar spherical fuzzy set ${\overline{{\mathbb{S}}^{\Gamma }}}_2$.

${\overline{{\mathbb{S}}^{\mathbf{\Gamma }}}}_2$	$4\mathit{PSFSs}$
${\breve{⨿}}_1$	$\left(0.421,0.167,0.312\right),\left(0.632,0.459,0.430\right),\left(0.697,0.217,0.065\right),\left(0.596,0.217,0.195\right)$
${\breve{⨿}}_2$	$\left(0.523,0.211,0.148\right),\left(0.692,0.216,0.056\right),\left(0.389,0.301,0.112\right),\left(0.364,0.008,0.112\right)$
${\breve{⨿}}_3$	$\left(0.679,0.372,0.213\right),\left(0.694,0.245,0.132\right),\left(0.752,0.321,0.033\right),\left(0.536,0.075,0.211\right)$

, respectively.

then

$${\mathfrak{T}}_X^{\Omega }=\{\overline{\overline{⌀}},{\overline{{\mathbb{S}}^{\Gamma }}}_1,{\overline{{\mathbb{S}}^{\Gamma }}}_2,\overline{\mathbb{X}}\}$$

is a 4PSF topology on X.

Now, let the absolute 4PSF on $\mathcal{Y}=\{{\breve{⨿}}_1,{\breve{⨿}}_3\}\subseteq X$ be is shown in the

Table 18. 4-polar spherical fuzzy set $\overline{\mathcal{Y}}$.

$\overline{\mathcal{Y}}$	$4\mathit{PSFSs}$
${\breve{⨿}}_1$	$\left(1.000,0.000,0.000\right),\left(1.000,0.000,0.000\right),\left(1.000,0.000,0.000\right),\left(1.000,0.000,0.000\right)$
${\breve{⨿}}_3$	$\left(1.000,0.000,0.000\right),\left(1.000,0.000,0.000\right),\left(1.000,0.000,0.000\right),\left(1.000,0.000,0.000\right)$

. Working is shown in

Table 19. 4-polar spherical fuzzy set ${{\mathbb{S}}^{\Gamma }}_1^{{}^{\prime }}$.

$\overline{\mathcal{Y}}\cap {\overline{{\mathbb{S}}^{\mathbf{\Gamma }}}}_1={\overline{{\mathbb{S}}^{\mathbf{\Gamma }}}}_1^{{}^{\prime }}$	$4\mathit{PSFSs}$
${\breve{⨿}}_1$	$\left(0.319,0.428,0.486\right),\left(0.398,0.546,0.622\right),\left(0.495,0.809,0.134\right),\left(0.525,0.239,0.284\right)$
${\breve{⨿}}_3$	$\left(0.635,0.489,0.217\right),\left(0.489,0.317,0.159\right),\left(0.719,0.563,0.443\right),\left(0.455,0.092,0.387\right)$

and

Table 20. 4-polar spherical fuzzy set ${\overline{{\mathbb{S}}^{\Gamma }}}_2^{{}^{\prime }}$.

$\overline{\mathcal{Y}}\cap {\overline{{\mathbb{S}}^{\mathbf{\Gamma }}}}_2={\overline{{\mathbb{S}}^{\mathbf{\Gamma }}}}_2^{{}^{\prime }}$	$4\mathit{PSFSs}$
${\breve{⨿}}_1$	$\left(0.421,0.167,0.312\right),\left(0.632,0.459,0.430\right),\left(0.697,0.217,0.065\right),\left(0.596,0.217,0.195\right)$
${\breve{⨿}}_3$	$\left(0.679,0.372,0.213\right),\left(0.694,0.245,0.132\right),\left(0.752,0.321,0.033\right),\left(0.536,0.075,0.211\right)$

.

Because $\overline{\mathcal{Y}}\cap \overline{\overline{⌀}}=\widetilde{\overline{\overline{⌀}}}$. Furthermore,

and $\overline{\mathcal{Y}}\cap X=\overline{\mathcal{Y}}.$

Thus, ${\mathfrak{T}}_{\mathcal{Y}}^{\Omega }=\{\widetilde{\overline{\overline{⌀}}},{\overline{{\mathbb{S}}^{\Gamma }}}_1^{{}^{\prime }},{\overline{{\mathbb{S}}^{\Gamma }}}_2^{{}^{\prime }},\overline{\mathbb{X}}\}$ is a 4PSF sub-topology of ${\mathfrak{T}}_X^{\Omega }.$

Definition 13.

Let (X, ${\mathfrak{T}}^{\Omega }$) be an mPSFTS and $\overline{{\mathbb{S}}^{\Gamma }}\subseteq mPSFS(X)$; then, the interior of $\overline{{\mathbb{S}}^{\Gamma }}$ is indicated as ${\overline{{\mathbb{S}}^{\Gamma }}}^{\circ }$ and described as the union of all open mPSF subsets included in $\overline{{\mathbb{S}}^{\Gamma }}$. Alternatively, it can be defined as the largest open mPSFS that includes $\overline{{\mathbb{S}}^{\Gamma }}$.

Example 6.

Let X=$\{{\breve{⨿}}_1,{\breve{⨿}}_2,{\breve{⨿}}_3\}$. Let us consider 4PSFSs ${\overline{{\mathbb{S}}^{\Gamma }}}_1$ and ${\overline{{\mathbb{S}}^{\Gamma }}}_2$ in X such that ${\mathfrak{T}}^{\Omega }=\{\overline{\overline{⌀}},S_1,S_2,\overline{\mathbb{X}}\}$ is the topology on X. ${\overline{{\mathbb{S}}^{\Gamma }}}_1$ is given in

Table 21. 4-polar spherical fuzzy set ${\overline{{\mathbb{S}}^{\Gamma }}}_1$.

${\overline{{\mathbb{S}}^{\mathbf{\Gamma }}}}_1$	$4\mathit{PSFSs}$
${\breve{⨿}}_1$	$\left(0.276,0.435,0.394\right),\left(0.254,0.337,0.325\right),\left(0.548,0.440,0.122\right),\left(0.248,0.462,0.282\right)$
${\breve{⨿}}_2$	$\left(0.239,0.332,0.419\right),\left(0.611,0.226,0.192\right),\left(0.440,0.459,0.523\right),\left(0.458,0.286,0.331\right)$
${\breve{⨿}}_3$	$\left(0.316,0.297,0.196\right),\left(0.632,0.149,0.218\right),\left(0.198,0.387,0.291\right),\left(0.627,0.312,0.112\right)$

, ${\overline{{\mathbb{S}}^{\Gamma }}}_2$ is given in

Table 22. 4-polar spherical fuzzy set ${\overline{{\mathbb{S}}^{\Gamma }}}_2$.

${\overline{{\mathbb{S}}^{\mathbf{\Gamma }}}}_2$	$4\mathit{PSFSs}$
${\breve{⨿}}_1$	$\left(0.412,0.229,0.323\right),\left(0.254,0.325,0.190\right),\left(0.630,0.382,0.110\right),\left(0.418,0.362,0.172\right)$
${\breve{⨿}}_2$	$\left(0.406,0.313,0.218\right),\left(0.621,0.210,0.082\right),\left(0.554,0.287,0.137\right),\left(0.554,0.256,0.231\right)$
${\breve{⨿}}_3$	$\left(0.652,0.267,0.134\right),\left(0.674,0.149,0.145\right),\left(0.731,0.329,0.290\right),\left(0.687,0.212,0.092\right)$

and $\overline{{\mathbb{S}}^{\Gamma }}$ is given in

Table 23. 4-polar spherical fuzzy set $\overline{{\mathbb{S}}^{\Gamma }}$.

$\overline{{\mathbb{S}}^{\mathbf{\Gamma }}}$	$4\mathit{PSFSs}$
${\breve{⨿}}_1$	$\left(0.416,0.344,0.389\right),\left(0.465,0.256,0.276\right),\left(0.597,0.385,0.049\right),\left(0.388,0.453,0.231\right)$
${\breve{⨿}}_2$	$\left(0.376,0.276,0.311\right),\left(0.619,0.225,0.089\right),\left(0.595,0.430,0.255\right),\left(0.597,0.210,0.231\right)$
${\breve{⨿}}_3$	$\left(0.654,0.271,0.123\right),\left(0.740,0.112,0.194\right),\left(0.291,0.372,0.115\right),\left(0.736,0.218,0.105\right)$

. Then,

Consider $\overline{{\mathbb{S}}^{\Gamma }}$ as

Then, the 4PSF interior of $\overline{{\mathbb{S}}^{\Gamma }}$ is

$${\overline{{\mathbb{S}}^{\Gamma }}}^{\circ }=\overline{\overline{⌀}}\cup {\overline{{\mathbb{S}}^{\Gamma }}}_1={\overline{{\mathbb{S}}^{\Gamma }}}_1$$

Theorem 2.

Let (X, ${\mathfrak{T}}^{\Omega }$) be an mPSFTS and let $\overline{{\mathbb{S}}^{\Gamma }}\in mPSFS(X)$.

Then, $\overline{{\mathbb{S}}^{\Gamma }}$ is open mPSFS $\iff {\overline{{\mathbb{S}}^{\Gamma }}}^{\circ }=\overline{{\mathbb{S}}^{\Gamma }}$.

Proof. 

If ${\overline{{\mathbb{S}}^{\Gamma }}}^{\circ }=\overline{{\mathbb{S}}^{\Gamma }}$, then ${\overline{{\mathbb{S}}^{\Gamma }}}^{\circ }$ is an open mPSFS. This means that $\overline{{\mathbb{S}}^{\Gamma }}$ is an open mPSFS.

Conversely, if $\overline{{\mathbb{S}}^{\Gamma }}$ is an open mPSFS, then the largest open mPSFS included in $\overline{{\mathbb{S}}^{\Gamma }}$ is itself $\overline{{\mathbb{S}}^{\Gamma }}$. Thus, ${\overline{{\mathbb{S}}^{\Gamma }}}^{\circ }=\overline{{\mathbb{S}}^{\Gamma }}$. □

Theorem 3.

Let (X, ${\mathfrak{T}}^{\Omega }$) be an mPSFTS and let $\overline{{\mathbb{S}}^{\Gamma }},{\overline{{\mathbb{S}}^{\Gamma }}}_1$, and ${\overline{{\mathbb{S}}^{\Gamma }}}_2\in$ mPSFS(X). Then, the following results hold:

(i)

${({\overline{{\mathbb{S}}^{\Gamma }}}^{\circ })}^{\circ }={\overline{{\mathbb{S}}^{\Gamma }}}^{\circ }$

(ii)

${\overline{{\mathbb{S}}^{\Gamma }}}_1⊑{\overline{{\mathbb{S}}^{\Gamma }}}_2\Rightarrow {\overline{{\mathbb{S}}^{\Gamma }}}_1^{\circ }⊑{\overline{{\mathbb{S}}^{\Gamma }}}_2^{\circ }$

(iii)

${({\overline{{\mathbb{S}}^{\Gamma }}}_1\sqcap {\overline{{\mathbb{S}}^{\Gamma }}}_2)}^{\circ }={\overline{{\mathbb{S}}^{\Gamma }}}_1^{\circ }\sqcap {\overline{{\mathbb{S}}^{\Gamma }}}_2^{\circ }$

(iv)

${({\overline{{\mathbb{S}}^{\Gamma }}}_1\bigsqcup {\overline{{\mathbb{S}}^{\Gamma }}}_2)}^{\circ }⊒{\overline{{\mathbb{S}}^{\Gamma }}}_1^{\circ }\bigsqcup {\overline{{\mathbb{S}}^{\Gamma }}}_2^{\circ }$

Definition 14.

Let (X, ${\mathfrak{T}}^{\Omega }$) be an mPSFTS and let $\overline{{\mathbb{S}}^{\Gamma }}\in$ mPSFS(X); then, closure of $\overline{{\mathbb{S}}^{\Gamma }}$ is indicated as ${\overline{{\mathbb{S}}^{\Gamma }}}^{\mathtt{cl}}$ and is described as the intersection of all closed mPSF supersets of $\overline{{\mathbb{S}}^{\Gamma }}$; it can also be defined as the smallest closed mPSFS of $\overline{{\mathbb{S}}^{\Gamma }}$.

Example 7.

Let X=$\{{\breve{⨿}}_1,{\breve{⨿}}_2,{\breve{⨿}}_3\}$ be a 4PSFTS. Let us consider 4PSFSs ${\overline{{\mathbb{S}}^{\Gamma }}}_1$ and ${\overline{{\mathbb{S}}^{\Gamma }}}_2$ of X as provided in Example 6. These 4PSFSs are open in 4PSFTS given in

Table 24. 4-polar spherical fuzzy set ${\overline{{\mathbb{S}}^{\Gamma }}}_1^c$.

${\overline{{\mathbb{S}}^{\mathbf{\Gamma }}}}_1^{\mathit{c}}$	$3\mathit{PSFSs}$
${\breve{⨿}}_1$	$\left(0.394,0.435,0.276\right),\left(0.325,0.337,0.254\right),\left(0.122,0.440,0.548\right),\left(0.282,0.462,0.248\right)$
${\breve{⨿}}_2$	$\left(0.419,0.332,0.239\right),\left(0.192,0.226,0.611\right),\left(0.523,0.459,0.440\right),\left(0.331,0.286,0.458\right)$
${\breve{⨿}}_3$	$\left(0.196,0.297,0.316\right),\left(0.218,0.149,0.632\right),\left(0.291,0.387,0.198\right),\left(0.112,0.312,0.627\right)$

and

Table 25. 4-polar spherical fuzzy set ${\overline{{\mathbb{S}}^{\Gamma }}}_2^c$.

${\overline{{\mathbb{S}}^{\mathbf{\Gamma }}}}_2^{\mathit{c}}$	$4\mathit{PSFSs}$
${\breve{⨿}}_1$	$\left(0.323,0.229,0.412\right),\left(0.190,0.325,0.254\right),\left(0.110,0.382,0.630\right),\left(0.172,0.362,0.418\right)$
${\breve{⨿}}_2$	$\left(0.218,0.313,0.406\right),\left(0.082,0.210,0.621\right),\left(0.137,0.287,0.554\right),\left(0.231,0.256,0.554\right)$
${\breve{⨿}}_3$	$\left(0.134,0.267,0.652\right),\left(0.145,0.149,0.674\right),\left(0.290,0.329,0.731\right),\left(0.092,0.212,0.687\right)$

. Then, their corresponding 4PSF closed sets is given in

Table 26. 4-polar spherical fuzzy set $\overline{{\mathbb{S}}^{\Gamma }}$.

$\overline{{\mathbb{S}}^{\mathbf{\Gamma }}}$	$4\mathit{PSFSs}$
${\breve{⨿}}_1$	$\left(0.233,0.317,0.450\right),\left(0.189,0.484,0.390\right),\left(0.108,0.487,0.651\right),\left(0.163,0.412,0.508\right)$
${\breve{⨿}}_2$	$\left(0.213,0.375,0.45\right),\left(0.071,0.382,0.653\right),\left(0.059,0.376,0.598\right),\left(0.221,0.396,0.591\right)$
${\breve{⨿}}_3$	$\left(0.120,0.365,0.718\right),\left(0.142,0.221,0.689\right),\left(0.286,0.342,0.733\right),\left(0.092,0.422,0.693\right)$

.

Consider $\overline{{\mathbb{S}}^{\Gamma }}$ as

Then, the 4PSF closure of $\overline{{\mathbb{S}}^{\Gamma }}$ is

$${\overline{{\mathbb{S}}^{\Gamma }}}^{\mathtt{cl}}=\overline{\mathbb{X}}\cap {\overline{{\mathbb{S}}^{\Gamma }}}_2^c={\overline{{\mathbb{S}}^{\Gamma }}}_2^c.$$

Theorem 4.

Let (X, ${\mathfrak{T}}^{\Omega }$) be an mPSFTS and let $\overline{{\mathbb{S}}^{\Gamma }},{\overline{{\mathbb{S}}^{\Gamma }}}_1$, and ${\overline{{\mathbb{S}}^{\Gamma }}}_2\in$ mPSFS(X). Then, the following results hold:

(i)

$\overline{{\overline{{\mathbb{S}}^{\Gamma }}}^{\mathtt{cl}}}={\overline{{\mathbb{S}}^{\Gamma }}}^{\mathtt{cl}}$

(ii)

${\overline{{\mathbb{S}}^{\Gamma }}}_1⊑{\overline{{\mathbb{S}}^{\Gamma }}}_2\Rightarrow {\overline{{\mathbb{S}}^{\Gamma }}}_1^{\mathtt{cl}}⊑{\overline{{\mathbb{S}}^{\Gamma }}}_2^{\mathtt{cl}}$

(iii)

$({\overline{{\mathbb{S}}^{\Gamma }}}_1^{\mathtt{cl}}\bigsqcup {\overline{{\mathbb{S}}^{\Gamma }}}_2)={\overline{{\mathbb{S}}^{\Gamma }}}_1^{\mathtt{cl}}\bigsqcup {\overline{{\mathbb{S}}^{\Gamma }}}_2^{\mathtt{cl}}$

(iv)

${\overline{{\mathbb{S}}^{\Gamma }}}_1^{\mathtt{cl}}\sqcap {\overline{{\mathbb{S}}^{\Gamma }}}_2⊒{\overline{{\mathbb{S}}^{\Gamma }}}_1^{\mathtt{cl}}\sqcap {\overline{{\mathbb{S}}^{\Gamma }}}_2^{\mathtt{cl}}$

Theorem 5.

Let (X, ${\mathfrak{T}}^{\Omega }$) be an mPSFTS and let $\overline{{\mathbb{S}}^{\Gamma }}\in mPSFS(X)$. Then,

(i)

${({\overline{{\mathbb{S}}^{\Gamma }}}^{\circ })}^c={({\overline{{\mathbb{S}}^{\Gamma }}}^c)}^{\mathtt{cl}}$

(ii)

${({\overline{{\mathbb{S}}^{\Gamma }}}^{\mathtt{cl}})}^c={({\overline{{\mathbb{S}}^{\Gamma }}}^c)}^{\circ }$.

Proof. 

(i) Let $\overline{{\mathbb{S}}^{\Gamma }}=\left\{{〈x,\left({\tilde{\mu }}^{(j)}(x),{\gamma }^{(j)}(x),{\tilde{\eta }}^{(j)}(x)\right)〉}_{j=1}^m:x\in X\right\}$ be an mPSFS in X.

Suppose that the collection of all open sets in (X, ${\mathfrak{T}}^{\Omega }$) which are contained in the set $\overline{{\mathbb{S}}^{\Gamma }}$ is provided by

$${\dot{\mathfrak{O}}}_i=\left\{{〈\breve{⨿},\left({\tilde{\mu }}_i^{(j)}(\breve{⨿}),{\gamma }_i^{(j)}(x),{\tilde{\eta }}_i^{(j)}(\breve{⨿})\right)〉}_{j=1}^m:\breve{⨿}\in X\right\},wherei\in I.$$

Now, the interior of $\overline{{\mathbb{S}}^{\Gamma }}$ is provided by

$${\overline{{\mathbb{S}}^{\Gamma }}}^{\circ }=\left\{{〈\breve{⨿},\left(ma{\breve{⨿}}_{i\in I}{\tilde{\mu }}_i^{(j)}(\breve{⨿}),mi{n}_{i\in I}{\gamma }_i^{(j)}(\breve{⨿}),mi{n}_{i\in I}{\tilde{\eta }}_i^{(j)}(\breve{⨿})\right)〉}_{j=1}^m:\breve{⨿}\in X\right\}$$

and

$${({\overline{{\mathbb{S}}^{\Gamma }}}^{\circ })}^c=\left\{{〈\breve{⨿},\left(mi{n}_{i\in I}{\tilde{\eta }}_i^{(j)}(\breve{⨿}),mi{n}_{i\in I}{\gamma }_i^{(j)}(\breve{⨿}),ma{\breve{⨿}}_{i\in I}{\tilde{\mu }}_i^{(j)}(\breve{⨿})\right)〉}_{j=1}^m:x\in X\right\}.$$

Now, let ${\overline{{\mathbb{S}}^{\Gamma }}}^c=\left\{{〈\breve{⨿},\left({\tilde{\eta }}^{(j)}(\breve{⨿}),{\gamma }^{(j)}\breve{⨿}\breve{⨿}),{\tilde{\mu }}^{(j)}(x)\right)〉}_{j=1}^m:\breve{⨿}\in \breve{⨿}\right\}$ be all possible closed sets in ($\breve{⨿}$, ${\mathfrak{T}}^{\Omega }$) which contain $\overline{{\mathbb{S}}^{\Gamma }}$, as provided by

$${\dot{\mathfrak{O}}}_i^c=\left\{{〈\breve{⨿},\left({\tilde{\eta }}_i^{(j)}(\breve{⨿}),{\gamma }_i^{(j)}(\breve{⨿}),{\tilde{\mu }}_i^{(j)}(\breve{⨿})\right)〉}_{j=1}^m:\breve{⨿}\in \breve{⨿}\right\},wherei\in I.$$

Therefore,

$${({\overline{{\mathbb{S}}^{\Gamma }}}^c)}^{\mathtt{cl}}=\left\{{〈\breve{⨿},\left(mi{n}_{i\in I}{\tilde{\eta }}_i^{(j)}(\breve{⨿}),mi{n}_{i\in I}{\gamma }_i^{(j)}(\breve{⨿}),ma{\breve{⨿}}_{i\in I}{\tilde{\mu }}_i^{(j)}(\breve{⨿})\right)〉}_{j=1}^m:\breve{⨿}\in X\right\}$$

Hence, ${({\overline{{\mathbb{S}}^{\Gamma }}}^{\circ })}^c={({\overline{{\mathbb{S}}^{\Gamma }}}^c)}^{\mathtt{cl}}$.

Now, we must verify that ${({\overline{{\mathbb{S}}^{\Gamma }}}^{\circ })}^c$ and ${({\overline{{\mathbb{S}}^{\Gamma }}}^c)}^{\mathtt{cl}}$ are mPSFS.

For this purpose, assume that $ma{\breve{⨿}}_{i\in I}{\tilde{\mu }}_i^{(j)}(\breve{⨿})={\tilde{\mu }}_k^{(j)}(\breve{⨿})$ for some $k\in I$.

Now, consider

${\left(mi{n}_{i\in I}{\tilde{\eta }}_i^{(j)}(x)\right)}^2+{\left(mi{n}_{i\in I}{\gamma }_i^{(j)}(x)\right)}^2+{\left(ma{\breve{⨿}}_{i\in I}{\tilde{\mu }}_i^{(j)}(x)\right)}^2$

$={\left(mi{n}_{i\in I}{\tilde{\eta }}_i^{(j)}(x)\right)}^2+{\left(mi{n}_{i\in I}{\gamma }_i^{(j)}(x)\right)}^2+{\left({\tilde{\mu }}_k^{(j)}(x)\right)}^2$

$\le {\left({\tilde{\eta }}_k^{(j)}(x)\right)}^2+{\left({\gamma }_k^{(j)}(x)\right)}^2+{\left({\tilde{\mu }}_k^{(j)}(x)\right)}^2$

$\le {\left({\tilde{\mu }}_k^{(j)}(x)\right)}^2+{\left({\gamma }_k^{(j)}(x)\right)}^2+{\left({\tilde{\eta }}_k^{(j)}(x)\right)}^2$

$\le 1$, as ${\dot{\mathfrak{O}}}_k$ is an mPSFS.

Hence, ${({\overline{{\mathbb{S}}^{\Gamma }}}^{\circ })}^c$ and ${({\overline{{\mathbb{S}}^{\Gamma }}}^c)}^{\mathtt{cl}}$ both lie in the mPSF domain.

We can prove (ii) in a similar way. □

Proposition 1.

Let (X, ${\mathfrak{T}}^{\Omega }$) be an mPSFTS and let $\overline{{\mathbb{S}}^{\Gamma }}\in mPSFS(X)$. Then,

(i)

$\overline{\overline{\overline{⌀}}}=\overline{\overline{⌀}}$

(ii)

${\overline{\mathbb{X}}}^{\circ }=\overline{\mathbb{X}}$

(iii)

${\overline{{\mathbb{S}}^{\Gamma }}}^{\circ }\subseteq \overline{{\mathbb{S}}^{\Gamma }}\subseteq {\overline{{\mathbb{S}}^{\Gamma }}}^{\mathtt{cl}}.$

Definition 15.

Let (X, ${\mathfrak{T}}^{\Omega }$) be an mPSFTS and let $\overline{{\mathbb{S}}^{\Gamma }}\in mPSFS(X)$. Then, the frontier of $\overline{{\mathbb{S}}^{\Gamma }}$ is indicated as $\mathtt{Fr}(\overline{{\mathbb{S}}^{\Gamma }})$, and is described as

$$\mathtt{Fr}(\overline{{\mathbb{S}}^{\Gamma }})={\overline{{\mathbb{S}}^{\Gamma }}}^{\mathtt{cl}}\cap {({\overline{{\mathbb{S}}^{\Gamma }}}^c)}^{\mathtt{cl}}.$$

Definition 16.

Let (X, ${\mathfrak{T}}^{\Omega }$) be an mPSFTS and let $\overline{{\mathbb{S}}^{\Gamma }}\in mPSFS(X)$. Then, the exterior of $\overline{{\mathbb{S}}^{\Gamma }}$ is indicated as ${Ext}(\overline{{\mathbb{S}}^{\Gamma }})$ and is described as

$$\mathtt{Ext}(\overline{{\mathbb{S}}^{\Gamma }})={({\overline{{\mathbb{S}}^{\Gamma }}}^c)}^{\circ }.$$

Example 8.

In Example 7, the frontier of $\overline{{\mathbb{S}}^{\Gamma }}$ is provided as follows:

$$\mathtt{Fr}(\overline{{\mathbb{S}}^{\Gamma }})={\overline{{\mathbb{S}}^{\Gamma }}}^{\mathtt{cl}}\cap {({\overline{{\mathbb{S}}^{\Gamma }}}^c)}^{\mathtt{cl}}={({\overline{{\mathbb{S}}^{\Gamma }}}_2)}^c\cap \tilde{X}={({\overline{{\mathbb{S}}^{\Gamma }}}_2)}^c$$

and the exterior as $\mathtt{Ext}(\overline{{\mathbb{S}}^{\Gamma }})={({\overline{{\mathbb{S}}^{\Gamma }}}^c)}^{\circ }=\overline{\overline{⌀}}.$

Proposition 2.

Let (X, ${\mathfrak{T}}^{\Omega }$) be an mPSFTS and let $\overline{{\mathbb{S}}^{\Gamma }}\in mPSFS(X)$; then, $\mathtt{Fr}(\overline{{\mathbb{S}}^{\Gamma }})=\mathtt{Fr}({\overline{{\mathbb{S}}^{\Gamma }}}^c)$.

Proof. 

By definition,

$\mathtt{Fr}(\overline{{\mathbb{S}}^{\Gamma }})={\overline{{\mathbb{S}}^{\Gamma }}}^{\mathtt{cl}}\cap {({\overline{{\mathbb{S}}^{\Gamma }}}^c)}^{\mathtt{cl}}={({\overline{{\mathbb{S}}^{\Gamma }}}^c)}^{\mathtt{cl}}\cap {\overline{{\mathbb{S}}^{\Gamma }}}^{\mathtt{cl}}={({\overline{{\mathbb{S}}^{\Gamma }}}^c)}^{\mathtt{cl}}\cap {{({\overline{{\mathbb{S}}^{\Gamma }}}^c)}^c}^{\mathtt{cl}}=\mathtt{Fr}({\overline{{\mathbb{S}}^{\Gamma }}}^c).$□

Proposition 3.

Let (X, ${\mathfrak{T}}^{\Omega }$) be an mPSFTS and let $\overline{{\mathbb{S}}^{\Gamma }}\in mPSFS(X)$; then,

(i)

$\mathtt{Ext}({\overline{{\mathbb{S}}^{\Gamma }}}^c)={\overline{{\mathbb{S}}^{\Gamma }}}^{\circ }$

(ii)

$\mathtt{Ext}(\overline{{\mathbb{S}}^{\Gamma }})\cup \mathtt{Fr}(\overline{{\mathbb{S}}^{\Gamma }})\cup {\overline{{\mathbb{S}}^{\Gamma }}}^{\circ }\ne \overline{\mathbb{X}}$

(iii)

${\overline{{\mathbb{S}}^{\Gamma }}}^{\circ }\cap \mathtt{Fr}(\overline{{\mathbb{S}}^{\Gamma }})\ne \overline{\overline{⌀}}.$

5. Multi-Criteria Group Decision Making by m-PSF Topology

Choice-making occurs in trading, business, and sciences, and often faces huge challenges. It differentiates between a minimal regime’s constant operational analyses and leaders’ extensive formulation and management. While collected data can be analyzed to reach inferences that can have major or unfavorable implications, ultimately officials must show a logical operational strategy for winning.

Before reaching a choice, decision-makers should assess a wide range of factors. Consequently, while coming to a conclusion, it is imperative that all of these variables are factored into the equation. In legal terms, a systematic approach to decision-making is essential to guarantee that all of the key data and information are properly considered.

Among several other methods, mathematics can assists in reaching conclusions based on the evidence provided by science. This excerpt provides an illustration of a strategy for handling the problem of multiple criterion group decision-making by employing the superiority inferiority ranking (SIR) and linear assignment model (LAM) within an mPSF framework.

MCDM with SIR method.

The essential steps for the extended SIR approach for mPSFS are outlined below.

1:

Determine the individual measure degree ${\beth }_k(k=1,2,...,l)$, then obtain the relative closeness coefficient using the formula provided below:

$${\beth }_k=\frac{d\left(W_{d_k},W_{D_R}^{-}\right)}{d\left(W_{d_k},W_{D_R}^{-}\right)+d\left(W_{d_k},W_{D_R}^{+}\right)}$$

where $W_{D_R}^{-}$ and $W_{D_R}^{+}$ denote the relative minimum and relative maxima, respectively, and can be calculated as follows:

$W_{D_R}^{-}=(min\{{\tilde{\mu }}_k\},max\{{\gamma }_k\},max\{{\tilde{\eta }}_k\})$

$W_{D_R}^{+}=(max\{{\tilde{\mu }}_k\},min\{{\gamma }_k\},min\{{\tilde{\eta }}_k\})$

2:

Normalize ${\beth }_k(k=1,2,...,l)$ using the formula

$$\overline{W_k}=\frac{{\beth }_k}{{\sum }_{k=1}^l{\beth }_k}$$

and denote them as an individual measure degree by

$$\overline{W}=\left(\overline{w_1},\overline{w_2},\dots ,\overline{w_n}\right)$$

3:

Acquire the amalgamated mPSF decision matrix and weight vector utilizing the mPSF operator to class individual viewpoints together into an aggregated frame of reference.

• the mPSFWAM aggregation operator for integrating individual decision matrices is
  $mPSFWAM({\mathbb{k}}_{ij}^{(1)},{\mathbb{k}}_{ij}^{(2)},...,{\mathbb{k}}_{ij}^{(l)})={\sum }_{k=1}^l{\overline{w}}_k{\mathbb{k}}_{ij}^{(l)}$
  $=\{\sqrt{1-{\prod }_{k=1}^l{(1-{\tilde{\mu }}_{(i)}^2(x))}^{{\overline{w}}_k}},\sqrt{{\prod }_{k=1}^l{(1-{\tilde{\mu }}_{(i)}^2(x))}^{{\overline{w}}_k}-{\prod }_{k=1}^l{(1-{\tilde{\mu }}_{(i)}^2(x)-{\tilde{\eta }}_{(i)}^2(x))}^{{\overline{w}}_k}},$${\prod }_{k=1}^l{\gamma }_{(i)}^{{\overline{w}}_k}(x),{\}}_{i=1}^m$
• the mPSFWAM aggregation operator for integrating th weights of individual attributes is
  $mPSFWAM({\varpi }_j^{(1)},{\varpi }_j^{(2)},...,{\varpi }_j^{(l)})={\sum }_{k=1}^l{\overline{w}}_k{\varpi }_j^{(l)}$
  $=\{\sqrt{1-{\prod }_{k=1}^l{(1-{\tilde{\mu }}_{(i)}^2(x))}^{{\overline{w}}_k}},\sqrt{{\prod }_{k=1}^l{(1-{\tilde{\mu }}_{(i)}^2(x))}^{{\overline{w}}_k}-{\prod }_{k=1}^l{(1-{\tilde{\mu }}_{(i)}^2(x)-{\tilde{\eta }}_{(i)}^2(x))}^{{\overline{w}}_k}},$${\prod }_{k=1}^l{\gamma }_{(i)}^{{\overline{w}}_k}(x),{\}}_{i=1}^m$

4:

Build a performance relationship based on relative performance using the formula

$$f_{\alpha \beta }=\frac{d\left(P_{\alpha \beta },P^{-}\right)}{d\left(P_{\alpha \beta },P^{-}\right)+d\left(P_{\alpha \beta },P^{+}\right)},$$

the superiority matrix

$$S_{\alpha \beta }={\displaystyle \underset{t=1}{\overset{m}{⨁}}}F\left(f_{\alpha \beta }-f_{t\beta }\right),$$

and the inferiority matrix

$$I_{\alpha \beta }={\displaystyle \underset{t=1}{\overset{m}{⨁}}}F\left(f_{t\beta }-F_{\alpha \beta }\right).$$

Activate where $F\left(P^K\right)=0.01$ if $0〈P^{\kappa }〈1$ and $F\left(P^{\kappa }\right)=0$ if $0\ge P^{\kappa }$ or $P^{\kappa }\ge 1$

5:

Compute the superiority and inferiority indexes as follows:

$$\begin{array}{cc}& {ϝ}^{\prime }\left(P_{\alpha }^{\kappa }\right)={\displaystyle \underset{\beta =1}{\overset{n}{⨁}}}{S}_{\alpha \beta }\overline{w_{\beta }}\hfill \\ & {ϝ}^{\gamma }\left(P_{\alpha }^{\kappa }\right)={\displaystyle \underset{\beta =1}{\overset{n}{⨁}}}{I}_{\alpha \beta }\overline{w_{\beta }}\hfill \end{array}$$

6:

Determine score functions of ${ϝ}^{\prime }\left(P_{\alpha }^{\kappa }\right)$ and ${ϝ}^{\gamma }\left(P_{\alpha }^{\kappa }\right)$.

7:

By following the rules below, determine the flow of superiority and inferiority.

Superiority flow rules (SFRs):

• $P_{\alpha }^{\kappa }>P_t^{\kappa }$ if $S({ϝ}^{\prime }(P_{\alpha }^{\kappa })<S({ϝ}^{\prime }(P_t^{\kappa }))$ and $S({ϝ}^{\gamma }(P_{\alpha }^{\kappa }))>S({ϝ}^{\gamma }(P_t^{\kappa }))$
• $P_{\alpha }^{\kappa }>P_t^{\kappa }$ if $S({ϝ}^{\prime }(P_{\alpha }^{\kappa })<S({ϝ}^{\prime }(P_t^{\kappa }))$ and $S({ϝ}^{\gamma }(P_{\alpha }^{\kappa }))=S({ϝ}^{\gamma }(P_t^{\kappa }))$
• $P_{\alpha }^{\kappa }>P_t^{\kappa }$ if $S({ϝ}^{\prime }(P_{\alpha }^{\kappa })=S({ϝ}^{\prime }(P_t^{\kappa }))$ and $S({ϝ}^{\gamma }(P_{\alpha }^{\kappa }))>S({ϝ}^{\gamma }(P_t^{\kappa }))$

Inferiority flow rules (IFRs):

• $P_{\alpha }^{\kappa }<P_t^{\kappa }$ if $S({ϝ}^{\prime }(P_{\alpha }^{\kappa })>S({ϝ}^{\prime }(P_t^{\kappa }))$ and $S({ϝ}^{\gamma }(P_{\alpha }^{\kappa }))<S({ϝ}^{\gamma }(P_t^{\kappa }))$
• $P_{\alpha }^{\kappa }<P_t^{\kappa }$ if $S({ϝ}^{\prime }(P_{\alpha }^{\kappa })>S({ϝ}^{\prime }(P_t^{\kappa }))$ and $S({ϝ}^{\gamma }(P_{\alpha }^{\kappa }))=S({ϝ}^{\gamma }(P_t^{\kappa }))$
• $P_{\alpha }^{\kappa }<P_t^{\kappa }$ if $S({ϝ}^{\prime }(P_{\alpha }^{\kappa })=S({ϝ}^{\prime }(P_t^{\kappa }))$ and $S({ϝ}^{\gamma }(P_{\alpha }^{\kappa }))<S({ϝ}^{\gamma }(P_t^{\kappa }))$

8:

Obtain the best possible outcome by coupling SFRs and IFRs next to each other

MCDM with LAM.

On the basis of attributes and structures, the classical linear assignment method (LAM) can be extended to mPSFs. The following algorithm explains the numerous processes that form the proposed mPSFLAM.

1:

Take into account the scores and alternative weights of decision-makers.

2:

Aggregate the score matrices and weights of decision-makers.

3:

Compute the score values of the aggregated decision matrix.

4:

Determine the rank frequency non-negative matrix ${{\rm Y}}_k^i$

5:

Establish a weighted rank frequency ℶ, where the ${\beth }_k^i$ receives the alternative contribution to the total ranking. The value is

$${\beth }_k^i=w_{i1}+w_{i2}+w_{i3}+\dots .+w_{i{{\rm Y}}_k^i}$$

6:

Calculate $\mathbb{P}=({\beth }_k^i)$. The LAM can be expressed in a linear programming format, as mentioned below:

$${\displaystyle \sum _{i=1}^m\sum _{i=1}^m}{\beth }_k^i\circ P_k^i$$

such that

$$\begin{array}{ccc}\hfill {\displaystyle \sum _{i=1}^m}{P}_k^i& =\hfill & \hfill 1\\ \hfill {\displaystyle \sum _{k=1}^m}{P}_k^i& =\hfill & \hfill 1\\ \hfill P_k^i& =\hfill & \hfill 0\\ \hfill \mathit{or}{P}_k^i& =\hfill & \hfill 1\end{array}$$

7:

Find the best possible answer by working through the linear assignment model and analyzing it.

8:

Rank the optimal alternatives.

6. Case Study

Numerous kinds of vehicles, including automobiles, buses, tractors, motorcycles, mopeds, pedestrians, animals, taxis, and others, use roads throughout the world. The invention of the vehicle is directly responsible for the growth of many nations’ economies and social structures. Nonetheless, every year, millions of people are killed and wounded in vehicle-related incidents. Each year, 1.35 million people are killed on the roads and highways of the world. Every day, more than 3700 people are killed in accidents involving cars, buses, motorcycles, bicycles, lorries, and pedestrians around the globe. More than half of those killed are cyclists, pedestrians, or motorcyclists. Gopalakrishnan has presented these statistics in [71]. According to estimates, crash-related injuries are the eighth-leading cause of death around the globe for people of all ages. Today, automotive accidents kill more people than HIV/AIDS. The global death toll is depicted in Figure 1.

Transportation system quality is one of the key indicators of the standard of living. The transportation system is essential to human survival. Automobile crashes are a major worry, as they risk people’s lives, health, and property. In addition, the management of the transportation system may be compromised by road mishaps. Due to the dangerous nature of this system, it might not be able to work properly. Therefore, traffic accident prediction models may be useful for comprehending the elements that lead to accidents as well as their frequency under different conditions.

Accidents are the largest cause of injury and death worldwide, and as a result, they contribute to a vast array of social and economic problems. Here, we use Albania as a case study for the creation of a fuzzy model for accident prediction. The conditions of the road and the flow of traffic are two major contributors to road accidents. It is feasible to reduce the number of accidents by investigating these factors. Research on road safety has revealed the accuracy of collision prediction models.

Accidents on the road are the leading cause of hospitalisation for teenagers; drivers between the ages of 18 and 24 account for 23% of all fatalities resulting from automotive accidents. Similar to the incidence rate, the recurrence rate is rather high. Following an initial accident, one in every four teenagers goes on to experience a recurrence during the subsequent year. Cognitive deficiencies are known to be present in teenagers, and can be a contributing factor in the development of risky behaviours. Risky behaviours are defined as repeated engagement in potentially dangerous situations, such as getting into vehicle accidents. There are two distinct groups of factors that appear to be linked to road accidents: (1) characteristics that are unique to the environment in which the accident occurred and (2) “human” factors, which appear to be the most significant of the two. Both of these groups of factors are discussed further below. Additionally, the development of a tighter connection to high speed driving increases the risk of becoming involved in a car accident, which is a risk that can be amplified by the pursuit of extreme sensations. Additional variables, such as the use of drugs (including alcohol, opioids, or “binge drinking”), have been identified as risk factors. In addition, it would appear that both using a cell phone while driving and having attention deficit disorder, whether or not it is accompanied by hyperactivity, are major factors in the chance of being involved in a car collision.

Below, we describe the factors that can potentially cause vehicle accidents.

1.

Speeding ($\gimel {\mathfrak{Y}}_1$)

Speeding continues to be the major cause of automobile accidents. According to the Royal Society for the Prevention of Accidents (RoSPA), improper speed leads to around 11% of reported injury incidents and 24% of fatal collisions. All collisions caused by speeding are fully preventable; drivers and riders must respect traffic regulations to ensure the safety of others. Keep in mind that speed restrictions govern the maximum speed, not the minimum speed; therefore, modifying speed to the road or weather conditions is perfectly reasonable. In addition to being aware of their speed, one of the most crucial pieces of advice for drivers and riders is to maintain a safe distance from the vehicle in front, sometimes known as the “two-second rule.” Keeping a safe distance from other vehicles dramatically lessens the probability of being involved in an accident. The following may occur in an accident due to speeding.

A.

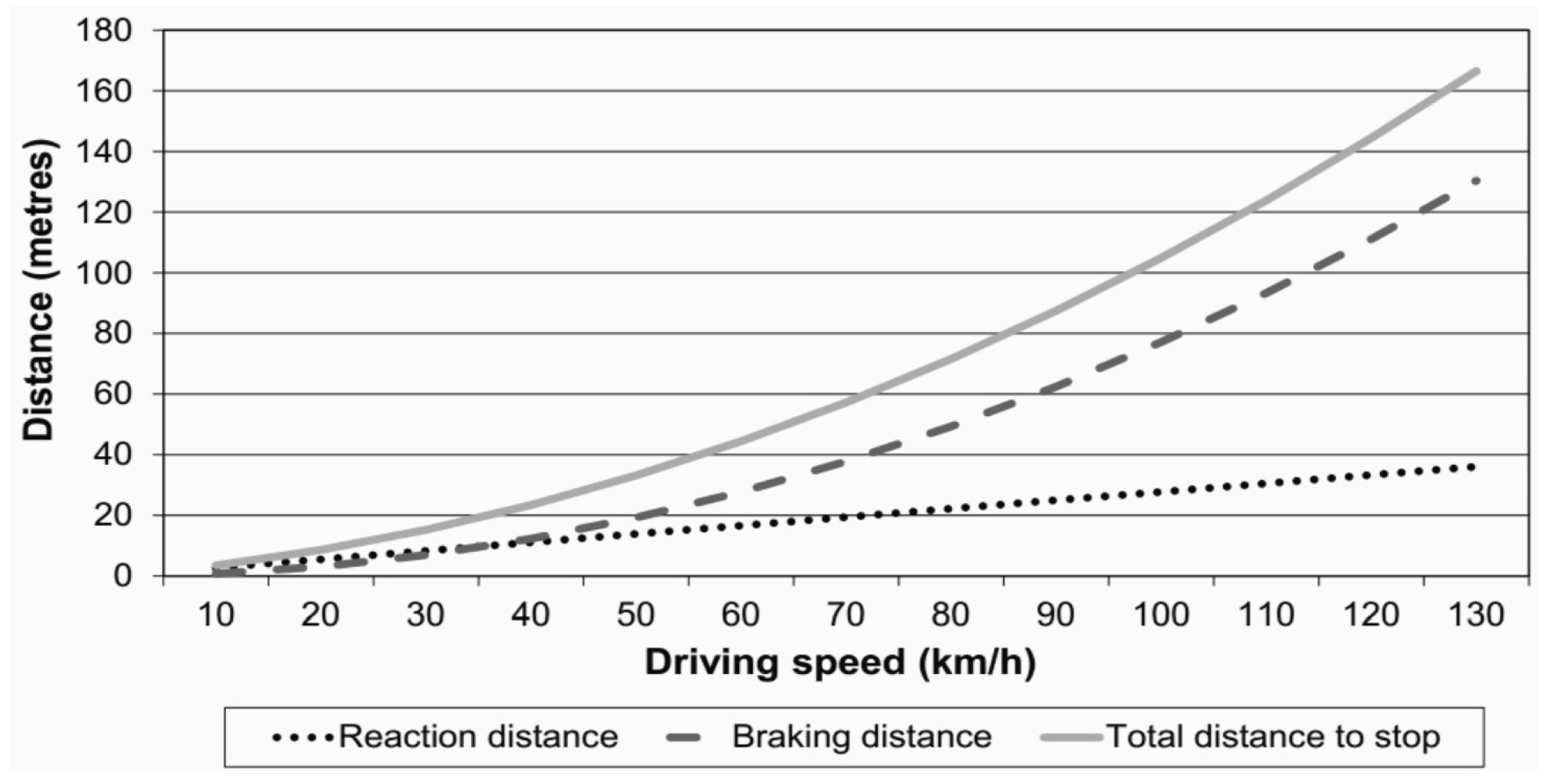
Lessened ability to drive and stop the car

There is a correlation between high rates of speed and the likelihood of becoming involved in an accident. The likelihood of a collision increases proportionally with the absolute speed of travel. Consider the fact that the driver needs a regular amount of time to respond effectively to unplanned events. As the speed of the vehicle rises, so does the distance it travels before reacting. When travelling at high speeds, there is less time to adapt to changes in the surroundings and less room to manoeuvre. In addition, as illustrated in Figure 2, the stopping distance is larger.

B.

Increased the likelihood of roll-over

When driving at high speeds, there is a significantly increased risk of becoming engaged in an accident involving a roll-over. It is highly uncommon for a car to flip over when it is engaged in an accident that occurs at a low speed, such as one that occurs in a parking lot. If even one of the vehicles is moving at a fast rate of speed, the probability that one of them may roll over is greatly increased, regardless of whether it is a car travelling at high speed or a lower-speed car struck by the high-speed vehicle.

2.

Overtaking ($\gimel {\mathfrak{Y}}_2$)

A.

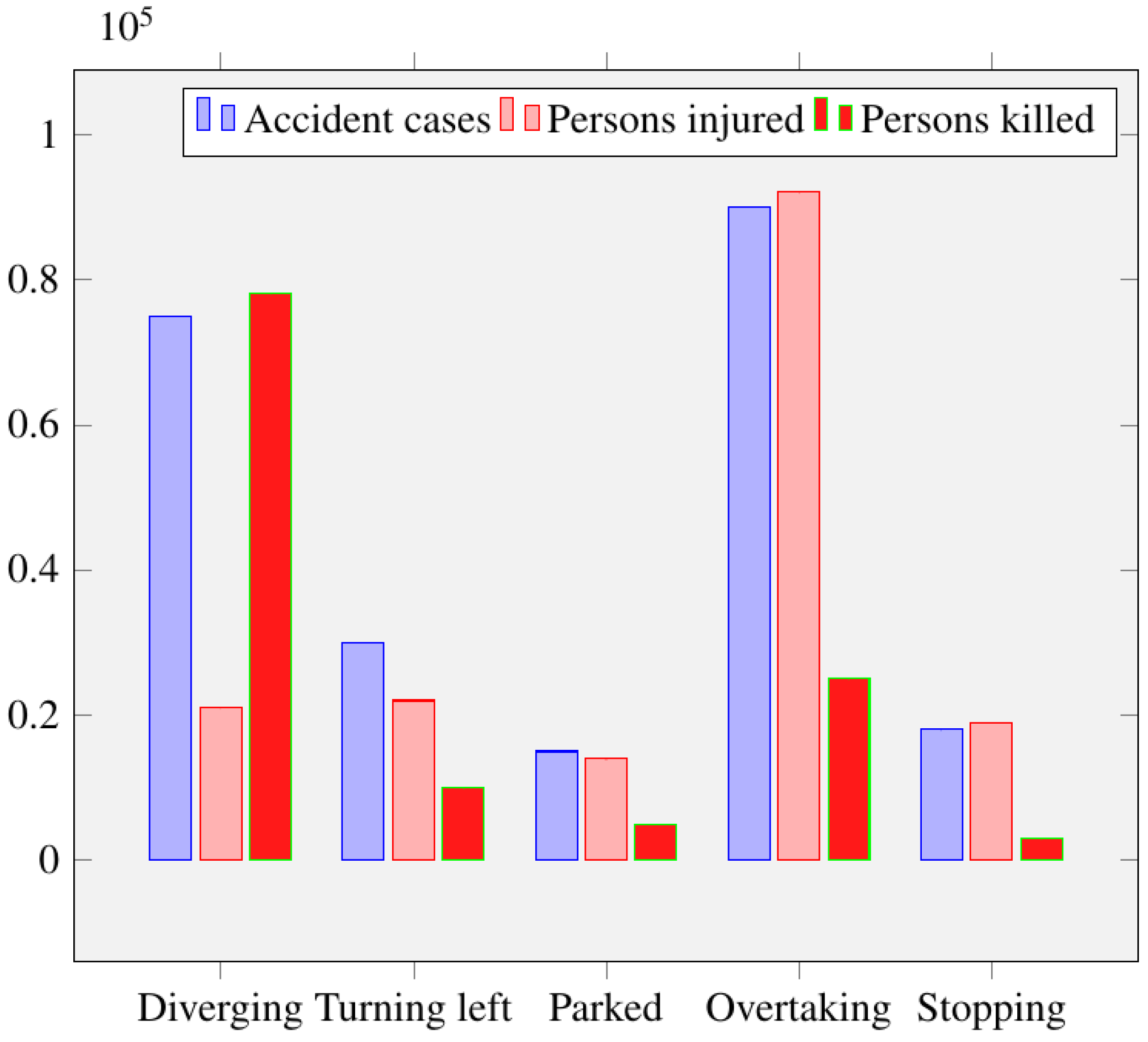
Non-adherence to lane driving. According to official statistics, this is one of the top five causes of accidents on Indian roads. There are 1214 car accidents every single day in India, and one person loses their life as a result of a road accident every four minutes. Figure 3 shows the number of accidents annually due to changing and/or not following the lane.

The number of deaths, which has been rising over the last few years, did not decrease despite the fact that there were fewer road traffic incidents overall. Instead, the number of fatalities has been steadily rising.

B.

Overtaking in an incorrect manner. If you have been driving for a long time and often go on lengthy journeys, you have likely witnessed accidents caused by drivers who failed to properly pass another car or who came perilously close to being struck by an oncoming vehicle when passing another vehicle. When attempting to pass another car on the road, it is common for drivers to underestimate the necessary space and time. This happens more often in rural areas. One of the most common errors that can lead to accidents when overtaking another vehicle is failing to give the proper signal to the cars in front of and behind them. Overtaking is one of the leading causes of accidents, as illustrated in Figure 4.

3.

Pedestrian negligence contributes to road accidents and endangers their own lives ($\gimel {\mathfrak{Y}}_3$)

A.

Running or Darting into the Road.

It is not unusual for children and adolescents to run into the street without first checking to see if there are vehicles approaching from the opposite direction. Because of this, there is a chance of an accident occurring in nearly any part of the city. It is likely that a motorist will not have the time to react in the appropriate manner when a pedestrian unexpectedly walks into the street. Because of this, they stand a good risk of colliding with the pedestrian, which may lead to serious injuries.

B.

Standing, Lying, Playing, or Working in a Roadway.

When a person is standing or loitering in the middle of the roadway, it can be difficult for a car to avoid colliding with the pedestrian. Even if a driver swerves to avoid striking a pedestrian, the driver behind that vehicle may not see the pedestrian in time. Pedestrians who are standing, lying down, or playing in the roadway at the time of an accident may be held liable.

The negligence of drivers may endanger the lives of roadside workers. In order to comply with safety standards, employees are frequently required to show road signs and wear apparel that is highly visible to drivers. Similarly, motorists are expected to exhibit heightened caution when driving close to a construction site.

7. Decision-Making

Consider the CCTV footage of an accident shown in Figure 5.

Consider a set of experts ${\mathfrak{E}}^{\daleth }=\left\{{\mathfrak{E}}_1^{\daleth },{\mathfrak{E}}_2^{\daleth },{\mathfrak{E}}_3^{\daleth }\right\}$ with the credibility weights $\mathcal{W}=$$\left\{W_{{\mathfrak{E}}_1^{\daleth }},W_{{\mathfrak{E}}_2^{\daleth }},W_{{\mathfrak{E}}_3^{\daleth }}\right\}$, criterion $\gimel \mathfrak{Y}=\left\{\gimel {\mathfrak{Y}}_1,\gimel {\mathfrak{Y}}_2,\gimel {\mathfrak{Y}}_3\right\}$, and alternatives ${\mathfrak{U}}^{\P }=\left\{{\mathfrak{U}}_1^{\P },{\mathfrak{U}}_2^{\P },{\mathfrak{U}}_3^{\P }\right\}$, which are highlighted in the Figure 5, namely, a red vehicle (${\mathfrak{U}}_1^{\P }$), two pedestrians (${\mathfrak{U}}_2^{\P }$), and a white vehicle (${\mathfrak{U}}_3^{\P }$). Let $P_{\alpha \beta }^k$ be the mPSFN assigned to $\alpha$th potential cause of accident with respect to $\beta$th by the $k^{\mathrm{th}}$ expert. Construct the mPSF decision matrix $P(k)$. Assume that $w_{\beta }^k$ represents the mPSF weights of symptom $S_{P_{\beta }}$ provided by the criteria decision matrix $\mathcal{W}$. The most effect patient is filtered using the proposed techniques.

The weights associated with experts’ assessments are provided in

Table 27. Weights associated with experts.

$W_{{\mathfrak{E}}_1^{\daleth }}$	$(0.63,0.15,0.23)(0.42,0.28,0.19)$
$W_{{\mathfrak{E}}_2^{\daleth }}$	$(0.59,0.18,0.09)(0.36,0.41,0.13)$
$W_{{\mathfrak{E}}_3^{\daleth }}$	$(0.81,0.07,0.13)(0.48,0.21,0.36)$

.

The minimum reference weight and maximum reference weight are given in the

Table 28. Minimum and maximum reference weight.

$W_{{\mathfrak{E}}^{\daleth }}^{-}$	$(0.59,0.18,0.23)(0.36,0.41,0.36)$
$W_{{\mathfrak{E}}^{\daleth }}^{+}$	$(0.81,0.07,0.09)(0.48,0.21,0.18)$

:

1.

Calculate the relative proximity coefficient using the following formula; for this purpose, we first need to determine the distances, as calculated in the

Table 29. Distance table for relative proximity.

$d\left(W_{{\mathfrak{E}}_1^{\daleth }},W_{{\mathfrak{E}}^{\daleth }}^{-}\right)$	0.1611
$d\left(W_{{\mathfrak{E}}_1^{\daleth }},W_{{\mathfrak{E}}^{\daleth }}^{+}\right)$	0.18303
$d\left(W_{{\mathfrak{E}}_2^{\daleth }},W_{{\mathfrak{E}}^{\daleth }}^{-}\right)$	0.1904
$d\left(W_{{\mathfrak{E}}_2^{\daleth }},W_{{\mathfrak{E}}^{\daleth }}^{+}\right)$	0.2423
$d\left(W_{{\mathfrak{E}}_3^{\daleth }},W_{{\mathfrak{E}}^{\daleth }}^{-}\right)$	0.2499
$d\left(W_{{\mathfrak{E}}_3^{\daleth }},W_{{\mathfrak{E}}^{\daleth }}^{+}\right)$	0.1304

.

The relative proximity coefficients are computed in are calculated in the

Table 30. Relative proximity coefficients.

${\mathit{\beth }}_{\mathit{k}}$	Values
${\beth }_1$	$0.4681$
${\beth }_2$	$0.4400$
${\beth }_3$	$0.6571$
sum	$1.5652$

.

2.

By normalizing the weights using

$$\mathcal{W}=\frac{{\beth }_k}{{\sum }_{k=1}^n{\beth }_k}$$

we obtain

$$\mathcal{W}=(0.2991,0.2811,0.4198).$$

The criteria weights assigned by the accident cause evaluators are presented in the

Table 31. Criteria weights assigned by the experts.

	$\gimel {\mathfrak{Y}}_1$	$\gimel {\mathfrak{Y}}_2$	$\gimel {\mathfrak{Y}}_3$
${\mathfrak{E}}_1^{\daleth }$	$(0.367,0.284,0.490)(0.516,0.211,0.178)$	$(0.245,0.387,0.421)(0.631,0.055,0.248)$	$(0.481,0.332,0.271)(0.322,0.210,0.433)$
${\mathfrak{E}}_2^{\daleth }$	$(0.251,0.365,0.418)(0.371,0.276,0.455)$	$(0.167,0.385,0.480)(0.512,0.320,0.009)$	$(0.672,0.024,0.218)(0.532,0.187,0.231)$
${\mathfrak{E}}_3^{\daleth }$	$(0.210,0.376,0.422)(0.798,0.007,0.156)$	$(0.292,0.328,0.473)(0.398,0.237,0.320)$	$(0.527,0.271,0.119)(0.480,0.278,0.159)$

. The decision matrices ${\mathfrak{E}}_1^{\daleth },{\mathfrak{E}}_2^{\daleth },{\mathfrak{E}}_3^{\daleth }$ assigned by doctors are provided in the

Table 32. Decision matrix by ${\mathfrak{E}}_1^{\daleth }$.

	$\gimel {\mathfrak{Y}}_1$	$\gimel {\mathfrak{Y}}_2$	$\gimel {\mathfrak{Y}}_3$
${\mathfrak{U}}_1^{\P }$	$(0.531,0.392,0.326)(0.424,0.283,0.317)$	$(0.612,0.215,0.117)(0.317,0.421,0.284)$	$(0.420,0.212,0.345)(0.823,0.135,0.089)$
${\mathfrak{U}}_2^{\P }$	$(0.434,0.281,0.156)(0.291,0.353,0.115)$	$(0.365,0.416,0.228)(0.813,0.056,0.133)$	$(0.391,0.123,0.433)(0.611,0.136,0.247)$
${\mathfrak{U}}_3^{\P }$	$(0.224,0.348,0.379)(0.593,0.186,0.345)$	$(0.632,0.315,0.262)(0.154,0.423,0.391)$	$(0.718,0.291,0.187)(0.384,0.241,0.412)$

,

Table 33. Decision matrix by ${\mathfrak{E}}_2^{\daleth }$.

	$\gimel {\mathfrak{Y}}_1$	$\gimel {\mathfrak{Y}}_2$	$\gimel {\mathfrak{Y}}_3$
${\mathfrak{U}}_1^{\P }$	$(0.522,0.178,0.231)(0.342,0.251,0.146)$	$(0.418,0.232,0.179)(0.534,0.242,0.387)$	$(0.623,0.156,0.241)(0.811,0.054,0.120)$
${\mathfrak{U}}_2^{\P }$	$(0.489,0.234,0.156)(0.378,0.188,0.369)$	$(0.554,0.210,0.114)(0.692,0.178,0.203)$	$(0.257,0.316,0.345)(0.630,0.179,0.311)$
${\mathfrak{U}}_3^{\P }$	$(0.812,0.109,0.089)(0.415,0.233,0.186)$	$(0.723,0.129,0.159)(0.346,0.287,0.436)$	$(0.628,0.195,0.249)(0.455,0.271,0.363)$

and

Table 34. Decision matrix by ${\mathfrak{E}}_3^{\daleth }$.

	$\gimel {\mathfrak{Y}}_1$	$\gimel {\mathfrak{Y}}_2$	$\gimel {\mathfrak{Y}}_3$
${\mathfrak{U}}_1^{\P }$	$(0.387,0.312,0.245)(0.562,0.089,0.431)$	$(0.426,0.178,0.329)(0.516,0.119,0.230)$	$(0.163,0.309,0.411)(0.589,0.178,0.254)$
${\mathfrak{U}}_2^{\P }$	$(0.584,0.267,0.123)(0.287,0.344,0.461)$	$(0.179,0.328,0.612)(0.451,0.245,0.361)$	$(0.560,0.322,0.143)(0.811,0.131,0.067)$
${\mathfrak{U}}_3^{\P }$	$(0.690,0.127,0.122)(0.389,0.287,0.497)$	$(0.447,0.235,0.331)(0.567,0.107,0.213)$	$(0.639,0.115,0.216)(0.383,0.264,0.419)$

, respectively.

3.

Furthermore, the aggregated mPSF-decision matrix is calculated and presented in the

Table 35. Aggregated decision matrix.

	$\gimel {\mathfrak{Y}}_1$	$\gimel {\mathfrak{Y}}_2$	$\gimel {\mathfrak{Y}}_3$
${\mathfrak{U}}_1^{\P }$	$(0.475,0.313,0.262)(0.473,0.206,0.290)$	$(0.493,0.207,0.204)(0.475,0.269,0.284)$	$(0.433,0.237,0.336)(0.747,0.133,0.150)$
${\mathfrak{U}}_2^{\P }$	$(0.519,0.263,0.141)(0.317,0.311,0.286)$	$(0.384,0.328,0.284)(0.673,0.169,0.228)$	$(0.450,0.283,0.255)(0.720,0.147,0.152)$
${\mathfrak{U}}_3^{\P }$	$(0.667,0.185,0.156)(0.472,0.242,0.338)$	$(0.604,0.239,0.251)(0.431,0.272,0.312)$	$(0.663,0.214,0.215)(0.405,0.205,0.400)$

. The aggregated weights are given in the

Table 36. Aggregated weights.

$W_{\gimel {\mathfrak{Y}}_1}$	$(0.278,0.347,0.440)(0.655,0.158,0.219)$
$W_{\gimel {\mathfrak{Y}}_1}$	$(0.249,0.363,0.459)(0.516,0.227,0.109)$
$W_{\gimel {\mathfrak{Y}}_1}$	$(0.565,0.244,0.180)(0.459,0.237,0.238)$

.

4.

Calculate the relative performance using the values of ${\mathcal{P}}^{+}$ and ${\mathcal{P}}^{-}$ given in the

Table 37. Values of ${\mathcal{P}}^{+}$ and ${\mathcal{P}}^{-}$.

${\mathcal{P}}^{+}$	$0.667,0.185,0.141)(0.747,0.133,0.150)$
${\mathcal{P}}^{-}$	$(0.384,0.328,0.336)(0.317,0.311,0.400)$

are shown in the

Table 38. Relative performance.

$d[P_{11},P^{+}]=0.2897$	$d[P_{11},P^{-}]=0.1753$	$f_{11}=0.3769$
$d[P_{12},P^{+}]=0.2694$	$d[P_{12},P^{-}]=0.2051$	$f_{12}=0.4322$
$d[P_{13},P^{+}]=0.2185$	$d[P_{13},P^{-}]=0.3806$	$f_{13}=0.6353$
$d[P_{21},P^{+}]=0.3627$	$d[P_{21},P^{-}]=0.1917$	$f_{21}=0.3458$
$d[P_{22},P^{+}]=0.2587$	$d[P_{22},P^{-}]=0.2993$	$f_{22}=0.5364$
$d[P_{23},P^{+}]=0.1879$	$d[P_{23},P^{-}]=0.3631$	$f_{23}=0.6590$
$d[P_{31},P^{+}]=0.2481$	$d[P_{31},P^{-}]=0.2877$	$f_{31}=0.5370$
$d[P_{32},P^{+}]=0.2867$	$d[P_{32},P^{-}]=0.2071$	$f_{32}=0.4194$
$d[P_{33},P^{+}]=0.3090$	$d[P_{33},P^{-}]=0.2495$	$f_{33}=0.4467$

.

$$\begin{array}{cc}\hfill S_{11}& ={\displaystyle \sum _{t=1}^3}\mathsf{\Phi }\left[f_{11}-f_{t1}\right]\hfill \\ & =\mathsf{\Phi }\left[f_{11}-f_{21}\right]+\mathsf{\Phi }\left[f_{11}-f_{31}\right]\hfill \\ \hfill S_{11}& =0.01\hfill \\ \hfill I_{11}& ={\displaystyle \sum _{t=1}^3}\mathsf{\Phi }\left[f_{t1}-f_{11}\right]\hfill \\ & =\mathsf{\Phi }\left[f_{21}-f_{11}\right]+\mathsf{\Phi }\left[f_{31}-f_{11}\right]\hfill \\ \hfill I_{11}& =0.01\hfill \end{array}$$

5.

First calculations are performed in order to get superiority and inferiority presented in the

Table 39. Values for superiority and inferiority.

$S_{12}=0.01$	$I_{12}=0.01$
$S_{13}=0.01$	$I_{13}=0.01$
$S_{21}=0$	$I_{21}=0.02$
$S_{22}=0.02$	$I_{22}=0$
$S_{23}=0.02$	$I_{23}=0$
$S_{31}=0.02$	$I_{31}=0$
$S_{32}=0$	$I_{32}=0.02$
$S_{33}=0$	$I_{33}=0.02$

. Further calculation are performed and the superiority index and inferiority indexes using the values listed in Table 39 are given in the

Table 40. Superiority index and inferiority index values.

Sr. No.	${\mathit{F}}^{\rangle }\left(P_{\mathit{i}}^{\mathit{K}}\right)$	${\mathit{F}}^{\langle }\left(P_{\mathit{i}}^{\mathit{K}}\right)$
1	$(0.6202,0.0519,0.3900)(0.1049,0.0434,0.3884)$	$(0.6202,0.0519,0.3900)(0.1049,0.0434,0.3884)$
2	$(0.0945,0.0693,0.9513)(0.1042,0.0538,0.9295)$	$(0.0401,0.0528,0.9837)(0.1056,0.0297,0.9701)$
3	$(0.0401,0.0528,0.9837)(0.1056,0.0297,0.9701)$	$(0.0945,0.0693,0.9513)(0.1042,0.0538,0.9295)$

.

$$F^{\rangle }\left(P_i^K\right)={\displaystyle \underset{j=1}{\overset{3}{⨁}}}{S}_{ij}{W}_{drj}$$

6.

The superiority rankings are provided in the

Table 41. Superiority rankings.

Function	Score Value	Rank
$F^{\rangle }\left(P_1^K\right)$	−0.8784	2
$F^{\rangle }\left(P_2^K\right)$	0.0441	1
$F^{\rangle }\left(P_3^K\right)$	−0.9498	3

.

7.

The inferiority rankings are provided in the

Table 42. Inferiority rankings.

Function	Score Value	Rank
$F^{\langle }\left(P_1^K\right)$	−0.9498	3
$F^{\langle }\left(P_2^K\right)$	0.0441	1
$F^{\langle }\left(P_3^K\right)$	−0.8784	2

.

8.

The optimal Solution is $P_2^k$. On the basis of this optimal value ${\mathfrak{U}}_2^{\P }$ is the main cause of the accident.

Numerical computation using LAM:

Step 1, Step 2 and Step 3 are the same as in the calculations for SIR.

Calculation of score function is given in the

Table 43. Score values of alternatives.

	$S_{P_1}$	$S_{P_2}$	$S_{P_3}$
$P_1^k$	$0.0781$	$0.1156$	$0.2681$
$P_2^k$	$0.0511$	$0.1658$	$0.2655$
$P_3^k$	$0.2182$	$0.1296$	$0.1548$

:

4.

The ranking of each alternative based on each criterion is provided in the

Table 44. Ranking of alternatives vs. criterion.

	$S_{P_1}$	$S_{P_2}$	$S_{P_3}$
1st	$P_3^k$	$P_2^k$	$P_1^k$
2nd	$P_1^k$	$P_1^k$	$P_2^k$
3rd	$P_2^k$	$P_3^k$	$P_3^k$

.

5.

The rank frequency matrix is based on the score values shown in the

Table 45. Rank frequency.

	1st	2nd	3rd
$P_1^k$	1	2	0
$P_2^k$	1	1	1
$P_3^k$	1	0	2

.

The normalized weights are W = (0.2975, 0.3562, 0.3463), and th weighted rank frequency matrix is calculated in the

Table 46. Rank frequency (weighted).

	1st	2nd	3rd
$P_1^k$	0.3463	0.6537	0
$P_2^k$	0.3562	0.3463	0.2975
$P_3^k$	0.2975	0	0.7025

.

6.

Construct the linear assignment model:

$$\begin{array}{cc}\hfill maxZ=& 0.3463P_{11}+0.6537P_{12}+0.3562P_{21}+0.3463\hfill \\ & P_{22}+0.2975P_{23}+0.2975P_{31}+0.7025P_{33}\hfill \end{array}$$

subject to

$\begin{array}{ccc}\hfill P_{11}+P_{12}+P_{13}& =\hfill & \hfill 1\\ \hfill P_{21}+P_{22}+P_{23}& =\hfill & \hfill 1\\ \hfill P_{31}+P_{32}+P_{33}& =\hfill & \hfill 1\\ \hfill P_{11}+P_{21}+P_{31}& =\hfill & \hfill 1\\ \hfill P_{12}+P_{22}+P_{32}& =\hfill & \hfill 1\\ \hfill P_{13}+P_{23}+P_{33}& =\hfill & \hfill 1\\ \hfill P_{ik}=1\mathit{or}0\mathit{for}i=1,2,3;k=1,2,3\end{array}$

7.

The optimal solution for the system is then $P_{12}=1,P_{21}=1,P_{33}=1;Z=1.7124$.

$$\mathfrak{P}=\left(\begin{array}{ccc}0& 1& 0\\ 1& 0& 0\\ 0& 0& 1\end{array}\right)$$

8.

The optimal rank order is $P_2^k>P_1^k>P_3^k$. On the basis of this optimal rank the alternatives are ranked as ${\mathfrak{U}}_2^{\P }>{\mathfrak{U}}_1^{\P }>{\mathfrak{U}}_3^{\P }$. Hence ${\mathfrak{U}}_2^{\P }$ is the main cause of accident whose CCTV footage is shown in the Figure 5.

8. Discussion

The first benefit of the proposed method (LAM) is that it lowers the subjectivity of decision-makers by explicitly calculating the proximity of each alternative to the best choice. This is the initial benefit. Using a collection of criterion-specific rankings as inputs, the linear assignment method can yield a general preference ranking of the available options. The SIR technique generalises the concepts of superiority and inferiority by taking into account the distinctions between criterion values and other forms of generalised criteria. As a consequence, it presents a model that is dependable, efficient, and objective for a full investigation of the relative importance of alternatives. The capacity of the decision-maker (DM) to alter the aggregation procedures depending on his or her perspective on compensation, trade-offs, and the types of information gathered is possibly the most significant aspect of the SIR method. As a result, the SIR methodology makes use of the qualities shared by the majority of MCDM techniques when working with unquantifiable, cardinal, and ordinal data. In order to address the MCDM issues, the beginning SIR technique has been used; real figures are used to evaluate the criteria.

9. Conclusions

Topics associated with mPSF topology have been examined in this work. Combining the notions of the mPSF-union and mPSF-intersection as well as the mPSF-absolute set and the mPSF-null set produces the mPSF-topology. Meanwhile, several components of mPSF-topology are specified, including mPSF-open sets, mPSF-closed sets, the mPSF-interior, mPSF-closure, and the mPSF-exterior. Other features include mPSF-open and mPSF-closed sets. In addition, this study emphasises the mPSF-base and the mPSF subbase. mPSF-topology is a type of fuzzy topology that is an extension of m-polar fuzzy topology and spherical fuzzy topology. In this article, we have demonstrated real-world applications of MCGDM using mPSF-sets and mPSF-topologies. SIR and LAM are two well-known and commonly used approaches that we employ. One of the phases is to create the appropriate algorithms and flowcharts to make the process easier to visualise. We extend the SIR and LAM to mPSFSs and apply it to obtain a ranking to find the main causes of road accidents. In addition, we include a case study illustrating the use of both techniques for evaluating the main reasons for roadside accidents.