Thermal Buckling and Postbuckling Behaviors of Couple Stress and Surface Energy-Enriched FG-CNTR Nanobeams
Abstract
:1. Introduction
2. Theoretical Formulation
2.1. Geometrical and Material Description
2.2. Governing Equations
3. Solution Methodology
3.1. Immovable SS Ends
3.2. Immovable CC Ends
4. Results and Discussion
4.1. Verification Study
4.2. Parametric Studies
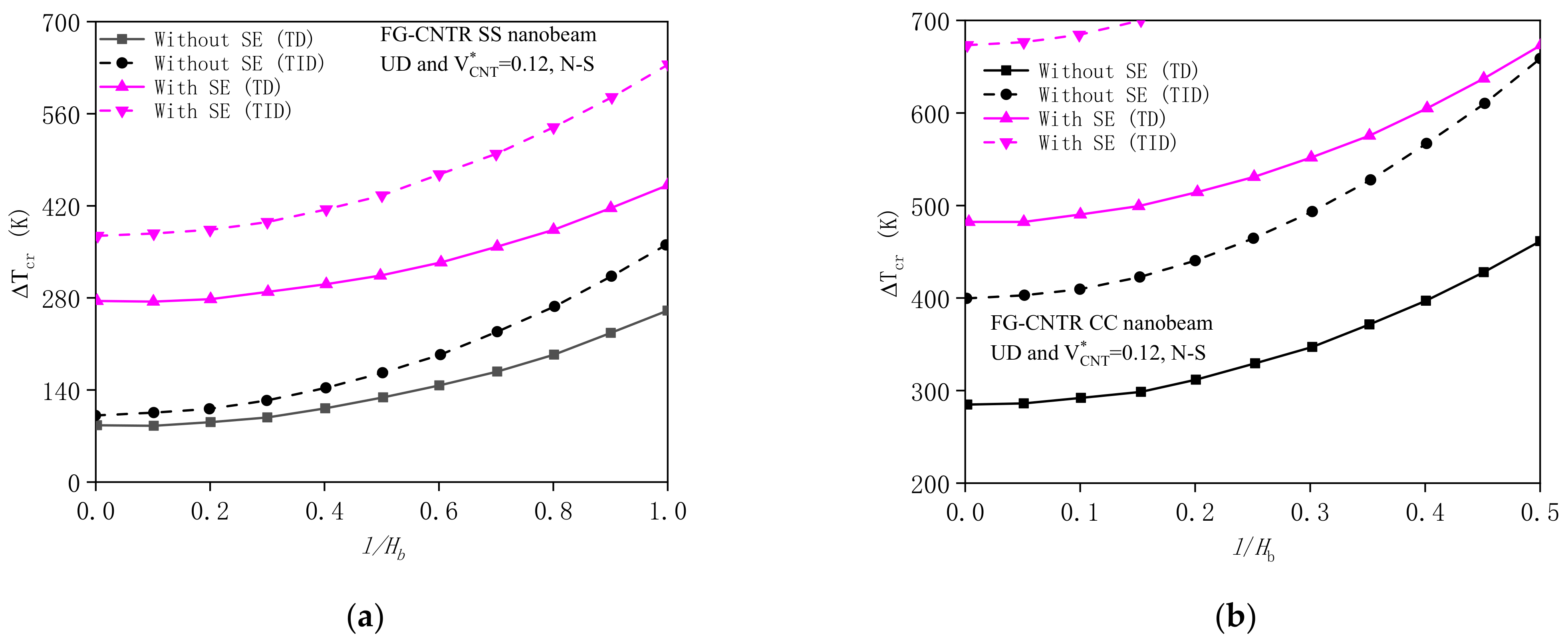
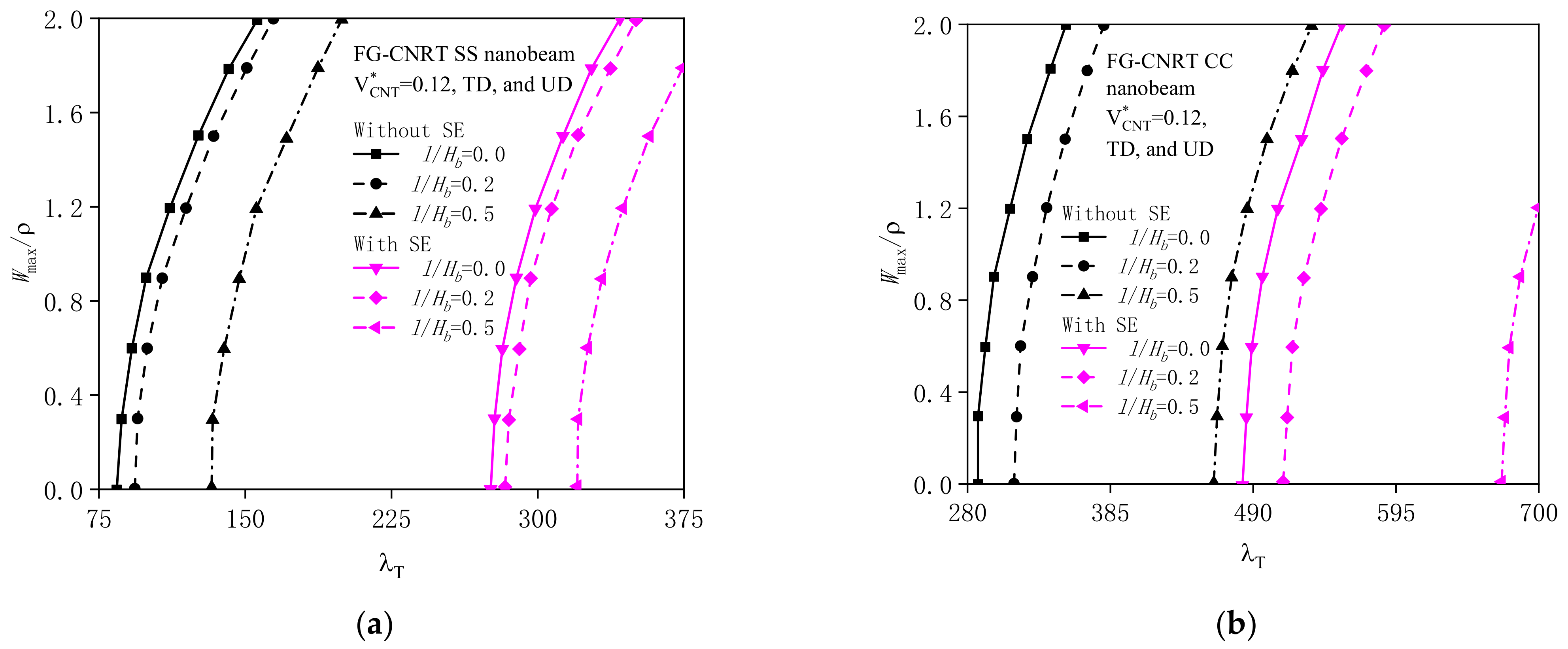
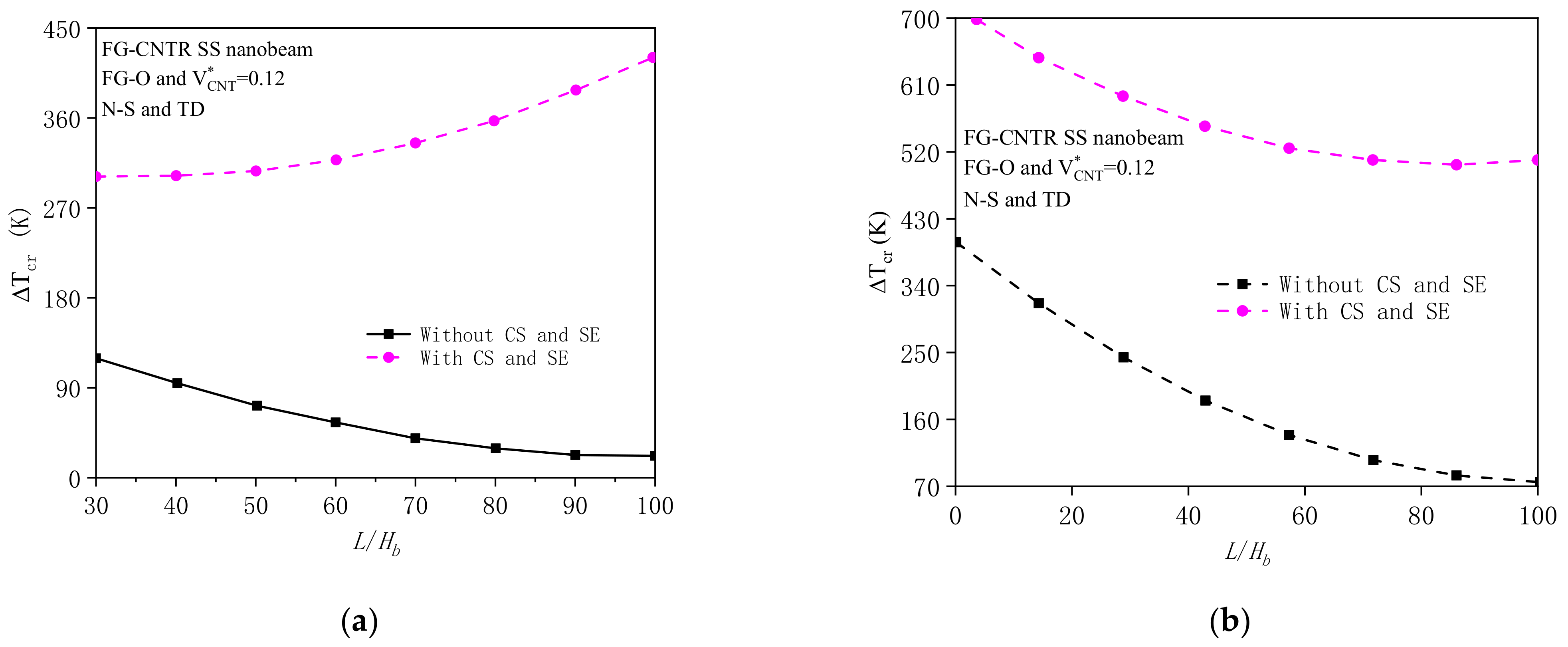
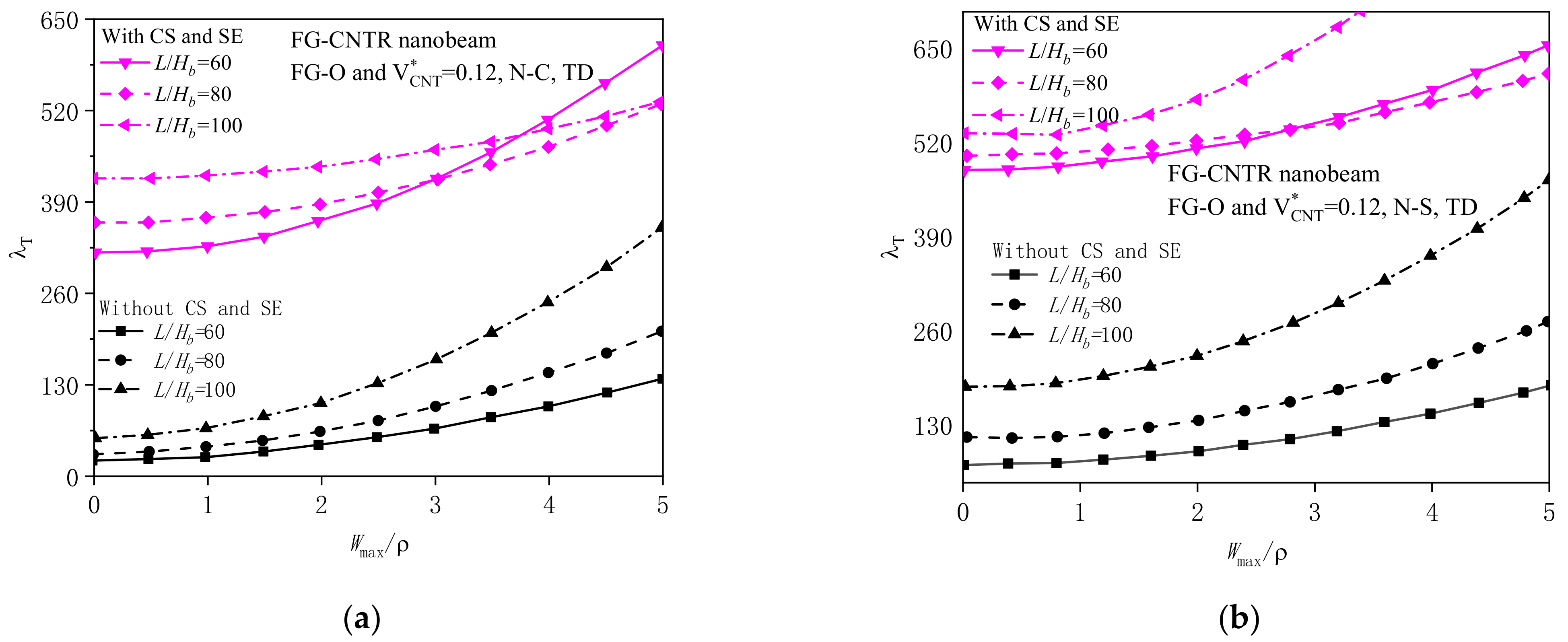
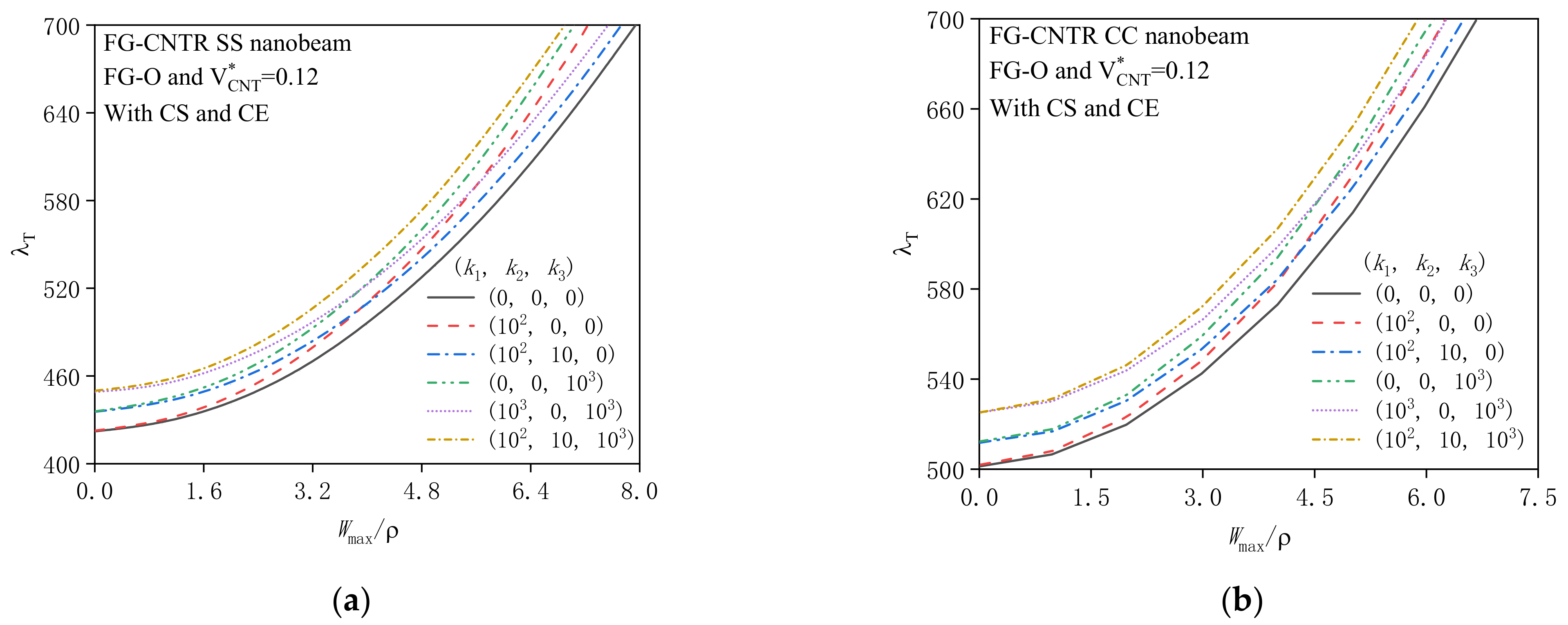
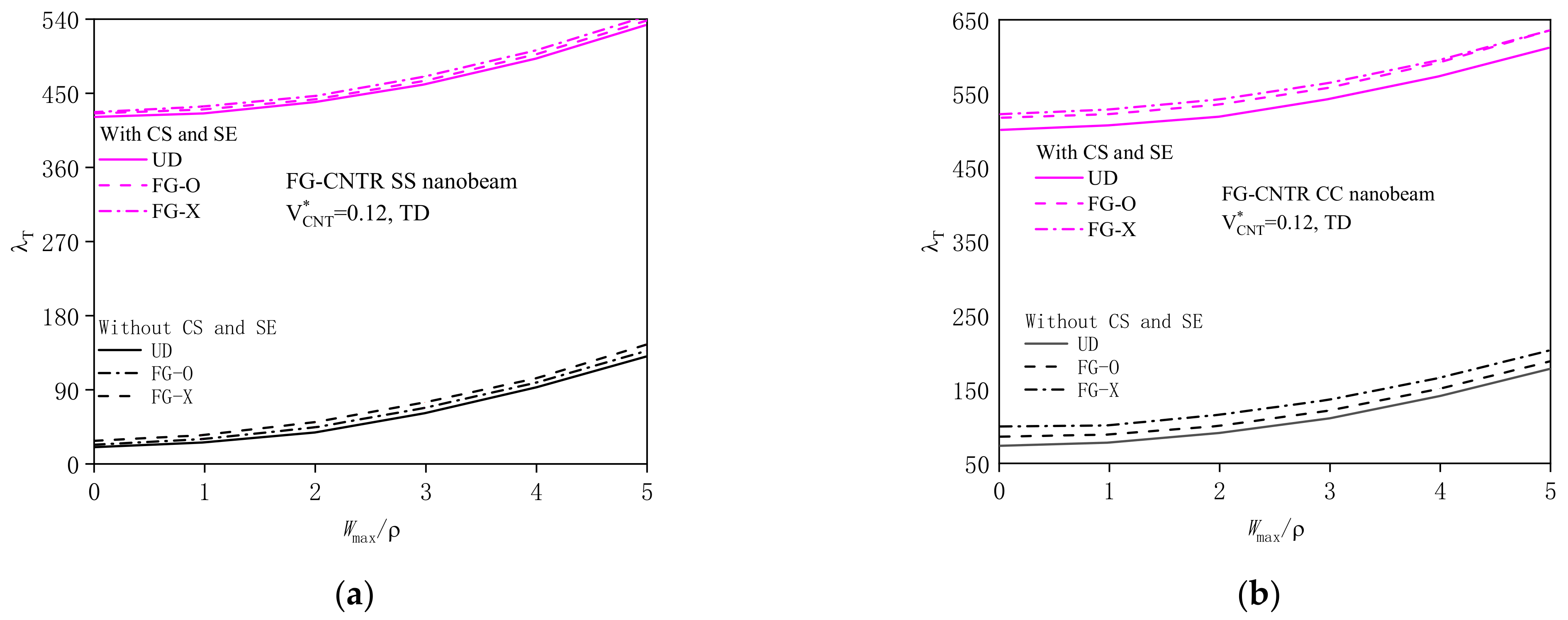
4.2.1. Effects of Surface Energy and Couple Stress
4.2.2. Effects of Geometrical Property and Substrate Stiffness
4.2.3. Effect of Material Properties
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Reddy, J.N. Nonlocal nonlinear formulations for bending of classical and shear deformation theories of beams and plates. Int. J. Eng. Sci. 2010, 48, 1507–1518. [Google Scholar] [CrossRef]
- Reddy, J.N. Microstructure-dependent couple stress theories of functionally graded beams. J. Mech. Phys. Solids 2011, 59, 2382–2399. [Google Scholar] [CrossRef]
- Ong, O.Z.S.; Ghayesh, M.H.; Losic, D.; Amabili, M. Coupled dynamics of double beams reinforced with bidirectional functionally graded carbon nanotubes. Eng. Anal. Bound. Elem. 2022, 143, 263–282. [Google Scholar] [CrossRef]
- Lam, D.C.; Yang, F.; Chong, A.; Wang, J.; Tong, P. Experiments and theory in strain gradient elasticity. J. Mech. Phys. Solids 2003, 51, 1477–1508. [Google Scholar] [CrossRef]
- Xie, Y.; Lei, J.; Guo, S.; Han, S.; Ruan, J.; He, Y. Size-dependent vibration of multi-scale sandwich micro-beams: An experimental study and theoretical analysis. Thin Wall. Struct. 2022, 175, 109115. [Google Scholar] [CrossRef]
- Li, Z.; He, Y.; Lei, J.; Han, S.; Guo, S.; Liu, D. Experimental investigation on size-dependent higher-mode vibration of cantilever microbeams. Microsyst. Technol. 2019, 25, 3005–3015. [Google Scholar]
- Li, Z.; He, Y.; Lei, J.; Guo, S.; Liu, D.; Wang, L. A standard experimental method for determining the material length scale based on modified couple stress theory. Int. J. Mech. Sci. 2018, 141, 198–205. [Google Scholar] [CrossRef]
- Lei, J.; He, Y.; Guo, S.; Li, Z.; Liu, D. Size-dependent vibration of nickel cantilever microbeams: Experiment and gradient elasticity. AIP Adv. 2016, 6, 105202. [Google Scholar] [CrossRef] [Green Version]
- Fleck, N.; Muller, G.; Ashby, M.; Hutchinson, J. Strain gradient plasticity: Theory and experiment. Acta Metall. Mater. 1994, 42, 475–487. [Google Scholar] [CrossRef]
- Liu, D.; He, Y.; Tang, X.; Ding, H.; Hu, P.; Cao, P. Size effects in the torsion of microscale copper wires: Experiment and analysis. Scripta Mater. 2012, 66, 406–409. [Google Scholar] [CrossRef]
- Polyzos, D.; Huber, G.; Mylonakis, G.; Triantafyllidis, T.; Papargyri-Beskou, S.; Beskos, D. Torsional vibrations of a column of fine-grained material: A gradient elastic approach. J. Mech. Phys. Solids 2015, 76, 338–358. [Google Scholar] [CrossRef]
- Guo, S.; He, Y.; Liu, D.; Lei, J.; Li, Z.; Ding, H. Torsional stress relaxation behavior of microscale copper wire. Mater. Sci. Eng. A 2017, 698, 277–281. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Mindlin, R.; Tiersten, H. Effects of couple-stresses in linear elasticity. Arch. Ration. Mech. An. 1962, 11, 415–448. [Google Scholar] [CrossRef]
- Toupin, R.A. Theories of elasticity with couple-stress. Arch. Ration. Mech. An. 1964, 17, 85–112. [Google Scholar] [CrossRef]
- Yang, F.; Chong, A.C.M.; Lam, D.C.C.; Tong, P. Couple stress based strain gradient theory for elasticity. Int. J. Solids Struct. 2002, 39, 2731–2743. [Google Scholar] [CrossRef]
- Hadjesfandiari, A.R.; Dargush, G.F. Couple stress theory for solids. Int. J. Solids Struct. 2011, 48, 2496–2510. [Google Scholar] [CrossRef] [Green Version]
- Mindlin, R.D. Second gradient of strain and surface-tension in linear elasticity. Int. J. Solids Struct. 1965, 1, 417–438. [Google Scholar] [CrossRef]
- Mindlin, R.; Eshel, N. On first strain-gradient theories in linear elasticity. Int. J. Solids Struct. 1968, 4, 109–124. [Google Scholar] [CrossRef]
- Cordero, N.M.; Forest, S.; Busso, E.P. Second strain gradient elasticity of nano-objects. J. Mech. Phys. Solids 2016, 97, 92–124. [Google Scholar] [CrossRef]
- Zhou, S.; Li, A.; Wang, B. A reformulation of constitutive relations in the strain gradient elasticity theory for isotropic materials. Int. J. Solids Struct. 2016, 80, 28–37. [Google Scholar] [CrossRef]
- Fu, G.; Zhou, S.; Qi, L. On the strain gradient elasticity theory for isotropic materials. Int. J. Eng. Sci. 2020, 154, 103348. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Murdoch, A.I. A continuum theory of elastic material surfaces. Arch. Ration. Mech. An. 1975, 57, 291–323. [Google Scholar] [CrossRef]
- Ma, X.; Chen, W. 24-DOF quadrilateral hybrid stress element for couple stress theory. Comput. Mech. 2014, 53, 159–172. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Murdoch, A.I. Surface stress in solids. Int. J. Solids Struct. 1978, 14, 431–440. [Google Scholar] [CrossRef]
- Thai, H.T.; Vo, T.P.; Nguyen, T.K.; Kim, S.E. A review of continuum mechanics models for size-dependent analysis of beams and plates. Compos. Struct. 2017, 177, 196–219. [Google Scholar] [CrossRef]
- Roudbari, M.A.; Jorshari, T.D.; Lü, C.; Ansari, R.; Kouzani, A.Z.; Amabili, M. A review of size-dependent continuum mechanics models for micro-and nano-structures. Thin Wall. Struct. 2022, 170, 108562. [Google Scholar] [CrossRef]
- Gao, X.L.; Mahmoud, F.F. A new Bernoulli–Euler beam model incorporating microstructure and surface energy effects. Z. Angew. Math. Phys. 2014, 65, 393–404. [Google Scholar] [CrossRef]
- Gao, X.L. A new Timoshenko beam model incorporating microstructure and surface energy effects. Acta. Mech. 2015, 226, 457–474. [Google Scholar] [CrossRef]
- Gao, X.L.; Zhang, G. A microstructure-and surface energy-dependent third-order shear deformation beam model. Z. Angew. Math. Phys. 2015, 66, 1871–1894. [Google Scholar] [CrossRef]
- Gao, X.L.; Zhang, G. A non-classical Kirchhoff plate model incorporating microstructure, surface energy and foundation effects. Contin. Mech. Therm. 2016, 28, 195–213. [Google Scholar] [CrossRef]
- Gao, X.L.; Zhang, G. A non-classical Mindlin plate model incorporating microstructure, surface energy and foundation effects. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20160275. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yin, S.; Deng, Y.; Zhang, G.; Yu, T.; Gu, S. A new isogeometric Timoshenko beam model incorporating microstructures and surface energy effects. Math. Mech. Solids 2020, 25, 2005–2022. [Google Scholar] [CrossRef]
- Zhang, B.; Shen, H.; Liu, J.; Wang, Y.; Zhang, Y. Deep postbuckling and nonlinear bending behaviors of nanobeams with nonlocal and strain gradient effects. Appl. Math. Mech. 2019, 40, 515–548. [Google Scholar] [CrossRef]
- Allahkarami, F.; Nikkhah-Bahrami, M. The effects of agglomerated CNTs as reinforcement on the size-dependent vibration of embedded curved microbeams based on modified couple stress theory. Mech. Adv. Mater. Struct. 2017, 25, 995–1008. [Google Scholar] [CrossRef]
- Thanh, C.L.; Phung-Van, P.; Thai, C.H.; Nguyen-Xuan, H.; Wahab, M.A. Isogeometric analysis of functionally graded carbon nanotube reinforced composite nanoplates using modified couple stress theory. Compos. Struct. 2018, 184, 633–649. [Google Scholar] [CrossRef]
- Zhang, B.; Li, H.; Liu, J.; Shen, H.; Zhang, X. Surface energy-enriched gradient elastic Kirchhoff plate model and a novel weak-form solution scheme. Eur. J. Mech. A-Solids 2021, 85, 104118. [Google Scholar] [CrossRef]
- Zhang, B.; Li, H.; Kong, L.; Shen, H.; Zhang, X. Coupling effects of surface energy, strain gradient, and inertia gradient on the vibration behavior of small-scale beams. Int. J. Mech. Sci. 2020, 184, 105834. [Google Scholar] [CrossRef]
- Eftekhari, S.A.; Toghraie, D. Vibration and dynamic analysis of a cantilever sandwich microbeam integrated with piezoelectric layers based on strain gradient theory and surface effects. Appl. Math. Comput. 2022, 419, 126867. [Google Scholar]
- Dangi, C.; Lal, R.; Sukavanam, N. Effect of surface stresses on the dynamic behavior of bi-directional functionally graded nonlocal strain gradient nanobeams via generalized differential quadrature rule. Eur. J. Mech. A-Solids 2021, 90, 104376. [Google Scholar] [CrossRef]
- Shanab, R.; Attia, M.; Mohamed, S. Nonlinear analysis of functionally graded nanoscale beams incorporating the surface energy and microstructure effects. Int. J. Mech. Sci. 2017, 131, 908–923. [Google Scholar] [CrossRef]
- Shaat, M.; Mahmoud, F.; Gao, X.L.; Faheem, A.F. Size-dependent bending analysis of Kirchhoff nano-plates based on a modified couple-stress theory including surface effects. Int. J. Mech. Sci. 2014, 79, 31–37. [Google Scholar] [CrossRef]
- Lu, L.; Guo, X.; Zhao, J. A unified size-dependent plate model based on nonlocal strain gradient theory including surface effects. Appl. Math. Model. 2019, 68, 583–602. [Google Scholar] [CrossRef]
- Duong, V.Q.; Tran, N.D.; Luat, D.T.; Thom, D.V. Static analysis and boundary effect of FG-CNTRC cylindrical shells with various boundary conditions using quasi-3D shear and normal deformations theory. Structures 2022, 44, 828–850. [Google Scholar] [CrossRef]
- Duc, D.H.; Thom, D.V.; Cong, P.H.; Minh, P.V.; Nguyen, N.X. Vibration and static buckling behavior of variable thickness flexoelectric nanoplates. Mech. Based. Des. Struc. 2022, 1–29. [Google Scholar] [CrossRef]
- Van Do, T.; Doan, D.H.; Tho, N.C.; Duc, N.D. Thermal buckling analysis of cracked functionally graded plates. Int. J. Struct. Stab. Dy. 2022, 22, 2250089. [Google Scholar] [CrossRef]
- Van Do, T.; Doan, D.H.; Duc, N.D.; Bui, T.Q. Phase-field thermal buckling analysis for cracked functionally graded composite plates considering neutral surface. Compos. Struct. 2017, 182, 542–548. [Google Scholar] [CrossRef]
- Shen, H.S.; Xiang, Y. Nonlinear analysis of nanotube-reinforced composite beams resting on elastic foundations in thermal environments. Eng. Struct. 2013, 56, 698–708. [Google Scholar] [CrossRef]
- Shen, H.S. Nonlinear bending of functionally graded carbon nanotube-reinforced composite plates in thermal environments. Compos. Struct. 2009, 91, 9–19. [Google Scholar] [CrossRef]
- Shen, H.S. A Two-Step Perturbation Method in Nonlinear Analysis of Beams, Plates and Shells; Higher Education Press: Beijing, China, 2013. [Google Scholar]
- Shen, H.S.; Zhang, C.L. Nonlocal beam model for nonlinear analysis of carbon nanotubes on elastomeric substrates. Comp. Mater. Sci. 2011, 50, 1022–1029. [Google Scholar] [CrossRef]
- Sahmani, S.; Bahrami, M.; Aghdam, M.M. Surface stress effects on the postbuckling behavior of geometrically imperfect cylindrical nanoshells subjected to combined axial and radial compressions. Int. J. Mech. Sci. 2015, 100, 1–22. [Google Scholar] [CrossRef]
- Shen, H.S.; Wang, Z.X. Nonlinear analysis of shear deformable FGM beams resting on elastic foundations in thermal environments. Int. J. Mech. Sci. 2014, 81, 195–206. [Google Scholar] [CrossRef]
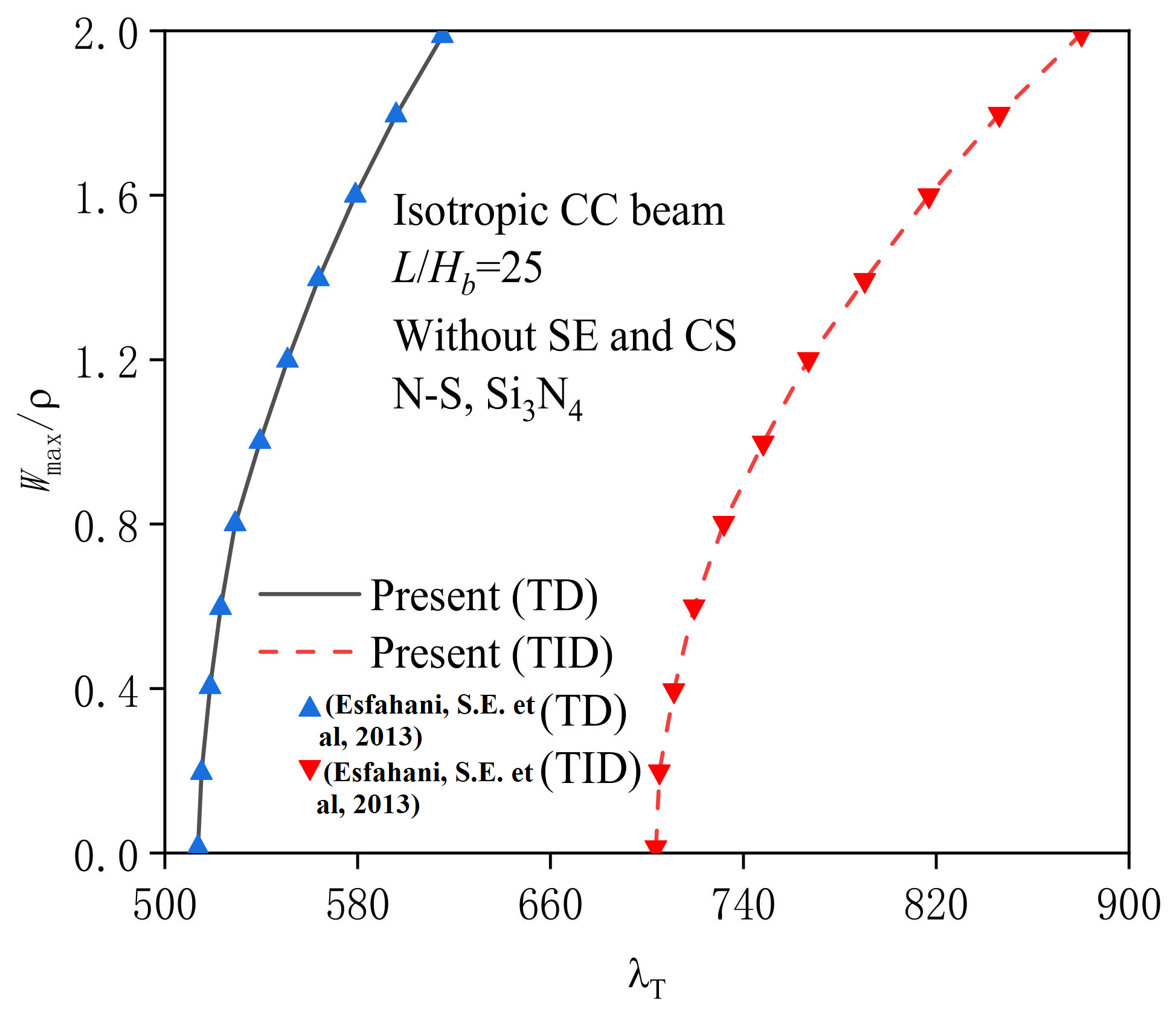
- Esfahani, S.E.; Kiani, Y.; Eslami, M.R. Non-linear thermal stability analysis of temperature dependent FGM beams supported on non-linear hardening elastic foundations. Int. J. Mech. Sci. 2013, 69, 10–20. [Google Scholar] [CrossRef]



| Materials | TID | TD | ||
|---|---|---|---|---|
| Shen and Wang [54] | Present | Shen and Wang [54] | Present | |
| SUS304 | 0.619 | 0.661 | 0.582 | 0.595 |
| Si3N4 | 1.350 | 1.355 | 1.185 | 1.189 |
| ZrO2 | 0.518 | 0.544 | 0.416 | 0.416 |
| Al2O3 | 1.379 | 1.406 | 1.326 | 1.342 |
| Materials | TID | TD | ||
|---|---|---|---|---|
| Esfahani et al. [55] | Present | Esfahani et al. [55] | Present | |
| Si3N4 | 5.338 | 5.421 | 3.916 | 3.916 |
| 3.263 | 3.315 | 2.659 | 2.659 | |
| 3.039 | 3.089 | 2.515 | 2.515 | |
| 2.898 | 2.946 | 2.416 | 2.416 | |
| SUS304 | 2.604 | 2.644 | 2.196 | 2.196 |
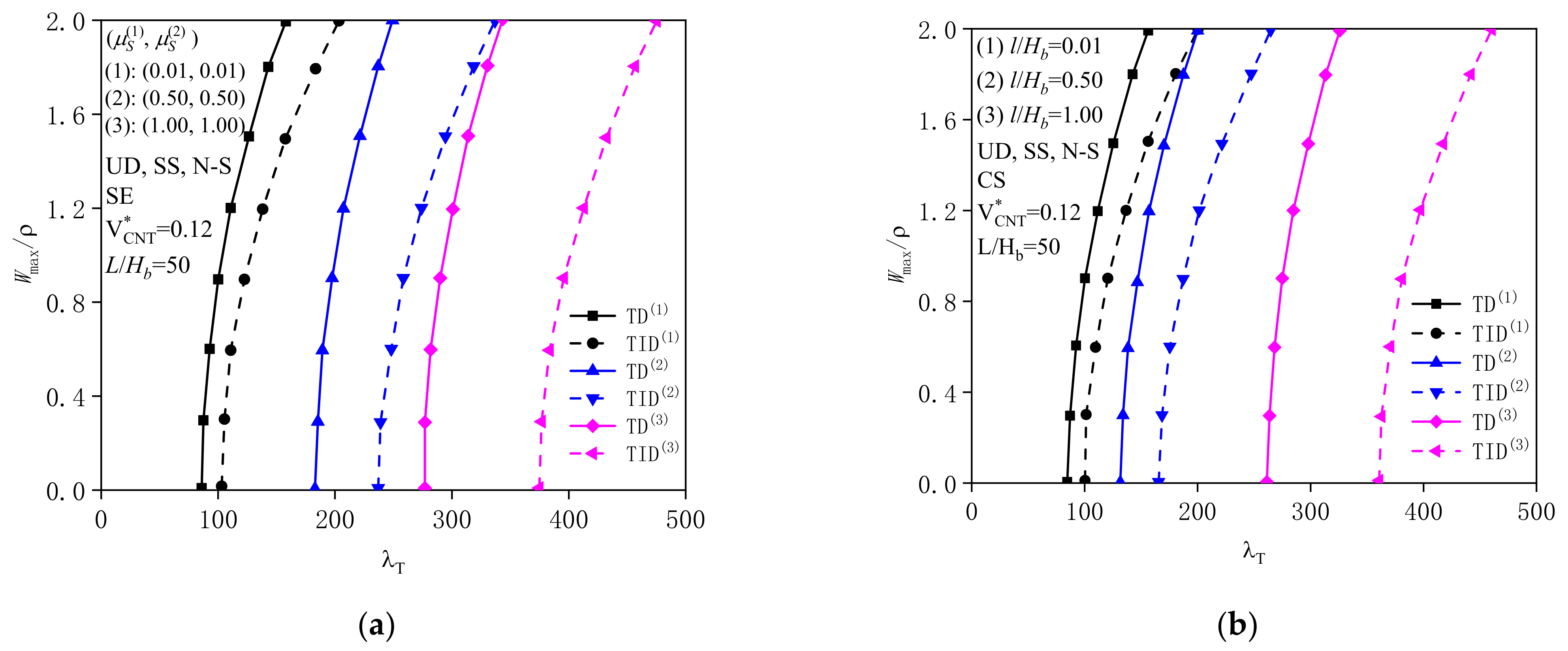
| BC | |||||||
|---|---|---|---|---|---|---|---|
| (0.0,0.0) | (0.01,0.01) | (0.3,0.3) | (0.4,0.4) | (0.5,0.5) | (1.0,1.0) | ||
| SS | TID | 99.666 | 102.403 | 181.784 | 209.157 | 318.649 | 373.396 |
| TD | 84.673 | 86.757 | 144.498 | 163.580 | 238.170 | 275.293 | |
| CC | TID | 398.665 | 401.411 | 481.068 | 508.536 | 536.004 | 673.345 |
| TD | 286.336 | 288.179 | 342.325 | 361.386 | 380.695 | 481.673 | |
| BC | |||||||
|---|---|---|---|---|---|---|---|
| 0.0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | ||
| SS | TID | 99.666 | 99.692 | 110.095 | 123.131 | 141.383 | 164.848 |
| TD | 84.673 | 84.692 | 92.488 | 102.092 | 115.266 | 131.816 | |
| CC | TID | 398.665 | 398.768 | 440.381 | 492.527 | 565.531 | 659.393 |
| TD | 286.336 | 286.403 | 313.451 | 347.616 | 396.229 | 460.486 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, L.; Zhang, B.; Li, C. Thermal Buckling and Postbuckling Behaviors of Couple Stress and Surface Energy-Enriched FG-CNTR Nanobeams. Symmetry 2022, 14, 2228. https://doi.org/10.3390/sym14112228
Kong L, Zhang B, Li C. Thermal Buckling and Postbuckling Behaviors of Couple Stress and Surface Energy-Enriched FG-CNTR Nanobeams. Symmetry. 2022; 14(11):2228. https://doi.org/10.3390/sym14112228
Chicago/Turabian StyleKong, Liulin, Bo Zhang, and Cheng Li. 2022. "Thermal Buckling and Postbuckling Behaviors of Couple Stress and Surface Energy-Enriched FG-CNTR Nanobeams" Symmetry 14, no. 11: 2228. https://doi.org/10.3390/sym14112228





