Discrete Dynamics of Balls in Cageless Ball Bearings

Abstract

Cageless ball bearings are often preferred as a back-up bearing for active magnetic bearings to support a falling rotor, but the contact between the balls of the cageless ball bearing may lead to the deterioration of the bearing performance and affect the dynamic stability of the rotor system. Thus, we studied the discrete dynamics of cageless ball bearings. First, a model is proposed to change the groove curvature center of the local outer raceway to control the ball velocity to achieve dispersion. Combined with the spatial geometry theory, the mathematical model of the discrete raceway is established, the collision between the balls is considered as an abruptly added constraint, and the non-smooth dynamics equation of the cageless ball bearing with a local discrete raceway is established. Then, the fourth-order Adams prediction correction algorithm is used to numerically solve the dynamic discretization of the ball, and the structural parameters of the discrete raceway are preferably selected, according to the phase diagram of the ball and the change in the angular spacing. The results show that the structure of the discrete raceway has a strong influence on the discrete dynamics of the ball.

1. Introduction

Research on cageless bearings has received increasing attention in recent years due to the wide application of cageless bearings in active magnetically levitated standby bearings [1,2]. When the active magnetic bearing system fails when power is unavailable, due to the absence of cage action, there are contact collisions during the motion of the adjacent rolling elements, and the uneven distribution of the rolling elements causes the bearing load/bearing performance of the standby bearing to decrease [3], which in turn affects the stability of the rotor during its fall. Therefore, how to control the rolling body motion has become the focus of research on cageless bearings. Existing scholars have performed research on the force and motion of rolling elements from the structural and dynamic aspects.

For the bearing raceway structure change, Xue and Lu et al. [4,5] proposed the outer ring three-valve wave structure raceway for the ideal assumption that there is no contact angle between the rolling body and the raceway, adjusted the contact force between the rolling body and the ring in the non-load bearing area, by designing the slope of the raceway flap, and increased the friction to improve the slippage phenomenon of the rolling body at high speed. Hamrock [6,7] considered the problem of rolling body slippage caused by the change in the contact angle of a bearing raceway under the action of centrifugal force, proposed to design the overall circular outer raceway as a double-flap arch symmetric three-point contact structure, established a proposed static model and used the Newtonian Rafelson method to iteratively obtain the contact angle change, and then determined the relative position of the center of the curvature of the double-flap raceway. Other studies [8,9] considered the relationship between the radius of the curvature of the outer ring arch raceway groove and the rolling body spin motion, based on the raceway control theory, and analyzed the change law of the rolling body and the raceway force under different speed conditions, in combination with the proposed dynamics of the bearing. The arch raceway is more suitable for controlling the rolling body spin and the sliding motion at a low speed. With the development of the wind turbine and aviation field, scholars have changed both the inner and outer raceway structure of the bearing to improve the bearing stability and load carrying capacity, and designed it as a four-point contact bearing [10,11]. Leblanc [12] combined the deformation coordination theory proposed by Harris to determine the four-point contact bearing rolling body and raceway contact geometry relationship, and derived the relative sliding velocity function model at the contact point. The study found that the four-point contact structure is conducive to sharing the load on the rolling body and then offset the sliding friction at the contact point. Halpin et al. [13] designed a double-arch raceway structure four-point contact bearing with a symmetric center of the curvature and equal radius of the curvature to control the sliding friction between the rolling element and raceway, and analyzed the sliding speed of the rolling element and the raceway contact by combining the clearance and arch size parameters of the double-arch raceway. When the bearing is subjected to a combined load, the same curvature value of the inner and outer raceway will lead to the deflection of the collar and thus reduce the frictional force on the rolling element, causing the sliding motion of the rolling element. Singh et al. [14] proposed to reduce the sliding rate as the design goal of a raceway structure, designed a variable curvature double elliptical raceway 4-point contact ball bearing model based on the principle of space geometry, established an elliptical raceway radius of the curvature analytical geometric model by analyzing the geometric relationship between the axial offset motion displacement of the rolling element and the contact point, and determined the applicable conditions of the different elliptical-type designs by comparing the range of contact force changes caused by the axial offset under three different combinations of elliptical raceway curvatures, which provides a reference for the design of the elliptical raceways. Korolev [15] considered the relationship between the raceway curvature ratio and contact wear and designed the inner ring raceway of the bearing with a continuous 20$°$ deflection angle from the lowest point of the raceway by controlling the direction of the frictional force in contact between the rolling body and the raceway to move the contact point between the rolling body and the raceway along the axis. This process improves the contact preload while controlling the resistance to the running rolling body, which helps to reduce the vibration level of the bearing.

For bearing dynamics, Townsend [16] analyzed the relationship between the rolling body and the raceway frictional resistance and the relative sliding speed characteristics under the assumption of the uniform distribution of rolling bodies not in contact with each other in cage free bearings. They began with the rolling body being subjected to the raceway frictional moment. Then, based on the research of Townsend, Zhilnikov [17] considered the initial motion stage of the cageless bearings. The rolling bodies’ contact with each other, was based on the deformation coordination principle to analyze the rolling bodies and the inner ring raceway contact characteristics, and they established the dynamics model of the cageless bearing, by obtaining the rolling bodies through the operation to exist first separately, and then have a discontinuous contact phenomenon. Such a random contact makes the rolling bodies produce a pile-up, which is the cause of the vibration in a cageless bearing. Conversely, Helfert [18] determined the cause of the discontinuous contact between the rolling bodies during the smooth motion of the cageless bearings, established a rolling element with a two-degree-of-freedom dynamics model for a single rolling body, using the Hertzian contact theory and the Eulerian dynamics theory, and found that the slippage of a rolling body causes the random continuous contact between the adjacent rolling bodies. Cole [19] comprehensively considered the rolling body discontinuous contact. The rolling body simultaneously withstood the front and rear ball force situation and derived the rolling body contact force vector function using the center-of-mass motion theorem to establish the rolling body rotation, the rotation nonlinear differential equations of motion, and the numerical iterative solution to determine the distribution area of the rolling bodies’ discontinuous contact. Kärkkäinen et al. [20,21] considered the contact problem of only bearing one adjacent rolling element force when the rolling element’s discontinuous contact is made, proposed the adjacent rolling element’s discontinuous normal force model as a compression spring damping model, combined with the rolling element position angle to establish the contact force segmentation function, and solved the dynamic characteristics of the cageless bearing, based on the segmented rolling element collision force using the fourth-order Runge-Kutta method. Although the model considers the discontinuity of the rolling element collision force, it does not consider the transient impact between the adjacent rolling elements, due to the difference in the rotational speed. Currently, the non-smooth characteristics are primarily studied for the discontinuous contact between the rotor and the cageless bearing [22,23]. Chávez et al. [24] studied the non-smooth characteristics of the discontinuous contact between the rotor and the inner ring raceway due to the impact when the rotor is dropped, and established the bearing non-smooth two-degrees-of-freedom differential equations of the motion by combining the intermittent contact-induced unbalanced impact force with the rotor-bearing relative vector displacement. The track diagram of the stable solution of the motion trajectory was solved using the Runge-Kutta method, which provided a judgment of the influence of the load shock on the stability of the bearing. Halminen [25,26] established the relative distance function at the contact point by analyzing the clearance between the rotor and the bearing collar, using the position coordinates of the inner ring and the rotor in space, as variables, determined the discontinuous collision force model by combining the relative motion velocity, and established a non-smooth multibody dynamics model for a cageless bearing, based on the elastic contact theory.

Due to the complex nature of the non-smooth dynamic models, the numerical solutions are also becoming an important alternative to the experimental verification of the dynamic properties of rotor bearings [27], and the numerical solution methods have an important impact on the dynamic accuracy of the rotor bearing systems. Ming et al. [28] proposed a numerical solution method of Paulsen for the non-smooth dynamic model of the rotor system in combination with the structural mechanics for the incomplete constraints of the rotor system. However, this method is primarily used for the analysis of the high-frequency impact characteristics formed by the rotor shaft itself. Deng et al. [29] considered the suppression effect of the bearings on the rotor system vibration, used the prediction correction algorithm to solve the rotor dynamic characteristics, and combined the result with the phase space diagram to analyze the rotor trajectory stability. Their algorithm effectively analyzed the influence of the coupling effect between the rotor and the bearings on the rotor dynamic characteristics. Roques [30] modeled the non-smooth dynamics of the rotor impact transients from the perspective of rotor motion and solved the post-contact velocity, using the display prediction correction method, which has a high accuracy for the solution of transient contact dynamics.

Therefore, to solve the problem of an unstable rotor operation caused by the collision of the rolling body contact of cageless bearings, this paper innovatively proposes the method of combining the analytical geometric curve features to design the raceway structure, and establishes the mathematical model of the discrete raceway space surface. This study is based on the research of the same group [31,32,33], from the perspective of the bearing structure design with the goal of controlling the dispersive motion of the rolling body using space geometry and analytical geometry, combined with the bearing kinematics theory. According to the kinematic contact characteristics between the rolling elements of the cageless bearing, a non-smooth kinetic model of the cageless bearing, including a local discrete groove is established, and the dynamic characteristics of the bearing are obtained by choosing the prediction correction algorithm for the sudden change in the contact force between the rolling elements. The local discrete raceway research in this paper combines the mathematical methods with engineering theories to provide new ideas for the design and development of new cageless bearings. for the dynamic performance analysis of the bearings, the influence of the ball-ball contact problem on the running stability of cageless bearings is avoided by simplifying the rolling element motion state and ignoring the ball-ball contact problem. Furthermore, the accuracy of the cageless non-smooth dynamic model is improved, using a numerical simulation instead of experiments.

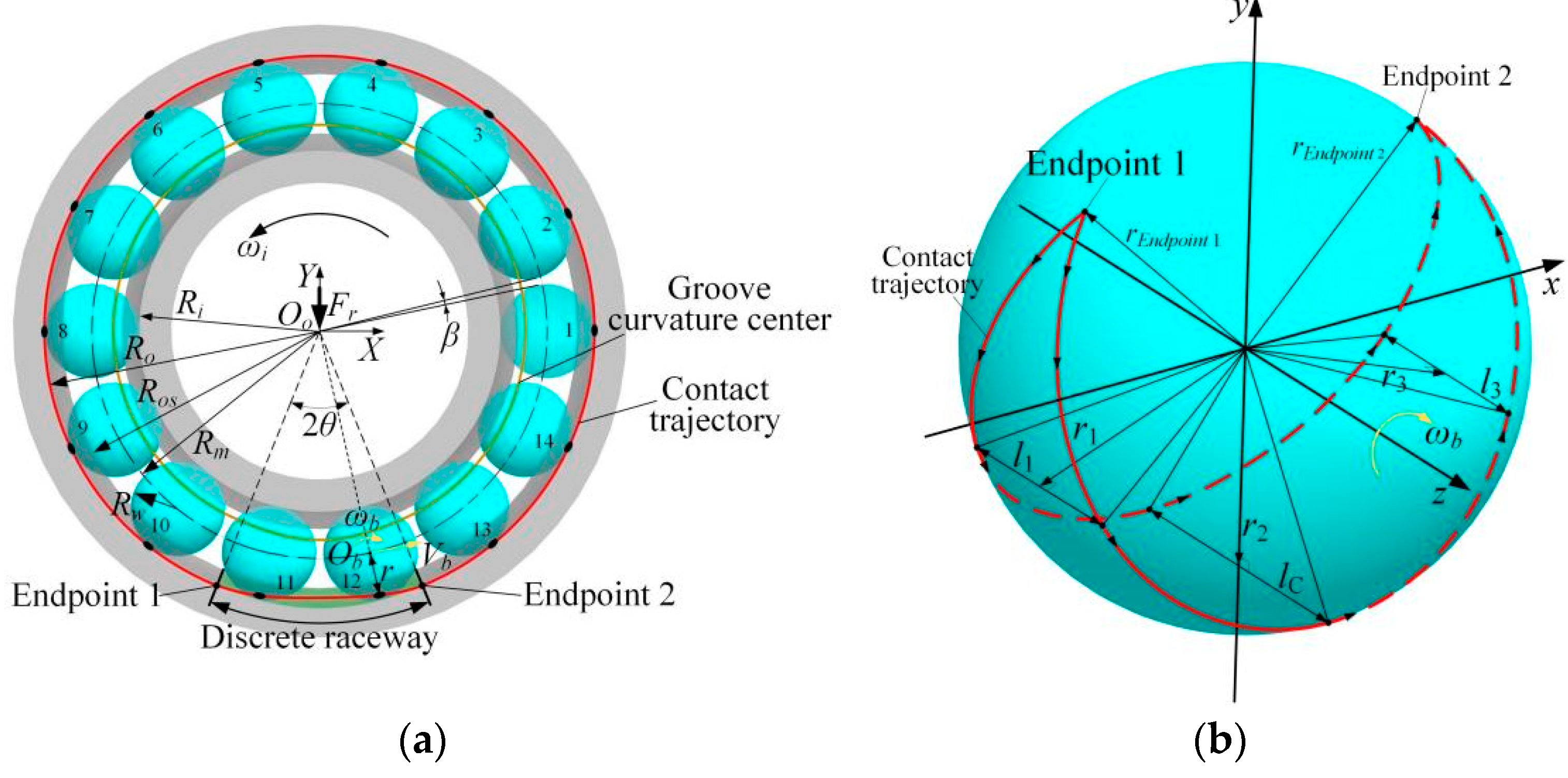
2. Discrete Raceway Principle and the Mathematical Model

2.1. Principle

From the perspective of the motion of the cageless ball bearing system, to achieve dispersion with adjacent balls, it is necessary to control the common rotation speed of the balls so that the common rotation speed of the balls varies in a regular manner. The proposed cageless ball bearing with a discrete raceway is shown in Figure 1a. The outer ring raceway consists of two parts: a conventional raceway and a discrete raceway, where the discrete raceway plays the role of separating the balls. We denote O_i(o) and O_b as the bearing center and ball center, respectively; R_i as the radius of the inner ring groove bottom; R_o as the radius of the outer ring groove bottom; R_m as the radius of the bearing pitch circle; R_w as the radius of the ball; and R_os as the outer shoulder radius. The annular span angle of the discrete raceway is 2θ, and r is the effective contact radius of the ball and the outer raceway (i.e., the radial distance between the contact point of the ball and the outer raceway and the ball center). Figure 1b shows the projection of the contact trajectory between the ball and the discrete raceway on the ball, and l is the axial span distance between the two contact points.

When the ball moves to the bearing area, the orbital velocity V_b and the self-rotation velocity w_b of the ball are approximately equal to the theoretical value under the larger load of the inner and outer rings [34]. By investigating the four-point contact bearings, Ref. [13] found that for a bearing system in which the inner ring rotates, and the outer ring is fixed, the orbital velocity of the ball is related to the effective contact radius r. The relative sliding velocities of the ball and the outer and inner rings are:

ΔV_o = V_b(r + R_m)/R_m − ω_br,

(1)

ΔV_i = ω_iR_i − (V_bR_i/R_m + ω_bR_w).

(2)

When the ball is purely rolling, the unit of the theoretical revolution speed of the ball is deg/s, and the relationship with the effective contact radius r is:

V_b = 180ω_iR_i(1 − R_w/(r + R_w))/πR_m.

(3)

Equation (3) shows that the effective contact radius r between the ball and the outer raceway can affect the ball orbit speed, and the revolution speed is the incremental function of the effective contact radius; thus, the ball orbit speed can be controlled by changing the effective contact radius r between the ball and the outer raceway. The contact trajectory of the ball and the outer raceway also consists of two parts. When the ball moves at the regular outer raceway, its contact trajectory is along the bottom of the groove of the outer raceway. When the ball moves at the discrete raceway, its contact trajectory becomes two spatial curves symmetrical about the X-Y plane, and the contact point will be shifted to the axial direction and the center of the ball, which leads to a change in the effective contact radius r. Therefore, when the ball passes through the discrete raceway, the track speed will change, which makes the adjacent ball in the discrete raceway produce a certain speed difference to realize the ball discrete. However, to determine the law of the change in the effective contact radius r, additional research on the structure of the discrete raceway is required.

2.2. Discrete Raceway Mathematical Model

The shape of the discrete raceway is similar to the outer raceway of the double half outer ring ball bearing, and its structure is shown in Figure 2. Both have two contact points with the ball, but the difference is that the angle ∠O_e1O_bO_e2 formed between the center of curvature of the two grooves of the discrete raceway and the center of the ball is changed; thus, the Line l and the effective contact radius r of the two contact points between the ball and the discrete raceway are changed.

Because the ball and the discrete raceway have two points of contact, the change in the effective contact radius makes the trajectory of the contact point into a space curve. To determine the change law of the effective contact radius, we can first determine the change law of the contact point of the ball and the discrete raceway. Taking the bearing center as the origin and establishing the coordinate system shown in Figure 1a, the coordinates of the contact point between the ball and the discrete raceway in the coordinate system are (x, y, z). Considering the symmetry of the discrete raceway structure, this paper adopts the double quadratic equation about the Y axis symmetry as the equation of the contact trajectory between the ball and the discrete raceway in the X-Y plane. Furthermore, to make the circle where the orbital motion of the ball in the discrete raceway region is constant, the parametric equation of the contact trajectory between the ball and the discrete raceway is as follows:

$$\{\begin{array}{l}y=a{x}^4+b{x}^2+c\hfill \\ z=\pm sqrt(R_w^2-{(sprt(x^2+{(a{x}^4+b{x}^2+c)}^2)-R_m)}^2).\hfill \end{array}$$

(4)

where a, b, and c are all coefficients that must be determined, and the ball passing through the two end points of the discrete raceway must ensure that the orbital velocity will not change abruptly (i.e., the effective contact radius r at the two end points of the derivative of 0):

$$\begin{array}{c}a=\frac{R_o\sin \theta \tan \theta +2R_o\cos \theta +2c}{2R_o^4{\sin }^4\theta }\\ b=\frac{4c-R_o\sin \theta \tan \theta -4R_o\cos \theta }{2R_o^2{\sin }^2\theta }.\\ c=(R_m+sqrt(R_w^2-l_C^2/4))\end{array}$$

(5)

where l_C is the maximum axial span between the ball and the two contact points of the discrete raceway, and the effective contact radius r is calculated by the following formula:

$$r=\{\begin{array}{cc}sqrt(x^2+y^2)-R_m& -R_o\sin \theta <x<R_o\sin \theta \\ R_w& else\end{array}.$$

(6)

In Figure 2, R_e is the radius of the groove curvature of the outer raceway. According to space geometry theory, and combined with the structure of the bearing raceway and the parameter equation of the contact trajectory, the parameter equation of the center of groove curvature of the discrete raceway is derived as:

$$O_e(x_e,y_e,z_e)=\{\begin{array}{c}{x}_e=\frac{x((R_w-R_e)sqrt(x^2+y^2)+R_m{R}_e)}{R_{w}sqrt(x^2+y^2)}\\ y_e=\frac{y((R_w-R_e)sqrt(x^2+y^2)+R_m{R}_e)}{R_{w}sqrt(x^2+y^2}\\ z_e=\mp \frac{z(R_w-R_e)}{R_w}\end{array}.$$

(7)

The change in the groove curvature center of the discrete raceway determines the change in the raceway shape, and the shape of the discrete raceway is a spatial surface obtained by a circle of the radius R_e with the groove curvature center as the scan path; thus, the mathematical model of the discrete raceway can be described by the center of the curvature of the groove of the discrete raceway.

2.3. Constraints for the Discrete Raceway Structures

Equations (4), (5) and (7) show that when the dimensional parameters of the bearing are determined, the structure of the discrete raceway is only related to θ and l_C; thus, it is necessary to combine the bearing structure and the discrete angular spacing of the discrete raceway to determine the reasonable range of θ and l_C.

Based on the bearing structure, the effective contact radius r of the ball and the discrete raceway cannot be larger than the radius of the ball and cannot be smaller than the difference between the radius of the outer shoulder R_os and the radius of the pitch circle R_m; then:

$$2\mathrm{s}prt(R_w^2-{(R_{os}-R_m)}^2)>l_C,$$

(8)

$$R_o-sqrt(x^2+y^2)>0.$$

(9)

From the perspective of motion, the angular distance between the adjacent balls after passing through the discrete raceway should be controlled to make the balls evenly distributed, but the balls will first decelerate and then accelerate when passing through the discrete raceway, and the adjacent balls will catch up and then move away from each other; thus, there are three possible situations: (1) the ball behind catches up with the ball in front, collides, and then separates after a given period of time; (2) adjacent balls come into contact but immediately separate; and (3) adjacent balls do not come into contact. Figure 3 shows the situation where the adjacent balls are just coming into contact.

At moment t0, the angular distance between Ball 1 and Ball 2 is β₀, and at moment t₁, the two balls are just coming into contact. Due to the symmetry of the discrete raceway, the orbital velocities of the two balls are the same when they are exactly in contact and the contact point of the two balls is on the Y-axis. However, after t1, the velocity of Ball 1 increases and the velocity of Ball 2 decreases; thus, the two balls will be separated immediately, and the angular separation of the two balls returns to β₀ after Ball 2 leaves the discrete raceway completely. Thus, when the angular distance between adjacent balls at time t₀ is less than β₀, the two balls will collide in the discrete raceway, and when the angular distance is greater than β₀, the two balls will not collide. The ball should be uniformly distributed outside the discrete raceway; then:

$${\beta }_0=({360}^{\circ }-\epsilon N)/N.$$

(10)

where N is the number of balls, and $\epsilon =2\arccos ((2R_m^2-R_w^2)/(2R_m^2))$.

We let $x=R_o\sin \phi ,\phi \in [-\theta ,\theta ]$. Then, the discrete angular spacing of the discrete raceway is calculated as follows:

$${\beta }_0=\frac{1}{2}{\displaystyle {\mathrm{\int }}_{-\epsilon /2}^{\epsilon /2}\frac{sqrt({(R_0\sin \phi )}^2+{(a{(R_o\sin \phi )}^4+b{(R_o\sin \phi )}^2+c)}^2)+R_w}{sqrt({(R_0\sin \phi )}^2+{(a{(R_o\sin \phi )}^4+b{(R_o\sin \phi )}^2+c)}^2)}}-\epsilon .$$

(11)

Equation (11) shows that the discrete angular spacing generated by the discrete raceway is independent of the rotational speed of the inner ring. However, the structure of the discrete raceway will affect how rapidly the ball speed changes, which may cause the ball to slide and make the discrete raceway fail. Thus, we use the numerical simulations to simulate the motion of the ball to determine the structural parameters of the discrete raceway.

3. Dynamic Model

To verify the discrete function of the discrete raceway and to determine the structure of the discrete raceway, this section analyzes the contact between the parts of the cageless ball bearing containing the discrete raceway. Because the random collision between the balls of the cageless ball bearing system can be regarded as a type of abruptly added constraint, thus, there is an abrupt change in the motion of the balls. Based on the non-smooth dynamics, the three-degree-of-freedom non-smooth dynamics equations of the cageless ball bearing system are established, and the phase space method is used to analyze the motion characteristics of the balls. The influence of slippage is considered, and the bearing system is subject to radial load only.

3.1. Differential Equation

The motion of the center of mass of the ball and the center of mass of the inner ring can be described by Newton’s law, and Figure 4 shows the forces acting on the ball and the inner ring, as well as the interaction between the parts.

In Figure 4a, F_i(o) is the normal contact force between the ball and the collar; F_bb is the collision force between the balls; F_fi(o) is the friction force between the balls and the collar; F_fbb is the friction force between the balls; G is the gravitational force of the balls; and F_w is the centrifugal force. In this paper, we only consider the case when the bearing is subjected to a radial load, and assume that there is no axial motion (Z-axis) in the bearing system, and the ball self-rotation axis will not be deflected, so the motion of the ball is described by three-degrees-of-freedom, which is the motion of the ball in the X-direction and Y-direction and the self-rotation motion of the ball, and the differential equations of the motion of the ball in the X-direction and Y-direction are as follows:

$$F_i+F_o+F_w+F_{bb}+F_{bb}^{’}+F_{fi}+F_{fo}+F_{fbb}+F_{fbb}^{’}+\left[\begin{array}{c}0\\ m_{b}g\end{array}\right]=\left[\begin{array}{c}{m}_b\ddot{x}\\ m_b\ddot{y}\end{array}\right],$$

(12)

The differential equation of motion in the direction of the rotation of the ball is as follows:

$$R_w(F_{fi}-F_{fbb}-F_{fbb}^{’})+r{F}_{fo}=J_r\ddot{\phi }.$$

(13)

where m_b is the mass of the ball, and J_r is the rotational inertia of the ball. The outer ring is fixed and the motion of the center of mass of the inner ring is described by two-degrees-of-freedom, i.e., the motion of the center of the mass of the inner ring in the X-direction and the Y-direction, and the differential equation of the motion of the center of the mass of the inner ring is as follows:

$$F_r+{\displaystyle \sum _{j=1}^N(F_{i(j)}+F_{fi(j)})}+\left[\begin{array}{c}0\\ m_{i}g\end{array}\right]=\left[\begin{array}{c}{m}_i\ddot{x}+C\dot{x}\\ m_i\ddot{y}+C\dot{y}\end{array}\right].$$

(14)

where m_i is the mass of the inner ring; F_r is radial load; j is the serial number of the ball; and C is the drag coefficient. The centrifugal force F_w in Equation (12) can be expressed as [35]

$$F_w=m_b{V}_b^2/{R^{\prime }}_m.$$

(15)

where ${R^{\prime }}_m$ is the radius of the pitch circle of the ball under the load.

3.2. Contact Force Calculation

In Figure 4b, r_i is the position vector of the center of the inner ring; r_b is the position vector of the center of the ball; r_bi is the relative position vector between the ball and the inner ring; r_bb is the relative position vector of two adjacent balls; δ_i is the contact deformation of the ball and the inner ring; and δ_b is the contact deformation of the adjacent balls.

$${\delta }_i=\{\begin{array}{cc}{R}_m-\left|{\mathit{r}}_{\mathit{b}\mathit{i}}\right|& R_m-\left|{\mathit{r}}_{\mathit{b}\mathit{i}}\right|>0\\ 0& R_m-\left|{\mathit{r}}_{\mathit{b}\mathit{i}}\right|<0\end{array},$$

(16)

$${\delta }_b=\{\begin{array}{cc}2R_w-\left|{\mathit{r}}_{\mathit{b}\mathit{b}}\right|& 2R_w-\left|{\mathit{r}}_{\mathit{b}\mathit{b}}\right|>0\\ 0& 2R_w-\left|{\mathit{r}}_{\mathit{b}\mathit{b}}\right|<0\end{array}.$$

(17)

Therefore, the contact force between the parts can be calculated by the Hertzian contact theory [36]. The direction of F_i is the same as r_bi, and the direction of F_bb is the same as r_bb. For the contact force between the ball and the outer ring containing a discrete raceway, the contact force is calculated by the geometric relationship between the ball and the outer ring from a point of contact to two points of contact within the instant. The method of contact deformation to calculate the contact force is not fully applicable because the contact depth within this instant is the same. However, the magnitude of the contact force from a point of contact force to the superposition of two points of contact force, results in a sudden change in the contact force, which does not agree with the real situation and brings difficulties to the numerical solution. Therefore, we use the method of equivalent stiffness, and the normal force F_o of the discrete raceway to the ball is regarded as the combined force of two contact points, and the contact deformation between the ball and the outer ring is:

$${\delta }_o=\{\begin{array}{cc}\left|{\mathit{r}}_{\mathit{b}}\right|-R_m& \left|{\mathit{r}}_{\mathit{b}}\right|-R_m>0\\ 0& \left|{\mathit{r}}_{\mathit{b}}\right|-R_m<0\end{array}.$$

(18)

Similarly, the Hertz contact theory is used to calculate the normal force F_o between the ball and the outer ring, and the direction of F_o is opposite to r_b. F′_o is the normal contact force of the contact point between the ball and the discrete raceway, and the relevant formula is:

$$F{’}_o=\frac{F_o{R}_w}{2sqrt(R_w^2-l^2/4)}.$$

(19)

3.3. Friction Calculation

The friction force is a function of the friction coefficient and normal force. In the numerical simulation of the friction coefficient, a constant value can also better simulate the ball movement, thus, we set μ = 0.007 [37]. The ball and the inner and outer rings of the friction force are calculated as:

$$F_{fi}=\frac{\mu \Delta V_i}{\left|\Delta V_i\right|}{F}_i,$$

(20)

$$F_{fo}=\frac{\mu \Delta V_o}{\left|\Delta V_o\right|}{F}_o.$$

(21)

The direction of the friction force is perpendicular to the direction of the contact force, and the friction force between the ball and the discrete raceway is:

$$F_{fo}=\frac{2\mu \Delta V_o}{\left|\Delta V_o\right|}{F^{\prime }}_o.$$

(22)

The direction vector of F_fo is $r_f=\left[1,dy/dx,dz/dx\right]$.

4. Numerical Simulation Results and Analysis

The collision between the balls of a cageless ball bearing makes the dynamics of the bearing system non-smooth, and the contact between the balls is a low-frequency phenomenon, for which the dynamics problem can be solved best using the prediction correction algorithm. In this paper, Equations (12)–(14) are programmed using MATLAB and solved using the fourth-order Adams predictive correction algorithm.

4.1. Initial Value

The specific parameters of the numerical simulation are shown in

Table 1. Parameter table.

Parameters	Value
Ball radial Rw (mm)	4.7625
Radius of the outer groove bottom Ro (mm)	27.765
Radius of the inner groove bottom Ri (mm)	18.24
Outer Shoulder Radius Ros (mm)	26
Number of balls N	14
Inner ring rotation speed ωi (rpm)	12,000
Radial load Fr (N)	1500

.

The serial number and initial position of the ball are shown in Figure 1a. The initial orbital velocity and spin speed of the ball are the theoretical values when there is no sliding, which are calculated by Equations (1) and (2).

4.2. Maximum Axial Span and the Circumferential Span Angle

Equations (8), (9), and (11), for the maximum axial span l_C and the circular span angle θ constraints in MATLAB, are used to solve the constraints, and the relationship between the two is shown in Figure 5.

l_C and θ are inversely related: the larger the maximum axial span l_C of the discrete raceway, the smaller the effective contact radius r is, and the greater the orbital speed of the ball drops. Furthermore, the larger the annular span angle θ of the discrete raceway, the longer the ball passes through the discrete raceway, thus, when the discrete angular span is determined, the larger the l_C of the discrete raceway, the faster the speed of the ball changes when it passes through the discrete raceway.

4.3. Results Analysis

When 14 balls are present, the discrete angular distance of the discrete raceway is β₀ = 1.8161°. Considering the numerical simulation result of l_C = 4.95 mm and θ = 35° as an example. Firstly, the angular spacing variation of any adjacent ball is analyzed, the angular spacing between Ball i and Ball i+1 is shown in Figure 6.

It can be seen from Figure 6, that the angular spacing of Ball i and Ball i+1 decreases rapidly at the beginning of the numerical solution. This is due to the fact that there is a certain error between the given initial value and the actual value, which makes the iterative process of the solution perturbed [38] and leads to inaccurate solution results, so the results at the early stage of the numerical simulation need to be discarded. As the solution continues, the prediction correction step of the selected solution algorithm causes the solution results to converge gradually and the variation of the angular spacing of Ball i and Ball i+1 becomes stable, so only the solution results of the stable phase are analyzed subsequently.

The local enlargement in Figure 6 shows the angular spacing variation of Ball i and Ball i+1 in one operation period, where stage a~b is the ball in the non-load bearing area. In this stage, the maximum value of the angular spacing of Ball i and Ball i+1 is about β₀, but due to the slipping motion of the ball [39], its angular spacing decreases by 0.033°, which is only 1.8% change compared to β₀, so the angular spacing variation of the ball in this stage can be neglected. In stages b~c and d~e, the ball moves in the non-discrete raceway region of the load-bearing zone, while in this stage, the ball hardly slips under the load of the inner and outer rings [34], so that the angular distance between Ball i and Ball i+1 is stabilized at β₀ in this stage. The c~d stage is the ball passing through the discrete raceway area. At this time, the angular distance of the two balls under the action of the discrete raceway shows a tendency of decreasing and then increasing, and the magnitude of its change is about β₀, so the balls within the discrete raceway are not uniformly distributed. The variation of the angular spacing of the balls in the discrete raceway is due to the change of the rotational speed of balls. In combination with the variation of the speed of three adjacent balls in Figure 7 when passing through the discrete raceway, the variation law of their angular spacing is analyzed.

At t₀, Ball i+1 moves into the discrete raceway and begins to decelerate, and the angular spacing between Ball i and Ball i+1 begins to decrease. At t₁, Ball i moves to the discrete raceway and begins to decelerate, and the angular spacing between Ball i and Ball i−1 begins to decrease. At t₂, Ball i collides with Ball i+1, and the angular spacing decreases to 0. The collision force causes the orbital velocity of Ball i to drop suddenly, but due to the collar friction, the velocity of Ball i will then rapidly increase to the theoretical orbital velocity. At this time, Ball i is still in the deceleration stage of the discrete raceway; thus, Ball i will decelerate again. At t₃, Ball i−1 begins to enter the discrete raceway, and the angular spacing between Ball i and Ball i+1 begins to decrease. At this time, the three balls are in the discrete raceway, concurrently. At t₄, Ball i collides with Ball i−1, Ball i suddenly accelerates under the action of the collision force, and the friction of the collar causes the speed of Ball i to drop to the theoretical value again quickly. At this time, Ball i is already in the acceleration phase, thus, Ball i accelerates again.

According to the analysis of Figure 6 and Figure 7, it is clear that when the annular span angle of the discrete raceway is too large to allow three balls to be in the discrete raceway concurrently, each ball may collide twice in the discrete raceway, which is detrimental to the ball movement, thus, the annular span angle of the discrete raceway should be sufficient for at most two balls to be in the discrete raceway, concurrently.

Table 2. 10 groups of numerical simulation results.

lC (mm)	$\theta (°)$	${\beta }_0 (°)$	Simulation Values of ${\beta }_0 (°)$	Difference
4.95	35	1.8153	1.8131	−0.0022
5	30.5	1.8176	1.8281	0.0105
5.05	27.5	1.8185	1.8323	0.0138
5.1	25.2	1.8171	1.8190	0.0019
5.15	23.5	1.8183	1.7932	−0.0251
5.2	22	1.8156	1.7552	−0.0604
5.4	18.167	1.8161	1.6589	−0.1572
5.6	15.774	1.8161	1.6594	−0.1567
5.8	14.062	1.8161	1.5416	−0.2645
6	12.717	1.8160	1.4538	−0.3622

compares the discrete angular spacing of 10 groups of discrete raceway structures.

Table 2 shows the difference between the numerical simulation results and the theoretical value of β₀ as the discrete angular spacing becomes larger and larger with the increase of l_C and the decrease of θ. Figure 8 shows the phase space diagram of Ball 1 under these 10 discrete raceway structure parameters.

From Figure 8, it can be seen that the phase space track of Ball i has different degrees of variation in the part of the region where X-velocity is positive, while it is stable and smooth in all other regions. This is because the discrete raceway is set in the bearing area (i.e., the lower part of the bearing shown in Figure 1a), and the direction of rotation of Ball i is counterclockwise, so the component of the linear velocity of the Ball i in the X-axis, when it passes through the discrete raceway, is in the positive direction. However, the ball changes its linear velocity of revolution under the action of the discrete raceway, which makes the tracks in Figure 8a–j have a significant change in the region where the X-velocity is positive.

In Figure 8a~Figure 8c, the annular span angles of the discrete raceway are 70°, 61°, and 55°, respectively. Since the annular span angle is greater than $2(\epsilon +{\beta }_0)={51.17}^{\circ }$, it can allow three balls to be in the discrete raceway region at the same time, and their corresponding phase space trajectories have two abrupt changes in the region of the positive X-velocity, which is because Ball i has collided with Ball i−1 and Ball i+1 successively, when passing through the discrete raceway in one cycle, so that the velocity of Ball i has one abrupt decrease and one abrupt increase. As can be seen from Table 2, these three discrete raceway structures are unreasonable because the annular span angle is too large, so that the ball has collided twice in the discrete raceway, although they make the ball have a good discrete effect. In Figure 8d~Figure 8f, the phase space track line of Ball i is stable and smooth, and the velocity change when the ball passes through the discrete raceway is also smooth, so there is no collision between the balls. Combined with Table 2, it can be seen that these three discrete raceway structures are also ideal for the discrete effect of the balls, so these three discrete raceway structures are reasonable. Ball i in Figure 8g and Figure 8h, has a chaotic velocity variation while passing through the discrete raceway, resulting in multiple abrupt changes. The velocity of Ball i in both Figure 8i and Figure 8j, varies periodically, but there is a sudden acceleration of the velocity during the descent, which means that Ball i is subjected to a sudden change in acceleration by the force of the abrupt change of the inner and outer rings, while passing through the discrete raceway at a certain point. The reason for the four phenomena in Figure 8g~Figure 8j, is that the annular span angle of these four discrete raceway structures is too small, which makes the ball unable to change a larger speed in a shorter time, and sliding occurs. From Table 2, we can also see that the discrete performance of these four discrete raceway structures, to the ball, does not reach the ideal value, so these four discrete raceway structures are not reasonable. It can also be seen from Figure 8, that for the cageless ball bearing containing the discrete raceway, the phase space trajectory of the balls, in the conventional raceway area, are smooth, which indicates that the balls are discrete under the action of the discrete raceway and avoid the collision between the balls. In the literature [39], through the study of the collision between the rolling elements in the cageless ball bearing, it is concluded that the rolling elements are more likely to collide in the transition zone between the load bearing area and the non-load bearing area, which is contrasted with the cageless ball bearing containing the discrete raceway designed in this paper, so the discrete raceway designed in this paper has obvious superiority to solve the collision between the balls of the cageless ball bearing. Figure 9 shows the variation in the orbital velocity of Ball i as it passes through the different discrete raceway structures.

When θ is less than 22°, the orbital velocity of the ball undergoes a rapid change and cannot reach the theoretical value in the discrete raceway. Therefore, under the premise of the discrete angular spacing β₀ = 1.816, and when the circumferential span angle of the discrete raceway is less than a certain value, the discrete raceway cannot guarantee the speed variation of the ball.

Thus, to ensure that the angular spacing of the ball through the discrete raceway is β = 1.816°, and that ball movement is smooth, the circumferential span angle of the discrete raceway should not allow three balls to be within the discrete raceway, concurrently. For the bearing size selected in this paper, the range of the circumferential span angle 2θ of the discrete raceway should be [44°, 2ε].

When θ is less than 22°, the orbital velocity of the ball undergoes a rapid change and cannot reach the theoretical value in the discrete raceway. Therefore, under the premise of the discrete angular spacing β₀ = 1.816, and when the circumferential span angle of the discrete raceway is less than a certain value, the discrete raceway cannot guarantee the speed variation of the ball.

Thus, to ensure that the angular spacing of the ball through the discrete raceway is β = 1.816°, and that ball movement is smooth, the circumferential span angle of the discrete raceway should not allow three balls to be within the discrete raceway, concurrently. For the bearing size selected in this paper, the range of the circumferential span angle 2θ of the discrete raceway should be [44°, 2ε].

5. Experiment

The experimental sample with the discrete raceway structure parameters of l = 5.1 mm and θ = 25.2°, was manufactured using the Five-axis NC machine with the machining accuracy of 0.002 mm, as shown in Figure 10, based on the design dimensions of the cageless ball bearing with the discrete raceway obtained by comparing the numerical solution results. The bearing sample was mounted to the vibration measurement test bench, as shown in Figure 11. The experimental speed is 3000 rpm, the radial load is 1.5 KN, and the sampling frequency is 5000 Hz. the vibration acceleration signal of the tested bearing is collected during the stable operation stage, as shown in Figure 12. From the figure, it can be seen that the vibration acceleration amplitude of the measured bearing is generally decreasing, and the collision of the ball in the ball bearing without the cage is the main cause of vibration, the decrease of the vibration acceleration signal indicates that the collision frequency of the ball under the action of the discrete raceway is gradually decreasing.

In order to further demonstrate the superiority of cageless ball bearings with a discrete raceway, the discrete motion experiments were conducted on conventional cageless ball bearings and cageless ball bearings with a discrete raceway. The ball motion was examined, using the high-speed photography equipment in Figure 11, the model of which is Phantom VEO 710L, with a frame rate of 10,000 Hz. The results of the high-speed photographic inspection of the conventional cageless ball bearings and the cageless ball bearings with the discrete raceway are shown in Figure 13 and Figure 14, respectively.

The experimental bearing in Figure 13, has an inner diameter of 35 mm, and the experimental bearing in Figure 14, is the bearing designed in this paper. From the results shown in Figure 13, it can be seen that the conventional ball bearing without a cage has ball contact at all four moments, which means that the bearing without the discrete raceway has more collisions during the operation and the angular spacing between the balls is not evenly distributed. From the results of Figure 14, it can be seen that the angular spacing of Ball 1 and Ball 2 marked in the figure, changes in these four moments when passing through the discrete raceway, which is corresponding to the results of the theoretical analysis, and there is almost no collision between the balls in these four moments, The angular spacing is more uniform compared with Figure 13. From the comparison results of the two groups of the high-speed photography experiments, it can be seen that the cageless ball bearing with the discrete raceway has a good discrete effect and a better performance than the conventional cageless ball bearing.

6. Conclusions

In this paper, a cageless ball bearing model with a discrete raceway that can disperse balls is proposed. Based on the principle that a ball effectively does not slip in the bearing area, the effective contact radius between the ball and the outer raceway is changed, and the mathematical model of the space surface of the discrete raceway is established. Considering that the ball collisions will produce a sudden addition of constraints, the kinetic equations of the cageless ball bearings with discrete raceways are established, based on non-smooth dynamics, the dispersion law, and motion characteristics of the ball under 10 types of discrete raceway structure parameters are solved, and the influence of the discrete raceways on the ball motion is analyzed using ball phase diagrams. The results show that the cageless ball bearing with a discrete raceway designed in this paper reduces the collision between the balls and has an obvious superiority, compared with the conventional bearings, and provides a new idea for the parametric design of the discrete raceway and provides a new direction for the design of cageless ball bearings.

According to the spatial surface mathematical model of the discrete raceway, the annular span angle 2θ of the discrete raceway and the axial span distance l_C of the contact point are determined as the structural parameters of the discrete raceway. Furthermore, l_C and θ are negatively correlated with the bearing raceway structure and the discrete angular spacing, as the constraint conditions. For the bearing size selected in this paper, the smaller the circumferential span angle of the discrete raceway, the larger the error of the discrete angular spacing and the less smooth the ball movement, under the working condition of an inner ring speed of 12,000 rpm and radial load of 1500 N. According to the phase diagram and the velocity variation of the ball, the range of the annular span angle of the discrete raceway is determined to equal [44°, 2ε], within which the angular spacing of a few balls inside the discrete raceway will be less than β₀, while all balls outside the discrete raceway are uniformly distributed.