An Insight of the Theoretical Physics of Ru-Alloyed Iron Pyrite Studied for Energy Generation
Abstract
:1. Introduction
2. Experimental
2.1. Materials and Method
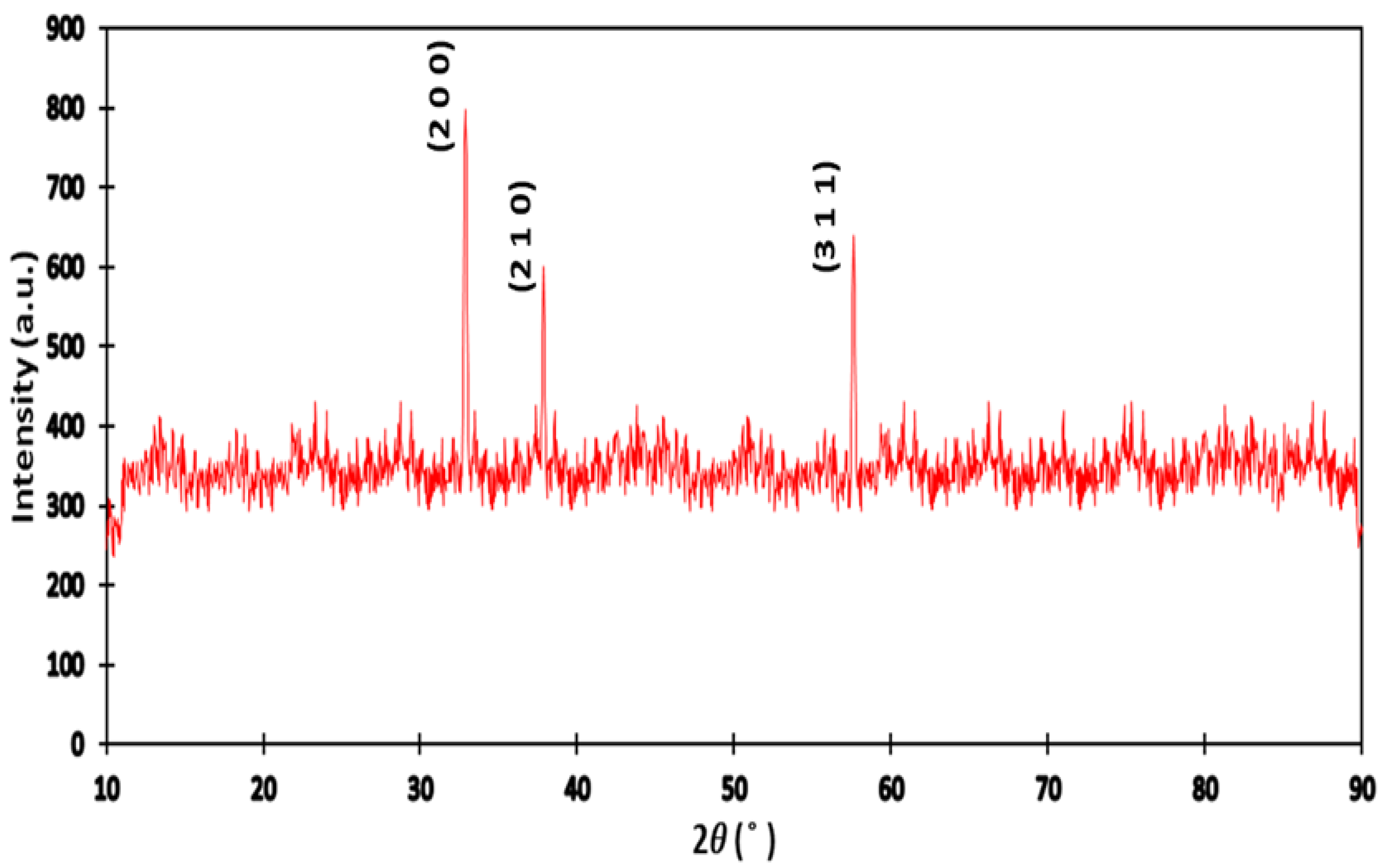
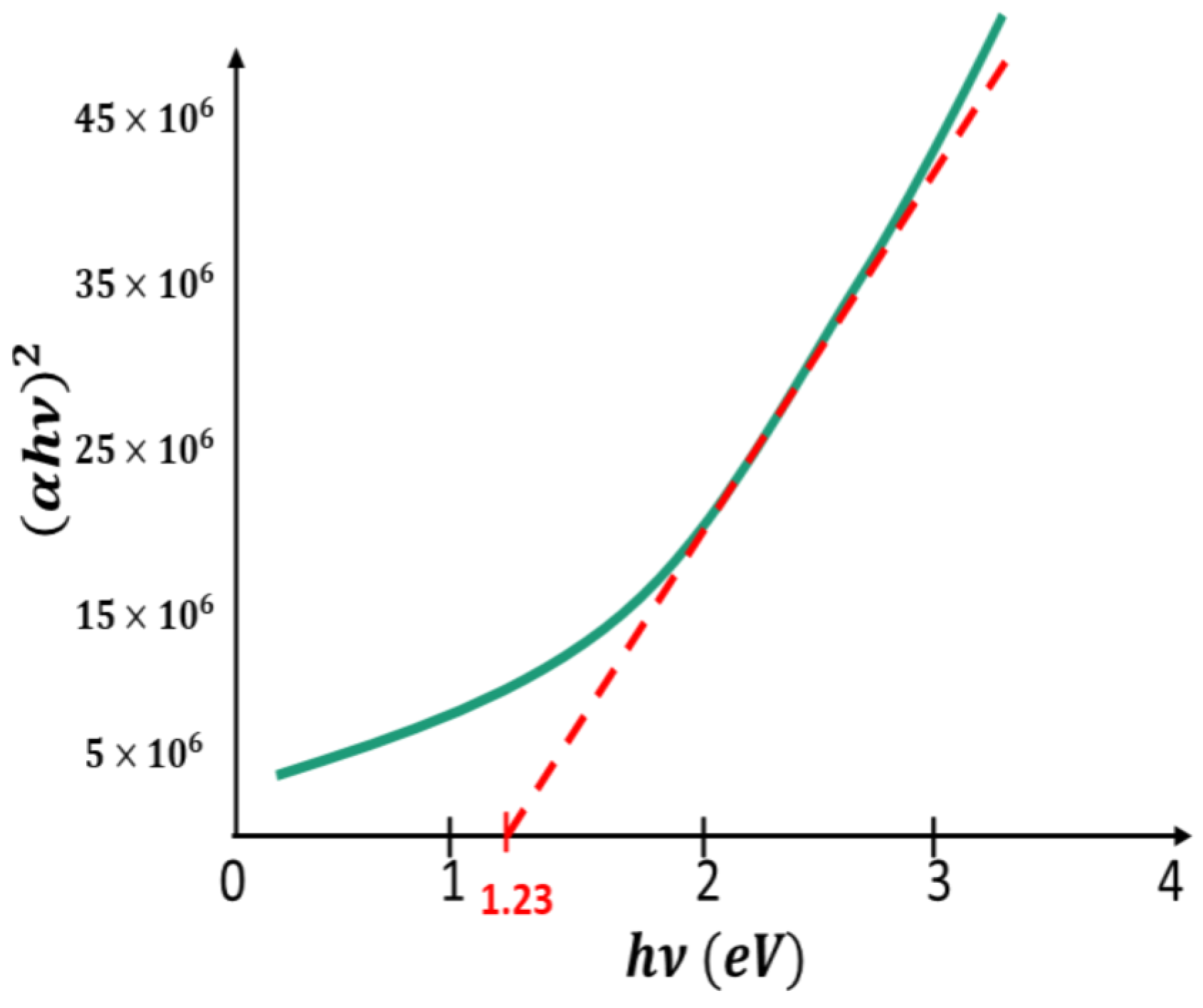
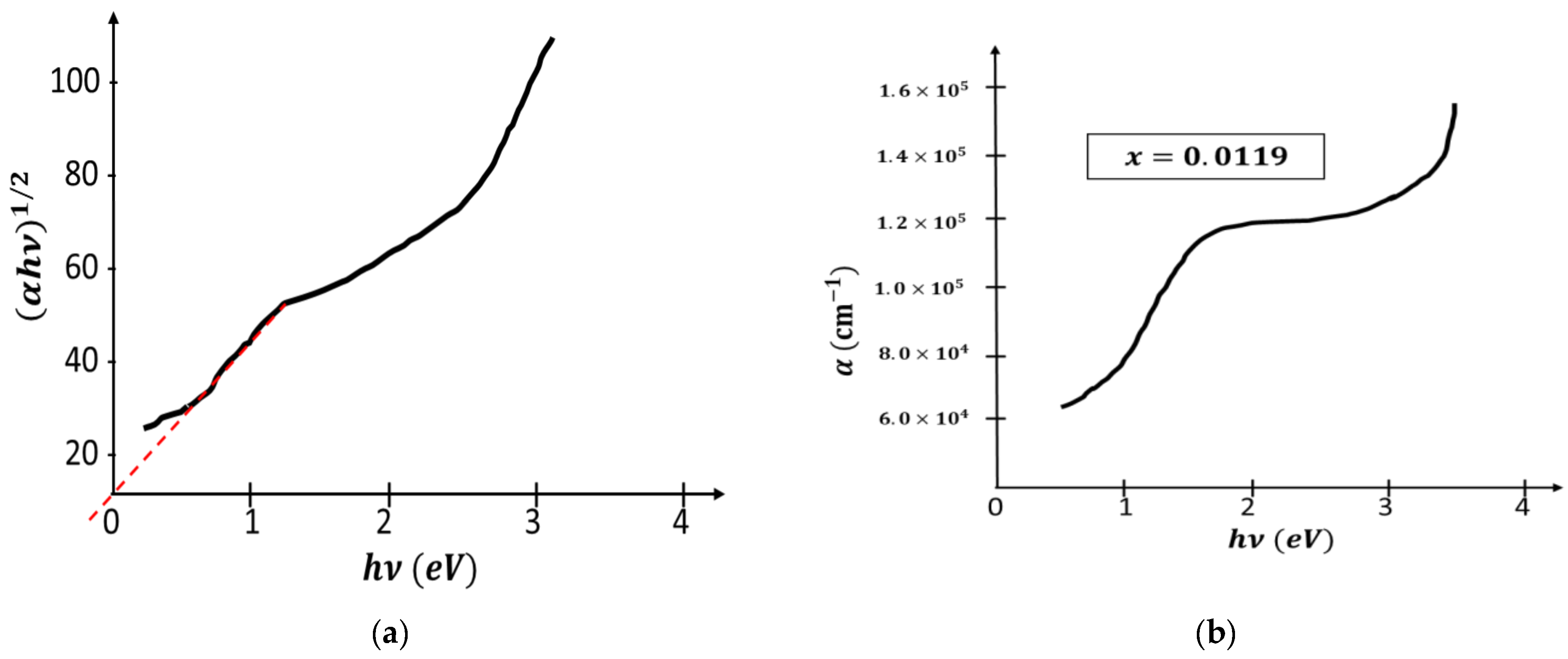
2.2. Characterization Techniques
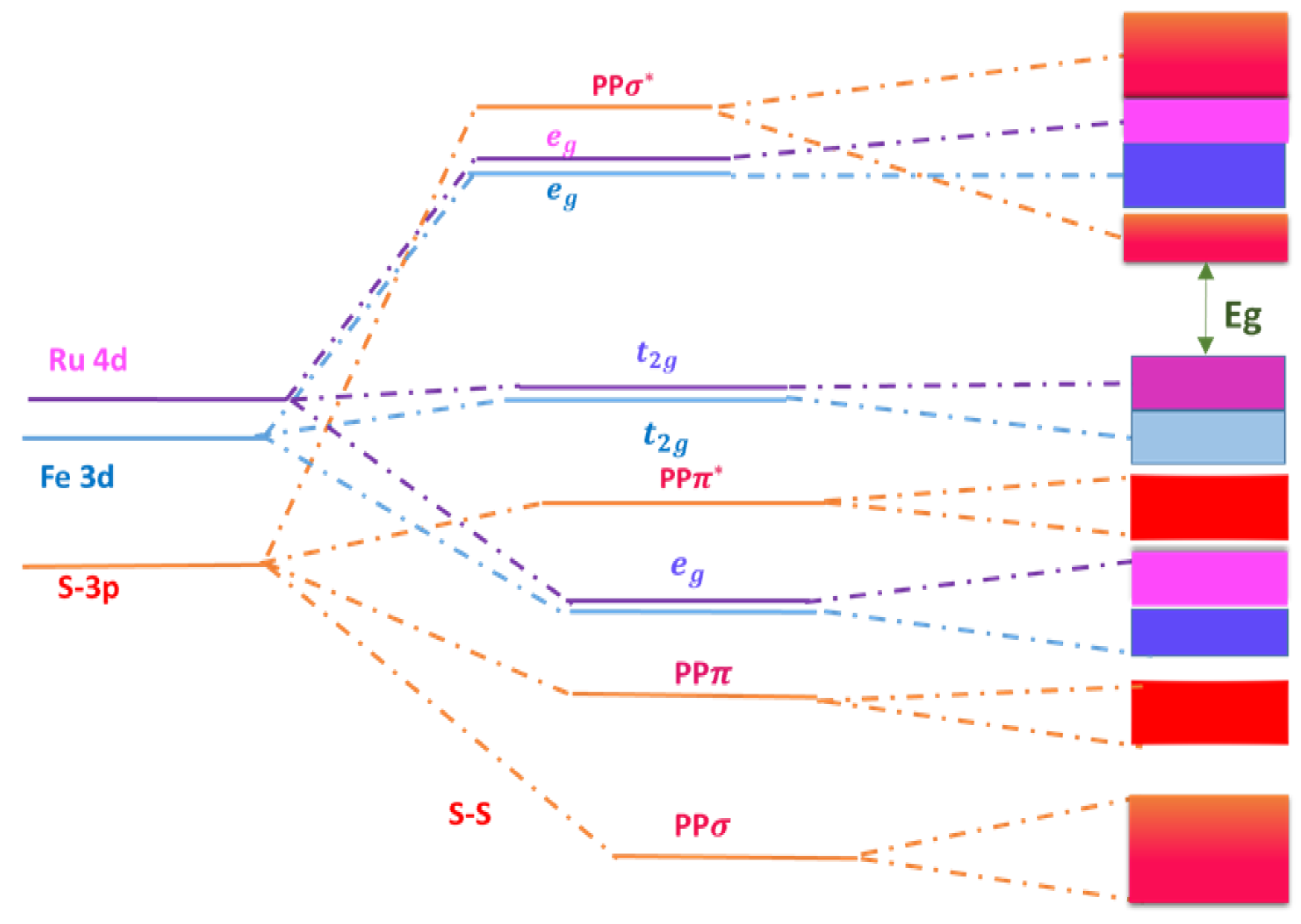
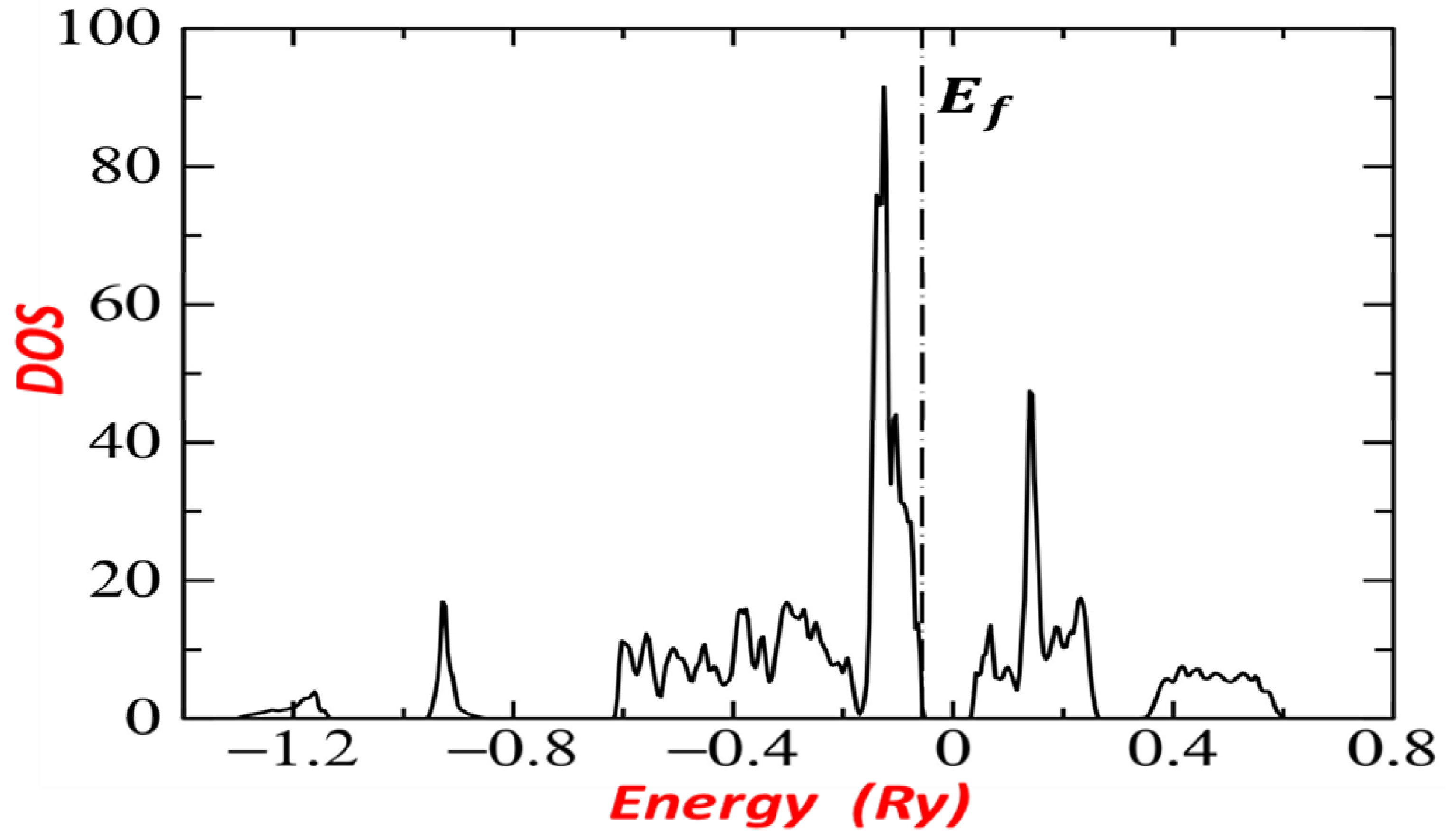
3. Calculated Band Energy of
3.1. Method
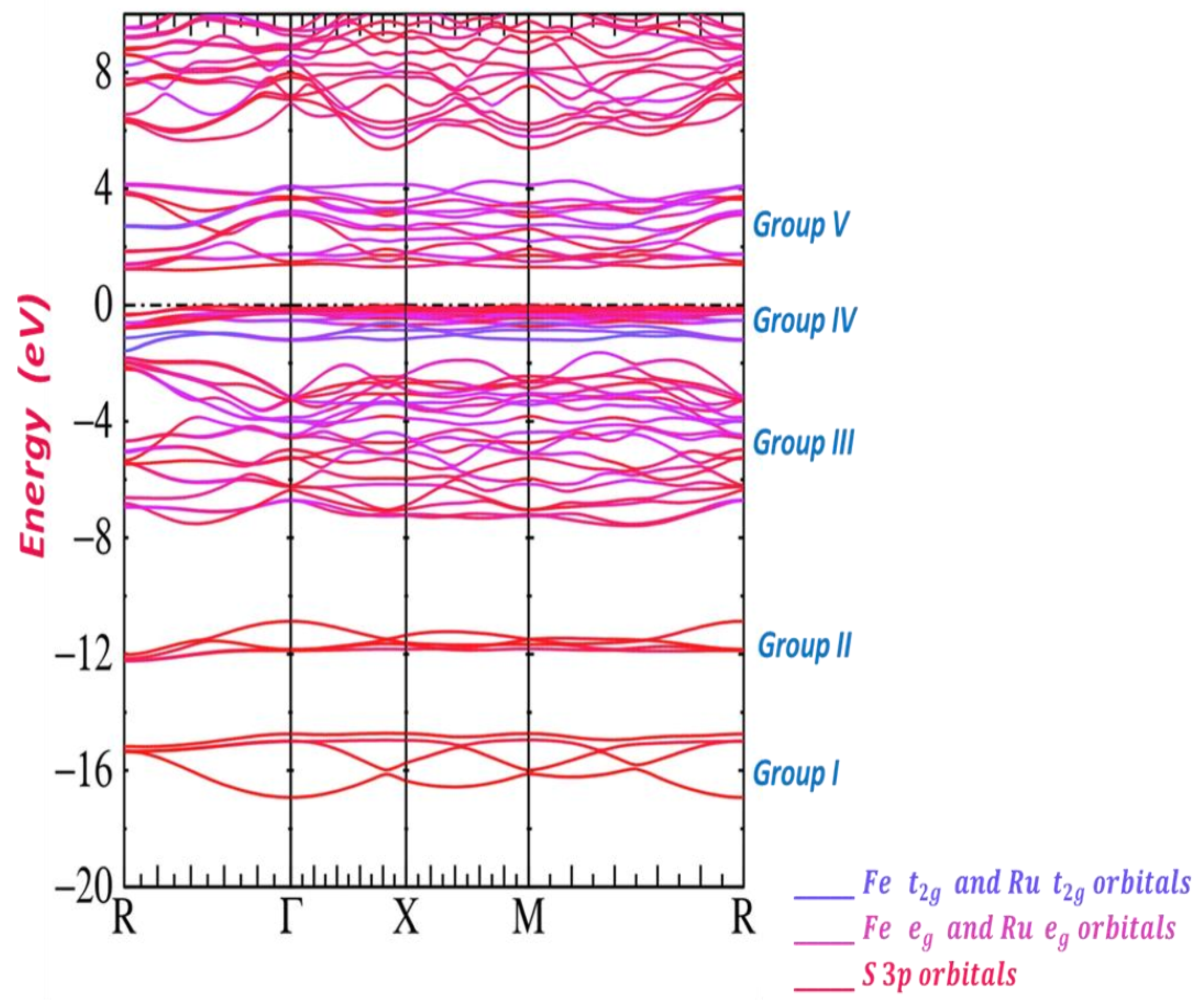
3.2. Band Structure
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ennaoui, A.; Fiechter, S.; Jaegermann, W.; Tributsch, H. Photoelectrochemistry of highly quantum efficient single-crystalline n-FeS2 (Pyrite). J. Electrochem. Soc. 1986, 133, 97. [Google Scholar] [CrossRef]
- Büker, K.; Alonso-Vante, N.; Tributsch, H. Photovoltaic output limitation of n-FeS2 (pyrite) Schottky barriers: A temperature-dependent characterization. J. Appl. Phys. 1992, 72, 5721. [Google Scholar] [CrossRef]
- Ennaoui, A.; Fiechter, S.; Pettenkoer, C.; Alonso-Vante, N.; Büker, K.; Bronold, M.; Höpfner, C.; Tributsch, H. Iron disulfide for solar energy conversion. Sol. Energy Mater. Sol. Cells 1993, 29, 289. [Google Scholar] [CrossRef]
- Murphy, R.; Strongin, D.R. Surface reactivity of pyrite and related sulfides. Sur. Sci. Rep. 2009, 64, 1–45. [Google Scholar] [CrossRef]
- Schlegel, A. Wachter, Optical properties, phonons and electronic structure of iron pyrite (FeS2). J. Phys. C Solid State Phys. 1976, 9, 3363. [Google Scholar] [CrossRef]
- Altermatt, P.P.; Kiesewetter, T.; Ellmer, K.; Tributsch, H. Specifying targets of future research in photovoltaic devices containing pyrite (FeS2) by numerical modelling. Sol. Energy Mater. Sol. Cells 2002, 71, 181. [Google Scholar] [CrossRef]
- Ennaoui, A.; Tributsch, H. Energetic characterization of the photoactive FeS2 (pyrite) interface. Sol. Energy Mater. 1986, 14, 461. [Google Scholar]
- Smestad, G.; Ennaoui, A.; Fiechter, S.; Tributsch, H.; Hofmann, W.K.; Birkholz, M.; Kautek, W. Photoactive thin film semiconducting iron pyrite prepared by sulfurization of iron oxides. Sol. Energy Mater. 1990, 20, 149. [Google Scholar] [CrossRef]
- Wadia, C.; Alivisatos, A.P.; Kammen, D.M. Materials availability expands the opportunity for large-scale photovoltaics deployment. Environ. Sci. Technol. 2009, 43, 2072. [Google Scholar] [CrossRef]
- Joshi, H.; Ram, M.; Limbu, N.; Rai, D.P.; Thapa, B.; Labar, K.; Laref, A.; Thapa, R.K.; Shankar, A. Modulation of optical absorption in m Fe_(1-x) Ru_x S_2 and exploring stability in new m RuS_2. Sci. Rep. 2021, 11, 6601. [Google Scholar] [CrossRef]
- Anantharaj, S.; Noda, S. Nickel selenides as pre-catalysts for electrochemical oxygen evolution reaction. Int. J. Hydrog. Energy 2020, 45, 15763–15784. [Google Scholar] [CrossRef]
- Hussain, R.A.; Hussain, I. Copper selenide thin films from growth to applications. Solid State Sci. 2020, 100, 106101. [Google Scholar] [CrossRef]
- Pesko, E.; Zero, Z.E.; Krzton-Maziopa, A. Electrocrystallization of nanostructured iron-selenide films for potential application in dye sensitized solar cells. Thin Solid Film. 2020, 709, 138121. [Google Scholar] [CrossRef]
- Luo, M.; Yu, H.; Hu, F.; Liu, T.; Shu, J. Metal selenides for high performance sodium ion batteries. Chem. Eng. J. 2020, 380, 122557. [Google Scholar] [CrossRef]
- Ao, K.L.; Shao, Y.; Chan, I.N.; Shi, X.; Pan, H. Design of novel pentagonal 2D transitional-metal sulphide monolayers for hydrogen evolution reaction. Int. J. Hydrog. Energy 2020, 45, 16201–16209. [Google Scholar] [CrossRef]
- Theerthagiri, J.; Senthil, R.A.; Nithyadharseni, P.; Lee, S.J.; Durai, G.; Kuppusami, P.; Madhavan, J.; Choi, M.Y. Recent progress and emerging challenges of transition metal sulfides based composite electrodes for electrochemical supercapacitive energy storage. Ceram. Int. 2020, 46, 14317–14345. [Google Scholar] [CrossRef]
- Sahoo, S.; Naik, K.K.; Late, D.J.; Rout, C.S. Electrochemical synthesis of a ternary transition metal sulfide nanosheets on nickel foam and energy storage application. J. Alloy. Compd. 2017, 695, 154–161. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, Y.N.; Law, M.; Wu, R.Q. Increasing the band gap of iron pyrite by alloying with oxygen. J. Am. Chem. Soc. 2012, 134, 13216–13219. [Google Scholar] [CrossRef]
- Sun, R.; Ceder, G. First-principles electronic structure and relative stability of pyrite and marcasite: Implications for photovoltaic performance. Phys. Rev. B Condens. Matter Mater. Phys. 2011, 84, 245211. [Google Scholar] [CrossRef] [Green Version]
- Sun, R.S.; Chan, M.K.Y.; Kang, S.Y.; Ceder, G. Intrinsic stoichiometry and oxygen-induced-type conductivity of pyrite FeS2. Phys. Rev. B Condens. Matter Mater. Phys. 2011, 84, 035212. [Google Scholar] [CrossRef]
- Ezzaouia, H.; Foise, J.W.; Gorochov, O. Crystal growth in tellurium fluxes and characterization of RuS2 single crystals. Mat. Res. Bull. 1985, 20, 1353–1358. [Google Scholar] [CrossRef]
- Sun, R.; Ceder, G. Feasibility of band gap engineering of pyrite FeS2. Phys. Rev. B 2011, 84, 245211. [Google Scholar] [CrossRef] [Green Version]
- Ouertani, B.; Ezzaouia, H.; Theys, B. Effect of ruthenium alloy on the band gap value of FeS2-pyrite. Colloids Surf. A Physicochem. Eng. Asp. 2017, 20, 13–19. [Google Scholar] [CrossRef]
- Sai, R.; Ezzaouia, H.; Muaffaq, M.M. Electronic structure of iron pyrite by the LMTO_ASA method. Results Phys. 2021, 22, 103950. [Google Scholar] [CrossRef]
- Ouertani, B.; Ouerfelli, J.; Saadoun, M.; Ezzaouia, H.; Bessaïs, B. Characterisation of iron oxide thin films prepared from spray pyrolysis of iron trichloride-based aqueous solution. Thin Solid Film. 2008, 516, 8584–8586. [Google Scholar] [CrossRef]
- Ouertani, B.; Ouerfelli, J.; Saadoun, M.; Bessais, B.; Hajji, M.; Kanzari, M.; Ezzaouiaa, H.; Hamdadoud, N.; Bernède, J.C. Characterization of FeS2-pyrite thin films synthesized by sulphuration of amorphous iron oxide films pre-deposited by spray pyrolysis. Mater. Lett. 2005, 59, 734–739. [Google Scholar] [CrossRef]
- Sai, R.; Gorochov, O.; Ezzaouia, H. The study of the electronic structure of RuS2. Results Phys. 2021, 26, 104393. [Google Scholar] [CrossRef]
- Foise, J.W.; Ezzaouia, H.; Gorochov, O. Crystal growth of p-type RuS2 using bismuth flux and its photoelectrochemical properties. Mat. Res. Bull. 1985, 20, 1421–1425. [Google Scholar] [CrossRef]
- Ezzaouia, H.; Heindl, R.; Loriers, J. Synthesis of ruthenium and osmium dichalcogenide single crystals. J. Mater. Sci. 1984, 165, 155. [Google Scholar] [CrossRef]
- Tsay, M.; Chen, S.; Chen, C.; Huang, Y. Preparation and characterization of iron-doped RuS2 single crystals. J. Cryst. Growth 1994, 144, 91–96. [Google Scholar] [CrossRef]
- Louie, S.G.; Ho, K.-M.; Cohen, M.L. Self-consistent mixed-basis approach to the electronic structure of solids. Phys. Rev. B 1979, 19, 1774. [Google Scholar] [CrossRef]
- Anderson, O.K. Coring and Core Analysis Handbook; Petroleum Publishing Company: Tulsa, OK, USA, 1975; p. 123060. [Google Scholar]
- Jan, J.P.; Skriver, H.L. Optical properties of single crystal thallium between 0.6 and 5 eV. J. Phys. F Met. Phys. 1977, 7, 1719. [Google Scholar] [CrossRef]
- Skriver, H.L. One-Electron Theory of Metals; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Hohenberg, P.; Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar]
- Hedin, L.; Lundqvist, B.I. Explicit local exchange-correlation potentials. J. Phys. C 1971, 4, 2064. [Google Scholar] [CrossRef]
- Andersen, O.K.; Jepsen, O.; Krier, G. Lectures on Methods of Electronic Structure Calculations; Kumar, V., Andersen, O.K., Mookerjee, A., Eds.; World Scientific Publishing Co.: Singapore, 1994; pp. 63–124. [Google Scholar]
- Andersen, O.K.; Arcangeli, C.; Tank, R.W.; Saha-Dasgupta, T.; Krier, G.; Jepsen, O.; Dasgupta, I. Tight-Binding Approach to Computational Materials Science; Colombo, L., Gonis, A., Turchi, P., Eds.; Materials Research Society: Pittsburgh, PA, USA, 1998; Volume 491, pp. 3–34. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nofal, M.M.; Sai, R.; Shawish, I.; Alaqeel, M.A. An Insight of the Theoretical Physics of Ru-Alloyed Iron Pyrite Studied for Energy Generation. Symmetry 2022, 14, 2252. https://doi.org/10.3390/sym14112252
Nofal MM, Sai R, Shawish I, Alaqeel MA. An Insight of the Theoretical Physics of Ru-Alloyed Iron Pyrite Studied for Energy Generation. Symmetry. 2022; 14(11):2252. https://doi.org/10.3390/sym14112252
Chicago/Turabian StyleNofal, Muaffaq M., Refka Sai, Ihab Shawish, and Muneerah A. Alaqeel. 2022. "An Insight of the Theoretical Physics of Ru-Alloyed Iron Pyrite Studied for Energy Generation" Symmetry 14, no. 11: 2252. https://doi.org/10.3390/sym14112252
APA StyleNofal, M. M., Sai, R., Shawish, I., & Alaqeel, M. A. (2022). An Insight of the Theoretical Physics of Ru-Alloyed Iron Pyrite Studied for Energy Generation. Symmetry, 14(11), 2252. https://doi.org/10.3390/sym14112252








