A CFD Validation Effect of YP/PV from Laboratory-Formulated SBMDIF for Productive Transport Load to the Surface
Abstract
:1. Introduction
- To validate the effective synthetic-based drilling mud formulated from the drilling fluid laboratory at Nazarbayev University.
- To validate the distribution of synthetic-based mud particles and cuttings in the wellbore.
- To investigate how rotating the drill pipe affects drilling mud transport capacity.
- To examine the effects of fluid hydraulics on transport cuttings based on the turbulence of solid-particle suspension.
2. Methods
2.1. Empirical Data
2.2. CFD–Eulerian–Eulerian Model
2.3. Drag Adaptation
2.4. Model Assumptions
- The flow of solid–liquid particles under surveillance is in a continuous phase.
- Particle-particle interactions do not result in a change in mass or form.
- Particles’ shapes are spherical and uniform.
- The synthetic and oil-based fluids are non-Newtonian and incompressible.
- The position of the drill pipe is in both a concentric and eccentric position.
- The walls of the drill pipe are smooth.
2.5. Governing Equations
2.6. CFD Model Implementation
Geometry, Grid & Boundary
3. Results and Discussion
3.1. Effects of Particle Diameter and Density
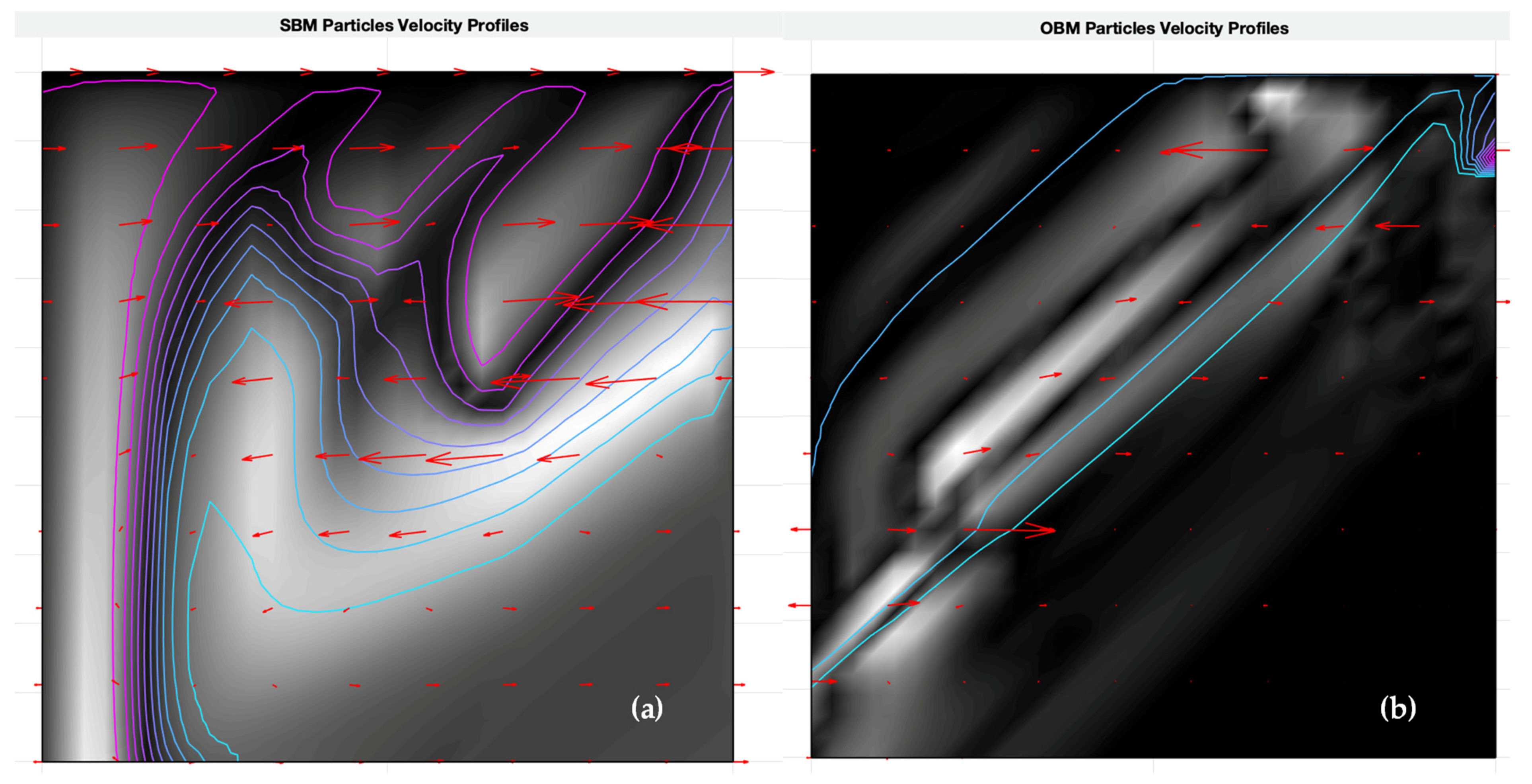
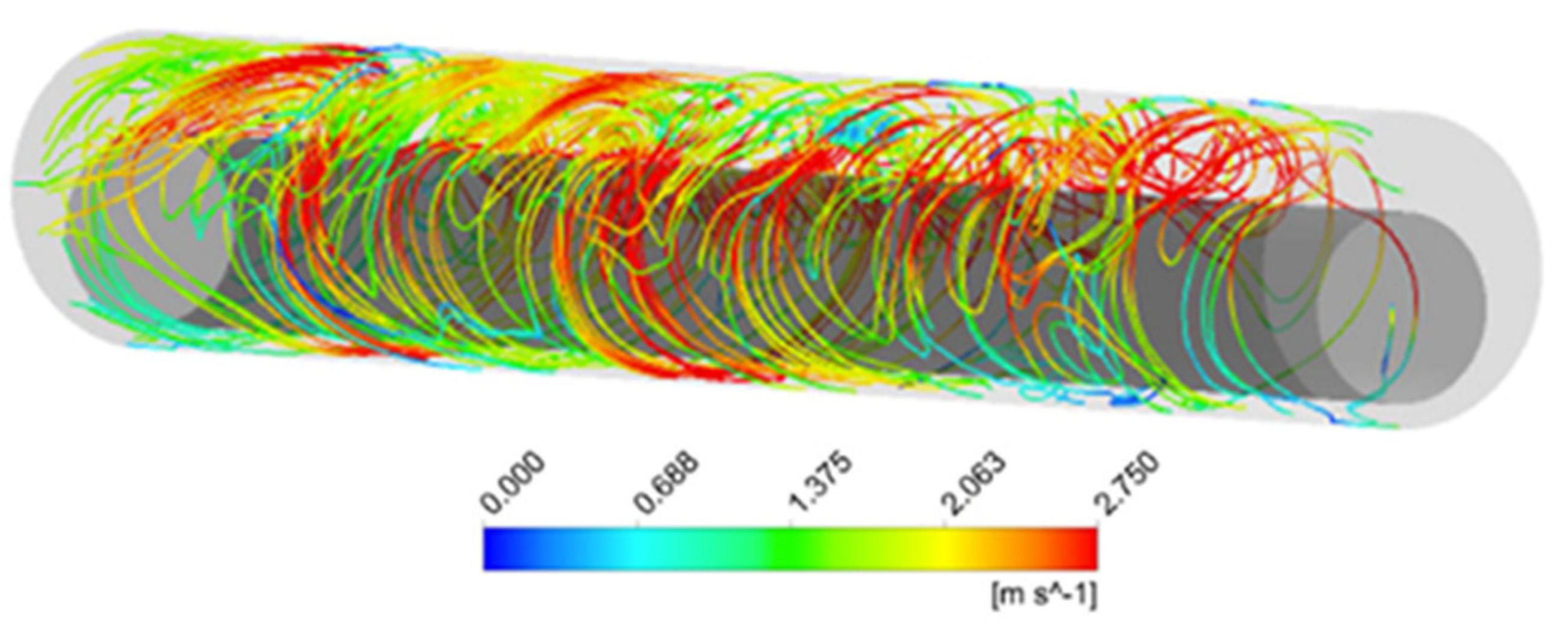
3.2. Effects of Pipe Rotation and Velocity Profiles on SBM/OBM
3.3. Effects of Fluid Rheology
4. Conclusions
- The CFD simulation validates the experimental results; the symmetrical results purport that the transport index or transport capacity for these two different drilling fluids (synthetic-based and oil-based muds) under surveillance were agreeably efficient and suitable for drilling operations.
- The smaller particles swiftly occupied the void spaces aiding the lift of cuttings to the surface. Particle diameters of 1 mm were spotted as suitable particle sizes for the enhancement of cuttings carriage. Also, the distribution of cuttings at any point of the annulus was only seen as efficient at the concentric positions.
- An 80 RPM pipe rotation maintained throughout the simulation favoured particles in the concentric annulus; movement of these particles was seen as uniformly distributed.
- The turbulence of the solid particles was caused by the velocity profiles of the smaller particles in question.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| CFD | computational fluid dynamic |
| RPM | revolution per minute |
| OBM | oil-based mud |
| SBM | synthetic-based mud |
| YP | yield point, lbf/100 ft2 |
| PV | plastic viscosity, lbf/100 ft2 |
| solid phase volume fraction | |
| liquid phase volume fraction | |
| drag coefficient | |
| particle diameter, m | |
| distance between centres, m | |
| eccentricity | |
| kinetic energy | |
| solid phase force, N | |
| lift force, N | |
| virtual mass force, N | |
| turbulence dispersion force, N | |
| gravity, m/s2 | |
| rate of dissipation | |
| interphase momentum exchange coefficient | |
| mass transfer from liquid phase to solid phase, kg/s | |
| mass transfer from solid phase to liquid phase, kg/s | |
| volume fraction pressure | |
| solids pressure, Pa | |
| solid phase density, kg/m3 | |
| liquid phase density, kg/m3 | |
| centre of inner tube | |
| particle Reynolds number | |
| centre of outer tube, m | |
| cuttings transport ratio | |
| viscosity, Pa·s | |
| fluid viscosity, Pa·s | |
| turbulence viscosity, Pa·s | |
| velocity of cuttings transport, m/s | |
| fluid velocity in annulus m/s | |
| liquid phase velocity m/s | |
| solid phase velocity m/s |
References
- Badrouchi, F.; Rasouli, V.; Badrouchi, N. Impact of hole cleaning and drilling performance on the equivalent circulating density. J. Pet. Sci. Eng. 2022, 211, 110150. [Google Scholar] [CrossRef]
- Huque, M.M.; Butt, S.; Zendehboudi, S.; Imtiaz, S. Systematic sensitivity analysis of cuttings transport in drilling operation using computational fluid dynamics approach. J. Nat. Gas Sci. Eng. 2020, 81, 103386. [Google Scholar] [CrossRef]
- Khan, J.A.; Irfan, M.; Irawan, S.; Yao, F.K.; Rahaman, M.S.A.; Shahari, A.R.; Glowacz, A.; Zeb, N. Comparison of machine learning classifiers for accurate prediction of real-time stuck pipe incidents. Energies 2020, 13, 3683. [Google Scholar] [CrossRef]
- Oseh, J.O.; Norddin, M.N.A.M.; Ismail, I.; Gbadamosi, A.O.; Agi, A.; Ismail, A.R. Experimental investigation of cuttings transportation in deviated and horizontal wellbores using polypropylene–nanosilica composite drilling mud. J. Pet. Sci. Eng. 2020, 189, 106958. [Google Scholar] [CrossRef]
- Ulker, E.; Sorgun, M. Comparison of computational intelligence models for cuttings transport in horizontal and deviated wells. J. Pet. Sci. Eng. 2016, 146, 832–837. [Google Scholar] [CrossRef]
- Wayo, D.D.K. Primary Evaluation of Filter Cake Breaker in Biodegradable Synthetic-Based Drill-In-Fluid. Master’s Thesis, Nazarbayev University, Astana, Kazakhstan, 2022. [Google Scholar] [CrossRef]
- Khan, J.A.; Irawan, S.; Dan, I.B.M.; Cai, B. Determining the difference of kick tolerance with single bubble and dynamic multiphase models: Evaluation of well-control with water/synthetic based muds. Ain Shams Eng. J. 2022, 13, 101678. [Google Scholar] [CrossRef]
- Pao, W.; Khan, J.A.; Ofei, T.N.; Irawan, S. Fill removal from horizontal wellbore using foam in different coiled tubing/annulus diameter ratios. Int. J. Oil Gas Coal Techbol. 2015, 9, 129–147. [Google Scholar] [CrossRef]
- Khan, J.A.; Pao, K.S. Fill removal with foam in horizontal well cleaning in coiled tubing. Res. J. App. Sci. Eng. Technol. 2013, 6, 2655–2661. [Google Scholar] [CrossRef]
- Bin Mohamad Noor, M.Z.; Chin, I.L.Y.; Irawan, S. Study of the transportation behavior of nanoparticles through low-porosity sand pack in the absence and presence of oil. J. Pet. Explor. Prod. Technol. 2019, 9, 2845–2851. [Google Scholar] [CrossRef]
- Epelle, E.I.; Obande, W.; Okolie, J.A.; Wilberforce, T.; Gerogiorgis, D.I. CFD modelling and simulation of drill cuttings transport efficiency in annular bends: Effect of particle size polydispersity. J. Pet. Sci. Eng. 2022, 208, 109795. [Google Scholar] [CrossRef]
- Epelle, E.I.; Gerogiorgis, D.I. Drill cuttings transport and deposition in complex annular geometries of deviated oil and gas wells: A multiphase flow analysis of positional variability. Chem. Eng. Res. Des. 2019, 151, 214–230. [Google Scholar] [CrossRef]
- Busch, A.; Johansen, S.T. Cuttings transport: On the effect of drill pipe rotation and lateral motion on the cuttings bed. J. Pet. Sci. Eng. 2020, 191, 107136. [Google Scholar] [CrossRef]
- Barooah, A.; Khan, M.S.; Khaled, M.; Rahman, M.A. Investigation of cutting transport in horizontal/deviated annulus using visualization and pressure drop techniques for two-phase slurry flow. J. Nat. Gas Sci. Eng. 2021, 100, 104460. [Google Scholar] [CrossRef]
- Huque, M.M.; Rahman, M.A.; Zendehboudi, S.; Butt, S.; Imtiaz, S. Investigation of cuttings transport in a horizontal well with high-speed visualization and electrical resistance tomography technique. J. Nat. Gas Sci. Eng. 2021, 92, 103968. [Google Scholar] [CrossRef]
- Oezkaya, E.; Baumann, A.; Eberhard, P.; Biermann, D. Analysis of the cutting fluid behavior with a modified micro single-lip deep hole drilling tool. CIRP J. Manuf. Sci. Technol. 2022, 38, 93–104. [Google Scholar] [CrossRef]
- Moraveji, M.K.; Sabah, M.; Shahryari, A.; Ghaffarkhah, A. Investigation of drill pipe rotation effect on cutting transport with aerated mud using CFD approach. Adv. Powder Technol. 2017, 28, 1141–1153. [Google Scholar] [CrossRef]
- Pang, B.; Wang, S.; Jiang, X.; Lu, H. Effect of orbital motion of drill pipe on the transport of non-Newtonian fluid-cuttings mixture in horizontal drilling annulus. J. Pet. Sci. Eng. 2018, 174, 201–215. [Google Scholar] [CrossRef]
- Erge, O.; van Oort, E. Modeling the effects of drillstring eccentricity, pipe rotation and annular blockage on cuttings transport in deviated wells. J. Nat. Gas Sci. Eng. 2020, 79, 103221. [Google Scholar] [CrossRef]
- Epelle, E.I.; Gerogiorgis, D.I. CFD modelling and simulation of drill cuttings transport efficiency in annular bends: Effect of particle sphericity. J. Pet. Sci. Eng. 2018, 170, 992–1004. [Google Scholar] [CrossRef]
- Pang, B.; Wang, S.; Wang, Q.; Yang, K.; Lu, H.; Hassan, M.; Jiang, X. Numerical prediction of cuttings transport behavior in well drilling using kinetic theory of granular flow. J. Pet. Sci. Eng. 2018, 161, 190–203. [Google Scholar] [CrossRef]
- GhasemiKafrudi, E.; Hashemabadi, S.H. Numerical study on cuttings transport in vertical wells with eccentric drillpipe. J. Pet. Sci. Eng. 2016, 140, 85–96. [Google Scholar] [CrossRef]
- Manjula, E.V.P.J.; Ariyaratne, W.K.H.; Ratnayake, C.; Melaaen, M.C. A review of CFD modelling studies on pneumatic conveying and challenges in modelling offshore drill cuttings transport. Powder Technol. 2017, 305, 782–793. [Google Scholar] [CrossRef]
- Vaziri, E.; Simjoo, M.; Chahardowli, M. Application of foam as drilling fluid for cuttings transport in horizontal and inclined wells: A numerical study using computational fluid dynamics. J. Pet. Sci. Eng. 2019, 194, 107325. [Google Scholar] [CrossRef]
- Ferroudji, H.; Rahman, M.A.; Hadjadj, A.; Ofei, T.N.; Khaled, M.S.; Rushd, S.; Gajbhiye, R.N. 3D numerical and experimental modelling of multiphase flow through an annular geometry applied for cuttings transport. Int. J. Multiph. Flow 2022, 151, 104044. [Google Scholar] [CrossRef]
- Awad, A.M.; Hussein, I.A.; Nasser, M.S.; Ghani, S.A.; Mahgoub, A.O. A CFD- RSM study of cuttings transport in non-Newtonian drilling fluids: Impact of operational parameters. J. Pet. Sci. Eng. 2022, 208, 109613. [Google Scholar] [CrossRef]
- Wang, G.; Dong, M.; Wang, Z.; Ren, T.; Xu, S. Removing cuttings from inclined and horizontal wells: Numerical analysis of the required drilling fluid rheology and flow rate. J. Nat. Gas Sci. Eng. 2022, 102, 104544. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Y.; Wang, R.; Yuan, Z.; Chen, Y.; Shao, B.; Ma, Y. Simulation study on cutting transport in a horizontal well with hydraulic pulsed jet technology. J. Pet. Sci. Eng. 2021, 196, 107745. [Google Scholar] [CrossRef]
- Rooki, R.; Ardejani, F.D.; Moradzadeh, A.; Norouzi, M. CFD Simulation of Rheological Model Effect on Cuttings Transport. J. Dispers. Sci. Technol. 2015, 36, 402–410. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, H.; Li, J.; Zhou, Y.; Lu, Z.; Ouyang, Y.; Tan, T.; Liu, K.; Wang, X.; Zhang, G. Simulation study on cuttings transport of the wavy wellbore trajectory in the long horizontal wellbore. J. Pet. Sci. Eng. 2022, 215, 110584. [Google Scholar] [CrossRef]
- Ofei, T.N.; Irawan, S.; Pao, W. CFD Method for Predicting Annular Pressure Losses and Cuttings Concentration in Eccentric Horizontal Wells. J. Pet. Eng. 2014, 2014, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Martyushev, D.A.; Govindarajan, S.K. Development and study of a visco-elastic gel with controlled destruction times for killing oil wells. J. King Saud Univ. Eng. Sci. 2022, 34, 408–415. [Google Scholar] [CrossRef]
- Ponomareva, I.N.; Galkin, V.I.; Martyushev, D.A. Operational method for determining bottom hole pressure in mechanized oil producing wells, based on the application of multivariate regression analysis. Pet. Res. 2021, 6, 351–360. [Google Scholar] [CrossRef]
- Elkatatny, S. Enhancing the stability of invert emulsion drilling fluid for drilling in high-pressure high-temperature conditions. Energies 2018, 11, 2393. [Google Scholar] [CrossRef] [Green Version]
- Murtaza, M.; Alarifi, S.A.; Kamal, M.S.; Onaizi, S.A.; Al-Ajmi, M.; Mahmoud, M. Experimental investigation of the rheological behavior of an oil-based drilling fluid with rheology modifier and oil wetter additives. Molecules 2021, 26, 4877. [Google Scholar] [CrossRef] [PubMed]
- Plastic Viscosity|Energy Glossary. Available online: https://glossary.slb.com/en/terms/p/plastic_viscosity (accessed on 10 July 2022).
- Mahto, V.; Sharma, V.P. Rheological study of a water-based oil well drilling fluid. J. Pet. Sci. Eng. 2004, 45, 123–128. [Google Scholar] [CrossRef]
- Okon, A.N.; Agwu, O.E.; Udoh, F.D. Evaluation of the cuttings carrying capacity of a formulated synthetic-based drilling mud. In Proceedings of the Society of Petroleum Engineers—SPE Nigeria Annual International Conference and Exhibition, NAICE, Lagos, Nigeria, 4–6 August 2015. [Google Scholar] [CrossRef]
- Pang, B.; Wang, S.; Lu, C.; Cai, W.; Jiang, X.; Lu, H. Investigation of cuttings transport in directional and horizontal drilling wellbores injected with pulsed drilling fluid using CFD approach. Tunn. Undergr. Space Technol. 2019, 90, 183–193. [Google Scholar] [CrossRef]
- API-13I. Recommended Practice for Laboratory Testing Drilling Fluids; American Petroleum Institute: Washington, DC, USA, 2018; Volume 2008, Available online: https://www.techstreet.com/standards/api-rp-13i-r2016?product_id=1613565 (accessed on 3 September 2022).
- Jahari, A.F.; Shafian, S.R.M.; Husin, H.; Razali, N.; Irawan, S. Quantification method of suspended solids in micromodel using image analysis. J. Pet. Explor. Prod. 2021, 11, 2271–2286. [Google Scholar] [CrossRef]
- Epelle, E.I.; Gerogiorgis, D.I. Transient and steady state analysis of drill cuttings transport phenomena under turbulent conditions. Chem. Eng. Res. Des. 2018, 131, 520–544. [Google Scholar] [CrossRef]
- Wayo, D.D.K.; Irawan, S.; Khan, J.A.; Fitrianti, F. CFD Validation for Assessing the Repercussions of Filter Cake Breakers; EDTA and SiO2 on Filter Cake Return Permeability. Appl. Artif. Intell. 2022, 36, 3099. [Google Scholar] [CrossRef]
- Foued, B.; Vamegh, R. Simulation of settling velocity and motion of particles in drilling operation. J. Pet. Sci. Eng. 2021, 196, 107971. [Google Scholar] [CrossRef]
- Ouchene, R.; Khalij, M.; Tanière, A.; Arcen, B. Drag, lift and torque coefficients for ellipsoidal particles: From low to moderate particle Reynolds numbers. Comput. Fluids 2015, 113, 53–64. [Google Scholar] [CrossRef]
- Gerhardter, H.; Prieler, R.; Mayr, B.; Knoll, M.; Mühlböck, M.; Tomazic, P.; Hochenauer, C. Evaluation of drag models for particles and powders with non-uniform size and shape. Powder Technol. 2018, 330, 152–163. [Google Scholar] [CrossRef]
- Chhabra, R.P.; Agarwal, L.; Sinha, N.K. Drag on non-spherical particles: An evaluation of available methods. Powder Technol. 1999, 101, 288–295. [Google Scholar] [CrossRef]
- Richardson, J.F. This Week’s Citation Classic NUMBER FEBRUARY 12. Sedimentation and Fluidisation. Richardson J F & Zaki W N. Part 1. Trans. Inst. Chem. Eng. 1979, 32, 35–53. Available online: http://garfield.library.upenn.edu/classics1979/A1979HZ20300001.pdf (accessed on 10 September 2022).
- Gera, D.; Gautam, M.; Tsuji, Y.; Kawaguchi, T.; Tanaka, T. Computer simulation of bubbles in large-particle fluidized beds. Powder Technol. 1998, 98, 38–47. [Google Scholar] [CrossRef]
- Wen, C.Y. Mechanics of fluidization. In The Chemical Engineering Progress Symposium Series; AIChE Chemical: New York, NY, USA, 1966; Volume 62, pp. 100–111. [Google Scholar]
- Gidaspow, D.; Bezburuah, R.; Ding, J. Hydrodynamics of Circulating Fluidized Beds: Kinetic Theory Approach; Illinois Institute of Technology Department of Chemical: Chicago, IL, USA, 1991. [Google Scholar]
- Shynybayeva, A. Eulerian–Eulerian Modeling of Multiphase Flow in Horizontal Annuli: Current Limitations and Challenges. Processes 2020, 8, 1426. [Google Scholar] [CrossRef]
- Duru, U.I.; Kerunwa, A.; Omeokwe, I.; Uwaezuoke, N.; Obah, B. Suitability of Some Nigerian Barites in Drilling Fluid Formulations. Pet. Sci. Eng. 2019, 3, 46. [Google Scholar] [CrossRef]
- Sauki, A.; Khamaruddin, P.N.F.M.; Irawan, S.; Kinif, I.; Ridha, S. Statistical relationship of drilled solid concentration on drilling mud rheology. J. Adv. Res. Fluid Mech. Therm. Sci. 2020, 69, 122–136. [Google Scholar] [CrossRef]
- Onugha, I.; Igwilo, K.; Duru, U.I. Reduction in annular pressure loss by mud rheology control—A means of mud pump pressure optimization, a case study of a Niger delta well. J. Basic App. Res. Int. 2019, 16, 172–183. [Google Scholar]
- Irawan, S.; Kinif, I.B. Solid Control System for Maximizing Drilling. Drilling 2018, 1, 192. [Google Scholar] [CrossRef]
- Minakov, A.V.; Zhigarev, V.A.; Mikhienkova, E.I.; Neverov, A.L.; Buryukin, F.A.; Guzei, D.V. The effect of nanoparticles additives in the drilling fluid on pressure loss and cutting transport efficiency in the vertical boreholes. J. Pet. Sci. Eng. 2018, 171, 1149–1158. [Google Scholar] [CrossRef] [Green Version]
- Erge, O.; van Oort, E. Time-dependent cuttings transport modeling considering the effects of eccentricity, rotation and partial blockage in wellbore annuli. J. Nat. Gas Sci. Eng. 2020, 82, 103488. [Google Scholar] [CrossRef]
- Biyanto, T.R.; Cordova, H.; Matradji; Anggrea, T.O.; Suryowicaksono, H.; Irawan, S. Stuck pipe optimization using duellist algorithm. In Proceedings of the The 3rd International Conference on Food and Agriculture, Jember, East Java, Indonesia, 7–8 November 2020; Volume 672. [Google Scholar] [CrossRef]
- Irawan, S.; Khaleeda, S.; Shakeel, M.; Fathaddin, M.T. Maximizing well productivity by using filter cake breaker for synthetic-based mud drill-in fluid (SBMDIF) system. Upstream Oil Gas Technol. 2021, 9, 100075. [Google Scholar] [CrossRef]
- Irawan, S.; Kinif, B.I.; Bayuaji, R. Maximizing drilling performance through enhanced solid control system. In Proceedings of the International Conference of Applied Science and Technology for Infrastructure Engineering, Surabaya, East Java, Indonesia, 5 August 2017; Volume 267. [Google Scholar] [CrossRef]


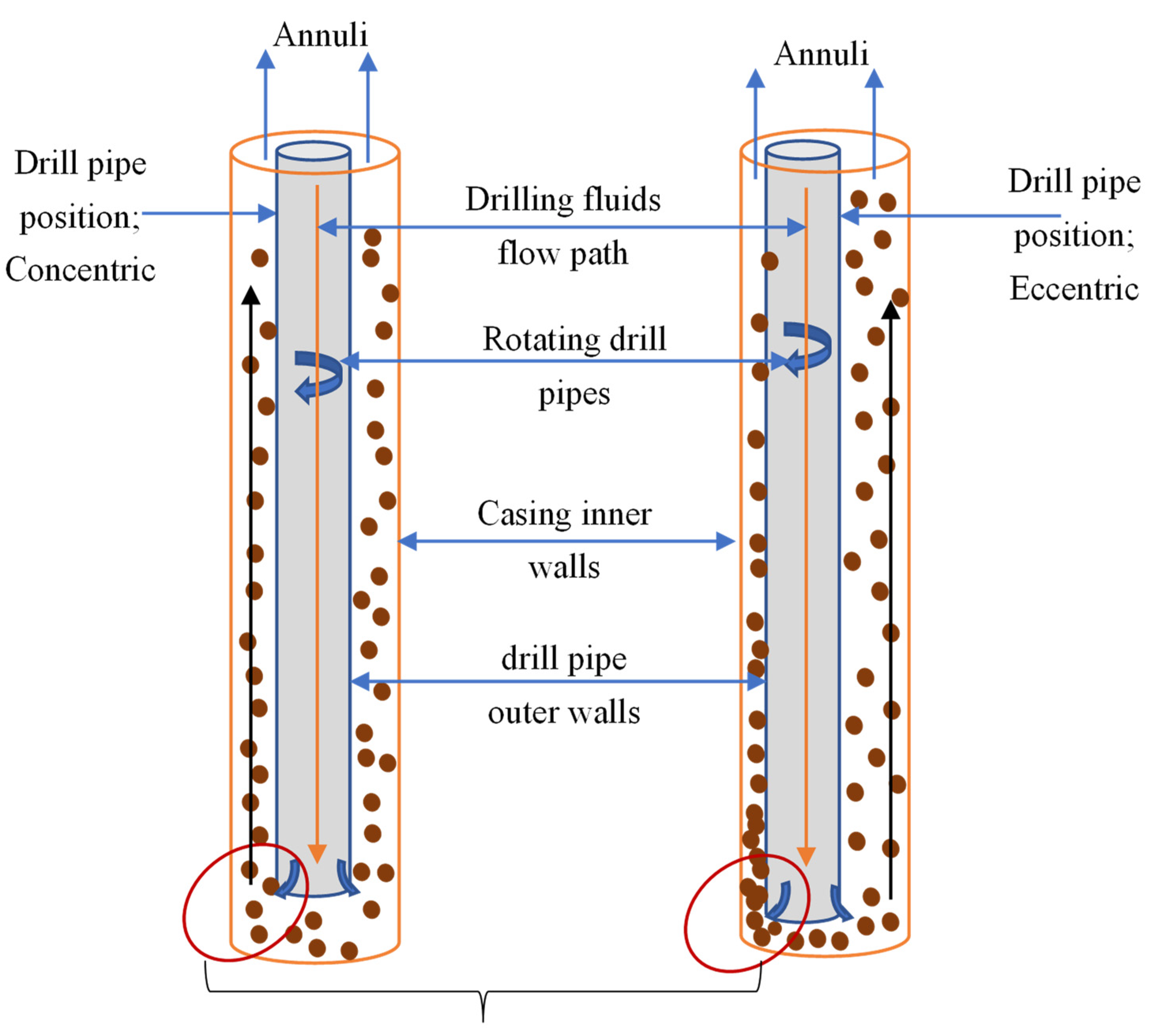
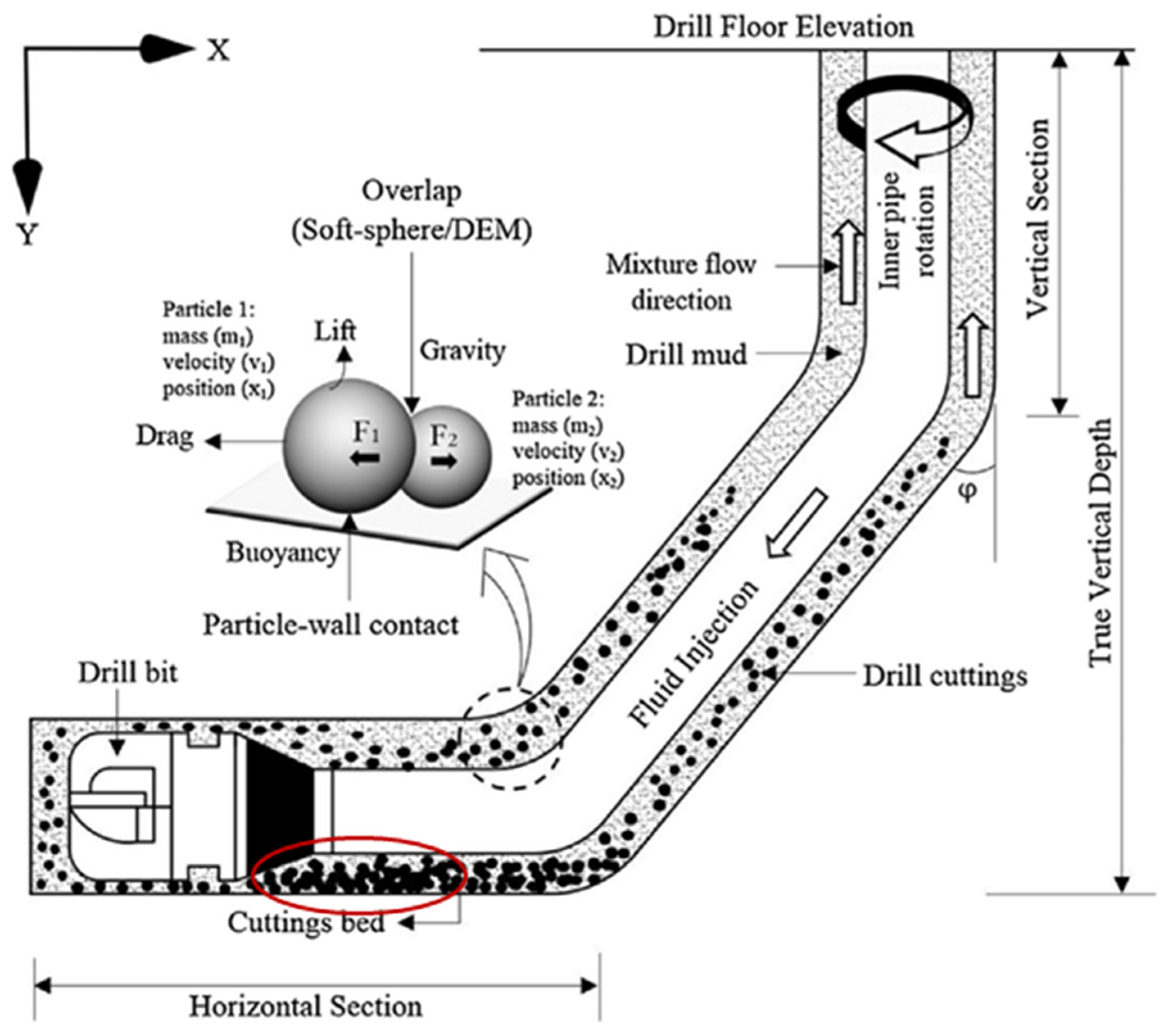
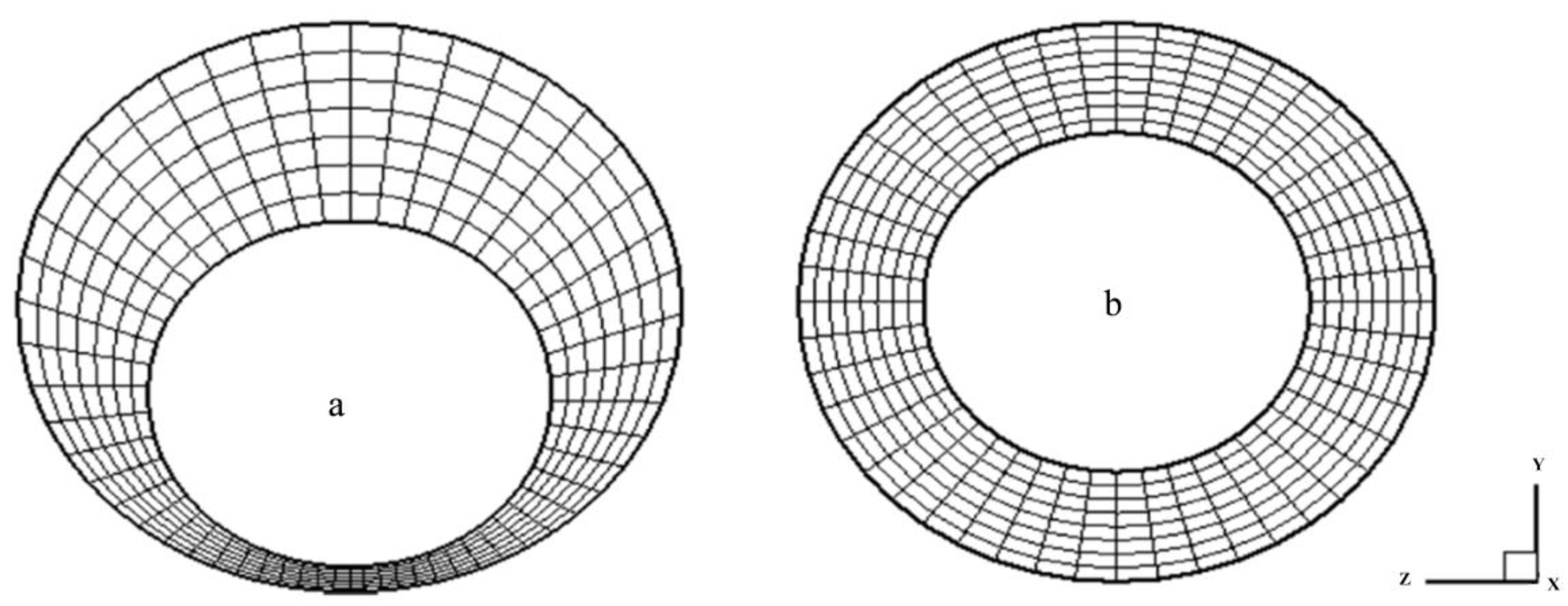
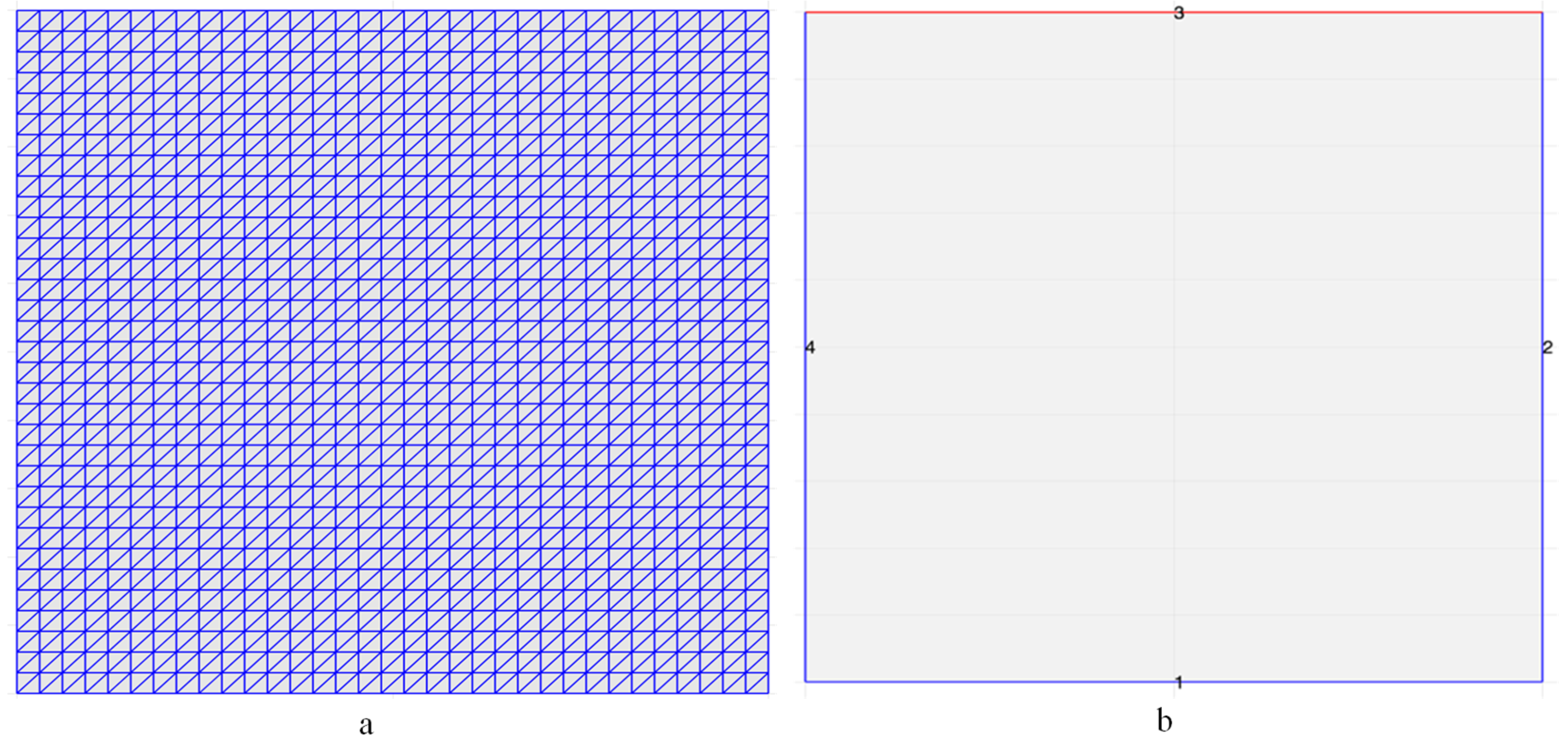



| Author | Yield Point (YP) | Plastic Viscosity (PV) | Transport Index (TI) | Average TI | Mud Type |
|---|---|---|---|---|---|
| Wayo’s Experiment [6] | 136.4 | 97.0 | 1.406 | 1.413 | Synthetic-Based |
| 133.4 | 93.8 | 1.422 | |||
| 135.3 | 95.9 | 1.411 | |||
| Okon’s Experiment [38] | 10 | 6 | 1.667 | 1.005 | Synthetic-Based |
| 13 | 17 | 0.765 | |||
| 14 | 24 | 0.583 | |||
| Murtaza’s Experiment [35] | 24.60 | 18 | 1.367 | 1.166 | Oil-based |
| 39.48 | 37.1 | 1.064 | |||
| 43.91 | 41.1 | 1.068 |
| Parameters for Computation | ||
| Synthetic-Based Mud | Oil-Based Mud | |
| Geometry | ||
| Drill pipe outer wall (mm) | 0, 1 | 0, 1 |
| Casing inner wall, (mm) | 0, 1 | 0, 1 |
| Annulus inlet/outlet, (mm) | 0, 1 | 0, 1 |
| Computational distance (Drill pipe & Casing) (mm) | 0.5, 0.7 | 0.5, 0.7 |
| Drill pipe eccentricity | 0.5, 0.7 | 0.5, 0.7 |
| Rheology | ||
| Fluid density (kg/m3) | 14,382 | 14,200 |
| Yield point (YP) (lbf/100 ft2) | 136.4, 133.4, 135.3 | 24.60, 39.48, 43.91 |
| Plastic viscosity (PV) (lbf/100 ft2) | 97.0, 93.8, 95.9 | 18, 37.1, 41.1 |
| Transport index | 1.406, 1.422, 1.411 | 1.367, 1.064, 1.068 |
| Particles | ||
| Mud particle diameter (mm) | 0.2, 0.5, 1 | 0.2, 0.5, 1 |
| Cuttings Particle diameter (mm) | 1, 3, 6 | 1, 3, 6 |
| Cuttings diameter (mm) | 1.2, 3.5, 7 | 1.2, 3.5, 7 |
| Cuttings density (kg/m3) | 2000 | 2000 |
| Other Variables | ||
| Mud-Nozzle inlet velocity, u (m·s−1) | 0, 10, 50 | 0, 10, 50 |
| Cuttings velocity, v (m·s−1) | 50, 60 | 50, 60 |
| Pressure (psi) | 100, 80 | 100, 80 |
| Pipe rotation (RPM) | 80 | 80 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wayo, D.D.K.; Irawan, S.; Bin Mohamad Noor, M.Z.; Badrouchi, F.; Khan, J.A.; Duru, U.I. A CFD Validation Effect of YP/PV from Laboratory-Formulated SBMDIF for Productive Transport Load to the Surface. Symmetry 2022, 14, 2300. https://doi.org/10.3390/sym14112300
Wayo DDK, Irawan S, Bin Mohamad Noor MZ, Badrouchi F, Khan JA, Duru UI. A CFD Validation Effect of YP/PV from Laboratory-Formulated SBMDIF for Productive Transport Load to the Surface. Symmetry. 2022; 14(11):2300. https://doi.org/10.3390/sym14112300
Chicago/Turabian StyleWayo, Dennis Delali Kwesi, Sonny Irawan, Mohd Zulkifli Bin Mohamad Noor, Foued Badrouchi, Javed Akbar Khan, and Ugochukwu I. Duru. 2022. "A CFD Validation Effect of YP/PV from Laboratory-Formulated SBMDIF for Productive Transport Load to the Surface" Symmetry 14, no. 11: 2300. https://doi.org/10.3390/sym14112300
APA StyleWayo, D. D. K., Irawan, S., Bin Mohamad Noor, M. Z., Badrouchi, F., Khan, J. A., & Duru, U. I. (2022). A CFD Validation Effect of YP/PV from Laboratory-Formulated SBMDIF for Productive Transport Load to the Surface. Symmetry, 14(11), 2300. https://doi.org/10.3390/sym14112300









